中国气象学会主办。
文章信息
- 杨 毅, 弓中强, 王金艳, 刘鑫华. 2012.
- YANG Yi, GONG Zhongqiang, WANG Jinyan, LIU Xinhua. 2012.
- 时间扩展取样集合卡尔曼滤波同化模拟探空试验研究
- Experiment study of the time-expanded sampling approach for the ensemble Kalman filter for simulated soundings assimilation
- 气象学报, 70(1): 101-108
- Acta Meteorologica Sinica, 70(1): 101-108.
- http://dx.doi.org/10.11676/qxxb2012.009
-
文章历史
- 收稿日期:2010-01-11
- 改回日期:2011-02-13
2. 中国气象局国家气象中心,北京,100081
2. National Meteorological Center of China Meteorological Administration, Beijing 100081, China
数值天气预报是一个初边值的问题,初值估计的越精确,预报的质量就越高。目前,主要通过同化各种观测资料来提高模式初始场的质量。三维变分(3D-Var)由于其节省计算资源,成为当今业务运用的主流方式(翁永辉等,2000;马旭林等,2009;Liang et al,2009; Yang et al,2009)。目前业务上三维变分所采用的背景误差协方差矩阵是均匀各向同性的(龚建东等,2006),且在一个季节内不随时间变化。四维变分(4D-Var)是三维变分的一个重要扩展,它考虑了观测资料在时间区间上的分布,是比较好的同化方法(许小永等,2004;张林等,2006),但在求目标函数梯度时仍需用伴随模式,而且,对于复杂模式,其伴随模式在理论上还有很多问题尚待解决,开发以及维护伴随模式对于四维变分系统同样是一个很大的难点。另外,四维变分巨大的计算量也是制约其在业务中广泛应用的重要障碍。而集合卡尔曼滤波(EnKF)是一个用蒙特卡罗(Anderson et al,1999)的短期集合预报方法来估计预报误差协方差的顺序同化方法,利用集合成员的样本方差来得到随流型变化的误差协方差,不需要像扩展卡尔曼滤波那样对观测算子和预报模式做切线性近似,解决了卡尔曼滤波应用在非线性系统中背景误差协方差矩阵的预报困难(Kalman,1960; Evensen,2003)。同时,由于集合卡尔曼滤波不需要像四维变分那样的积分伴随模式,工作程序非常简单,又可以不断估计和更新预报误差协方差,自从海洋学家Evensen(1994)首次将其应用和推广到同化领域中以来,一直受到人们广泛的关注,并成为资料同化方法研究的一个热点。有关集合卡尔曼滤波在资料同化中的应用已有大量的研究(Houtekamer et al,1998; Anderson et al,1999; Mitchell et al,2000; Whitaker et al,2002; Hamill et al,2000,2002; Zhang et al,2005; 朱江等,2006)。从理论上讲,只有当集合成员数与模式的自由度一致时,预报样本才能准确反映预报误差协方差矩阵的特征。由于实际计算条件的限制,在样本数很少时,传统的集合卡尔曼滤波通常会低估预报误差协方差,特别是模式有误差的时候,最终会导致滤波发散。但增加样本数又意味着大幅度增加计算量。如何减少集合卡尔曼滤波同化预报循环系统的巨额计算量,成为集合卡尔曼滤波能否在实际业务中得到广泛应用的一个挑战。针对中尺度模式的同化问题,Gao等(2008)提出一种双分辨率集合卡尔曼滤波方法来提高同化效率,减少计算量。这一方法用一组低分辨率模式的预报样本为自身和一个高分辨率的样本提供背景误差协方差,同时利用高分辨率样本来调整低分辨率样本的集合平均,这样低分辨率样本能吸收到高分辨率样本的信息。利用模拟的雷达资料所作的同化试验表明,双分辨率集合卡尔曼滤波既能节省非常多的计算时间,又能达到接近高分辨率集合卡尔曼滤波同化的效果。
对集合卡尔曼滤波应用的另一个挑战就是如何处理模式误差,特别是模式偏差,这也是所有同化方法面临的问题。模式误差和天气系统真实状态的非线性相关通常是未知的,且很难估计。未知的模式误差能导致滤波(卡尔曼滤波或集合卡尔曼滤波)发散,即在多次同化预报循环时,使得同化分析的集合平均逐渐偏离观测,逐渐偏离真实状态。为了避免或减轻未知模式误差或其他原因所导致的滤波发散,常用一些经验方法处理,例如Anderson(2001)方差放大法和Mitchell等(2000)模式误差参数化法。然而原始的模式误差问题仍旧在很大程度上未得到解决。所以,探索从别的方面来解决或缓解这个问题可能是更加有效的途径。由于数值模式预报经常存在时间误差,此类误差通常表现为用数值模式预报的天气系统比真实的天气系统发展(或传播)得快或慢。许多模式检验方面的研究表明,模式时间误差和由时间误差导致的空间误差,在模式预报中往往普遍存在(Manobianco et al,1999; Mass et al,2002)。由于此类模式时间误差的存在,那么在分析时刻前(或后)某时刻的预报场比分析时刻的预报场可能更能代表真实场。然而,在没有先验估计情况下,此类时间误差通常被当成平均为零的统计学上的随机误差。为此,Xu等(2008)利用一组较少的预报样本通过时间扩展取样的方法来进行集合样本取样,以此来构建较多样本集合计算背景误差协方差,从而节省了大量的计算资源。即不仅在分析时刻取样,同时也在分析时刻前、后进行取样,这样,局地的预报误差方差也许可从上述的时间扩展取样样本统计得到。虽然,该时间扩展取样方法是基于模式预报存在的时间误差提出的,但并不直接处理模式误差,其应用也不必局限于此。Xu等(2008)在浅水方程模式所做的理想试验表明,此方案以较小的集合样本数既可得到接近其数倍集合数所得到的分析效果,节省了大量的预报时间,并且,即使集合预报的初始化无系统的时间误差,集合卡尔曼滤波也能得到较好的分析结果。但浅水方程是非常简单的模式,而在业务中应用的数值天气模式都非常复杂。另外,在实际业务运行中主要以同化大尺度网观测为主。大尺度的观测系统主要是无线电探空网或其他探空资料(例如廓线)。这一方法是否适应于现有的中尺度模式以及探空资料尚需进一步研究。本文将基于新一代中尺度天气预报模式WRF,利用时间扩展取样集合卡尔曼滤波来同化模拟的探空观测,检验不同的取样策略对同化结果的影响,考察该方法是否也适合于复杂的中尺度模式。 2 同化系统
如上所述,为了减少集合卡尔曼滤波同化预报循环系统的巨额计算量和减轻模式误差引起的滤波发散等问题,Xu等(2008)提出了利用一组较少的预报样本通过时间扩展取样进行集合卡尔曼滤波分析,不仅从分析时刻的预报场取样,同时还从分析时刻前后的预报场取样,以此来构建较大的样本集合计算背景误差协方差,这样就减少了预报的样本数,从而节省了大量的计算资源。即假设用来预报的成员样本个数为Nb(以下称为基本样本成员),时间扩展取样不仅在分析时刻t=tj(每次循环的分析时刻)取样(传统的做法,得到Nb个样本成员),同时也在分析时刻前后每间隔Δt的时刻取样,共取M次(得到扩展的样本:Nb×2M个)。则所有样本成员的时间可表达为t=tj+mΔt(其中m=0,±1,±2,…,±M),很明显,通过时间扩展取样,集合成员数由N=Nb变为N=(2M+1)×Nb=Nb+Nb×2M(基本样本个数+扩展样本个数)。这样,在不增加预报样本数的情况下,扩大了分析样本的数目,从而在保证集合样本数目足够大的情况下,减少了计算量,同时也考虑到了模式误差问题。
本文将基于Whitaker等(2002)的不加扰动观测的集合卡尔曼滤波(EnSRF),采用时间扩展取样进行同化模拟探空试验。由于有限样本数会导致取样误差,以致过度低估了分析误差协方差,通常需要采取局地化处理。一般都认为,每个观测只对一定影响半径内的状态变量有影响,即在三维空间采取一定的截断半径,过滤距观测点较远处的虚假相关,同时也减少不加扰动观测的集合卡尔曼滤波分析的计算量,因为仅在截断半径内的状态变量被更新。具体而言,采用Houtekamer等(2001)方案中对预报误差协方差乘以一个舒尔积。即一个简洁的平滑相关函数,此函数仅仅依赖于给定的观测和状态变量之间的三维距离。在本文中此平滑相关函数采用一个简单的5阶分段有理函数(Gaspari et al,1999)。 3 模式和模拟的观测资料
采用WRF中尺度预报模式,初边界条件采用NCEP 的1°×1°再分析资料。水平分析格点数为101×101,垂直28层,水平格距20 km,分析区域中心为(31.5°N,112.5°E),积分步长120 s,主要物理过程有: Lin微物理过程,Rrtm长波辐射方案,Dudhia短波方案,MYJ莫宁-奥布霍夫近地面方案,热量扩散陆面过程方案,Eta MYJ TKE边界层方案,KF(new Eta)浅对流积云参数化方案。分析变量为6个:风的3个分量u、v、w,扰动位温Tp,扰动位势hp,水汽混合比qv。
试验的“真实场”是以NCEP资料为初边界条件,从2002年7月20日18时(世界时,下同)开始预报的预报场。集合卡尔曼滤波同化试验在7月20日18时的“背景场”是7月18日00时—25日00时6 h一次的NCEP资料的平均场,初始集合场是在此“背景场”上,对除了垂直速度以外的5个分析变量叠加一组平均为0的高斯随机扰动,在高斯扰动场垂直方向上,每层的标准差为此时“背景场”误差(背景场和真实场之差)的标准差。然后将此组集合预报6 h直至21日00时开始同化,以后6 h同化一次,共9个同化循环。
模拟的探空观测是在“真实场”中加入随机扰动误差产生
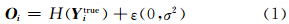
模拟的探空从第5个格点开始每隔15个水平点取一个,垂直方向每隔一个格点取一个,这样就相当于有36个探空。假定观测误差和背景误差相当,则u、v的扰动标准均为2 m/s,Tp、hp和qv的扰动标准分别为0.8 K、30 m2/s2和0.5 g/kg。4 试验设计及结果讨论
时间扩展取样同化试验,可以根据不同的取样间隔Δt和最大取样次数M来设计。为了考察时间扩展取样相对于传统取样的效果,首先进行使用传统不加扰动观测的集合卡尔曼滤波的两组控制试验CTL20和CTL60,即N=Nb分别为20和60,M=0。在时间扩展取样试验中2MΔt≤2T,T为同化循环的时间间隔,这里T= 6 h。设计了7组时间扩展取样同化试验,基本样本数Nb=20,试验名称命名格式为ExpΔtM(表 1)。
| 试验名称(ExpΔtM) | 基本样本数Nb | 取样间隔Δt(h) | 取样次数M | 总的样本数N | 垂直截断半径(单位:格点数) | 水平截断半径(单位:格点数) | 放大因子β |
| CTL20 | 20 | / | 0 | 20 | 3 | 20 | 1.28 |
| CTL60 | 60 | / | 0 | 60 | 3 | 30 | 1.22 |
| Exp0.5h1 | 20 | 0.5 | 1 | 60 | 3 | 30 | 1.20 |
| Exp1h1 | 20 | 1 | 1 | 60 | 3 | 30 | 1.18 |
| Exp2h1 | 20 | 2 | 1 | 60 | 3 | 30 | 1.14 |
| Exp3h1 | 20 | 3 | 1 | 60 | 3 | 30 | 1.10 |
| Exp4h1 | 20 | 4 | 1 | 60 | 3 | 30 | 1.08 |
| Exp6h1 | 20 | 6 | 1 | 60 | 3 | 30 | 1.00 |
| Exp1h2 | 20 | 1 | 2 | 100 | 3 | 35 | 1.10 |
为了定量地给出各组试验同化的效果,以集合平均的均方根误差为评判标准
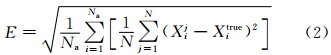
Hamill等(2001)指出,局地化中截断半径的大小和集合成员数成正比。为了考察时间扩展取样同化试验效果,首先需调整水平、垂直截断半径和放大影响因子,将两组控制试验CTL20和CTL60的同化效果调到最优。类似Caya等(2005)做法,使按式(3)求算的6个分析变量在9次同化循环分析中的均方根误差平方和达到最小。
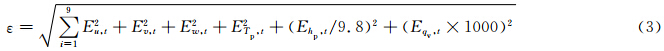
对样本数为60的控制试验CTL60,先固定水平截断半径为5倍格距,放大因子β为1,变化垂直截断半径,以使式(3)达到最小。试验结果表明,ε对垂直截断半径的变化不太敏感,为了节省机时,将以后所有的试验垂直截断半径都取3倍垂直格距。
经多次试验统计后得知,样本数20的CTL20,在水平截断半径为20倍格距,放大因子β为1.28时,ε=14.72984,达到最优;样本数60的CTL60,在水平截断半径为30倍格距,放大因子β为1.22时,ε=12.4,达到最优。
在分析时刻前后每半小时取一次样的试验Exp0.5h1,采取与CTL60一样的30倍格距的水平截断半径和3倍格距的垂直截断半径,调整放大因子β为1.20时,ε=13.43375,达到极小。
剩余的时间扩展取样同化试验ExpΔt1,采取和Exp0.5h1相同的水平和垂直截断半径,但由于取样间隔时间变长,集合成员之间相关性变小,就仅仅调小放大因子β(表 1)。
由于时间扩展取样试验Exp1h2集合成员数N=(2×2+1)×20=100,样本数变大,所以,将水平截断半径扩大为35倍格距,放大因子β缩小为1.10。
从各组试验在所有格点上统计的6个分析诊断变量分析前后集合平均的均方根误差随同化循环次数的变化(图 1)可知,在两组控制试验中,样本数多(CTL60)的效果明显好于样本数少(CTL20)的试验。另外所有试验所有分析变量均方根误差随时间总体上都在下降,并且,每次同化后误差下降幅度也变小,说明随着观测信息融入模式中,模式分析场越来越接近真实场。
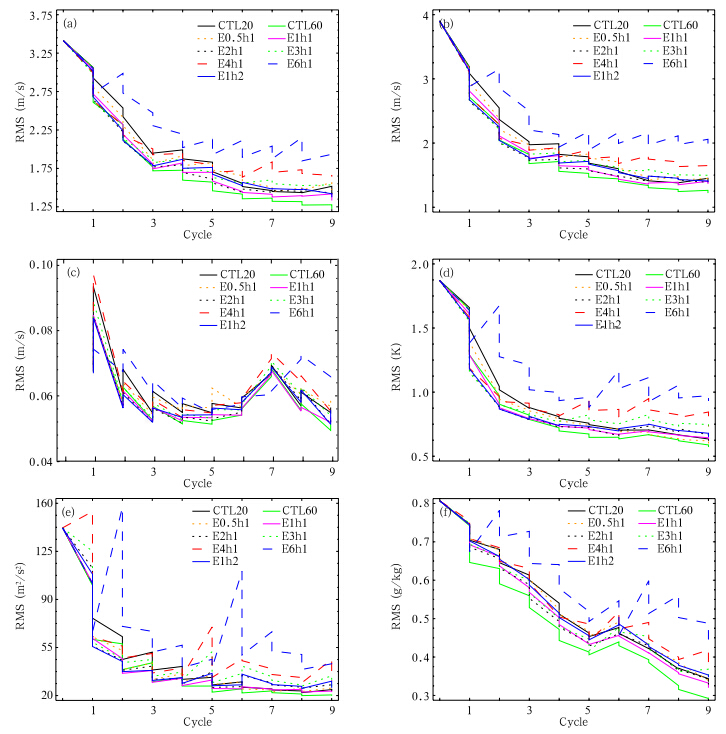 |
| 图 1 各组试验在全局的集合平均预报和分析的均方根误差随同化循环次数的变化(a.u,b.v,c.w,d.Tp,e.hp,f.qv)Fig. 1 Changes in the RMS errors of the ensemble mean forecasts and the analyses over the entire domain with the number of cycle for each experiment for(a)u,(b)v,(c)w,(d)Tp,(e)hp,and (f)qv |
从图 1还可看出,试验Exp6h1的误差远大于其他几组试验,说明取样间隔时间太长,集合成员之间相关性太小,导致同化分析效果很差。但并非取样间隔短同化效果就一定很好,如在Δt为0.5 h的Exp0.5h1试验的前3—4个循环中,其同化效果虽好于控制试验CTL20,但却比除了取样间隔非常大的试验(如Exp4h1和Exp6h1)以外的所有试验都差,在此后的同化循环内的效果则接近控制试验CTL20,只是仍好于取样间隔比较大的试验(Δt=3、4、6 h)。这说明取样时间间隔太短,成员之间相似性太大,同化效果也会很差。同样,Δt为4 h的试验Exp4h1的误差也明显高于其他取样间隔时间较短的试验(Δt=0.5、1、2、3 h)。但是,在前几个循环内同化效果还是比控制试验CTL20好,例如,对于u、Tp、qv的前2个循环,对v、w和hp的前4个循环。以后同化效果逐渐变差,并且,误差大于控制试验CTL20。说明通过放大取样时间窗增加了集合样本数,同时使得样本之间相关性缩小,在同化初期还是取得较好的同化效果。
Δt为3 h的试验Exp3h1与Δt分别为2、1 h的试验(Exp2h1、Exp1h1、Exp1h2)在前4个循环内的误差相当,并都比控制试验CTL20小,此后,试验Exp3h1的误差甚至大于控制试验CTL20,说明对本试验来说,样本取样时间间隔为3 h还是太长。而Δt分别为2、1 h的试验(Exp2h1、Exp1h1、Exp1h2)同化效果比其他扩展取样同化试验好,但总体上看,在所有扩展取样同化试验中,Δt为1 h取样一次(M=1)的试验Exp1h1效果最好。所以,对于本试验时间扩展取样的时间间隔不宜太长。
另外,再分析每次最大取样次数M对同化效果的影响。从图 1可以清楚看出,M=2的试验Exp1h2同化效果明显不如M=1的Exp1h1,甚至不好Exp2h1。这说明虽然经过多次取样后增加了样本数,但由于取样太频繁,样本成员之间相关性加大,分析的效果并不一定变好。
从以上分析可知,扩展取样时间间隔Δt不能取得太长也不能太短,但总能找到一个合适的Δt使同化效果接近于样本数为Nb×(1+Nb×2M)传统集合卡尔曼滤波分析的效果;取样次数也不能太频繁(M不能太大),否则样本数虽然增加了,但样本成员之间太接近,相关性太高,分析效果同样不好。
对各组试验也计算了均方根误差比率R=E/F(Anderson,2001),F为
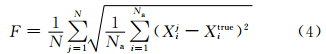
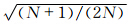 ,对样本数为60时,R的期望值约为0.713(图 2中蓝线);对样本数为100时,R的期望值约为0.711。当R>
,对样本数为60时,R的期望值约为0.713(图 2中蓝线);对样本数为100时,R的期望值约为0.711。当R>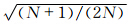 时,则集合方差低估了集合平均误差,R<
时,则集合方差低估了集合平均误差,R<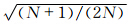 时,则为高估了集合平均误差。
时,则为高估了集合平均误差。
分析各组试验的各个分析变量均方根误差比率R在各个循环分析前后的变化(图 2)可知,所有试验在分析后的R基本都大于其期望值(0.713或0.711),说明在分析过程中,低估了集合平均误差,这样会导致滤波发散,所以,在下一次分析
前乘上一个大于1的协方差放大因子β还是有必要的。控制试验CTL60(图中黑线)在分析前后的R都比较接近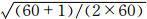 =0.713,这说明基本样本数多,分析的效果最好。可清楚看出,时间扩展取样的时间间隔太短(E0.5h1,图中红虚线)或太长(E1h6,图中黑虚线)时,均方根误差比率R在分析同化后都远大于0.713。这也同样说明取样时间间隔太短或太长得到的样本集合容易低估误差协方差,分析效果较差。相对而言,试验E1h1(每隔1 h取一次样,共取一次)的R在分析前后都比较接近期望值0.713,其他试验基本在分析后远大于0.713。所以,对本试验,时间扩展取样的时间间隔Δt等于1 h时候效果最好。
=0.713,这说明基本样本数多,分析的效果最好。可清楚看出,时间扩展取样的时间间隔太短(E0.5h1,图中红虚线)或太长(E1h6,图中黑虚线)时,均方根误差比率R在分析同化后都远大于0.713。这也同样说明取样时间间隔太短或太长得到的样本集合容易低估误差协方差,分析效果较差。相对而言,试验E1h1(每隔1 h取一次样,共取一次)的R在分析前后都比较接近期望值0.713,其他试验基本在分析后远大于0.713。所以,对本试验,时间扩展取样的时间间隔Δt等于1 h时候效果最好。
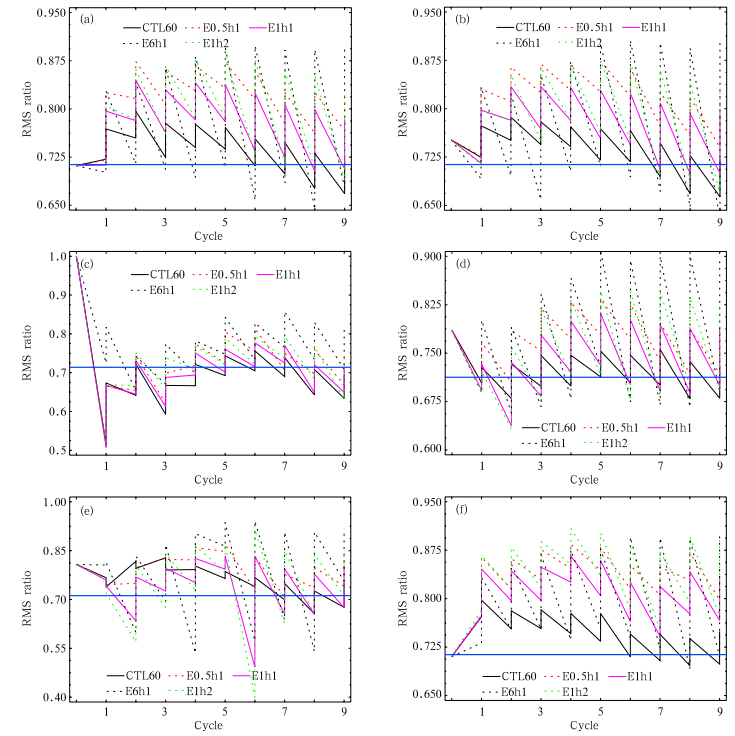 |
| 图 2 各组试验在全局的集合平均预报和分析的均方根误差比率随同化循环次数的变化(a.u,b.v,c.w,d.Tp,e.hp,f.qv;蓝线是0.713)Fig. 2 Changes in the RMS ratio of the ensemble mean forecasts and analyses over the entire domain with the number of cycle for each experiment for(a)u,(b)v,(c)w,(d)Tp,(e)hp,and (f)qv |
另外,试验Exp1h2相对于试验Exp1h1,虽然经过增加取样次数(M=2),集合样本数增加了,但其分析前后R的增幅基本上都大于试验Exp1h1,其同化分析效果总体还是不如试验Exp1h1。从均方根误差比率R的变化同样也说明对于本试验而言,增加取样次数M虽增大了集合样本数,但不一定能提高同化效果。5 结 论
本文基于WRF模式,针对不同取样时间间隔Δt和分析时刻前后最大取样次数M,开展了一系列时间扩展取样集合卡尔曼滤波同化模拟探空比较试验,同化时间间隔为6 h,共同化9次。试验结果表明时间扩展取样时间间隔Δt 取的太长或太短,则样本成员之间相关性太小或太大,最终分析效果都不太好;另外,每次取样次数M并不是越大越好,即使增加了分析样本成员数,但样本之间相关性变大,分析效果同样也不太理想。但是,通过时间扩展取样增加了样本数,在分析初期的几个同化循环里面,即使Δt 过大或过小,同化效果都好于样本数比较少的控制试验(样本数为基本预报样本数的传统集合卡尔曼滤波)。总是能找到合适的取样时间间隔Δt和最大取样次数M,使分析结果接近样本数为扩展后的总样本数的传统集合卡尔曼滤波分析的效果,并明显优于用基本样本分析的传统集合卡尔曼滤波。以本文所取个例为例,在Δt为1 h,M为1时,同化分析效果达到最优。
| 龚建东,赵刚,2006.全球资料同化中误差协方差三维结构的准确估计与应用Ⅱ:背景误差协方差调整与数值试验分析.气象学报,64(6):684-698 |
| 马旭林,庄照荣,薛纪善等,2009.GRAPES非静力数值预报模式的三维变分资料同化系统的发展.气象学报,67(1):50-60 |
| 翁永辉,徐祥德,柏晶瑜.2000.应用TOVS资料变分分析技术增加青藏高原地区模式初始场信息.气象学报,58(6):679-691 |
| 许小永,郑国光, 刘黎平. 2004.多普勒雷达资料4DVAR同化反演的模拟研究.气象学报,62(4):410-422 |
| 张林,倪允琪.2006.雷达径向风资料的四维变分同化试验.大气科学,30(3):433-440 |
| 朱江,汪萍. 2006.集合卡尔曼平滑和集合卡尔曼滤波在污染源反演中的应用.大气科学,30(5):871-882 |
| Anderson J L, Anderson S L. 1999. A Monte Carlo implementation of the nonlinear filtering problem to produce ensemble assimilations and forecasts. Mon Wea Rev, 127: 2741-2758 |
| Anderson J L. 2001. An ensemble adjustment Kalman filter for data assimilation. Mon Wea Rev, 129: 2884-2903 |
| Caya A, Sun J, Snyder C. 2005. A comparison between the 4D-Var and the ensemble Kalman filter techniques for radar data assimilation. Mon Wea Rev, 133: 3081-3094 |
| Evensen G. 1994. Sequential data assimilation with a nonlinear quasi-geostrophic model using Monte Carlo methods to forecast error statistics. J Geophys Res, 99: 10143-10162 |
| Evensen G. 2003. The ensemble Kalman filter: Theoretical formulation and practical implementation. Ocean Dyn, 53: 343-367 |
| Gao Jidong, Xue Ming, 2008. An efficient dual-resolution approach for ensemble data assimilation and tests with assimilated Doppler radar data. Mon Wea Rev, 136: 945-963 |
| Gaspari G, Cohn S E. 1999. Construction of correlation functions in two and three dimensions. Quart J Roy Meteor Soc, 125: 723-757 |
| Hamill T M, Snyder C. 2000. A hybrid ensemble Kalman filter-3D variational analysis scheme. Mon Wea Rev, 128: 2905-2919 |
| Hamill T M, Whitaker J S, Snyder C. 2001. Distance-dependent filtering of background error covariance estimates in an ensemble Kalman filter. Mon Wea Rev, 129: 2776-2790 |
| Hamill T M, Snyder C. 2002. Using improved background error covariances from an ensemble Kalman filter for adaptive observations. Mon Wea Rev, 130: 1552-1572 |
| Houtekamer P L, Mitchell H L. 1998. Data assimilation using an ensemble Kalman filter technique. Mon Wea Rev, 126:796- 811 |
| Houtekamer P L, Mitchell H L. 2001. A sequential ensemble Kalman filter for atmospheric data assimilation. Mon Wea Rev, 129: 123-137 |
| Kalman R E. 1960. A New Approach to Linear Filtering and Prediction Theory. Trans ASME J Basic Eng, 82D: 35-46 |
| Liang Aimin, Zhang Qinghong, Liu Kaiyu, et al. 2009. The 3D-Var data assimilation experiments on a dense fog event over the Central Plain of China. Acta Meteor Sinica, 23(1): 116-127 |
| Manobianco J, Nutter P A. 1999. Evaluation of the 29-km Eta model Part II: Subjective verification over Floida. Wea Forecasting, 14, 18-37 |
| Mass C F, Ovens D, Westrick K, et al. 2002. Does increasing horizontal resolution produce more skillfull forecasts. Bull Amer Meteor Soc, 83, 407-430 |
| Mitchell H L, Houtekamer P L. 2000. An adaptive ensemble Kalman filter. Mon Wea Rev, 128: 416-433 |
| Whitaker, J S, Hamill T M. 2002. Ensemble data assimilation without perturbed observations. Mon Wea Rev, 130: 1913-1924 |
| Xu Qin, Wei Li, Lu Huijuan, et al. 2008. Time-expanded sampling for ensemble-based filters: Assimilation experiments with a shallow-water equation model. J Geophys Res, 113: D02114, doi:10.1029/2007JD008624 |
| Yang Yi, Qiu Chongjian, Gong Jiandong, et al. 2009. The WRF 3D-Var system combined with physical initialization for assimilation of doppler radar data. Acta Meteor Sinica, 23(2):129-139 |
| Zhang Shuwen, Li Haorui, Zhang Weidong, et al, 2005. Estimating the soil moisture profile by assimilating near-surface observations with the Ensemble Kalman Filter (EnKF). Adv Atmos Sci, 22(6): 936-945 |
 2012, Vol. 70
2012, Vol. 70

