中国气象学会主办。
文章信息
- 陈 敏, Huang Xiangyu, Wang Wei. 2012.
- CHEN Min, HUANG Xiang-Yu, WANG Wei. 2012.
- 数字滤波初始化DFI在高水平分辨率模式中的应用
- Difficulties in the implementation of the digital filter initialization in a high resolution numerical weather forecast model
- 气象学报, 70(1): 109-118
- Acta Meteorologica Sinica, 70(1): 109-118.
- http://dx.doi.org/10.11676/qxxb2012.010
-
文章历史
- 收稿日期:2010-01-13
- 改回日期:2011-03-17
2. 美国国家大气研究中心,博尔德,科罗拉多,美国
2. National Center for Atmospheric Research,Boulder, Colorado 80307-3000, USA
在以往的研究中,数字滤波初始化(DFI)的作用通常体现在以下几个方面:消除由于客观分析和插值等原因造成的质量场和风场不平衡导致的噪声;产生与模式动力场一致的初始条件,如水物质、垂直速度等;在初始条件中无相关的云水及其他水物质分析场时,采用数字滤波初始化能够缩短云和降水产生的调整适应时间。
对于冷启动预报而言,数字滤波初始化在上述几个方面确实能够产生很好的初始化效果,这早已被大量的研究和实际应用所证实。而对于高频更新的同化-预报循环(如1 h)而言,确实由于其循环更新频率过快,模式无法在短时间内衰减掉由于初始场不平衡而导致的噪声,此噪声有可能会被带入下个循环,从而降低资料同化及预报的性能,甚至导致循环崩溃,在这种情况下数字滤波初始化作为一个高效的初始化过程对循环的稳定维持起到了不可或缺的作用(Benjamin et al,2004)。但是,应注意,迄今为止见到的上述应用基本上针对的水平分辨率最高在15 km左右(Huang et al,1993,1994;Chen et al,2006;Lynch et al,1992)。近年来更高分辨率的短期区域数值天气预报正越来越多地从科研阶段走向业务应用,其目的是为灾害性天气、特别是为强对流天气提供更加精准的预报。目前,世界上许多业务中心的区域模式分辨率已经达到2—4 km,并且,可以预计在未来的5—10 a内1 km分辨率的模式将基本普及(Lean et al,2008)。而且,预报模式水平分辨率的提高也使模式初始场中的高频噪声更加显著,从而数字滤波初始化方法在高水平分辨率预报中的应用更具有必要性。
但是,正如Fillion(2002)指出的,数字滤波初始化应用的前提假设是最快的不平衡重力惯性波在平衡的背景场气流中准线性地传播,而且,其在频率谱上与有天气意义的波动不重叠。这一前提假设在粗分辨率条件下通常较易满足,因为在较粗分辨率情形下,模式可解析的有天气意义的波动与高频噪声可以存在较为清楚的界限,从而在设置滤波的切断频率时往往通过经验即可决定。例如针对27 km分辨率的预报,切断周期设为1 h即可滤除模式中虚假的高频振荡(Huang et al,1993;Chen et al,2006)。但是,对于3 km、甚至1 km左右分辨率的数值天气预报,由于其本身具有的高水平分辨率,使模式能够解析的重力波具有波长更短、频率更高的性质,在高分辨率条件下,模式中有天气意义的波动与高频噪声的界线更加模糊。如果考虑同化初猜场中已经有重力内波存在的情况,例如采用同化-预报循环进行深对流预报,无论前次循环预报提供的初猜场动力平衡与否,一旦其中已经具备了与深对流相关的强垂直速度分布,在此基础上进行变分同化分析,在最小化开始之初既已有重力波被激发出来(Fillion,2002)。虽然初始化需解决的问题仍是消除在同化过程中形成的虚假重力波,同时又要能够保留初猜场中原有的具备天气意义的波动,但是在数值模式高水平分辨率的条件下,数字滤波初始化应用的前提条件是否依然成立?如果对此问题缺乏了解,数字滤波初始化在高水平分辨率快速更新同化-预报循环中能否获得成功应用是存在疑问的。
因此,本文以一次深对流过程为例,在3 km水平分辨率条件下采用不同滤波参数配置进行数字滤波初始化试验,试图对高水平分辨率预报初始场中高频噪声特征、如何区分具有天气意义的高频信号和虚假噪声、数字滤波初始化在数值预报模式(WRF)高水平分辨率条件下的应用性能等一系列相关问题给出初步的认识。 2 WRF模式的数字滤波初始化及分析-预报循环
应用的数值模式为WRFV2.2,并基于此版本建立WRF的数字滤波初始化方法(Huang et al,2007),并对绝热的后向积分过程进行了修改。考虑到多数物理过程是不可逆的,需要在后向积分过程中关闭所有的非绝热物理过程,但是发现,如果仅仅关闭相应物理选项的参数,虽然能够达到关闭物理过程的目的,实际上却在初始条件中取消了相应物理预报量的初值,特别是若简单地取消显式云物理过程,在相应的后向积分过程中会导致所有的水物质预报量,诸如云水、雨水、冰、雪等含量丢失以及不守恒。因此,在对后向积分过程修改中仍然保留了相应云物理方案的启动,而是关闭其执行过程,这样能够在后向积分过程中仍然保留水物质预报量伴随动力场的平流、辐合、辐散等合理的行为,只取消其相变的物理过程。此措施部分解决了数字滤波初始化方案最初版本中滤波后预报降水率显著偏低的问题。
基于WRF三维变分同化和WRF模式建立了快速更新的分析-预报循环系统(简称BJ-RUC)(范水勇等,2009)。为研究高分辨率的数字滤波初始化性能,本文的个例研究均在BJ-RUC的3 km区域上进行。与BJ-RUC略有不同的是,由BJ-RUC的9 km区域冷启动预报经单向嵌套(NDOWN)技术 形成 3 km区域(图 1)的边界条件。水平网格点数为172×199,垂直方向为38层,所用的积分时间步长为20 s。主要物理过程包括:WSM6云物理方案,YSU PBL边界层方案,Noah陆面模式,RRTM长波、Dudhia短波辐射方案,无对流参数化方案。
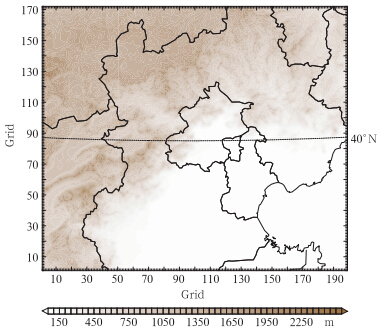 |
| 图 1 3 km预报区域范围及地形高度Fig. 1 Forecast domain and the terrain height with 3 km resolution of the BJ-RUC |
2007年8月1日在河北地区发生了一次较强的飑线过程,在其快速向东南移动的过程中触发了北京城区的短时局地暴雨。这次过程降水主要集中在8月1日12—18时(世界时,下同)。
针对此次强对流过程进行3 km分辨率的预报和数字滤波初始化试验。试验的起始时刻为2007年8月1日12时。由于模式的6 h预报通常较3 h具有更好的动力平衡性、即此时的模式预报场中虚假的高频振荡已经基本被阻尼干净,而且经过6 h的积分,模式大气中已经形成了细致的中尺度结构,可以当作“无噪声”的对照试验。因此,在起始于2007年8月1日06时的3 km区域 6 h预报的基础上对多种观测资料进行三维变分同化,即采用所谓的“热启动”形式来生成预报的初始条件,以研究数字滤波初始化的滤波效率及其对初始场中原有高频天气信息的可能影响。 3.1 WRF模式中表征噪声水平的物理量
通常用平均绝对地面气压倾向(DPSDT)来表示数值模式的噪声水平和平衡状况(Lynch et al,1992),其总体倾向诊断量(N1)表达式为
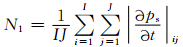
 的扰动形式
的扰动形式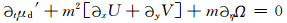 进行求解,其中,μd′为整层干空气质量的扰动量,m为地图尺度因子,Ω=μd /m,方程中具体符号的意义请参考文献(Wang et al,2007)。
进行求解,其中,μd′为整层干空气质量的扰动量,m为地图尺度因子,Ω=μd /m,方程中具体符号的意义请参考文献(Wang et al,2007)。
因此,在WRF模式中定义了平均绝对地面干空气气压倾向(DMUDT)(Huang et al,2007),即单位时间内模式网格点上干空气气压变化的趋势,并且设计了其总体倾向(N2)诊断量
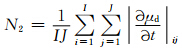
各个试验的具体参数配置见表 1。BG试验的初始条件为起始于2007年8月1日06时的6 h预报场,从图 2a3—e3给出的垂直速度分布可以看出,BG的北京地区已经形成了有组织的对流中尺度结构; 以BG为初猜场进行观测资料的三维变分同化后形成NOI试验及其他数字滤波初始化试验的初始场。分析NOI试验的平均绝对地面干空气气压倾向时间序列(图 3b)可以发现,在积分过程中NOI试验的干空气气压倾向值呈现出周期为15 min(0.25 h)的高频振荡的形式,在积分的前3 h尤其明显。假设此0.25 h以及更短周期的高频振荡是需要滤除的目标噪声,以此进行滤波初始化试验的设计。
| 试验名称 | 是否进行数字滤波初始化 | 滤波时间窗(h) | 切断频率(h) | 初始条件来源 |
| BG | 否 | - | - | 起始于2007年8月1日06时的6 h预报场 |
| NOI | 否 | - | - | 在BG的基础上进行三维变分同化后形成 |
| T0.2C0.3 | 是 | 0.2 | 0.3 | 在BG的基础上进行三维变分同化后形成 |
| T0.7C0.3 | 是 | 0.7 | 0.3 | 在BG的基础上进行三维变分同化后形成 |
| T0.06C0.03 | 是 | 0.067 | 0.03 | 在BG的基础上进行三维变分同化后形成 |
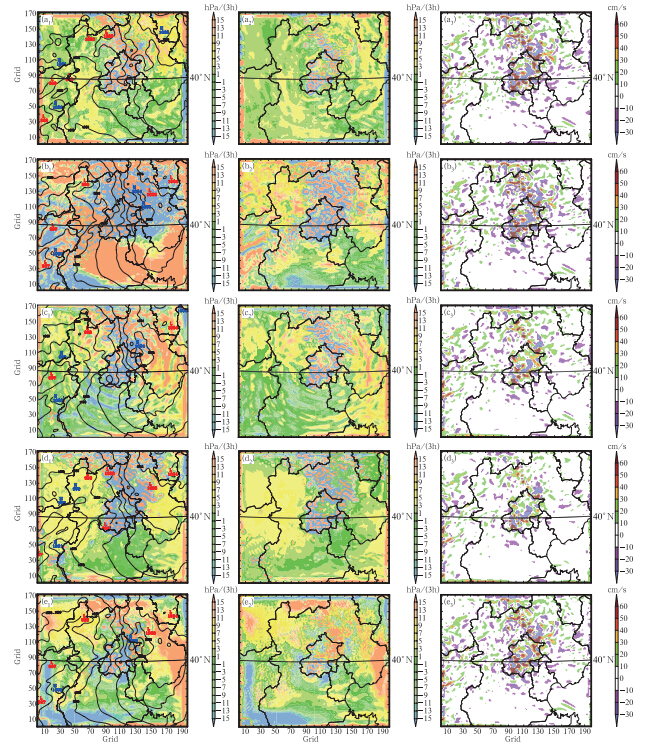 |
| 图 2 预报阶段第1步积分(t=20 s)时刻的地面气压场(等值线,单位: hPa)和平均绝对地面气压倾向(a1-e1),平均绝对地面干空气气压倾向(a2-e2)水平分布以及700 hPa的垂直速度(a3-e3)(a. BG试验,b. NOI试验,c. T0.2C0.3试验,d. T0.7C0.3试验,e. T0.06C0.03试验)Fig. 2 Surface pressure fields(unit: hPa) and the DPSDT(a1-e1),the DMUDT(a2-e2) and the vertical velocity at 700 hPa(a3-e3)(a. the BG experiment,b. the NOI experiment,c. the T0.2C0.3 experiment,d. the T0.7C0.3 experiment,e. the T0.06C0.03 experiment) |
因此,为了滤除周期为0.3 h(当然也包含了0.25 h及更短周期)的高频波、并且尽可能不影响其他波动结构,将滤波初始化的目标噪声切断周期设置为0.3 h,相应地将滤波时间窗设为0.2 h,即给定切断频率的最小滤波时间窗(Huang et al,1993),将此试验命名为T0.2C0.3;T0.7C0.3试验是将滤波时间窗延长至0.7 h,以研究不同时间窗长度的滤波性能;此外还设计了针对超高频振荡(切断周期为0.03 h)进行的滤波试验T0.06C0.03(滤波时间窗为4 min),以探索超高频振荡在模式初始条件中的表现及其在后续预报阶段中的影响。 3.3 噪声水平
从平均绝对地面气压倾向的时间序列分布(图 3)可以看到,BG试验作为一个“无噪声”的参考预报,在有较强的中尺度天气信息状况下,模式在达到动力平衡状态后的噪声水平基本上维持在4 hPa/(3 h)左右;NOI试验代表的3 km分辨率模式噪声在初始时刻具有极高的噪声水平,并且在积分过程中表现为明显的周期约15 min的高频振荡。对比NOI的平均绝对地面干空气气压倾向时间序列,最初的高频噪声中大部分是由于模式的非静力过程所引起的; T0.06C0.03试验在积分的最初阶段有效地将NOI的干空气气压倾向值从20 hPa/(3 h)降低至约10 hPa/(3 h),这表明NOI初始场中大量的虚假噪声具有超高频的性质;T0.2C0.3试验虽然将整个预报过程中的干空气气压倾向值降低了约40%,但是T0.2C0.3和T0.06C0.03两个试验均未对NOI高频振荡的振幅、频率等起到任何的抑制作用;仅有T0.7C0.3试验将平均绝对地面气压倾向和干空气气压倾向降至与BG几乎一致的水平,且积分过程中的高频振荡也几乎完全消除,即对于同一切断频率,要将高频波动抑制到理想的程度必须延长滤波时间窗。
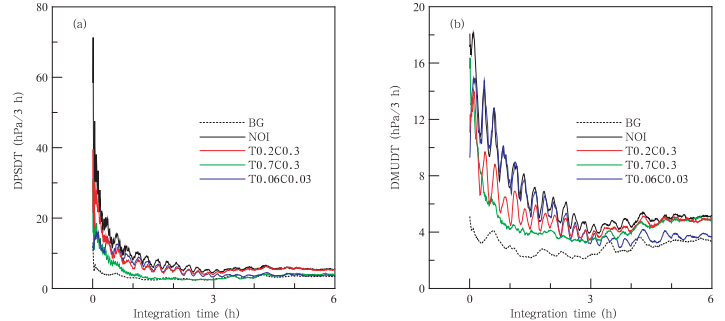 |
| 图 3 各个预报试验平均绝对地面气压倾向(a)和干空气气压倾向(b)的时间序列分布Fig. 3 Time series of the DPSDT(a) and the DMUDT(b)from the different experiments |
图 2给出的是各个试验在积分第1步地面气压和地面干空气气压变化倾向(N1和N2)的水平分布。作为一个“无噪声”的参考预报,BG试验在3 km范围内的大部分区域平均绝对地面气压倾向值处于±5 hPa/(3 h),但是有绝对值在15 hPa/(3 h)以上的平均绝对地面气压倾向和干空气气压倾向大值区存在,其范围对应于初始场中强垂直运动发生的位置,因而此部分即代表同化初猜场中具有天气意义的信息,而非虚假的高频振荡;NOI试验在整个预报区域内均具有很高的平均绝对地面气压倾向和干空气气压倾向,基本无法辨认出细致的中尺度结构;NOI与BG试验平均绝对地面气压倾向和干空气气压倾向分布的差别反映了在BG基础上通过同化过程所获得的额外高频波动,其中,既有具有天气意义的高频信息,也必然包含了同化过程造成的动力场和质量场不平衡而形成的高频噪声(Chen et al,2006)。由于在同化过程中未针对垂直速度和云水、雨水、冰和雪等预报量进行客观分析,因此,在NOI的初始条件中垂直速度场和水成物含量与BG保持一致,同样也从BG中继承了二者之间的既有平衡。但是此垂直速度和水成物含量与NOI初始条件中经客观分析获得的其他预报量之间仍然存在动力上的不协调,需要在未来的积分过程中做进一步的调整。
T0.06C0.03试验虽然只是滤除了NOI中部分的超高频波动,但平均绝对地面气压倾向的分布中已经可以部分显露出中尺度天气信号的特征,且其干空气气压倾向呈现出更多的空间小尺度结构;T0.2C0.3和T0.7C0.3试验在积分第1步的平均绝对地面气压倾向和干空气气压倾向总体分布形式与BG已经十分相似,NOI中极高的平均绝对地面气压倾向和干空气气压倾向在大部分区域内都已降至合理的水平,而平均绝对地面气压倾向和干空气气压倾向高值区也与这两个试验预报的强垂直速度范围相对应。虽然在当前分辨率条件下,由此可以认为0.3 h对于达到消除高频噪声的目的而言是一个较为合理的切断周期,但只有当滤波的时间窗长度达到0.7 h后积分过程中周期为0.25 h的高频振荡才能被完全抑制。
将T系列试验与NOI/BG进行对比后可以发现,T0.06C0.03试验对垂直速度(图 2a3—e3)的改变最不明显;而T0.7C0.3和T0.2C0.3与NOI/BG试验相比,垂直速度的分布范围明显缩小,且强度也显著的削弱,其中,T0.7C0.3试验更为显著,这说明在滤除高频噪声的同时,初始条件中的垂直速度及其所代表的有天气意义的高频波动也被一并削弱了。 3.4 初始化增量
初始化增量是经历初始化过程后的模式变量相对于原初始场的增量。对任何初始化方案而言,必须满足的一个重要前提就是初始化过程对于模式初始条件的改变必须尽可能的小,一般来说,初始化增量应当小于分析增量以确保不损害初值中包含的有用信息,而Daley(1993)认为,初始化增量甚至应当小于观测误差。可以用NOI和BG初始条件中各预报要素的全场平均均方根偏差来表示三维变分同化带来的分析增量,初始化增量则通过各初始化方案与NOI的全场平均均方根偏差来表示。
对比各预报要素初始化增量与分析增量(表 2),T0.06C0.03方案造成的初始化增量远远小于模式的分析增量;而T0.7C0.3和T0.2C0.3两个方案的初始化增量相当显著,尤其是动力上的改变,其中T0.7C0.3试验V的初值增量甚至达到了与分析增量相当的量级,说明T0.7C0.3方案在具有最为显著的滤波效果的同时,对原初始场的改变也最为明显。
| T(K) | U(m/s) | V(m/s) | W(m/s) | Q(g/kg) | ||
| 分析增量 | NOI-BG | 0.716 | 1.265 | 0.785 | 0 | 0.692 |
| T0.06C0.03-NOI | 0.118 | 0.168 | 0.166 | 0.093 | 0.087 | |
| 初始化增量 | T0.2C0.3-NOI | 0.195 | 0.378 | 0.354 | 0.179 | 0.145 |
| T0.7C0.3-NOI | 0.364 | 0.591 | 0.618 | 0.236 | 0.213 |
对比图 4给出的各个试验方案预报前3 h的逐时降水同样可以发现,NOI的预报较BG更加接近实况,这反映了资料同化确实在初猜场基础上增加了有用的中尺度信息这一事实;T0.06C0.03试验预报的降水结构和量级与NOI几乎完全一致;T0.2C0.3和T0.7C0.3试验的整体降水预报结构和分布与NOI十分相似,但在北京北部地区部分小降水中心较NOI有所减弱或者消失;其中T0.7C0.3 试验预报的降水结构与NOI有较大的差别,首先是积分前2 h预报的雨区范围明显缩小,发生在北京北部的降水被显著削弱或者干脆消失,另外,积分至第2小时,北京城区出现了额外的降水极大中心,说明该初始化方案对NOI初始场的修改一方面弱化了模式的降水预报,另一方面也较大地改变了原初始场中的高频天气信号。这与T0.2C0.3和T0.7C0.3 试验显著削弱了初始场中垂直速度的强度和范围也是一致的。
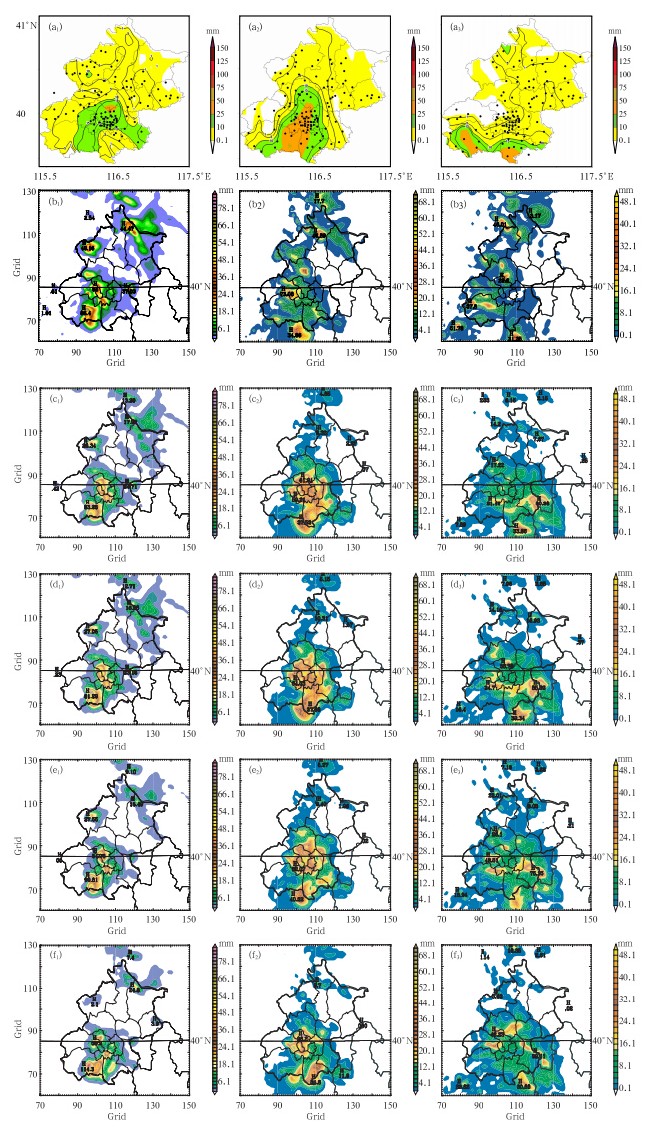 |
| 图 4 北京地区自动站1 h降水观测(a)和各个试验(b-f)预报的逐时累积降水对比(a1-f1. 积分第1小时,实际时间为2007年8月1日12-13时;a2-f2. 积分第2小时,实际时间为13-14时;a3-f3. 积分第3小时,实际时间为14-15时;(b. BG试验,c. NOI试验,d. T0.06C0.03试验,e. T0.2C0.3试验,f. T0.7C0.3试验)Fig. 4 Observed(a) and the forecasted(b-f)1 h accumulated precipitation for the runs of(b)BG,(c)NOI,(d)T0.06C0.03,(e)T0.2C0.3 and (f)T0.7C0.3 with(a1-f1) t=0-1 h,valid at 12-13 UTC 1 Aug 2007;(a2-f2)t=1-2 h,valid at 13-14 UTC 1 Aug 2007; and (a3-f3)t=2-3 h,valid at 15-16 UTC 1 Aug 2007 |
通过对一次深对流个例进行数字滤波初始化试验后发现,当模式的水平分辨率达到3 km左右,即使在“无噪声”状态下,有天气意义的信息在模式中也可以具有与虚假高频噪声一致的表现形式,即地面气压倾向也可以达到 15 hPa/(3 h)以上的量级。在采用WRF变分同化对观测资料进行客观分析后,在背景场基础上增加大量具备天气意义信息的同时,也激发了大量的高频噪声。此高频噪声不仅在预报范围内表现为平均绝对地面气压倾向和干空气气压倾向的高值区,并且,在积分过程中也表现为周期约15 min的高频振荡,通常需要约3 h的积分时间才能通过模式本身的频散和耗散机制将之阻尼至较低的水平。
因此,在针对高分辨率模式进行数字滤波初始化时,原有的应用于低分辨率模式的初始化配置参数已不适用,必须根据高分辨率噪声的特点重新设计相应的滤波方案。当滤波的切断频率缩小至0.03 h-1时,滤除的可能是此分辨率条件下无气象意义的超高频波动,虽然此方案对原初始场的改变微小、且对预报效果的影响微乎其微,但从噪声的抑制方面来看,实质上并未达到滤除高频振荡的目的。从T0.2C0.3和T0.7C0.3试验的结果来看,在目前尚无有效技术手段对同样频率的波动进行区分的条件下,如果希望获得理想的初始化效果,则必然会削弱初始场中原有的具有天气意义的波动。因此,必须考虑的一个问题是,对于当前许多更新周期为3 h 或者更长的同化预报循环系统而言,付出额外的计算代价来执行数字滤波初始化是否值得?
WRF模式本身在动力框架的设计上已经包含了很好的噪声阻尼机制(Wicker et al,2002;Skamarock et al,2005)。从本文给出的结果也可以看到,即使在高水平分辨率条件下,WRF模式中由于初始场不平衡激发的高频噪声通常在3 h内就基本上衰减到可以接受的水平,即通常3 h或者周期更长的同化-预报更新循环系统即使没有经历初始化过程也能维持循环稳定的原因。另外,正如上面一再指出的,如果在资料同化阶段未产生水成物与垂直速度的分析增量,两者之间仍然维持从前次循环获得的平衡状态,云和降水产生的模式调整适应问题将比冷启动预报大为缓解。从噪声和模式调整适应这两点来看,其虽然可以帮助模式较快达到平衡状态,但对于周期在3 h以上的更新循环预报系统,数字滤波初始化的应用或许并不十分必需。
首先,数字滤波初始化的应用需要付出额外的计算代价,根据Smimova等(2009)的结果,执行一个数字滤波初始化过程需要耗费一个正常24 h预报10%的计算时间,尤其在进行业务应用时,计算代价是必须考虑的重要因素。其次,如前述结果,数字滤波初始化的确能对特定切断频率的高频振荡进行滤波,但数字滤波初始化无法区分滤除掉的信号究竟是具有天气意义的高频信号,还是虚假的高频噪声。如果要达到滤除高频噪声的理想效果,比如将模式的平均绝对地面气压倾向/干空气气压倾向值降低至背景场的“无噪声”水平,并且,消除积分过程中的高频振荡,必须延长滤波时间窗,但这是以增加额外积分时间以及有可能损害气象上有意义的波动为代价的。滤波效果越显著,滤波结果对初始场的改变越大,这两个方面实质上是冲突的,因此,在应用数字滤波初始化时必须在滤波效果可接受和保证预报性能两方面之间进行妥协。
需要指出的是,虽然有时数字滤波初始化的应用会带来降水预报效果的提高,但这不能成为数字滤波初始化是否投入实际业务应用的决定性因素,因为毕竟数字滤波初始化最根本的功能是从初始条件中去掉虚假噪声,而实际上并没有向初始条件中加入额外有用的信息,因此,要期望通过应用数字滤波初始化来提高模式预报性能是不现实的。
因此,能够真正发挥数字滤波初始化滤除高频噪声、改善模式调整适应能力的应用主要包括:
(1)以冷启动方式形成预报初始条件;(2)更新频率为1 h或者更高的更新同化-预报循环;(3)如果同化雷达径向风速度,从而产生垂直速度分析增量,或者同化雷达反射率等非常规观测资料,在初始条件中产生水物质分析增量,可以通过数字滤波初始化的应用,尽快缩短初始场的协调时间。
此外,如同Fillion(2002)提出的,也许可以对数字滤波初始化进行一定的扩展,例如,采用仅对平衡初猜场在同化后获得的分析增量进行滤波,从而避免破坏原有初猜场中的气象信息,即所谓的“增量数字滤波初始化”方法来解决本文提出的数字滤波初始化无法区分噪声和天气信号的问题,这将是未来值得尝试的一种手段。
| 范水勇,陈敏等. 2009. 北京地区高分辨率快速循环同化预报系统性能检验和评估. 暴雨灾害, 28(2): 119-125 |
| Benjamin S G, Dévényi D, Weygandt S S,et al. 2004. An hourly assimilation-forecast cycle: The RUC. Mon Wea Rev, 132(2): 495-518 |
| Chen Min, Huang Xiang-Yu. 2006. Digital filter initialization for MM5. Mon Wea Rev, 134(4): 1222-1236 |
| Daley R. 1993. Atmospheric Data Analysis. Cambridge Univ Press |
| Fillion L. 2002. Variational assimilation of precipitation data and gravity wave excitation. Mon Wea Rev, 130(2): 357-371 |
| Huang Xiang-Yu, Lynch Peter. 1993. Diabatic digital-filtering initialization: Application to the HIRLAM model. Mon Wea Rev, 121(2): 589-603 |
| Huang Xiang-Yu, Cederskov A, Erl K, et al. 1994. A comparison between digital filtering initialization and nonlinear normal-mode initialization in a data assimilation system. Mon Wea Rev, 122(5): 1001-1015 |
| Huang Xiang-Yu, Chen Min, et al. 2007. Development of digital filter initialization for WRF and its implementation at IUM//8th Annual WRF User's Workshop |
| Lean H W, Clark P A, Dixon M, et al. 2008. Characteristics of high-resolution versions of the met office unified model for forecasting convection over the United Kingdom. Mon Wea Rev, 136(9): 3408-3424 |
| Lynch Peter, Huang Xiang-Yu. 1992. Initialization of the HIRLAM Model using a digital filter. Mon Wea Rev, 120(6): 1019-1034 |
| Smirnova T G, Peckham S, Benjamin, S G, et al. 2009. Implementation and Testing of WRF DFI |
| Skamarock W C, Klemp J B, Dudhia J, et al. 2005. A description of the Advanced Research WRF Version 2. NCAR Tech Notes-468+ STR |
| Wang W, Barker D, Bray J, et al. 2007. User's Guide for Advanced Research WRF (ARW) Modeling System Version 2.2. Mesoscale and Microscale Meteorology Division-National Center for Atmospheric Research (MMM-NCAR) |
| Wicker L J, Skamarock W C. 2002. Time-splitting methods for elastic models using forward time schemes. Mon Wea Rev, 130(8): 2088-2097 |
 2012, Vol. 70
2012, Vol. 70

