中国气象学会主办。
文章信息
- 赵俊虎, 王启光, 支 蓉, 封国林. 2012.
- ZHAO Junhu, WANG Qiguang, ZHI Rong, FENG Guolin. 2012.
- 中国极端温度的群发性研究
- A study of the extreme temperature group-occurring events in China
- 气象学报, 70(2): 302-310
- Acta Meteorologica Sinica, 70(2): 302-310.
- http://dx.doi.org/10.11676/qxxb2012.029
-
文章历史
- 收稿日期:2010-03-17
- 改回日期:2011-10-28
2. 国家气候中心,中国气象局气候研究开放实验室,北京,100081;
3. 扬州大学物理科学与技术学院,扬州,225002
2.Laboratory for Climate Studies, National Climate Center, China Meteorological Administration, Beijing 100081, China;
3. College of Physics Science and Technology, Yangzhou University, Yangzhou 225002, China
极端事件是人们十分关注的问题,其传统的基本假设是时间序列中的各事件互不相关(Gumbel,1958),在这种情况下极端事件的统计规律仅取决于原序列的概率密度函数,在以往对其进行预测研究时完全采用随机模拟的方法。但近来大量的研究表明,洪涝、地震和经济学等领域的极端事件并非随机的,仍然有一定的规律可循(Bunde et al,1998;封国林等,1998),即极端事件序列具有长程相关性的特征。王启光等(2008)通过对混沌序列分析发现,长程相关性和极端事件的可预测性有比较好的定性关系,并且,极端天气气候事件的长程相关性具有区域分布的特征(封国林等,2009;王启光等,2009)。
此外,受大气环流变化和区域地形的影响,中国的极端天气气候事件具有明显的区域群发性特征。很多学者已从不同的角度研究了极端事件的群发性。翟盘茂等(1999)对极端降水事件变化趋势的研究发现,近30 a中国长江流域频繁发生洪水,而北方却出现持久、严重的干旱,形成南涝北旱的空间分布格局。钱维宏等(2007)对中国近40 a极值气候的变化研究发现,中国极端温度事件的时空变化具有明显的区域群发性,黄河、东北等地暖日增加显著,而冷日的显著减少区则集中在中国的北方。杨萍等(2010)将J阶最近邻距离丛集点提取算法及其一系列理论研究成果用于揭示中国极端气候事件群发性的年代际空间演变特征。王启光等(2010)通过构造理想时间序列,从理论上研究了极端事件再现时间序列的长程相关性和群发性的物理特性,并指出时间序列的长程相关性是导致极端事件群发性的原因。大量统计事实也表明,极端天气气候事件在发生频次、影响范围和破坏程度上都表现出越来越明显的群发性特征。从极端天气气候事件群发性的特点和规律来看,大体上可分为两类:一是时间上的群发,如2009年秋—2010年春,中国西南5省区发生持续性少雨事件,造成了西南地区的3季连旱;二是空间上的群发,如2008年1月—2月初,中国南方大范围地区发生了历史罕见的低温雨雪冰冻灾害。以上两种类型群发性极端事件均可能形成重大灾害,值得深入研究。
事实上对极端事件的描述,不仅有频次和强度,还有极端事件的再现时间,即持续重大异常的极端事件下次何时发生,这也是一个值得研究的问题。对其进行研究有助于深入了解极端事件的发生规律并为预测提供理论基础。本文从极端事件再现时间的角度,探讨极端最高、最低气温(以下简称“极端高、低温”)的长程相关性和时间上的群发性的关联。此外,通过定义群发指数,研究了极端高、低温再现时间序列群发指数的空间分布、年际和年代际变化。 2 极端事件再现时间和方法介绍 2.1 极端天气、气候事件的定义
从统计学的角度看,极端天气、气候事件是一种小概率事件。为了克服传统定义中绝对阈值法所得到的极端事件无法顾及不同区域的气候和地理差异的缺陷,本文采用百分位法定义极端温度事件(Bonsal et al,2001;杨萍等,2008),定义85百分位对应的事件为中等极端事件,记为85th;90和95百分位对应的事件为较强极端事件,分别记为90th和95th。 2.2 长程相关性指数计算方法
Peng等(1994)提出了去趋势涨落分析(Detrended fluctuation analysis,DFA),作为一种序列长程相关性分析工具,能有效地滤去各阶趋势成分,很好地处理非平稳数据,消除其中的伪相关现象,检测非平稳时间序列中的相关性。DFA方法是判断是否存在非线性时间序列长程相关的工具,已被广泛应用于自然科学甚至社会科学的各个领域。DFA本质上是随机游走理论的一种修正均方根分析方法,对于一个给定长度为N的时间序列{x(i),i=1,2,3,…,N},其计算方法(封国林等,2009)步骤如下:
(1)计算时间序列x(i)的距平累加值
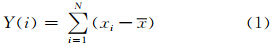
(2)将Y(i)分成Ns个不重叠的间隔为s的区间v,Ns=N/s,对每个区间v用最小二乘法进行拟合,得到局部趋势,滤去其趋势后的时间序列记为Ys(k)(表示原序列与拟合值之差)
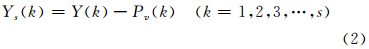
(3)计算每个区间滤去趋势后的方差
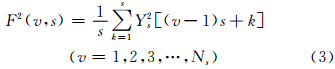
(4)对所有等长度区间的方差求均值并开方,计算标准DFA波动函数
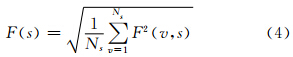
(5)对于存在长程相关性的序列,F(s)与s呈幂律关系

在(F(s),s)的双对数坐标中,利用最小二乘法拟合,其直线部分的斜率即为标度指数α。根据随机游走理论,当0<α<0.5时,表示时间序列是非持久的,只有短期记忆性,当前事件不会对长期的未来事件产生影响;当α=0.5时,表示原序列是白噪声,例如布朗运动;当0.5<α<1.0时,表示序列具有长程相关特征,即当前发生的事件和未来事件存在长程相关性,时间序列具有长期记忆性,且标度指数α越大记忆性越好,即时间序列可预测性也越强。 2.3 极端事件再现时间
时间序列{x(i),i=1,2,3,…,N}在给定的百分位阈值q条件下,极端事件的数目Nq可以确定,便可以构建一条对应的极端事件序列xq(i),定义2次相邻极端事件发生的间隔为极端事件再现时间rq(j)(王启光等,2010)

当N→∞时,有
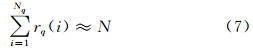
此时定义极端事件序列的平均再现时间Rq
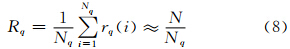
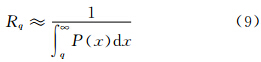
由此可见,Rq、q和P(x)紧密相关,其实质内涵是极端事件的阈值如何确定,如何真正揭示极端事件的分布规律,这一直是极值理论关注的热点问题之一。
2.4 再现时间概率分布
采用傅里叶滤波变换的方法生成标度指数α分别为0.5、0.7、0.8、0.9的4个时间序列,样本量为2×106,其均值为0,方差为1。4个理想时间序列在85th、90th、95th条件下再现时间概率分布如图 1。α=0.7、0.8、0.9时,在不同百分位阈值条件下的概率分布与α=0.5的高斯白噪声随机序列存在明显差异。当rq/Rq<0.5时,具有长程相关性的序列在相同百分位阈值条件下,极端事件再现时间的概率P(r)比随机序列大得多;同时当rq/Rq>4时,具有长程相关性序列在某一百分位阈值条件下再现时间大值的分布概率也明显大于随机序列,说明具有长程相关性的系统,其再现时间有向两端(极小或极大)聚集的倾向,导致极端事件的群发。因此,将rq<0.5Rq时的再现时间定义为小值再现时间,表示两次相邻极端事件时间间隔较短;将rq>4Rq的再现时间定义为大值再现时间,表示两次相邻极端事件时间间隔较长。
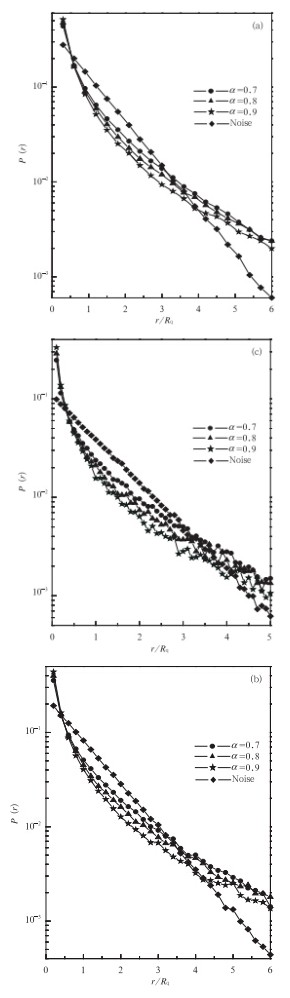 |
| 图 1 不同百分位阈值条件下理想时间序列再现时间概率分布(a.85th,b.90th,c.95th)Fig. 1 Probability distribution of the ideal time-series’ reproduction time under the different percentile threshold(a.85th,b.90th,and c.95th) |
为研究观测资料中极端事件长程相关性的区域分布情况,采用中国194个国际交换站1961年1月—2008年12月的逐日最高、最低气温资料进行研究,对缺测较多或者不满48 a连续观测的站点予以剔除,经检验有167个站点满足上述要求,对仍存在的个别缺测使用插值方法补足。由于篇幅,下文仅研究了90百分位对应的极端事件。
从167个站点极端高、低温事件再现时间序列标度指数的分布(图 2)可以看出,中国各站点极端高温事件标度指数值范围为0.6—0.74,极端低温事件标度指数值为0.65—0.75,均存在较好的长程相关性,且二者标度指数α值总体上均呈纬向分布,但有一定的区别。极端高温事件标度指数α在长江以南地区尤其是云贵高原较小,基本为0.6—0.68,表明这些区域极端高温事件长程相关性较弱;而在长江以北地区标度指数α值的范围基本在0.68以上,尤其是新疆北部部分地区和东北北部地区标度指数α值为0.72—0.74,表明这些区域极端高温事件长程相关性较强。极端低温事件标度指数α分布则具有黄河以北地区较大而华南沿海地区较小的特点。
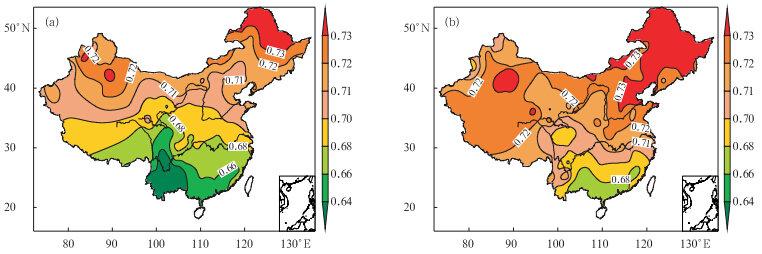 |
| 图 2 极端温度标度指数的分布(a.极端高温,b.极端低温)Fig. 2 Distribution of the extreme temperature’s scaling exponent(a. extreme high temperature,and b. extreme low temperature) |
此外,不论是极端高温还是极端低温,其标度指数大体上都呈纬向分布,北高南低。这可能与大气环流以及地形有关。冬季,北半球中高纬度对流层中部盛行以极地为中心的沿纬圈的西风环流。“十月突变”以后,东亚大槽加强,中国整个大地开始受冬季风控制。11—12月,东亚上空西风急流中心强度再一次明显加强,达到一年中最强,并稳定于30°N 附近,东亚大槽也更为强大、稳定,自此中国开始了隆冬季节。此时,影响中国的主要是寒潮天气过程,冷空气强,影响范围大。北方天气比较稳定,一定程度导致了温度变化具有较好的长程记忆性,因此,中国北方地区的标度指数值较大。中国南部,由于冷空气南下和南海高压与印缅槽的共同作用,有降水天气,天气不稳定,导致温度变化大,长程记忆性差,因此,标度指数值相对较小。夏季,北半球中纬度对流层中上层的西风带向北撤退至40°N以北,中心强度减弱。7月以后,西风急流再一次北撤至45°—60°N,其强度为一年中最弱。此时,北半球大范围环流呈稳定的夏季模式。由于中国北方还是主要受西风带的影响,天气比较稳定,一定程度导致了温度变化具有较好的长程记忆性,因此,其标度指数值较大。而中国西南部由于受印度季风、西南涡等多种天气系统的影响,晴雨多变,天气不稳定,温度变化的不确定性较大,长程记忆性差一些,相应的标度指数值相对较小。
对比图 2a、b发现,由于夏季西风带北撤,同一纬度上极端高温的标度指数要比极端低温的标度指数小,这也说明了受西风带影响大的地区天气形势稳定,温度的记忆性强,长程相关性好,标度指数大;反之,长程相关性差,标度指数小。这样就从侧面建立了长程相关性与气候系统记忆性的可能联系。封国林等(2001)、何文平等(2006a,2006b)、王启光等(2008)对洛伦茨系统的研究表明,洛伦茨系统具有长程相关性,动力学系统的记忆性和长程相关性紧密相连,且长程相关性越强,可预测性越强。由此 可见,研究系统的长程相关性是预报和预测的基础之一。 4 群发性 4.1 群发指数
从第2.3节分析可知,极端事件的小值再现时间的概率P(rq<0.5Rq)比随机序列大得多,且小值再现时间(rq<0.5Rq)的出现分布概率约高于大值的再现时间(rq/Rq>4)概率两个数量级,因此,应着重关注极端事件的小值再现时间群发情况。
为了定量描述极端事件的群发性,本文定义了群发指数Cl
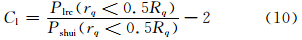
分别计算了2.3节中α=0.7、0.8、0.9的3条长程相关性序列在不同百分位阈值下的群发指数Cl(图 3),当α=0.9时,Cl>0.6;当α=0.8时,0.4<Cl<0.6;当α=0.7时,Cl<0.4。结果显示在不同百分位阈值条件下,对同一个时间序列而言,其Cl基本一致,表明了群发指数Cl的稳定性。它揭示了系统固有的属性,群发指数可以用来定量地比较极端事件群发性的强弱,是一个对极端事件进行分类和评估的有效工具。基于此,定义Cl>0.6的Cl为Ⅰ级群发指数,表示极端事件群发性最强;0.4 ≤Cl≤0.6时Cl为Ⅱ级群发指数,表示极端事件群发性较强;Cl<0.4时Cl为Ⅲ级群发指数,表示极端事件群发性最弱。
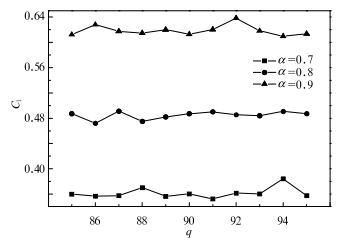 |
| 图 3 α分别为0.7、0.8、0.9的3个序列在不同百分位下群发指数Fig. 3 Group-occurring indices of the three sequences under the different percentile with α equal 0.7,0.8 and 0.9,respectively |
图 4给出了中国东部地区极端高温年代际群发指数的空间分布,其中红色区域为Ⅰ级高值区域,群发性最强;黄色区域为Ⅱ级区域,群发性较强;绿色区域为Ⅲ级低值区域,群发性最弱。极端高温群发指数不同年代的空间分布较为复杂。20世纪60年代,Ⅰ级群发区域位于华北东部和长江以南大部分地区,除东北西部外中国东部大部分地区属于Ⅱ级区域;70和80年代Ⅰ级群发区域逐渐向南北方向发展,其中70年代,华北北部、东北北部和南部以及华东出现了大范围的Ⅰ级高值区,80年代Ⅰ级高值区呈明显的南北分布,东北大部分地区、内蒙古、中南南部以及华东东部为Ⅰ级群发区,而黄河下游则出现大范围的群发低值区;到了90年代,群发高值区集中于长江中下游地区。21世纪最初10年,Ⅰ级群发区分布零散,呈东西分布,Ⅱ级群发区域面积 扩大。从Ⅰ级高群发区域在各个年代的分布特点看,先纬向南北分布,后经向东西分布。
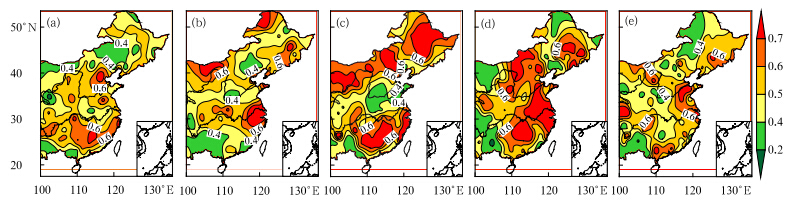 |
| 图 4 极端高温群发指数年代际变化的空间分布(a、b、c、d.20世纪60、70、80、90年代,e.21世纪最初10年)Fig. 4 Spatial distribution of the inter-decadal variance of the group-occurring index of extreme high temperature(a. 1960s,b. 1970s,c. 1980s,d. 1990s,and e. 2000s) |
从中国东部地区极端低温年代际群发性指数的空间分布(图 5)可以看出,20世纪60年代,极端低温的Ⅰ级高群发区域范围较大,主要在东北地区;70年代,Ⅰ级高群发区范围较60年代有所扩大,主要以东北大部分地区以及黄河下游与长江下游之间为主;80年代,极端低温Ⅰ级群发区范围明显减少,只有东北北部、华北北部和长江中下游部分地区;90年代,Ⅰ级高群发区域主要在东北东南部以及黄河下游与长江下游之间,Ⅱ级群发区范围较小,而Ⅲ级区域范围较大;21世纪最初10年,极端低温Ⅰ级高群发区进一步减少,分布在东北东南部和华北部分地区。
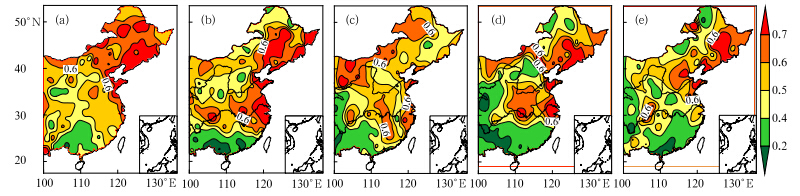 |
| 图 5 极端低温群发指数年代际变化的空间分布(a、b、c、d.20世纪60、70、80、90年代,e.21世纪最初10年)Fig. 5 Spatial distribution of the inter-decadal variance of the group-occurring index of extreme low temperature(a. 1960s,b. 1970s,c. 1980s,d. 1990s,and e. 2000s) |
翟盘茂等(1997)对中国近40年最高最低温度变化的研究发现,最高和最低气温的变化在各个区域内部存在差异。最高温度在夏季,华北、黄淮流域和四川盆地为降温区,而增温主要发生在川藏交界,西北东部地区夏季平均最高气温有下降趋势,这与图 4中极端高温群发指数在西北地区东部和黄淮流域下游呈下降趋势相吻合。其研究同时指出,冬季时中国西北、华北、东北等纬度较高的地区最低温度趋势明显增暖,在黄河以南最低温度增暖趋势随纬度降低有所减缓。这也与图 5中西北、华北、东北等纬度较高的地区极端低温Ⅰ级群发区域在20世纪60年代、70年代范围较大,而到了80年代、90年代一直到21世纪最初10年极端低温Ⅰ级群发区域范围明显减少一致。对比图 4和图 5发现,极端高温Ⅰ级群发区域总体面积变化不大,而极端低温Ⅰ级群发区域面积明显减少,可见从年代际尺度来说极端低温事件群发性的减弱很有可能为年代际气候变暖贡献了主要作用,这一结论与魏凤英(2008)的研究结论一致。 4.4 极端高、低温群发指数分布
从极端温度群发指数的分布(图 6)可以直观地看到最近的48 a中国极端高、低温Ⅰ级群发区域的中心位置。极端高温Ⅰ级群发区域主要在新疆的西北部、华东和华中大部分地区以及东北部分地区,表明这些地区极端高温事件容易群发;Ⅲ级群发区域在西南部分地区,表明这些区域极端高温不易群发。极端低温群发指数大体上呈纬向分布,北高南低,其中Ⅰ级群发区域主要在新疆大部分地区、华北东部以及东北南部,表明这些地区极端低温事件容易群发,而长江以南大部分地区为Ⅱ级和Ⅲ级群发区域,即这些地区极端低温不易群发。
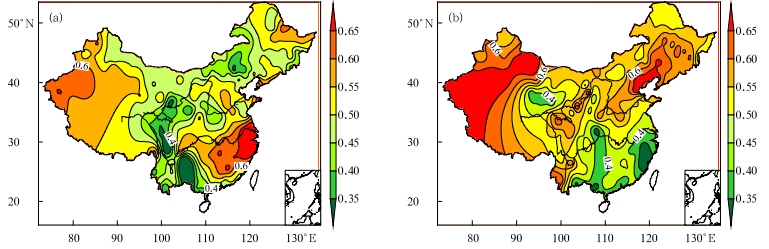 |
| 图 6 极端温度群发指数分布(a.极端高温,b.极端低温)Fig. 6 Group-occurring indices of the extreme temperature in China(a. extreme high temperature,and b. extreme low temperature) |
由图 6可以看出极端高、低温Ⅰ级群发区域相对集中,从图 6a中国东南部Ⅰ级群发区域中选取4个站点,采用逆向计算的方法,首先从每个站点1961—2008年日最高温度序列中剔除1961年数据,即由1962—2008年组成高温序列;其次剔除1962年数据,即由1961和1963—2008年组成高温序列……依此类推,分别计算剔除1 a数据后序列的群发指数。为了较直观地了解被剔除年份温度序列的群发指数,分别计算4个站点极端高温群发指数相对原序列群发指数的变化百分位,然后求其平均值,结果如图 7a所示。由于是剔除数据后分析,且用原序列群发指数减去剔除数据后序列的群发指数,因此,若群发指数变化百分位为正,则意味着所剔除的年份群发指数比原序列群发指数大,即这1年相对背景温度场群发指数是一个上升过程,反之为下降过程。由图 7a可知,极端高温Ⅰ级群发区域群发指数在20世纪60年代初至70年代初为下降趋势,从70年代中期开始上升,一直到80年代后期上升趋势才趋于平缓。
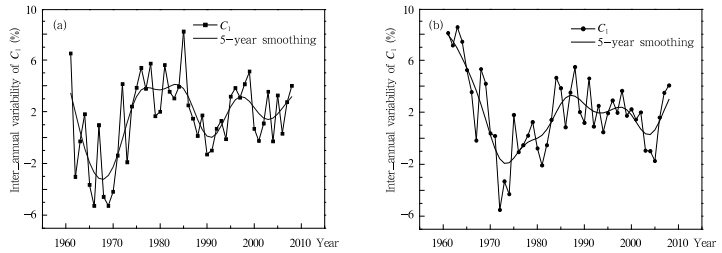 |
| 图 7 Ⅰ级群发区域群发指数的年际变化(a.极端高温,b.极端低温)Fig. 7 Inter-annual variations of the group-occurring index in the level-Ⅰgroup-occurring region(a. extreme high temperature,and b. extreme low temperature) |
同样,从图 6b中国东北Ⅰ级群发区域选取4个站点,对每个站点1961—2008年日最低温度序列,逐次剔除1 a温度数据,考察其群发指数的年际变化情况,结果如图 7b所示。极端低温Ⅰ级区群发区域群发指数在20世纪60年代上升,70年代下降,80和90年代有不同程度的上升,21世纪最初10年群发指数先下降后上升。
总体而言,极端高温Ⅰ级群发区域群发指数增长趋势趋于平缓,而极端低温Ⅰ级群发区域群发指数有下降趋势。这与任国玉等(2005)对中国气温变化研究最新进展的研究结论一致,其研究指出,在最近的50 a,中国地面气温的增加主要是平均最低气温明显上升的结果,全中国范围内极端最低气温也明显升高,而极端最高气温升高不显著。中国与温度相关的极端事件强度和发生频率一般呈降低趋势或稳定态势,与低温有关的极端事件强度和发生频率明显减小,而与高温相关的极端事件强度和发生频率并没有明显增强。 5 标度指数与群发指数的关联性
由2.2节分析可知,具有长程相关性的时间序列其极端事件再现时间的概率分布函数明显不同于随机序列。各理想序列在相同的阈值条件下,其平均极端事件再现时间不变,但是具有长程相关性的序列其极端事件再现时间序列的小值出现概率增大,说明具有长程相关性的系统,其极端事件再现时间有向两端(极小或极大)聚集的倾向,从而导致极端事件的群发。通过对比图 2与6发现:极端事件的标度指数高的地方其群发指数也高,二者在全中国的分布呈较好的对应关系。其中,极端高温标度指数与群发指数空间相关系数为0.281,极端低温标度指数与群发指数空间相关系数为0.598,均通过了0.01的显著性检验。以上通过实际温度资料的计算验证了王启光等(2010)利用理想时间序列研究指出的时间序列长程相关性可能是导致极端事件群发性的根本原因这一结论,为极端事件的预测提供了一定依据。 6 结 论
通过研究百分位阈值条件下中国极端高温、低温事件再现时间序列的长程相关性和群发性,得出以下结论:
(1)具有长程相关性的时间序列其再现时间的概率分布函数明显不同于随机序列,且其小值出现概率增大,导致极端事件的群发。
(2)不论是高温还是低温,其极端事件再现时间序列标度指数大体上都呈纬向分布,北高南低,这可能与大气环流形势以及地形有关。
(3)从年际变化的角度看,极端高温Ⅰ级群发区域群发指数增长趋于平缓,而极端低温Ⅰ级群发区域群发指数有下降趋势,这与近几十年来全球变暖吻合。在年代际时间尺度上,极端高温Ⅰ级群发区域总体面积变化不大,而极端低温Ⅰ级群发区域面积明显减少,因此,极端低温事件的群发性减弱很有可能是年代际气候变暖的主要原因。
(4)具有长程相关性的系统,其极端事件再现时间有向两端(极小或极大)聚集的倾向,从而导致极端事件的群发。通过相关性分析,也发现标度指数和群发指数呈很好的正相关,其相关系数通过99.9%的显著性检验,说明时间序列的长程相关性可能是导致极端事件群发性的根本原因。群发指数是一个对极端事件进行分类和评估的有效工具,为评估极端事件的可预测性提供参考。
| 封国林,曹鸿兴.1998.自忆预报模式中记忆特性的探讨.应用气象学报,9(2):219-224 |
| 封国林,戴新刚,王爱慧等.2001.混沌系统中可预报性的研究.物理学报,50(4):606-611 |
| 封国林,王启光,侯威等.2009.气象领域极端事件的长程相关性.物理学报,58(4):2853-2861 |
| 何文平,封国林,董文杰等.2006a.Lorenz系统的可预报性.物理学报,55(2):969-977 |
| 何文平,封国林,高新全等.2006b.准周期外力驱动下Lorenz系统的动力学行为.物理学报,55(6):3175-3179 |
| 钱维宏,符娇兰,张玮玮.2007.近40年中国平均气候与极值气候变化的概述.地球科学进展,22(7):673-684 |
| 任国玉,郭军,徐铭志等.2005.近50年中国地面气候变化基本特征.气象学报,63(6):942-956 |
| 魏凤英.2008.中国冬半年最低气温概率分布特征.气候变化研究进展,4(1):8-11 |
| 王启光,支蓉,张增平.2008.Lorenz系统长程相关性研究.物理学报,57(8):5343-5350 |
| 王启光,侯威,郑志海.2009.东亚区域大气长程相关性.物理学报,58(9):6640-6650 |
| 王启光,侯威,郑志海等.2010.极端事件再现时间长程相关性与群发性研究.物理学报,59(10):7491-7497 |
| 杨萍,侯威,封国林.2008.基于去趋势波动分析方法确定极端事件阈值.物理学报,57(8):5333-5342 |
| 杨萍,侯威,封国林.2010.中国极端气候事件的群发性规律研究.气候与环境研究,15(4):365-370 |
| 翟盘茂,任福民.1997.中国近四十年最高最低温度变化.气象学报,55(4):418-429 |
| 翟盘茂,任福民,张强.1999.中国降水极值变化趋势检测.气象学报,57(2):208-216 |
| Bonsal B R,Zhang X,Vincent L A,et al.2001.Characteristics of daily and extreme temperatures over Canada.J Climate,14:1959-1976 |
| Bunde E K,Bunde A,Havlin S,et al.1998.Indication of a universal persistence law governing atmospheric variability.Phys Rev Lett,81:729-732 |
| Gumbel E J.1958.Statistics of Extremes.New York:Columbia University Press |
| Peng C K,Buldyrev S V,Havlin S,et al.1994.Mosaic organization of DNA nucleotides.Phys Rev E,49(2):1685-1689 |
 2012, Vol. 70
2012, Vol. 70

