中国气象学会主办。
文章信息
- 张雅乐, 俞永强, 段晚锁. 2012.
- ZHANG Yale, YU Yongqiang, DUAN Wansuo. 2012.
- 四个耦合模式ENSO后报试验的“春季预报障碍”
- The spring prediction barrier of ENSO in retrospective prediction experiments as shown by the four coupled ocean-atmosphere models
- 气象学报, 70(3): 506-519
- Acta Meteorologica Sinica, 70(3): 506-519.
- http://dx.doi.org/10.11676/qxxb2012.042
-
文章历史
- 收稿日期:2010-07-14
- 改回日期:2011-03-17
2. 中国科学院大气物理研究所大气科学和地球流体力学数值模拟国家重点实验室,北京,100029
2. State Key Laboratory of Numerical Modeling for Atmospheric Sciences and Geophysical Fluid Dynamics, Institute of Atmospheric Physics, CAS, Beijing 100029, China
春季可预报性障碍(SPB)是ENSO预测的一个显著特征,是ENSO可预报性研究中的一个关键问题。所谓春季可预报性障碍,即是指大多数气候模式在预报ENSO事件时,模式及持续性预报技巧在大约4、5月间快速下降,导致预报结果产生较大不确定性的一种现象(Webster et al,1992;Webster,1995)。
对春季预报障碍的特征和原因,许多研究工作提出了可能的机理,并希望找到克服春季可预报性障碍的方法,但到目前为止还没有统一的结论。在已有的研究中,主要有以下观点:Webster等(1992)提出南亚季风爆发引起赤道太平洋信风的季节变化与热带太平洋海-气耦合系统相互作用是产生春季可预报性障碍的原因;Chen等(1995)和Xue等(1997)提出,海温距平方差的季节性变化在春季最小,数值模式不容易捕捉到有用的信息,使得ENSO预报产生春季可预报性障碍现象;Torrence等(1998)认为,ENSO总是倾向于在春季从冷位相转为暖位相,此时ENSO的信噪比最小;Samelson等(2001)认为春季可预报性障碍是ENSO的一个固有属性;Chen等(1995,2004)则认为Zebiak-Cane模式的春季预报障碍现象可能不是真实ENSO系统所固有的而是模式本身的问题造成的,可以通过改进初始场,减弱甚至消除春季可预报性障碍;Flügel等(1998)认为预报技巧对季节的依赖性与初始场有关;Samelson等(2001)用线性不稳定理论提出暖位相发展期预报障碍,即ENSO在发展期可预报性低;Mu等(2007a)用一个理论ENSO模式(Wang et al,1996),在不考虑模式误差的基础上,通过条件非线性最优扰动(CNOP)方法,从初始误差增长的角度研究了ENSO事件预报不确定性的季节依赖性,指出条件非线性最优扰动型误差在厄尔尼诺事件发展期的春季增长最大,并且随着初始误差的增大变得越来越明显。
也有研究从误差的角度探讨ENSO可预报问题的季节依赖性。刘新超等(2008)和Yu等(2009)分别用Zebiak-Cane模式做了一组回报试验和加入条件非线性最优扰动方法的理论试验,指出海温距平的误差在ENSO的生长阶段发生明显的春季可预报障碍。虽然Zebiak-Cane模式物理概念清晰、计算量小,目前不少与ENSO有关的工作均使用这一类型的模式(Chen et al,1995),但模式就ENSO事件海-气相互作用的刻画,尤其对拉尼娜事件的预测能力还有待提高。并且,Yu等(2009)专注于初始误差和春季可预报性障碍关系的理论试验,并没有考虑模式误差的作用。实际预测中,预报的不确定性不仅来自于初始误差,同时需要考虑模式误差的作用。因此,本文利用海-气耦合模式对过去20多年的ENSO事件进行了回报试验,其误差包含了初始误差和模式误差的共同作用,并通过对CliPAS试验的结果分析,讨论复杂耦合气候系统模式对ENSO事件预报的季节依赖性。
本文分析的4个模式有3个来自目前正在实施的CliPAS计划,已有大量工作对其所用模式从不同时间尺度和空间以及主要的气候事件都进行了的评估。如Wang等(2009)研究了欧亚季风主要模态的可预报性。Kim等(2008)研究了模式季节内的可预报性和预报技巧,并对耦合模式的平均态及其与季节可预报性的关系进行了探讨。对ENSO的预报,这些集合预报模式对ENSO的预报都有较好的预报能力(Wang et al,2009); Jin等(2008)分析Niño3.4指数发现持续6个月的超前预报中,一步法模式的海温集合预报相关系数最高,绝大多数模式对ENSO的预测,相关系数都明显好于持续性预报,一半以上的模式相关好于动力-统计模式。模式海温年平均和季节循环平均态的预测与观测存在一定距离,仍有待提高。本文同时分析了中国科学院大气物理研究所新发展的耦合模式FGOALS的回报试验结果,Yan等(2009)对模式季节预测的结果已经进行评估,讨论了FGOALS短期气候可预报性,认为对热带海-气相互作用有较强的预测能力,对ENSO的可预报性达到9个月。
本研究有如下特点:(1)通过多个海-气耦合模式ENSO回报试验的结果比较讨论春季可预报性障碍。耦合气候系统模式可以更真实地反映海洋、大气、海冰和陆面的复杂相互作用,回报试验结果又经对各自6—15个不等的预报成员进行集合平均得出,过滤了预报中可能存在的随机信息,这种集合预报方法甚至比用高分辨率模式产生的单一预报更精准。值得注意的是这些参数化方案、次网格物理过程、垂直水平分辨率等各不相同的模式,对ENSO的预报是否都会出现可预报性障碍?各模式的预测结果是否会体现出相似的特点甚至有一致规律可循?模式相互比较的同时也与观测进行比较,在一致中发现不同,在此基础上进一步探讨产生ENSO春季预报障碍究竟是ENSO事件本身的极限问题,还是模式在预报中产生的误差所导致?(2)把ENSO事件分为冷、暖事件分别研究,与ENSO发展的锁相特点联系在一起,通过讨论厄尔尼诺事件和拉尼娜事件各自发展期、衰减期的误差增长特征分析春季预报障碍。ENSO事件一般在前一年8—11月开始增长,到年底发展至峰值,次年春季处在迅速衰减冷暖位相转换期(Jin et al,2008)。发展至衰减的过程中,各跨越了一次春季,但这相邻两年出现在春季的海-气相互间作用肯定不同,于是,按Niño3.4 指数的逐月变化,本文将冷、暖事件的发展过程进一步细分为发展期和衰减期,通过讨论期间误差发展分析春季预报障碍。这将有助于更细致地分析春季可预报性障碍现象及其产生的机制。 2 ENSO回报试验介绍和分析方法 2.1 资料介绍
采用来自CliPAS计划中3个海-气耦合模式的回报试验资料。CliPAS计划归属于亚太经济合作组织(APEC)气候中心(APCC),该计划的一个重要目标是发展有效的多模式集合预报系统,以便更好地研究全球季节-季节内气候变化的可预报性问题。目前回报试验由来自全球12个研究中心7个一步法和7个两步法共14个气候模式参与,同时还包含了欧洲中期天气预报中心(ECWMF)7个一步法海气耦合模式(Wang,2009)。在这21个集合预报模式的回报试验资料中,有3个模式提供了超前预报1—12个月的海表温度(SST)资料,分别是一步法的美国地球流体动力学实验室(GFDL)模式和夏威夷大学(UH)模式(记作GFDL,UH),以及两步法的韩国国立首尔大学(SNU)统计-动力模式(记作SNU)。
GFDL模式海洋部分OM3.1(Gnanadesikan et al,2006; Griffies et al,2005)基于MOM4 编码,垂直方向50层,水平分辨率是纬向1°,经向分辨率采用 B型网格示踪的方式在29.5°S—29.5°N从1°渐变加密至赤道(1/3)°。海洋表面由海表风应力、热通量驱动(Delworth et al,2006)。
UH模式海洋部分是两层半的赤道上层海洋模式,水平分辨率1°(纬向)×2°(经向),观测的气候态海表风场和热通量驱动经单独海洋模式积分10年的结果作为初始场(Fu et al,2004; Wang et al,2004)。
SNU统计-动力模式系统对海表温度的预报基于4个不同的预报模式:赤道太平洋海表温度的中等调和动力模式、滞后线性回归模式、位相投影模式PPM和持续预报模式。之后将4个模式的预报结果进行简单的平均,水平分辨率2°×2°(Kug et al,2004)。回报试验结果由6个集合成员集合而成(Wang et al,2009)。
CliPAS计划所有模式都用NCEP/DOE再分析资料作为初始场,一步法模式均由10个集合成员组成,两步法SNU模式由15个集合预报成员组成。资料的水平分辨率统一插值到2.5°×2.5°,预报初始时刻为2月1日、5月1日、8月1日和11月1日,覆盖时段从1979年到2005年不等。
同时,本文还选取中国科学院大气物理研究所(IAP)大气科学和地球流体数值模拟国家重点实验室(LASG)发展的耦合模式(记作FGOALS)。海洋分量模式是LASG/IAP发展的一个气候系统海洋模式(LICOM)1.0版本(张学洪等,2003; Liu et al,2004),模式的物理参数化过程可以有多种选择,模式的垂直方向30层,水平分辨率1°×1°,预报初始时刻为1月1日、4月1日、7月1日和10月1日,覆盖时段从1982年到2008年(Yan et al,2009)。
所用的观测数据:(1)英国大气数据中心(BADC)提供的全球表层海温资料(GISST);(2)美国大气海洋局气候预测中心CMAP降水资料(Xie,1997);(3)美国国家海洋与大气管理局国家环境预测中心和国家大气研究中心(NOAA NCEP-NCAR CDAS-1)850 hPa纬向风场(u)再分析资料(Kalnay et al,1996)。
考虑到观测与预报时空一一对应,具有相同的格点分辨率和时间跨度,将FGOALS回报试验资料和观测资料插值为水平分辨率2.5°×2.5°,选取模式和观测资料共有的时间跨度为1982年1月—2003年12月。 2.2 ENSO事件发展期和衰减期的定义
ENSO事件最主要的特征是中东太平洋地区海表温度在厄尔尼诺年异常升高,在拉尼娜年异常降低,Barnston等(1997)指出,Nino3.4指数可以很好地刻画ENSO事件的变化。所以本文取Nino3.4区(5°S—5°N,170°—120°W)作为考察范围,采用美国国家海洋与大气管理局(NOAA)气候预测中心(CPC)提供的Nino3.4指数衡量一次冷、暖事件的发生、发展及消亡。
首先,将3个月滑动平均的Nino3.4指数超过+0.5℃(低于-0.5℃)定义为一次厄尔尼诺(拉尼娜)事件。由于ENSO事件在发展和衰减阶段位相特征并不一致,因此,基于观测Nino3.4指数把每一次ENSO事件划分为发展期和衰减期,分别考虑预报的不确定性。厄尔尼诺(拉尼娜)事件发展期定义为Nino3.4指数从大于-0.5℃(小于0.5℃)发展到峰值的时段,记作“G”;从峰值下降(上升)到-0.5℃(0.5℃)的时段为厄尔尼诺(拉尼娜)事件的衰减期,记作“D”(图 1),按上述定义给出观测和模式模拟的1982—2003年5次厄尔尼诺事件(1982/ 1983、1986/1987、1991/1992、1997/1998和2002/2003年)和4次拉尼娜事件(1984/1985、1988/1989、1995/1996和1998/1999年)。
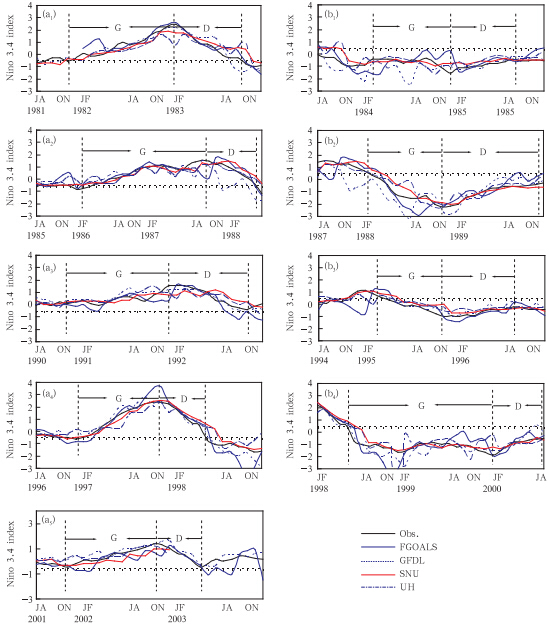 |
| 图 1 1982—2003年的5次厄尔尼诺事件(a)和4次拉尼娜事件(b)Nino 3.4指数分布(“G”表示生长期,“D”表示衰减期)Fig. 1 Time-dependent Nino 3.4 indexes of the five El Niño events(a) and the four La Ni a events(b)during 1982-2003(The start-months of predictions for these events are marked on the horizontal axis. The letter “G” indicates the growing-phase predictions and the letter “D” indicates the decaying-phase ones) |
引入动力学方法(刘新超等,2009)研究预报误差发展的季节依赖性问题。用范数‖T′(τ)‖=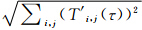 度量模式的预报误差,其中T′i,j(τ) 代表τ时刻格点(i,j)上预报与观测的海表温度异常之差。预报误差在各个季节的发展趋势可通过计算曲线γ(t)=‖T′(τ)‖的斜率k反映,k表示预报误差在各个季节的增长率,正(负)值表示预报误差的增长(衰减),绝对值越大意味预报误差增长(衰减)越快。
度量模式的预报误差,其中T′i,j(τ) 代表τ时刻格点(i,j)上预报与观测的海表温度异常之差。预报误差在各个季节的发展趋势可通过计算曲线γ(t)=‖T′(τ)‖的斜率k反映,k表示预报误差在各个季节的增长率,正(负)值表示预报误差的增长(衰减),绝对值越大意味预报误差增长(衰减)越快。
本文将一年分为四个季节:3—5月(MAM)定义为春季,相应的6—8月(JJA)为夏季,9—11月(SON)为秋季,12月至次年2月(DJF)为冬季。由于所用预报资料不包含初始分析场资料,故无法得到初始时刻所在季节预报误差的斜率k。 3 ENSO事件预报误差发展的季节依赖性 3.1 ENSO回报试验的春季预报障碍
在研究预报误差发展的季节依赖性之前,首先对模式的预报能力加以简单评估。观测与各模式间以及持续性预报的Nino3.4指数距平相关系数(ACC)随预报时效的演变(图 2)表明,随着超前预报时间的增加,观测与模式的相关性和持续性预报均逐渐减小,但是所有耦合模式的预报技巧均高于持续性预报技巧,说明模式对于ENSO事件具有相当的预测能力。但当超前预报时间增加到7—8个月时,大多模式的相关系数依然保持在0.6以上,并且在更长时间的预报中下降并不明显,因此,可以认为所选用分析的模式对ENSO的可预报性能达到9个月甚至更长。结合图 1和2,模式虽然不能预测出与观测完全吻合的ENSO事件,但位相和振幅与观测比较一致;从Nino3.4指数的距平相关系数更加证实,模式有9个月以上的预报时效,且好于对应的持续性预报,由此可以认为模式的预报能力较强。
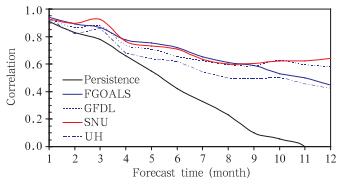 |
| 图 2 Nino 3.4指数相关系数随预报时效的演变(结果经6个月滑动平均)Fig. 2 Temporal changes in the correlations between the mean monthly Niño 3.4 indexes(The results are based on the 6 month running mean) |
接着总体研究回报试验均值的季节依赖性。把各个模式不同初始月和观测的 Nino3.4区海温做逐月相关(图 3),从图 3看到,7/8月开始预报,相关系数在超前9个月的预报随着预报时效的增加缓慢递减,并且4个模式均保持在0.6以上,而从下一年3月开始,相关系数快速下降,到5、6月相关性最差,5个模式都在0.2左右。从10/11月开始预报,相关系数在提前6个月的预报中保持在0.83以上,这与夏季开始预报情况一致,但当预报次年春季时,相关系数也出现迅速下降。而从1/2月开始预报,预报与观测的相关性只在提前3个月的预报较高,当预报跨越当年春季时,同样出现
快速下降的情形。这与 Webster等(1992)和Webster(1995)的结论一致,他们用Latif-Graham模式(Latif et al,1994)和Cane-Zebiak 模式(Cane and Zebiak: personal communication)将赤道太平洋海温的预报与观测的相关系数也在春季(4—6月)下降明显。同时,Webster等(1992)对南方涛动指数(SOI)进行的滞后相关也发现无论从哪个月开始,相关系数在接下来的春季(3—5月)都有很迅速地下降,并将这种现象称作“出现在春季的相关障碍”。
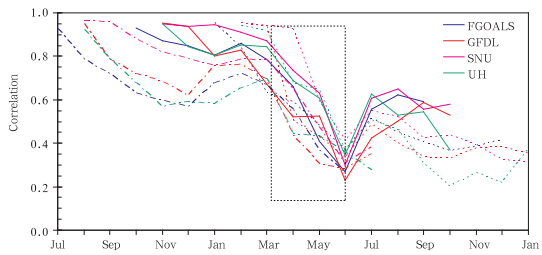 |
| 图 3 1982—2003年观测和气候模式Nino 3.4区海表温度的相关系数(点划线:起始预报月为7/8月,实线:起始预报月为10/11月,点状虚线:起始预报月为1/2月)Fig. 3 Correlations between the SST predictions using the coupled models and the observations for the Nino 3.4 area(The four colors indicate the four models,respectively,where July/August(dash-dotted line),October/November(solid line) and January/ February(dotted line)are used as the start-months of the predictions) |
总之,4个模式与观测的相关系数均强烈依赖于季节变化。无论从哪个月开始预报,相关性从3月开始出现明显下降,并在6月最低,这段时间正处于春季,说明本文考察的4个模式在进行预测时均出现了春季预报障碍。 3.2 ENSO事件预报误差发展的季节依赖性
上节总体考察了各个模式ENSO预测技巧的季节依赖性,这是一个统计平均特征,每一次ENSO事件都各不相同,冷暖事件也有各自的特征,并且具有不对称性。接着按照之前的划分方法,研究模式在每次厄尔尼诺(拉尼娜)事件的发展期和衰减期是否均会出现春季预报障碍。
在本文讨论的ENSO事件中,存在个别较特殊的厄尔尼诺(拉尼娜)事件。例如,1986/1987年厄尔尼诺事件不符合大多数厄尔尼诺事件位相锁相在年底的特征,且持续时间较长(图 1),从而使1985年8、11月和1986年2、8、11月的预报均处于该次厄尔尼诺事件的发展期,此处选离峰值最近的1986年8、11月和1987年2月为发展期的起始预报月;同时,衰减期约出现在1987年8月至1988年4月,这期间不包括整个春季,故不讨论此次事件衰减期跨春季预报的情形。
因篇幅所限,4个模式的预报误差随时间发展的斜率未一一给出。在本文分析的夏、秋、冬三个季节开始的预报中,秋季开始预报,较其他季节能完整地预测出ENSO事件的发展过程。再者,春季正好处在提前2个季度预报的时间尺度上,具有较稳定的预测能力(Wang et al,2009),还可同时得到春季前后两个季节的误差发展状况。因此无论从ENSO事件本身的发展规律到预报时效,以及季节配置上,秋季开始的预报都很具有代表性。下文给出FGOALS和GFDL两个耦合模式从秋季开始预报的误差随时间发展的斜率。3.2.1 发展期
首先讨论厄尔尼诺事件的发展期(表 1),FGOALS误差斜率均在春季最大,其他季节预报误差的发展倾向于负斜率,即误差衰减。GFDL除1991/1992年厄尔尼诺事件,最大正斜率同样出现在春季,此后的冬季误差发展为负,预报技巧明显提高。另外2个模式对5次厄尔尼诺事件发展期预测,误差随时间的最大增长率均出现在春季。
| 时间 | FGOALS模式 | GFDL模式 | ||||
| 冬季(DJF) | 春季(MAM) | 夏季(JJA) | 冬季(DJF) | 春季(MAM) | 夏季(JJA) | |
| 1982/1983 | / | / | / | 3.397 | 3.494 | -3.029 |
| -1.438 | 3.466 | -7.442 | -0.414 | 3.952 | -1.996 | |
| 1986/1987 | 0.019 | 1.252 | -1.747 | 0.691 | 1.916 | -2.437 |
| / | / | / | 4.367 | 12.159 | 5.715 | |
| 1991/1992 | -1.978 | 1.528 | -2.645 | 7.704 | -7.626 | -0.090 |
| 1.332 | -6.730 | -5.047 | 3.056 | -3.758 | 1.128 | |
| 1997/1998 | -1.783 | 10.634 | 6.057 | 4.533 | 5.830 | -3.887 |
| 1.938 | 8.283 | -21.559 | 0.473 | 0.905 | -1.098 | |
| 2002/2003 | 0.379 | 3.279 | 1.620 | 5.539 | 6.410 | -12.073 |
| -6.521 | 1.098 | 0.929 | 7.460 | -5.370 | 3.031 | |
| 注:每年的第1行代表发展期,第2行代表衰减期。黑体字表示春季预报误差最大增长率。 | ||||||
此外,还分析了其他季节起始预报在厄尔尼诺事件发展期的误差增长率,与秋季开始的预报类似,FGOALS、SNU和UH模式预报误差的最大增长均发生在春季,预报误差增长的斜率在其他季节都很小,尤其在冬季大多为负增长。GFDL除1991/1992年厄尔尼诺事件,误差也在春季增长最快。由图 1可知,模式在预测1991/1992年厄尔尼诺事件时,锁相没有出现在年底,峰值提前出现在春末夏初,对此次事件的预测与观测不符,可能是导致预报误差最快增长在这次事件中没有出现在春季的原因。
类似地,分析拉尼娜事件发展期,由表 2可知,10/11月开始预报,FGOALS、GFDL有2次预报误差最大增长率出现在春季,SNU、UH各3次。从7/8月开始预报,除1984/1985年拉尼娜事件,FGOALS、SNU两个模式预报误差均在春季增长最快,UH模式预报事件发展期误差的最大正斜率均出现在了春季;1/2月开始预报,对1984/1985年拉尼娜事件,4个模式对预测最大预报误差都没有出现在春季,FGOALS和GFDL预报误差其他3次拉尼娜事件最大增长率出现在春季,SNU和UH 2次出现在春季。
| 时间 | FGOALS模式 | GFDL模式 | ||||
| 冬季(DJF) | 春季(MAM) | 夏季(JJA) | 冬季(DJF) | 春季(MAM) | 夏季(JJA) | |
| 1984/1985 | 10.081 | -4.888 | -4.928 | 13.206 | -9.123 | -7.604 |
| -4.856 | -1.113 | -1.275 | 0.187 | -1.621 | 3.380 | |
| 1988/1989 | -2.289 | 6.819 | -5.921 | 9.586 | -5.139 | -0.872 |
| -1.303 | 0.322 | 2.497 | -3.866 | 5.416 | 3.887 | |
| 1995/1996 | -6.675 | -4.585 | -3.084 | 0.824 | 3.331 | -2.887 |
| -0.810 | 1.767 | -4.141 | 8.370 | 4.526 | -5.114 | |
| 1998/1999 | 1.938 | 8.283 | -21.559 | 0.473 | 0.905 | -1.098 |
| -7.561 | -4.179 | 1.104 | 5.150 | -10.455 | 9.908 | |
| 注:每年的第1行代表发展期,第2行代表衰减期。黑体字表示春季预报误差最大增长率。 | ||||||
各个季节对拉尼娜事件发展期的预报,模式在预报1984/1985年和1995/1996年2次拉尼娜事件时,误差发展的季节依赖性均不明显。与其他几次拉尼娜事件相比,这两次事件强度比较弱,也许意味着预报误差发展的季节依赖性与ENSO事件的强弱有关。在Jin等(2008)的研究中也曾有类似推断,认为预报与观测的相关性在振幅强的ENSO事件的表现要好于弱ENSO事件。3.2.2 衰减期
由表 1看到,不同的初始时刻,厄尔尼诺事件的衰减期发生预报障碍的季节也不同。7/8月开始的预报,误差最大增长率以秋季和春季居多;10/11月开始预报,1991/1992年厄尔尼诺事件,4个模式预报误差在冬季增长最快,其余事件模式预报误差最大增长率依然在春季。1/2月开始预报,UH模式不明显,其他3个模式预报误差均在春季发展最快。由此可见,厄尔尼诺事件衰减期发生预报障碍的季节也依赖于预报的初始季节。
对于跨春季预报拉尼娜事件的衰减期,无论从表 2或是未给出的分析中,对不同起始预报月,所有模式预报误差最大增长率分散出现在每个季节,并且模式间也没有一致的规律可循,无法看出明显的春季预报障碍。
综上所述,对ENSO事件生长位相进行预报时,误差在春季发展最快,在其他季节误差的发展非常小,因此,模式的ENSO预报技巧表现出明显春季预报障碍现象。对于衰减期的预报,模式对厄尔尼诺事件的预测因初始时刻不同体现出不同的季节依赖性,刘新超等(2008)和Yu等(2009)用Zebiak-Cane模式的回报试验和理论试验也指出海温距平的误差在厄尔尼诺事件的生长阶段会出现明显的春季(4—6月)可预报障碍,而衰减期则没有明显的春季预报障碍现象;在预测拉尼娜事件时,无论从何时开始预报,预报误差最大增长率均未出现季节依赖现象。 3.3 厄尔尼诺和拉尼娜事件误差发展的不对称性
厄尔尼诺事件和拉尼娜事件在振幅、结构和时间演变等方面均表现为显著的非对称性(Jin et al,2003; An et al,2001; Burgers et al,1999; Kang等,2002; Kessler,2002)。从表 1可以发现模式的预报技巧以及误差的发展在厄尔尼诺事件和拉尼娜事件位相存在不对称性。分析可知,从不同时刻开始的预报,4个模式预报厄尔尼诺事件的季节依赖性强于拉尼娜事件;并且,厄尔尼诺/拉尼娜事件生长位相的季节依赖性强于衰减位相。因此,预报误差随季节的增长率具有明显的不对称性。
从误差的角度分析发现,将所有厄尔尼诺事件和拉尼娜事件的预报误差分别做集合平均(图 4),可以看到无论从哪个月开始预报,4个模式对厄尔尼诺事件发展期的预报误差在春季都有明显增长,表明在春季预报技巧明显下降。厄尔尼诺事件衰减期和拉尼娜事件发展期虽然也有明显增长,但是4个模式体现的不如厄尔尼诺事件的发展期一致。
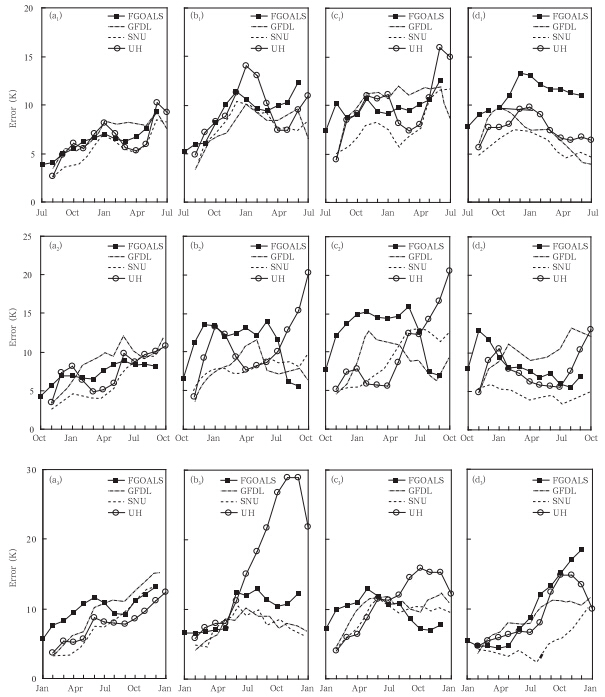 |
| 图 4 ENSO事件误差逐月增长趋势(单位:K)(a.厄尔尼诺事件生长期,b.厄尔尼诺事件衰减期,c.拉尼娜事件生长期,d.拉尼娜事件衰减期;a1—d1.起始预报月为7/8月,a2—d2.起始预报月10/11月,a3—d3.起始预报月1/2月)Fig. 4 Monthly prediction error growing trend for the ENSO events(unit: K)(a. the growing-phase of the El Niño events,b. the decaying-phase of the El Niño events,c. the growing-phase of the La Nina events,d. the decaying-phase of the La Nina events. The start-months of the predictions are July/August(a1-d1),October/November(a2-d2) and January/February(a3-d3)) |
再将每个模式的预报误差按发展期和衰减期加以分析(图 5),从图中各个模式发展期发现,虚线明显位于实线之上,即发展期厄尔尼诺事件误差小于拉尼娜事件,说明发展期厄尔尼诺事件可预报性比拉尼娜事件强;在衰减期,虚线位于实线的下方,即模式对于拉尼娜事件误差小于厄尔尼诺事件,衰减期厄尔尼诺事件较难预报。ENSO事件在误差大小上呈现出非对称性的特点。
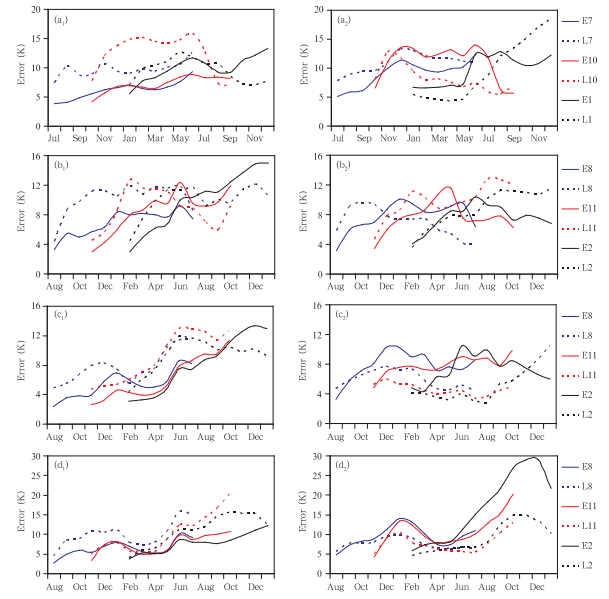 |
| 图 5 模式预报ENSO事件生长期(a1—d1)和衰减期(a2—d2)的逐月预报误差(a. FGOALS模式,b. GFDL模式,c. SNU模式,d. UH模式;实线为厄尔尼诺事件,E8指厄尔尼诺事件,8月起报,其他同;虚线为拉尼娜事件,L8指拉尼娜事件,8月起报,不同颜色代表不同起报月)Fig. 5 Prediction errors in the growing-phase(a1-d1) and the decaying-phase(a2-d2)of the ENSO events(Solid line: the El Niño events; dashed line: the La Ni a events. The different colors indicate the different start-months of the predictions) |
在目前的ENSO预报中,春季可预报障碍是一个普遍存在的现象。近年来,人们也从不同角度分析了春季预报障碍产生的机理,综合而言,目前倾向于春季预报障碍现象与季节循环、初始误差以及ENSO事件本身有紧密联系(Mu et al,2007a,2007b)。本文所用模式预测的海表温度异常无论从相关系数,或误差随季节的发展都体现出了明显的春季可预报障碍。有研究指出,春季是海-气相互作用最不稳定的季节,误差也容易在春季发展或者增长,因而导致了春季预报障碍。故此,通过比较分析在不同季节观测和模式预测的降水和风场对赤道中东太平洋海温距平的响应,探讨海-气相互作用强度的季节依赖性及其与春季预报障碍的联系。
由于受到模式资料不全的限制,图 6和7分别给出四个季节观测和两个模式(GFDL和FGOALS)预测的降水场与850 hPa纬向风场关于Nino3.4指数回归系数的空间分布。由图 6a可见,春季降水场回归系数在整个赤道太平洋地区超过2.4 mm/(d·K),暖池和冷舌地区更升至3.2 mm/(d·K)以上,而回归系数在其他3个季节普遍低于1.6 mm/(d·K)。此现象说明在春季随着海温升高,整个赤道太平洋地区的降水强度明显增加;同 时,在赤道中东太平洋850 hPa纬向风场对海表温度的回归系数也于春季达到最大,整个赤道地区几乎都被正值覆盖,在另外3个季节,赤道太平洋地区出现了西正东负的分布特点(图 7a)。以上说明,对于同样强度赤道中东太平洋海温距平,在春季大气环流的响应最为强烈。如果再结合Bjerknes(1969)提出的海-气正反馈机制,当赤道中东太平洋海表温度为正(负)异常时,可以引起沃克环流减弱(增强)并导致海表出现西(东)风距平,西(东)风应力距平可以使埃克曼上翻减弱(增强),从而海温正(负)异常进一步加强。因此,表面风场和海温距平的回归系数实际上在一定程度上代表了海-气相互作用的强度,例如在一些简化模式中风应力对海温距平的回归系数也称之为耦合系数(Battisti et al,1999)。因此由上述观测资料分析可知,在春季风应力与Nino3.4指数回归系数最大,应该是海-气相互作用最不稳定的季节,很容易导致初始的海温异常快速增长。
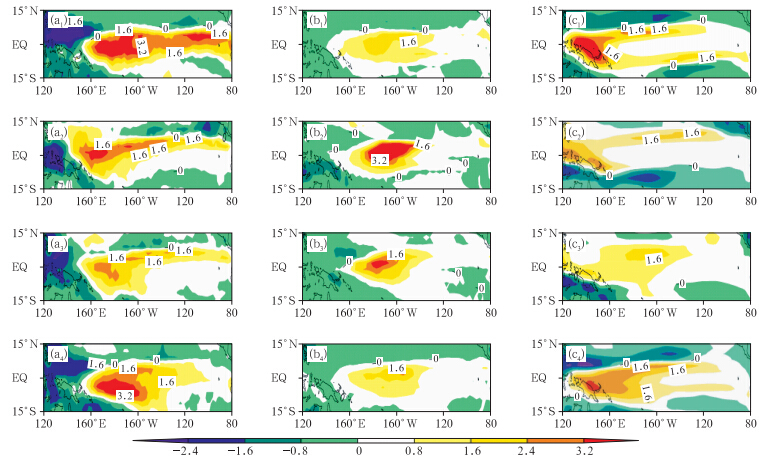 |
| 图 6 春(a1—c1)夏(a2—c2)秋(a3—c3)冬(a4—c4)四季降水场与Nino 3.4指数回归系数的分布(a. 观测,b. FGOALS模式,c. GFDL模式,单位:mm/(d·K))Fig. 6 Seasonally evolving patterns of the precipitation and the Niño 3.4 index regression analysis(a. observation,b. FGOALS,c. GFDL; a1-c1. spring(MAM),a2-c2.summer(JJA),a3-c3. autumn(SON),a4-c4. winter(DJF); unit: mm/(d·K)) |
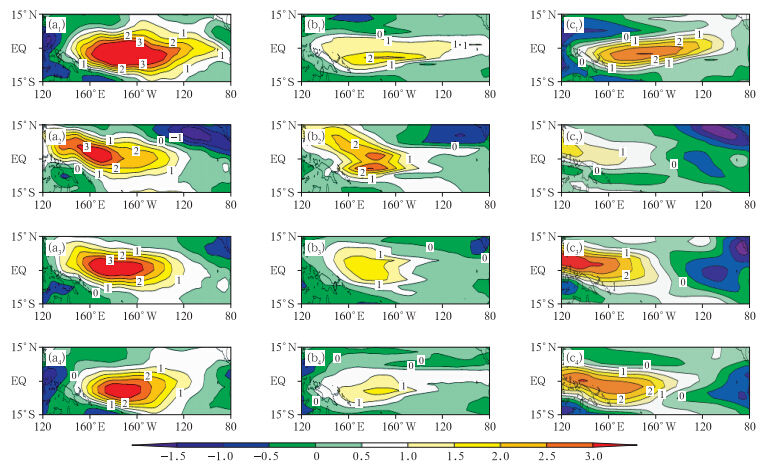 |
| 图 7 同图 6,但为850 hPa纬向风场(单位:m/(s·K))Fig. 7 As in Fig. 6 but for 850 hPa zonal wind(unit: m/(s·K)) |
FGOALS模式预测结果表明,降水场(图 6b)和纬向风场(图 7b)在赤道太平洋地区位相的分布与观测都比较一致。赤道东太平洋地区,降水回归系数均在0.8 mm/(d·K)以上,部分地区则高至3.2 mm/(d·K),而在其他季节,热带东太平洋的降水对海温的响应则明显减弱,接近0值,夏、秋2个季节的部分洋面甚至出现负值。尽管与观测相比强度整体偏弱,但模式对太平洋,尤其对赤道东太平洋降水场四季刻画都与观测较吻合。图 7b中850 hPa纬向风场的回归系数显示,春季整个太平洋都被西风距平覆盖,而到了夏季,西风异常明显回撤,Nino3区洋面上空已经被东风异常控制。秋冬两季,出现西风异常的区域更小,中东太平洋减弱的西风异常逐渐被东风异常取代。
GFDL模式预测大气环流场对海温距平的响应表明,降水场(图 6c)回归系数与观测的位相空间分布特征一致,与FGOALS模式类似,对降水场预测偏弱。赤道太平洋降水场回归系数春季明显高于其他3个季节,尤其在暖池达2.4 mm/(d·K),东太平洋春季回归系数保持在0.8—1.6 mm/(d·K),而在其他3个季节,降水场回归系数只有0—0.8 mm/(d·K),与以上分析相同,GFDL模式中降水场对海温的响应在春季最为强烈。GFDL模式850 hPa纬向风场(图 7c)的回归系数与观测位相空间分布类似,但东风距平西伸范围过大且强度过强。春季太平洋洋面,模式对纬向西风异常的刻画尤为凸显,尤其在中东太平洋更被西风距平主导,而其他3个季节日界线以东洋面,则呈现强的东风异常纬向环流型。
如前所述,图 6和7中,与观测相比,东太平洋降水场预测值徧小(FGOALS模式相对最小),而西风异常偏弱、东风异常范围偏大,强度偏强(GFDL模式最为明显)。风场同时会对海温产生正反馈作用,而暖的海温会使降水增加,Sun等(2009)在研究中更加指出,降水会随着海温的升高出现比海温更迅速地增加,且观测中降水的增加会远远超过模式预测的降水增量。
为进一步探讨模式比观测的降水偏小、东风距平偏强的原因,又对赤道东太平洋Nino3.4区的大气850 hPa纬向风场与海温距平回归进行逐月分析。如图 8所示,观测表明赤道东太平洋在1—2月西风异常开始增大,在春季西风异常增加迅速,并在4—5月达峰值,之后逐渐减弱,8月前后降至最低,秋季又有小幅增加,但异常幅度远远小于春季。这与图 7a也有很好的对应关系。比较发现,FGOALS模式对西风异常的预测整体弱于观测,尤其从2月开始直至整个春季,回归系数只有1 m/(s·K),低于观测1 m/(s·K),且峰值比观测滞后1个月左右。GFDL模式纬向风场位相与观测一致,春季西风异常发展,峰值出现于4月,之后逐渐减弱,但强度也明显低于观测。到7月之后,回归系数由正变负,说明西风异常已经被东风异常取代,几乎12个月均比观测低。图 8不仅从另一个角度展现了图 7 的特点,从观测出发更支持了本文的观点,同时,模式西风距平弱甚至变为负值,按照Bjerknes(1969)正反馈理论,模式西风距平对海温响应预测偏弱使得对海洋正反馈偏弱,不利于海温进一步变暖,负的西风异常不仅不会使海温增暖,还会驱使海温变冷,这种海-气相互作用可能是导致模式预测的四季降水偏小的原因,尤其对春季降水影响最为显著。这与严邦良等(2002)得出赤道西太平洋西风异常易发生在春季,从而引起海-气相互作用不稳定的观点一致。
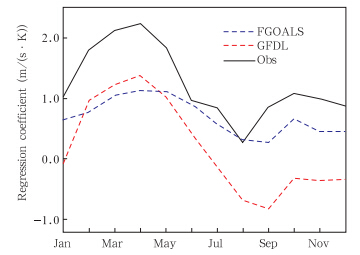 |
| 图 8 850 hPa纬向风场与Nino 3.4指数逐月回归系数的分布Fig. 8 Monthly regression coefficients of 850 hPa zonal wind and the Nino 3.4 index |
综上所述,模式对ENSO事件的预测,预报误差的发展在厄尔尼诺事件发展期和拉尼娜事件发展期都体现了比较明显的季节依赖性现象,发生春季预测障碍;而衰减期不如增长期明显,最大预报增长对于不同初始时刻,发生预报障碍的季节有所不同。此外,研究中尝试将ENSO事件的发展期和衰减期定义为峰值前后一年,发现所得结果类似。即只要春季包含在考察的时段内,春季误差增长的性质不依赖于发展期和衰减期定义,而依赖于ENSO事件本身,即ENSO事件的不同位相。
通过4个集合预报模式预测ENSO事件季节依赖性的研究发现,预报误差的发展在ENSO事件不同阶段有如下特点:厄尔尼诺事件发展期、衰减期和拉尼娜事件发展期预报误差最大增长率都出现在春季,存在比较明显的季节依赖性现象,发生春季预测障碍;而对拉尼娜事件衰减位相预报中,预报误差最大增长没有出现在固定的季节,不具有季节依赖性。而针对ENSO事件冷、暖位相生长期和衰减期春季出现不同季节依赖性特征的问题,在未来的工作中需要进行更深入地探讨。
发现ENSO事件模式预报误差和误差的发展具有非对称性,即厄尔尼诺事件的季节依赖性比拉尼娜事件显著,厄尔尼诺(拉尼娜)事件发展期出现的春季预测障碍现象比衰减期更明显。
通过回归分析,认为造成春季预报障碍可能的机制是大气环流场对海洋的响应在春季最强,从而使得海-气相互作用在春季最不稳定,导致模式在预报过程中的误差在此季节最易增大,预报技巧在春季下降最快,从而出现春季预报障碍。对两个模式的分析进一步验证了由观测得到的结论。
本文从海洋-大气相互作用的角度阐述了春季预报障碍产生的原因。同时,诸多研究认为季节循环预测的好坏对ENSO的预测有重要影响,模式对季节循环强度以及位相预测的准确性在季节分析中起着非常重要的作用,严邦良等(2002)结合观测与模式结果认为因赤道西太平洋西风异常易出现在春季,导致海-气相互作用不稳定的观点与本文一致,其深入探讨了在厄尔尼诺事件发生阶段和成熟、衰减阶段,大气环流基本态对赤道太平洋西风异常形成的作用。本文从赤道中东太平洋海温距平引起的风应力又可以反过来加强原来的海温异常即Bjerkness正反馈过程的角度,指出春季海-气相互作用最不稳定,造成模式对ENSO事件预报技巧在春季下降明显,产生春季预报障碍。Jin等(2008)发现对平均态的年循环预测偏差大的模式,对ENSO的预测偏差也相对较大。Yan等(2009)对FGOALS模式的评估中也提出,夏季中太平洋降水预测偏强的原因可能是对海表温度平均态预测的偏差造成。应该指出,本文的研究还非常初步,主要是分析了海-气相互作用不稳定性与春季预报障碍的关系,而赤道太平洋季节循环和ENSO的相互作用及其物理过程还有待进行更深入的研究。
致谢: 感谢严厉博士和Junyi Lee博士在模式数据方面提供的帮助,感谢穆穆研究员的修改建议。
| 刘新超, 段晚锁, 朱克云. 2008. Zebiak-Cane数值模式的可预报性分析. 气候与环境研究, 13(2): 135-149 |
| 严邦良, 张人禾. 2002. 热带西太平洋大气气候基本态与厄尔尼诺期间赤道附近西风异常. 海洋学报, 24(2): 39-50 |
| 张学洪, 俞永强, 刘海龙. 2003. 海洋环流模式的发展和应用Ⅰ: 全球海洋环流模式. 大气科学, 27(4): 607-617 |
| An S I, Wang B. 2001. Mechanisms of locking of the El Ni o and La Ni a mature phases to boreal winter. J Climate, 14(9): 2164-2176 |
| Barnston A G, Chelliah M, Goldenberg S B. 1997. Documentation of a highly ENSO-related SST region in the equatorial Pacific. Atmos Ocean, 35: 367-383 |
| Battisti D S, Sarachik E S, Hirst A C. 1999. A consistent model for the large scale steady surface atmospheric circulation in the tropics. J Climate 12:2956-2964 |
| Bjerknes J. 1969. Atmospheric teleconnections from the equatorial Pacific. Mon Wea Rev, 97(3): 163-172 |
| Burgers G, Stephenson D B. 1999. The “normality” of El Ni o. Geophys Res Lett, 26(8): 1027-1030 |
| Chen D K, Zebiak S E, Busalacchi A J, et al. 1995. An improved procedure for El Ni o forecasting: implications for predictability. Science, 269(5231): 1699-1702 |
| Chen D K, Cane M A, Kaplan A, et al. 2004. Predictability of El Ni o over the past 148 years. Nature, 428(6984): 733-736 |
| Delworth T L, Broccoli A J, Rosati A, et al. 2006. GFDL’s CM2 global coupled climate models-Part Ⅰ: Formulation and simulation characteristics. J Climate, 19(5): 643-674 |
| Flügel M, Chang P. 1998. Does the predictability of ENSO depend on the seasonal cycle? J Atmos Sci, 55: 3230-3243 |
| Fu X H, Wang B. 2004. The boreal-summer intraseasonal oscillations simulated in a hybrid coupled atmosphere-ocean model. Mon Wea Rev, 132(11): 2628-2649 |
| Gnanadesikan A, Dixon K W, Griffies S M, et al. 2006. GFDL’s CM2 global coupled climate models, Part II: The baseline ocean simulation. J Climate, 19(5), doi:10.1175/JCLI3630.1 |
| Griffies S M, Gnanadesikan A, Dixon K W, et al. 2005. Formulation of an ocean model for global climate simulations. Ocean Sci, 1: 45-79 |
| Jin E K, Kinter J L III, Wang B, et al. 2008. Current status of ENSO prediction skill in coupled ocean-atmosphere models. Climate Dyn, 31(6): 647-666 |
| Jin F -F, An S -I, Timmermann A, et al. 2003. Strong El Ni o events and nonlinear dynamical heating. Geophys Res Lett, 30(3): 1120, doi:10.1029/2002GL016356 |
| Kalnay E, et al. 1996. The NCEP/NCAR 40-Year Reanalysis Project. Bull Amer Meteor Soc, 77: 437-471 |
| Kang I S, Jin K, Lau K M, et al. 2002. Intercomparison of atmospheric GCM simulated anomalies associated with the 1997-1998 El Ni o. J Climate, 15(19): 2791-2805 |
| Kessler W S, 2002. Is ENSO a cycle or a series of events? Geophys Res Lett, 29(23): 2125-2159 |
| Kim H M, Kang I S, Wang B, et al. 2008. Interannual variations of the boreal summer intraseasonal variability predicted by ten atmosphere-ocean coupled models. Climate Dyn, 30(5): 485-496 |
| Kug J-S, Kang I-S, Lee J Y, et al. 2004. A statistical approach to Indian Ocean sea surface temperature prediction using a dynamical ENSO prediction. Geophys Res Lett 31:L09212 |
| Latif M, Barnett T P, Cane M A, et al. 1994. A review of ENSO prediction studies. Climate Dyn, 9(4-5): 167-179 |
| Liu H L, Zhang X H, Li W, et al. 2004. An eddy-permitting oceanic general circulation model and its preliminary evaluation. Adv Atmos Sci, 21(5): 675-690 |
| McPhaden M J. 2003. Tropical Pacific Ocean heat content variations and ENSO persistence barriers. Geophys Res Lett, 30(9): 1480 |
| Mu M, Duan W S, Wang B. 2007a. Season-dependent dynamics of nonlinear optimal error growth and El Ni o-Southern Oscillation predictability in a theoretical model. J Geophys Res, 112: D10113 |
| Mu M, Xu H, Duan W S. 2007b. A kind of initial errors related to “spring predictability barrier” for El Ni o events in Zebiak-Cane model. Geophys Res Lett, 34: L03709 |
| Samelson R M, Tziperman E. 2001. Instability of the chaotic ENSO: The growth-phase predictability barrier. J Atmos Sci, 58(23): 3613-3625 |
| Sun D Z, Yu Y Q, Zhang T. 2009. Tropical water vapor and cloud feedbacks in climate models: A further assessment using coupled simulations. J Climate, 22(5): 1287-1304 |
| Torrence C, Webster P, 1998. The annual cycle of persistence in the El Ni o-Southern Oscillation. Quart J Roy Meteor Soc,124:1985-2004 |
| Wang B, Fang Z. 1996. Chaotic oscillations of tropical climate: A dynamic system theory for ENSO. J Atmos Sci, 53(19): 2786-2802 |
| Wang B, Lee J Y, Shukla J, et al. 2009. Advance and prospectus of seasonal prediction: assessment of the APCC/CliPAS 14-Model Ensemble Retrospective Seasonal Prediction (1980-2004). Climate Dyn, 33(1): 93-117 |
| Wang C, Picaut J. 2004. Understanding ENSO physics: A review. Earth Climate: The ocean-atmosphere interaction. Geophys Monogr Amer Geophys Union, 147: 21- 48 |
| Webster P J, Yang S. 1992. Monsoon and ENSO: Selectively interactive systems. Quart J Roy Meteor Soc, 118(507): 877-926 |
| Webster P J. 1995. The annual cycle and the predictability of the tropical coupled ocean-atmosphere system. Meteor Atmos Phys, 56(1-2): 33-55 |
| Xie P, Arkin P A. 1997. Global precipitation: A 17-year monthly analysis based on gauge observations, satellite estimates, and numerical model outputs. Bull Amer Meteor Soc, 78: 2539-2558 |
| Xue Y, Cane M A, Zebiak S E. 1997. Predictability of a coupled model of ENSO using singular vector analysis. Part I: Optimal growth in seasonal background and ENSO cycles. Mon Wea Rev, 125(9): 2043-2056 |
| Yan L, Yu Y Q, Wang B, et al. 2009. ENSO hindcast experiments using a coupled GCM. Atmos Ocean Sci Lett, 2(1): 7-13 |
| Yu Y S, Duan W S, Xu H, et al. 2009. Dynamics of nonlinear error growth and season-dependent predictability of El Ni o events in the Zebiak-Cane model. Quart J Roy Meteor Soc, 135(645): 2146-2160 |
 2012, Vol. 70
2012, Vol. 70

