中国气象学会主办。
文章信息
- 赵 娟, 王 斌, 刘娟娟. 2012.
- ZHAO Juan, WANG Bin, LIU Juanjuan. 2012.
- 预分析初始扰动样本对降维投影四维变分同化性能的影响
- Influence of pre-analyzing the initial perturbation sample on DRP-4DVar assimilation performance
- 气象学报, 70(3): 549-561
- Acta Meteorologica Sinica, 70(3): 549-561.
- http://dx.doi.org/10.11676/qxxb2012.045
-
文章历史
- 收稿日期:2010-09-28
- 改回日期:2011-04-20
2. 中国科学院大气物理研究所大气科学和地球流体力学数值模拟国家重点实验室(LASG),北京,100029
2. State Key Laboratory of Numerical Modeling for Atmospheric Sciences and Geophysical Fluid Dynamics (LASG), Institute of Atmospheric Physics, Chinese Academy of Sciences, Beijing 100029, China
无论对于变分同化方法,还是集合卡尔曼滤波,背景误差协方差对同化结果都有着举足轻重的影响。作为确定权重的重要因素,背景误差协方差决定了观测对背景场修正的尺度和结构,即控制了观测信息在模式空间内的传播方式,以及通过平衡约束关系使得观测信息在不同模式变量之间传播。那么如何准确估计背景误差协方差成为影响同化结果的关键因素。由于实际大气模式的自由度很大,背景误差协方差矩阵(简称为 B 矩阵)的维数通常达到107×107,所以为了适应业务数值天气预报的需求,一些同化系统将背景误差协方差简化为均匀、各向同性的协方差模型,例如高斯相关模型、二阶自回归相关模型(Thiebaux,1976)和贝塞尔函数相关模型(Hollingsworth et al,1986)等。为了统计出更合理的背景误差协方差,Dee(1995)采用极大似然法对误差协方差模型的参数不断更新统计,Xu等(2001a,2001b,2002)运用多层最小二乘方法来对协方差模型的参数进行更准确的估计,Derber等(2003)利用递归滤波方法能够得到各向异性和非均匀的背景误差协方差。基于集合思想的同化方法,如集合卡尔曼滤波利用集合预报结果统计出随流型演变的背景误差协方差(Evensen,1994)。由Wang等(2010)提出的降维投影四维变分同化(DRP-4DVar)方法也是利用集合样本来统计背景误差协方差,避免了传统四维变分同化中同化窗始端的背景误差协方差总是固定不变的缺陷,使得背景误差协方差不仅在同化窗内隐式发展,而且,在同化窗之间也保持着流依赖的特征。但是,集合成员的数量远小于复杂大气模式的自由度,难以包含真实大气中所有可能的状态,即出现样本误差,从而导致对背景误差协方差的不准确估计以及出现虚假的远距离相关,产生分析误差。
想要改进背景误差协方差,可以先从如何有效地减少样本误差的角度来着手。一方面要求样本与实际大气中可能的误差分布一致,尽可能将观测包含进来,另一方面要求样本的离散度足够大。尽管降维投影四维变分同化方法中已经采用局地化技术(Hamill et al,2001; Ott et al,2004)和膨胀因子(Anderson,2007)来减小样本误差的影响,但分析前对初始扰动样本的预处理过程以及样本的生成方法仍然很重要。通过分析对比不同样本生成方法对降维投影四维变分同化性能的影响(Zhao et al,2010),发现基于三维变分同化系统的 B 矩阵生成的初始扰动样本比基于历史预报产生的样本更具有优势,使得降维投影四维变分同化能够取得更好的同化效果。本文尝试探索如何对生成的初始扰动样本做预处理,在样本中加入实际观测的信息,从而有效改进背景误差协方差的流依赖特性,以期进一步提高降维投影四维变分同化方法的性能。 2 预分析初始扰动样本
在传统四维变分同化中,通过在同化窗内进行多次非线性迭代,将观测信息引入背景场,来不断修正背景场,从而得到最优的分析场。而且,在同化窗内利用切线性模式和伴随模式来隐式发展背景误差协方差,使得协方差具有随流型演变的特征,从而能够将观测信息在模式空间内合理地传播,并保持不同分析变量之间的平衡约束关系;该做法的缺陷是积分切线性和伴随模式需要耗费大量机时,难以满足业务预报的时效性需求。而降维投影四维变分同化是将分析变量投影到由一组基向量构建的子空间中,在维数远小于模式空间的样本空间中直接求解代价函数的极小值,取代了传统四维变分同化中的非线性迭代过程,节省了大量机时(Wang et al,2010)。重要的一点是,降维投影四维变分同化利用由历史预报结果得到的集合样本来统计背景误差协方差,由于总是使用提前一天至两天的短期数值预报结果来准备初始扰动样本,使得统计的误差协方差具有流依赖的特征,并利用样本之间的时空对应关系巧妙替代了传统四维变分同化在同化窗内隐式发展误差协方差的方式,公式推导过程见文献(Wang et al,2010)。严格来说,流依赖是要求与实际大气的流型演变一致,而就数值预报模式的发展现状而言,历史预报结果中仍然包含模式误差,使得由历史样本统计得到的背景误差协方差与实际的天气形势不是完全一致的。因此,想要使背景误差协方差真正地随天气形势变化,还需要在集合样本中加入实际的观测信息。
集合卡尔曼滤波通过在每步同化循环中分析集合成员来将历史观测信息引入样本中,不断改善由样本统计得到的背景误差协方差的流依赖特性。借鉴这个思路,可以在对背景场做分析之前,利用降维投影四维变分同化系统本身对每个样本预先进行分析,使统计出的背景误差协方差包含观测信息。但是,与集合卡尔曼滤波的处理方式有根本的区别,以循环同化过程为例,集合卡尔曼滤波是通过在每步循环同化中分析样本,用历史观测信息的累积来更新背景误差协方差,本文则是利用一次循环同化中同化窗内的观测信息来改善背景误差协方差的结构和特征,从而改进本次循环的分析结果,而下一次循环时再从新的历史预报集合中取样。由于仅使用一个同化窗内的观测进行重复的迭代,使得集合离散度的减小非常有限;在预分析样本时,对观测数据加上随机扰动,相应的观测误差也增大,从而能够有效避免循环同化过程中集合卡尔曼滤波常出现的滤波发散现象。基本的操作流程如图 1所示。图中的t0是每次循环的同化窗始端时刻,x1(t0)……xm(t0)(m是样本的数量)是每次循环同化时重新收集的提前一天至两天的历史预报集合,取样方法见文献(Zhao et al,2010);
利用降维投影四维变分同化系统本身对其做预先分析后得到新的扰动样本xa1(t0)……xma(t0),用于统计背景误差协方差。
 |
| 图 1 预分析样本的操作流程Fig. 1 Flowchart of pre-analyzing the perturbation samples |
单点观测试验的分析增量轨迹表征了四维变分同化系统中背景误差协方差在同化窗内的演变(Thépaut et al,1991):
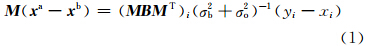
试验采用中尺度天气预报模式WRF-ARW(Skamarock et al,2008),模式水平分辨率为30 km,模拟区域的水平格点数为100×100,垂直方向共有31层,模式层顶为50 hPa。选用的次网格物理过程包括:Ferrier(new Eta)微物理方案,Betts-Miller-Janjic积云对流参数化方案(Janjić,1994,2000;Betts,1986;Betts et al,1986),YSU边界层方案(Hong et al,2006)和RRTM辐射方案(Mlawer et al,1997)。
6 h同化窗设定为2007年7月8日00时至06时(世界时,下同)。参照试验(CTRL)是以2007年
7月7日18时NCEP的FNL资料作为初始场,向前积分30 h的预报结果。第1组同化试验(EXP1)是利用降维投影四维变分同化系统直接同化单个观测;第二组同化试验(EXP2)则是利用降维投影四维变分同化系统本身对同化窗始端的集合样本进行预先分析,再同化单个观测,其中,用于分析样本的观测是在单点观测数据上添加了随机扰动的。为了提供所谓的“真值”和相应的“观测”用于对比两组同化试验,以ECMWF再分析资料(ERA-Interim)为初值,从2007年7月7日00时至9日00时的48 h连续积分结果作为“真实场”(记为TRUTH)。从8日06时的“真实场”中选定34.7°N,113.0°E,η=0.525处的温度值作为同化窗末端的单点观测。 3.2 B 矩阵空间分布特征对比分析
在EXP1试验中,观测代价函数下降了65%,而EXP2试验中的观测代价函数有更显著的下降,达到了75%,表明预分析样本后得到的分析场中包含了更多的观测信息。图 2—4中温度增量的时间演变显示出,降维投影四维变分同化系统不仅能够很好地拟合观测,而且,其 B 矩阵在同化窗内是不断随流型演变的。在同化窗始端,分析增量值较小,呈各向异性分布,且中心位于观测点的上游(图 2);到同化窗中间和末端,增量轨迹逐渐趋向于背景场的分布,沿着等温线延伸(图 3、图 4)。
 |
| 图 2 同化窗始端(2007年7月8日00时)模式层η=0.525上的温度增量(a.EXP1-CTRL,b.EXP2-CTRL,(c.TRUTH-CTRL;阴影为温度增量,黑色等值线为对应时刻的背景场温度,“十”字叉为观测点的位置)Fig. 2 Temperature increments(shaded)at the model layer η=0.525 at the beginning(00:00 UTC 08 July 2007)of assimilation window(a. EXP1-CTRL,b. EXP 2-CTRL,c. TRUTH-CTRL; The black contours are for the temperature(℃)in the CTRL run; The cross sign indicates the observation location) |
 |
| 图 3 同图 2,但为在同化窗中间时刻(2007年7月8日03时)的温度增量和背景温度场Fig. 3 As in Fig. 2 but for the temperature increments and the background field at the middle of assimilation window(03:00 UTC 08 July 2007) |
 |
| 图 4 同图 2,但为在同化窗末端(2007年7月8日06时)的温度增量和背景温度场Fig. 4 As in Fig. 2 but for the temperature increments and the background field at the end of assimilation window(06:00 UTC 08 July 2007) |
由于TRUTH试验能够提供“真值”,因此,将CTRL试验与其对比即可得到“真实”的背景误差分布。为了方便对比两组同化试验中的 B 矩阵,图 2—4中给出了TRUTH与CTRL试验的温度场差值,即“真实”的背景误差的相反值。在同化窗始端,两组同化试验的 B 矩阵结构与“真实”的背景场误差很相似,呈西南—东北向倾斜式分布,相对于 EXP1试验,对样本预分析的EXP2试验中 B 矩阵只是略好(图 2)。在同化窗中间和末端,EXP1试验的度增量明显偏小,而经过样本预分析后,EXP2试验对增量值及其分布形势有较为显著的改进(图 3、图 4),说明利用降维投影四维变分同化系统本身对每个样本进行预先分析,能够使统计出的背景误差协方差与“真实”的背景误差更加接近,改进了 B 矩阵的流依赖特性。 4 观测系统模拟试验
观测系统模拟试验所使用的数值模式及各项模式参数与单点试验一致,CTRL试验和模拟的“真实场”也是相同的。将同化窗内TRUTH中基本模式变量场(温度、水汽混合比、纬向风和经向风)投影到观测空间得到同化窗口内的观测,观测场的位置信息来源于对应时刻的实际探空和地面观测站点。为了节省预处理样本过程所耗费的机时,本文只利用一组78 h历史预报结果(从2007年7月6日00时起预报至9日06时),来生成72个初始扰动样本。利用降维投影四维变分同化系统对7月8日00时的背景场和6 h同化窗内的观测资料进行同化后得到分析场,作为新的模式初值向前预报,即为同化试验(ASSM)。为了将观测信息引入背景误差协方差改进其流依赖特性,利用降维投影四维变分同化系统本身对同化窗始端的集合样本进行预先分析,进行3组敏感性试验(ASSM1、ASSM2和ASSM3),考察样本的预分析过程对同化结果的影响。几组试验的基本设置如表 1所示。在ASSM1试验中,仅对前36个样本进行预先分析,而后36个样本仍使用原先的历史预报样本;ASSM2试验的设计与ASSM1恰好相反;而ASSM3试验中对所有72个样本都进行了预分析。
|
试验名称 | 是否同化观测资料 | 使用的样本个数 | 预分析样本个数 |
| CTRL | 否 | 0 | 0 |
| ASSM | 是 | 72 | 0 |
| ASSM1 | 是 | 72 | 36(1—36) |
| ASSM2 | 是 | 72 | 36(37—72) |
| ASSM3 | 是 | 72 | 72(1—72) |
为了考察预分析初始扰动样本对同化结果的影响,以分析时刻(2007年7月8日00时)的“真实 场”为验证标准,将同化试验ASSM、ASSM1、ASSM2和ASSM3的分析场分别减去对应垂直层上的TRUTH值。图 5给出了η=0.163层上4组同化试验的分析场与TRUTH的纬向风(U风)偏差。从中可以看到,ASSM1试验的纬向风偏差几乎在整个模拟区域内都小于ASSM试验的偏差,尤其是在偏差较大的正值区域(35°—43°N,110°—125°E)和负值区域(25°—34°N,108°—120°E)内,ASSM1试验对ASSM试验的分析有明显改进。对比3组对样本进行了预分析的试验结果发现(图 5b—5d),整体而言,对所有初始扰动样本进行了预分析的ASSM3试验的分析场是最优的,其次是ASSM2试验,而ASSM1试验相对较差。此外,η=0.922层上的湿度场分布也出现了类似的趋势(图 6),对初始样本做过预分析的3组同化试验(ASSM1、ASSM2和ASSM3)中分析场的水汽混合比偏差明显小于未对样本做过预处理的ASSM试验,其中,对所有样本做了预分析的ASSM3试验的分析误差最小,其与TRUTH最为接近。这说明经过预分析的初始扰动样本能够估计出更好的背景误差协方差,使观测信息在模式空间内更加合理地传播,从而提高分析场的精度。
 |
| 图 5 模式层η=0.163上的纬向风偏差水平分布(a. ASSM-TRUTH,b. ASSM1-TRUTH,c. ASSM2-TRUTH,d. ASSM3-TRUTH)Fig. 5 Zonal wind differences(m/s)on the model layer η=0.163 between the assimilation runs and the truth run(a. ASSM-TRUTH,b. ASSM1-TRUTH,c. ASSM2-TRUTH,d. ASSM3-TRUTH) |
 |
| 图 6 模式层η=0.922上的水汽混合比偏差水平分布(a. ASSM-TRUTH,b. ASSM1-TRUTH,c. ASSM2-TRUTH,d. ASSM3-TRUTH)Fig. 6 As in Fig. 5 but for the water vapor mixing ratio differences(g/kg)on the model layer η=0.922 |
分别计算了背景场和分析场中4个基本模式变量(温度、水汽混合比、纬向风和经向风)在各模式垂直层上的均方根误差。温度场(图 7a)在对流层低层和高层分别出现误差的极大值,而中层的误差值相差不大。相应地,分析后改进最显著的地方就是在分析前(即背景场)误差值最大的垂直层附近。在大部分垂直层上,ASSM试验的温度场误差小于背景场的误差;而对初始扰动样本做过预分析的3组同化试验(ASSM1、ASSM2、ASSM3),在每层上均对温度场有明显改进,且显著优于ASSM试验的分析。背景场的湿度误差在水汽分布较为集中的对流层低层出现极大值(图 7b),而ASSM试验正是在其误差极大值的垂直层附近有显著改进;对于纬向风和经向风(图 7c、7d),分析误差的垂直分布趋势也是类似的。总体而言,对于这4个模式变量,除了在少数几个垂直层上以外,同化试验ASSM的分析误 差几乎都明显小于背景场误差。相对于未对样本做过预分析的ASSM试验,使用了经过预分析的样本的3组同化试验(ASSM1、ASSM2、ASSM3)均对ASSM试验有进一步的改进,且改进的幅度很大,甚至在很多垂直层上将背景场误差减小了一半以上。例如,ASSM3试验在第6层(η=0.922)上将湿度场误差减小了67.8%,而在第22层上(η=0.163)将纬向风的误差减小了59.2%。比较采用预分析样本的3组同化试验分析结果发现,对72个样本都进行预先分析的ASSM3试验的分析误差在所有模式垂直层上都是最小的,其次是对后一半样本做了预分析的ASSM2试验,对前一半样本做预分析的ASSM1试验的结果相对而言较差。
 |
| 图 7 背景场(黑色虚线)与不同试验的分析场均方根误差的垂直廓线(a. 温度,b. 水汽混合比,c. U风,d. V风)Fig. 7 Vertical profiles of root mean square errors(RMSEs)for(a)temperature(K),(b)water vapor mixing ratio(g/kg),(c)U-wind(m/s),and (d)V-wind(m/s)(The results from the background field,ASSM,ASSM1,ASSM2 and ASSM3 analyses are denoted by black-dashed-line,black-solid-line,green-solid-line,blue-solid-line and red-solid-line,respectively) |
同化观测资料不仅为了改进模式的初始场,更重要的是提高数值预报水平,所以,将4组同化试验的分析场作为新的模式初值分别向前积分对比它们的预报效果。图 8给出了12 h预报,即在2007年7月8日12时预报的各模式变量均方根误差的垂直廓线。尽管ASSM试验的改进幅度不及分析时刻明显,但其预报误差在大部分垂直层上仍小于参照试验的误差。4组同化试验的预报结果之间,除了在温度场上的差别较小外,ASSM1、ASSM2和ASSM3试验的预报仍然明显好于ASSM试验,而它们三者之间的差别不明显。仔细辨别后发现,ASSM3试验的预报在整体上是最优的。
 |
| 图 8 同图 7,但为2007年7月8日12时的预报结果Fig. 8 As in Fig. 7 but for the forecasts at 12:00 UTC 8 July 2007 |
为了综合考察集合样本的预分析对同化结果的整体影响,图 9比较了CTRL试验和4组同化试验的分析和预报结果中,基本模式变量在模拟区域内的均方根误差随时间的演变情况。ASSM试验的正效果从分析时刻(图 9中00时)一直持续至预报24 h,甚至在24 h之后也仍然有明显改进(图略)。相对于ASSM试验,对初始扰动样本做预分析能够对同化结果有进一步的改进,且其优势一直贯穿于整个24 h预报中。分析ASSM1、ASSM2和ASSM3试验的误差发展曲线可以看出,在分析时刻,ASSM3试验的4个模式变量误差都是最小的,ASSM2的分析误差稍大,ASSM1的最大,这与前面模式变量的均方根误差垂直分布情形吻合(图 7);虽然预报误差均随时间逐渐增大,但在预报12 h 之前基本上都是ASSM3的预报是最优的。从统计的每3 h累计降水的均方根误差演变(图 10)看到,从3—21 h每3 h累积降水量预报中,ASSM试验的预报误差均小于CTRL试验的误差;ASSM2和ASSM3试验的降水预报相对于ASSM表现出显著优势。在大部分模拟时段内,ASSM3的降水预报是最优的。整体而言,对初始扰动样本进行预先分析,不仅能够进一步改进模式变量场的分析和预报,还能提高对降水的模拟能力,尤其是对所有样本都进行预分析能得到最优的分析和预报。
 |
| 图 9 不同试验的分析场和预报场均方根误差随时间的演变(a. 温度,b. 水汽混合比,c. U风,d. V风)Fig. 9 Root mean square errors(RMSEs)with respect to time for(a)temperature(K),(b)water vapor mixing ratio(g/kg),(c)U-wind(m/s),and (d)V-wind(m/s)(The analysis and forecast results from CTRL,ASSM,ASSM1,ASSM2 and ASSM3) |
 |
| 图 10 同图 9,但为降水的均方根误差的时间演变Fig. 10 As in Fig. 9 but for precipitation |
图 11对比了各组试验所模拟的2007年7月8日00时至9日00时24 h累积降水分布情况。TRUTH中降水带呈准东西向分布,两个强降水中心分别位于(33°N,113°E)和(34°N,118°E)附近。然而,CTRL试验漏报了112°E以西的强降水。经过分析后,ASSM试验对西边的降水有所改进,但是,模拟的雨带形状和强降水中心的位置仍与TRUTH有较大差距;而在ASSM3试验中,雨带的形状与TRUTH更加接近,基本模拟出了两个强降水中心,只是强降水中心的位置稍有偏移。
 |
| 图 11 各组试验模拟的24 h累计降水空间分布(a. TRUTH,b. CTRL,c. ASSM,d. ASSM3)Fig. 11 Distribution of 24 h accumulated precipitation from(a)TRUTH,(b)CTRL,(c)ASSM,and (d)ASSM3 |
综合以上试验结果发现,对样本进行预先分析能够在原来分析的基础上,进一步改进同化结果,而且不仅提高了基本模式变量的预报精度,还有效地改善了对强降水的模拟能力。这主要是由于通过对样本做预先分析,将观测信息引入了背景误差协方差,使得误差协方差不仅随着数值模式的预报而不断演变更新,而且具备了实际大气的误差发展特征,实现了背景误差协方差在真正意义上的流依赖,从而进一步提高了同化系统的性能。 5 结论与讨论
为了改进降维投影四维变分同化系统中的背景误差协方差,在对背景场做分析之前,利用降维投影四维变分同化系统本身对每个初始扰动样本进行预先分析,使得统计出的背景误差协方差包含观测信息,即背景误差协方差不仅随着数值模式的预报而演变,而且具有了实际大气的误差发展特征,实现了背景误差协方差在真正意义上的流依赖。但是,不同于集合卡尔曼滤波中用历史观测信息的累积来更新误差协方差,本文是利用同化窗内的观测信息来改善本次同化过程中使用的背景误差协方差的结构和特征,而下一次同化时用于统计协方差的样本仍是由提前一天至两天的历史预报得到,因此,对历史扰动样本进行预分析后集合的离散度不会明显减小,能够避免集合卡尔曼滤波在循环同化中常出现的滤波发散现象。尽管对样本的预分析过程增加了耗费的机时,但是,由于降维投影四维变分同化系统本身的经济省时特性,且对每个样本的分析可以通过实现计算机并行来减小计算量,因此,整个同化过程的计算代价仍然可以满足业务数值预报的需求。
通过单点观测试验发现,预分析样本能够改进同化窗内背景误差协方差的空间结构和流依赖特性。观测系统模拟试验结果表明,相对于未对样本做过预分析的同化试验,使用了经过预分析样本的3组同化试验均能够得到更好的分析场。其中,对所有初始扰动样本都进行了预分析的同化试验的分析误差在所有模式垂直层上都是最小的,而且,它的变量预报场在整体上也是最优的。除了进一步改进模式变量场的分析和预报外,对样本作预分析还有效地改善了对强降水的模拟能力。
本文仅利用理想试验初步地探索了预分析样本对降维投影四维变分同化系统性能的影响,
虽然取得了令人鼓舞的结果,但有关观测信息是如何一步一步地通过预分析过程进入到背景误差协方差中,再如何通过新的背景误差协方差来改进同化系统的分析结果,这些内在的机理还需要进一步的深入分析。此外,用来生成“真实场”的模式和同化的模式是相同的,因此试验中没有考虑模式误差,预报误差的唯一来源即为初始场的误差。而在实际观测的情况下,模式误差是不可忽略的。因此,预分析样本的新思路还需要在实际观测的情况下做进一步的试验和研究。
| Anderson J L. 2007. An adaptive covariance inflation error correction algorithm for ensemble filters. Tellus A, 59A(2): 210-224 |
| Betts A K. 1986. A new convective adjustment scheme. Part I: Observational and theoretical basis. Quart J Roy Meteor Soc, 112(473): 677-691 |
| Betts A K, Miller M J. 1986. A new convective adjustment scheme. Part II: Single column tests using GATE wave, BOMEX, ATEX and arctic air-mass data sets. Quart J Roy Meteor Soc, 112(473): 693-709 |
| Dee D P. 1995. On-line estimation of error covariance parameters for atmospheric data assimilation. Mon Wea Rev, 123(4): 1128-1145 |
| Derber J C, Purser R J, Wu W S, et al. 2003: Flow-dependent Jb in a global grid-point 3D-Var. Proc. ECMWF annual seminar on recent developments in data assimilation for atmosphere and ocean. Reading, UK, 2003(8-12) Sept |
| Evensen G. 1994. Sequential data assimilation with a nonlinear quasi-geostrophic model using Monte Carlo methods to forecast error statistics. J Geophys Res, 99(C5): 10143-10162 |
| Hamill T M, Whitaker J S, Snyder C. 2001. Distance-dependent filtering of background error covariance estimates in an ensemble Kalman filter. Mon Wea Rev, 129(11): 2776-2790 |
| Hollingsworth A, Lnnberg P. 1986. The statistical structure of short-range forecast errors as determined from radiosonde data. Part I: The wind field. Tellus A, 38A(2): 111-136 |
| Hong S Y, Lim J O J. 2006. The WRF single-moment 6-class microphysics scheme (WSM6). J Korean Meteor Soc, 42(2): 129-151 |
| Janjić Z I. 1994. The step-mountain eta coordinate model: further developments of the convection, viscous sublayer, and turbulence closure schemes. Mon Wea Rev, 122(5): 927-945 |
| Janjić Z I. 2000. Comments on "Development and Evaluation of a Convection Scheme for Use in Climate Models". J Atmos Sci, 57(21): 3686 |
| Mlawer E J, Taubman S J, Brown P D, et al. 1997. Radiative transfer for inhomogeneous atmospheres: RRTM, a validated correlated-k model for the longwave. J Geophys Res, 102(D14): 16663-16682 |
| Ott E, Hunt B R, Szunyogh I, et al. 2004. A local ensemble Kalman filter for atmospheric data assimilation. Tellus A, 56A(5): 415-428 |
| Skamarock W C, Klemp J B, Dudhia J, et al. 2008. A description of the Advanced Research WRF version 3. NCAR Tech. Note NCAR/TN-475+STR, 113 |
| Thépaut J N, Courtier P. 1991. Four-dimensional variational data assimilation using the adjoint of a multilevel primitive-equation model. Quart J Roy Meteor Soc, 117(502): 1225-1254 |
| Thiebaux H J. 1976. Anisotropic correlation functions for objective analysis. Mon Wea Rev, 104(8): 994-1002 |
| Wang B, Liu J J, Wang S D, et al. 2010. An economical approach to four-dimensional variational data assimilation. Adv Atmos Sci, 27(4): 715-727, doi: 10.1007/s00376-009-9122-3 |
| Xu Q, Wei L, Tuyi A V, et al. 2001a. Estimation of three-dimensional error covariances. Part Ⅰ: Analysis of height innovation vectors. Mon Wea Rev, 129(8): 2126-2135 |
| Xu Q, Wei L. 2001b. Estimation of three-dimensional error covariances. Part Ⅱ: Analysis of wind innovation vectors. Mon Wea Rev, 129(12): 2939-2954 |
| Xu Q, Wei L. 2002. Estimation of three-dimensional error Covariances. Part Ⅲ: Height-wind forecast error correlation and related geostrophy. Mon Wea Rev, 130(4): 1052-1062 |
| Zhao Juan, Wang Bin. 2010. Sensitivity of the DRP-4DVar performance to perturbation samples obtained by two different methods. Acta Meteor Sinica, 24(5): 527-538 |
 2012, Vol. 70
2012, Vol. 70

