中国气象学会主办。
文章信息
- 张培昌, 王振会, 胡方超. 2012.
- ZHANG Peichang, WANG Zhenhui, HU Fangchao. 2012.
- 双/多基地天气雷达探测小椭球粒子群的雷达气象方程
- Radar meteorological equations for bistatic/multistatic weather radar systems detecting small spheroid raindrops
- 气象学报, 70(4): 867-874
- Acta Meteorologica Sinica, 70(4): 867-874.
- http://dx.doi.org/10.11676/qxxb2012.072
-
文章历史
- 收稿日期:2011-02-13
- 改回日期:2011-05-05
2. 南京信息工程大学大气物理学院, 南京, 210044
2. School of Atmospheric Physics, Nanjing University of Information Science & Technology, Nanjing 210044, China
单部多普勒天气雷达能够探测数百千米范围内降水云的回波强度、平均径向速度与速度谱宽,并可形成多种气象产品供监测、预警灾害性天气使用,但在反演风场时必须作一定假设,这就使反演结果的适用性受到限制。采用双/多基地天气雷达探测时,既比采用多部多普勒天气雷达经济得多,又能实现同时探测同一目标进行风场反演而不需作假设。因此,一些学者先后开展了这方面的探测研究。Wurman等(1993,2001)、Satoh等(2003)构建了第1部双/多基地天气雷达系统网络,外场试验表明,它具有探测复杂天气和大气流场的潜力。Aydin等(1998)研究了雨滴和冰雹对S波段的双/多基地双偏振散射特征。Protat等(1999)建立的双基地雷达系统已于1995年底正式运行,根据三维的双基地多普勒天气雷达资料,采用变分法反演风场供机场使用,并开展对中小尺度天气系统的研究。日本也做了类似的工作。近几年来,中国安徽四创电子股份有限公司及中国信息产业部南京第14研究所分别研制出了C波段和S波段的双/多基地天气雷达系统,准备进行外场试验。
双/多基地天气雷达系统是由一个主站(包括具有发射与接收的完整雷达系统)和一个或多个设置在一定距离外的子站(仅有接收系统)组成。主站发射的雷达波束遇到降水目标时,其后向散射波被主站接收,侧向散射波同时被子站接收。当要从子站估算回波功率理论值或由子站实测回波功率反演回波强度即雷达反射率因子时,必须有适用于双/多基地天气雷达接收子站的雷达气象方程。莫月琴等(2005)推导出球形降水粒子群的双基地雷达气象方程,并分析了其探测能力。对于像暴雨中的大雨滴以及冰粒、雹粒等降水粒子,一般均为非球形状,其散射特性与球形粒子有差异,通常可以用椭球形粒子去逼近得到散射特性解析解,也可以针对具体形状采用离散偶极子法(即DDA)(Draine et al,1994;Collinge et al,2004)计算得到散射特性数值解。小旋转椭球逼近得到的解析解可以作实时处理、便于业务应用,而离散偶极子法计算量大,如何将其应用于建立雷达气象方程及实现业务化使用尚需进一步研究(郭丽君等,2012)。目前,中国在沿海及主要防汛区正式布网的多普勒天气雷达,以S波段为主。若再配备多个接收子站构建成多基地雷达系统,则对上述非球形降水粒子一般可以作为小椭球粒子处理,但在建立双基地接收子站的雷达气象方程时,还要考虑有效照射体内整个粒子群的情况。
基于上述分析,推导出了小旋转椭球散射的方向函数和侧向散射截面的表达式。然后,分别考虑发射水平偏振波与垂直偏振波这两种情况,当小椭球粒子群旋转轴作一致铅直取向和在空间作均匀随机取向时,分别导出适用于双/多基地天气雷达接收子站的一组雷达气象方程。有了这组方程,不仅可以反演出非球形粒子群的回波强度,还能对双基地双线偏振多普勒天气雷达系统反演出发射水平偏振波与垂直偏振波时侧向散射和后向散射的反射率比(BBRh、BBRy)。 2 小旋转椭球散射方向函数β(θ,φ)表达式 2.1 坐标系的建立
在主站天线上建立的直角坐标系为OX′Y′Z′,其中,X′轴始终在水平方向,Y′方向是雷达天线发射波束的能流密度方向,Z′方向与天顶之夹角即为天线仰角(图 1中δ),也是Y′方向与水平面之夹角。发射波电场Ei在OX′Z′平面内偏振,它与X′轴的夹角为α。当α=0时为发射水平偏振波,α= 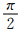 时为发射垂直偏振波。椭球上建立的直角坐标系为oξηζ。主站天线上与粒子上这两个直角坐标系之间的取向关系用方向余弦α1、α2、α3、β1、β2、β3、υ1、υ2、υ3来描述,其中(α1、β1、υ1)、(α2、β2、υ2)和(α3、β3、υ3)分别是X′、Y′和Z′三轴在oξηζ坐标系中的方向余弦。对于图 1中的旋转椭球,oξ、oη轴与椭球的相等轴一致,oζ轴与旋转轴一致。
时为发射垂直偏振波。椭球上建立的直角坐标系为oξηζ。主站天线上与粒子上这两个直角坐标系之间的取向关系用方向余弦α1、α2、α3、β1、β2、β3、υ1、υ2、υ3来描述,其中(α1、β1、υ1)、(α2、β2、υ2)和(α3、β3、υ3)分别是X′、Y′和Z′三轴在oξηζ坐标系中的方向余弦。对于图 1中的旋转椭球,oξ、oη轴与椭球的相等轴一致,oζ轴与旋转轴一致。
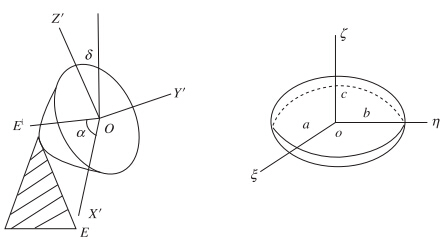 |
| 图 1 主站天线直角坐标系与椭球形粒子直角坐标系Fig. 1 Two rectangular coordination systems for the transmitting antanna and a spheroid raindrop,respectively |
设入射波为简谐波,振幅Ei0取为单位振幅,即Ei0=1,ω是角频率,入射波Ei在OX′及OZ′上的2个分量为
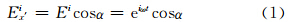
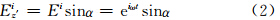
椭球受入射场极化后,在3个轴上分别形成3个电偶极矩Pξ、Pη、Pζ,产生的散射场分别为(张培昌等,2000)
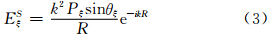

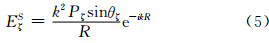
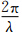 ,λ是入射波波长,R 是所考虑的散射方向上某一点离椭球的矢径距离,| R |=R,ξ、η、ζ 三个轴与 R 之间的夹角分别为θξ、θη、θζ,与建立在椭球上的球坐标(R,θ,φ)之间关系(图 2)
,λ是入射波波长,R 是所考虑的散射方向上某一点离椭球的矢径距离,| R |=R,ξ、η、ζ 三个轴与 R 之间的夹角分别为θξ、θη、θζ,与建立在椭球上的球坐标(R,θ,φ)之间关系(图 2)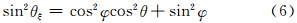
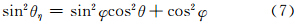

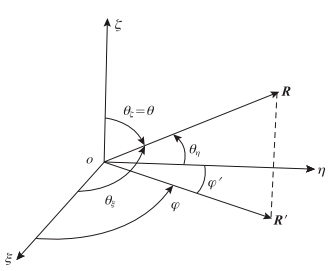 |
| 图 2 散射方向角(θξ,θη,θζ)和(θ,φ)的关系Fig. 2 Relationship between(θξ,θη,θζ) and (θ,φ)for the scattering direction |
图 2中 R ′是 R 在oξη平面上的投影。φ是ξ轴与 R ′的夹角,θ是ξ轴与 R 的夹角。
3个电偶极矩Pξ、Pη、Pζ产生的散射场ESξ、ESη、ESζ分别形成散射能流密度为(张培昌等,1995)
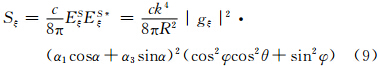
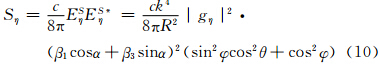
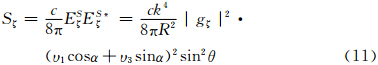
但是应指出,因为已取Ei0=1,故Si= 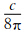 (Ei0)2=
(Ei0)2= 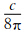 ,即式(9)—(11)中
,即式(9)—(11)中 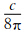 =Si是入射波能流密度。gξ、gη、gζ是椭球在3个轴方向上的极化系数。α1、α3、β1、β3、υ1、υ3是前面描述过的OX′Y′Z′坐标系与oξηζ坐标系间的方向余弦。
=Si是入射波能流密度。gξ、gη、gζ是椭球在3个轴方向上的极化系数。α1、α3、β1、β3、υ1、υ3是前面描述过的OX′Y′Z′坐标系与oξηζ坐标系间的方向余弦。
当发射水平偏振波时,α=0,这时Ei//X′轴。但X′轴与oξηζ坐标系的关系取决于粒子在空间中的取向,故α1、β1、υ1可以在0—1取值。这样式(9)—(11)变为
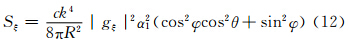
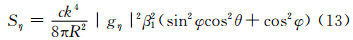
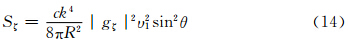
当发射垂直偏振波时,α= 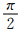 ,Ei//Z′轴,α3、β3、υ3可以在0—1取值,式(9)—(11)就简化成
,Ei//Z′轴,α3、β3、υ3可以在0—1取值,式(9)—(11)就简化成
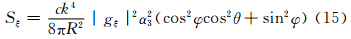
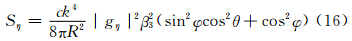
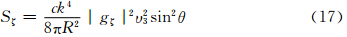
需要指出的是,某一方向(θ,φ)上的散射能流密度应是Sξ(θ,φ,R)、Sη(θ,φ,R)、Sζ(θ,φ,R)在该方向上产生的散射能流密度的总和。 2.3 小椭球散射的方向函数β(θ,φ)及侧向散射截面
据粒子散射的方向函数β(θ,φ)定义式(张培昌等,2001)有
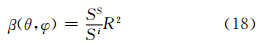
当发射水平偏振波时,将式(12)—(14)分别代入式(18),并注意Si= 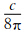 ,得到各电偶极矩分量Pξ、Pη、Pζ产生的散射方向函数为
,得到各电偶极矩分量Pξ、Pη、Pζ产生的散射方向函数为
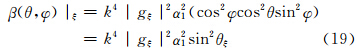
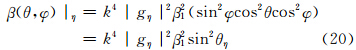
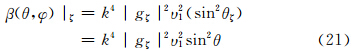
当发射垂直偏振波时,将式(15)—(17)代入式(18)后得
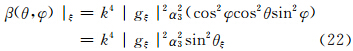
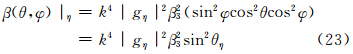
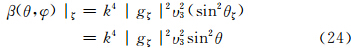
类似于后向散射截面的定义,侧向散射截面σB同样可定义为
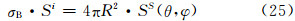
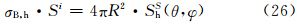
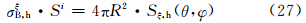
注意到,Sξ,h(θ,φ)·R2/Si=β(θ,φ)|ξ,代入式(27)可得
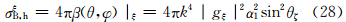
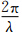 代入后就有
代入后就有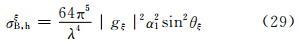
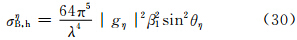
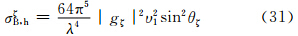
椭球在(θ,φ)方向上的总散射截面σB,h应为三者之和,即有
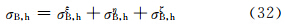
当发射垂直偏振波时,作上面同样处理可得
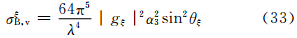
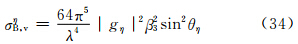

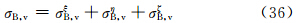
单基地时降水粒子群的雷达气象方程(张培昌等,2001)为
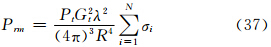
双基地时有(莫月琴等,2005)
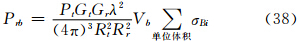

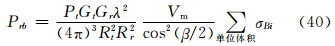
主站天线辐射强度不均匀时,用函数ft(θt,φt)表示其方向性,在该函数具有高斯特性的一般情况下,单基地降水目标的雷达气象方程(张培昌等,2001)为

双基地时降水目标的雷达气象方程通过下面推导获得:
设ft(θt,φt)及fr(θr,φr)分别是主站和子站天线辐射的方向函数。假设在有效照射体Vb内粒子尺度谱处处相同,并认为对同一个Vb内所有粒子而言,由于Rt和Rr远大于h/2(h/2为单基地时的有效照射深度),故可以认为β以及θξ、θη、θζ角都是不变的,则有下面微分形式的雷达气象方程
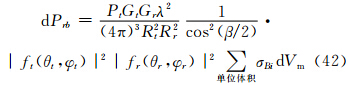
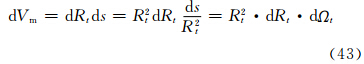
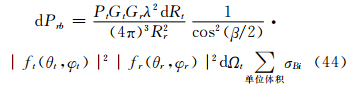
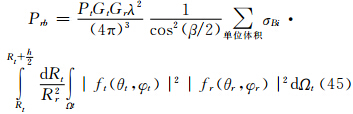
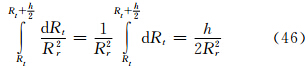
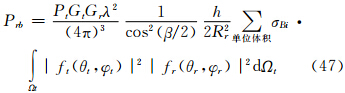
若认为接收天线辐射在半功率点间均匀时,这时半功率点以内fr(θr,φr)=1,代入式(47)中,并注意到主站天线具有高斯特性,按照张培昌等(2001)有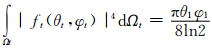 ,同理可得
,同理可得
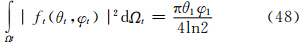
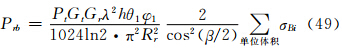
(1)双基地时的式(49)与单基地时的式(41)的主要差异在于后向散射截面σi与侧向散射截面σBi不相同。另外,由于两者的有效照射体积Vb与Vm不同,子站与单基地站天线方向性函数不同,使式(49)中多出了一个因子 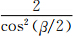 。
。
(2)双基地中方程(38)或(49)中的σBi均代表总的侧向散射截面,即当发射水平偏振波时σBi为σB,h,i由式(30)确定,发射垂直偏振波时σBi为σB,v,i由式(32)确定。 3.3 考虑发射与接收不同偏振波时的双基地雷达气象方程 3.3.1 发射水平偏振波
设主站雷达以任意仰角δ向云降水区发射水平偏振波,如图 1所示。这时,α=0,cosα=1,sinα=0。
一般双基地雷达系统子站的接收天线为裂缝天线,是直立式水平安置的固定天线,由入射波在椭球上产生的3个电偶极矩分量Pξ、Pη、Pζ在接收天线处的散射能流密度,分别为由水平偏振时式(12)—(14)决定的Sξ、Sη、Sζ;其相应的侧向散射截面,分别为由水平偏振时式(29)决定的σξB,h、σηB,h、σζB,h。3.3.1.1 小椭球群旋转轴一致铅直取向时
此时总有X′⊥ζ,故α21+β21=1,υ1=0,代入式(30),得到
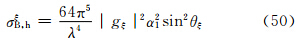
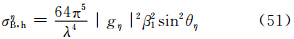

于是,主站天线辐射在半功率点间均匀及不均匀时的雷达气象方程(38)及(49)中的σBi用式(50)—(52)代替,得到
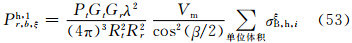

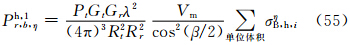
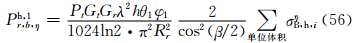


注意,实际到达子站天线处的回波功率应是上述方程中3个分量之总和,即有
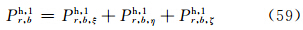
由于此情况下,α1、β1、υ1的取值与主站雷达仰角δ无关,所以,到达子站天线处的回波功率也与主站雷达仰角δ无关。3.3.1.2 小椭球旋转轴在空间无规则取向时
这时小椭球旋转轴在空间各个方向上取向的概率相等,方向余弦取各种取向的平均后有:α12 =β12 =υ12 = 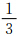 ,于是式(29)—(31)变为
,于是式(29)—(31)变为
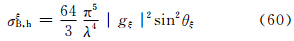
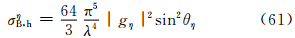
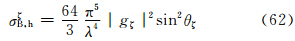
因此,主站天线辐射在两半功率点间均匀及不均匀时的雷达气象方程(38)及(49)中的σBi,可以分别用式(60)—(62)中的σB,hξ、σB,hη、σB,hζ代替,从而得到以下3组雷达气象方程:

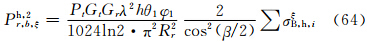
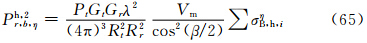
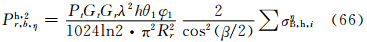
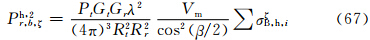
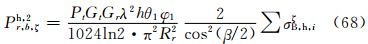
在式(63)—(68)中,σξB,h、σηB,h、σζB,h必须用式(60)—(62)进行估算。由于椭球旋转轴在空间无规则取向,入射波可以在椭球3个轴向ξ、η、ζ上产生电偶极矩Pξ、Pη、Pζ,到达子站天线处的总回波率Ph,2r,b应是上面相应3式之和。3.3.2 主站发射垂直偏振波
这时α= 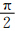 ,cosα=0,sinα=1,Pξ、Pη、Pζ产生的在接收天线处的散射能流密度Sξ、Sη、Sζ及侧向散射截面σξB,v、σηB,v、σζB,v分别由垂直偏振时的式(15)—(17)及(33)—(35)决定。3.3.2.1 小椭球旋转轴在空间一致铅直取向时
,cosα=0,sinα=1,Pξ、Pη、Pζ产生的在接收天线处的散射能流密度Sξ、Sη、Sζ及侧向散射截面σξB,v、σηB,v、σζB,v分别由垂直偏振时的式(15)—(17)及(33)—(35)决定。3.3.2.1 小椭球旋转轴在空间一致铅直取向时
此情况下,α3、β3、υ3随主站天线仰角δ变化而改变。因此,先由主站天线仰角确定Z′轴在oξηζ坐标系中的方向余弦α3、β3、υ3,代入式(33)—(35)计算σξB,v、σηB,v、σζB,v,然后代替雷达气象方程(40)及(49)中的σBi,得到相应的雷达气象方程为
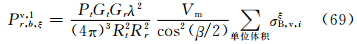
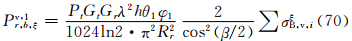

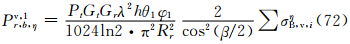


同样,实际到达子站天线处的回波功率应是上述方程中3个分量之总和,即有
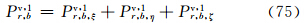
注意式(75)中3个分量可能都不为0,表示入射波为垂直偏振时一致铅直取向的椭球群的侧向散射截面可能由包含铅直分量在内的3个正交分量组成。这具体依赖于主站天线仰角。但入射波为水平偏振时到达子站天线处的回波功率与主站天线仰角无关。
在主站天线仰角δ=0(即主站天线作水平探测)时,Z′//ζ,α3=β3=0,υ3=1,这样式(33)—(35)成为

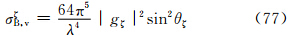
因为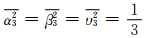 ,于是式(33)—(35)变成
,于是式(33)—(35)变成
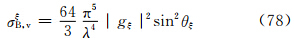

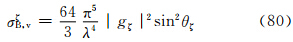
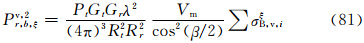


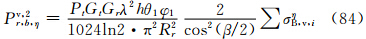
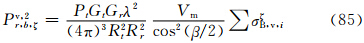
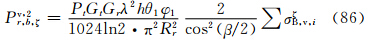
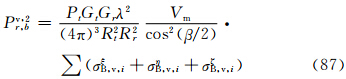
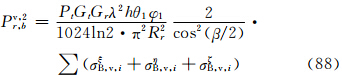
实际上,比较式(60)—(62)和(78)—(80)可见相应式右边完全相同,所以,式(63)—(68)在数值上和式(81)—(86)完全相同。其原因是在小椭球旋转轴在空间作无规则取向时,粒子群的整体散射特征与入射波的偏振方向无关。4 结 论
详细推导了小椭球散射的方向函数及侧向散射截面的表达式。然后,考虑主站天线辐射强度均匀和不均匀时发射水平偏振波与垂直偏振波两种情况下,当小椭球粒子群旋转轴作一致铅直取向和在空间作均匀随机取向时,分别建立适用于双/多基地雷达接收子站的一组雷达气象方程。主要结论如下:
(1)小椭球散射方向函数β(θ,φ)不仅与θ,φ有关,还与两个直角坐标OX′Y′Z′及oξηζ的配置情况有关,这是由于当入射波以不同的仰角及方位角射到旋转轴任意取向的椭球上时,会在ξ、η、ζ方向的a、b、c三个轴上产生不同的极化电偶极矩分量Pξ、Pη、Pζ,从而影响β(θ,φ)│ξ,η,ζ的不同分布。
(2)入射波无论是水平偏振波还是垂直偏振波,小椭球粒子的总侧向散射截面σB恒是Sξ,h(v)、Sη,h(v)、Sζ,h(v)在(θ,φ)方向上造成的侧向散射截面之和(见式(32)和(36))。
(3)双基地雷达气象方程与单基地雷达气象方程相比较,其差别在于侧向散射截面σBi与后向散射截面σi不相同,另外,有效照射体积Vb与Vm不同,子站与单基地站天线方向性函数不同,使双基地雷达气象方程多出了一个因子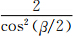 (见式(49))。
(见式(49))。
(4)双基地雷达气象方程,在主站天线辐射在半功率点内均匀时为式(40),不均匀时为式(49),其中,σBi均代表总的侧向散射截面且与入射波偏振方式有关(分别为σB,h见式(32),σB,v见式(36))。
(5)给出了小椭球群旋转轴一致铅直取向情况下的双基地雷达气象方程,这些方程与入射波偏振方式、主站发射天线辐射在半功率点内均匀与否有关(见式(53)─(58)、(69)─(74))。入射波为垂直偏振时一致铅直取向的椭球群的侧向散射截面可能由包含铅直分量在内的3个正交分量组成。这具体依赖于主站天线仰角。但入射波为水平偏振时到达子站天线处的回波功率与主站天线仰角无关。
(6)给出了小椭球群旋转轴在空间无规则取向时的双基地雷达气象方程,这些方程与主站天线仰角、入射波偏振方式等无关,但与主站发射天线辐射在半功率点内均匀与否有关(见式(63)—(68))。
应该指出,方程中涉及的α1、α3、β1、β3、υ1、υ3以及θξ、θη、θζ这些量都能转换成双基坐标中的已知量,另外,关于双/多基地天气雷达探测小椭球粒子群的侧向散射能力,这些均将在另一篇论文中讨论。
| 郭丽君,王振会,董慧杰等. 2012. 基于DDA数据的非球形粒子散射截面的快算研究. 高原气象,待刊 |
| 莫月琴, 刘黎平, 徐宝祥等. 2005. 双基地多普勒天气雷达探测能力分析. 气象学报, 63(6): 994-1005 |
| 张培昌, 王振会. 1995. 大气微波遥感基础. 北京: 气象出版社, 412 pp |
| 张培昌, 殷秀良. 2000. 小旋转椭球粒子群的微波散射特性. 气象学报, 58(2): 250-256 |
| 张培昌, 戴铁丕, 杜秉玉. 2001. 雷达气象学. 北京: 气象出版社, 88 |
| Aydin K, Park S H, Walsh T M. 1998. Bistatic dual-polarization scattering from rain and hail at S-and C-band frequencies. J Atmos Ocean Technol, 15(5): 1110-1121 |
| Collinge M J, Draine B T. 2004. Discrete-dipole approximation with polarizabilities that account for both finite wavelength and target geometry. J Opt Soc Amer A, 21(10): 2023-2028 |
| Draine B T, Flatau P J. 1994. Discrete-dipole approximation for scattering calculations. J Opt Soc Amer A, 11(4): 1491-1499 |
| Protat A, Zawadzki I. 1999. A variational method for real-time retrieval of three-dimensional wind field from multiple-doppler bistatic radar network data. J Atmos Ocean Technol, 16(4): 432-449 |
| Satoh S, Wurman J. 2003. Accuracy of wind fields observed by a bistatic Doppler radar network. J Atmos Ocean Technol, 20(8): 1077-1091 |
| Wurman J, Heckman S, Boccippio D. 1993. A bistatic multiple-Doppler radar network. J Appl Meteor, 32(12): 1802-1814 |
| Wurman J, Randall M, Burghart C. 2001. Bistatic radar networks//30th International Conference on Radar Meteorology. Munich, Germany, 130-133 |
 2012, Vol. 70
2012, Vol. 70


