中国气象学会主办。
文章信息
- 龚志强, 侯 威, 封国林. 2012.
- GONG Zhiqiang, HOU Wei, FENG Guolin. 2012.
- 赤道中东太平洋海温关联指数及其与ENSO强弱作用年相关的研究
- Study of tropical middle-eastern Pacific sea surface temperature correlation index and probale correlation with ENSO effects
- 气象学报, 70(5): 1074-1083
- Acta Meteorologica Sinica, 70(5): 1074-1083.
- http://dx.doi.org/10.11676/qxxb2012.090
-
文章历史
- 收稿日期:2011-02-21
- 改回日期:2012-05-22
2. 扬州大学物理科学与技术学院,扬州,225002
2. Department of Physics, Yangzhou University, Yangzhou 225002, China
气候系统是一个开放的复杂巨系统,系统内部既包括近邻区域的同步耦合作用,又包括远程区域间的遥相关作用,各种作用错综交错必然导致气候系统具有复杂的关联结构。气候系统内部区域之间能量、动量和信息的传递和交换等,必然导致区域间的关联作用是动态变化的,其关联结构特征自然随之发生变化;但就宏观整体而言,系统的关联结构特征则是动态稳定的(Carlson et al,2000;杨培才等,2005;胡隐樵,2002; 万仕全等,2005)。海表温度场及其内在关联作用是气候系统结构复杂性的重要表现形式之一。ENSO则是海表温度场中最显著的年际变化信号,厄尔尼诺年赤道中东太平洋区域温度显著升高,拉尼娜年则表现出相反的特征。赤道中东太平洋地区的海温变化,一方面是海-气耦合等热力过程中的重要热力源(Bjerknes,1969;Philander,1981;邢如楠等,1995);另一方面赤道太平洋与赤道大西洋等地区的海温变化存在显著的遥相关作用(Parthasarathy et al,1985;封国林等,2008;支蓉等,2009;王晓娟等,2009;Wang et al,2012);此外,赤道中东太平洋海温异常和东亚季风等在不同的阶段均有不同程度的影响(李崇银等,1999;施能,1996;黄荣辉等,1994)。因此,赤道中东太平洋地区的海温是气候变化诊断和预测中最强的年际变化信号之一,必然对整个海表温度场内部的关联作用,乃至对环流系统内部的关联作用等都产生重要的影响(Walker,1925)。值得指出的是,赤道中东太平洋区域海表温度对气候系统关联结构的影响是如何体现的,这种影响是否稳定,这些问题都没有得到很好的解答。Sterl等(2007)研究了ENSO遥相关作用的稳定性特征,发现ENSO发生显著变化具有一定的来源于取样变率的随机性。但Sterl等的研究没有提出一种有效的方法来衡量ENSO对系统关联结构影响,同时也未能对ENSO事件的作用强和弱的情况有区别的进行分析。在赤道中东太平洋指数定义方面,主要是以海表温度的距平值作为气候变化研究的主要指数,如Nino3指数、Nino3.4指数等。此外,Tsonis等(2008)和Yamasaki等(2008)指出,厄尔尼诺年和拉尼娜年赤道中东太平洋海温对其他区域的作用是不同的,且存在一定的强弱变化。但事实上,赤道中东太平洋海温异常偏高或异常偏低与该区域在气候系统中作用的强弱配置并非是等价的,而这方面的研究则相对较少。
基于以上科学问题,采用美国国家环境预报中心(NCEP)再分析海温资料,根据赤道中东太平洋区域在海表温度场中作用的年际变化特征定义赤道中东太平洋海温关联指数(TPTI),并和传统的一些定义比较,讨论该关联指数定义的有效性;对厄尔尼诺和拉尼娜年根据其作用的强弱进行分类,给出可能的原因;最后将这一关联指数应用于中国夏季降水的研究,讨论赤道中东太平洋海表温度作用强弱与中国夏季降水的可能联系。2 资料和方法 2.1 资料
温度资料来源于美国国家环境预报中心(NCEP)和美国国家大气研究中心(NCAR)的逐日再分析资料(Kistler et al,2001),分辨率为5°×5°,沿纬向有72个格点,沿经向有36个格点,总计2592个格点。资料时段为1948—2005年,对数据作距平处理以滤除日温度资料中包含的季节振荡信号。同时采用中国国家气候中心提供的全中国731站常规逐日降水数据,资料时段1951—2005年。 2.2 TPTI的定义
图 1a为全球地表温度场经验正交分解展开的第1模态,其方差贡献为5.6%,在赤道太平洋、赤道印度洋和大西洋存在3个正值中心,北太平洋为负值中心,其中,以赤道中东太平洋区的关联中心最为明显。对赤道东太平洋的研究比较广泛,且定义了Nino3、Nino4、Nino3.4指数,ENSO指数等。这些指数大多基于海表温度值或等值线中心值等进行定义并以此来定量描述气候变化信号的强弱等。这类指数定义的优点在于能够体现信号的强弱,在赤道中东太平洋区域气候变化的研究中取得了一系列成果。值得指出的是,定义各种指数的最终目的在于研究不同区域间气候变化的相互作用,而温度的高低并不能直接体现这种相互作用。因此,有必要从直接体现关联作用的角度定义赤道中东太平洋海温指数,继而定量描述该区域对全球气候变化作用的时空特征。本文是在龚志强等(2008,2009)构建温度关联网络的基础上,尝试结合关联度这一网络结构特征量定义赤道中东太平洋海温关联指数。结合经验正交函数分解展开赤道中东太平洋主要关联区的分布(图 1a),选取(10°S—10°N,180°—90°W)为研究区域(图 1b)。该区域覆盖了经验正交函数分解展开第1模态中赤道中东太平洋区域的主要显著关联区,因此,具有一定的代表性。此外,结合海表温度场复杂网络节点关联度(龚志强等,2008,2009)的分布,该区域也是网络中起关键作用的核心区域(图 1c)。
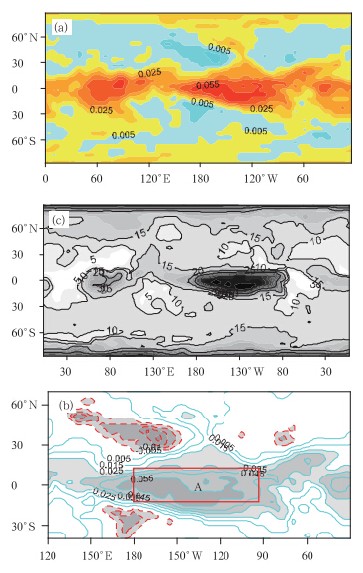 |
| 图 1 NCEP海表温度场经验正交分解展开第1模态(a),赤道中东太平洋温度场异常关联区(b)和温度关联网络节点关联度的空间分布(c)Fig. 1 First mode of the EOF of the sea surface temperatures(SSTs)of the NCEP(a),the tropical middle-eastern Pacific abnormal correlation area of SSTs(b) and the degree distribution of global temperature correlation networks(c) |
对标准化的逐日格点温度序列,根据式(1)计算任意两个格点间的相关系数Cij,
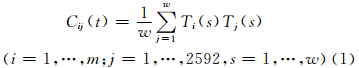
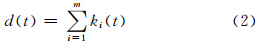
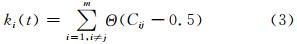
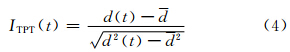
TPTI的意义在于:一方面体现了温度关联网络空间关联结构特征的变化,就网络的性质而言,TPTI越大则相应区域网络的平均关联度越大,即某一区域内部格点之间相互关联的程度则越高,必然使体现网络连通程度的结构特征量平均集聚系数(S)(Watts et al,1998)越高,而任意两格点建立联系(相互作用)需要经过的中间格点也越少,即体现格点间作用中间过程复杂程度的结构特征量——平均路径长度(L)则较小(龚志强,2008)。以春季为例,图 2a—c给出了TPTI与S为同相变化,与L则是反相变化,相关系数分别为0.72和-0.69。另一方面,支蓉等(2009)研究揭示了全球范围与赤道中东太平洋气候变化有显著关联的区域为北太平洋、赤道印度洋、赤道大西洋和(20°—40°S,150°—160°W)区域。因此,TPTI是赤道中东太平洋海表温度与这4个区域的海表温度间相互作用强度的体现。
 |
| 图 2 春季TPTI指数(a)、网络平均集聚系数(b)和平均路径长度(c)的年际变化曲线Fig. 2 Spring TPTI(a),the average cluster coefficient(b) and the average route length of temperature correlation networks(c) |
本文关键区域是根据全球2 m高温度场顶点度分布的高值区和经验正交函数分解展开第1模态的显著性区域,进而选定赤道中东太平洋的10°S—10°N,180°—90°W作为主要研究区域,与传统的厄尔尼诺区域既有联系又有区别。此外,采用2.5°×2.5°的2 m气温资料,选取(5°S—5°N,180°—90°W)作为主要研究区域,按照上述方法计算指数。两种指数四季的相关系数分别为0.30、0.31、0.26和0.28(通过了0.05的信度检验),具有一定差异,但总体特征类似,从而验证了本文结果的可能性。
图 3给出了四季TPTI年际变化曲线。四季的TPTI存在一定的相似性,这说明赤道中东太平洋是一年中全球海表温度场中稳定的强作用区域。此外,TPTI也存在显著的年际和年代际特征等。赤道太平洋的海温变化与太平洋年代际振荡(PDO)、 Nino3、Nino4和Nino3.4指数等均有一定的联系。表 1给出了1966—2005年四季的TPTI与赤道中东太平洋海表平均温度T、太平洋年代际涛动指数、南方涛动指数 、厄尔尼诺指数、ENSO指数和赤道中东太平洋海表温度经验正交函数分解第1模态的时间系数(tEOF)等的相关系数。TPTI与各种指数大都显著相关,且大部分通过了0.05的信度检验。
 |
| 图 3 四季TPTI指数曲线(a. 冬,b. 春,c. 夏,d. 秋)Fig. 3 TPTI series for the four seasons(a. winter,b. spring,c. summer,d. autumn) |
| 季节 | T | tEOF | PDO | Nino 3 | Nino 4 | Nino 3.4 | ENSO |
| 冬 | 0.29 | 0.17 | 0.36 | 0.23 | 0.13 | 0.18 | 0.29 |
| 春 | 0.27 | 0.47 | 0.41 | 0.06 | 0.19 | 0.13 | 0.32 |
| 夏 | 0.31 | 0.40 | 0.43 | 0.29 | 0.24 | 0.31 | 0.39 |
| 秋 | 0.28 | 0.42 | 0.27 | 0.15 | 0.27 | 0.14 | 0.27 |
从图 2亦可看出,TPTI等指数中存在显著的均值和趋势突变,为此结合滑动t检验、启发式分割算法和MK趋势检测法对TPTI和其余5种常规指数做突变检测分析。表 2列出了突变检测结果,显然 、tEOF、ENSO和PDO在1976年前后存在一次显著的突变,而TPTI春、夏、秋3个季节在20世纪70年代中后期存在一次与之相对应的突变,突变时间略滞后前面几种指数,但冬季TPTI未检测出突变。由此可见,全球温度突变并非同步引起气候系统内部相互作用的变化,而是当温度变化从一部分区域先开始,然后逐步影响其他区域的气候变化,这种作用效果积累到一定程度时引起全球范围内区域之间相互作用的整体变化。肖栋等(2007)、Xiao等(2007)的研究在一定程度上验证了气候突变从某一区域开始逐步影响其他区域,从大气底层开始向高层传播这一机制的可能性。
| 检验方法 | TPTI | T | tEOF | Nino 3.4 | ENSO | PDO | |||
| 春 | 夏 | 秋 | 冬 | ||||||
| 滑动t检验 | 1979 | 1977,1993 | 1979 | — | 1976 | 1975,1995 | — | 1976 | 1976,1987 |
| 启发式分割算法 | 1979* | 1973 | 1979 | — | 1976 | 1975,1995 | 1976* | 1977 | 1976 |
| MK趋势检测法 | 1979 | 1973 | 1977 | — | 1978 | 1984 | 1982* | 1977,1997 | 7976 |
| 注:“*”表示通过了0.10的信度检验,未标注的突变通过了0.05的信度检验。 | |||||||||
小波分析的结果也表明,近40 a的TPTI在20世纪80年代以前是5 a的准周期信号占主导,80年代中后期以来这一信号逐渐消失,同时出现8 a的准周期振荡信号,显然这种周期信号的变化是伴随其突变同步发生的,是突变的另外一种重要表现。海温场、ENSO指数和Nino 3.4指数中均存在3—5和10—15 a的准周期振荡,第1模态的时间系数tEOF中存在3—5和8—10 a的准周期振荡,太平洋年代际涛动指数中则以8—10 a的周期信号最为显著。在此采用功率方法进一步检验这些周期信号的有效性,结果表明,各种指数中5或3—5 a的周期信号均通过了0.05的信度检验。
通过上面TPTI与各种传统指数的比较表明,TPTI不仅能够体现赤道中东太平洋区域与其他区域之间关联作用的强弱变化,同时也和各种传统指数具有很好的相似性,因此,TPTI的定义具有一定的代表性。4 TPTI与厄尔尼诺和拉尼娜的可能联系
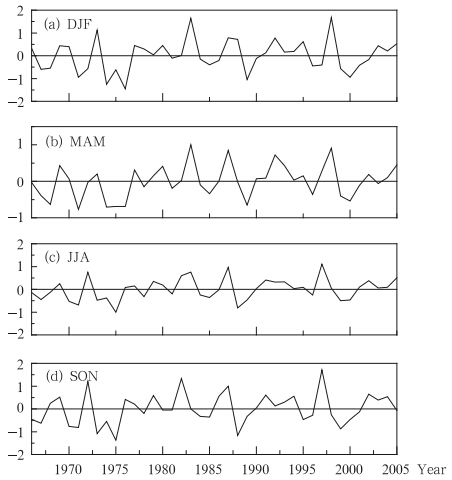
图 4可以看出,TPTI在1972、1973、1976、1982、1988、1996、1997、1998和2002年异常偏高,这些年份均对应了赤道中东太平洋区海温异常偏冷或异常偏暖的年份。李崇银等(2000)给出了近40年的强厄尔尼诺年为1972—1973、1982—1983、1986—1988、1991—1992、1997—1998年;强拉尼娜年为1970—1971、1974—1976、1988—1989、1998—2000年。显然指数异常偏强的年份基本对应了较强的厄尔尼诺或拉尼娜事件。但并不是所有的厄尔尼诺或拉尼娜事件对应的TPTI都高,这说明厄尔尼诺或拉尼娜事件本身可以分为作用强和弱的情况。根据图 4中TPTI和赤道中东太平洋海温距平,可将厄尔尼诺或拉尼娜事件分为强作用事件和弱作用事件两类(表 3)。
 |
| 图 4 TPTI(a)及赤道中东太平洋海表温度距平(b)的年际变化Fig. 4 Series of the TPTI and the tropical middle-eastern sea surface temperatures anomaly from 1966-2005 |
| 年份 | S | k | L | ||
| 厄尔尼 | 高值年 | 1972,1976,1982,1997,2002 | 0.628 | 23.737 | 6.007 |
| 诺事件 | 低值年 | 1969,1979,1986,1991,2004 | 0.609 | 19.186 | 7.855 |
| 拉尼娜 | 高值年 | 1973,1988,1998 | 0.627 | 22.435 | 5.671 |
| 事件 | 低值年 | 1967,1970,1975,1984,1999 | 0.623 | 19.430 | 6.979 |
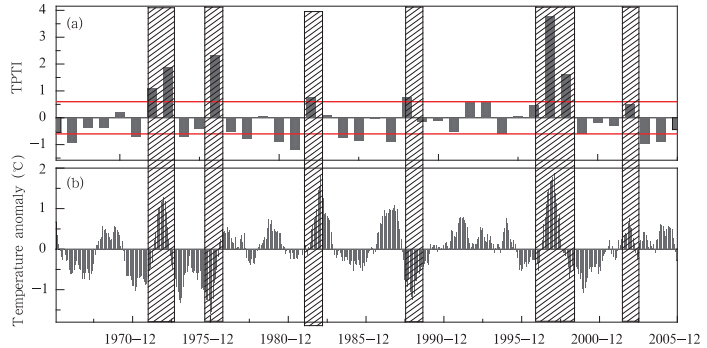
TPTI的异常主要有两方面原因:(1)赤道中东太平洋地区温度同步变化的覆盖面积;(2)赤道中东太平洋对其他区域温度变化的作用。表 3中集聚系数(S)反应了赤道中东太平洋区域海温变化的同步性,集聚系数越高说明同步性变化越好,因此,厄尔尼诺和拉尼娜强作用事件比弱作用事件的集聚系数明显要高。此外,从图 5a可以看出,厄尔尼诺事件TPTI高值年赤道中东太平洋显著关联区域的中心主要分布在赤道印度洋和大西洋及部分 邻近的大陆区域、北太平洋部分区域、澳大利亚以东,30°S附近区域、北大西洋部分区域;而图 5c中厄尔尼诺事件TPTI低值年主要表现为与赤道中东太平洋区域的正相关,此外仅与菲律宾群岛附近的暖池区有一定的正相关。显然,弱指数年赤道中东太平洋与其他区域的作用明显较弱。从图 5b、d可以看出,拉尼娜事件TPTI偏强年主要作用区域与厄尔尼诺指数偏强年类似,但关联作用 的面积及强度均偏大,同时增加了赤道西太平洋暖池区及60°S附近的部分区域;TPTI低值年的关联区域无论是面积和强度等均明显小于指数偏强年的情况。
 |
| 图 5 厄尔尼诺年(a、 c)和拉尼娜年(b、 d)对应TPTI偏强(a、 b)和偏弱(c、 d)年份的显著关联区域分布Fig. 5 Correlation-remarkable areas for El Niño(a,c)/La Niña(b,d)of high(a,b)/low(c,d)TPTIs |
在分析TPTI定义的意义和有效性的基础上,采用1966—2005年中国511个站的逐日降水资料,着重分析TPTI与中国夏季降水的年际变化关系。图 6a、b分别为TPTI与中国511个站夏季降水的相关系数分布和中国夏季降水距平经验正交函数分解第1特征向量的分布。图 6a中,相关系数从华北至华南基本呈现“-+-”的分布特征,正相关中心位于长江流域的中下游地区,这些地区的相关性均通过0.10的信度检验,部分地区的相关性通过了0.05的信度检验。负相关区主要分布在黄河流域、华北地区和华南等,相关系数也通过0.10的信度检验。此外,中国西北地区以正相关为主,均与TPTI有一定的相关性。黄荣辉(1990)、黄荣辉等(2006a,2006b)对中国夏季降水主要模态的研究亦得出了类似的结论。因此,在TPTI较强的年份,长江流域、西北地区降水易偏多,黄河流域、华北和华南大部分地区则降水易偏少;TPTI偏弱年情况相反。从中国511个站夏季降水距平经验正交函数分解展开第1模态特征向量(方差贡献为10.4%)的空间分布(图 6b)可见,华北至华南呈“+-+”的分布特征,这种分布与图 6a中相关系数的空间分布特征基本相反,经验正交函数分解第1模态的正(负)高值区与TPTI和中国夏季降水的负(正)相关高值区基本吻合,进而验证了TPTI与中国夏季降水联系的可能性。中国夏季降水经验正交函数分解第1模态时间系数和TPTI的年际变化曲线的相关系数为-0.38,通过了0.05的信度检验。可以看出,中国夏季降水主要模态的年际变化趋势与TPTI的年际变化趋势具有一定的反相关性,且在1980年前后出现显著的年代际变化。黄荣辉等(2006a,2006b)、戴新刚等(2003)研究中也发现中国夏季降水在20世纪70年代后期出现突变。
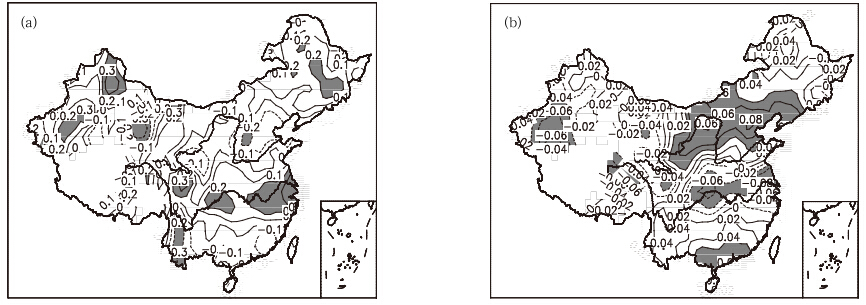 |
| 图 6 夏季TPTI指数与中国夏季降水的相关系数分布(a)和1966—2005年中国511个站夏季降水距平经验正交函数分解第1模态(解释方差为总方差的10.4%)特征向量分布(b)(阴影表示相关检验通过90%的区域,下同)Fig. 6 Distribution of the correlaiton coefficients between China summer precipitation and the summer TPTI(a),and the first EOF mode(variance contribution is 10.4%)of China summer precipitation field(1966-2005)(b),(shadow denotes negative value areas; the same below) |
从TPTI与夏季降水的相关系数分布(图 7)可见,春季的TPTI与东北地区的降水呈正相关(部分地区的相关性通过了0.05的信度检验),与华北地区呈负相关,与长江中下游地区呈正相关(长江中游地区的相关性通过了0.10的信度检验),与华南则呈负相关,华北至华南的“-+-”三极型特征依然存在(图 7a)。前冬的TPTI与长江中下游地区降水呈正相关(长江下游地区的相关性通过了0.05的信度检验),华北至华南的“-+-”三极型特征依然存在(图 7b)。春季TPTI与中国夏季降水经验正交函数分解第1模态时间系数的相关系数为-0.24(达到一定的显著性水平),因此TPTI具有应用于夏季降水预测的潜在可能性。
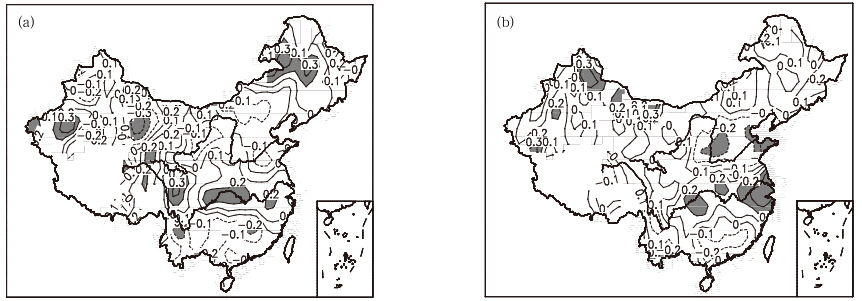 |
| 图 7 春季(a)和冬季(b)TPTI与中国夏季降水的相关系数分布Fig. 7 As in Fig. 6(a)but for spring(a) and winter(b) |
下面从TPTI强弱年的合成分析入手,分析不同TPTI对应的中高纬度的高度场差异的配置情况。根据TPTI年际变化情况,选取指数最高的7年和最低的7年分别作为赤道中东太平洋对全球气候变化作用异常偏强和偏弱的年份。作用异常偏强年有:1972、1973、1976、1982、1988、1997和1998年;异常偏弱年有:1967、1971、1978、1981、1987、2003和2004年。
从TPTI异常偏强年份夏季的对流层高层200 hPa、中层500 hPa和低层850 hPa位势高度距平场(图 8a、c、e)可以看出,TPTI异常偏强的年份,80°E向西至160°W范围内高度场距平中心呈“-+-”的波列状分布。从低层至高层,这一波列始终稳定存在,这也说明了中纬度地区位势高度距平场存在一定的正压性特征。在TPTI偏弱年(图 8b、d、f),对流层高、中、低层位势高度距平中心基本呈“+-+”的反位相变化。TPTI偏强年份和偏弱年份中高纬度环流场的反位相配置,必然会引起中国区域降水异常的反位相变化。此外,TPTI高值年,欧亚大陆120°E以西、西伯利亚和西北太平洋均存在北高南低的“+-”高度距平中心,这种配置是不利于南方的季风影响中国北方地区,同时也不利于西北太平洋的水汽向亚欧输送,容易引起中国夏季降水尤其东北夏季降水相对偏少;反之,指数偏弱年份,欧亚大陆120°E以西“+-”的环流形势明显减弱,西伯利亚和西北太平洋则存在北低南高“-+”的高度场距平中心,对中国降水有促进作用。
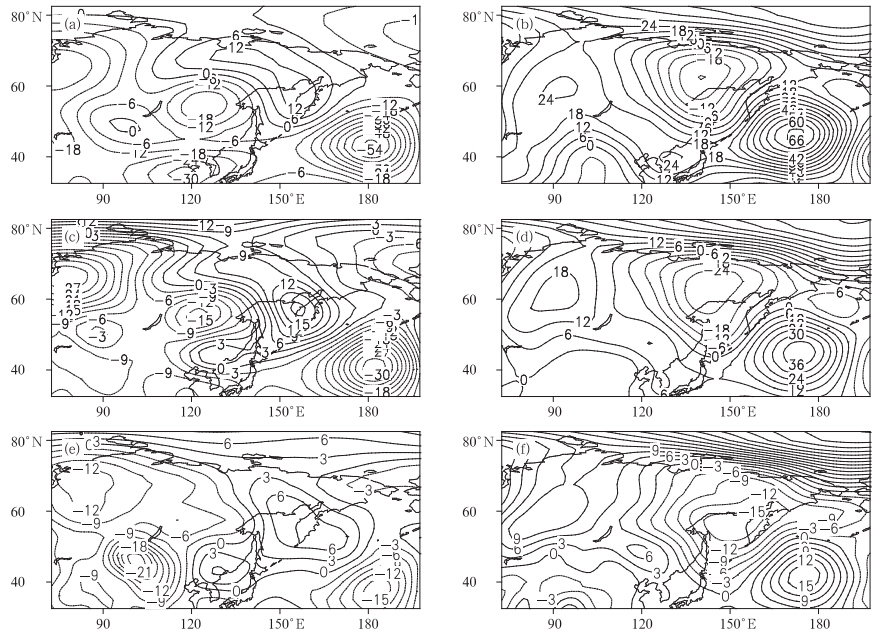 |
| 图 8 TPTI偏强(a、c、e)、偏弱(b、d、f)年份夏季200(a、b)、500(c、d)和850(e、f)hPa上合成的位势高度距平场Fig. 8 Composite summer high fields of 200(a,b),500(c,d),850(e,f)hPa for the years of high(a,c,e) and low(b,d,f)TPTIs |
气候系统中短程关联和遥相关的交织作用构成了一种既包含短程连边又包含长程连边的复杂网络,温度关联网络的构建及其结构特征量的分析从一个全新的角度展现了气候系统的空间结构特征。温度关联网络中关键区域对网络整体性质的变化在一定程度上可能起主导作用,对关键区域的研究就显得尤为重要。因此,有必要对关键区域作用的强弱进行定义,并以指数的形式进行定量描述。基于温度关联网络对赤道中东太平洋区域在网络中作用的年际变化特征定义赤道中东太平洋温度关联指数(TPTI),TPTI指数较以往通过温度距平值等的定义能更深入地体现该区域海表温度异常对全球气候变化作用的强弱。与平均温度、Nino3、 Nino3.4指数、太平洋年代际涛动指数等的比较具有一定的一致性,说明TPTI的定义具有一定的可行性。
TPTI偏强的年份基本对应强厄尔尼诺年和拉尼娜年,主要原因在于这些年份温度同步变化的覆盖区域较广,赤道中东太平洋与其他地区的关联作用较强。通过TPTI的计算发现,TPTI偏强和偏弱的厄尔尼诺年和拉尼娜年对应的高度场配置存在显著差异,厄尔尼诺和拉尼娜事件本身也包含了对全球气候变化强作用年和弱作用年两种情况。
TPTI是从整体角度描述赤道中东太平洋区域的海表温度在全球温度场内部的作用强弱,因此,对所有年份均能分为强作用年、弱作用年和正常年3种情况,TPTI的强作用年和弱作用年均以0.5倍方差为强(弱)值年的衡量标准。海表温度接近常年的年份,TPTI以接近常年或偏小为主,对应赤道中东太平洋区域海温对其他地区的作用接近正常或略偏低,符合已有的认识,故本文对海表温度正常年份没有进一步区分强、弱作用年;对于厄尔尼诺(拉尼娜)事件发生的年份,TPTI值则以偏大为主,但也有对应TPTI偏小的年份,这和传统意义上对厄尔尼诺(拉尼娜)年的认识有一定的差别。本文将两种情况下的年份分为强和弱作用年,并结合相关数据和图形进行了检验。总体而言,大值年对应拉尼娜或者厄尔尼诺事件的概率较高,但不是完全一致,这也进一步说明了拉尼娜和厄尔尼诺事件作用的复杂性,在一定程度解释了同种性质的海温事件所对应的气候特征可能是不同的。
从TPTI与其他指数的相关性来看,TPTI与赤道中东太平洋海表温度的经验正交函数分解第1模态、太平洋年代际涛动指数和ENSO指数的相关性较好。春季和夏季TPTI与中国夏季降水经验正交函数分解第1模态的相关系数分别为-0.24和-0.38,接近或通过0.05的显著性检验,此外,TPTI与中国降水由南到北“-+-”的分布型是存在的,进一步验证了夏季降水华北-长江-华南的三极型分布。
| 戴新刚, 汪萍, 丑纪范. 2003. 华北汛期降水多尺度特征与夏季季风年代际衰变. 科学通报, 48(23): 2483-2487 |
| 封国林, 龚志强, 支蓉. 2008. 气候变化检测与诊断技术的若干新进展. 气象学报, 66(6): 892-905 |
| 龚志强, 周磊, 支蓉等. 2008. 1—30 d尺度温度关联网动力学统计性质的研究. 物理学报, 57(8): 5351-5360 |
| 龚志强, 王晓娟, 支蓉等. 2009. 中国近58年温度极端事件的区域特征及其与气候突变的联系. 物理学报, 58(6): 4342-4352 |
| 胡隐樵. 2002. 大气热力学导论:大气非平衡态非线性热力学. 北京: 地质出版社, 406pp |
| 黄荣辉. 1990. 引起我国夏季旱涝的东亚大气环流异常遥相关及其物理机制的研究. 大气科学, 14(1): 108-117 |
| 黄荣辉, 孙凤英. 1994. 热带西太平洋暖池的热状态及其上空的对流活动对东亚夏季气候异常的影响. 大气科学, 18(2): 141-151 |
| 黄荣辉, 蔡榕硕, 陈际龙等. 2006a. 我国旱涝气候灾害的年代际变化及其与东亚气候系统变化的关系. 大气科学, 30(4): 545-560 |
| 黄荣辉, 陈际龙, 黄刚等. 2006b. 中国东部夏季降水的准两年周期振荡及其成因. 大气科学, 30(4): 545-560 |
| 李崇银, 穆明权. 1999. 厄尔尼诺的发生与赤道西太平洋暖池次表层海温异常. 大气科学, 23(5): 513-521 |
| 李崇银. 2000. 气候动力学引论. 北京: 气象出版社, 514pp |
| 施能. 1996. 北半球冬季大气环流遥相关的长期变化及其与我国气候变化的关系. 气象学报, 54(6): 675-683 |
| 王晓娟, 龚志强, 周磊等. 2009. 温度关联网络稳定性分析I:极端事件的影响. 物理学报, 58(9): 6651-6658 |
| 万仕全, 封国林, 董文杰等. 2005. 气候代用资料动力学结构的区域与全球特征. 物理学报, 54(11): 5487-5493 |
| 肖栋, 李建平. 2007.全球海表温度场中主要的年代际突变及其模态. 大气科学, 31(5): 839-854 |
| 邢如楠, 巢纪平. 1995. 热带海洋对风应力异常的响应. 海洋学报, 17(2): 44-50 |
| 杨培才, 周秀骥. 2005. 气候系统的非平稳行为和预测理论. 气象学报, 63(5): 556-570 |
| 支蓉, 龚志强, 周磊等. 2009. 基于矩阵理论的全球温度资料的尺度性研究. 物理学报, 58(3): 2113-2120 |
| Bjerknes J. 1969. Atmospheric tele-connections from the equatorial Pacific. Mon Wea Rev, 97(3): 163-172 |
| Carlson J, Doyle J. 2000. Highly optimized tolerance: Robustness and design in complex systems. Phys Rew Lett, 84(11): 2529-2532 |
| Kistler R, Kalnay E, Collins W, et al. 2001. The NCEP/NCAR 50 year reanalysis: Monthly means CD-ROM and documentation. Bull Amer Meteor Soc, 82(2): 247-268 |
| Parthasarathy B, Pant G B. 1985. Seasonal relationship between Indian summer monsoon rainfall and southern oscillation. J Climatol, 5(4): 369-378 |
| Philander S G H. 1981. The response of Equatorial Oceans to a relaxation of the trade winds. J Phys Oceanogr, 11(2): 176-189 |
| Sterl A, Oldenborgh G J, Hazeleger W, et al. 2007. On the robustness of ENSO teleconnections. Climate Dyn, 29(5): 469-485 |
| Tsonis A A, Swanson K L. 2008. Topology and predictability of El Ni o and La Ni a networks. Phys Rev Lett, 100(22): 228502 |
| Walker G T. 1925. Correlation in the seasonal variations of weather-a further study of world weather. Mon Wea Rew, 53(6): 252-254 |
| Wang X J, Zhi R, He W P, et al. 2012. Collective behaviour of climate indices in the North Pacific air-sea system and its potential relationships with decadal climate changes. Chinese Physics B, 21(2): 029201 |
| Watts D J, Strogatz S H. 1998. Collective dynamics of “smallworld” networks. Nature, 393(6684): 440-442 |
| Xiao D, Li J P. 2007. Spatial and temporal characteristics of the decadal abrupt changes of global atmosphere-ocean system in 1970s. J Geophys Res, 112(D24S22): doi: 10.1029/2007JD008956 |
| Yamasaki K, Gozolchiani A, Havlin S. 2008. Climate networks around the globe are significantly affected by El Ni o. Phys Rev Lett, 100(22): 228501 |
 2012, Vol. 70
2012, Vol. 70


