中国气象学会主办。
文章信息
- 韩秀珍, 李三妹, 窦芳丽. 2012.
- HAN Xiuzhen, LI Sanmei, Dou Fangli. 2012.
- 气象卫星遥感地表温度推算近地表气温方法研究
- Study of obtaining high resolution near-surface atmosphere temperature by using the land surface temperature from meteorological satellite data
- 气象学报, 70(5): 1107-1118
- Acta Meteorologica Sinica, 70(5): 1107-1118.
- http://dx.doi.org/10.11676/qxxb2012.093
-
文章历史
- 收稿日期:2011-07-29
- 改回日期:2012-02-15
气温是各种植物生理、水文、气象、环境等模式或模型中的一个非常重要的近地表气象参数输入因子(Prihodko et al,1997)。目前近地表气温资料指的是由气象观测站收集得到的观测站点附近约1.5 m高度的大气温度,由于受地形等因素影响,气象站点密度低且离散,在人烟稀少的广阔地区布置的气象观测站更是非常稀疏,甚至根本没有观测站点,因此,在监测范围上受到极大的限制。通过站点气温插值方法,虽然能获得具有一定精度的面气温分布,但由于插值方法本身无法精确描述出植被覆盖、坡向等因素的影响,尤其在站点稀疏地区,仅通过插值方法无法精确地反映出气温的区域分布差异。因此,如何获取连续的面气温分布一直是学者的研究热点之一。王旻燕等(2005)利用单时相双光谱分裂窗算法以GMS 5/VISSR红外资料反演地表温度,揭示了中国几类典型下垫面晴空地表温度的日变化及季节变化特征。张敏等(2005)利用聊城市1981—2000年的日平均地面温度和气温资料,分析了地、气温差值的逐日、逐月变化规律,建立了以日平均气温为基础的日平均地温逐日预测模型,取得了一定的效果。李超等(2009)对草地下垫面地表温度和近地面气温进行了对比研究,并利用2002—2005年合肥站的资料分析了草地下垫面条件下地表温度和气温的年变化、季节变化和日分布特征。柯灵红等(2011)提出了一种基于高程-温度回归关系的空间重建算法,对2008年青藏高原MODIS地表温度影像异常低值像元进行了重建,得到空间完整的地表温度时间序列。姜会飞等(2004)利用气象统计学和气候学的原理及方法,分析北京市海淀地面气象观测站1955—1999年的逐日平均气温资料和1981—1999年逐日地面温度资料,建立了以气温为基础的地温预测模型,并探索地、气温差的年变化规律。
近年来,随着卫星遥感地表温度算法和业务产品的日趋成熟,利用遥感反演得到的地表温度结果为近地表气温的估算提供了新的思路。遥感观测连续性好,资料覆盖范围广,受地面影响小,可弥补常规站点观测的不足。利用近5年的遥感旬地表温度与全中国2340个站点观测的气温的统计结果表明,90%以上站点两者间的相关系数在0.9以上,表明卫星遥感地表温度与近地表气温存在较好的相关,因此,利用卫星遥感资料反演的地表温度可用于获取面分布的近地表气温。如何利用卫星遥感地表温度数据推算近地表气温分布近年来逐渐受到学者们的重视,不少学者就气温和地表温度的相关关系进行了不同程度的分析,以获取地表温度向气温转换的有效途径。Cresswell等(1999)基于Meteosat地表温度数据,建立了地表温度和近地表气温的经验太阳天顶角模式,用于推算近地表气温分布。Mostovoy等(2005)利用MODIS地表温度数据,在密西西比河流域建立了2 m高处的日最高和最低近地表气温与地表温度的统计关系,用来计算密西西比河流域的近地表气温。Colombi等(2007)利用MODIS地表温度数据推算出日平均近地表气温,并将结果用于水文和环境模式中。Riddering等(2006)利用两周合成的NOAA/AVHRR数据反演出的地表温度数据,建立了复杂地形条件下的遥感地表温度与近地表气温的拟合关系,取得了较好的效果,同时利用SEVIRI和MODIS资料,采用经验回归的方法建立了高时间和空间分辨率的地表温度和气温推算模型,用于准实时的气温估算。祝善友等(2009)利用2005年气象卫星热红外亮温数据与同步气象站点数据进行相关分析,建立了分季度、分时段的两种气温遥感反演模型。齐述华等(2005)利用气温时间尺度转换模型将297个气象观测站获得的最高和最低气温资料计算MODIS卫星过境时刻的气温。上述工作在卫星遥感地表温度和近地表气温的相互转换中取得了较好的效果,然而大部分模型考虑的因子较为单一,尚不能适用于大范围地区。基于此,本文利用1998—2007年1 km 空间分辨率的NOAA/AVHRR旬最高地表温度数据和常规气象观测站点旬平均最高气温数据,依据遥感地表温度和近地表气温存在较强的相关性的研究结果,通过经验回归和拟合方式,充分考虑植被指数、土地覆盖类型、海拔高度、季节、太阳高度角、风速、气压等影响因子,建立了卫星遥感旬最高地表温度与旬平均最高气温间的推算模型,并将结果与常规气象站点气温观测值以及江西省气象局提供的站点插值气温进行精度检验分析。结果表明,利用卫星遥感地表温度推算的气温误差在3℃左右,在站点密集地区与常规气象站点插值气温趋势一致,而在山区和站点稀疏地区精度明显高于常规站点插值气温。2 数据及预处理分析
卫星遥感地表温度产品基于NOAA-14、16和18卫星1998—2007年中国标准化处理数据集,采用分裂窗算法反演得到,标准化处理包括归一化辐射定标、投影变换、几何精校正、数据合成和滤波等处理,本套卫星数据集由中国国家卫星气象中心遥感应用室提供。常规气象观测数据选取1998—2007年中国2340个加密气象观测站的气温、降水等要素,以及756个基本站点的0 cm地温要素,常规观测数据由中国国家气象中心农业气象中心提供,考虑到地表温度为旬最高值,因此,气温和0 cm 地温进行了旬平均最高值统计,得到旬平均最高气温和旬平均最高0 cm地温。为进行对比分析,选取江西省气象局气候中心提供的1998—2007年基于中国2340个加密气象观测站采用克立金插值算法得到的旬平均最高气温插值数据。辅助数据包括国际地圈生物圈计划(IGBP)的中国土地覆盖类型数据、高程数据、气候分区数据、MODIS多年月平均植被指数数据等。3 主要技术方法 3.1 近地表气温、0 cm地温以及卫星遥感地表温度三者间的相关分析
卫星遥感地表温度定义为卫星探测像元范围内的陆地表面温度平均值,站点0 cm地温则是指气象台站观测点处的地面温度,两者在物理意义上较为接近,主要存在面和点的区别。在实际的地表温度反演中,0 cm地温常用来对地表温度反演结果进行精度检验,是台站观测多种温度要素中与遥感反演地表温度最接近的物理量。理论上,两者应该存在较好的相关性。利用2002—2008年中国756个基本站点旬平均最高0 cm地温和站点位置对应的相应时次卫星遥感旬最高地表温度进行采样及相关性分析,结果表明在可用的687个站点中,二者平均相关系数可以达到0.84,相关性最好的站点相关系数超过0.98,超过60%的站点相关系数在0.9 以上。从新疆淖毛湖站 2002—2008年旬最高地表 温度与旬平均最高0 cm地温散点分布(图 1)可见,两者相关性很高,相关系数为0.99。
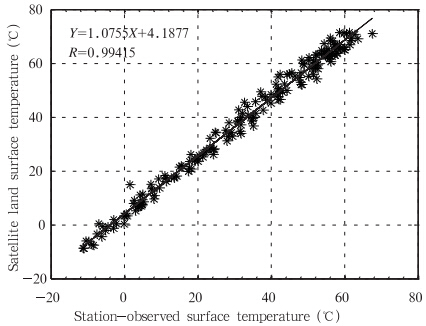 |
| 图 1 新疆淖毛湖站2002—2008年卫星遥感旬最高地表温度与站点观测旬平均最高0 cm地温散点分布Fig. 1 Scatter plot between the satellite l and surface temperatures and the station-observed surface temperatures from 2002 to 2008 in Zhuomao Lake station,the Xinjiang Uygur Autonomous Region |
从物理意义上说,0 cm地温与气温应该存在一定的相关关系。利用1971—2008年中国756个基本站获取的旬平均最高0 cm地温和旬平均最高气温资料,通过对每个站点的旬平均最高0 cm地温和旬平均最高气温进行相关分析,发现95%以上的站点二者相关系数在0.75以上,81%以上的站点二者相关系数超过0.9,其中,最大相关系数为0.993,最小相关系数为0.571,全部通过α=0.05的置信度检验。表 1为旬平均最高0 cm地温和旬平均最高气温站点回归分析情况。图 2给出吐鲁番、昌都、木里和丽江4个站点的旬平均最高气温与旬平均最高0 cm地温的散点分布。
| 要素 | 数值 | 要素 | 数值 | 要素 | 数值 |
| 站点数 | 731 | 平均标准偏差(℃) | 3.93 | 最大偏差最小值(℃) | 7.73 |
| 最小相关系数 | 0.57 | 标准偏差最小值(℃) | 2.39 | 最大偏差最高值(℃) | 25.2 |
| 最大相关系数 | 0.99 | 标准偏差最大值(℃) | 8.64 | 最大偏差整体均值(℃) | 13.12 |
| 相关系数大于0.75的站点百分比(%) | 95.2 | 偏差平均值最小值(℃) | 1.81 | 最小偏差最小值(℃) | 0.0 |
| 相关系数大于0.9的站点百分比(%) | 81.1 | 偏差平均值最大值(℃) | 7.32 | 最小偏差最高值(℃) | 0.153 |
| 整体平均相关系数 | 0.93 | 偏差平均值总体平均值(℃) | 3.18 | 最小偏差整体均值(℃) | 0.006 |
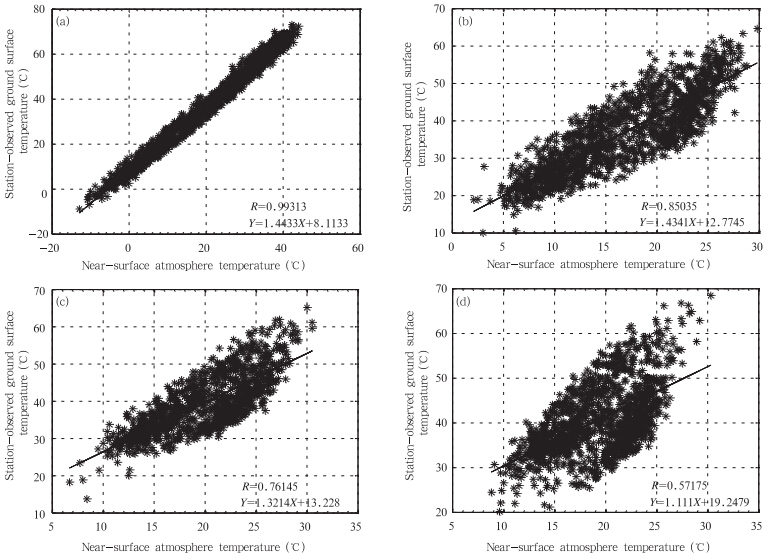 |
| 图 2 4站点旬平均最高0 cm地温和旬平均最高气温的散点分布(a. 吐鲁番,b. 昌都,c. 木里,d. 丽江)Fig. 2 Scatter plot of the ten-days average station-observed ground surface maximum temperatures and near-surface atmosphere maximum temperatures at(a)Turpan,(b)Changdu,(c)Muli,and (d)Lijiang stations |
站点旬平均最高气温和旬平均最高0 cm地温的分析结果表明,二者确实存在较好的相关关系。由于卫星遥感地表温度与0 cm地温有着较强的相关性,卫星遥感地表温度与气温必然也存在着一定的联系。利用获取的中国2340个加密气象观测站2004—2008年的站点旬平均最高气温与对应的卫星遥感旬最高地表温度进行的统计分析表明,仅有21个站的相关系数低于0.75,且最小相关系数为0.544,85%以上的站点相关系数在0.9以上,其中,相关系数低于0.75的站点主要分布在海南岛,相关系数在0.75—0.90的站点主要分布在华南南部、西南地区南部以及青藏高原东部等地(图 3)。
 |
| 图 3 卫星遥感旬最高地表温度与对应站点旬平均最高气温的相关系数分布Fig. 3 Correlation coefficients between the satellite ten-days maximal l and surface temperatures and ten-days average maximal near-surface atmosphere temperatures |
图 4给出相关系数不同的吐鲁番、昌都、木里和丽江4个站点的卫星遥感旬最高地表温度与旬平均最高气温的散点分布,可见相关系数较低的站点散点分布较为离散,但整体相关性仍较好。
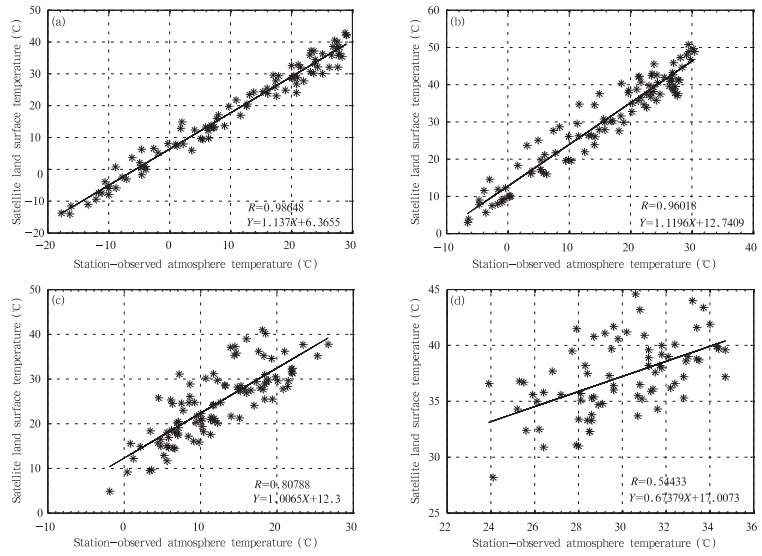 |
| 图 4 4站点卫星遥感旬最高地表温度和站点旬平均最高气温的散点分布(a. 吐鲁番,b. 昌都,c. 木里,d. 丽江)Fig. 4 Scatter plot of the ten-days average maximal satellite l and surface temperatures and station-observed atmosphere temperatures at(a)Turpan,(b)Changdu,(c)Muli,and (d)Lijiang stations |
综上所述,旬平均最高气温、旬平均最高0 cm地温以及卫星遥感旬最高地表温度存在较强的线性相关关系,这为基于卫星遥感地表温度推算近地表气温从而获取连续分布的旬气温分布数据提供了可能(Prihodko et al,1997;齐述华等,2005;Cresswell et al,1997; Mostovoy et al,2005; Colombi et al,2007)。 3.2 主要影响因子分析
地表温度与近地表气温虽然存在着较好的相关关系,但两者的相关性受到多种因素的影响。由于地表温度是表征地物表面冷热程度的物理量,其变化受到地物性质、干湿状况等影响,而气温是表征大气冷热程度的物理量,大气流动性强,易受周围环境的影响。由于地物与大气的导热性、热容性等都存在差异,并且,不同地物之间热容性也不同,水的热容性大,裸地热容性小,因此,在寻找地温与气温的相关关系时,必须考虑地物及环境等多种因素的影响(Prihodko et al,1997;Cresswell et al,1999)。
按照地表温度的反演原理,地表温度与土地覆盖类型、植被指数等关系密切。反演地表温度采用的分裂窗算法,通过考虑地表湿度、土地覆盖类型及植被指数对比辐射率的影响,根据分裂窗通道的亮度温度,采用普朗克函数最终求得地表温度。而气温变化受到气压、大气湿度、风速等影响。因此,归纳起来,影响地表温度和气温关系变化的因素包括大气湿度、地表湿度、气压、风速、植被指数、土地覆盖类型等。大气湿度和地表湿度对于气温以及地表温度的变化有着重要的影响,湿度增大,温度变化缓慢。风速通过影响大气运动对地表和大气的热量传递或传输起到重要的作用。气压反映了空气稀薄程度,影响大气的热量吸收和传输,进而影响到气温和地表温度的变化。植被指数和土地覆盖类型则通过影响地表比辐射率,直接影响到地表温度的变化,通常来说,植被稀疏区和裸土区,地表温度变化比高植被覆盖区温度变化快,而由于大气的流动性,气温受植被指数和土地覆盖类型的影响没有地表温度明显,因此,在不同的植被指数和土地覆盖条件下,气温和地表温度的关系变化亦不同。
在上述影响因子中,对地表温度和气温的相关性影响较大的是地表湿度和大气湿度,而影响地表湿度和大气湿度的主要因素为降水量。通过分析站点旬降水量对地表温度和气温相关性的影响可知,旬内降水量越大,气温和地表温度的相关性越低。分析16个站点在不同旬降水量时,旬平均最高气温与旬平均最高0 cm地温的相关系数分布(图 5)可见,当旬总降水量低于50 mm时,各站点的气温与地温相关性较为连续,在0.9以上,尤其当旬总降水量低于10 mm时,二者的相关性接近1.0,而当旬总降水量超过50 mm时,旬平均最高气温与旬平均最高0 cm地温的相关系数存在较大的波动,部分站点的相关系数低于0.9,最低可降至0.7左右。
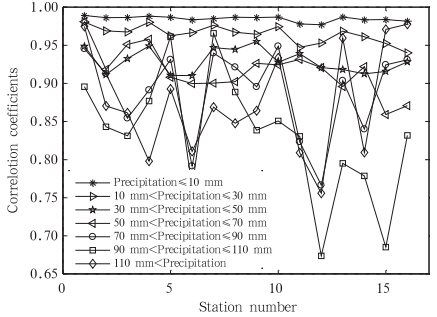 |
| 图 5 不同降水量站点旬平均最高气温与旬平均最高0 cm地温间的相关系数分布Fig. 5 Plot of correlation coefficients between the ten-days average maximal station-observed l and surface temperatures and atmosphere temperatures for the different precipitation grades |
降水量对气温与地表温度相关性计算的影响,主要表现在两个方面:(1)旬内云覆盖量的增多,云量的增加不仅影响卫星遥感晴空资料的获取率,碎云等的存在对于地表温度的反演精度也会带来较大影响;(2)旬内地表湿度或含水率的增大,由于同一地区地表温度的变化率随地表湿度的增大而下降,致使地表温度和气温的相关性与地表湿度较小时有所不同,从而导致地表温度和气温推算的偏差。 3.3 基于地表温度的近地表气温推算模型 3.3.1 线性回归模型
根据3.1节的分析,旬平均最高近地表气温、旬平均最高0 cm地温以及卫星遥感旬最高地表温度存在较好的相关性,并且这种关系在同一站点表现为较强的线性相关。因此,旬平均最高近地表气温(T)与旬最高地表温度(TLS)的关系可表达为
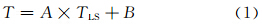
根据3.2节的分析,气温和地表 温度受到多种因素的影响,包括大气湿度、气压、风速、地表湿度、土地覆盖类型、植被指数等。尽管地表温度和气温存在较强的线性关系,然而这种线性关系常常表现为分段线性相关,即在不同大气和下垫面条件下,回归系数和常数项并不固定,而是随着下垫 面条件和大气环境的改变而变化。因此,式(1)可以表述为式(2)
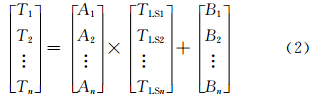
根据式(2),确定不同条件下的回归系数A和回归常数项B是利用卫星遥感地表温度推算气温的关键所在。3.3.2 分类与回归模型的建立
根据地表温度与气温推算模型的影响因子分析结果,影响地表温度和气温相关性的因子主要包括风速、大气湿度、降水量(地表湿度)、土地覆盖类型及植被指数等。由于卫星遥感地表温度数据为0.01°×0.01°空间分辨率的栅格数据,土地覆盖类型和植被指数可以通过遥感资料获取,与地表温度数据在空间上完全匹配,而风速、大气湿度、降水等要素为站点离散观测资料,在空间上无法与卫星遥感地表温度数据匹配,并且,站点观测时间与卫星观测时间不一致,在利用地表温度推算气温时,无法直接将这些因素使用到推算模型中。分析表明,风速、湿度、降水这些因子具有一定的季节性和气候分布特征,在相同季节、同一气候带中,风速、大气湿度和降水量具有一定的相似性,因而其对地表温度和气温相关性的影响相似(中国气候区划,1959;毛飞等,2009;郑景云等,2010)。这样,地表温度与气温推算模型的因子主要确定为以下4类:
季节:主要根据逐月的地表温度和气温的回归系数进行归类,一般情况下分为春(3—5月)、夏(6—8月)、秋(9—11月)、冬(12、1、2月)四个季节。
气候分区:主要根据中国气候区划图进行划分,一共分为9类(表 2)。
| 分类 | 气候区 | 气候区细分 |
| 1 | 中热带 | 中热带湿润区 |
| 2 | 北热带 | 北热带湿润区 |
| 北热带亚干旱区 | ||
| 北热带亚湿润区 | ||
| 3 | 南亚热带 | 南亚热带湿润区 |
| 4 | 中亚热带 | 中亚热带湿润区 |
| 5 | 北亚热带 | 北亚热带湿润区 |
| 6 | 南温带 | 南温带湿润区 |
| 南温带亚湿润区 | ||
| 南温带亚干旱区 | ||
| 南温带干旱区 | ||
| 7 | 中温带 | 中温带湿润区 |
| 中温带亚湿润区 | ||
| 中温带亚干旱区 | ||
| 中温带干旱区 | ||
| 8 | 北温带 | 北温带湿润区 |
| 9 | 高原区 | 高原湿润区 |
| 高原亚湿润区 | ||
| 高原亚干旱区 | ||
| 高原干旱区 |
土地覆盖类型:采用IGBP的全球土地覆盖分类结果,一共分为17类。
植被指数:按照植被指数分为4大类:小于0.2、0.2—0.4、0.4—0.6、大于0.6。
根据上述分类原则,对中国主要陆地区域进行分类,一共获取了851种类型。基于这851类别,利用1998—2007年卫星遥感中国主要陆地区域逐旬地表温度及相应旬的站点旬平均最高气温数据,通过空间匹配处理等,建立 各类型的卫星遥感旬地表温度和旬平均最高气温样本表,利用线性回归获取每一种类别的旬最高地表温度和旬平均最高气温的回归系数和回归常数项,从而建立起旬最高地 表温度和旬平均最高气温间的推算模型。
在这851种推算模型中,相关性最好的模型遥感反演旬平均最高地
表温度和旬平均最高气温间相关系数高达0.98以上,超过27%的模型相关系数在0.9以上,超过75%的模型相关系数在0.7以上。通过对每一种模型进行α=0.05的置信度检验,91%以上的模型均通过检验。检验未通过的类型主要分布在华南南部包括广西南部、海南、广东南部等地。总体来说,北方地区旬最高地表温度和旬平均最高气温的相关系数明显高于南方地区,季节分布上秋冬季好于春夏季,植被稀疏地区好于植被稠密区。表 3为类型4(土地覆盖类型为农地,气候分区为中亚热带湿润区)在不同季节和植被指数时的旬平均最高气温和卫星遥感旬最高地表温度间的推算模型分析表。
| 季节 | 植被指数分类 | 样本数 | 相关系数 | 回归系数 | 回归常数(℃) | 偏差平方和 | 平均标准偏差(℃) | 回归平方和 | 最大偏差(℃) | 最小偏差(℃) | 偏差平均值(℃) |
| 春 | 4 | 666 | 0.88616 | -6.436058 | 0.882356 | 3282.87624 | 2.248559 | 12006.22172 | 6.064027 | 0.000666 | 1.7899 |
| 夏 | 4 | 2039 | 0.633757 | 11.805958 | 0.485404 | 8636.341615 | 1.430773 | 5797.198925 | 6.295832 | 0.000162 | 1.661187 |
| 秋 | 4 | 527 | 0.937266 | -3.640841 | 0.836058 | 1409.769339 | 2.696387 | 10190.13856 | 4.470372 | 0.00643 | 1.340562 |
| 冬 | 4 | 312 | 0.879391 | -4.470917 | 0.757416 | 1182.924347 | 2.149222 | 4035.762287 | 5.368509 | 0.00618 | 1.564979 |
| 春 | 3 | 2060 | 0.900514 | -7.290349 | 0.874965 | 11005.02591 | 2.341128 | 47199.78055 | 6.371046 | 0.004256 | 1.907583 |
| 夏 | 3 | 712 | 0.503209 | 13.637818 | 0.415344 | 3980.213879 | 1.163269 | 1349.618481 | 6.165344 | 0.013227 | 1.963917 |
| 秋 | 3 | 1924 | 0.947353 | -4.184618 | 0.834031 | 4802.862909 | 2.847865 | 42044.54819 | 5.514686 | 0.000655 | 1.254503 |
| 冬 | 3 | 1709 | 0.897813 | -4.802932 | 0.767195 | 5518.544077 | 2.330295 | 22937.53088 | 5.84361 | 0.002864 | 1.464382 |
| 春 | 2 | 1649 | 0.910347 | -8.066725 | 0.878645 | 8939.925111 | 2.399484 | 43258.16868 | 6.531943 | 0.000048 | 1.92067 |
| 夏 | 2 | 69 | 0.658233 | 8.824569 | 0.465875 | 292.12615 | 1.481007 | 223.333271 | 5.117141 | 0.008673 | 1.728986 |
| 秋 | 2 | 1633 | 0.944489 | -4.134374 | 0.821817 | 3932.350591 | 2.774406 | 32498.53626 | 5.3914 | 0.001571 | 1.236793 |
| 冬 | 2 | 2131 | 0.870123 | -3.598623 | 0.721523 | 7081.734505 | 2.099283 | 22074.90033 | 5.682467 | 0.000183 | 1.470074 |
| * 均通过F检验。 | |||||||||||
基于建立的卫星遥感旬最高地表温度和站点旬平均最高气温的推算模型,利用NOAA/AVHRR 1998—2007年反演的卫星遥感旬最高地表温度数据集和旬最大植被指数数据集,结合气候分区、土地覆盖数据,考虑季节影响,建立了1998—2007年10年逐旬的0.01°×0.01°旬平均最高气温数据集。从2007年1月上旬(图 6a)、4月上旬(图 6b)、7月上旬(图 6c)和10月上旬(图 6d)利用卫星遥感旬最高地表温度推算的旬平均最高气温的分布可见,通过卫星遥感地表温度推算得到的0.01°×0.01°旬平均最高气温分布连续,细节特征突出,尤其在西北地区,较好地反应了气温的空间分布特征。
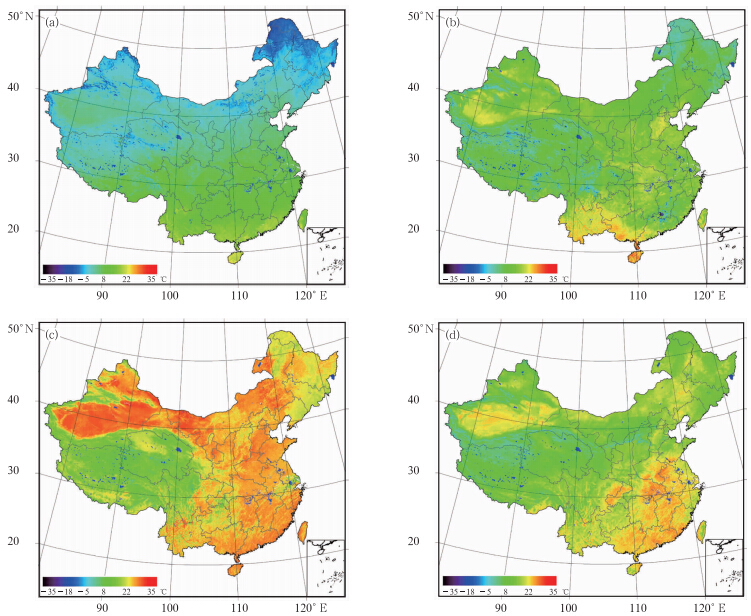 |
| 图 6 2007年1月上旬(a)、4月上旬(b)、7月上旬(c)和10月上旬(d)卫星遥感中国旬最高地表温度推算旬平均最高气温的分布Fig. 6 Simulated 1 km-resolution 10 days average maximal near-surface atmosphere temperatures based on the satellite l and surface temperatures using the proposed estimative model for the first ten-days of January(a),April(b),July(c) and October(d)2007 |
为检验模型精度,可采用常规站点观测的温度值检验和站点插值的气温数据对比检验两种方法。常规站点观测的温度值检验主要通过获取的站点旬平均最高气温值资料与推算气温逐旬误差、逐月累计误差、年度累计误差以及单站点的平均误差分布分析。站点插值气温数据对比检验主要将推算的气温数据集与采用常规方法插值得到的相应空间分辨率的气温数据集进行对比,分析其在空间分布上的差异,并比较两者分别采用常规站点观测的温度值检验结果。精度分析采用的数据为2002—2003年未参与建模的数据集。4.2.2 检验结果4.2.2.1 逐旬分析结果
从逐旬结果分析,基于卫星遥感地表温度推算的气温分布在细节特征上较插值气温更为合理,可有效反映出因地形、高程等因素造成的气温在局部区域上的差异,尤其在西部站点稀疏区,避免了插值气温误差较大,分布极为不连续等缺点,同时插值气温会产生因插值方法造成的“耀斑”现象,即在局部区域出现圆形的异常高温区或低温区。图 7给出2002年1月、4月、7月及10月上旬卫星遥感地表温度推算气温和插值气温与站点观测气温间的散点分布。从散点分布图分析,利用卫星遥感地表温度推算的气温在分布趋势上与站点观测气温较为一致,与插值气温分析结果对比,两者总体来说具有较好的一致性。
 |
| 图 7 2002年1月(a)、4月(b)、7月(c)及10月(d)上旬0.01°×0.01°旬平均最高气温精度检验结果(a1—d1.推算气温,a2—d2.插值气温)Fig. 7 Scatter plot of the accuracy evaluation between 1 km-resolution near-surface temperatures and station-observed atmosphere temperatures in the first 10 days of January(a),April(b),July(c) and October 2002(a1—d1. simulated temperatures from satellite l and surface temperatures,and a2—d2. interpolated grid temperatures) |
基于旬分析结果,逐站点计算出推算气温(TS)与站点观测气温(T)的绝对误差,进行逐月和逐年气温累计差统计,得到月或年气温累计误差分布(S△τ),以分析推算气温在季节分布上的差异。
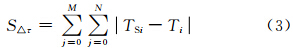
表 4为2002—2003年卫星遥感地表温度推算气温和插值气温与常规站点气温月、年累计温差的对比检验分析。
| 月 | 站点数 | 推算气温差<3℃站点所占百分数(%) | 插值气温差<3℃站点所占百分数(%) | 推算气温累计误差(℃) | 插值气温累计误差(℃) |
| 1 | 9104 | 76.54877 | 72.16608 | 18884.3 | 21986.7 |
| 2 | 8999 | 78.786532 | 65.96288 | 17805.8 | 24832.0 |
| 3 | 9054 | 56.450188 | 67.50607 | 28022.8 | 24569.2 |
| 4 | 9140 | 66.017505 | 66.57549 | 23907.7 | 25196.1 |
| 5 | 8976 | 67.947861 | 69.96435 | 22415.8 | 23038.1 |
| 6 | 7295 | 72.268677 | 74.3523 | 16855.3 | 15668.0 |
| 7 | 7085 | 75.850388 | 59.37897 | 15026.0 | 20823.6 |
| 8 | 7017 | 75.929885 | 65.58358 | 14658.7 | 19819.6 |
| 9 | 9103 | 70.888718 | 76.57915 | 21328.9 | 21116.0 |
| 10 | 9432 | 78.445717 | 70.01696 | 18713.4 | 23016.8 |
| 11 | 9440 | 68.898305 | 76.25
| 23773.9 | 20833.0 |
| 12 | 8974 | 84.722532 | 79.06173 | 15049.5 | 19049.8 |
| 年平均 | 103619 | 72.608305 | 70.53147 | 236442.1 | 259948.9 |
从表 4分析,利用卫星遥感地表温度数据推算的气温数据,平均72.6%以上的站点温差在3℃以内,高于插值气温的70.5%。对于年度绝对累计误差,推算气温较插值气温降低了11753.4℃。从季节分布上分析,冬季结果最好,夏季次之,冬夏两季推算气温明显好于插值气温,秋季二者精度相近,春季推算气温略差于插值气温。总体上来说,推算气温在精度上要高于插值气温。4.2.2.3 误差空间分布分析
对于同一站点,计算其逐旬推算气温和观测气温的绝对差值,再对绝对差值进行累加,计算其旬平均差值(△T ——)。利用所有获取的站点旬平均差值绘制其空间分布图,分析温度误差的空间分布特征。
利用式(4)可计算得到卫星遥感地表温度推算气温(图 8a)和插值气温(图 8b)与站点观测气温的旬平均温差分布,分析图 8可见,在站点密集的平原地区,利用卫星遥感地表温度推算的气温在分布趋势上与插值气温较为一致,尤其在华北平原和东北平原上,插值气温结果甚至优于推算气温。但是,在中南部山区、西南山区以及西北站点稀疏区,基于地表温度推算的气温分布明显好于插值气温。从整体分布上看,地表温度推算的气温误差分布较为平均,大部分站点误差在3℃以内,而插值气温的误差分布具有明显的地域性特征,误差大于3℃的站点数明显高于推算气温。
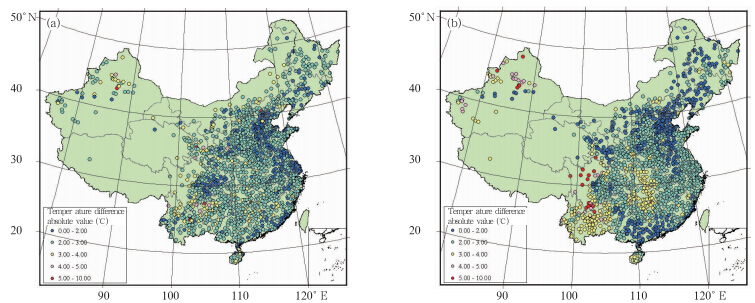 |
| 图 8 卫星遥感地表温度推算气温(a)和插值气温(b)分别与站点观测气温的旬平均温差分布(2002—2003年)Fig. 8 Accumulated 10 days average temperature differences between 1 km-resolution atmosphere temperatures from satellite l and surface temperatures(a) and the interpolated atmosphere temperatures(b) and the station-observed atmosphere temperatures for 2002-2003 |
综上所述,卫星遥感地表温度推算近地表气温分布虽然存在一定的误差,但气温分布总体趋势上与站点观测结果较为一致,具有一定的可参考性。从季节分布来看,冬季最好,夏季和秋季次之,春季较差。与站点插值结果对比分析显示,二者总体趋势一致,但卫星遥感地表温度推算的气温结果层次更丰富,细节特征更为突出,尤其在站点稀少区域和地形复杂山区,插值气温分辨率粗,而卫星遥感推算的气温分布连续,可较好地反映温度的空间分布特征;此外,插值气温因插值方法本身会带来一定的“耀斑”现象,而地表温度推算的气温可有效避免该现象。当然,插值气温在东部站点密集的平坦地区,误差小,误差整体趋势上甚至略好于卫星遥感地表温度推算的结果,并且,插值气温不受云覆盖等天气条件的影响,数据获取率较高。因此,为获取高空间分辨率的旬值气温数据,可充分利用二者的优势,在西部站点稀疏地区以及地形条件复杂的山区,采用卫星遥感地表温度推算的气温结果,在东部站点密集的平坦地区,可以以插值气温为主,同时为避免插值气温的耀斑现象,参考卫星遥感地表温度推算的气温,而在有云条件下,则采用插值气温。
引起误差的原因可归纳为以下几点:(1)地表温度反演存在一定的误差。由于卫星遥感地表温度反演产品精度一般在2—3℃,少数情况甚至会超过5℃,在这种精度条件下,基于该产品推算的气温也必然受到影响。(2)气候分区虽然在一定程度上可以反映出降水、气压和风速的区域分布特征,但是这些因素波动性大,即使在同一站点,短时间内也可能出现较大的变化,而气候分区无法体现这种波动性,在同一气候分区相同季节以及相同下垫面条件下,该推算模型建立的地表温度和气温间的线性相关始终是固定的,这必然带来较大的误差。(3)采用的卫星遥感地表温度数据来自于旬最大亮温合成结果,因而是旬最高值或较高值,仅为某一个时刻的温度值,而气温采用的是旬平均最高气温值,是旬内日平均最高温度基础上求得的平均温度,这两个物理值在观测时间上存在较大的差异,这种差异也会影响到二者间的相关关系。 5 讨论与改进
总体来说,利用卫星遥感地表温度产品推算气温具有较好的可行性,可以作为获取旬值气温的新方法之一。本文的研究可归纳为以下几点:
(1)卫星遥感旬最高地表温度与旬平均最高气温存在着较好的相关,并且,这种相关表现为较强的线性相关。基于这种线性相关关系,可以建立起卫星遥感旬最高地表温度与旬平均最高气温间的推算模型,从而为获取高空间分辨率的近地表旬平均最高气温分布数据集提供新的技术手段。
(2)尽管二者之间存在较好的线性相关,这种相关关系受到多个因子的影响,包括降水、气压、风速、植被指数和土地覆盖类型等。
(3)通过考虑多个因子的影响,将中国主要陆地区域分为851种类别,通过采样和回归分析,建立的基于卫星遥感地表温度的气温推算模型取得了较好的精度,利用该模型建立的高空间分辨率近地表旬平均最高气温数据在精度上好于传统的插值气温数据,尤其在站点稀疏地区和地形复杂地区,有效弥补了传统的基于站点气温插值法的不足。
由于无法获取到与卫星遥感地表温度数据空间分辨率一致的降水、气压和风速等数据,该推算模型采用气候分区,结合下垫面分类的方法最大程度地避免这些动态因子的影响,尽管如此,仍无法准确地反映出降水、气压和风速等动态因子对气温和地表温度相关性的影响,因而成为该模型最主要的不足,也是该模型需要改进的主要地方。
致谢: 文中用到的气象观测数据由公益性行业(气象)科研专项“精细化农业气候区划及其应用系统研究(GYHY(QX)2007-6-7)”项目组提供,插值数据由江西省气象局气候中心提供,在此表示感谢。
| 姜会飞, 廖树华, 叶尔克江等. 2004. 地面温度与气温关系的统计分析. 中国农业气象, 25(3): 1-4 |
| 柯灵红, 王正兴, 宋春桥等. 2011. 青藏高原东北部MODIS地表温度重建及其与气温对比分析. 高原气象, 30(2): 277-287 |
| 李超, 刘厚通, 迟如利等. 2009. 草地下垫面地表温度与近地面气温的对比研究. 光学技术, 35(4): 635-639 |
| 毛飞, 孙函, 冯明等. 2009. 中华人民共和国气象行业标准——干湿气候区划分. 北京: 中国气象科学研究院,48pp |
| 齐述华, 王军邦, 张庆员元等. 2005. 利用MODIS遥感影像获取近地层气温的方法研究. 遥感学报, 9(5): 570-575 |
| 王旻燕, 吕达仁. 2005. GMS 5反演中国几类典型下垫面晴空地表温度的日变化及季节变化. 气象学报, 63(6): 957-968 |
| 张敏, 张荣霞, 王新燕. 2005. 聊城市地面温度与气温的相关分析. 山东气象, 25(4): 19-20 |
| 郑景云, 尹云鹤, 李炳元. 2010. 中国气候区划新方案. 地理学报, 65(1): 3-13 |
| 中国科学院自然区划工作委员会. 1959. 中国气候区划(初稿). 北京: 科学出版社 |
| 祝善友, 张桂欣, 尹球等. 2009. 基于多源极轨气象卫星热红外数据的近地表气温反演研究. 遥感技术与应用, 24(1): 27-31 |
| Colombi A, Pepe M, Rampini A, et al. 2007. Estimation of daily mean air temperature from MODIS LST in Alpine areas. EARSeL eProceedings, 6(3): 38-46 |
| Cresswell M P, Morse A P, Connor S J. 1997. Improved estimates of ambient air temperature for large area studies of vector bionomics. Transactions of the Royal Society of Tropical Medicine and Hygiene, 91(5): 502 |
| Cresswell M P, Morse A P, Thomson M C, et al. 1999. Estimating surface air temperatures, from Meteosat land surface temperatures, using an empirical solar zenith angle model. Int J Remote Sensing, 20 (6): 1125-1132 |
| Mostovoy G V, Mostovoy R, King K R, et al. 2005. Using MODIS LST data for high-resolution estimates of daily air temperature over Mississippi//Proceedings of the 3rd International Workshop on the Analysis of Multi-Temporal Remote Sensing Images. IEEE, CD Rom, 76-80 |
| Prihodko L, Goward S N. 1997. Estimation of air temperature from remotely sensed surface observations. Remote Sensing Environ, 60(3): 335-346 |
| Riddering J P, Queen L P. 2006. Estimating near-surface air temperature with NOAA AVHRR. Canadian J Remote Sensing, 32(1): 33-43 |
 2012, Vol. 70
2012, Vol. 70

