中国气象学会主办。
文章信息
- 陶建军, 胡向辉, 李朝奎. 2012.
- TAO Jianjun, HU Xianghui, LI Chaokui. 2012.
- 台风中涡旋波1波扰动的形成机制及其变化特征
- The formation mechanism and change characteristics of the wavenumber-1 vortex Rossby wave in the typhoon
- 气象学报, 70(6): 1200-1206
- Acta Meteorologica Sinica, 70(6): 1200-1206.
- http://dx.doi.org/10.11676/qxxb2012.101
-
文章历史
- 收稿日期:2011-08-31
- 改回日期:2012-05-23
由于台风中的螺旋云带是台风系统的一个重要组成部分,其变化直接影响着台风的灾害强度和移动路径,因此,长期以来有不少学者致力于其研究(余志豪,2002; Abdullah,1966; Chow et al,2002; Corbosiero et al,2006; 黄泓等,2008;黄思训等,2007;周秀骥等,2006;钟科等,2002;Montgomery et al,1997,1998; Moller et al,1999;Wang,2002a,2002b;陆汉城等,2007;钟玮等,2008;徐祥德等,2004;陶建军等,2008,2009;陈永林等,2009)。讨论的重点是形成机制及演变过程。最初有学者认为,螺旋云带是一种重力波,但由于在传播速度等问题上与实际不符,因此,Montgomery等(1997)提出了涡旋罗斯贝波的概念,因为其涡度方程中基本气流的涡度η的径向梯度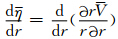 在动力学上等价于科里奥利参数f 随纬度变化的梯度(
在动力学上等价于科里奥利参数f 随纬度变化的梯度(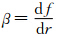 )而得名,这一概念得到很多学者的赞同。随后即有不少学者做过相关的研究。按照波动理论,涡旋罗斯贝波存在径向波数和切向波数,从卫星云图(图 1)和雷达回波上看,涡旋罗斯贝波多呈螺旋结构,因而在以往的研究中多注重切向波数1波和2波。Moller等(1999)利用正压模式,通过数值方法研究了基本涡旋中的一个初始位涡扰动演变为1波型涡旋罗斯贝波的过程。随后Wang(2002a,2002b)在三维模式下,利用数值方法研究了台风中螺旋云带的形成过程,也出现了1波和2波型涡旋罗斯贝波。近年来,陆汉城等(2007)利用飓风Bonnie(1998)高分辨率模拟资料,采用非对称波分量分离方法,也发现平衡流条件下1波型扰动的中尺度波动特征以涡旋波性质为主。因此,无论是从实际观测结果,还是理论研究来看,1波型和2波型涡旋罗斯贝波是客观存在的。如上所述,很多研究者都认为是环境场的涡度梯度激发出涡旋罗斯贝波,并将涡度梯度
)而得名,这一概念得到很多学者的赞同。随后即有不少学者做过相关的研究。按照波动理论,涡旋罗斯贝波存在径向波数和切向波数,从卫星云图(图 1)和雷达回波上看,涡旋罗斯贝波多呈螺旋结构,因而在以往的研究中多注重切向波数1波和2波。Moller等(1999)利用正压模式,通过数值方法研究了基本涡旋中的一个初始位涡扰动演变为1波型涡旋罗斯贝波的过程。随后Wang(2002a,2002b)在三维模式下,利用数值方法研究了台风中螺旋云带的形成过程,也出现了1波和2波型涡旋罗斯贝波。近年来,陆汉城等(2007)利用飓风Bonnie(1998)高分辨率模拟资料,采用非对称波分量分离方法,也发现平衡流条件下1波型扰动的中尺度波动特征以涡旋波性质为主。因此,无论是从实际观测结果,还是理论研究来看,1波型和2波型涡旋罗斯贝波是客观存在的。如上所述,很多研究者都认为是环境场的涡度梯度激发出涡旋罗斯贝波,并将涡度梯度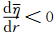 作为涡旋罗斯贝波的成波机制。不过以往的研究工作多放在数值模拟或诊断分析上,波动形成物理机制的研究尚少,这种波动生成和发展的物理机制目前还不甚清楚。陶建军等(2008,2009)曾从简单的正压无辐散涡度方程出发,取特定的基本流分布,使其满足
作为涡旋罗斯贝波的成波机制。不过以往的研究工作多放在数值模拟或诊断分析上,波动形成物理机制的研究尚少,这种波动生成和发展的物理机制目前还不甚清楚。陶建军等(2008,2009)曾从简单的正压无辐散涡度方程出发,取特定的基本流分布,使其满足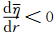 ,结果发现,将m=2代入频率方程时,扰动的增长率会很大,2波型扰动可以通过平流效应从基本流吸取能量而快速增长,用其可以解释台风和云系双臂(2波)形成的物理机制。不过当时并没有讨论1波不稳定发展的物理机制问题。但是,无论是从卫星云图等实际情况还是从数值模拟或诊断分析来看,1波扰动是客观存在的,所以对1波扰动的形成和发展的物理机制有必要进行更深入的探讨和研究。因此,本文将深入研究以下几个问题:(1)1波的稳定性,即在正压条件下,1波扰动是否也会从基本切向流吸取能量发展;(2)如果扰动发展的话,那么发展的物理机制怎样;(3)1波扰动在发展演变过程是否也和2波的发展过程一样。如果以上研究的结果是肯定的话,就进一步说明台风中确实存在涡旋罗斯贝波1波扰动。研究结果对于增强台风的预报准确率具有一定的意义。
,结果发现,将m=2代入频率方程时,扰动的增长率会很大,2波型扰动可以通过平流效应从基本流吸取能量而快速增长,用其可以解释台风和云系双臂(2波)形成的物理机制。不过当时并没有讨论1波不稳定发展的物理机制问题。但是,无论是从卫星云图等实际情况还是从数值模拟或诊断分析来看,1波扰动是客观存在的,所以对1波扰动的形成和发展的物理机制有必要进行更深入的探讨和研究。因此,本文将深入研究以下几个问题:(1)1波的稳定性,即在正压条件下,1波扰动是否也会从基本切向流吸取能量发展;(2)如果扰动发展的话,那么发展的物理机制怎样;(3)1波扰动在发展演变过程是否也和2波的发展过程一样。如果以上研究的结果是肯定的话,就进一步说明台风中确实存在涡旋罗斯贝波1波扰动。研究结果对于增强台风的预报准确率具有一定的意义。
 |
| 图 1 2011年台风梅花的卫星云图 Fig. 1 Satellite cloud pictures of Typhoon Muifa(2011) |
利用含基流的柱坐标下的线性涡度方程(余志豪,2002; Montgomery et al,1998;陶建军等,2009)
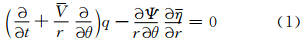

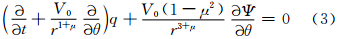
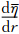 =
=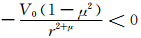 ,满足涡旋罗斯贝波的成波条件。
,满足涡旋罗斯贝波的成波条件。
考虑涡度场的发展过程,先讨论初始时刻的不稳定,可寻求以下形式的涡度场的初始解(陶建军等,2008,2009)
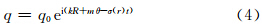
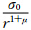 ,式(4)解表示一螺旋状的涡度场,当|kr|(kr是k的实部)很小时,则表示涡旋的涡度场呈不对称分布,螺旋结构不明显。由式(4),可设流函数为(陶建军等,2008,2009)
,式(4)解表示一螺旋状的涡度场,当|kr|(kr是k的实部)很小时,则表示涡旋的涡度场呈不对称分布,螺旋结构不明显。由式(4),可设流函数为(陶建军等,2008,2009)

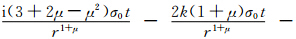
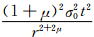 。流函数与涡度的关系则为
。流函数与涡度的关系则为
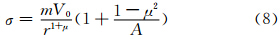
由于A为一复数,故σ亦为复数,令σ=σr+iσi,当σi为正时,扰动可出现不稳定增长。当m=1时,σi与kr和ki的关系如图 2所示。可以看出,当kr为很小的负值、ki接近1时,扰动的增长率将很大。由于解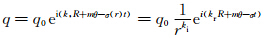 ,可见ki接近1意味着初始扰动主要集中在涡旋中心附近,扰动随半径增加而递减。|kr|很小表示解为1波非对称涡度扰动,但螺旋结构不明显(图 3)。这与Thomas等(1993)研究飓风时取的初始基本场解相似,他们讨论了基本场演变为2波螺旋结构的过程,不过当时假定最大风速以外η=0,亦即
,可见ki接近1意味着初始扰动主要集中在涡旋中心附近,扰动随半径增加而递减。|kr|很小表示解为1波非对称涡度扰动,但螺旋结构不明显(图 3)。这与Thomas等(1993)研究飓风时取的初始基本场解相似,他们讨论了基本场演变为2波螺旋结构的过程,不过当时假定最大风速以外η=0,亦即 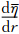 =0,因此,螺旋结构未出现发展过程。而本文结论说明,涡旋中非对称1波扰动可以从基本流场中吸取能量增长,且增长速度可以很大,这意味着即使初始时刻涡度场出现微小的非对称扰动,这种扰动会在较短时间内增长加强。由于基本流对扰动悬臂的作用,将使扰动演变为螺旋状形态。不过由于扰动旋臂的缠卷越来越紧,ω(r,t)将很快增大,由式(7)可知,径向速度也很快变小,增长率也很快减小,即当
=0,因此,螺旋结构未出现发展过程。而本文结论说明,涡旋中非对称1波扰动可以从基本流场中吸取能量增长,且增长速度可以很大,这意味着即使初始时刻涡度场出现微小的非对称扰动,这种扰动会在较短时间内增长加强。由于基本流对扰动悬臂的作用,将使扰动演变为螺旋状形态。不过由于扰动旋臂的缠卷越来越紧,ω(r,t)将很快增大,由式(7)可知,径向速度也很快变小,增长率也很快减小,即当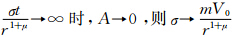 ,此时螺旋波不再发展,因此,这种不稳定将受到时间限制,不会呈自然指数增长。不过,当初始时刻增长率较大时,扰动会在短时间内发展成规模。
,此时螺旋波不再发展,因此,这种不稳定将受到时间限制,不会呈自然指数增长。不过,当初始时刻增长率较大时,扰动会在短时间内发展成规模。
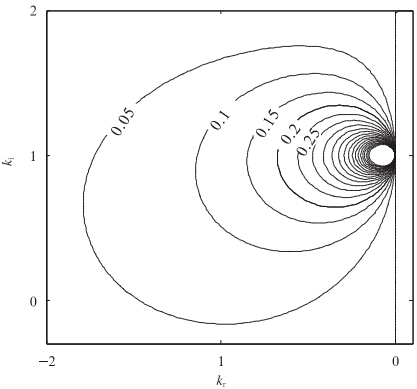 |
| 图 2 r=1处扰动增长率(对于台风,单位为10-3)与径向波数k的关系(μ=0.5,V0=0.4,m=1,下同) Fig. 2 Relationship between the disturbance growth rate and the radial wave number at r=1(μ=0.5,V0=0.4,and m=1 are set; the same below) |
下面讨论为什么当μ<1,k取小的负数时扰动会迅速发展。对于1波初始涡度扰动,由式(7)可得扰动的切向和径向速度分别为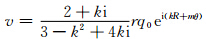 和
和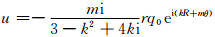
图 3a是发展型扰动对应的总涡度场和扰动速度矢量场。图中的A点表示在平均基流涡度场上叠加了正的涡度扰动值,B点具有负的扰动值,整个涡度场呈非对称状。可见对于发展型扰动,扰动涡度产生的速度场将基本场正涡度区平流至扰动场的正涡度区(A点),使扰动涡度增大,扰动涡度的增大又将使扰动速度增大,这时平流作用也跟着增大,这是一种正反馈过程。如图 3a中A点扰动正涡度将增大,B点负涡度增大,扰动加强,整个涡度场的非对称性将进一步加强,加上基本流对扰动悬臂的缠卷作用,扰动逐渐演变为螺旋状(图 6)。
 |
| 图 3 扰动物理机制示意图(等值线为总的涡度场,矢量为初始扰动速度,取μ=0.6,V0=0.4,m=1,初值为q0r=0.0,q0i=0.03; a.发展型,kr=-0.06,ki=1.1; b.衰减型,kr=0.2,ki=0.8) Fig. 3 Physical mechanism sketch map for the development disturbance(a) and the decay disturbance(b)(Contours are for the total vorticity field,and the initial disturbance velocity are denoted by vectors. μ=0.6,V0=0.4; m=1; q0r=0.0,and q0i=0.03 are set; Set kr= -0.06,ki=1.1 in Fig(a); and set kr=0.2,ki=0.8 in Fig(b)) |
相反,图 3b为衰减型扰动,这时图中A点具有负的涡度平流,B点具有正的涡度平流,扰动将减弱,涡度场趋于对称结构。
可见扰动是从基本切向流吸取能量增长的。但由于扰动涡度场结构的快速变化,平流效应会停止,扰动增长也将停止。值得注意的是,图 3的基本流涡度场正好满足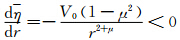 ,即涡旋罗斯贝波的成波条件。在这里,
,即涡旋罗斯贝波的成波条件。在这里,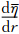 <0也是涡旋罗斯贝波形成和发展的充分必要条件。
<0也是涡旋罗斯贝波形成和发展的充分必要条件。
由式(8)亦可知,增长率与轮廓系数μ有关,轮廓系数越大,即台风范围越小,增长率越小,意味着尺度较小的台风其螺旋波动发展较慢;相反,尺度较大的台风螺旋波动发展较快,后文的数值计算结果也印证了这一点。4 扰动场的演变
前面定性分析了1波扰动初始时刻的不稳定性及扰动的发展机制,但由于频率中含变量r,随着时间的增加,
波动振幅不再是r的缓变量,所以,要进一步了解扰动的增长变化过程,必须利用数值计算方法。
下面讨论扰动场随时间发展演变过程和螺旋臂的形成。如果将式(3)的解写为
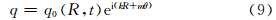

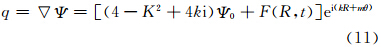
式中,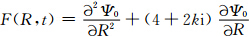 ,所以
,所以

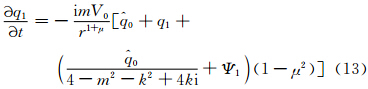
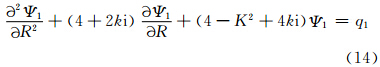
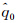 为初始值,与R和t无关,即假设初始时刻涡度场径向分布较为均匀。
为初始值,与R和t无关,即假设初始时刻涡度场径向分布较为均匀。
将式(13)、(14)化为差分方程,先利用初值(q0r=0.01,q0i=0,Ψ1,t=0=0,q1,t=0=0),通过式(13)求出下一时刻的q1,再由式(14)用追赶法解出Ψ1,如此循环,可得q1的时间变化序列值。计算时,径向取400个格点,R的积分区域为0—2;边界值近似取上一时刻的插值。参数取μ=0.5,V0=0.4,m=1,kr=-0.04,ki=0.8。
从计算得到的扰动振幅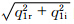 的时间变化过程(图 4)可以看出,虽然模式是线性方程,但随着时间的增长,扰动并未呈指数增长,而是出现周期振 荡,且离中心越近,扰动发展越快,减弱也快,振荡的周期越短,距离中心越远,则扰动发展越慢,周期越长,整体上看,扰动向外拓展。分析式(8)可知,当σt很大(即当
的时间变化过程(图 4)可以看出,虽然模式是线性方程,但随着时间的增长,扰动并未呈指数增长,而是出现周期振 荡,且离中心越近,扰动发展越快,减弱也快,振荡的周期越短,距离中心越远,则扰动发展越慢,周期越长,整体上看,扰动向外拓展。分析式(8)可知,当σt很大(即当 →∞)时,ω(r,t)→∞,A→∞,则σ→
→∞)时,ω(r,t)→∞,A→∞,则σ→ 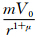 ,此时螺旋波不再发展,即虽然是线性方程,但扰动不会出现呈自然指数形式增长。
,此时螺旋波不再发展,即虽然是线性方程,但扰动不会出现呈自然指数形式增长。
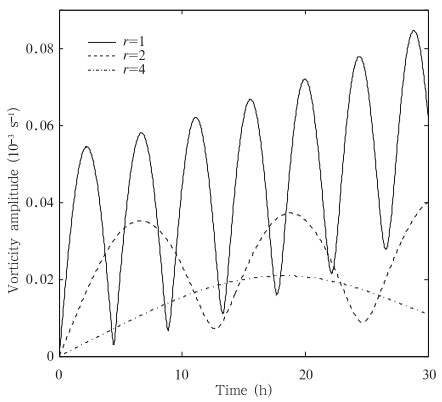 |
图 4 在不同半径处扰动振幅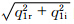 随时间的变化 Fig. 4 Temporal change of the disturbance amplitude 随时间的变化 Fig. 4 Temporal change of the disturbance amplitude 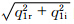 for the different radii for the different radii |
从不同轮廓系数μ下的距中心r=2(200 km)处扰动振幅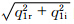 的时间变化(图 5)可见,轮廓系数μ越大,即台风的范围越小时,振幅变化的幅度越小,螺旋波相对较弱,变化的频率也越低,相反,轮廓系数μ越小,即台风的范围越大时,振幅变化的幅度也越大,螺旋云带也会越强。
的时间变化(图 5)可见,轮廓系数μ越大,即台风的范围越小时,振幅变化的幅度越小,螺旋波相对较弱,变化的频率也越低,相反,轮廓系数μ越小,即台风的范围越大时,振幅变化的幅度也越大,螺旋云带也会越强。
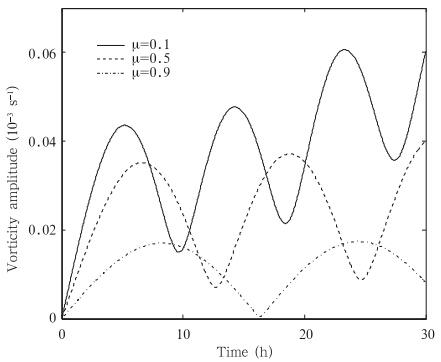 |
图 5 在r=2处不同轮廓系数μ下的扰动振幅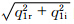 随时间的变化 Fig. 5 Temporal change of the disturbance amplitude 随时间的变化 Fig. 5 Temporal change of the disturbance amplitude 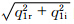 for the different profile coefficient μ at r=2 for the different profile coefficient μ at r=2 |
从扰动的演变过程(图 6)可看出一个有趣的现象,首先,随着时间的增长,1波扰动逐步发展,初始时刻,扰动不是很明显,随着时间的增长,至6 h,显现1波扰动,随后扰动一边随着基本流旋转,一边向外扩展和传播,这些都符合实际大气的情况。此外,从18 h扰动涡度场的螺旋带的分布特点以及结构形式可以看出,扰动随切向分布是不均匀的,在某些象限扰动始终明显突出,这与钟玮等(2008)的涡度场的分布相似。也与 Moller等(1999)和Montgomery等(1998)关于1波的研究结果相似,不过Moller等(1999)和Montgomery等(1998)的结果是由已有的中尺度涡旋转变而成,而本研究的结果是扰动通过平流效应从基本流吸收能量发展演变而形成,可能更具有普遍意义。此外,扰动的结构形式以及螺旋云带在某一象限突出且向外传播的这一特点也与实际雷达回波较为吻合(包澄澜,1980;Corbosiero et al,2006; 陈永林等,2009)。
 |
| 图 6 1波扰动的发展过程(a—d.0、6、12、18 h;μ=0.5,V0=0.4;kr=-0.04,ki=0.8,m=1,初值为q0r=0.01,q0i=0.01;填充彩色为涡度值) Fig. 6 Development process for the 1-wave disturbance(a. 0 h,b. 6 h,c. 12 h,d. 18 h; μ=0.5,V0=0.4; kr=-0.04,ki=0.8,m=1 are set. Initial value: q0r=0.01,q0i=0.01;vorticity value is coloured) |
利用柱坐标下的流体涡度方程,在最简单的基本流下求解析解,研究了涡旋中涡旋罗斯贝波扰动中1波的不稳定发展及其机制。结果表明,当基本流涡度梯度小于0(即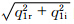 <0)时,由于扰动速度场对于基本涡度场的强平流效应,1波(m=1)扰动可从基本流吸取能量而出现不稳定快速增长,其增长率受时间限制,并形成螺旋带状向外扩展。
<0)时,由于扰动速度场对于基本涡度场的强平流效应,1波(m=1)扰动可从基本流吸取能量而出现不稳定快速增长,其增长率受时间限制,并形成螺旋带状向外扩展。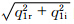 <0不仅是涡旋罗斯贝波的成波条件,还是其形成和发展的必要条件。研究还表明,大尺度台风的螺旋云带比小尺度台风的螺旋云带发展更快。这些都符合实际大气的情况。这里涡度场的螺旋状分布特点以及结构形式与Moller等(1999)关于1波的研究结果相似,扰动结构的分布和变化也与实际雷达回波相似(包澄澜,1980;Corbosiero et al,2006;陈永林等,2009)。
<0不仅是涡旋罗斯贝波的成波条件,还是其形成和发展的必要条件。研究还表明,大尺度台风的螺旋云带比小尺度台风的螺旋云带发展更快。这些都符合实际大气的情况。这里涡度场的螺旋状分布特点以及结构形式与Moller等(1999)关于1波的研究结果相似,扰动结构的分布和变化也与实际雷达回波相似(包澄澜,1980;Corbosiero et al,2006;陈永林等,2009)。
| 包澄澜. 1980. 热带天气学. 北京: 科学出版社, 250-300 |
| 陈永林, 王智, 曹晓岗等. 2009. 0509号台风 (Matsa) 登陆螺旋云带的增幅及其台前飑线的特征研究. 气象学报, 67(5): 828-839 |
| 黄泓, 张铭. 2008. 热带气旋螺旋云带动力不稳定的性质. 气象学报, 66(1): 81-89 |
| 黄思训, 蔡其发, 项杰等. 2007. 台风风场分解. 物理学报, 56(5): 3022-3027 |
| 陆汉城, 钟玮, 张大林. 2007. 热带风暴中波动特征的研究进展和问题. 大气科学, 31(6): 1140-1150 |
| 陶建军, 李朝奎. 2008. 流体涡旋中螺旋波不稳定发展的理论研究. 地球物理学报, 51(3): 650-656 |
| 陶建军, 李朝奎. 2009. 涡旋中双臂形成的物理机制及其演变. 物理学报, 58(6): 4313-4318 |
| 徐祥德, 张胜军, 陈联寿等. 2004. 台风涡旋螺旋波及其波列传播动力学特征:诊断分析. 地球物理学报, 47(1): 35-41 |
| 余志豪. 2002. 台风螺旋云带——涡旋Rossby波. 气象学报, 60(4): 502-506 |
| 钟科, 康建伟, 余清平. 2002. 飓风中的涡旋Rossby波. 气象学报, 60(4): 436-442 |
| 钟玮, 陆汉城, 张大林. 2008. 非对称型强飓风中的准平衡流特征分析. 地球物理学报, 51(3): 663-666 |
| 周秀骥, 罗哲贤, 高守亭. 2006. 涡旋自组织的两类可能机制. 中国科学(D), 36(2): 201-208 |
| Abdullah A J. 1966. The spiral bands of a hurricane: A possible dynamic explanation. J Atmos Sci, 23(4): 367-375 |
| Chow K C, Chan K L, Lau A K H. 2002. Generation of moving spiral bands in tropical cyclones. J Atmos Sci, 59(20): 2930-2950 |
| Corbosiero K L, Molinari J, Aiyyer A R, et al. 2006. The structure and evolution of hurricane Elena (1985). Part II: Convective asymmetries and evidence for vortex Rossby waves. Mon Wea Rev, 134(11): 3073-3091 |
| Montgomery M T, Kaiienbach R J. 1997. A theory of vortex Rossby wave and application to spiral bands and intensity changes in hurricanes. Quart J Roy Meteor Soc, 123(538): 436-453 |
| Montgomery M T, Enagonio J. 1998. Tropical cyclogenesis via convectively forced vortex Rossby waves in a three-dimensional quasigeostrophic model. J Atmos Sci, 55(20): 3176-3207 |
| Moller J D, Montgomery M T. 1999. Vortex Rossby waves and hurricane intensification in a bar tropic model. J Atmos Sci, 56: 1674-1687 |
| Thomas A G, Wayne H S. 1993. Hurricane spiral bands. J Atmos Sci, 50(20): 3380-3403 |
| Wang Y Q. 2002a. Vortex Rossby wave in numerically simulated tropical cyclone. Ⅰ:Overall structure, potential vorticity, and kinetic energy budgets. J Atmos Sci, 59(7): 1213-1238 |
| Wang Y Q. 2002b. Vortex Rossby wave in numerically simulated tropical cyclone. Ⅱ:The role in tropical cyclone structure and intensity change. J Atmos Sci, 59(7): 1239-1262 |
 2012, Vol. 70
2012, Vol. 70

