中国气象学会主办。
文章信息
- 权维俊, 韩秀珍, 陈洪滨. 2012.
- QUAN Weijun, HAN Xiuzhen, CHEN Hongbin. 2012.
- 基于AVHRR和VIRR数据的改进型Becker“分裂窗”地表温度反演算法
- A modified Becker’s split window approach for retrieving land surface temperature from the AVHRR and VIRR data
- 气象学报, 70(6): 1356-1366
- Acta Meteorologica Sinica, 70(6): 1356-1366.
- http://dx.doi.org/10.11676/qxxb2012.114
-
文章历史
- 收稿日期:2011-04-06
- 改回日期:2011-08-03
2. 北京市气候中心,北京,100089;
3. 国家卫星气象中心,北京,100081
2. Beijing Municipal Climate Center, Beijing 100089, China;
3. National Satellite Meteorological Center, Beijing 100081, China
地表温度(L and surface temperature,LST)是一个非常重要的环境参数,在潜热和感热通量的估算中有着直接或间接的作用,而且,在地质学、水文学、植被监测、全球环流模式(GCM)等其他应用领域也依赖于对地表温度的了解。因此,在空间和时间上可靠的大范围地表温度估算产品在许多研究中都是至关重要的(Quattrochi et al,2000)。由于卫星能够提供地基观测难以提供的全球范围内的地表温度产品,利用卫星热红外通道观测数据进行地表温度反演研究是定量遥感中的热点问题之一。甚高分辨率辐射计(AVHRR)是搭载在由美国国家海洋和大气管理局(NOAA)负责运行的极轨业务环境卫星(POES)上的扫描辐射计。搭载在TIROS-N、NOAA-6、NOAA-8和NOAA-10上的第一代AVHRR(AVHRR/1)拥有4个通道,分别是可见光通道(0.58—0.68 μm)、近红外通道(0.725—1.0 μm)、中红外通道(3.55—3.93 μm)和热红外通道(10.3—11.3 μm);第2代AVHRR(AVHRR/2)搭载在NOAA-7、NOAA-9、NOAA-11、NOAA-12和NOAA-14 上(简记为AVHRR-7、-9、-11、-12、-14),与第1代AVHRR相比增加了一个11.5—12.5 μm的“分裂窗”通道;第3代AVHRR(AVHRR/3)搭载在NOAA-15、 NOAA-16、NOAA-17、NOAA-18和METOP卫星上(简记为AVHRR-15、-16、-17、-18、-M),这一代AVHRR又多出一个1.58—1.64 μm的短波红外通道(NOAASIS,2011)。中国于2008年5月27日成功发射了第2代极轨气象卫星的首发星——风云三号A星(FY-3A),其搭载的可见光红外扫描辐射计(Visible and InfraRed Radiometer,VIRR)拥有10个观测通道,其中,前6个通道的光谱范围与AVHRR相应通道的光谱范围相同或接近,FY-3是中国目前综合探测能力最强的应用卫星(杨军等,2009)。
中外科学家在利用AVHRR热红外通道观测数据反演地表温度方面已经做了大量的工作(Price,1984;Becker et al,1990)。其主要方法是所谓的“分裂窗”方法,该方法利用AVHRR通道4、5的亮温差来纠正海表温度和地表温度反演中的大气影响(Quattrochi et al,2000)。分裂窗算法的基本特点是地表温度可以表示成通道4、5亮温的线性组合(McClain et al,1983;Price,1984;Prata et al,1991;Ulivieri et al,1994)。但Sobrino等(1993)提出的算法有所不同,因为在其算法中,地表温度是通道4、5亮温的一个2次多项式,其中,2次项用来说明通道4、5亮温差中的非线性变化部分。值得注意的是,这些分裂窗算法是针对不同AVHRR传感器而提出的,例如Price(1984)算法、Becker等(1990)算法、Sobrino等(1993)算法分别是根据AVHRR-7、-9、-11而提出的。不同AVHRR的通道4、5的光谱响应函数存在差异,这对热红外通道亮温的计算是有影响的(Czajkowski et al,1998)。因此,如果将基于AVHRR-9数据提出的Becker和Li的分裂窗算法应用于其他AVHRR数据,地表温度的反演误差可达2.3 K(Czajkowski et al,1998)。杨虎等(2006)利用MODTRAN 4(Berk et al,1999)在4种标准大气、12种地表温度和一系列在0.90—1.0变化的地表比辐射率组合下的模拟结果,并结合AVHRR-16、-17的通道4、5的光谱响应函数重新计算了Becker和Li算法中的参数,提出了适合于AVHRR-16、-17的改进型分裂窗算法。
本文在已有研究的基础上,从辐射传输方程出发,根据MODTRAN模拟数据结合AVHRR和VIRR热红外通道光谱响应函数,提出一个适用于AVHRR和VIRR的具有较高精度的改进型Becker和Li分裂窗地表温度反演算法,以提高利用不同AVHRR和VIRR数据反演的地表温度的可比性,从而满足在气候变化研究中对长序列、高分辨率地表温度数据的需求。在改进Becker和Li算法的过程中,首先利用MODTRAN 4模拟了6种标准大气、10种CO2混合比(与NOAA和FY-3A卫星运行年份相对应)、6种边界温度、18种典型地物和2个光谱间隔组成的共12960种条件下,到达卫星的热红外光谱辐亮
度数据;然后结合AVHRR和VIRR通道4、5的光谱响应函数对该光谱辐亮度数据进行加权平均运算和亮温计算,得到了温度数据集(TS,T4,T5);最后根据该温度数据集采用最小二乘法重新计算Becker和Li分裂窗地表温度反演算法中的各参数,从而提出了适用于AVHRR和VIRR的改进型分裂窗地表温度反演算法。并利用改进型算法对一景AVHRR-17数据进行了地表温度反演,将反演结果与MODIS的地表温度产品进行了对比分析。2 理论基础 2.1 辐射传输方程
处于局地热力平衡的晴空大气,热红外谱段大气的散射效应可以忽略(Becker,1987)。在这种情况下,卫星传感器接收的辐亮度(图 1)(Kahle et al,1980;Becker,1987;Sobrino et al,2004a)为
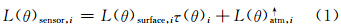
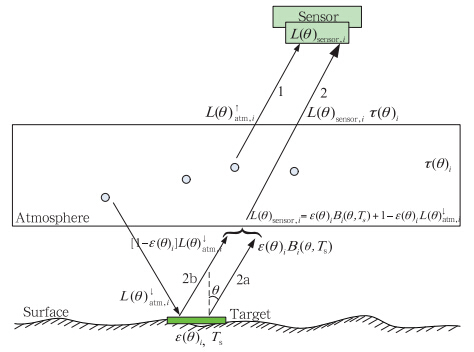 |
| 图 1 到达卫星传感器的热红外辐亮度 Fig. 1 Thermal radiance reaching at the sensor on a satellite |
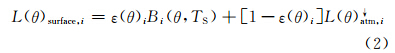
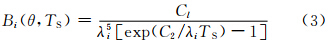
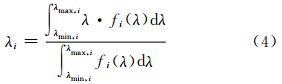
大气对地表发射的热红外辐射的衰减与两个热红外通道观测的辐亮度之差成比例(McMillin,1975)。Becker等(1990)经过理论推导提出,真实的地表温度可以表示为卫星两个相邻通道亮温的线性组合,其系数依赖于光谱比辐射率而不依赖于大气条件。Becker和Li的“分裂窗”地表温度反演方程为
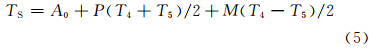
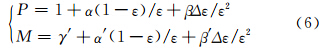
为了获取式(6)中的系数A0 、α、β、γ′、α′和β′,需要一个温度数据集(TS,T4,T5)。然而,通过地表温度的星地同步观测方法来获取该数据集实际上是很困难的,利用模式计算的大气透过率、大气和地表发射的热辐射来构建该数据集是一个可行的办法(Becker et al,1990)。为此,利用MODTRAN 4模拟的12960种不同地表和大气条件组合下的辐亮度数据来构建温度数据集,模拟时的MODTRAN输入参数设置为
(1)6种标准大气,即副极地冬季大气、中纬度冬季大气、1976 美国标准大气、副极地夏季大气、中纬度夏季大气和热带大气。水汽含量选用这些标准大气的缺省值,分别为0.38、0.87、1.44、2.12、2.98和4.19 g/cm2,代表了从非常干燥大气到湿润大气的条件。
(2)由于CO2的混合比以1%—2%的年增长率增加,且1995年的推荐值为(355—360)×10-6(V/V)(Kneisys et al,1995),考虑到不同NOAA和FY-3A卫星运行年份所对应的CO2混合比会有所差异,以1995年的CO2 混合比为基准值,采用线性插值方法得到卫星运行年份相对应的CO2 混合比作为MODTRAN的输入参数,相应于从NOAA-7(1981年)到NOAA-18或FY-3A(目前),CO2 混合比在(349—373)×10-6(V/V)。
(3)MODTRAN模式中的边界温度(TBOUND项)由标准大气0 km高度的基准温度 T0和一个温度偏移量ΔT组成。ΔT的取值为-5、0、5、10、15和20 K,这样对每一种标准大气,总共设置了6个初始边界温度,代表了从比基准温度低5 K到高20 K的一个较大的变化范围。对应的6种标准大气初始边界温度的值分别为257.2、272.2、288.2、287.2、284.2和299.7 K。
(4)考虑到地表状况的真实性,使用了John Hopkins大学(JHU)的0.4—14 μm光谱比辐射率数据库(Salisbury et al,1991,1992,1994;Korb et al,1996)。共选用了18种典型地物,分别为4种土壤、4种岩石、3种植被、3种水体和4种不同粒度的雪,并计算了通道4、5的比辐射率(表 1)。
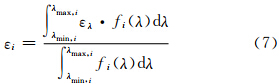
| 地表类型 | AVHRR-7 | AVHRR-9 | AVHRR-11 | AVHRR-12 | AVHRR-14 | |||||
| 通道4 通道5 | 通道4 通道5 | 通道4 通道5 | 通道4 通道5 | 通道4 通道5 | ||||||
| 土壤 | ||||||||||
| 细沙壤土 | 0.9646 0.9752 | 0.9644 0.9748 | 0.9645 0.9752 | 0.9651 0.9756 | 0.9643 0.9759 | |||||
| 粗沙壤土 | 0.9729 0.9743 | 0.9730 0.9736 | 0.9729 0.9742 | 0.9726 0.9749 | 0.9729 0.9754 | |||||
| 含有机质的壤土 | 0.9734 0.9788 | 0.9733 0.9783 | 0.9733 0.9788 | 0.9736 0.9793 | 0.9731 0.9796 | |||||
| 粘土 | 0.9780 0.9807 | 0.9779 0.9801 | 0.9779 0.9807 | 0.9780 0.9812 | 0.9780 0.9817 | |||||
| 岩石 | ||||||||||
| 玄武岩 | 0.9040 0.9555 | 0.9032 0.9532 | 0.9039 0.9547 | 0.9072 0.9572 | 0.9048 0.9584 | |||||
| 花岗岩 | 0.9123 0.9534 | 0.9106 0.9529 | 0.9117 0.9534 | 0.9160 0.9538 | 0.9094 0.9540 | |||||
| 石灰石 | 0.9677 0.9772 | 0.9675 0.9767 | 0.9677 0.9771 | 0.9684 0.9776 | 0.9675 0.9779 | |||||
| 粉砂岩 | 0.9631 0.9691 | 0.9632 0.9681 | 0.9631 0.9689 | 0.9628 0.9700 | 0.9632 0.9707 | |||||
| 植被 | ||||||||||
| 草地 | 0.9824 0.9885 | 0.9822 0.9884 | 0.9824 0.9884 | 0.9830 0.9885 | 0.9823 0.9885 | |||||
| 落叶树 | 0.9735 0.9731 | 0.9736 0.9730 | 0.9735 0.9730 | 0.9733 0.9732 | 0.9737 0.9732 | |||||
| 针叶树 | 0.9889 0.9907 | 0.9889 0.9906 | 0.9889 0.9907 | 0.9890 0.9908 | 0.9890 0.9909 | |||||
| 水体 | ||||||||||
| 海水 | 0.9904 0.9866 | 0.9904 0.9872 | 0.9904 0.9868 | 0.9904 0.9862 | 0.9903 0.9859 | |||||
| 海水泡沫 | 0.9905 0.9874 | 0.9905 0.9879 | 0.9905 0.9875 | 0.9905 0.9870 | 0.9904 0.9867 | |||||
| 纯净水 | 0.9907 0.9862 | 0.9907 0.9867 | 0.9907 0.9863 | 0.9907 0.9857 | 0.9906 0.9854 | |||||
| 雪 | ||||||||||
| 霜 | 0.9933 0.9912 | 0.9932 0.9913 | 0.9932 0.9913 | 0.9933 0.9911 | 0.9929 0.9910 | |||||
| 粗粒子雪 | 0.9864 0.9642 | 0.9869 0.9652 | 0.9865 0.9645 | 0.9848 0.9635 | 0.9864 0.9629 | |||||
| 中等粒子雪 | 0.9916 0.9806 | 0.9918 0.9810 | 0.9916 0.9807 | 0.9907 0.9802 | 0.9916 0.9800 | |||||
| 细粒子雪 | 0.9956 0.9898 | 0.9958 0.9900 | 0.9957 0.9899 | 0.9952 0.9897 | 0.9957 0.9895 | |||||
| 土壤 | ||||||||||
| 细沙壤土 | 0.9647 0.9758 | 0.9652 0.9752 | 0.9645 0.9757 | 0.9645 0.9759 | 0.9645 0.9749 | |||||
| 粗沙壤土 | 0.9728 0.9744 | 0.9724 0.9751 | 0.9728 0.9745 | 0.9729 0.9755 | 0.9728 0.9757 | |||||
| 含有机质的壤土 | 0.9734 0.9791 | 0.9736 0.9793 | 0.9733 0.9791 | 0.9733 0.9798 | 0.9731 0.9796 | |||||
| 粘土 | 0.9779 0.9808 | 0.9779 0.9812 | 0.9779 0.9808 | 0.9779 0.9818 | 0.9780 0.9820 | |||||
| 岩石 | ||||||||||
| 玄武岩 | 0.9051 0.9561 | 0.9092 0.9579 | 0.9045 0.9562 | 0.9042 0.9592 | 0.9067 0.9583 | |||||
| 花岗岩 | 0.9130 0.9545 | 0.9173 0.9530 | 0.9118 0.9543 | 0.9116 0.9538 | 0.9105 0.9517 | |||||
| 石灰石 | 0.9679 0.9775 | 0.9685 0.9776 | 0.9679 0.9775 | 0.9677 0.9780 | 0.9678 0.9774 | |||||
| 粉砂岩 | 0.9630 0.9693 | 0.9628 0.9704 | 0.9630 0.9693 | 0.9631 0.9710 | 0.9632 0.9712 | |||||
| 植被 | ||||||||||
| 草地 | 0.9826 0.9885 | 0.9832 0.9886 | 0.9825 0.9885 | 0.9824 0.9886 | 0.9827 0.9884 | |||||
| 落叶树 | 0.9735 0.9731 | 0.9733 0.9732 | 0.9735 0.9731 | 0.9735 0.9733 | 0.9736 0.9734 | |||||
| 针叶树 | 0.9890 0.9908 | 0.9891 0.9908 | 0.9890 0.9908 | 0.9890 0.9909 | 0.9890 0.9909 | |||||
| 水体 | ||||||||||
| 海水 | 0.9904 0.9865 | 0.9904 0.9861 | 0.9904 0.9865 | 0.9904 0.9857 | 0.9903 0.9855 | |||||
| 海水泡沫 | 0.9905 0.9873 | 0.9905 0.9869 | 0.9905 0.9873 | 0.9905 0.9866 | 0.9904 0.9864 | |||||
| 纯净水 | 0.9907 0.9861 | 0.9907 0.9855 | 0.9907 0.9861 | 0.9907 0.9852 | 0.9905 0.9850 | |||||
| 雪 | ||||||||||
| 霜 | 0.9932 0.9912 | 0.9932 0.9910 | 0.9931 0.9911 | 0.9932 0.9910 | 0.9928 0.9910 | |||||
| 粗粒子雪 | 0.9859 0.9639 | 0.9839 0.9632 | 0.9862 0.9639 | 0.9864 0.9626 | 0.9855 0.9629 | |||||
| 中等粒子雪 | 0.9913 0.9805 | 0.9902 0.9801 | 0.9914 0.9804 | 0.9916 0.9799 | 0.9911 0.9800 | |||||
| 细粒子雪 | 0.9955 0.9898 | 0.9949 0.9896 | 0.9956 0.9898 | 0.9956 0.9895 | 0.9954 0.9996 | |||||
(5)从表 1可见,同一地物在不同的AVHRR和VIRR通道4、5平均比辐射率有一定的差异,因此,在模拟时,分别选用10.0—12.0、11.0—13.0 μm两个光谱区间进行。3.2 构建温度数据集
温度数据集中的地表温度TS为MODTRAN模拟时输入的边界温度,TS=T0+ΔT;通道4、5的亮温T4、T5需要根据MODTRAN输出结果中的光谱辐亮度数据和光谱响应函数来计算。
在MODTRAN的输出文件tape 7中的TOTAL RAD项是到达卫星传感器的总的光谱辐亮度,即L(λ)等于TOTAL RAD。根据NOAA/NESDIS 对AVHRR热红外通道的定标方法(Robel,2007,2009),要将MODTRAN模拟的光谱辐亮度转换为通道的亮温需进行以下两步操作:
(1)计算热红外通道4和5的加权平均光谱辐亮度LE,i
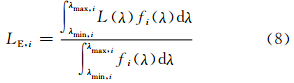
(2)根据逆普朗克公式将通道的加权平均光谱辐亮度转换为通道的亮温
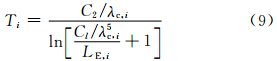
值得注意的是,AVHRR/2的通道4、5的中心波长将随不同温度范围而变化(表 2)。
| 传感器 | 温度范围(K) | 中心波长(μm) | |
| 通道4 | 通道5 | ||
| AVHRR-7 | 180—225 | 10.797 | 11.903 |
| 225—275 | 10.790 | 11.898 | |
| 275—320 | 10.785 | 11.892 | |
| AHVRR-9 | 180—225 | 10.770 | 11.843 |
| 225—275 | 10.764 | 11.837 | |
| 275—320 | 10.759 | 11.832 | |
| AVHRR-11 | 180—225 | 10.790 | 11.885 |
| 225—275 | 10.783 | 11.879 | |
| 275—320 | 10.778 | 11.874 | |
| 270—310 | 10.779 | 11.875 | |
| AVHRR-12 | 190—230 | 10.869 | 11.952 |
| 230—270 | 10.863 | 11.947 | |
| 270—310 | 10.857 | 11.942 | |
| 290—330 | 10.855 | 11.939 | |
| AVHRR-14 | 190—230 | 10.773 | 11.984 |
| 230—270 | 10.766 | 11.979 | |
| 270—310 | 10.760 | 11.974 | |
| 290—330 | 10.757 | 11.971 | |
对AVHRR/3和VIRR,亮温的计算采用了固定中心波长结合校正系数的方法取代AVHRR/2采用的非固定中心波长的方法来进行定标(Robel,2009; 国家卫星气象中心,2009)
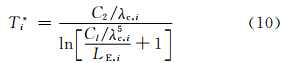

| 传感器 | 通道 | 中心波长(μm) | A | B |
| AVHRR-15 | 4 | 10.806 | 0.337810 | 0.998719 |
| 5 | 11.906 | 0.304558 | 0.999024 | |
| AVHRR-16 | 4 | 10.902 | 0.332380 | 0.998522 |
| 5 | 11.931 | 0.674623 | 0.998363 | |
| AVHRR-17 | 4 | 10.796 | 0.271683 | 0.998794 |
| 5 | 11.907 | 0.309180 | 0.999012 | |
| AVHRR-18 | 4 | 10.774 | 0.436645 | 0.998607 |
| 5 | 12.001 | 0.253179 | 0.999057 | |
| VIRR | 4 | 10.829 | 0.200025 | 0.997917 |
| 5 | 12.045 | 0.131499 | 0.998205 |
根据式(9)、(11)计算的AVHRR和VIRR通道4、5的亮温被用于计算平均亮温和亮温差(图 2)。通道4、5的亮温平均值与地表温度有较好的线性关系(图 2a),亮温差也与地表温度有近似线性关系(图 2b)。由此可见,地表温度可用亮温平均值与亮温差的线性关系式来表示,本文采用了Becker和Li的线性方程式(5)。
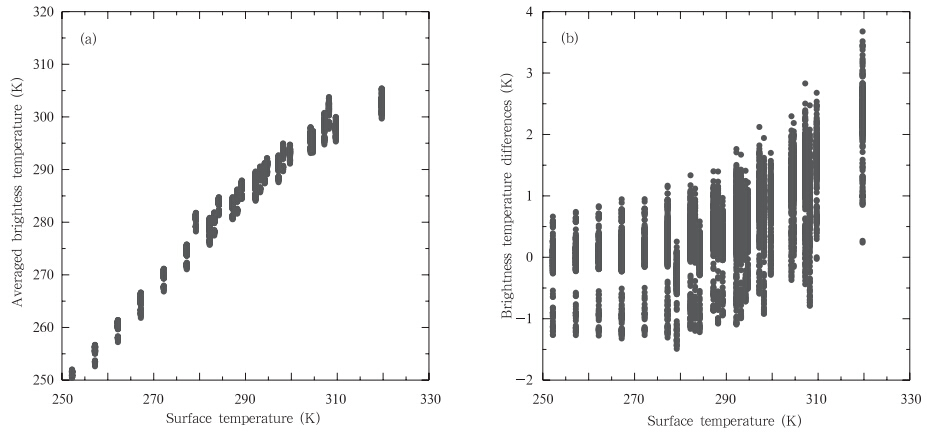 |
| 图 2 通道4、5的(a)平均亮温(T4+T5)/2及(b)亮温差(T4-T5)/2与地表温度的比较 Fig. 2 Comparison of the averaged brightness temperature(T4+T5)/2(a) and brightness temperature differences(T4-T5)/2(b)with the surface temperature |
地表比辐射率是影响亮温的一个重要地表参数(图 3),当地表温度为284.2 K、大气为中纬度夏季大气时,平均比辐射率对通道4、5的亮温平均值的影响最大可达6 K;地表比辐射率差值Δε对通道4、5的亮温差的影响也可达3 K。
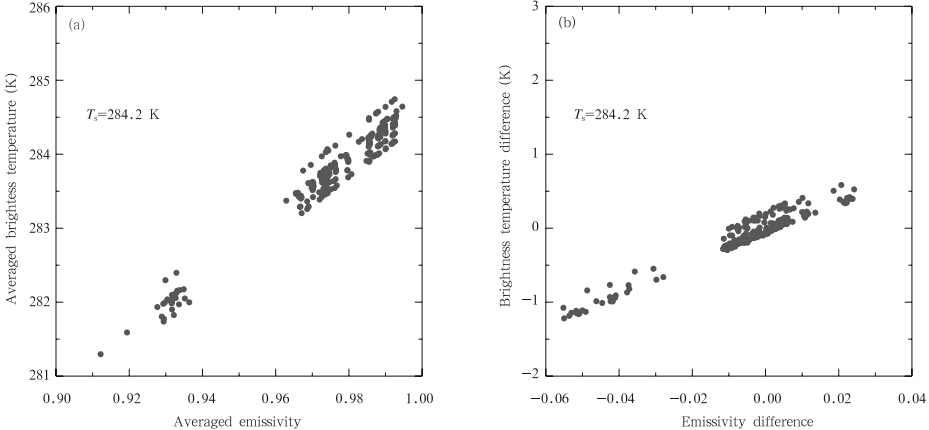 |
| 图 3(a)平均亮温(T4+T5)/2与地表比辐射率平均值及(b)亮温差(T4-T5)/2与地表比辐射率差值的关系 Fig. 3 Scatter plots of the averaged brightness temperature(T4+T5)/2 versus average emissivities(a),and the brightness temperature difference(T4-T5)/2 versus emissivity differences(b) |
利用最小二乘法,根据温度数据集(TS,T4,T5)重新计算了适用于AVHRR和VIRR的Becker和Li分裂窗地表温度反演算法中的相关参数(表 4)。
| 传感器 | A0 | α | β | γ′ | α′ | β′ | R2 |
| AVHRR-7 | -0.0261 | 0.1365 | -0.5275 | 6.6165 | -1.5186 | 7.1324 | 0.97 |
| AVHRR-9 | 0.1605 | 0.1316 | -0.5628 | 7.0883 | -1.9270 | 8.0914 | 0.97 |
| AVHRR-11 | 0.0601 | 0.1341 | -0.5440 | 6.8484 | -1.9935 | 7.4087 | 0.97 |
| AVHRR-12 | -0.0360 | 0.1398 | -0.5287 | 6.5730 | -0.7266 | 8.0381 | 0.97 |
| AVHRR-14 | 0.0101 | 0.1309 | -0.4817 | 5.8932 | 0.7642 | 7.8168 | 0.97 |
| AVHRR-15 | -0.0647 | 0.1345 | -0.5352 | 6.6874 | -1.4043 | 7.9145 | 0.97 |
| AVHRR-16 | -1.1999 | 0.1315 | -0.5176 | 6.0441 | 3.7319 | 11.0475 | 0.96 |
| AVHRR-17 | -0.2552 | 0.1326 | -0.5250 | 6.5005 | -0.5190 | 8.3842 | 0.97 |
| AVHRR-18 | -0.0118 | 0.1377 | -0.4659 | 5.7318 | 0.3840 | 6.7264 | 0.97 |
| VIRR | -0.1400 | 0.1197 | -0.4891 | 5.6538 | 5.6543 | 12.9238 | 0.97 |
为了验证改进型Becker和Li的分裂窗地表温度反演算法,选取了2008年4月27日03时12分(世界时,下同)的一景晴空AVHRR-17图像,利用本文所提出的改进型算法反演了地表温度,其中,地表比辐射率估算采用归一化植被指数方法(Vande Griend et al,1993;Valor et al,1996)。这景图像的空间范围为(38.8°—41.6°N,114.8°—117.6°E),覆盖了北京及周边地区,研究区的主要地表类型为森林、裸地、水体、农田和城市用地等。最后将反演结果同日本东京大学的MODIS的地表温度产品(http://webmodis.iis.u-tokyo.ac.jp/)进行了对比分析。
4.1 基于归一化植被指数方法的地表比辐射率的估算
式(6)中的系数P和M依赖于AVHRR或VIRR通道4、5的地表比辐射率,一个可行的地表比辐射率获取方法是归一化植被指数方法。该方法通过归一化植被指数的分级来估算地表比辐射率。
(1)归一化植被指数小于0.2
认为是裸土像元,它在AVHRR和VIRR通道4、5的地表比辐射率可用表 1中的土壤和岩石的比辐射率的平均值来代替。即AVHRR-7、-9、-11、-12、-14、-15、-16、-17、-18和VIRR通道4的裸土的比辐射率(εS,4)分别为0.9545、0.9541、0.9544、0.9555、0.9542、0.9547、0.9559、0.9545、0.9544和0.9545;通道5的裸土的比辐射率(εS,5)分别为:0.9705、0.9697、0.9704、0.9712、0.9717、0.9709、0.9712、0.9709、0.9719和0.9714。
(2)归一化植被指数大于0.5
认为完全由植被覆盖,这时通常假定AVHRR和VIRR通道4、5的地表比辐射率为一个常数,典型的值为0.99(Sobrino et al,2004b)。
(3)归一化植被指数在[0.2,0.5]
像元是由裸土和植被所构成的混合像元,地表比辐射率为


式(12)中的dεi项包含了自然表面的几何分布效应和内反射效应,对平坦地表可以忽略,但对粗糙表面(例如森林)其值可以达到2%(Sobrino,1989)。该项一个很好的近似式为
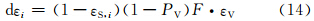
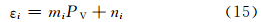
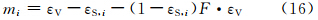
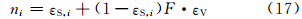
计算AVHRR和VIRR的系数m、n(表 5)。
| 传感器 | m4 | n4 | m5 | n5 |
| AVHRR-7 | 0.0107 | 0.9793 | 0.0034 | 0.9866 |
| AVHRR-9 | 0.0109 | 0.9791 | 0.0038 | 0.9862 |
| AVHRR-11 | 0.0108 | 0.9792 | 0.0035 | 0.9865 |
| AVHRR-12 | 0.0103 | 0.9797 | 0.0031 | 0.9869 |
| AVHRR-14 | 0.0109 | 0.9791 | 0.0029 | 0.9871 |
| AVHRR-15 | 0.0106 | 0.9794 | 0.0033 | 0.9867 |
| AVHRR-16 | 0.0101 | 0.9799 | 0.0031 | 0.9869 |
| AVHRR-17 | 0.0107 | 0.9793 | 0.0033 | 0.9867 |
| AVHRR-18 | 0.0108 | 0.9792 | 0.0028 | 0.9872 |
| VIRR | 0.0107 | 0.9793 | 0.0030 | 0.9870 |
由于很难获取卫星过境时的地面同步地表温度 观测值,对于卫星遥感反演的地表温度的验证是一个非常困难的任务。此外,根据卫星数据反演的地表温度与地面观测的地表温度颇为不同,卫星是在一个较大的瞬时视场(IFOV)上对地物进行观测的,实际上是一个像元内的所有地物地表温度的平均值,而地面地表温度观测的范围则要小很多。本文采用了同一研究区域、同一时刻的MODIS的地表温度产品对其进行了对比分析(图 4,MODIS的地表温度产品由日本东京大学提供)。
 |
| 图 4(a)日本东京大学提供的2008年4月27日03时12分北京及周边地区的MODIS Level 2地表温度产品,(b)本算法用同地区、同时相的AVHRR-17 1B数据反演的地表温度 Fig. 4 Comparison between the MODIS Level 2 LST products(MOD11)measured at 03:12 UTC 27 April 2008 over the Beijing area,which were provided by the University of Tokyo in Japan(a),and that retrieved from the AVHRR-17 image using the modified algorithm developed in this paper(b)over the same region at the same time |
可见两种地表温度产品的分布特征总体非常相似,但使用本文方法得到的地表温度(图 4b)在植被稀疏的区域(图中的红色斑块表示的土壤、裸地和城市用地等)要比MODIS的地表温度高一些;而在植被浓密区域(图中蓝色斑块表示的森林等地区)则要低一些。从两种地表温度产品的散点图(图 5)可见,虽然大部分点匹配不是很完美,但其都分布在1:1线的附近。平均绝对偏差为0.6 K,相关系数达到0.88,均方根偏差为2.1 K,说明两种地表温度产品的一致性尚好。由于是与同类型的MODIS地表温度产品的对比,因此,并不是说本文提出的改进型Becker和Li的分裂窗地表温度反演算法的精度就是2.1 K。
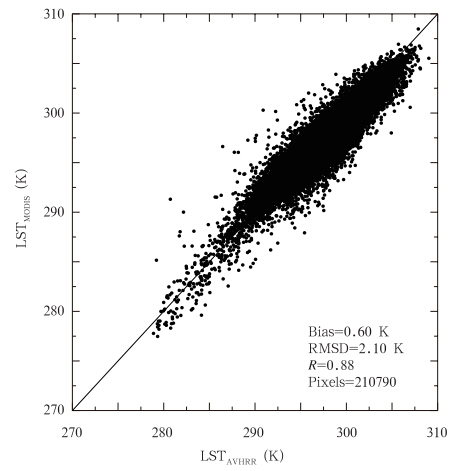 |
| 图 5 MODIS Level 2地表温度产品与本文提出的改进型Becker和Li算法用AVHRR-17数据反演的地表温度产品的散点图 Fig. 5 Scatter plot of the LST from the MODIS Level 2 product vs. that derieved from the AVHRR-17 using the modified Becker and Li’s split window algorithm developed in this paper |
从频率直方图(图 6a)上可见,两种地表温度产品的概率分布也较为相似;两种地表温度产品差值的频率直方图(图 6b)显示,大约有69.6%的像元的地表温度差值在±2 K以内,37% 的像元的差值在±1 K以内。
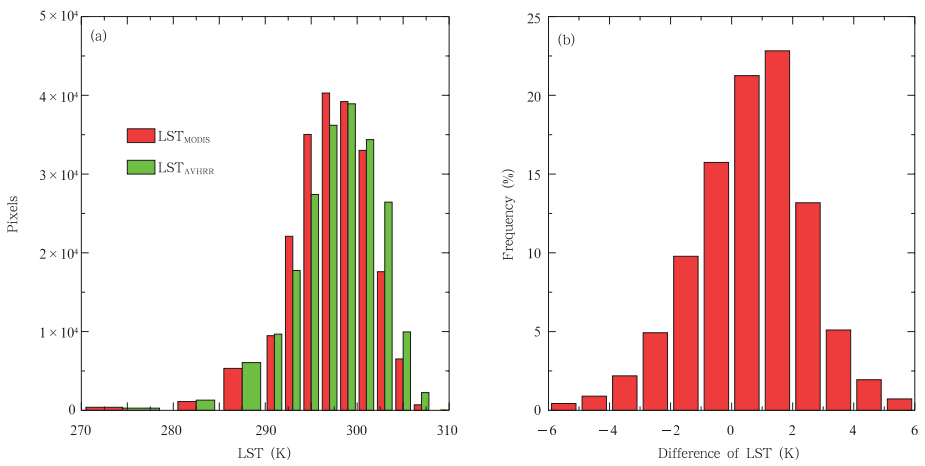 |
| 图 6 MODIS与AVHRR反演的(a)地表温度、(b)地表温度差值的频率分布 Fig. 6 Histograms of the MODIS LST and those derived from the AVHRR data using the modified Becker’s LST retrieval algorithm(a) and their differences(b) |
利用MODTRAN 4辐射传输模式模拟了不同大气和地表条件下到达卫星传感器热红外通道的光谱辐亮度;结合AVHRR和VIRR通道4、5的光谱响应函数计算了通道平均光谱辐亮度,进而根据逆普朗克函数计算了通道亮温并建立了温度数据集(TS,T4,T5);根据建立的温度数据集,采用最小二乘法计算了适用于AVHRR和VIRR的改进型Becker和Li 的分裂窗地表温度反演算法中相关参数。利用该改进型算法对一景覆盖北京及周边地区的AVHRR-17数据进行了地表温度反演,并将反演结果与日本东京大学的MODIS地表温度产品进行了对比,结果表明两者具有较好的一致性。
利用本文发展的改进型Becker和Li的分裂窗地表温度算法可以实现对从NOAA-7至NOAA-18卫星的AVHRR以及FY-3A的VIRR观测数据进行地表温度的反演,这将提高来自不同AVHRR以及VIRR数据反演的地表温度产品的可比性,从而提高AVHRR和VIRR的地表温度产品在气候变化研究中的应用效益。然而地表温度反演是一个非常复杂的问题,反演过程中存在诸多困难,例如地表比辐射率的准确估算、地表温度反演结果的验证等。本文虽然做了对比分析和验证,但仍然需要对该改进型算法在不同地区、不同地表和大气条件下的地表温度反演结果进行验证,这将在下一步的工作中得到解决。
| 国家卫星气象中心. 2009. FY-3A扫描辐射计(VIRR) L1数据定标方法及相关参数//扫描辐射计相对光谱响应函数技术报告. 国家卫星气象中心, 1-2 |
| 杨虎, 杨忠东. 2006. 中国陆地区域陆表温度业务化遥感反演算法及产品运行系统. 遥感学报, 10(4): 600-607 |
| 杨军, 董超华, 卢乃锰等. 2009. 中国新一代极轨气象卫星——风云三号. 气象学报, 67(4): 501-509 |
| Becker F. 1987. The impact of spectral emissivity on the measurement of land surface temperature from a satellite. Int J Remote Sens, 8(10): 1509-1522 |
| Becker F, Li Z L. 1990. Towards a local split window method over land surfaces. Int J Remote Sens, 11(3): 369-393 |
| Berk A, Anderson G P, Acharya P K, et al. 1999. MODTRAN4 user’s manual, air force research laboratory space vehicles directorate air force materiel command HANSCOM AFB, MA 01731-3010: 10-35 |
| Carson T N, Ripley D A. 1997. On the relation between NDVI, fractional vegetation cover, and leaf area index. Remote Sens Environ, 62(3): 241-252 |
| Czajkowski K P, Goward S N, Ouaidrari H. 1998. Impact of AVHRR filter function on surface temperature estimation from the split window approach. Int J Remote Sens, 19(10): 2007-2012 |
| Kahle A B, Madura D P, Soha J M. 1980. Middle infrared multispectral aircraft scanner data: Analysis for geological applications. Appl Opt, 19(14): 2279-2290 |
| Kneisys F X, Robertson D C, Abreu L W, et al. 1995. Appendix A MODTRAN 3 user instructions. The MODTRAN 2/3 and LOWTRAN 7 Model, 233-234 |
| Korb A R, Dybwad P, Wadsworth W, et al. 1996. Portable FTIR spectroradiometer for field measurements of radiance and emissivity. Appl Opt, 35(10): 1679-1692 |
| McClain E P, Pichel W G, Walton C C. 1983. Comparative performance of AVHRR-based multichannel sea surface temperatures. J Geophys Res, 90(C6): 11587-11601 |
| McMillin L M. 1975. Estimation of sea surface temperatures from two infrared window measurements with different absorption. J Geophys Res, 80(36): 5113-5117 |
| NOAASIS (NOAA Satellite and Information Service). 2011. Advanced Very High Resolution Radiometer-AVHRR, http://noaasis.noaa.gov/NOAASIS/ml/avhrr.html |
| Prata A J, Platt C M R. 1991. Land surface temperatures measurements from AVHRR//5th AVHRR Data Users Conference. Tromso, Norway: 433-438 |
| Price J C. 1984. Land surface temperature measurements from the split window channels of the NOAA 7 advanced very high resolution radiometer. J Geophys Res, 89(D5): 7231-7237 |
| Quattrochi D A, Luvall J C. 2000. Thermal remote sensing in land surface processes. Boca Raton: CRC Press, 13-32 |
| Robel J. 2007. AVHRR Level 1b data base. NOAA polar orbiter data user’s guide, 1-24 |
| Robel J. 2009. Calibration of NOAA KLM instruments. NOAA KLM user’s guide with NOAA-N, -N’ supplement, 7: 1-11 |
| Salisbury J W, D’Aria D M, Jarosevich E. 1991. Midinfrared (2.5—13.5 micrometers) reflectance spectra of powdered stony meteorites. Icarus, 92(2): 280-297 |
| Salisbury J W, D’Aria D M. 1992. Emissivity of terrestrial materials in the 8—14 μm atmospheric window. Remote Sens Environ, 42(2): 83-106 |
| Salisbury J W, Wald A, D’Aria D M. 1994. Thermal-infrared remote sensing and Kirchhoff’s law 1. Laboratory measurements. J Geophys Res, 99(B6): 11897-11911 |
| Sobrino J A. 1989. Desarrollo de un modelo teórico para implementarla medida de la temperatura realizada mediante teledetección. Aplicación a un campo de naranjos. Valencia, Spain: University of Valencia, 169-170 |
| Sobrino J A, Caselles V, Becker F. 1990. Significance of the remotely sensed thermal infrared measurements obtained over a citrus orchard. ISPRS Photogramm Enginee Remote Sens, 44(6): 343-353 |
| Sobrino J A, Caselles V, Coll C. 1993. Theoretical split window algorithms for determining the actual surface temperature. II Nuovo Cimento, 16(3): 219-236 |
| Sobrino J A, Jiménez-Mu oz J C, El-Kharraz J, et al. 2004a. Single-channel and two-channel methods for land surface temperature retrieval from DIAS data and its application to the Barrax site. Int J Remote Sens, 25(1): 215-230 |
| Sobrino J A, Jiménez-Mu oz J C, Paolini L. 2004b. Land surface temperature retrieval from LANDSAT TM 5. Remot Sens Environ, 90(4): 434-440 |
| Ulivieri C, Castronuovo M M, Francioni R, et al. 1994. A split window algorithm for estimating land surface temperature from satellite. Adv Space Res, 14(3): 59-65 |
| Valor E, Caselles V. 1996. Mapping land surface emissivity from NDVI: Application to European, African and South American areas. Remote Sens Environ, 57(3): 167-184 |
| Van de Griend A A, Owe M. 1993. On the relationship between thermal emissivity and the normalized difference vegetation index for natural surfaces. Int J Remote Sens, 14(6): 1119-1131 |
 2012, Vol. 70
2012, Vol. 70

