中国气象学会主办。
文章信息
- 潘 旸, 沈 艳, 宇婧婧, 赵 平. 2012.
- PAN Yang, SHEN Yan, YU Jingjing, ZHAO Ping. 2012.
- 基于最优插值方法分析的中国区域地面观测与卫星反演逐时降水融合试验
- Analysis of the combined gauge-satellite hourly precipitation over China based on the OI technique
- 气象学报, 70(6): 1381-1389
- Acta Meteorologica Sinica, 70(6): 1381-1389.
- http://dx.doi.org/10.11676/qxxb2012.116
-
文章历史
- 收稿日期:2011-05-31
- 改回日期:2012-04-16
开发高时空分辨率和高精度的降水分析产品对于灾害性天气监测、数值预报和模式检验以及中尺度天气动力分析都非常迫切和重要。近年来,中国气象局已经布设了一套分布较为密集的地面观测网,在中国共建设了3万多个自动气象观测站,绝大多数位于中国的东部和南部(图 1)。基于这些自动站的逐时降水观测资料,中国国家气象信息中心开发了一套高时空分辨率的中国降水格点分析产品(Chinese Precipitation Analyses,CPA),该产品在中国东部和南部具有较高的质量和精度(沈艳等,2012)。但由于中国西部地区的站点比较稀疏,降水格点分析产品在这些地区的精度尚不能满足业务和科研的需要。卫星资料由于空间覆盖广阔、观测频次高而逐步受到气象学家的重视,随着卫星遥感探测技术的发展,已能够弥补广袤海洋和无人区地面观测站稀少的缺陷。因此,从20世纪末开始,国际上不少研究机构都相继推出了卫星反演的降水产品,如PERSIANN(Precipitation Estimation From Remotely Sensed Information Using Artificial Neural Network)(Hsu et al,1997)、CMORPH(Climate Prediction Morphing Technique)(Joyce et al,2004)、TRMM-3B42RT(Tropical Rainfall Measuring Mission)(Huffman et al,2007)等。这些卫星产品都能较好地把握中国地区降水的空间分布,然而精度较差,多数产品描述的3 h累积降水量都偏低20%左右(Shen et al,2010),显然尚不能满足现代气象业务和科研的需求,仍需要地面观测资料对其进行订正。例如,TRMM-3B42采用地面观测的月降水量进行订正,能将偏差控制在-0.4%,取得了较显著的改进(Shen et al,2010)。所以,开发卫星和地面观测降水的融合产品已是国际上发展高质量降水产品的一个趋势。
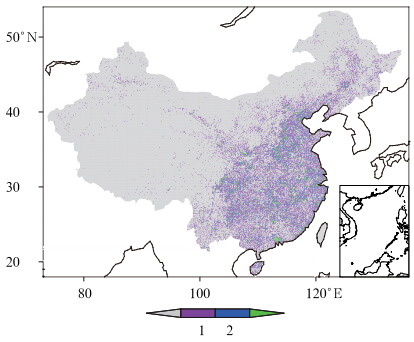 |
| 图 1 中国区域0.1°×0.1°经纬度网格内雨量计个数分布 Fig. 1 Gauge numbers in the 0.1°×0.1° lat/lon resolution grid boxes over China |
在此趋势推动下,国际上相关研究机构开发了各种融合技术,例如:GPCP数据集采用的误差方差反比加权法(Huffman,1995)、CMAP数据集采用的适用于海表温度资料融合分析的泊松法(Reynolds,1988; Xie et al,1997),以及GPCP 1DD(One Degree Daily)数据集(Huffman et al,2001)和TRMM-3B42(Huffman et al,2007)采用月尺度的卫星与雨量计降水的比率来订正更短时间尺度的卫星反演降水。但这些方法多是针对月或日降水。同时,由于国际上难以获取中国地区较为密集的站点资料,这些降水产品的空间分辨率均在1.0°×1.0°左右,因而这些方法是否适用于逐时和更高空间分辨率的降水融合还有待进一步研究。中国国家卫星气象中心也研制了中国区域风云系列卫星反演逐时降水0.1°×0.1°的融合产品,采用的是同时考虑距离因子和站点相对于格点取向的智能型客观分析方法(Lu et al,2004)。但是,由于风云系列的卫星估测降水仅由红外遥感资料通过统计方法估计而成,本身误差较大,引入站点资料订正后虽然有效提高了有站点分布地区降水的精度,但对降水空间结构的连续性影响很大(潘旸等,2011),特别是在站点密度变化非常剧烈的地区,降水的精度还有待进一步提高。
最优插值(Optimum Interpolation,OI)最早由Eliassem(1954)和Gandin (1965)应用于气象领域的研究,Reynolds等(1994)曾采用该方法融合了卫星反演和海洋浮标、船舶观测的全球海表温度,取得非常好的效果。与上述其他降水资料融合方法相比,最优插值的优点在于它既考虑了各种观测误差的自相关关系,又考虑了不同观测间的相关关系,这样权重函数不仅是距离的单变量关系,还考虑了不同观测间误差的相互影响,并且,最优插值只在分析点一定范围内求解最优值,特别适合降水这种时空变率较大的单要素的分析。Xie等(2011)就采用这种方法在逐日、0.25°×0.25°尺度上成功地建立了卫星反演与地面站观测降水融合的概念模型,可是降水的误差根据时空尺度不同,变化非常剧烈(Hong et al,2006),这种方法是否适用于更高时空分辨率的降水资料融合,还有待进一步研究和试验。
因此,本文采用最优插值技术开展了中国地区0.1°×0.1°逐时降水的融合试验,卫星反演降水资料选用美国国家海洋大气局(National Oceanic and Atmospheric Administration,NOAA)气候预测中心(Climate Prediction Center,CPC)研制的CMORPH,该资料在东亚地区的精度较高(Xie et al,2007;Shen et al,2010),且与中国国家卫星气象中心的风云系列卫星估测降水产品相比,能更合理地反映降水的空间结构(潘旸等,2011)。2 资料及处理方法
CMORPH是以被动微波反演降水量为基准,对连续的静止卫星红外图像采用运动矢量方法估计被动微波反演降水的空间传播特征,进而做出高质量降水估计产品(Joyce et al,2004)。其时间间隔为30 min,空间分辨率为8 km,覆盖了60°S—60°N的区域。在融合前,将30 min间隔的原始数据累加成逐时降水值,再插值成0.1°×0.1°分辨率的格点资料。由于最优插值的基本假设要求所有不同来源观测的误差相互独立,并且,不存在系统误差,所以,针对CMORPH资料的系统性偏差,还采用概率密度匹配(Probability Density Function,PDF)方法进行订正,即利用一定时空范围内降水概率密度相对稳定的特性,将CMORPH逐时降水的概率密度分布调整到与地面观测一致(宇婧婧等,待刊)。
地面观测采用的是中国3万个自动气象观测站雨量计记录的逐时降水量。中国国家气象信息中心对该资料进行了严格的质量控制,包括气候学界限值检查、区域界限值检查、时间一致性检查和空间一致性检查(任芝花等,2010)。在此基础上,采用“气候背景场”的优化插值方法(沈艳等,2010),对质量控制后的自动站逐时降水进行空间插值,生成时空分辨率为逐时、0.1°×0.1°格点分析产品(沈艳等,2012)。该产品每个时次每个格点上包含两个变量:一个是该时次网格内的平均降水率,另一个是该时次该网格点内包含的雨量计观测数(图 1)。在融合时,只选取网格上至少有一个雨量计观测的格点降水值(以下称为“有效格点”)参与最优插值分析。从2009年汛期开始中国国家气象信息中心对中国区域自动站实时传输业务进行了考核,资料可用率达到81.6%,具有相对稳定且较好的质量,因而本文选取2009年6、7、8月的资料,针对受关注较多的夏季降水进行试验和分析。
在检验本融合试验产品精度时,还用了中国国家卫星气象中心发布的FY-2C静止气象卫星(简称“FY-2C”)逐时0.1°×0.1°的降水融合产品作对比评估。该产品以FY-2C搭载的可见光和红外自旋扫描辐射计(VISSR)遥感探测的红外资料为主,选用云顶温度梯度、云体相对于云团中心的偏移量、云团移动速度作为影响因子回归得到卫星降水估计,再以中国2400个国家级地面站常规雨量计观测的逐时降水资料对卫星估测降水进行订正(Lu et al,2004)。3 最优插值降水分析 3.1 最优插值融合原理
最优插值分析首先需要一个初估场,卫星反演降水的空间覆盖率高,将其设为初估场。在网格内有站点分布的格点上,中国降水格点分析产品的精度较高,将其作为观测值。每一个格点上的降水分析值Ak等于该点的初估值Fk加上该格点上观测值与初估值的偏差,而这个偏差由一定范围内n个格点上已知的观测值Oi与初估值Fi的偏差加权估计得到
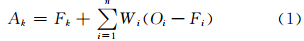
分析点上分析值的误差方差为
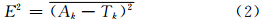
假设,观测误差和初估场误差不相关,即
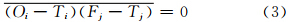
将式(1)代入式(2),再结合式(3),则分析误差方差可化为
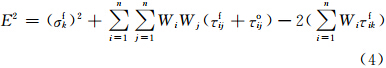
针对式(4)利用最小二乘法构建线性方程
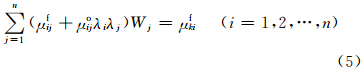
可以通过求解式(5)确定权重Wi,最后得到分析误差的最小方差估计
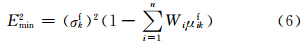
在最优插值中求解Wi时要求σio、μijo、 σif和μijf均为已知量,需要对地面观测和卫星反演降水的误差以及误差的相关性进行预先的估计,一般可通过统计方法给定。以下分析所用的误差均用均方差表示,样本统计时段为2009年6—8月。 3.2.1 观测误差标准差(σio)
降水格点分析产品的误差表现出依赖时空分辨率、站网密度以及雨强而变化的特征(North et al,1989;Schneider et al,1993;Rudolf et al,1994)。文中地面观测降水的误差除了考虑降水量本身外,还考虑了网格内观测站数的影响,即网格内观测站越多,网格点上分析值越能“真实”地代表该网格区域内的平均降水量。
在台站分布密集的区域(24°—30°N,110°—118°E),选取该区域中的有效网格上的中国降水格点分析产品分析值为样本。以该网格内站点观测的算术平均值代表格点的“真值”,按照雨强大小分成多个等级,计算每个等级内所有样本的平均雨强和均方差。分别统计在网格内不同的观测站点个数下,分析误差随雨强的变化关系(图 2):在不同观测站点个数下,分析误差均随雨强增大而呈近似为幂指数增加的趋势;随着站点个数的增加,分析误差则呈减小趋势,且减小幅度逐渐降低,例如降水量为15 mm/h、站数从1增加到2时,分析误差减小了2/3,而站数从2增加到3时,分析误差仅减小了1/3。另外,当雨强在5 mm/h以下时,分析误差随观测站数的变化不大。
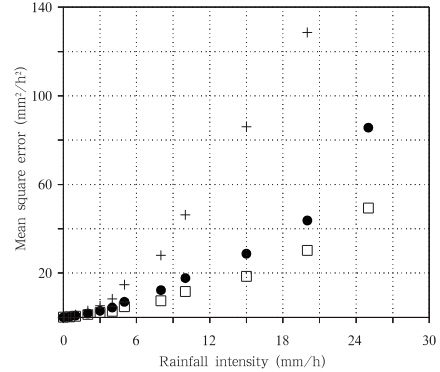 |
| 图 2 0.1°×0.1°网格内不同站点个数下均方误差随雨强的变化关系(+、●和□分别表示网格内自动站个数为1、2和3个) Fig. 2 Mean square errors computed for the different gauge numbers in a 0.1°×0.1° grid box vs. the precipitation(+,●,and □ are for one,two,and three gauges in a grid box,respectively) |
由上述分析可知,观测场误差方差的估计方程可简化成与雨强成正相关,而与站点个数成反相关。3.2.2 观测误差协相关(μijo)
在地面观测降水的空间相关性定义中,通常认为不同台站的观测相互独立,各个站之间的误差不相关,每个台站的观测误差只与自身的观测有关,所以,观测场误差的空间相关可以定义为
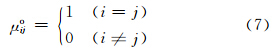
实际上,经过格点分析之后,格点间降水的误差存在一定相关。为了计算简化,再考虑到格点化时,东部站网密度较大的地区搜索半径实际上不足20 km,可以假设中国降水格点分析场各有效格点间的误差协相关近似满足式(7)所示的关系。3.2.3 初估场误差标准差(σfi)
卫星反演降水误差也受到降水变率、时空取样等多种因素的影响(Barrett et al,1981;Hong et al,2006),一般认为它遵循这样一个规律:降水误差方差与降水强度成正比,与样本数成反比。对于CMORPH卫星反演降水,其空间样本分布非常均一,所以,误差主要受降水强度的影响。
由于有效格点上的中国降水格点分析产品分析值可信度较高,可将其作为“真值”。在一定时空范围内,取所有有效格点上的卫星反演降水为样本,分别计算不同强度降水下卫星反演降水与“真值”的均方偏差,作为卫星反演降水的误差。图 3给出误差与卫星反演降水强度的对应关系,可见与观测降水误差类似,卫星反演降水的误差随着降水量值增大也近似呈幂指数增加。
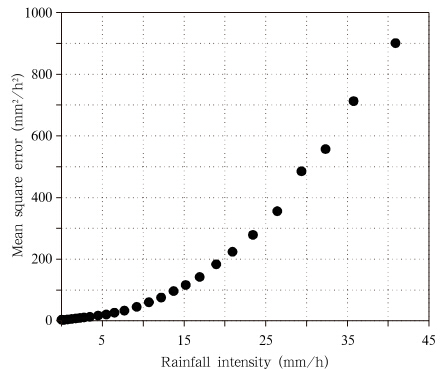 |
| 图 3 卫星反演降水(CMORPH)的均方误差与雨强的散点分布(以(30°N,112°E)格点为中心10°×10°网格区域内样本为例) Fig. 3 Mean square errors of the CMORPH vs. the precipitation(Sampled from an area of 10°×10° lat/lon centered at the grid of 112°E,30°N) |
与地面观测降水不同,卫星的观测手段决定了它总是在一片区域内同时进行观测,并且,用概率密度函数匹配方法对卫星反演降水系统误差进行订正也是在一定区域内取样,这就造成了卫星反演降水误差具有相对较强的空间相关性。
仍以有效格点上的中国降水格点分析产品分析值作为“真值”,在一定时空范围内,取所有任意两个有效格点(本身除外)的距离和卫星反演降水值与“真值”的偏差协方差来构建初估场误差的协相关μijf。将距离以10 km为等分,计算每段距离等分中平均的误差协相关系数,得到不同距离下协相关系数的变化(图 4)。可以看到,卫星反演降水误差的空间相关性随距离增加而减小,并可以用负指数函数来拟合。
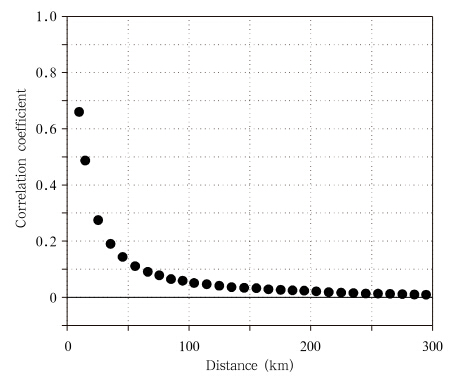 |
| 图 4 任意两格点上卫星反演降水均方根误差的相关系数与两点间距离的关系(以(30°N,112°E)格点为中心的10°×10°网格区域内样本为例) Fig. 4 Correlation coefficients of the CMORPH’s mean square errors between two different grids vs. the distance(Sampled from an area of 10°×10° lat/lon centered at the grid of 112°E,30°N) |
基于上述误差分析,卫星反演与地面观测降水 的误差及空间相关性均可通过大量样本统计拟合后,以确定一个相对稳定的误差估计经验公式,从而求解权重函数Wi。不难看到,卫星反演降水的误差比地面观测的大,可以预见在东部站网密集的地区,地面信息对融合产品的影响将比较显著。4 融合试验效果检验
针对2009年6—8月中国区域的降水,采用上述最优插值方法进行了初步的融合试验。针对试验结果(COMB),从单时次的个例分析和独立样本检验的统计分析两个方面检验该融合方法的效果和精度。在统计分析时采用的评估指标包括平均偏差(Bias)、均方根误差(RMSE)、相对误差(RE)和相关系数(CC)。为了更严格地对融合方法进行评估,去除了地面降水分析值、卫星反演降水和融合降水同时为0的样本(约占总样本数的80%)。 4.1 单时次个例分析
图 5给出一次华南地区强降水天气过程中某一时刻(2009年7月2日00时,世界时,下同)的融合试验结果。从站点观测来看,在华南中部,有一条横亘湘赣闽的强降水区(图 5a),该地区站点分布较密集,融合降水的中心结构和强度与中国降水格点分析产品非常相似(图 5b、d),与地面自动站观测降水的分布形态也很接近(图 5a),而卫星反演降水产品与它们略有差异(图 5c),如:湘赣交界的降水中心明显分裂,横亘闽中的降水中心强度偏弱并分裂为东西两个小中心等。此外,融合降水在西部站点稀疏的地方,如青海西部地区,中国降水格点分析产品中由插值带来成片的虚假降水分布被消除了,保留了卫星反演降水分布零散的特征,空间结构更为合理。
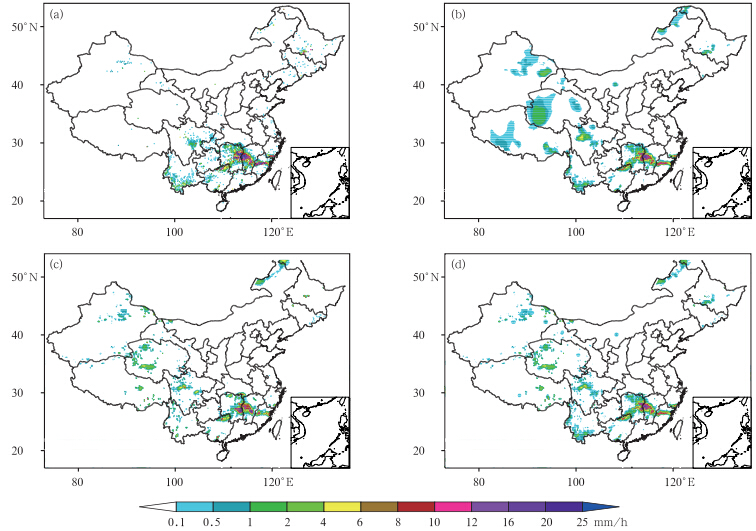 |
| 图 5 2009年7月2日00时中国区域雨强(mm/h)(a.地面自动气象站观测,b.中国降水格点分析场,c.卫星反演降水,d.融合降水) Fig. 5 Hourly precipitation(mm/h)at 00:00 UTC 2 July 2009 over China:(a)AWS,(b)CPA,(c)CMORPH,and (d)COMB |
从融合降水分别与中国降水格点分析产品及卫星反演降水的散点分布上也可以看到相同的情况(图 6):网格内观测站个数越多,融合降水与中国降水格点分析产品的散点分布越集中,线性拟合线与y=x越接近;而在没有观测的地方(图 6中gauge=0处),融合降水与卫星降水更接近。这结果与融合的基本思路是一致的。
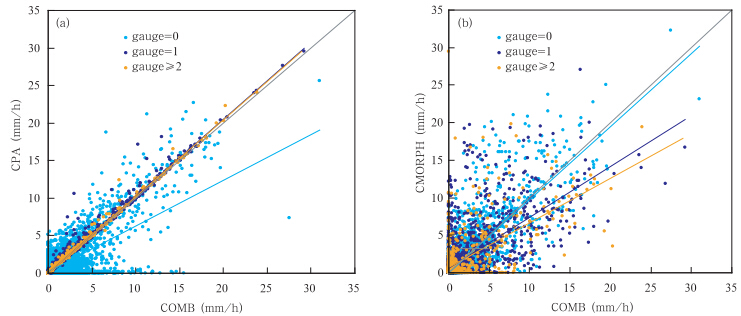 |
| 图 6 2009年7月2日00时不同观测站点个数下融合降水分别与(a)中国降水格点分析场、(b)卫星反演降水的散点分布(彩色线表示相应的线性拟合线,灰色线表示y=x) Fig. 6(a)Scatter diagrams of the hourly precipitations from the COMB and the CPA; and (b)the same as(a)but from the COMB and the CMORPH(the colorful lines are the linear fitting for the different gauge numbers,1,2 and 3,respectively. Grey lines denotes y=x) |
为了定量评估该方案的融合效果,利用2009年夏季的降水进行独立样本检验。将网格内有3个及以上观测的站点保留起来(如图 1所示,共有1278个网格4433个站点,约占全部自动站的15%),只用余下的站点进行格点化分析,再与卫星资料融合,检验时则以网格内包含3个及以上观测信息的中国降水格点分析产品分析值为“真值”,并在这些网格上对融合值进行检验,由于格点化和融合时完全没有用到格点内的观测信息,所以,称这种检验为“独立样本检验”。
图 7是2009年6—8月独立样本检验的平均偏差和相关系数的逐日变化。与融合前的卫星反演降水产品的精度相比,虽然融合降水的平均偏差只是 从-0.037 mm/h提高到-0.004 mm/h,但基本在0值附近小幅摆动,摆动幅度明显减小;平均的空间相关系数由0.368大幅提高到0.778,且融合前相关系数多在0.2—0.6大幅变化,而融合后的相关系数绝大多数为0.7—0.9。卫星反演降水融合产品的均方根误差也从融合前的2.267 mm/h下降至1.271 mm/h,减幅接近50%;相对误差更是从57.93%大幅下降至15.964%(表 1)。融合前后统计指标的变化表明,与单纯的卫星反演降水相比,融合产品在降水量值和空间分布上均与地面资料更为接近,该融合方法能够稳定且有效地引入地面观测信息从而提高卫星反演降水的精度。
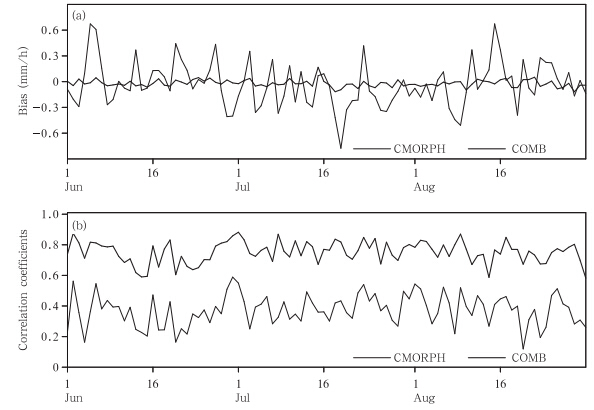 |
| 图 7 2009年6—8月独立检验统计值的逐日变化(a.平均偏差(mm/h),b.相关系数) Fig. 7 Daily(a)bias(mm/h),and (b)correlation coefficients from June to August of 2009 on the independent grids |
| 偏差(mm/h) | 相关系数 | 均方根误差(mm/h) | 相对误差(%) | |
| CMORPH | -0.037 | 0.368 | 2.209 | 57.930 |
| 融合 | -0.004 | 0.778 | 1.271 | 15.964 |
| FY-2C | 0.162 | 0.392 | 2.267 | 48.338 |
图 8是2009年7月1日00时—3日23时的中国降水格点分析场分别与融合降水和FY-2C降水的散点分布。显然,融合降水散点分布要比FY-2C的降水更加集中,融合降水的相关系数和均方根误差分别为0.84和1.420 mm/h,优于FY-2C的0.50和2. 512 mm/h,说明在这些独立的检验网格上,融合值比FY-2C的降水更接近地面观测。
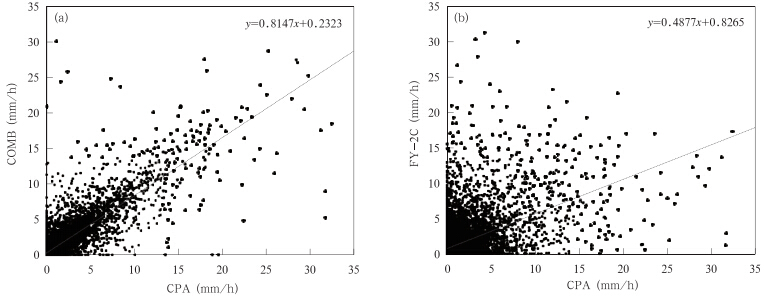 |
| 图 8 2009年7月1日00时—3日23时中国降水格点分析值分别与(a)融合降水值、(b)FY-2C融合降水值的散点分布 Fig. 8 Scatter diagrams of the hourly precipitations during the period from 00:00 UTC 1 July 2009 to 23:00 UTC 3 July 2009 from(a)the COMB and the CPA; and (b)the FY-2C and the CPA |
从2009年6—8月平均的统计评估结果上看(表 1),FY-2C的偏差偏高了0.162 mm/h,均方根误差和相对误差均比融合降水的大,相关系数只有0.392,也比融合降水的要低,表明融合降水的精度要高于FY-2C的融合产品,这与个例检验的结果一致。这说明2400站的站网密度下尚不能准确反映0.1°×0.1°网格上的降水信息,有必要融入更高密度站网的观测信息。5 总结和讨论
本文采用最优插值技术在0.1°×0.1°逐时的时空尺度上开展了卫星与地面观测降水的融合试验。以卫星反演降水为初估场,以地面降水的格点分析场为观测,以资料数量和质量相对较稳定的2009年6—8月的样本为例,统计确定了如下的误差关系:(1)观测误差近似与降水强度成正比,与观测站点数成反比;(2)初估场误差随降水强度增大近似成幂指数增加;(3)初估场误差协相关随距离成负指数单调递减。将这些关系通过拟合量化后用于最优插值中权重函数的求解。融合试验个例检验证明,该方案符合融合的基本思路,即在站点分布越密集的地区,融合降水的值与地面格点分析值越接近;在站点稀疏地区,融合值与卫星反演降水值更接近。针对2009年6—8月的降水对融合试验的效果进行了独立样本检验。结果表明,与融合前的卫星反演降水相比,融合后降水的平均偏差更接近于0;相对误差、均方根误差大幅减小,减幅均在50%左右;相关系数提高了1倍。说明该融合方案能够稳定且有效地引入地面观测信息以提高卫星反演降水的精度。与FY-2C的同类型产品相比,融合试验产品的精度也更高。
对地面和卫星资料合理准确的误差估计是保证最优插值方法精度和产品质量的关键,上述结果表明,用最优插值方法融合的逐时0.1°×0.1°降水场达到了比较合理和理想的效果,本文定义的误差关系基本能正确反映两种资料的误差特征。但是,现用的误差估计方程均是基于夏季东部站网密集地区的样本量化确定的,产品在这些时段和地区的质量较好,然而在冬季和站网密度稀疏的情况下,该误差关系的准确性有所降低,这可能会影响冬季和西部地区融合产品的精度。此外,除了降水量本身和样本数,误差估计尚没有考虑其他因子(Xu et al,2010),这些都会影响误差估计的准确性,所以产品的精度仍有改进的空间。
致谢: 感谢美国NOAA气候预测中心的谢平平博士提供最优插值分析源程序,并在最优插值误差分析中给予指导。感谢中国国家气象信息中心周自江研究员在研究过程中给予的宝贵建议。
| 潘旸, 宇婧婧, 廖捷等. 2011. 地面和卫星降水产品对台风莫拉克降水监测能力的对比分析. 气象, 37(5): 564-570 |
| 任芝花, 赵平, 张强等. 2010. 适用于全国自动站小时降水资料的质量控制方法. 气象, 36(7): 123-132 |
| 沈艳, 冯明农, 张洪政等. 2010. 我国逐日降水量格点化方法. 应用气象学报, 21(3): 279-286 |
| 沈艳,潘旸,徐宾等.2012.最优插值对降水量空间分析中的参数优化.成都信息工程学院学报,27(2):219-224 |
| 宇婧婧, 沈艳, 潘旸等. 待刊. 概率密度匹配法对中国区域卫星降水资料的改进.应用气象学报 |
| Barrett E C, Martin D W. 1981. The Use of Satellite Data in Rainfall Monitoring. London: Academic Press, 340pp |
| Eliassem A. 1954. Provisional report on calculation of spatial covariance and autocorrelation of the pressure field. Inst Weather and Climate Research, Acad Sci, Oslo, Report No. 5 |
| Gandin L S. 1965. Objective Analysis of Meteorological Fields. Jerusalem: Israel Program for Scientific Translations, 242pp |
| Hong Y, Hsu K L, Moradkhani H, et al. 2006. Uncertainty quantification of satellite precipitation estimation and Monet Carlo assessment of the error propagation into hydrologic response. Water Resources Res, 42(8): W08421, doi: 10. 1029/2005 WR004398 |
| Hsu K L, Gao X G, Sorooshian S, et al. 1997. Precipitation estimation from remotely sensed information using artificial neural networks. J Appl Meteor, 36(9): 1176-1190 |
| Huffman G J, Adler R F, Rudolf B, et al. 1995. Global precipitation estimates based on a technique for combing satellite-based estimates, rain gauge analysis, and model precipitation information. J Climate. 8:1284-1295 |
| Huffman G J, Adler R F, Morrissey M M, et al. 2001. Global precipitation at one-degree daily resolution from multisatellite observations. J Hydro Meteor, 2(1): 36-50 |
| Huffman G J, Adler R F, Bolvin D T, et al. 2007. The TRMM Multisatellite Precipitation Analysis (TMPA): Quasi-global, multiyear, combined-sensor precipitation estimates at fine scales. J Hydro Meteor, 8(1): 38-55 |
| Joyce R J, Janowiak J E, Arkin P A, et al. 2004. CMORPH: A method that produces global precipitation estimates from passive microwave and infrared data at high spatial and temporal resolution. J Hydro Meteor, 5: 487-503 |
| Lu N M, You R, Zhang W J. 2004. A fusing technique with satellite precipitation estimate and raingauge data. Acta Meteor Sinica, 18(2): 141-146 |
| North G R, Nakamoto S. 1989. Formalism for comparing rain estimation designs. J Atmos Oceanic Techn, 6(6): 985-992 |
| Reynolds R W. 1988. A real-time global sea surface temperature analysis. J Climate, 1: 75-86. |
| Reynolds R W, Smith T M. 1994. Improved global sea surface temperature analyses using optimum interpolation. J Climate, 7(6): 929-948 |
| Rudolf B, Hauschild H, Rueth W, et al. 1994. Terrestrial precipitation analysis: Operational method and required density of point measurements. NATO ASI Series, 1(26): 173-186 |
| Schneider U, Rudolf B, Rueth W. 1993. The spatial sampling error of areal mean monthly precipitation totals analyzed from gauge measurements. Fourth Int. Conf. on precipitation, Iowa City, IA, 80-82 |
| Shen Y, Xiong A Y, Wang Y, et al. 2010. Performance of high-resolution satellite precipitateon products over China. J Geophys Res, 115: D02114, doi: 10. 1029/2009JD012097 |
| Xie P P, Arkin P A. 1997. Global precipitation: A 17-year monthly analysis based on gauge observations, satellite estimates, and numerical model outputs. Bull Amer Meteor Soc, 78(11): 2539-2558 |
| Xie P P, Chen M Y, Yatagai A, et al. 2007. A gauge-based analysis of daily precipitation over East Asia. J Hydro Meteor, 8(3): 607-626 |
| Xie P P, Xiong A Y. 2011. A conceptual model for constructing high-resolution gauge-satellite merged precipitation analyses. J Geophys Res, 116: D21106, doi: 10. 1029/2011JD016118 |
| Xu B, Yoo S, Xie P. 2010. Quantifying error in the CMORPH satellite precipitation estimates // 2010 AGU Annual Assembly. San Francisco, CA |
 2012, Vol. 70
2012, Vol. 70

