中国气象学会主办。
文章信息
- 杜牧云, 刘黎平, 胡志群, 杨川. 2013.
- Dn Muyun, Lin Liping, Hn Zhiqnn, Yang Chnan. 2013.
- 双线偏振多普勒雷达资料质量分析
- An analysis of dual-linear polarimetric doppler radar data quality
- 气象学报, 71(1): 146-158
- Acta Meteorologica Sinica, 71(1): 146-158.
- http://dx.doi.org/10.11676/qxxb2013.012
-
文章历史
- 收稿日期:2011-11-15
- 改回日期:2012-04-14
2. 武汉中心气象台, 武汉, 430074
2. Wuhan Central Meteorological Observatory, Wuhan 430074, China
双线偏振多普勒雷达通过交替发射或者同时发射水平和垂直偏振波,并接收两个偏振方向的回波信号的方法,不仅可以探测到降水系统的回波强度(ZH),还可以探测到差分反射率因子(ZDR)、差传播相移(ΦDP)、差传播相移率(KDP)以及零滞后互相关系数(ρHV(0))等参数(Seliga et al,1976;Doviak et al,2000)。但在实际探测过程中,资料质量容易受到地物遮挡、系统及环境噪声、信号衰减等因素的影响,因此,在利用资料进行降水估测或水凝物相态识别等应用前需对资料质量进行分析。
地物杂波的识别是一个复杂而又必须解决的实际问题。对于多普勒天气雷达,常用的方法主要分为两种。第一种是根据地物信号与气象信号多普勒功率谱的差异,利用凹槽滤波器来处理地物回波。该方法经常把径向速度为0的降水回波误判为地物杂波,尤其是对大面积的地物进行滤波时,为此,美国的WSR-88D雷达、中国的CINRAD/SA雷达等采用预先规定滤波区域的方法来尽可能地减小对降水回波的影响。该方法对雷达波正常传播(NP)情况下的地物处理效果较好,但对由雷达波异常传播而产生的超折射地物回波(AP)却无能为力。第二种方法主要是根据地物和降水观测量的空间分布特征差异来设计程序进行识别。美国大气研究中心(NCAR)利用模糊逻辑法综合使用反射率因子、径向速度和速度谱宽识别地物杂波,但也存在0速度区回波过度识别的问题。刘黎平等(2007)改进了Kessinger提出的模糊逻辑方法,提高了对超折射杂波的识别效果,但对一些孤立的降水回波仍会产生错误识别。江源等(2009)在刘黎平等(2007)的工作基础上,发展了适合中国CINRAD/SA雷达的地物回波识别方法,能有效减少对降水回波的误判,但多普勒雷达对降水和地物混合区的识别仍存在困难。对于偏振雷达而言,由于地物杂波的差分反射率因子ZDR往往会偏离气象回波正常的取值范围(-2—6 dB),通常明显偏低,偶尔也会明显偏大;差传播相移ΦDP在地物处也会出现明显异于降水回波的大幅度波动;零滞后互相关系数ρHV(0)较气象回波正常取值范围(一般大于0.9)偏小很多。因此,在识别地物方面,特别是在地物与降水回波混合的情况下具有更为明显的优势。美国强风暴实验室(NSSL)的Ryzhkov等(2003)根据KOUN雷达在数年间收集的98个气象与非气象回波资料,提出了识别地物杂波的模糊基参数设置,并在实际的业务应用中取得了较好的识别效果。
差分反射率因子ZDR是反映云雨气象目标特征的主要参数之一,其在定量估测降水、降水粒子相态识别等方面有着广泛的应用(张鸿发等,1996),因此,差分反射率因子ZDR的订正问题对于偏振雷达的成功应用起着至关重要的作用。不仅可以提高定量估测降水的精度,还可以提高水凝物类型识别的水平,对于提高气象保障水平有着重要意义。例如,Gourley等(2003)在运用基于反射率因子和差分反射率因子的公式进行降水估测时发现,即使保证差分反射率因子ZDR满足0.2 dB的精度要求,估测的降水率仍会存在15%的误差。
差传播相移ΦDP是一个距离积累量,随着距离的增加而变化。在实际探测中,由于地物等非气象目标的干扰、大气环境场的扰动、气象目标自身的涨落,以及雷达系统各种噪声及误差的影响,差传播相移ΦDP存在抖动起伏现象。Hubbert等(1993)利用有限冲激响应(FIR)和无限冲激响应(IIR)低通滤波器剔除高频噪声以保留差传播相移ΦDP的平均走势。Hubbert等(1995)改进了该方法,提出了迭代滤波的方法。从实际应用情况来看,该方法得到了一定的效果,但一般处理时间较长。中国在差传播相移ΦDP资料处理方面的研究尚少,对ΦDP数据的质量控制局限于滑动平均和中值滤波等预处理方法。曹俊武(2006)对双线偏振雷达资料的平滑方法进行了相关分析。何宇翔等(2009)根据差传播相移ΦDP的特点引入了卡尔曼滤波方法。
车载双线偏振雷达每次移动到新的观测地点都需进行拆卸和重新组装,其相关参数会因此发生改变。这种变化会直接影响资料的后续分析及应用。经过升级改造后雷达的探测性能和参数同样会有所不同。对这方面进行研究有助于了解雷达的具体探测性能及改造后探测资料质量的改进情况。目前这方面的研究还相对较少。曹俊武等(2006)对升级改造后的3836C波段双线偏振多普勒雷达的技术状况做了简要介绍,并利用该雷达实测的一次降水过程资料分析了资料质量情况及其对降水粒子的探测性能。
虽然双线偏振雷达被认为是探测和研究降水粒子结构的一种有效手段,并且已取得了较多的研究成果,但是对于某一特定的双线偏振雷达,要对其进行资料分析和预处理以评价其探测性能仍然是一个相当棘手的难题。Liu等(2010)对C波段双线偏振多普勒雷达资料进行分析后发现,双通道接收机的不匹配导致差分反射率因子ZDR存在明显偏差,且信噪比偏低时噪声对差分反射率因子ZDR和零滞后互相关系数ρHV(0)的影响明显,经过噪声订正和系统误差订正后资料质量得到显著提升。在此基础上,本文对该雷达完成改造后其探测性能的提升情况做了进一步研究,并以该雷达2011年在云南洱源观测的一次降水过程为例,对雷达原始资料进行了质量分析,为资料的后续应用奠定了基础。
2 资料分析方法简介2.1 纯地物回波及地物与降水混合回波的特征及其识别方法2.1.1 纯地物回波及地物与降水混合回波的偏振特征分析图 1为2011年8月12日14时35分(北京时,下同)0.9°仰角晴空模式下的纯地物回波和2011年8月15日18时01分 0.9°仰角下地物与降水混合回波的PPI(plan position indicating)。其中,红色方框标示地物与降水的混合区域,红色箭头指示未受降水回波影响的纯地物回波。图中最大观测距离为75 km,距离圈间隔为15 km,每条径向射线的间隔为30°,雷达位于圆心处(下同)。由于雷达西面近处有多座风力发电塔,因此,整个外场观测期间都设置了探测静默区域(255°—300°),雷达在该区域内不发射电磁波。图中资料已经过孤立杂波剔除和弱信号抑制等预处理。
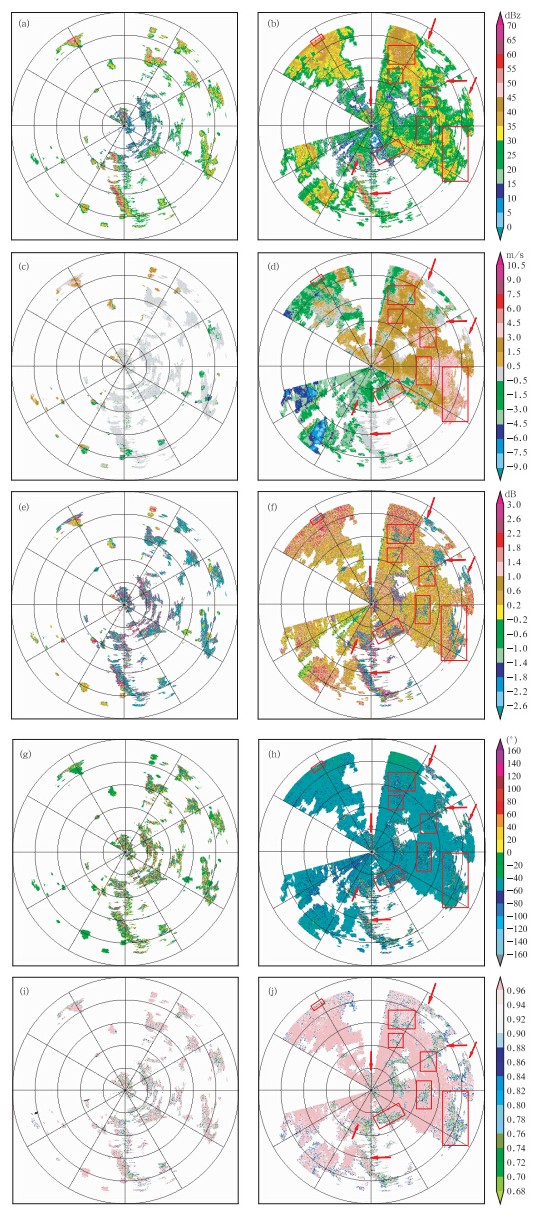 |
| 图 1 纯地物回波及地物与降水混合回波的各雷达参量PPI(a.ZH、c.Vr、e.ZDR、g.ΦDP、i.ρHV(0)纯地物回波;b.ZH、d.Vr、f.ZDR、h.ΦDP、j.ρHV(0)地物与降水混合回波) Fig. 1 PPI of radar measurements of pure ground clutter and mixed ground clutter and precipitation echoes((a)ZH,(c)Vr,(e)ZDR,(g)ΦDP,and (i)ρHV(0)for pure ground clutter echoes,and (b)ZH,(d)Vr,(f)ZDR,(h)ΦDP,and (j)ρHV(0)for mixed echoes) |
在纯地物情况下,差分反射率因子ZDR(图 1e)较之气象回波(通常为-2—6 dB)明显偏大或者偏小,表现为正负极值;差传播相移ΦDP(图 1g)的波动幅度也明显偏大,完全异于降水回波;尽管有少许地物回波的零滞后互相关系数ρHV(0)(图 1i)比降水回波的理论值(一般大于0.9)偏小很多,但绝大部分的ρHV(0)都在0.9以上,即气象回波和纯地物回波在零滞后互相关系数ρHV(0)方面并未表现出明显差异。上述地物偏振特性与Ryzhkov等(2003)的研究结论完全一致。当地物与降水回波混合后,未受降水回波影响的地物回波(红色箭头标示)仍表现出纯地物回波的常规特性和偏振特性,而地物与降水混合回波(红色方框标示)的差分反射率因子ZDR(图 1f)和差传播相移ΦDP(图 1h)同样表现出明显的地物偏振特性,但回波面积明显减小。对两种情况下回波的强度、形状及轮廓进行对比观察后发现,由于雷达参量是根据雷达有效照射体积内所有目标物按照强度加权得到的,当强度较强的地物回波与降水回波混合后,由于其强度比降水回波要大,在雷达有效照射体积内占主导地位,因此,经过强度加权后对外仍表现出明显的地物回波特征;而强度相对较弱的地物回波则被强度较强的降水回波所淹没,从而其偏振参量表现出降水回波的特征。受到地物回波的影响,混合回波的零滞后互相关系数ρHV(0)(图 1j)较纯地物回波和降水回波都有明显的降低,因此,对地物与降水混合回波的识别具有重要作用。综上所述,结合雷达常规参量和偏振参量对地物回波进行识别,并在此基础上,利用偏振参量对地物与降水混合回波做进一步的识别。
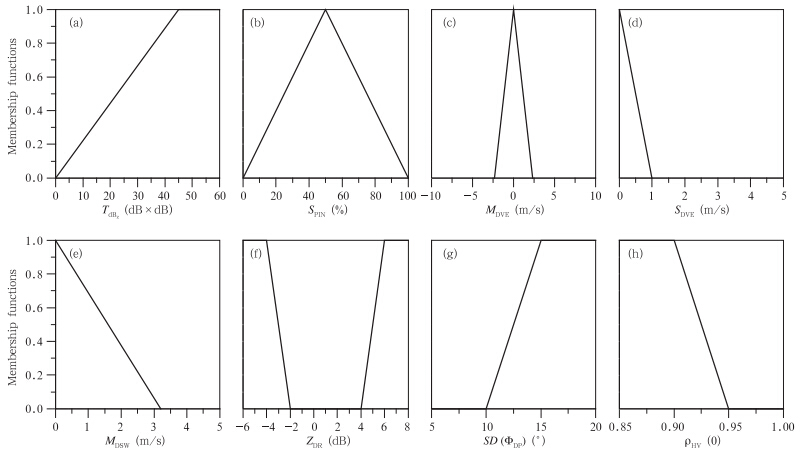
2.1.2 纯地物回波识别方法在刘黎平等(2007)及江源等(2009)(后简称“常规识别模式”)的研究基础上,本文通过添加差分反射率因子ZDR、差传播相移纹理SD(ΦDP)和零滞后互相关系数ρHV(0)这3个参量构建出适合双线偏振雷达的地物回波识别模式(后简称“综合识别模式”)。由于缺乏体扫资料,最终确定采用由单一仰角下观测得到的几个物理量来区分地物和降水回波,其中,包括从回波强度中提取的2个物理量:回波强度的纹理TdBZ、沿径向的库间变化程度SPIN;从径向速度和速度谱宽中提取的3个物理量:径向速度的区域平均值MDVE、标准差SDVE、速度谱宽的区域平均值MDSW;反映探测目标偏振特性的3个物理量:差分反射率因子ZDR,差传播相移纹理SD(ΦDP)及零滞后互相关系数ρHV(0)共计8个雷达参量作为所采用的模糊逻辑识别模式的输入参数,相关参数的定义详见刘黎平等(2007)。其中,用梯形折线表示各常规参量的隶属函数,而偏振参量则选择不对称T函数作为隶属函数的基本形式(式(1)),输入的各雷达参量都已经过相应的质量控制。识别模式的输出结果为1(地物回波)或0(非地物回波)。由于该方法不追求地物和降水回波的具体量值,而是通过宽松的分级原则将回波信号进行分类,从而不受统计公式的影响,不会因为某一具体值的设置不够准确而对最终结果产生太大的影响,具有较强的兼容性和扩展性。
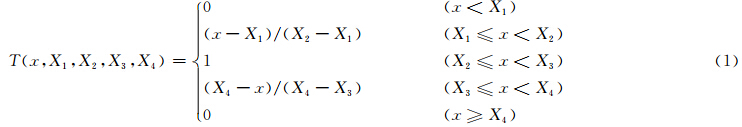
图 2即为各输入变量的隶属函数。在用贡献度相加的方法计算地物回波的权重度(R)时,采取等权重系数法,即各输入变量的权重系数都为1。若计算结果R≥0.5,就认为当前回波为地物回波,否则为非地物回波。
 |
| 图 2 地物识别的各输入参量的隶属函数 (a.TdBZ,b.SPIN,c.MDVE,d.SDVE,e.MDSW,f.ZDR,g.SD(ΦDP),h.ρHV) Fig. 2 Membership functions of input parameters for ground clutter detection (a.TdBZ,b.SPIN,c.MDVE,d.SDVE,e.MDSW,f.ZDR,g.SD(ΦDP),h.ρHV) |
在纯地物回波的识别基础上,根据地物与降水混合回波的偏振特性,利用差分反射率因子ZDR,差传播相移纹理SD(ΦDP)及零滞后互相关系数ρHV(0)作为输入参量,并利用模糊逻辑法构建了混合回波识别模式。识别模式的输出结果为1(地物与降水混合回波)或0(非混合回波)。其中,各输入参量的隶属函数设置如图 2所示,且权重度的计算同样采用贡献度相加的方法。由于混合回波的零滞后互相关系数ρHV(0)明显小于纯地物回波和降水回波,因此,被设为混合回波识别模式的主要贡献量,其权重系数设为1.2,另两个偏振参量的权重系数则设为1。
2.2 ZDR系统误差订正Liu等(2010)利用车载C波段双线偏振多普勒雷达的垂直扫描数据进行了差分反射率因子ZDR随信噪比(SNR)变化的研究及其系统误差订正,订正后的差分反射率因子ZDR数据质量得到显著提升。杜牧云等(2011)在此工作基础上,对雷达垂直扫描时偏振资料随信噪比和高度(H)的变化情况做了进一步的分析,并发现在利用垂直扫描数据进行差分反射率因子ZDR系统误差订正时,信噪比及高度对差分反射率因子ZDR资料的影响较大,需对垂直扫描数据进行筛选和质量控制。整个过程分为4步:
(1)根据差分反射率因子ZDR及零滞后互相关系数ρHV(0)随信噪比和高度的分布情况确立资料选择的信噪比阈值及高度范围:SNR>SNRT且HTL<H<HTH,其中,SNRT为信噪比阈值,HTL和HTH分别为高度下限和上限。
(2)对筛选出来的数据做进一步的质量控制,以指定信噪比间隔(例如0.5 dB)对差分反射率因子ZDR数据分段求均值,并设置散点阈值TZDR,逐点求解各点差分反射率因子ZDR与其对应信噪比区间差分反射率因子均值的绝对偏差ΔZDR=|ZDR-DR|。
(3)对绝对偏差进行判断,若ΔZDR>TZDR则认为该点是离散点,将其剔除。重复前两步直到无散点数据出现。
(4)对剩下的差分反射率因子ZDR数据求整体均值和分段均值,此时得到的随信噪比变化的分段均值曲线即为差分反射率因子ZDR系统误差的订正曲线,而整体均值则为差分反射率因子ZDR系统误差的订正均值。
2.3 系统初始相位分析车载C波段双线偏振多普勒雷达为双发双收(SHV)模式,在该模式下为了保证发射电磁波的极化状态为线性的,需要水平通道和垂直通道的差传播相移ΦDP为0。在实际情况下,往往由于两个通道的不完全匹配导致差传播相移存在一定的偏差。Liu等(2010)利用测试信号对车载C波段双线偏振多普勒雷达进行了差传播相移订正,并用靠近雷达的气象回波边缘的差传播相移求解雷达的系统差传播相移。陈晓辉等(2010)采用如下方法获得系统初始相位:沿径向寻找2 km以外的第一个连续1 km的零滞后互相关系数ρHV(0)大于0.9的数据段,然后取该段所有差传播相移ΦDP的平均值作为该径向的系统初始相位。杜牧云等(2011)对车载C波段双线偏振多普勒雷达差传播相移ΦDP随信噪比和高度的变化情况做了进一步分析后发现,当信噪比较小(小于15 dB)时,差传播相移ΦDP资料波动明显,资料不可用;且距离雷达3 km以内的ΦDP观测值不稳定,即使是在有降水回波的情况下抖动也非常大。因此,从3 km处开始,以第一个连续 1 km(距离库长为75 m)信噪比大于15 dB,零滞后互相关系数ρHV(0)大于0.9的距离库段内的差传播相移ΦDP均值作为该径向的系统初始相位。
2.4 差传播相移ΦDP分类处理及差传播相移率KDP估算目前,对差传播相移ΦDP资料的质量控制主要集中在滤波方法的研究方面。杜牧云等(2011)通过对大量差传播相移ΦDP资料的特征分析,构建出一套系统的差传播相移ΦDP资料分类处理方法。该方法根据差传播相移ΦDP资料的实际情况将其分为非气象信号、较好气象信号、较差气象信号和差气象信号四类,并进行分类处理。该方法对差传播相移ΦDP资料做了较为全面的处理,在最大程度地保留回波信号中的气象信息的同时,也保证了差传播相移ΦDP资料的整体质量,利用处理后的差传播相移ΦDP估算的差传播相移率KDP的数据分布也更加合理。
差传播相移率KDP是通过变距离法(Ryzhkov et al,2003; Wang et al,2009)对分类处理后的差传播相移ΦDP资料进行最小二乘法拟合而得到的。当距离库(库长为75 m)的回波强度ZH>45 dBz时,差传播相移率KDP值由前后各10个库(共21个库,约1.5 km)的差传播相移ΦDP拟合得到;当35 dBz<ZH<45 dBz时,差传播相移率KDP值
由前后各20个库(共41个库,约3 km)的差传播相移ΦDP拟合得到;而当回波强度ZH<35 dBz时,差传播相移率KDP值由前后各30个库(共61个库,约4.5 km)的差传播相移ΦDP拟合得到。上述处理方法的好处在于减少观测资料扰动所产生的误差,且采用较短的拟合距离可以减少强回波受周围弱回波区的影响,从而保持强回波区的特征。
3 C波段双线偏振雷达资料质量分析3.1 地物及地物和降水混合回波的识别效果分析C波段双线偏振多普勒雷达2011年8月15日在云南洱源观测到一次大范围层状云降水过程。图 3为18时01分0.9°仰角下两种地物识别模式的识别结果PPI。图中紫色区域为纯地物回波,橘红色区域为地物与降水混合回波。雷达资料已经过孤立杂波剔除,噪声抑制等预处理。可见两种模式都能较好地识别出主要的、强度较强的地物回波。但对位于0速度区的降水回波(图 3a中蓝色方框),常规识别模式(图 3a)出现了明显的误判。产生误判的原因是降水回波移动缓慢,其径向速度Vr(图 1d)数值较小,接近于0。图 4a、b、c为穿过0速度区降水回波径向(图 3a中蓝线标示)的差传播相移ΦDP和差分反射率因子ZDR距离廓线图,可以看到明显的降水回波特征,即差传播相移ΦDP的波动幅度较小,无明显波动;零滞后互相关系数ρHV(0)全部大于0.9,且大部分在0.95以上。常规识别模式对混合回波(图 3b中红色方框)的识别效果很差,基本无法识别,这是因为地物回波和降水回波混合以后,其径向速度和速度谱宽受降水回波影响,表现为明显的非0值。综合识别模式(图 3b)很好地解决了0速度区过度识别的问题,对混合回波的识别效果较常规识别模式也有所提升,但仍漏掉了较多的地物回波。图 4d、e、f为穿过混合回波径向(图 3b中红线标示)的差传播相移ΦDP和零滞后互相关系数ρHV(0)距离廓线图。从图中虚线标示区域可看到,差传播相移ΦDP出现了大幅波动,其对应的零滞后互相关系数ρHV(0)也明显偏小,基本低于0.9,有些点甚至低于0.7。由其对应的差分反射率因子ZDR(图 1f)、差传播相移ΦDP(图 1h)和零滞后互相关系数ρHV(0)(图 1j)的PPI可以看到,差分反射率因子ZDR较降水回波的理论值(-2—6 dB)明显偏大或者偏小,表现为正负极值;差传播相移ΦDP的波动幅度也明显偏大,完全异于降水回波;而零滞后互相关系数ρHV(0)较之降水回波的理论值(一般大于0.9)也偏小很多。在综合识别模式上叠加混合回波识别模式对地物回波和混合回波进行了较好地识别,识别的地物回波位置和轮廓与各偏振参量PPI图中表现出地物特性的区域也基本吻合,识别效果令人满意。
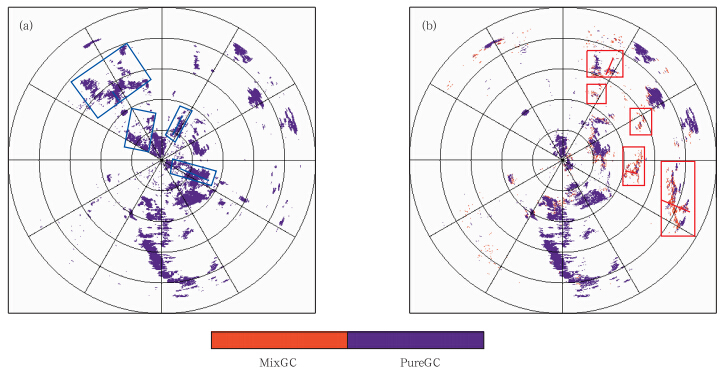 |
| 图 3 2011年8月15日18时01分0.9°仰角不同识别模式的地物识别PPI(a.常规识别模式,b.综合与混合回波联合识别模式) Fig. 3 PPI images from(a)the results by the conventional recognition algorithm,and (b)the results by the comprehensive recognition algorithm with the mixed echo class at 18:01 BT 15 August 2011 at the elevation angle of 0.9° |
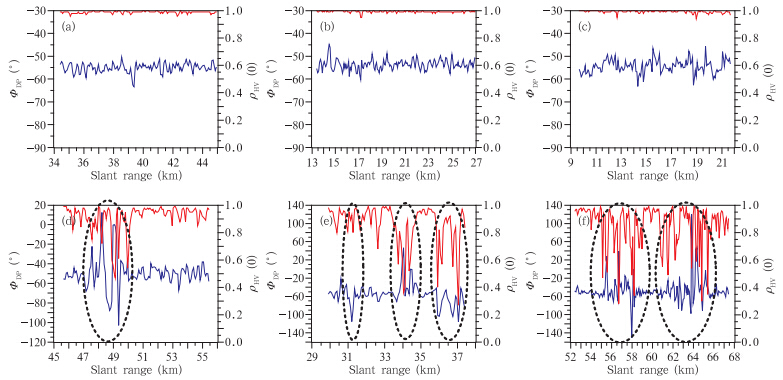 |
| 图 4 图 3a、b中的从左往右蓝线和红线标示径向的ΦDP和ρHV(0)距离廓线(a.324.6°,b.20.3°,c.113.9°,d.25.9°,e.101.1°,f.111.3°方位角) Fig. 4 Radial profiles of ΦDP and ρHV(0)in different azimuths marked by blue and red lines from left to right in Fig. 3(a,b)(a. azimuth in 324.6°,b. azimuth in 20.3°,c. azimuth in 113.9°,d. azimuth in 25.9°,e. azimuth in 101.1°,f. azimuth in 111.3°) |
图 5为C波段双线偏振多普勒雷达改造前2009年9月15日在广东珠海(图 5a、b、c)和改造后2011年8月15日在云南洱源(图 5d、e、f)观测的差分反射率因子ZDR和零滞后互相关系数ρHV(0)分别与信噪比SNR的散点分布(红线为以信噪比0.5 dB为间隔的均值线)。图中资料已经过地物杂波剔除,孤立杂波剔除,噪声订正等预处理。
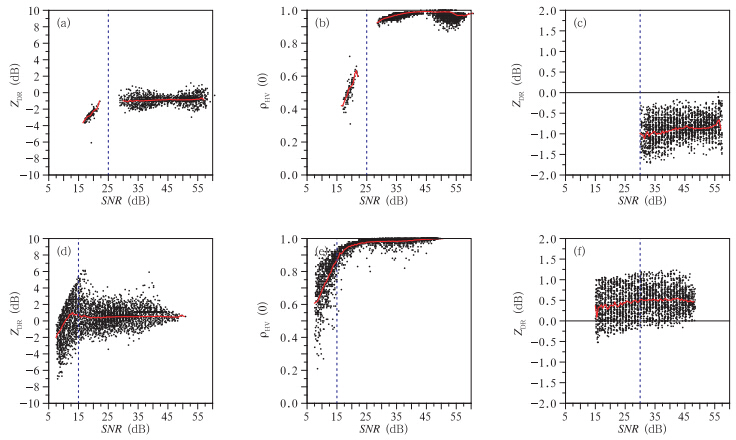 |
| 图 5 雷达改造前后信噪比分别与ZDR和ρHV(0)的散点分布(a. 改造前SNR-ZDR,b. 改造前SNR-ρHV(0),c. 改造前用系统误差订正的SNR-ZDR,d. 改造后SNR-ZDR,e. 改造后SNR-ρHV(0),f. 改造后用于系统误差订正的SNR-ZDR) Fig. 5 Scatter plots of SNR-ZDR and SNR-ρHV(0)before and after radar upgrade(a. the scatter plot of SNR-ZDR before upgrade,b. the scatter plot of SNR-ρHV(0)before upgrade,c. the scatter plot of SNR-ZDR from system error correction data before upgrade,d. the scatter plot of SNR-ZDR after upgrade,e. the scatter plot of SNR-ρHV(0)after upgrade,f. the scatter plot of SNR-ZDR from system error correction data after upgrade) |
从图 5a、d的对比中发现,雷达改造后其信号探测能力得到显著提高。改造前,当信噪比SNR低于25 dB时,差分反射率因子ZDR受噪声影响很大,测量值出现较大误差,其对应的零滞后互相关系数ρHV(0)也明显偏小,远低于理论值(一般大于0.9),且都随着信噪比的降低而呈减小趋势。这说明当信噪比偏低时探测数据整体质量较差,回波信号淹没在噪声之中,数据变得不可信。随着信噪比的增大,差分反射率因子ZDR的分布趋于平稳,而零滞后互相关系数ρHV(0)也基本都大于0.9并迅速向1靠拢。改造后,其信噪比阈值降低到了15 dB,即只有当信噪比小于15 dB时,差分反射率因子ZDR和零滞后互相关系数ρHV(0)资料才会出现较大误差,信噪比大于15 dB时,差分反射率因子ZDR和零滞后互相关系数ρHV(0)资料整体质量较好。因此,通过设置信噪比阈值来筛选数据,并对筛选出的差分反射率因子ZDR资料做进一步的质量控制(见2.2节),从
经过质量控制处理后ZDR与信噪比的散点分布(图 5c、f)可以看出,雷达改造后的ZDR随信噪比的分布更加平稳,尤其是在信噪比较大时(大于30 dB),改造前的差分反射率因子ZDR随信噪比呈现出明显的波动上升趋势,改造后的差分反射率因子ZDR随信噪比几乎呈直线分布,无明显波动。改造前后其变化方差分别为1.898 dB(改造前)和0.113 dB(改造后),最大偏差分别为2.165 dB(改造前)和0.975 dB(改造后)。由此可见,改造后的雷达系统运行更加稳定,差分反射率因子ZDR系统误差随信噪比的变化也更加平稳,无明显波动。此外,还发现雷达经过升级改造并更换观测地点以后,由于雷达硬件方面的更新及移动到新的观测地点时雷达需进行拆卸与重新组装,其差分反射率因子ZDR系统误差发生了很大的变化。
利用垂直扫描数据进行差分反射率因子ZDR系统误差订正前后(图 6)的对比可清楚看到,在用垂直扫描数据对差分反射率因子ZDR进行系统误差订正前(图 6a),ZDR值整体偏大,其拟合直线(蓝线)与理论直线(红线)之间存在明显偏差。其中,理论直线为使用散射模式计算出的理论结果(Bringi et al,2001)。用垂直扫描数据对差分反射率因子ZDR进行系统误差订正后(图 6b),ZDR的分布更加合理,拟合直线与理论直线更加吻合。此外,当回波强度ZH相对较小(ZH<25 dBz)时,其差分反射率因子ZDR值都比较小,在0值附近摆动。随着回波强度ZH的增大(25 dBz<ZH<45 dBz),订正后的差分反射率因子ZDR值基本为0.2—2 dB,且都随着回波强度ZH的增大呈现出明显的上升变化趋势,这种偏振参数的变化特性同Ryzhkov等(2003)的研究成果一致,说明经过订正的差分反射率因子ZDR资料对降水粒子的特性反映是有效合理的,比较符合实际情况,可以对其进行后续分析。对该雷达探测的其他过程资料进行分析也能得到相同结论(图略)。
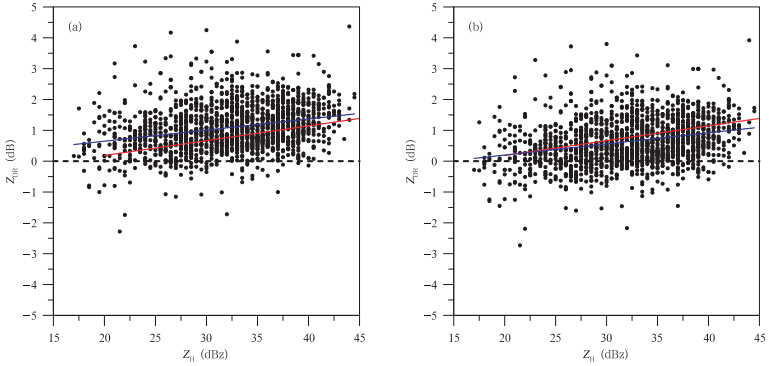 |
| 图 6 图 3降水资料ZH-ZDR的散点分布(a.ZDR系统误差订正前,b.ZDR系统误差订正后) Fig. 6 Scatter plots of ZH-ZDR from the precipitation data in Fig. 3 (a. ZH-measured ZDR,b. ZH-corrected ZDR) |
在对雷达资料进行地物杂波剔除、孤立杂波剔除、弱回波抑制等预处理的基础上,对比分析了雷达改造前后其径向初始相位ΦDP(0)随方位角以及不同仰角、不同时次的相对变化。图 7a、b分别为2009年9月15日01时54分(改造前)和2011年9月4日18时54分(改造后)不同仰角下径向初始相位ΦDP(0)随方位角的变化趋势对比。图 7c、d则分别为相邻4个时次最低仰角下径向初始相位ΦDP(0)随方位角的变化趋势对比。其中,趋势曲线为对每10个点进行最小二乘法拟合得到的,不同仰角、不同时次的趋势曲线以不同的颜色标示。
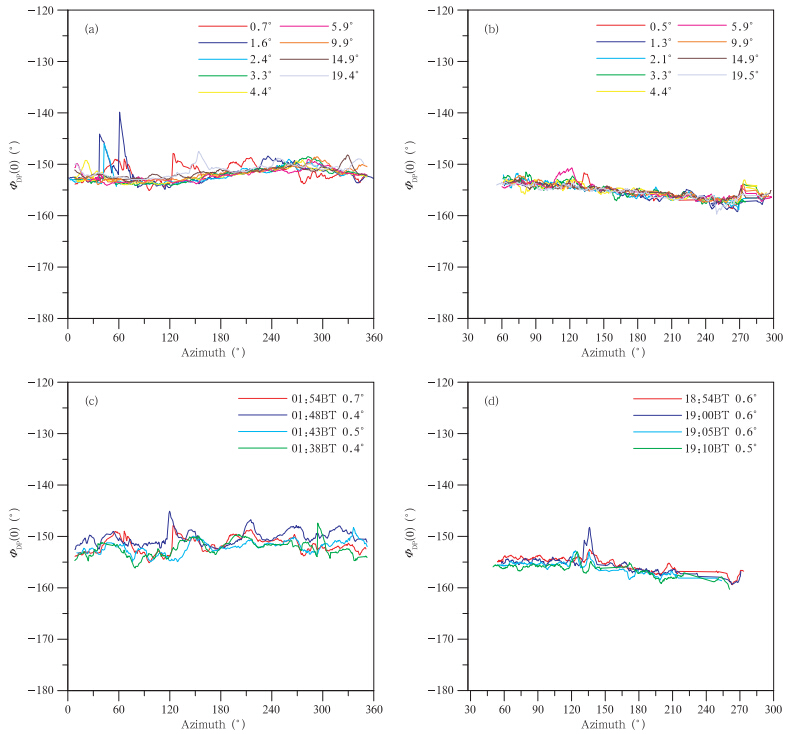 |
| 图 7 雷达改造前后方位角与ΦDP(0)分布(a、c.改造前,b、d.改造后) Fig. 7 Scatter plots of amizuth and ΦDP(0)before(a,c) and after(b,d)radar upgrade |
由图 7a、b可清楚地看到,随着仰角的抬升,径向初始相位ΦDP(0)随方位角的变化趋于平稳,出现较大波动的几个方位集中在低仰角,这主要是受未完全剔除的孤立地物的影响。改造后(图 7b)与改造前(图 7a)相比,径向初始相位ΦDP(0)随方位角的波动幅度更小,整体分布更加平稳且不同仰角下的趋势也更加一致。从图 7c、d不难发现,对应相邻的不同时次,改造前(图 7c)径向初始相位ΦDP(0)随方位角的变化趋势基本一致,但不同时次之间仍存在明显差异。改造后(图 7d)不同时次的趋势曲线之间的吻合度明显提高,且几条曲线几乎重合在一起。上述分析结果表明,改造后的雷达系统在观测过程中更加稳定,系统初始相位随仰角和时间的波动性更小。对其他过程资料的分析也能得到相同的结论(图略)。
3.4 差传播相移率KDP分析以反射率因子ZH和差传播相移率KDP的资料一致性来分析和判断KDP的质量情况。图 8a、b分别为回波强度ZH与经平滑处理(平滑距离约2 km)和分类处理后的差传播相移ΦDP通过变距离法拟合得到的差传播相移率KDP的散点分布。
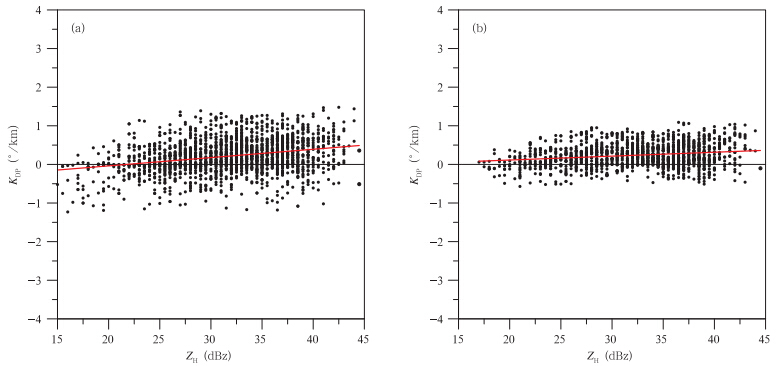 |
| 图 8 图 3降水资料ZH-KDP散点分布(a. 差传播相移ΦDP经平滑处理后拟合差传播相移率KDP,b. 差传播相移ΦDP经分类处理后拟合差传播相移率KDP) Fig. 8 Scatter plots of ZH-KDP from the precipitation data in Fig. 3(a. ΦDP processed using moving average method,b. ΦDP processed using classification processing method) |
由图 8可看到,差传播相移ΦDP经两种方法处理后拟合的差传播相移率KDP都随着回波强度ZH的增大呈现出明显的上升变化趋势(图中红线为数据拟合直线),但相较于常规的平滑处理方法(图 8a),差传播相移ΦDP经分类处理后拟合的差传播相移率KDP(图 8b)更加收敛,其值稳定在0°—1°/km的范围内,且负值点明显更少。上述偏振参量的变化特性同Ryzhkov等(2003)的研究结果一致,说明分类处理法对差传播相移ΦDP的处理效果要优于常规的平滑处理方法,差传播相移ΦDP经分类处理后拟合的KDP资料对降水粒子的特性反映也是合理有效的,比较符合实际情况,可以对其进行后续分析。对其他过程资料进行分析也能得到相同的结论(图略)。
4 结 论双偏振天气雷达是下一代天气雷达的一个重要发展方向,其在研究云微物理机制、定量估测降水、人工影响天气等工作中都将发挥巨大的作用,在实际的业务观测中也有着广泛的应用潜力。本文通过对中国气象科学研究院灾害天气国家重点实验室的车载C波段双线偏振多普勒雷达2011年完成升级改造后观测的一次大范围层状云降水过程的资料分析,以及与改造前观测资料的对比分析,得出如下结论:
(1)该雷达经过升级改造后,信号探测能力得到显著提升。差分反射率因子ZDR随信噪比明显波动的情况基本消除,系统初始相位在探测过程中也更加平稳,随方位的变化明显减小。
(2)改造前,在信噪比小于25 dB时,差分反射率因子ZDR受噪声影响而存在明显的测量误差,而零滞后互相关系数ρHV(0)也迅速减小,明显低于理论值,资料变得不再可信。经过升级改造,其信噪比探测阈值由25 dB降低到15 dB。
(3)结合地物的常规特性和偏振特性,利用模糊逻辑法建立的综合识别模式能有效地识别地物,并明显改善了常规识别模式对0速度区降水回波的过度识别问题。叠加使用混合回波识别模式对地物与降水混合回波的识别也更具优势,识别效果令人满意。
(4)该雷达系统获取的这次降水过程与国外同类产品探测到的结果相类似,对降水粒子偏振特性的反映都比较合理,资料质量较好,可作为后续分析使用。
| 曹俊武. 2006. 双线偏振多普勒雷达的资料质量控制及降水粒子相态识别方法的研究[D]. 北京: 中国气象科学研究院与南京信息工程大学 |
| 曹俊武, 刘黎平, 陈晓辉等. 2006. 3836C波段双线偏振多普勒雷达及其在一次降水过程中的应用研究. 应用气象学报, 17(2): 192-200 |
| 陈晓辉, 曹俊武, 胡志群等. 2010. 车载X波段双线偏振多普勒天气雷达及其数据处理系统. 气象, 36(8): 116-125 |
| 杜牧云, 刘黎平, 胡志群等. 2011. C波段双线偏振多普勒雷达资料质量分析. 暴雨灾害, 30(4): 328-334 |
| 何宇翔, 吕达仁, 肖辉等. 2009. X波段双线极化雷达反射率的衰减订正. 大气科学, 33(5): 1027-1037 |
| 江源, 刘黎平, 庄薇. 2009. 多普勒天气雷达地物回波特征及其识别方法改进. 应用气象学报, 20(2): 203-213 |
| 刘黎平, 吴林林, 杨引明. 2007. 基于模糊逻辑的分步式超折射地物回波识别方法的建立和效果分析. 气象学报, 65(2): 252-260 |
| 张鸿发, 徐宝祥, 王致君等. 1996. 用双线偏振雷达的差分反射率 技术测量降雨和雨滴谱的研究. 气象学报, 54(2): 154-165 |
| Bringi V N, Chandrasekar V. 2001. Polarimetric Doppler Weather Radar: Principles and Applications. Cambridge: Cambridge University Press, 636pp |
| Doviak R J, Bringi V N, Ryzhkov A, et al. 2000. Considerations for polarimetric upgrades to operational WSR-88D Radars. J Atmos Oceanic Technol, 17(3): 257-277 |
| Gourley J J, Kaney B, Maddox R A. 2003. Evaluating the calibrations of radars: A software approach. 31th Conference on Radar Meteorology, 459-462 |
| Hubbert J, Chandrasekar V, Bringi V N, et al. 1993. Processing and interpretation of coherent dual-polarized radar measurements. J Atmos Oceanic Technol, 10(2): 155-164 |
| Hubbert J, Bringi V N. 1995. An iterative filtering technique for the analysis of copolar differential phase and dual-frequency radar measurements. J Atmos Oceanic Technol, 12(3): 643-648 |
| Liu L P, Hu Z Q, Fang W G, et al. 2010. Calibration and data quality analysis with mobile C-band polarimetric radar. Acta Meteor Sinica, 24(4): 501-509 |
| Ryzhkov A V, Zrnic D S, Burgess D, et al. 2003. Observation and classification of echoes with the polarimetric WSR-88D radar. Report of National Severe Storms Laboratory, Norman, Oklahoma, 19-26 L. A |
| Seliga T A, Bringi V N. 1976. Potential use of radar differential reflectivity measurements at orthogonal polarizations for measuring precipitation. J Appl Meteor, 15(1): 69-76 |
| Wang Y T, Chandrasekar V. 2009. Algorithm for estimation of the specific differential phase. J Atmos Oceanic Technol, 26(12): 2565-2578 |
 2013, Vol. 71
2013, Vol. 71

