中国气象学会主办。
文章信息
- 曹经福, 江志红, 任福民, 徐振亚. 2013.
- Cao Jingfu, Jiang Zhihong, Ren Fumin, Xn Zhenya. 2013.
- 广义线性统计降尺度方法模拟日降水量的应用研究
- An application of the generalized linear statitical downscaling method to simulating daily precipitation
- 气象学报, 71(1): 167-175
- Acta Meteorologica Sinica, 71(1): 167-175.
- http://dx.doi.org/10.11676/qxxb2013.014
-
文章历史
- 收稿日期:2011-10-12
- 改回日期:2012-04-06
2. 中国气象科学研究院灾害天气国家重点实验室, 北京, 100081;
3. 南京大学, 灾害性天气研究所, 南京, 210093
2. State Key Laboratory of Severe Weather, Chinese Academy of Meteorological Sciences, Beijing 100081, China;
3. Institute of Severe Weather and Climate, Nanjing University, Nanjing 210093, China
降尺度是进行区域气候研究的重要技术手段。降尺度主要有动力降尺度(张东峰等,2005;许吟隆等,2005)和统计降尺度(Huth,2002)两类,统计降尺度因其计算量小,易于实现而得到广泛应用。
在针对降水的降尺度研究方面,范丽军(2006)利用主分量分析和逐步回归相结合的统计降尺度方法对中国1961—1990年30 a的降水进行模拟分析,发现在当前气候条件下,对区域平均降水的模拟较好。Hellstrōm等(2001)用多元线性回归方法估计了瑞典的月降水,取得了显著效果。Mpelasoka等(2001)成功地用人工神经网络(ANN)模拟了新西兰的月平均降水。王冀等(2010)指出,统计降尺度模型(SDSM)对于模拟月尺度降水量整体上小于实测值,这一点在对降水极大值的模拟上表现更为明显。Widmann等(2003)选取降水量作为预报因子,利用奇异值分解方法模拟季节降水,取得良好效果。
然而,对于日降水量的降尺度问题,较多工作集中在广义线性模型(GLM)的应用上。刘永和等(2000)建立模拟日降水量的广义线性模型,发现基于NCEP再分析资料和广义线性模型的天气发生器对降水变率具有很强的解释和模拟能力。Chandler等(2002)提出了用伯努利分布描述降水发生的广义线性模型,取得了显著的效果;Yang等(2005)利用伽马分布描述降水量的时空广义线性模型,并已用于统计降尺度(Fealy et al,2007);根据日降水量具有非负性、存在大量0值及非0值的偏态分布的特点,杨赤等(2009)基于Tweedie分布发展了日降水量统计降尺度GLM-Kriging模型,对主要降水过程的模拟取得了较高的准确度。然而,在上述研究中,广义线性模型降尺度方法对于长时间序列以及不同区域(如高原与平原)的逐日降水模拟涉及的尚少,而这方面的研究对于气候变化模拟而言其重要性是显而易见的。
本文利用广义线性模型统计降尺度方法,结合NCEP/NCAR再分析资料,对1960—2010年青藏高原和长江下游两个区域的台站日降水量进行模拟,探讨和验证广义线性模型对日降水量的模拟能力。
2 资料与广义线性模型2.1 广义线性模型设要分析的n×1随机因变量向量为Y=(Y1,Y2,…,Yn)T,所有因变量都受到p个自变量的影响,这些自变量用n×p的矩阵X来表示(其每个元素用Xij表示相应于Yi的第j个自变量值),Y的均值向量为μ=(μ1,μ2,…,μn)T,则自变量X与因变量Y的关系用广义线性模型(Chandler,2005)可表示为

式(1)给出了广义线性模型的一般表示,对于日降水量,本文采用类似于Tweedie(1984)提出的一种泊松-伽马复合分布,后来被称为Tweedie分布。所谓Tweedie分布,是设一日内发生了N次降水事件,N服从均值为λ的泊松分布,每次降水事件的降水量Ri服从伽马分布G(-α,γ),日降水量Y由N次降水量Ri相加得到,即
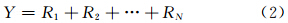

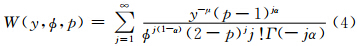
Tweedie分布的均值E(Y)=μ,方差σ(Y)=φμp。当p=1时,该分布趋向于泊松分布;当p=2时,该分布趋向于伽马分布;当1<p<2时,随机变量Y可取0,即无降水情形。此时可得无降水的离散概率为
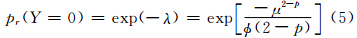
那么,利用Tweedie分布的广义线性模型进行日降水的统计降尺度时,自变量x主要为数值模式输出的反映大尺度环流形势或天气形势、对局地降水有影响的物理量,连接函数取自然对数函数,则得到如下模型
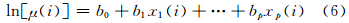
广义线性模型的参数可以采用最大似然法来估计,式(6)中的系数采用的似然公式为

在降尺度研究时,常常将环流因子和温度因子作为大尺度变量场的首选,该因子既可以被大尺度数值模式很好地模拟,又对地面气候要素有重要的影响。由于水循环的变化可能导致未来降水的变化,因此,不少研究发现进行降水预测时包含一个湿度因子是非常有用的(Ruping et al,2002)。
所用资料包括青藏高原和长江下游(图 1)的观测日降水量和NCEP逐日再分析资料。广义线性模型与优选格点回归(OPR)方法的预报量均为观测日降水量。广义线性模型的预报因子为NCEP逐日海平面气压、逐日地面温度场,以及850、500 hPa逐日比湿场和位势高度场资料,用双线性插值方法分别插值到两区域的站点上;优选格点回归的预报因子为NCEP逐日降水量。选取1960—2005年为降尺度建模时段,2006—2010年为模型独立样本检验时段。
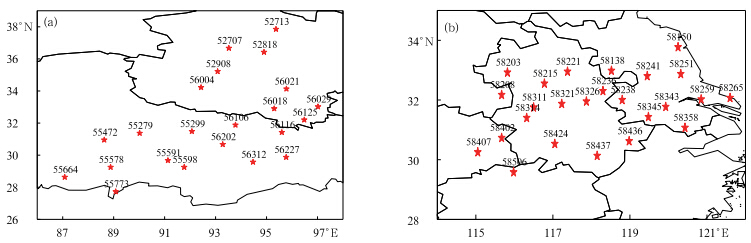 |
| 图 1 青藏高原23个站点(a)和长江下游25个站点(b)的分布 Fig. 1 Distribution of the stations over the Tibetan Plateau(a) and the lower valley of the Yangtze River(b)used in this study |
为了考察广义线性模型的降尺度效果,评估广义线性模型对日降水量的模拟能力,应选择一个参照方法,以期通过降尺度结果的对比分析更客观地认识和刻画出广义线性模型的模拟能力。本文选取优选格点回归(徐振亚等,2012)作为参照方法,优选格点回归是针对简单插值方法所存在之不足而提出来的降尺度方法,包括相邻格点选定、优选相邻格点和回归模型建立3个步骤。徐振亚等(2012)通过对逐日最高气温的降尺度研究发现优选格点回归较之简单插值方法具有明显优势。
3.1 建模期区域降尺度效果从建模期广义线性模型和优选格点回归模拟的青藏高原和长江下游区域日降水量结果(表 1)可发现,1月青藏高原和长江下游广义线性模型模拟结果与观测值的区域平均相关系数达0.74和0.79,7月也均超过0.5,而优选格点回归模拟结果与观测值几乎不相关(相关系数接近0)。从均方根误差来看,广义线性模型模拟两地区的结果在1月和7月均相应减少,其中,7月长江中下游地区相对于优选格点回归减小最多(减小6.8 mm)。此外,分析无降水模拟准确率发现,在青藏高原1月广义线性模型模拟的准确率达85.2%,高于优选格点回归模拟的45.3%,7月广义线性模型模拟的准确率亦达60.32%,而优选格点回归只有27.1%;长江下游1月和7月广义线性模型模拟的准确率均大于65%,但优选格点回归却只有35%左右。
| 时间 | 模型 | 青藏高原 | 长江下游 | ||||
| 相关系数 | 均方根误差(mm) | 无降水模拟准确率(%) | 相关系数 | 均方根误差(mm) | 无降水模拟准确率(%) | ||
| 1月 | 广义线性模型 | 0.74 | 0.23 | 85.2 | 0.79 | 2.2 | 76.1 |
| 优选格点回归 | -0.03 | 1.47 | 45.3 | 0.04 | 4.49 | 35.03 | |
| 7月 | 广义线性模型 | 0.52 | 4.62 | 60.32 | 0.62 | 13.54 | 65.34 |
| 优选格点回归 | -0.09 | 6.31 | 27.1 | -0.02 | 20.34 | 35.49 | |
从建模期广义线性模型和优选格点回归模拟两区域日降水偏差的空间分布(图 2)可看出,广义线性模型和优选格点回归模拟的日降水量大部分偏大,仅1月广义线性模型模拟两区域的少数台站偏小(图 2a、e),7月优选格点回归模拟两区域的少数台站(图 2d、h)偏小。1月广义线性模型模拟两区日降水量偏差大多不足10 mm,虽然7月存在较大偏差,达58 mm,但相对于优选格点回归仍具有明显优势,特别是在长江下游优选格点回归的偏差高达328.75 mm(图 2h)。此外,广义线性模型和优选格点回归模拟两区域1月日降水量的偏差明显小于7月。可见,广义线性模型对日降水量的模拟能力有明显优势。
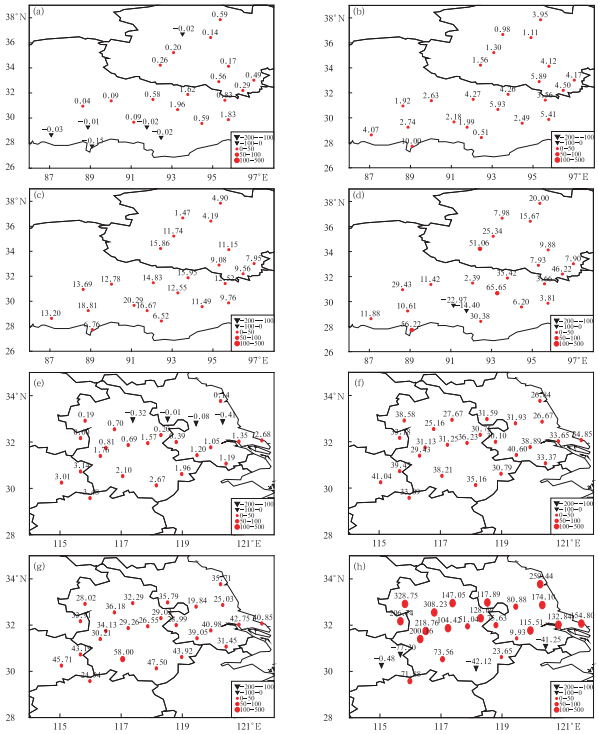 |
| 图 2 建模期广义线性模型(a、c、e、g)和优选格点回归(b、d、f、h)模拟日降水量的偏差分布(单位:mm)(a、b.青藏高原1月,c、d.青藏高原7月,e、f.长江下游1月,g、h.长江下游7月) Fig. 2 Spatial distribution of biases of daily precipitation during the simulative period(unit:mm)for the Tibetan Plateau by GLM in January(a) and by OPR in January(b),by GLM in July(c) and by OPR in July(d); and for the lower valley of the Yangtze River by GLM in January(e) and by OPR in January(f),by GLM in July(g) and by OPR in July(h) |
从检验期广义线性模型和优选格点回归分别对青藏高原和长江下游区域模拟结果(表 2)可发现,广义线性模型模拟两地区的降水量与观测降水的相关系数均超过0.5,明显好于优选格点回归(不足0.1)。优选格点回归模拟的均方根误差大于广义线性模型,最大出现在7月长江下游,达25 mm,而广义线性模型仅为19.46 mm。广义线性模型模拟两地区的无降水准确率均大于优选格点回归,1月青藏高原达最大值,为82.63%,而优选格点回归仅为40.64%。
| 时间 | 模型 | 青藏高原 | 长江下游 | ||||
| 相关系数 | 均方根误差(mm) | 无降水模拟准确率(%) | 相关系数 | 均方根误差(mm) | 无降水模拟准确率(%) | ||
| 1月 | 广义线性模型 | 0.58 | 0.21 | 82.63 | 0.67 | 3.18 | 69.82 |
| 优选格点回归 | -0.02 | 2.42 | 40.64 | 0.01 | 5.33 | 31.22 | |
| 7月 | 广义线性模型 | 0.51 | 5.74 | 58.94 | 0.53 | 19.46 | 63.19 |
| 优选格点回归 | -0.07 | 8.36 | 24.21 | -0.02 | 25 | 30.95 | |
从检验期1月和7月的广义线性模型和优选格点回归模拟青藏高原和长江下游日降水偏差的空间分布(图 3)可见,1月和7月广义线性模型模拟两地区的日降水量大部分偏大,此外,7月有部分台站偏小(图 3c、d、g、h)。其中,广义线性模型偏差绝对值最大出现在7月青藏高原,为-23.47 mm,广义线性模型模拟结果的偏差远小于优选格点回归。
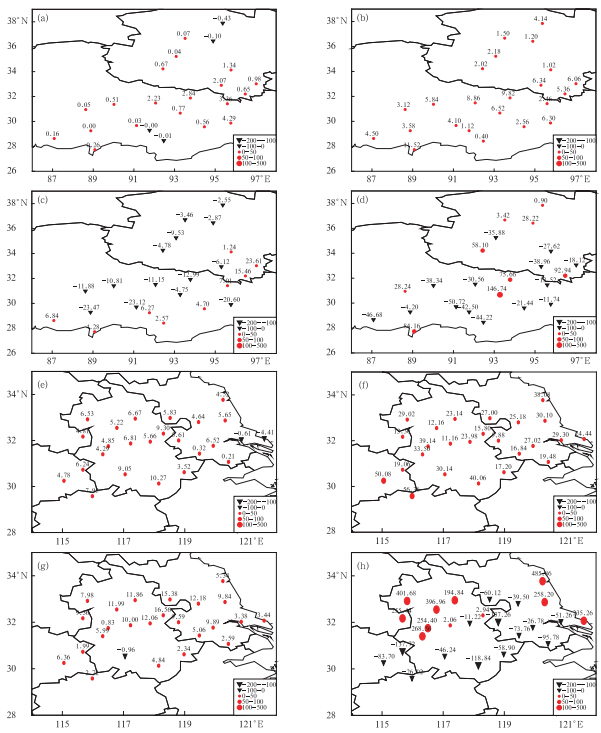 |
| 图 3 检验期广义线性模型(a、c、e、g)和优选格点回归(b、d、f、h)模拟日降水的偏差分布(单位:mm)(a、b.青藏高原1月,c、d.青藏高原7月,e、f.长江下游1月,g、h.长江下游7月) Fig. 3 Spatial distribution of biases of daily precipitation during the test period(unit:mm)for the Tibetan Plateau by GLM in January(a) and by OPR in January(b),by GLM in July(c) and by OPR in July(d); and for the lower valley of the Yangtze River by GLM in January(e) and by OPR in January(f),by GLM in July(g) and by OPR in July(h) |
综上所述,广义线性模型对日降水量的模拟能力效果较好,明显优于优选格点回归,广义线性模型可以较好地反映出气候模式对区域气候特征的模拟。
3.3 代表站降尺度效果为了检查广义线性模型对台站过程降水的模拟效果,分别从高原区和平原区选出隆子站和南通站检验期的结果进行分析。
从隆子站2008年1、7月广义线性模型和优选格点回归模拟结果与观测序列的对比(图 4)可看出,广义线性模型模拟日降水量的效果明显好于优选格点回归,如1月24日观测降水量为0.5 mm,广义线性模型模拟值为0.35 mm,而优选格点回归模拟为无降水,7月17—27日有类似情况;广义线性模型模拟无降水或弱降水时偏大程度小于优选格点回归,如7月8—10日观测无降水,优选格点回归模拟结果均有降水,而广义线性模型仅在7月10日模拟有少量降水。从南通站2008年1月和7月广义线性模型和优选格点回归的模拟结果与观测序列的对比(图 5)可以看出其结果与隆子站类似。
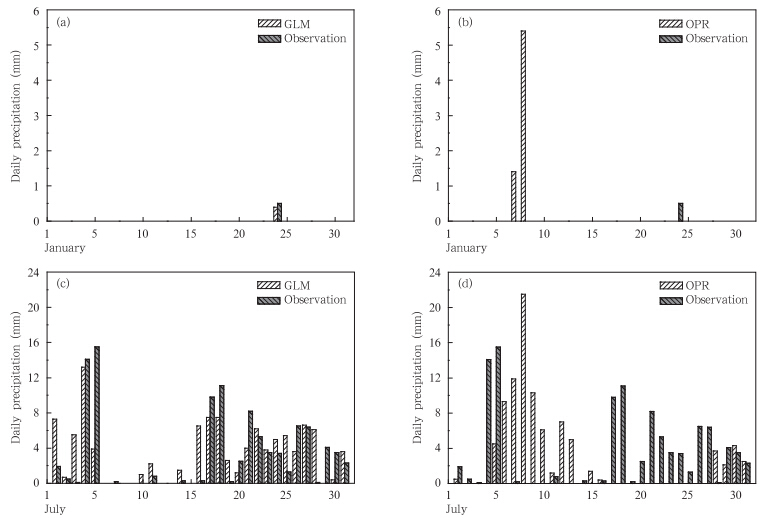 |
| 图 4 广义线性模型(a、c)和优选格点回归(b、d)模拟2008年1月(a、b)和7月(c、d)隆子站的日降水量及其与观测的对比 Fig. 4 Comparison between the observed daily precipitations and the simulated daily precipitations at the Longzi station in 2008(a)by GLM in January,(b)by OPR in January,(c)by GLM in July,and (d)by OPR in July |
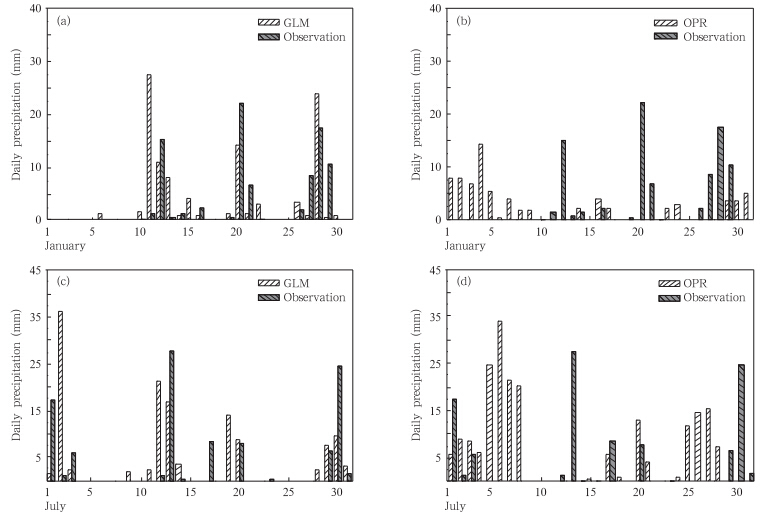 |
| 图 5 广义线性模型(a、c)和优选格点回归(b、d)模拟2008年1月(a、b)和7月(c、d)南通站的日降水量及其与观测的对比 Fig. 5 As in Fig. 4 but for the Nantong station |
为了进一步了解广义线性模型的降尺度效果,以南通站为例,分析检验期内观测与广义线性模型模拟的日降水量的概率密度函数(图 6)可知,无论1月还是7月,广义线性模型模拟与观测的概率密度函数均相当接近,对大降水和无降水都具有较好的模拟能力;而相对来看7月结果更加吻合,1月对小于5 mm的弱降水模拟存在偏大现象。
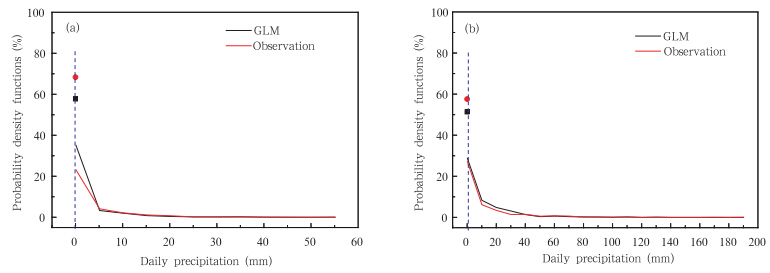 |
| 图 6 南通站观测与检验期广义线性模型模拟的台站日降水量的概率密度函数(%)(a.1月,b.7月) Fig. 6 Probability density functions of the observed daily precipitation and the simulated daily precipitation by GLM during the test period(a)January,and (d)July |
综上所述,广义线性模型模拟降水极值的效果良好,误差较小,较好地还原了站点的主要降水过程,但对于弱降水的模拟仍存在偏大的现象。4 结论和讨论
通过检验广义线性模型对于日降水量的模拟效果,得出以下结论:
(1)评估建模期广义线性模型模拟效果,表明广义线性模型对日降水量具有良好的模拟能力。模拟结果与观测值的相关程度较好,两区域1月平均相关系数达0.75左右,7月也均超过0.5;模拟结果大部分台站日降水为湿偏差,但偏差量值较小;模拟的无降水准确率较高,高原区域1月平均可达85.2%。
(2)检验期广义线性模型模拟效果显示,广义线性模型对日降水量仍表现出较好的模拟能力。广义线性模型模拟两区域的日降水大部分为湿偏差,而7月有部分台站为干偏差;从相关系数、均方根误差、模拟的无降水准确率来看效果均略低于建模期广义线性模型模拟效果。
(3)广义线性模型可以模拟出台站的主要降水过程。对检验期两区域代表站的分析表明,广义线性模型模拟降水极值的效果良好,误差较小,但对于弱降水的模拟仍有的偏多;从降水序列的模拟来看,广义线性模型较好地还原了站点的主要降水过程。
广义线性模型的多项模拟能力与优选格点回归的对比结果显示,广义线性模型对日降水的模拟能力明显优于优选格点回归,其原因可能主要来自两个方面:广义线性模型可以用于拟合非正态分布的随机变量,适合于描述像日降水这样的非负取值的随机变量;广义线性模型采用模式输出的逐日温、压、湿等大气环流场作为预报因子,而优选格点回归直接选取大尺度数值模式的降水因子,由于通常模式对大气环流因子模拟的可靠性比降水高,这也直接影响了降尺度的效果。
上述研究表明,广义线性模型对日降水量的降尺度效果良好,适合应用于气候领域的相关研究。
致谢:研究过程中作者与陈德亮教授、欧廷海博士、李维京研究员和杨赤博士进行了有益的讨论,在此对他们的大力支持和鼓励深表谢意!
| 范丽军. 2006. 统计降尺度方法的研究及其对中国未来区域气候情景的预估[D].北京:中国科学院大气物理研究所, 1-178 |
| 刘永和, 张万昌, 朱时良等. 2000. 基于广义线性模型和NCEP资料的降水随机发生器. 大气科学, 34(3): 599-610 |
| 王冀, 王承伟, 许秀红. 2009. SDSM 降尺度方法在月尺度预报中的应用//第26届中国气象学会年会预测与公共服务分会场论文集,67-77 |
| 许吟隆, 黄晓莹, 张勇等. 2005. 中国21世纪气候变化情景的统计分析. 气候变化研究进展, 1(2): 80-83 |
| 徐振亚, 任福民, 杨修群等. 2012. 日最高温度统计降尺度方法的比较研究. 气象科学, 32(4): 395-402 |
| 杨赤, 严中伟, 邵月红. 2009. 基于Tweedie分布的日降水量统计降尺度模型. 北京师范大学学报 (自然科学版), 45(5-6): 531-536 |
| 张冬峰, 高学杰, 赵宗慈等. 2005. RegCM3区域气候模式对中国气候的模拟. 气候变化研究进展, 1(3): 119-121 |
| Chandler R E, Wheater H S. 2002. Analysis of rainfall variability using generalized linear models: A case study from the west of Ireland. Water Resour Res, 38(10): 1192 |
| Chandler R E. 2005. On the use of generalized linear models for interpreting climate variability. Environmetrics, 16(7): 699-715 |
| Fealy R, Sweeney J. 2007. Statistical downscaling of precipitation for a selection of sites in Ireland employing a generalised linear modelling approach. Int J Climatol, 27(15): 2083-2094 |
| Hellstrōm C, Chen D, Achberger C, et al. 2001. Comparison of climate change scenarios for Sweden based on statistical and dynamical downscaling of monthly precipitation. Climate Res, 19(1): 45-55 |
| Huth R. 2002. Statistical downscaling of the daily temperature in Central Europe. J Climate, 15(13): 1731-1742 |
| Mpelasoka F S, Mullan A B, Heerdegen R G. 2001. New Zealand climate change information derived by multivariate statistical and artificial neural networks approaches. Int J Climate, 21: 1415-1433 |
| Ruping M, David M S. 2002. Statistical-dynamical seasonal prediction based on principal component regression of GCM ensemble integrations. Mon Wea Rev, 130(9): 2167-2187 |
| Tweedie M C K. 1984. An index which distinguishes between some important exponential families //Ghosh J K, Roy J. Applications and New Directions//Proceedings of the Indian Statistical Institute Golden Jubilee International Conference. Calcutta: Indian Statistical Institute, 579-604 |
| Widmann M, Bretherton C S, Salathe C S Jr. 2003. Statistical precipitation downscaling over the Northwestern United States using numerically simulated precipitation as a predictor. J Climate, 16(5): 799-816 |
| Yang C, Chandler R E, Isham V S, et al. 2005. Spatial-temporal rainfall simulation using generalized linear models. Water Resour Res, 41(11): W11415, doi: 10.1029/2004WR003739 |
 2013, Vol. 71
2013, Vol. 71


