中国气象学会主办。
文章信息
- 陈超辉, 李崇银, 谭言科, 曾新民, 周祖刚. 2013.
- CHEN Chaohui, LI Chongyin, TAN Yanke, ZENG Xinmin, ZHOU Zugang. 2013.
- 随机强迫对集合预报效果的影响研究
- Study of the drift of ensemble forecast effects caused by stochastic forcing
- 气象学报, 71(3): 505-516
- Acta Meteorologica Sinica, 71(3): 505-516.
- http://dx.doi.org/10.11676/qxxb2013.040
-
文章历史
- 收稿日期:2012-09-06
- 改回日期:2013-02-19
2. 中国科学院大气物理研究所, LASG, 北京, 100029
2. State Key Laboratory of Numerical Modeling for Atmospheric Sciences and Geophysical Fluid Dynamics (LASG), Institute of Atmospheric Physics, Chinese Academy of Sciences, Beijing 100029, China
迄今,集合数值天气预报发展已近半个世纪,其理论与技术得到了极大丰富与发展,但研究内容仍然主要是围绕初值不确定性、模式不确定性以及集合预报产品释用三个方面。在处理初值不确定性方面,集合预报形成了一条不断向前发展的产生初值扰动集合的理论主线。如蒙特卡罗法(Leith,1974)、时间滞后平均法(Hoffman et al,1983)、增长模培育法(Toth et al,1993,1997)、奇异矢量法(Buizza et al,1995;Molteni et al,1996)、观测扰动法(Houtekamer et al,1996,1998),以及新近发展的集合卡尔曼滤波变换法(Bishop et al,2001,2003;Wang et al,2003;Wei et al,2006)、集合变换法(Wei et al,2008)等,这些方法尽管在理论上越来越完善,但其本质仍然只是在分析值附近对初值的可能概率密度分布进行采样,较少考虑扰动的发展与模式本身内在特性的关系,比如模式的系统性偏差或模型内在随机性。即现行的初值集合预报理论主要基于完美模式假定,但模式永远不可能完美,因此,模式本身对扰动发展及其演变的影响不应忽略。在处理模式不确定性方面,集合预报从最初仅考虑物理过程参数化不完善的多参数化集合预报方案发展到多模式多参数化方案,并且对于各数值预报业务中心的预报不确定性,也从最初的“poor man”技术(Ebert et al,2001)及其延伸的超级集合预报(Krishnamurti et al,2000,2007,2009)发展到目前全球交互式集合预报TIGGE(The THORPEX Interactive Gr and Global Ensemble),这些描述模式不确定性的方法在一定程度上可以增加集合预报系统的发散度,减少集合平均预报的系统误差。但这些基于多参数化或多模式的集合预报方法能完全代表模式不确定性吗?Palmer(2001)和Wilks(2005)的研究表明,这些方式尽管在天气和气候集合预报方面取得了较大成功,但仍不能表征动力系统所有的不确定性,并且,对于模式中除次网格变化外剩下的一切不确定性建议采用非局地随机动力参数化描述。周秀骥(2005)分析也指出,起源于分子热运动的宏观微尺度的随机力是大气本身固有的属性,例如太阳辐射的起伏,以及陆地海洋等下边界与大气过程的随机耦合,使大气变化过程承受着不同时空尺度结构的随机强迫。这些决定着大气过程的突变以及新的大气平衡态的形成,但在以往的牛顿力学框架中,通常认为随机性过程与必然性过程相互独立,随机不确定性因子对必然过程不起决定性作用,一般视为小量而被忽略,或者只考虑其耗散作用。Lorenz(1975)也曾指出,气候模式最终会演变为随机动力模式,即随机数将会出现在积分过程的每个时间步上。
再者,目前对于数值模式只有大尺度大气运动的物理机制是较为清楚的,而次网格参数化过程普遍采用相对简单的确定性模型,即通过可分辨尺度变量表示不可分辨次网格尺度过程的效果,导致大气模式中可分辨与不可分辨变量之间缺乏独立性,可能会产生系统性的误差。因此,基于这种传统计算范式的数值模式,无论是多参数还是多模式,只能描述大气系统变化不确定性的一部分,这就表明天气和气候预报模式中仍然存在一些不确定性源,而这些不确定性源通常在模式中可采用高效非局地随机动力过程来描述。例如目前较前沿的随机参数化扰动方案以及随机全倾向扰动方案(Hou et al,2008)都是基于随机动力积分,其主要目的都是用于集合预报增加系统离散度,初步研究也表明,这种方法在长时间的季节尺度以及气候尺度集合预报中特别有用(Batté et al,2012)。尽管如此,在随机动力积分过程中,关于非局地随机强迫对集合预报效果的影响,从已有研究来看都是一个全新的科学问题。鉴于上述分析,本文主要是在数值模式积分过程中,引入能够代表模式内在随机不确定性的非局地随机动力过程,探究随机强迫引起集合预报效果的变化规律,其中,主要是针对比较典型的高斯白噪声和红噪声随机强迫对集合预报效果的影响,为进一步改善集合预报效果与发展集合预报理论提供科学依据。2 理论分析与模式说明2.1 传统的集合预报计算范式
传统的集合预报计算范式可以描述如下:在一个非线性数值模式中,对于每个集合预报成员Xj(当j=0时,表示控制预报)可以看作是下面的时间积分
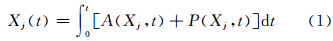
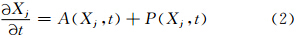
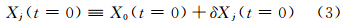
与传统的集合预报计算范式相比,引入随机动力过程的集合预报计算范式主要是在数值模式动力框架部分引入能够描述模式内在随机性的方案。即对于每个集合预报成员Xj的时间积分为
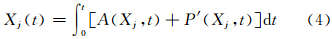
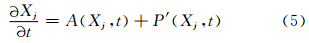
目前,建立P′模型主要有两种思路:
第1种是在传统计算范式的参数化过程P的系数部分引入随机过程
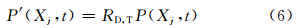
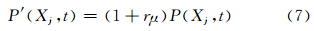
第2种是考虑在数值模式的倾向上直接加入随机强迫项,这种方法又可称为随机全倾向扰动

初步研究表明,上述两种方法都能增加集合离散度,提高概率预报技巧,且比基于传统计算范式的多参数化过程或多模式集合预报方案所描述的模式不确定性效果更好,但这两种思路哪种更有优势,目前尚无相关研究。尽管在这两种处理模式内随机性的思路显示出较好的应用前景,但目前仍主要集中在增加集合离散度和改善概率预报技巧方面,而对于引入随机强迫造成集合预报效果变化的规律研究仍是空白。故本文主要针对典型的高斯白噪声强迫以及服从一阶马尔科夫链分布的红噪声强迫所引起的集合预报效果变化进行研究。
2.3 模式说明本文选用Lorenz 96模式(Lorenz et al,1995,1998,2005)为试验模式,它较Lorenz 1963年提出的3个变量的热对流“点模式”更适宜于研究大气模型。目前,很多学者将其广泛用于大气科学领域引入新技术或者新应用方面的研究,例如,目标观测以及资料同化等领域。Lorenz96模式对初值异常敏感且非线性作用强,它的动力框架可描述为
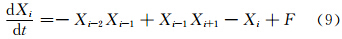
在实际天气系统中,由于次网格尺度变化物理机制很难采用一种确定性模型进行完全描述,因此,基于考虑模式内在随机性,给出集合预报计算新范式,即在模式倾向上引入随机强迫项ηk,ηk 取为空间不相关但时间相关的随机强迫。即随机动力框架可描述为
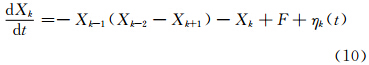
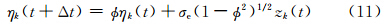
目前用于集合预报的数值模型基本上还没有考虑到这一点,因此,在集合预报系统中探讨随机强迫对集合预报效果的影响是一个很有意义的问题。文中模式真值采用完美模式假定下模式自然运行得到,即对于F等于8或18的系统,真值通过Lorenz96系统自然运行50个单位时间后截取的值作为真值,积分步长为0.025,得到的气候平均态与气候标准差见表 1。模式分析值是在真值的基础上考虑分析误差产生,模式初值是在模式分析值的基础上考虑初始误差得到。为便于讨论,分析误差和初始误差都取为气候标准差的10%。
| 强迫项 | 真值(式(9)) | 非随机强迫σe=φ=0 | 白噪声强迫σe=0.4,φ=0 | 红噪声强迫σe=0.4,φ=0.4 | |
| F=8 | 气候平均 | 2.4893 | 2.4336 | 2.4331 | 2.4888 |
| 气候标准差 | 3.7091 | 3.6876 | 3.7037 | 3.7006 | |
| F=18 | 气候平均 | 3.1129 | 3.2584 | 3.1886 | 3.2134 |
| 气候标准差 | 6.8619 | 6.9109 | 6.8916 | 6.8930 |
通常考虑模式不确定性主要是通过引入不同的数值模式或不同的物理参数化方案,本文主要研究模式动力过程的内在随机不确定性对集合预报结果的影响,包括模式确定性倾向之外的一切未知不确定性,这里首先讨论随机强迫对数值模式的气候态影响。本部分主要给出3种具体不同的积分范式对数值模式气候态的影响,积分范式分别为非随机强迫(即传统的数值模式计算范式)、白噪声强迫和红噪声强迫,其中,后两者主要是根据式(11)的规律分类得到。表 1是真值(通过式(9)自然运行得到)以及Lorenz 96模式采用3种不同积分计算范式得到的气候平均及气候标准差结果,可以看出随机强迫对数值模式气候态的影响。
从表 1可知,不管是气候平均还是气候标准差,3种积分计算范式得到的模式气候态都能接近真值的气候态,但对于不同的计算范式,其接近真值气候态的程度不同。当F=8时,气候平均值方面,红噪声强迫较非随机强迫(即传统的数值预报积分计算范式)更接近真值的气候平均态,白噪声强迫结果与非随机强迫结果相近,但白噪声强迫得到的气候标准差更接近真值的气候标准差。当F=18时,可以发现白噪声、红噪声随机强迫计算范式得到的气候平均值与气候标准差都较非随机强迫更接近真值的气候平均与气候标准差。即从表 1中所引入随机强迫的计算范式结果看,随机强迫对数值模式气候态的影响有正效果,尤其是当F=8时,红噪声强迫所得到的气候平均值基本等于真值的气候平均。
上面仅对气候均值和气候标准差做了简单分析,事实上与表 1中气候平均和气候标准差相联系的是各计算范式得到的变量样本概率密度分布,因此,可以用变量概率密度分布表示接近真值气候态的全貌(图 1)。
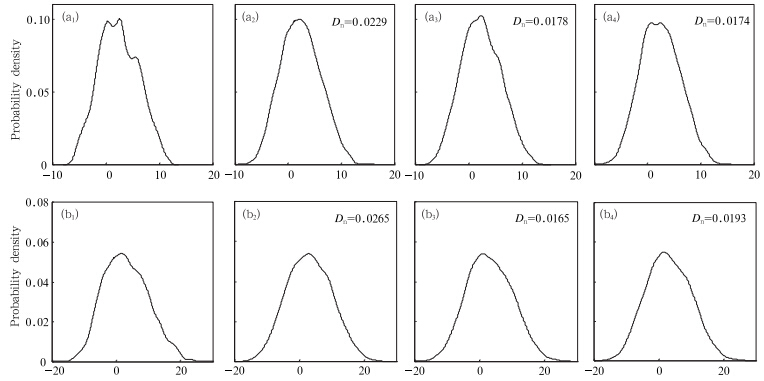 |
| 图 1 真值(a1、b1)、非随机强迫(a2、b2)、白噪声强迫(a3、b3)和红噪声强迫(a4、b4)所对应的模式变量概率密度分布(a. F=8的模式系统,b. F=18的模式系统;图上Dn是衡量各计算范式变量样本分布与真值分布的近似程度) Fig. 1 Probability density distribution of the corresponding model variable to the truth value(a1,b1),non-stochastic forcing(a2,b2),white noise forcing(a3,b3) and red noise forcing(a4,b4)(a. system of F=8,b. system of F=18,Dn representing the distance of probability density distribution between each computational paradigm and truth value) |
从图 1可以看到,各计算范式变量的概率密度分布都能反映真值概率密度分布的主体结构,但引入随机强迫的变量分布较未引入随机强迫的变量分布能更详细描述真值概率分布细节,即引入随机强迫较传统的数值模式计算范式更有价值,尤其在变量概率密度分布峰值附近,引入随机强迫对数值模式气候态的贡献显著。这里可采用Kolmogorov-Smirnov统计客观度量各积分计算范式变量与真值的概率密度分布一致性
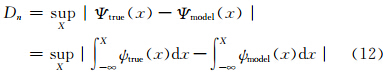
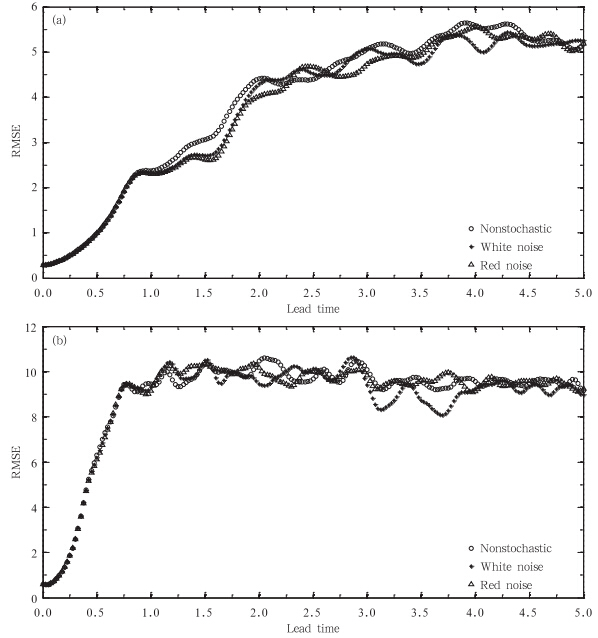 |
| 图 2 非随机强迫、白噪声强迫和红噪声强迫对应的预报结果与真值的均方根误差随时间的演变(a. F=8,b. F=18) Fig. 2 RMSE evolution of the results yielded by non-stochastic forcing,white noise stochastic forcing and red noise stochastic forcing respectively away from the truth value(a. system of F=8,b. system of F=18) |
从式(11)可看出,非随机强迫、白噪声强迫、红噪声强迫的归类主要取决于滞-1自协相关系数(φ)与白噪声振幅(σe)。该模型的物理意义在于当前时刻数值模式的随机不确定性是由前一时刻的随机不确定性和当前时刻的随机干扰造成,φ值表示前一时刻随机不确定性对当前时刻随机不确定性的重要性。如果φ=0,就表示前后两个相邻时刻,模式内随机不确定性相互独立,即数值模式随机强迫仅取决于独立同分布的白噪声随机干扰。
下面就针对白噪声强迫引起集合预报效果的变化问题进行讨论。图 3表示在不同振幅的高斯白噪声强迫下(即式(11)中φ=0),10个成员的Lorenz96模式系统集合预报效果变化特征,试验中分析误差和初始误差如上所述,都为气候标准差的10%,白噪声强迫的振幅在0—3倍分析误差范围内变化。图 3a表示F=8时白噪声强迫引起的系统集合预报效果的变化规律,图 3b则对应F=18时的结果,数值越小代表集合预报效果越好。
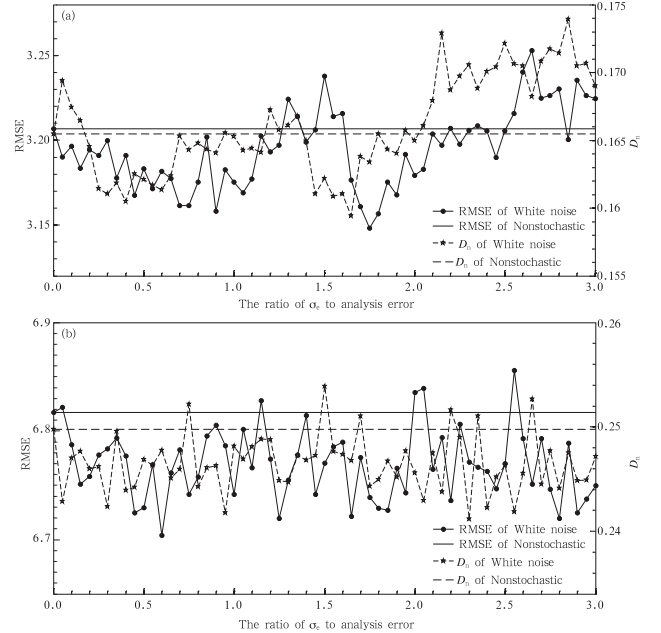 |
| 图 3 不同大小的σe对应的白噪声强迫引起集合预报效果的变化(a. F=8,b. F=18) Fig. 3 Variations of the EPS effects drift caused by white noise stochastic forcing of the different sizes of σe(a. system of F=8,b. system of F=18) |
从图 3可知,对于白噪声影响下的集合预报,白噪声由小到大变化时,集合预报的均方根误差和Dn值都在一定范围内波动,白噪声大小不同,所得集合预报的均方根误差和Dn值一般也不同。与非随机强迫的集合预报效果相比,可以发现大部分白噪声对应的集合预报效果优于非随机强迫的集合预报结果,并且发现当σe值在分析误差1倍以内,白噪声随机强迫对集合预报基本都有正效果,且在σe值与分析误差的比率为1.75附近,系统的均方根误差最小。此外,还可发现一个重要结论,即集合预报的效果并没有随白噪声强迫增大而单调地变差或变好,而是处在一定范围内的白噪声所对应的集合预报结果都能优于非随机强迫集合预报效果,即所对应的均方根误差和Dn值分布在水平横线下方。注意图上的均方根误差和Dn值的分布有细微的差别,但两者总体结论一致。这是由于两者的衡量角度不同,这里均方根误差表示所有时间步、空间点集合平均预报的效果平均,而Dn值是表征集合平均预报变量分布与真值分布的累积概率最大绝对差异。
上面是针对积分所有时刻集合预报的平均效果评估,通过评估可知引入白噪声随机强迫可以改进集合平均预报,同时得出随着高斯白噪声增大,集合预报效果的变化是非单调的。下面进一步分析积分时间为2时,不同σe对集合平均预报效果的影响,结果如图 4所示。
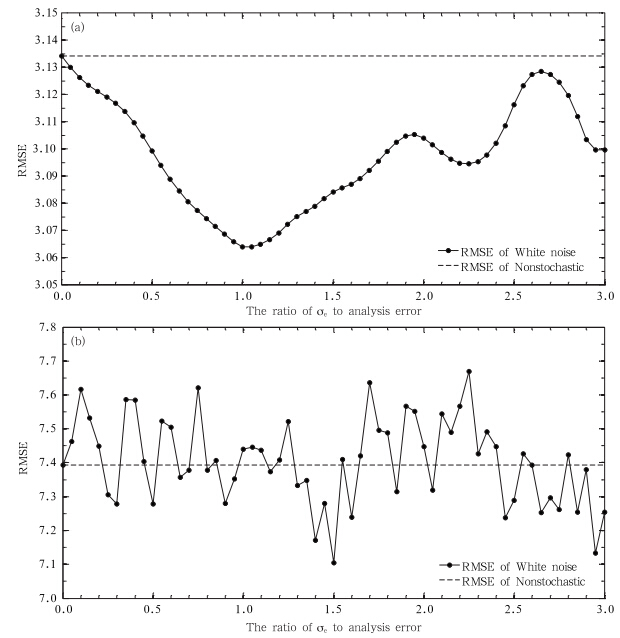 |
| 图 4 积分时间为2时,不同σe对应的白噪声强迫引起集合平均预报效果的变化(a. F=8,b. F=18) Fig. 4 Variations of the EPS effects drift caused by white noise stochastic forcing of the different sizes of σe at a lead time of 2 units(a. system of F=8,b. system of F=18) |
图 4与图 3的区别在于图 3是积分所有时刻的效果平均,而图 4特指积分时间为2时的集合平均预报效果随σe变化的规律。从图 4可知,Lorenz96模式加入不同σe对应的白噪声过程后,集合平均预报效果是不同的,且发现引入恰当的高斯型白噪声强迫,能够对集合平均预报效果有所改善。对于F=8的系统,可以发现积分时间为2时引入白噪声的集合预报效果均比没有噪声状态下的集合预报效果好;对于F=18的系统,发现仅在一定范围内的白噪声强迫对应的集合预报效果比没有噪声状态下的集合预报效果好。此外,从图 4a、b对比可知,对于不同的非线性系统,相同比率大小的白噪声既可产生正效果,也可产生负效果,即白噪声强迫对于不同的非线性系统产生的效果是不同的,但总体而言,对于一个具体的系统,随着白噪声强迫的增大,集合预报效果的变化是非单调的,且在恰当范围内的白噪声强迫都能使集合预报效果优于非随机强迫的集合预报结果。
前面分析了白噪声过程对集合预报效果的影响,本部分主要针对影响随机强迫不确定性的另一个因素对集合预报效果的影响进行讨论。即研究滞-1自协相关系数φ引起集合预报效果的变化特征,这里φ∈[-1,1],且从图 3、4的均方根误差分析看,σe相对于分析误差的比率不妨取为1,集合预报系统成员仍取为10个,其余试验设计同上。下面讨论引入红噪声过程的集合预报效果变化特征(图 5)。图 5表示不同φ值对应的10个成员的Lorenz96模式系统集合预报效果的变化特征。图 5a表示F=8时红噪声强迫引起的系统集合预报效果的变化规律,图 5b则对应F=18时的结果,φ值表示积分前后时间步随机强迫的相关性,绝对值越大,表示相关性越大。
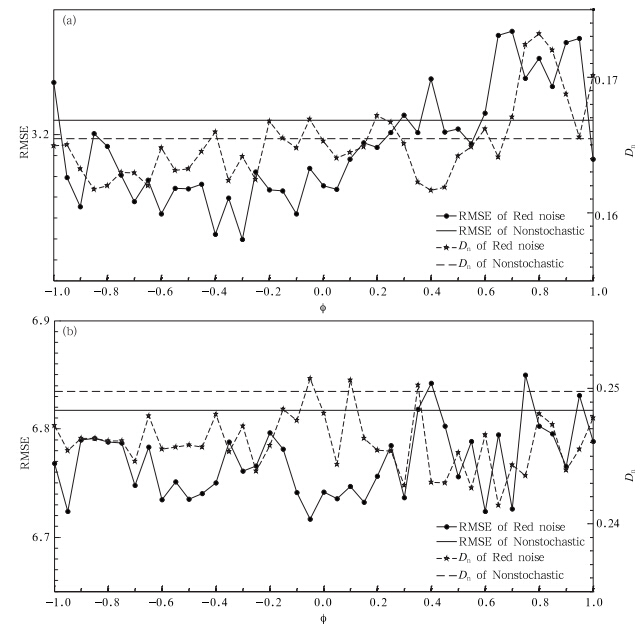 |
| 图 5 不同滞-1自协相关系数φ对应的红噪声强迫引起集合预报效果的变化(a. F=8,b. F=18) Fig. 5 Variations of the EPS effects drift caused by red noise stochastic forcing with the different φ(a. system of F=8,b. system of F=18) |
从图 5可发现引入红噪声强迫过程的集合预报,相关系数φ由-1变化到1时,度量集合预报效果的均方根误差和Dn值都在一定范围内变化,φ不同,所得集合预报的均方根误差和Dn值一般也不同,并且与非随机强迫的集合预报效果相比(即水平横线对应的结果),可以发现对于F为8或18的非线性系统,绝大部分红噪声过程对应的集合预报效果优于非随机强迫的集合预报结果。再者,与白噪声过程的集合预报效果(即图 5中横坐标φ=0对应的点)相比,红噪声强迫对应的集合预报可能更具价值,尤其是在φ的负值区,但其改善效果随相关系数φ值的正负分布不具有对称性。例如在图 5a中,大部分小于0的φ值对应的均方根误差小于φ=0时的均方根误差,而在φ>0时,均方根误差一般较φ=0时的均方根误差大;在图 5b中,尽管均方根误差相对效果分布与图 5a的有所不同,但随相关系数φ值的正负分布,集合预报效果同样非对称变化。Dn值的总体分布特点类似,不同在于用Dn值度量时,可以发现红噪声过程的集合预报效果明显优于白噪声过程的集合预报,即φ=0对应的Dn较大部分φ对应的Dn值大。
此外,集合预报效果也没有随φ值变化而单调地变差或变好,而是处于某些范围内的φ值所对应的集合预报结果都能优于白噪声强迫集合预报和非随机强迫集合预报,但从均方根误差和Dn值总体分布看,红噪声过程的集合预报优于非随机强迫集合预报的程度相比它优于白噪声过程的集合预报程度更明显。并且对于不同的非线性系统,同一个φ值对应的集合预报改善效果也可能不同,这表明开展随机强迫集合预报时,随机参数φ的选择也依赖于模型。
前面图 5是针对积分所有时刻集合平均预报的效果平均,而这里仅给出积分时间为2时不同φ对集合平均预报效果的影响,结果如图 6所示,Lorenz96模式加入不同φ对应的红噪声过程后,集合平均预报效果是不同的。对于恰当的φ值,它能够改善集合平均预报,但随φ的正负分布,集合预报效果呈非单调非对称变化。如对于F=8的系统,可以发现引入红噪声的集合预报效果均比没有噪声状态下的集合预报效果好,但只有部分φ值对应的效果优于白噪声集合预报(φ=0的结果);而对于F=18的系统,发现仅在一定范围内的φ对应的集合预报效果比非随机强迫或白噪声强迫的集合预报效果好。此外,由图 6a、b对比可知,非线性系统不同,相同大小的φ产生的效果也可能不同,即表明φ的选择依赖于模型。
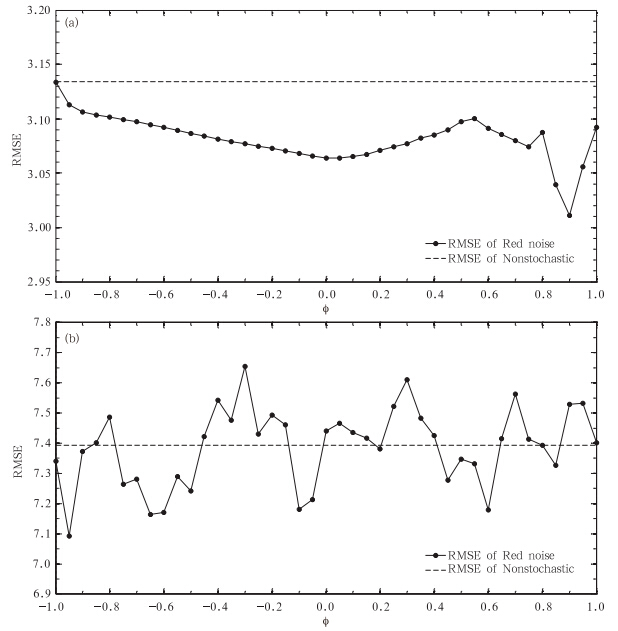 |
| 图 6 积分时间为2时,不同滞-1自协相关系数φ对应的红噪声强迫引起集合平均预报的效果变化 (a. F=8,b. F=18) Fig. 6 Variations of the EPS effects drift caused by red noise stochastic forcing with the different φ at a lead time of 2 units(a. system of F=8,b. system of F=18) |
数值预报积分过程中引入非局地随机动力过程是一种新的计算范式,必然对现行集合预报理论及应用带来新的研究内容。基于此观点,首先在理论部分分析了传统的集合预报计算范式与考虑模式内在随机性的集合预报计算范式的概念与方法,从两者的本质区别可知,开展随机强迫引起集合预报效果的影响研究既有严密的数学基础又有一定的物理意义和科学内涵。在理论分析的基础上,本文基于Lorenz 96模式动力框架开展了随机强迫对模式气候态的影响、高斯白噪声强迫和红噪声强迫对集合预报效果的影响的研究,并通过均方根误差和Dn对比分析,得到一些有意义的结果。
(1)数值模式积分过程中引入恰当的随机强迫构成的新计算范式,对刻画数值模式的气候态有正的影响效果。从气候平均值与气候标准差看,非随机强迫(即传统的数值模式计算范式)、随机强迫(包括白噪声强迫和红噪声强迫的新计算范式)得到的模式气候态都能接近真实气候态,但其各自接近真实气候态的程度不同。总体而言,对于F=8与F=18的模式系统,随机强迫得到的气候平均值与气候标准差都较非随机强迫更接近真值的气候平均与气候标准差。尤其是当F=8时,红噪声强迫所得到的气候平均值基本等于真值的气候平均。此外,从随机强迫起作用的时间看,随机强迫的正效果主要体现在长时效阶段。
(2)引入的绝大部分白噪声随机强迫得到的集合预报效果优于非随机强迫的集合预报结果,且白噪声随机强迫不同,所得的集合预报均方根误差和Dn值一般也不同。尤为重要的是白噪声随机强迫由小到大变化时,集合预报效果并没有随白噪声强迫增大而单调地变差或变好,而是处在一定范围内的白噪声随机强迫所对应的集合预报效果都能优于非随机强迫集合预报效果。从积分时间为2时的集合平均预报效果可知,对于F=8的情况,引入白噪声随机强迫的系统均比没有噪声状态下的集合平均预报效果好;对于F=18的情况,仅处在一定范围内的白噪声随机强迫对应的系统比没有噪声状态下的集合平均预报效果好。这也反映了非线性系统不同,相同比率的白噪声随机强迫产生的效果也不同。
(3)与白噪声随机强迫不同,红噪声强迫不仅取决于σe相对于分析误差的比率,还取决于滞-1自协相关系数φ。为便于讨论,σe相对于分析误差的比率不妨取为1,系数φ由-1到1变化,发现φ不同,所得集合预报的均方根误差和Dn值一般不同,并且对于F为8或18的非线性系统,绝大部分红噪声随机强迫对应的集合预报效果优于非随机强迫的集合预报结果,但仅部分φ值对应的红噪声强迫集合预报优于白噪声随机强迫的集合预报结果。更为重要的是,引入红噪声随机强迫得到的相对改善效果随系数φ值的正负分布不具有对称或单调的变化。此外,积分时间为2时的结论类似,且对于不同的非线性系统,同一个φ值所对应的集合预报改善效果也可能不同,表明φ值的选择依赖于模型。
(4)引入恰当的随机强迫在刻画模式气候态和集合平均预报方面都具价值。从理论上说,这种增加模式复杂度的计算范式,相比传统的计算范式可能更能探测到相空间重要的邻近区域,从而更好地描述模式系统的不确定性。但需指出,本文的结论是基于初始扰动误差方差与分析误差方差大小一致的情况下得出的,对于初始扰动误差方差与分析误差方差不一致的情况仍需进一步研究。文中模式气候态和集合平均预报效果不仅与随机强迫的参数选择相关,还取决于非线性模式系统,随着研究进一步深入,相信随机强迫引起集合预报效果的影响研究会有更好的应用前景。
| 周秀骥. 2005. 大气随机动力学与可预报性. 气象学报, 63(5): 806-811 |
| Batté L, Déqué M. 2012. A stochastic method for improving seasonal predictions. Geophys Res Lett, 39: L09707, doi:10.029/2012GL051406 |
| Bishop C H, Etherton B J, Majumdar S J. 2001. Adaptive sampling with the ensemble transform Kalman filter. Part I: Theoretical aspects. Mon Wea Rev, 129: 420-436 |
| Bishop C H, Reynolds C A, Tippett M K. 2003. Optimization of the fixed global observing network in a simple model. J Atmos Sci, 60(12): 1471-1489 |
| Buizza R, Palmer T N. 1995. The singular vector structure of the atmospheric global circulation. J Atmos Sci, 52(9): 1434-1456 |
| Buizza R, Miller M J, Palmer T N. 1999. Stochastic representation of model uncertainties in the ECMWF ensemble prediction system. Quart J Roy Meteor Soc, 125(560): 2887-2908 |
| Ebert E E. 2001. Ability of a poor man’s ensemble to predict the probability and distribution of precipitation. Mon Wea Rev, 129: 2461-2480 |
| Hoffman R N, Kalnay E. 1983. Lagged average forecasting, an alternative to Monte Carlo forecasting. Tellus A, 35A(2): 100-118 |
| Hou D C, Toth Z, Zhu Y, et al. 2008. Impact of a stochastic perturbation scheme on NCEP Global Ensemble Forecast System//Proceedings of the 19th AMS Conference on Probability and Statistics, New Orleans, Louisian |
| Houtekamer P L, Lefaivre L, Derome J, et al. 1996. A system simulation approach to ensemble prediction. Mon Wea Rev, 124: 1225-1242 |
| Houtekamer P L, Mitchell H L. 1998. Data assimilation using an ensemble Kalman filter technique. Mon Wea Rev, 126: 796-811 |
| Krishnamurti T N, Kishtawal C M, Shin D W, et al. 2000. Improving tropical precipitation forecasts from a multianalysis super-ensemble. J Climate, 13: 4217-4227 |
| Krishnamurti T N, Gnanaseelan C, Chakraborty A. 2007. Prediction of the diurnal change using a multimodel superensemble. Part I: Precipitation. Mon Wea Rev, 135: 3613-3632 |
| Krishnamurti T N, Mishra A K, Chakraborty A, et al. 2009. Improving global model precipitation forecasts over India using downscaling and the FSU super-ensemble. Part I: 1-5-Day Forecasts. Mon Wea Rev, 137: 2713-2735 |
| Leith C E. 1974. Theoretical skill of Monte Carlo Forecasts. Mon Wea Rev, 102(6): 409-418 |
| Lorenz E N. 1975. Climatic predictability//The Physical Basis of Climate and Climate Modelling, WMO GARP Publ Ser, (16): 132-136. Geneva: World Meteor Organ, 265 pp |
| Lorenz E N. 1995. Predictability: A problem partly solved//Seminar on Predictability, Volume I. ECMWF, Reading, UK, 1-18 |
| Lorenz E N, Emanuel K A. 1998. Optimal sites for supplementary weather observations: Simulation with a small model. J Atmos Sci, 399-414 |
| Lorenz E N. 2005. Designing chaotic models. J Atmos Sci, 62: 1574-1587 |
| Molteni F, Buizza R, Palmer T N, et al. 1996. The ECMWF ensemble prediction system: Methodology and validation. Quart J Roy Meteor Soc, 122(529): 73-119 |
| Palmer T N. 2001. A nonlinear dynamical perspective on model error: A proposal for non-local stochastic-dynamic parameterization in weather and climate prediction models. Quart J Roy Meteor Soc, 127(527): 279-304 |
| Toth Z, Kalnay E. 1993. Ensemble forecasting at NMC: The generation of perturbations. Bull Amer Meteor Soc, 74(12): 2317-2330 |
| Toth Z, Kalnay E. 1997. Ensemble forecasting at NCEP and the breeding method. Mon Wea Rev, 125(12): 3297-3319 |
| Wang X G, Bishop C H. 2003. A comparison of breeding and ensemble transform Kalman filter ensemble forecast schemes. J Atmos Sci, 60(9): 1140-1158 |
| Wei M, Toth Z, Wobus R, et al. 2006. Ensemble transform kalman filter-based ensemble perturbations in an operational global prediction system at NCEP. Tellus A, 58(1): 28-44 |
| Wei M, Toth Z, Wobus R, et al. 2008. Initial perturbations based on the ensemble transform(ET) technique in the NCEP global operational forecast system. Tellus A, 60(1): 62-79 |
| Wilks D S. 2005. Effects of stochastic parametrizations in the Lorenz ′96 system. Quart J Roy Meteor Soc, 131(606): 389-407 |
 2013, Vol. 71
2013, Vol. 71

