中国气象学会主办。
文章信息
- 刘永柱, 沈学顺, 李晓莉. 2013.
- LIU Yongzhu, SHEN Xueshun, LI Xiaoli. 2013.
- 基于总能量模的GRAPES全球模式奇异向量扰动研究
- Researeh on the singular vector perturbation of the GRAPES global model based on the total energy norm
- 气象学报, 71(3): 517-526
- Acta Meteorologica Sinica, 71(3): 517-526.
- http://dx.doi.org/10.11676/qxxb2013.043
-
文章历史
- 收稿日期:2012-08-15
- 改回日期:2013-01-31
数值模式的初值误差、模式物理过程参数化的不确定性以及大气运动的非线性特点,使得单一的确定性数值预报存在较大的不确定性。集合预报提供了一种估计大气状态概率密度函数(PDF)的方法(Ehrendorfer,1994a,1994b),它通过构建一组能描述大气初值误差分布特征的扰动初值成员,利用这些扰动初值进行模式预报,进而给出大气状态概率密度函数的预报,来提供数值预报不确定性的信息。对于初始场的扰动,理想的扰动场结构应该与实际分析场中误差的分布一致,从而使叠加扰动场后的集合成员的初始场可以被认为是大气初始状态概率密度函数的样本,并且,不同集合成员的预报随时间的演变也要足够发散以尽可能地包含大气可能出现的状态。
在过去的几十年里,不同的初始扰动技术应用于集合预报,其中主要有奇异向量法(SV)(Buizza et al,1995)、增长模繁殖法(Toth et al,1997)、集合转换(ET)(Bishop et al,1999)及重新尺度化集合转换方法(ETR)(Wei et al,2006)、集合卡尔曼滤波方法(EnKF)(Houtekamer et al,2005)以及非线性方法如条件非线性最优扰动(CNOP)法(Mu et al,2003)。这些初值扰动技术是从不同角度来估计大气初始状态的概率密度函数,并且进行集合成员初值的取样。已有研究利用简化模式进行不同扰动方法的比较(Hamill et al,2000; Bowler,2006),及对采用不同扰动技术的3个全球集合预报业务系统(European Center for Medium-Range Weather Forecasts,ECMWF,National Centers for Environment Prediction,NCEP及Meteorological Service of Canada,MSC)的对比(Buizza et al,2005)。 相对于其他扰动技术而言,奇异向量法具有完备的数学理论基础,基于大气数值模式的切线性及伴随模式计算出的奇异向量扰动反映了分析误差在相空间中增长最快的扰动,利用奇异向量构造的集合预报初始扰动是模拟初始大气误差概率密度函数的最佳方法之一(Ehrendorfer,1997)。奇异向量扰动法在ECWMF全球集合预报业务系统中得到了成功的应用(Buizza et al,1997)。
GRAPES全球模式是中国气象局自主研发的新一代数值天气预报模式(薛纪善等,2008),建立基于奇异向量法的GRAPES全球集合预报系统也是未来的发展目标。目前GRAPES全球模式干动力框架下的切线性和伴随模式已经完成,这为GRAPES全球模式奇异向量扰动技术的研究和发展提供了条件。奇异向量求解中权重模的确定对奇异向量的结构有着显著的影响。已有研究表明,以总能量模为权重模的奇异向量比较适合作为集合预报初值扰动(Buizza et al,1997)。因此,本文将根据GRAPES全球模式的自身特点,推导适合其模式预报变量的GRAEPS奇异向量求解所需的总能量模,通过奇异向量检验方法和切线性近似方法验证GRAPES奇异向量求解的正确性,并通过试验来分析奇异向量结构及其线性演变特征,论证基于总能量权重模的GRAPES 奇异向量结构的合理性,为GRAPES全球集合预报系统的研发奠定坚实的技术基础。2 GRAPES 奇异向量计算介绍
GRAPES全球模式是一个非静力的、半隐式半拉格朗日的均匀经纬格点全球数值预报模式,其动力框架采用高度地形追随坐标“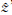 ”,其预报变量为风的3个分量(u,v,w)、扰动位温
”,其预报变量为风的3个分量(u,v,w)、扰动位温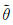 =θ-θr、扰动无量纲气压变量
=θ-θr、扰动无量纲气压变量 =Π-Πr和水物质q,可记为向量X=(u,v,w,
=Π-Πr和水物质q,可记为向量X=(u,v,w,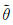 ,
, ,q)T,其中,Πr为参考无量纲气压,θr为参考位温(薛纪善等,2008)。
,q)T,其中,Πr为参考无量纲气压,θr为参考位温(薛纪善等,2008)。
对于GRAPES全球模式的切线性及伴随模式(目前不包括线性化物理过程参数化方案),需要计算的预报变量包括纬向风u、经向风v、扰动位温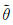 和扰动无量纲气压
和扰动无量纲气压 的扰动向量,可记为x=(u′,v′,
的扰动向量,可记为x=(u′,v′,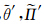 )T。
)T。
奇异向量是在线性模式中一定时间间隔内增长最快的一组扰动。一个初始扰动向量x经过GRAPES切线性模式(记为:矩阵算子L)向后积分t时刻得到了演化扰动向量xt(xt=Lx),则GRAPES奇异向量扰动的求解问题就是演化向量xt与初始向量x的模比值的极大化问题。
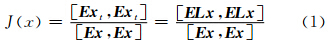
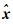 (
(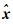 =Ex,x=E-1
=Ex,x=E-1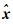 ),式(1)可进一步变化为
),式(1)可进一步变化为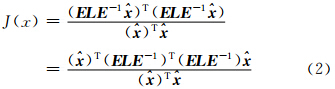
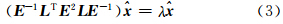
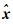 是(ELE-1)T·(ELE-1)属于λ的特征向量。那么,
是(ELE-1)T·(ELE-1)属于λ的特征向量。那么,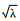 就是矩阵(ELE-1)的奇异值,
就是矩阵(ELE-1)的奇异值,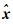 就是矩阵(ELE-1)的右奇异向量,也就是本文所要计算的GRAPES模式的奇异向量。3 GRAPES奇异向量总能量模的推导
就是矩阵(ELE-1)的右奇异向量,也就是本文所要计算的GRAPES模式的奇异向量。3 GRAPES奇异向量总能量模的推导由式(3)可以看出,权重算子E是衡量扰动大小的重要因子,也承担着物理空间变量(x)和欧拉空间向量(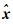 )进行转换的作用。如前所述,本文要研究和建立基于GRAPES模式切线性模式扰动变量的总能量模权重算子E,将扰动变量(u′,v′,
)进行转换的作用。如前所述,本文要研究和建立基于GRAPES模式切线性模式扰动变量的总能量模权重算子E,将扰动变量(u′,v′,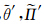 )的不同单位转换为相同的能量单位。
)的不同单位转换为相同的能量单位。
在静力平衡大气中,从海平面延伸至大气上界的铅直气柱内,GRAPES全球模式的干总能量可以表示为动能和势能之和
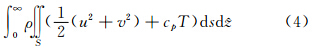
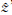 ”下,式(4)中的模式变量替换为切线性模式的扰动变量,则可得到在铅直气柱内切线性模式的干总能量为扰动动能和扰动势能之和
”下,式(4)中的模式变量替换为切线性模式的扰动变量,则可得到在铅直气柱内切线性模式的干总能量为扰动动能和扰动势能之和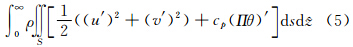
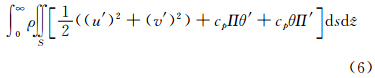
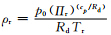 计算得到,Rd是空气的干气体常数,p0是标准大气压(1013 hPa),Tr是参考温度(300 K)。由于GRAPES全球模式中的预报变量采用的是扰动无量纲气压变量
计算得到,Rd是空气的干气体常数,p0是标准大气压(1013 hPa),Tr是参考温度(300 K)。由于GRAPES全球模式中的预报变量采用的是扰动无量纲气压变量 和扰动位温
和扰动位温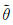 ,所以式(6)中的cpΠθ′相应的转换为cpΠr
,所以式(6)中的cpΠθ′相应的转换为cpΠr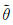 ′,cpθΠ′相应的转换为cpθr
′,cpθΠ′相应的转换为cpθr ′。那么式(6)可以变化为
′。那么式(6)可以变化为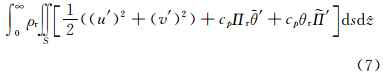
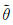 ′和
′和 ′的内积定义,需要对式(7)第3项引入参考位温θr,则扰动
′的内积定义,需要对式(7)第3项引入参考位温θr,则扰动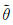 ′的内积可表示为
′的内积可表示为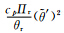 ,同样对于式(7)第4项引入参考Πr,则扰动
,同样对于式(7)第4项引入参考Πr,则扰动 ′的内积可表示为
′的内积可表示为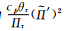 。 依据上述变换和公式Tr=Πrθr,就可以得到扰动向量x的内积定义
。 依据上述变换和公式Tr=Πrθr,就可以得到扰动向量x的内积定义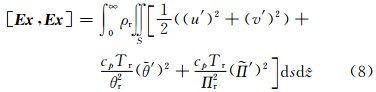
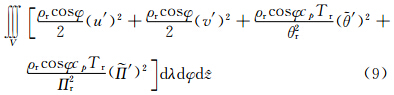
结合式(1)和式(9)中推导出的GRAPES 奇异向量计算的总能量模公式,可以得出基于总能量模的变换算子E分别对应于GRAPES切线性模式的4个扰动变量(u′,v′,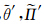 )在式(9)的系数
)在式(9)的系数
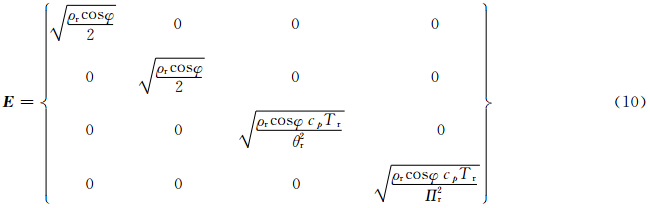
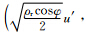
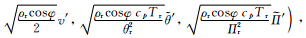 能量模算子E保证了向量
能量模算子E保证了向量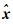 具有相同的单位信息,又反映了GRAPES 奇异向量是相空间中能量增长最快的初始扰动。4 基于总能量模的GRAPES奇异向量计算
具有相同的单位信息,又反映了GRAPES 奇异向量是相空间中能量增长最快的初始扰动。4 基于总能量模的GRAPES奇异向量计算对于式(3)定义的奇异向量及奇异值求解,由于切线性算子L相当于一个高维(>106)的稀疏矩阵,一般采用Lanczos迭代算法(Simon,1984)来计算前面最大奇异值对应的部分GRAPES 奇异向量。Lanczos算法是一种将对称矩阵通过正交相似变换成三对角矩阵的算法,并得到奇异值最大的一部分奇异向量,这种方法是求解维数很大的稀疏矩阵特征值问题的最有效方法之一。在具体求解奇异向量时,本文采用了NAG(Numerical Algorithm Group Ltd,Oxford)开发的Lanczos算法程序库。基于这个程序库,刘永柱等(2010)也开展了区域GRAPES模式奇异向量计算求解研究。本文将在结合并行版本的GRAPES全球切线性和伴随模式进一步开展全球GRAPES奇异向量的计算研究。
从数学定义上看,所需计算的GRAPES奇异向量事实上就是式(3)中的矩阵算子(E-1LTE2LE-1)的特征向量,该矩阵算子由5部分组成,结合Lanczos算法的循环迭代流程,本文设计了GRAPES奇异向量的计算流程:
(1)第一步,启动Lanczos算法,把欧拉向量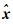 (注意第一次迭代时,引入一个随机向量作为启动迭代算法的
(注意第一次迭代时,引入一个随机向量作为启动迭代算法的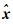 )运用本文定义的总能量模变换算子E的逆E-1转换成初始扰动向量x=(u′,v′,
)运用本文定义的总能量模变换算子E的逆E-1转换成初始扰动向量x=(u′,v′,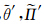 )T;
)T;
(2)第二步,对初始扰动向量进行并行GRAPES切线性模式L向前积分t时段,得到演化扰动向量xt*=(u′,v′,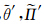 )tT;
)tT;
(3)第三步,在对xt进行总能量变换算子Etx2转换,得到输入GRAPES伴随模式LT的伴随扰动向量xt*=(u′*,v′*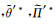 )tT;
)tT;
(4)第四步,对xt*利用并行GRAPES伴随模式LT向后积分t时段,得到初始时刻的伴随梯度向量x0*=(u′*,v′*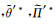 )T;
)T;
(5)第五步,对x0*实施E-1转换后得到了欧拉向量;
(6)第六步,欧拉向量 经过Lanczos算法程序计算后,又重新得到了新的欧拉向量
经过Lanczos算法程序计算后,又重新得到了新的欧拉向量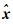 ,然后再重复前5步,一直到循环迭代结束。最后得到一组增长最快的奇异向量扰动,也就是本文所希望获得的GRAPES奇异向量。
,然后再重复前5步,一直到循环迭代结束。最后得到一组增长最快的奇异向量扰动,也就是本文所希望获得的GRAPES奇异向量。
为了体现全球不同纬度地区天气系统不稳定性的不同特征,也使所计算出的GRAPES 奇异向量能更显著地出现在所关注区域内天气系统的不稳定区,本文借鉴了ECWMF采用的分目标区计算奇异向量的技术(Buizza,1994),分别计算了3个目标区的GRAPES奇异向量:北半球中高纬度(30°—80°N)、南半球中高纬度(80°—30°S)和低纬度热带区域(30°S—30°N)。由于当前使用的GRAPES全球切线性和伴随模式中还不包括线性化的湿物理过程参数化方案,无法有效描述出热带区域系统的不稳定特点,所以,对于热带区域的GRAPES 奇异向量计算,本研究仅是建立了其计算模块,未对其结构进行深入分析。
由以上奇异向量的求解流程可以看出,全球GRAEPS奇异向量计算过程复杂,需要把GRAEPS全球切线性模式、伴随模式和变换算子E组成一个矩阵算子(ELE-1),采用Lanczos迭代算法来对(ELE-1)进行奇异值分解。由于(ELE-1)并不是一个“真正”的矩阵,且维数巨大,它比一般矩阵的奇异值分解要复杂很多,因此,需要对所计算的GRAPES 奇异向量的正确性进行验证,本文采用的验证技术为刘永柱等(2010)发展的奇异向量检验法(具体细节在此不再详述)。
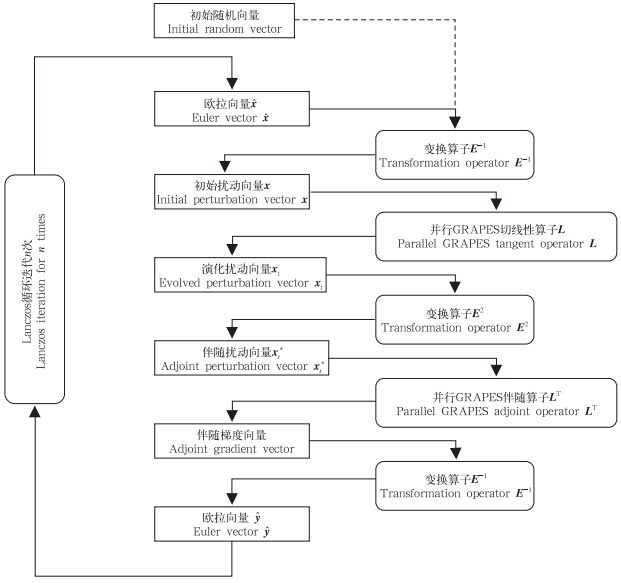 |
| 图 1 GRAPES奇异向量计算流程 Fig. 1 Flow chart for the GRAPES SV calculation |
本文开展了2010年6月1—10日连续10天的GRAPES 奇异向量的计算试验。试验的基本设置为:分析场为每日00时(世界时,下同)NCEP 的FNL分析场;GRAPES全球切线性和伴随模式的水平分辨率为2.5°,垂直方向为37层,不包括线性化物理参数化方案;奇异向量计算的最优化时间间隔为48 h;Lanczos算法的最大迭代次数为40次,其奇异值计算精度为0.01。 奇异向量的计算在两个目标区域进行:(1)北半球中高纬度区域(30°—80°N),求得的GRAPES奇异向量记为NH SVs;(2)南半球中高纬度区域(80°—30°S),求得的GRAPES奇异向量记为SH SVs。
首先基于2010年6月1日00时的试验结果,利用奇异向量检验法来验证奇异向量的计算正确性。具体验证步骤如下:(1)对奇异向量实施E-1运算,得到物理空间上的扰动向量xi;(2)对xi运用GRAPES切线性算子L向后积分最优时间间隔48 h,得到物理空间上的演化扰动向量xit=Lxi;(3)对演化扰动向量xit运用E变化得到欧拉空间上的演化向量Exit;(4)对Exit依次实施E运算、GRAPES伴随算子LT反向积分48 h,得到物理空间上的变换扰动向量xi*。根据奇异向量检验方法,变化扰动向量xi*和扰动向量xi在空间结构应该是相同的,只是扰动量值的差对应奇异值的平方σi2。
图 2给出了北半球中高纬度区域第1奇异向量(简称SV01)的扰动位温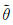 ′和变换后的
′和变换后的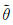 ′*在模式第7层(大约850 hPa),14层(大约500 hPa)和第20层(大约200 hPa)上的空间结构比较,为了更好的展示结果,扰动值均放大了1000倍,且对
′*在模式第7层(大约850 hPa),14层(大约500 hPa)和第20层(大约200 hPa)上的空间结构比较,为了更好的展示结果,扰动值均放大了1000倍,且对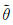 ′*除以σi2(11.4238)。从图 2中可以看出,在这3层上
′*除以σi2(11.4238)。从图 2中可以看出,在这3层上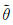 ′(阴影)与缩小σi2倍的
′(阴影)与缩小σi2倍的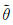 ′*(等值线)基本上是重合的,这表明NH SV01的扰动位温
′*(等值线)基本上是重合的,这表明NH SV01的扰动位温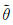 ′和变换后的′*具有相同的空间结构,只是扰动量值上存在着σ2i倍数的差异,这种转换关系完全符合特征向量分解的几何意义。分析南、北半球中高纬度区域其他奇异向量的扰动变量及变化扰动变量的结构,也得到了相同的结果,这说明本文所计算的GRAPES 奇异向量在数理基础上是正确的。
′和变换后的′*具有相同的空间结构,只是扰动量值上存在着σ2i倍数的差异,这种转换关系完全符合特征向量分解的几何意义。分析南、北半球中高纬度区域其他奇异向量的扰动变量及变化扰动变量的结构,也得到了相同的结果,这说明本文所计算的GRAPES 奇异向量在数理基础上是正确的。
 |
图 2 北半球中高纬度区域第1奇异向量的位温扰动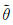 ′(阴影)和变换后的 ′(阴影)和变换后的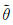 ′*(等值线)的空间结构比较(a. 模式第7层,b. 第14层,c. 第20层) Fig. 2 Comparison between the potential temperature perturbation ′*(等值线)的空间结构比较(a. 模式第7层,b. 第14层,c. 第20层) Fig. 2 Comparison between the potential temperature perturbation 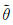 ′(shaded) and the evolved ′(shaded) and the evolved 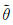 ′*(contour)of the NH SV01(a. model level 7,b. model level 14,c. model level 20) ′*(contour)of the NH SV01(a. model level 7,b. model level 14,c. model level 20) |
5.2 GRAPES奇异向量线性及非线性时间演变特征
本文继续以2010年6月1日00时的试验结果为例,来研究所计算出的奇异向量扰动在切线性模式中随大气轨迹基本气流的演化特征,以了解其如何从基本气流中获得能量,来促使扰动的不断增强。主要分析比较了奇异向量扰动在GRAPES切线性模式中24、48 h的演变。此外,还进行奇异向量扰动在GRAPES全球预报模式中非线性演变的分析,具体就是对未扰动的初始场和增加奇异向量扰动后的初始场分别进行GRAPES全球非线性模式的48 h积分,计算两者预报结果的差值,即为奇异向量扰动的非线性演变。比较在较短时间(48 h以内)小扰动在切线性模式及非线性模式中演变的一致性是一种常用的检验切线性模式正确性的技术(Errico et al,1993;Buizza,1995)。通过比较奇异向量扰动的24 h及48 h的线性及非线性演变的相似性进一步验证GRAPES切线性模式的正确性。
图 3给出了6月1日模式14层(约500 hPa)上北半球中高纬度第1奇异向量在初始时刻00时、经过24、48 h线性演变的结构,以及经过48 h非线性演变的结构,为了更好地展示结果,扰动量值均放大了1000倍。可以看出,初始时刻第1奇异向量的位温扰动主要位于蒙古国西北处500 hPa高空槽前斜压性较强的气压梯度大值区,同时,在位温扰动大值区对应的位置也存在一个明显的反气旋结构的扰动风速区,其中扰动位温正值区和扰动风速的辐散区相配合(图 3a)。经过24 h的GRAPES全球切线性模式的线性演变(图 3b),北半球中高纬度第1奇异向量的主要结构随基本气流向下游移动,其位置仍位于500 hPa高空槽气压梯度大的斜压区,且位温扰动的暖中心更暖,冷中心更冷,同时风速扰动也相应一起增长,这说明扰动不断从基本气流的斜压变化中获得能量。经过48 h的线性演变后(图 3c),第1奇异向量的主要扰动也主要对应于基本气流的大气压梯度区,且由于从基本气流中获得更多能量而使位温扰动冷暖中心的范围和扰动幅度都在快速增长,并且,在增大的冷扰动中心后出现了一个暖中心的扰动,相应的风速扰动也在持续的增长和扩展。通过分析更多试验的南、北半球中高纬度其他奇异向量在相空间中的线性演变也得到了类似的结论:GRAPES 奇异向量一般位于大气斜压梯度大的地方,并且,其随时间的线性演变不断从基本气流的斜压变化中获得能量,促进扰动幅度和范围持续的变大。 这也说明GRAPES奇异向量所处的位置正是大气基本气流中的斜压最不稳定的地方,也是导致未来预报不确定性的敏感性区域。
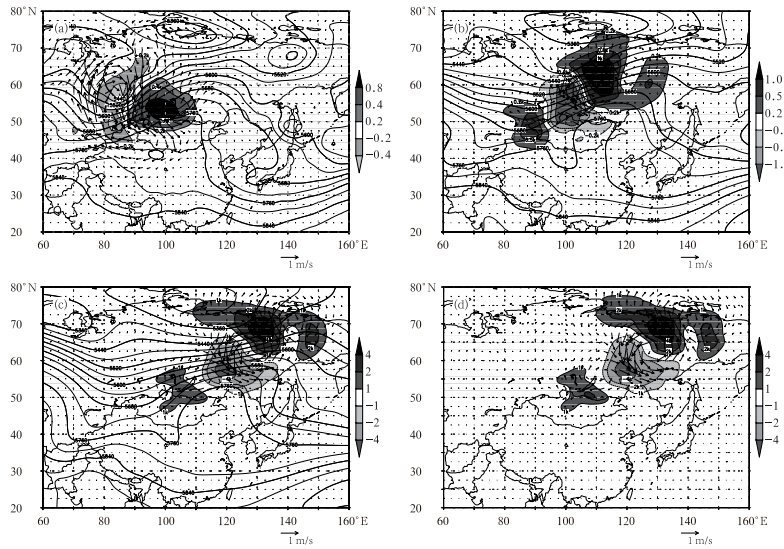 |
| 图 3 北半球中高纬度第1奇异向量风速与位温扰动(阴影)在模式14层的线性和非线性的时间演变(等值线)及500 hPa位势高度(a.初始时刻,b.24 h线性演变,c.48 h线性演变,d. 48 h非线性演变) Fig. 3 Linear and non-linear evolution of the wind speed and potential temperature perturbation(shading)at model level 14,and 500 hPa geopotential height(contour)(a.initial time,b. 24 h linear evolution,c. 48 h linear evolution,d. 48 h non-linear evolution) |
此外,对比北半球中高纬度第1奇异向量的48 h 线性演变结构(图 3c)和48 h非线性演变结构(图 3d)可以看出,两者的位温扰动和风速扰动在大小、形状和位置上非常相似,说明在最优时间间隔(48 h)内北半球中高纬度第1奇异向量的切线性近似很好。其他奇异向量扰动的线性演变和非线性演变结果也具有很好的切线性近似,这进一步验证了基于GRAPES全球切线性和伴随模式与本文定义的总能量模公式GRAPES奇异向量的结构是合理的。5.3 GRAPES奇异向量扰动能量垂直结构分析
在此进一步分析奇异向量扰动的能量垂直分布,以全面了解其结构特征。图 4给出了10天试验的南、北半球第1和第6奇异向量(NH SV01、NH SV06、SH SV01和SH SV06)总能量的垂直分布。可以看出,GRAPES奇异向量的总能量模主要分布在模式第4层到第16层中间(图中的两条水平线之间),相当于850—400 hPa的对流层内,个别GRAPES 奇异向量的总能量模较大的值出现在模式24层(相当于对流层顶)上下(图 2b),这说明中高纬度的斜压不稳定区域主要集中在对流层内,斜压不稳定是中高纬度天气尺度扰动发生发展的主要机制,从而验证了采用总能量作为求解GRAPES奇异向量的模定义能够很好地反映中高纬度天气的斜压不稳定特征。
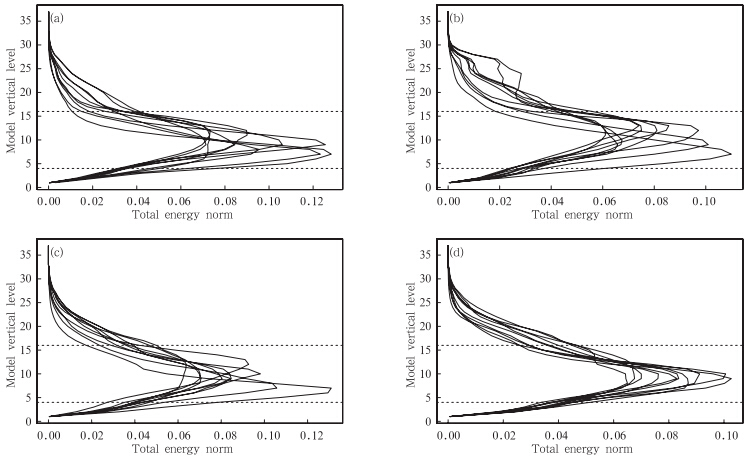 |
| 图 4 10天试验的GRAPES 奇异向量总能量模的垂直分布(a.北半球第1奇异向量,b.北半球第6奇异向量,c.南半球第1奇异向量,d.南半球第6奇异向量) Fig. 4 Vertical distribution of the total energy of the GRAEPS SVs during the 10 days experiment(a. NH SV01,b. NH SV06,c. SH SV01,d. SH SV06) |
由式(9)可知,GRAPES 奇异向量的总能量可以分成动能与势能两部分,在此进一步分析奇异向量扰动总能量及其分量——动能及势能的时间演变。对于图 4中的4个奇异向量扰动,图 5分别给出了其总能量、动能及势能在初始时刻及最优化时间间隔(48 h)时的垂直结构。可以看出,北半球中高纬度第1奇异向量在初始时刻的势能大概占了总能量60%的比重,动能和势能的最大值都分布在模式第9层上下,经过最优时间间隔线性演化后,演化奇异向量的总能量、动能和势能都迅速增长,其中,势能的增长要明显快于动能的增长,在总能量中大约占75%的比重,且其主要集中在对流层中下层。南半球中高纬度第1奇异向量的势能线性演变(图 5c)与北半球基本相似,但动能在对流层上层比北半球第1奇异向量的动能增长更快。
对于北半球中高纬度第6奇异向量,其能量线性演变特征与其第1奇异向量明显不同,在初始时刻第6奇异向量总能量的垂直分布在对流层内分布更广,动能分量大概占65%的比重,经过48 h的线性演化其第6奇异向量的总能量显著增长,在对流层上层和下层表现出最大值和次大值的峰值结构。分析动能和势能对总能量分布的贡献,发现动能分量在对流层上层的峰值起主导作用,而势能在对流层下层峰值贡献显著(图 5b)。 南半球中高纬度第6奇异向量的总能量及其各分量的线性演变特征(图 5d)与北半球第6奇异向量很相似,这表明由于对流层上层气温较低,存在风速急流,GRAPES奇异向量扰动动能更容易从基本气流中获得能量促进其发展,而在对流层中下层,气流受到地形的摩擦和地面热力作用的影响,温度变化比较明显,奇异向量扰动的势能在该层随时间演变过程较易从温度变化中得到扰动能量,来促使其增长。
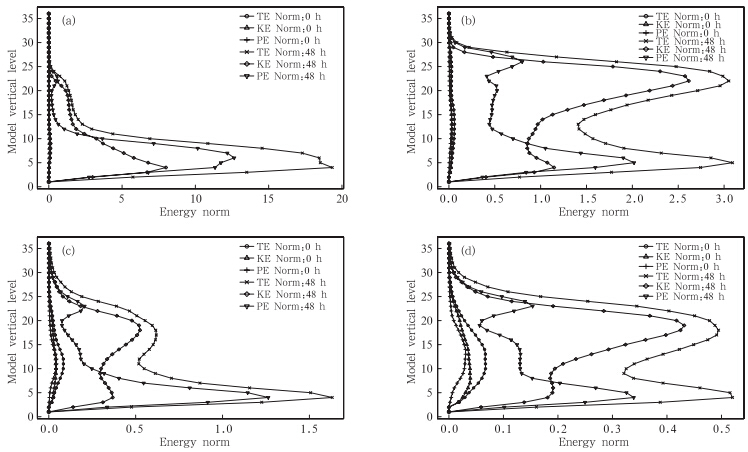 |
| 图 5 GRAPES 奇异向量总能量(TE)、动能(KE)和势能(PE)在初始时刻和经过48 h切线性积分的垂直分布 (a.北半球第1奇异向量,b.北半球第6奇异向量,c.南半球第1奇异向量,d.南半球第6奇异向量) Fig. 5 Vertical distribution of the TE,KE and PE of the GRAEPS SVs at the initial time,and the time after(48 h)tangent linear integration (a. NH SV01,b. NH SV06,c. SH SV01,d. SH SV06) |
从GRAPES 奇异向量能量模的垂直分布及其线性演变特征可以看出,基于本文定义的GRAPES总能量模公式能够在中高纬度区域得到切线性相空间中增长最快的奇异向量,其能够反映中高纬度对流层不同层的特点和斜压不稳定特征。
本文是基于干动力框架下GRAPES切线性和伴随模式来求解奇异向量的,由于缺乏物理过程的切线性和伴随模块,所获得的奇异向量对大气相空间中扰动的真实增长的描述并不完整。随着未来GRAPES模式切线性及伴随模式的完善(引入线性化的物理过程参数化方案),将继续深入开展有线性物理过程影响的奇异向量的研究及分析。6 结论和讨论
针对GRAPES全球模式及其干动力框架下的切线性模式的变量特点,推导出了适合集合预报初值扰动的GRAPES奇异向量的总能量模公式,并基于GRAPES模式的切线性模式、伴随模式,及Lanzcos算法,建立GRAPES奇异向量的计算求解模块,并通过奇异向量检验方法验证了其求解的正确性。此外,对奇异向量结构的线性和非线性演变分析,也证明奇异向量切线性近似是正确的。
通过对中高纬度的GRAPES 奇异向量水平结构的线性演变分析,证实了在最优时间间隔内GRAPES奇异向量能够快速增长,并能体现中高纬度大气斜压不稳定的特征。分析在初始时刻和最优化时间间隔时刻GRAPES奇异向量总能量及其分量——动能和势能的垂直分布,也发现本文所计算的奇异向量能够体现出中高纬度地区对流层中不同层的斜压不稳定增长特征。 这为建立基于奇异向量扰动的GRAPES全球奇异向量集合预报系统奠定了技术基础。
由于GRAPES全球模式中的物理过程相关的切线性和伴随模式正在研发中,热带区域的不稳定是由积云的发展等引起的,所以关于热带低纬度区域的能量模公式的设计需要引入湿能量,今后会进一步深入研究和发展GRAPES奇异向量的湿能量模。
| 刘永柱,杨学胜,王洪庆.2010.基于切线伴随技术计算GRAPES-Meso模式的奇异向量.热带气象学报,26(4):421-428 |
| 薛纪善,陈德辉.2008.数值预报系统GRAPES的科学设计与应用.北京:科学出版社,136pp |
| Bishop C H, Toth Z. 1999. Ensemble transformation and adaptive observations. J Atmos Sci, 56(11): 1748-1765 |
| Bowler N E. 2006. Comparison of perturbation strategies on a simple model. Tellus, 58A: 538-548 |
| Buizza R. 1994. Localization of optimal perturbations using a projection operator. Quart J Roy Meteor Soc, 120(520): 1647-1681 |
| Buizza R, Palmer T N. 1995. The singular-vector structure of the atmospheric global circulation. J Atmos Sci, 52(9): 1434-1456 |
| Buizza R.1995.Optimal perturbation time evolution and sensitivity of ensemble prediction to perturbation amplitude.Quart J Roy Meteor Soc,121(527):1705-1738 |
| Buizza R, Gelaro R, Molteni F, et al. 1997. The impact of increased resolution on predictability studies with singular vectors. Quart J Roy Meteor Soc, 123(543): 1007-1033 |
| Buizza R, Houtekamer P L, Toth Z, et al. 2005. A comparison of the ECMWF, MSC, and NCEP global ensemble prediction systems. Mon Wea Rev, 133(5): 1076-1097 |
| Ehrendorfer M. 1994a. The liouville equation and its potential usefulness for the prediction of forecast skill, PartⅠ: Theory. Mon Wea Rev, 122(4): 703-713 |
| Ehrendorfer M. 1994b. The liouville equation and its potential usefulness for the prediction of forecast skill, partⅡ: applications. Mon Wea Rev, 122(4): 714-728 |
| Ehrendorfer M. 1997. Predicting the uncertainty of numerical weather forecasts: a review. Meteor Z, 6: 147-183 |
| Errico R M, Vukivevic T, Raeder K. 1993. Examination of the accuracy of a tangent linear model. Tellus, 45(5): 462-477 |
| Globu G H, Van Loan C F. 1996. Matrix Computations//Hopkins Fulfillment Service. 3rd ed. Baltimore: The Johns Hopkins University Press |
| Hamill T M, Snyder C, Morss R E. 2000. A comparison of probabilistic forecasts from bred, singular-vector, and perturbed observation ensembles. Mon Wea Rev, 128(6): 1835-1851 |
| Houtekamer P, Mitchell L. 2005. Ensemble kalman filtering. Quart J Roy Meteor Soc, 131: 3629-3289 |
| Mu M,Duan W S,Wang B.2003.Conditional nonlinear optimal perturbation and its applications.Nonlinear Proc Geophys,10(6):493-501 |
| Simon H D.1984.The Lanczos algorithm with partial reorthogonal-ization.Mathematics of Compution,165(42):115-142 |
| Toth Z, Kalnay E. 1997. Ensemble forecasting at NCEP and the breeding method. Mon Wea Rev, 125: 3297-3319 |
| Wei, M, Toth Z, Wobus R, et al. 2006. Ensemble Transform Kalman Filter-based ensemble perturbations in an operational global prediction system at NCEP. Tellus, 58(1): 28-44 |
 2013, Vol. 71
2013, Vol. 71

