中国气象学会主办。
文章信息
- 张培昌, 王蕙莹, 王振会. 2013.
- ZHANG Peichang, WANG Huiying, WANG Zhenhui. 2013.
- 双/多基地天气雷达探测小椭球降水粒子的侧向散射能力
- Study of the side-scattering capability of bistatic/multistatic weather radar system detecting small spheroid raindrops
- 气象学报, 71(3): 538-546
- Acta Meteorologica Sinica, 71(3): 538-546.
- http://dx.doi.org/10.11676/qxxb2013.047
-
文章历史
- 收稿日期:2012-09-21
- 改回日期:2013-02-06
2. 南京信息工程大学大气物理学院, 南京, 210044
2. School of Atmospheric Physics, Nanjing University of Information Science and Technology, Nanjing 210044, China
单部多普勒天气雷达能够获取探测范围内降水回波的强度、平均径向速度与速度谱宽,并可形成一系列气象产品供监测灾害性天气使用,但风场反演时需作一定假设。采用双/多基地天气雷达探测时,能够不作假设实现同时探测同一目标进行风场反演。因此,一些学者先后开展了这方面的探测研究。Wurman等(1993,2001)、Satoh等(2003)构建了第一部双/多基地天气雷达系统网络,Protat等(1999)根据三维的双基
地多普勒天气雷达资料,采用变分法反演风场。McGill大学建立的双基地雷达系统已于1995年底正式运行,给机场提供精确的三维风场,并开展对中小尺度天气系统的研究。Aydin等(1998)研究了雨滴和冰雹对S波段的双/多基、双偏振散射特征。中国安徽四创电子股份有限公司及信息产业部南京第14研究所分别研制出C波段和S波段的双/多基地天气雷达系统,准备进行外场试验。
双/多基地天气雷达系统是由一个主站(包括具有发射与接收的完整雷达系统)和一个或多个设置在一定距离外的子站(仅有接收系统)组成。主站发射的雷达波束遇到降水目标时,其后向散射波被主站接收,同时侧向散射波被子站接收。子站获得的回波功率大小与降水粒子侧向散射能力有关。莫月琴等(2005)推导并估算出了小圆球形降水粒子的侧向散射能力。但暴雨中的大雨滴、冰粒、雹粒等一般均为非球形,通常可以用椭球形粒子去逼近,其散射特性与球形粒子有差异。
本文在前期工作(张培昌等,2012)的基础上,首先给出小椭球粒子侧向散射截面和后向散射截面的函数表达式,为了能使用双基地天气雷达中探测到的量进行估算,将函数表达式中相关参数用双基地坐标系中的量表示。在对小椭球粒子侧向散射能力进行定义后,分别推导出发射水平偏振波与垂直偏振波时估算侧向散射能力的算式,并通过仿真计算,获得各高度上侧向散射能力的分布情况,对这些分布情况进行分析后,得到一些可供参考的结果。2 坐标系的建立
在主站天线上建立的直角坐标系为O′X′Y′Z′(图 1),其中X′轴始终在水平方向,Y′方向是雷达天线发射波束的能流密度方向,发射波电场Ei偏振方向与X′轴的夹角为α。当α=0时为发射水平偏振波,α=π/2时为发射垂直偏振波。椭球上建立的直角坐标系为Oξηζ。对于图 1中的旋转椭球,Oζ轴为旋转轴,Oξ、Oη轴为相等轴。
 |
| 图 1 主站天线直角坐标系与椭球形粒子直角坐标系 Fig. 1 Two rectangular coordination systems for the transmitting antenna and a spheroid raindrop,respectively |
设R是所考虑的散射方向上某一点离椭球的距离矢量,距离|R|=R,ξ、η、ζ三个轴与R的夹角分别为θξ、θη、θζ,它们与建立在椭球上的球坐标(R,θ,φ)的关系从图 2中可得
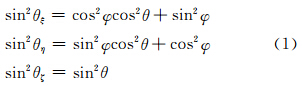
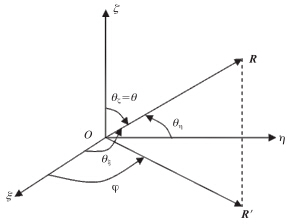 |
| 图 2 散射方向角(θξ,θη,θζ)与(θ,φ)的关系 Fig. 2 Relationship between(θξ,θη,θζ) and (θ,φ)for the scattering direction(for further details see the text) |
图 2中,R′是R在Oξη平面上的投影。φ是ξ轴与R′的夹角,θ是ζ轴与R的夹角。3 小椭球粒子的侧向散射截面
入射波以不同的仰角及方位角射到旋转轴任意取向的椭球上时,会在ξ、η、ζ方向长度分别为a、b、c的3个椭球轴上产生不同的极化电偶极矩分量Pξ、Pη、Pζ,椭球相对接收站会产生3个侧向散射截面。3.1 发射水平偏振波时侧向散射截面的表达式
由小椭球粒子3个电偶极矩分量产生的侧向散射截面在ξ、η、ζ方向上分别为(张培昌等,1995)
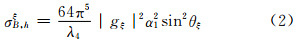
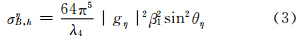
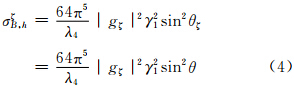
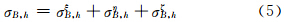
发射垂直偏振波时,小椭球粒子3个电偶极矩分量产生的侧向散射截面在ξ、η、ζ方向上分别为

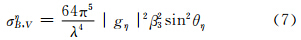
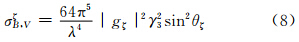
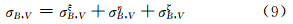
双基地雷达系统坐标系Oxyz是这样建立的(图 3):Oxyz坐标系的原点放在主站,即主站坐标为O(0,0,0),令x轴指向正东,y轴指向正北,并作为方位角at的起始位置,z轴垂直指向,图 3中at和et分别表示主站相对于椭球目标的方位角和仰角,Rt表示主站到目标的距离。子站(接收站)坐标为O1(x1,y1,z1),为简便起见,假设主站与子站在同一水平面高度上,相距的距离即基线长度为L0,a1、e1分别是子站相对椭球目标的方位角及仰角。
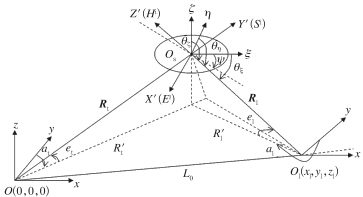 |
| 图 3 双基地系统中各坐标间的关系 Fig. 3 Relationship among the various coordinate in the bistatic radar system |
椭球目标位于坐标Os(xs,ys,zs)处。在椭球上建立一个与发射天线上的坐标系平行的OsX′Y′Z′坐标系。当发射水平偏振波时,Ei就在OsX′轴方向上,这时Y′方向是入射波能流密度方向,Z′是发射波磁场Hi的方向。另外,还在椭球上建立一个与椭球3个轴平行的Osξηζ直角坐标系。
令R1为椭球散射时射向子站的径向距离矢量,R′1是R1在OXY平面上的投影,R1在Osξη平面上的投影线与ξ轴的夹角为φ,R1与ζ轴的夹角为θ,故(R,θ,φ)是建立在椭球上的球坐标。
θξ、θη、θζ分别是ξ、η、ζ三轴与散射方向R1的夹角,它们与(θ,φ)的关系见式(1)。4.2 用双基地雷达系统坐标Oxyz表示sin2θξ、sin2θη、sin2θζ
首先推导sin2θξ在双基地系统中的表示式。为了清晰,将图 3改绘成图 4。
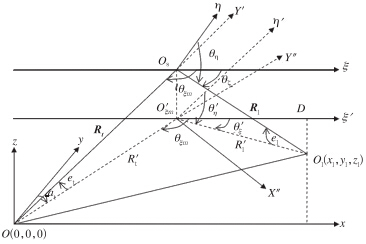 |
| 图 4 双基地系统中各坐标变量关系的另一种描述 Fig. 4 Alternative diagram for the relationship among the coordinate variables in the bistatic radar system |
图 3中的Os、Rt、R1、OsX′、OsY′、Osξ、Osη在Oxy平面上的投影分别为Os′、Rt′、R1′、O′sX″、O′sY″、Os′ξ′、Os′η′(图 4),由图 4可知,Os′ξ′//Ox轴,故R1′在Os′ξ′上的投影值为
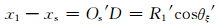
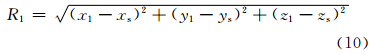
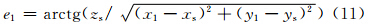
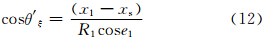
注意到建立在Osξηζ坐标系上的球坐标(R,θ,φ),φ角是由Osξ轴开始按顺时针进行计算的,θ角自Osζ轴开始按顺时针向下计算,则有
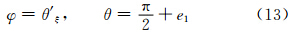
另外,据式(1)及图 4中几何关系可得
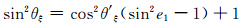
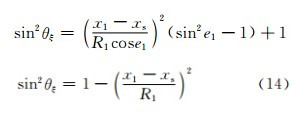
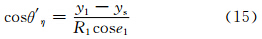
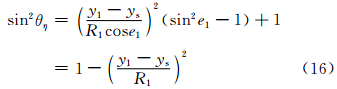
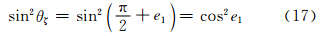
设sin2θξ在后向方向上的值用sin2θξm表示,由于电偶极矩Pξ的入射能流密度在水平的η方向上,故其后向方向在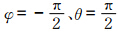 的方向,则据式(1)可得
的方向,则据式(1)可得


根据图 4中各角的几何及三角关系,可得一组公式
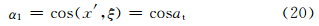
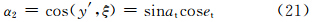
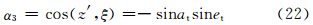
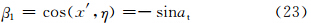
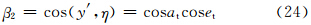
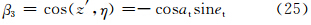
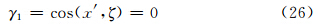

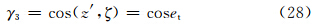
将式(18)、(19)结果代入式(2)、(3)、(4)后可得各个后向散射截面分别为
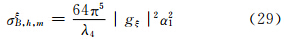
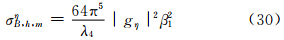
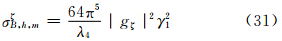
5.2 小椭球粒子在接收站方向的侧向散射能力的表示式
为了用小椭球粒子在接收站方向总的侧向散射截面与后向散射截面之比(RTh)来表示相应方向上的侧向散射能力,故可用式(2)、(3)、(4)之和,除以式(29)、(30)、(31)之和来获得,并注意到对于旋转扁椭球而言,在ξ、η轴方向上存在相等轴——a与b轴,故有gξ=gη,且γ1=0,则有
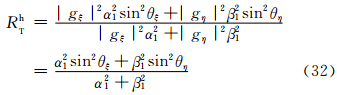
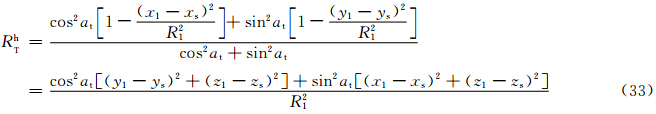
将上述式(18)、(19)结果代入式(6)、(7)、(8)后,可得各个后向散射截面分别为
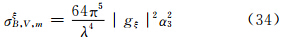
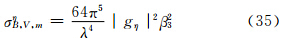
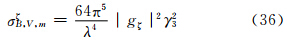
为了用小椭球粒子在接收站方向总的侧向散射截面与后向散射截面之比(RTv)来表示相应方向上的散射能力,故可以用式(6)、(7)、(8)之和除以式(34)、(35)、(36)之和,并注意到对于旋转扁椭球而言,在ξ、η轴方向上存在相等轴——a与b轴,故有gξ=gη,则
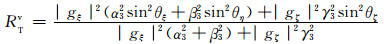
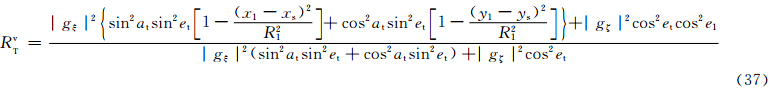
上式中(张培昌等,2000)
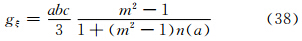
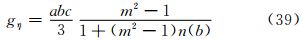
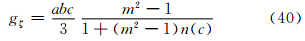
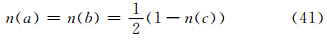
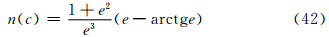

7 小椭球粒子侧向散射能力的仿真试验
设在双基地坐标中O(0,0)为主站雷达坐标,O1(20,0)为子站接收天线坐标,即基线长度L0=20 km。目标位置(XS,YS,ZS)是变数,从图 3、4中可知et、at可以由(XS,YS,ZS)确定。其中,Rt以及Rt在水平面上的投影R′t已转化成(XS,YS,ZS)决定的量,R1及R1在水平面上的投影R′1,已由(XS,YS,ZS)和(X1,Y1,Z1)共同确定。通过仿真计算可以得到粒子侧向散射能力随高度的分布。 因此,只要给定一个(XS,YS,ZS)值,就可分别由式(33)、(37)计算出发射水平偏振波和垂直偏振波到小旋转扁椭球粒子上时的侧向散射能力在不同高度上的分布。7.1 发射水平偏振波时
由0.1 km高度水平面(图 5a)上可见,在主站与子站的基线及向左、向右的延线附近,存在侧向散射能力高值区:当离开基线垂直向上或向下距离增大时,侧向散射能力先逐渐变小到最小值后,再逐渐增大。在基线左、右的延线上也基本呈这种分布,仅在主站与子站的垂直方向上存在侧向散射能力的最低区域。2.0 km高度水平面(图 5b)上的侧向散射能力分布情况与图 5a基本相似,仅子站上下的弱侧向散射值0.1消失了,即侧向散射能力稍有提高。5.0 km高度水平面(图 5c)上的侧向散射能力分布情况与图 5b基本相似,但主站与子站上、下的弱侧向散射值进一步提高。
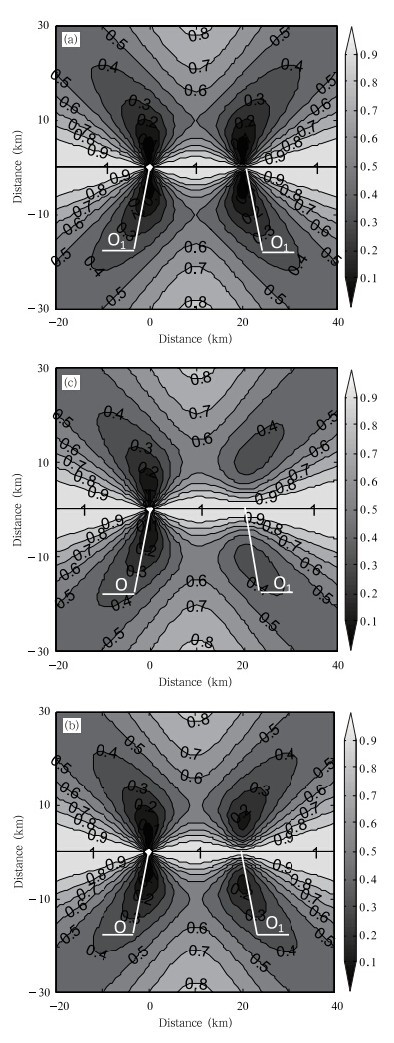 |
| 图 5 水平偏振时侧向散射能力随高度的分布 (a.0.1 km高度,b. 2.0 km高度,c. 5.0 km高度) Fig. 5 Side-scattering capability distributions at the different altitudes for horizontal polarization at the altitude of 0.1 km(a),2.0 km(b),and 5.0 km(c) |
不同高度上侧向散射能力呈上述分布及变化的原因,可以根据瑞利散射方向函数(图 6)给予解释,图 6a中小旋转扁椭球粒子位于坐标原点,y、x、z坐标方向分别与入射电磁波能流密度、电场以及磁场方向一致,在yOz平面内散射方向函数是个圆(图 6b),表明在离粒子等半径的距离上散射能流密度是处处相同的,在xOy平面内散射方向函数呈横的8字形(图 6c),这表明在y轴方向的前向与后向,具有最大的散射能流密度,而在x轴方向上无散射波能流密度(张培昌等,2001)。因为发射水平偏振波时,散射方向函数在发射方向上近似呈8字形分布,它在基线中心点垂直方向上某特定距离点处射向子站的侧向散射,恰好来自8字形的腰部,故最弱,在这特定距离点的上方或下方,侧向散射来自散射方向函数其他部位,侧向散射能力就如图 5中那样逐渐变化。应注意,在对离地面一定高度平面上的气象目标探测中,发射波束的仰角不为0°,且各探测点上的仰角与方位角均不相同,这时发射波束将斜穿扁椭球粒子,由电场使其极化产生的电偶极矩和方向函数也将发生变化,这是不同等高面上形成侧向散射能力分布图的物理原因。在实际双基地雷达探测时,主站发射波束有一定宽度,子站接收天线波束更是宽达几十度,在接收的有效照射体内存在大量散射粒子,它们也不会完全呈一致的取向,故实际的侧向散射能力要比上述仿真分布强。
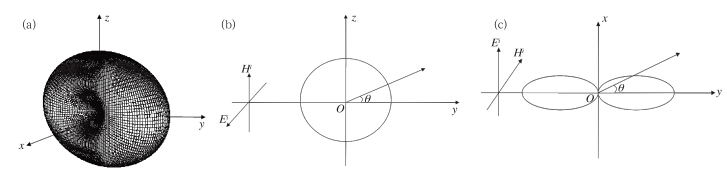 |
| 图 6 瑞利散射方向函数图 (a. 立体图,b. yOz剖面图,c. xOy剖面图) Fig. 6 Rayleigh scattering function diagram (a. three-dimensional diagram,b. yOz cross section diagram,c. xOy cross section diagram) |
取式中等效半径re=0.076 cm,轴比a/c=7/3,复折射指数m=2.764+1.412i,根据式(36)—(42)计算得到以下3个高度平面上的侧向散射能力的分布(图 7)。
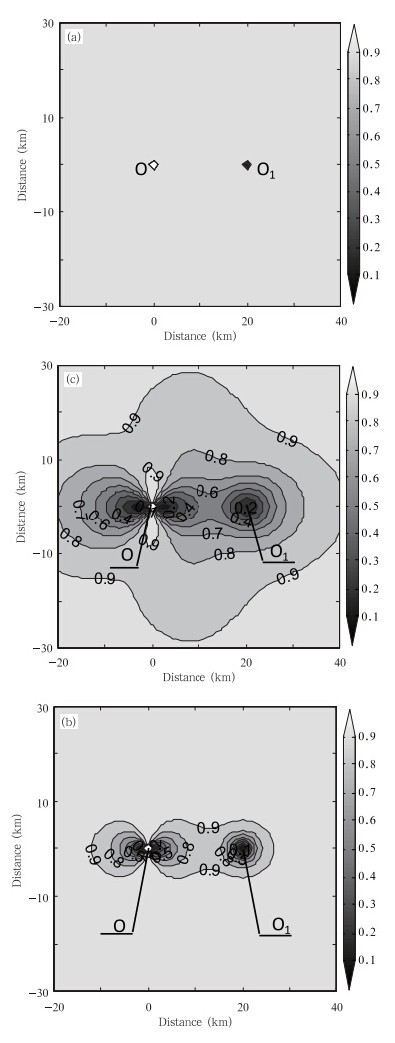 |
| 图 7 垂直偏振时侧向散射能力随高度的分布 (a.0.1 km高度,b. 2.0 km高度,c. 5.0 km高度) Fig. 7 As in Fig. 6 but for vertical polarizationat the altitude of 0.1 km(a),2.0 km(b),and 5.0 km(c) |
由0.1 km高度水平面上(图 7a)可见,无论被探测的扁旋转椭球粒子处在该平面上(除主站与子站的位置以外)的任何处,侧向散射能力均为最大值。当高度升高到2.0 km时,在主站与子站的相应位置左、右两侧出现了侧向散射能力小值区,越靠近主站与子站,侧向散射能力越小,最小达0.1(图 7b)。当高度升高到5.0 km时,这种两侧出现的侧向散射能力的小值区面积进一步扩大(图 7c)。以上侧向散射能力分布及随高度的变化,仍可用瑞利散射方向函数分布值随天线仰角不同引起对扁椭球粒子极化产生的偶极矩不同给予解释,当仰角为0°时,垂直偏振使扁椭球极化发生在短轴方向,产生的电偶极矩小,散射方向函数值也较小,随着仰角抬高,极化产生的电偶极矩变大,散射方向函数值也变大,仰角为90°时达最大。还应注意,当以0°仰角发射垂直偏振波时,若探测高度就在天线高度上,则被探测目标无论处在此高度平面上哪一点,其在此高度平面上产生的散射方向函数均呈圆形分布,故它射向子站的侧向散射能力均接近最大值1.0(图 7a)。当高度升高到2.0和5.0 km时,发射波束的仰角就不为0°,且该高度平面各探测点的仰角与方位角均不相同,这时发射波束将斜穿扁椭球粒子,由入射电场使其极化产生的电偶极矩和方向函数也将随仰角增大而变大,这是不同等高面上形成侧向散射能力分布如图 7b与图 7c那样变化的物理原因。
以上虽然仅是对单个小椭球降水粒子侧向散射能力的仿真,但可以推断,当雷达波束有效照射体内存在一群小椭球降水粒子时,若它们的旋转轴是一致铅垂取向,其侧向散射能力应与上述结果基本相同;若旋转轴在空间作均匀随机取向,其结果应与小球形粒子侧向散射能力基本相似。由于目前中国尚无双线偏振多普勒双/多基地天气雷达设备,因此,还缺乏实际资料的对照验证,这里只能先做一些前期的基础理论分析研究。
根据上述小椭球粒子侧向散射能力的仿真试验结果,可以给出双/多基地天气雷达接收子站的布站建议:(1)鉴于降水粒子侧向散射能力比后向散射能力弱,故子站离主站距离一般不宜太远,可以按主站发射功率去确定基线,一般在几十千米左右;(2)由图 5知,发射水平偏振波时,几个高度平面上除基线方向及垂直于基线中心点方向附近散射很弱外,在东北、西北、东南、西南方向散射均较强;从图 7可知,发射垂直偏振波时,2 km及其以上高度平面上,除主站与子站相对应的位置附近散射很弱外,其他位置上侧向散射能力均很大。综合以上情况考虑,建议主站的南北方向以及东北、西北、东南、西南方向,分别设置接收子站,形成多条基线,这样可以保证降水云出现在主站附近一定距离内的任意方向或多个方向时,总会有一个以上子站能接收到较强的回波。8 结 语
(1)首先给出发射水平与垂直偏振波条件下,小扁椭球粒子在各粒子坐标上的侧向散射截面以及总的侧向散射截面的表达式,在建立双基地雷达系统中各种坐标系间各量的关系后,将其中相关参数用双基地雷达坐标系中的量表示,并获得后向散射截面的表达式。
(2)定义小扁椭球粒子在接收站方向总的侧向散射截面与总的后向散射截面之比来表示小扁椭球粒子总的侧向散射能力,并分别推导出发射水平与垂直偏振波条件下估算侧向散射能力的算式。
(3)通过仿真计算,获得发射水平与垂直偏振波时,各高度上小扁椭球粒子侧向散射能力分布情况,得到如下结果:发射水平偏振波时,在低高度的等高面上,当离开基线垂直向上或向下距离增加时,侧向散射能力先逐渐变小到最小值后,再逐渐增大。在基线左、右的延线上也基本呈这种分布,仅在主站与子站的垂直方向上存在侧向散射能力的最低区域。随着等高面高度升高,侧向散射能力分布情况基本相似,仅子站上下的弱侧向散射值有了提高。发射垂直偏振波时,在低高度水平面上无论被探测的扁旋转椭球粒子处在该平面上(除主站与子站的位置以外)的任何处,侧向散射能力均为最大值。当高度增加时,在主站与子站相对应位置左右两侧出现了侧向散射能力小值区,越靠近主站与子站,侧向散射能力越小,当高度继续增加时,这种两侧出现的侧向散射能力的小值区面积进一步扩大。侧向散射能力呈上述分布及变化的原因,可以根据瑞利散射方向函数图给予定性的解释。
(4)为了使子站能获得较强的回波,子站应设置在主站周围一定半径以内,并在不同方向设置不同子站,以便形成多子站系统、提高探测效率。
| 莫月琴, 刘黎平, 徐宝祥等. 2005. 双基地多普勒天气雷达探测能力分析. 气象学报, 63(6): 994-1005 |
| 张培昌, 王振会. 1995. 大气微波遥感基础. 北京: 气象出版社, 41 |
| 张培昌, 殷秀良. 2000. 小旋转椭球粒子群的微波散射特性. 气象学报, 58(2): 250-256 |
| 张培昌, 戴铁丕, 杜秉玉. 2001. 雷达气象学. 北京: 气象出版社, 88 |
| 张培昌, 王振会, 胡方超. 2012. 双/多基地天气雷达探测小椭球粒子群的雷达气象方程. 气象学报, 70(4): 867-874 |
| Aydin K, Park S H, Walsh T M. 1998. Bistatic dual-polarization scattering from rain and hail at S-and C-band frequencies. J Atmos Ocean Technol, 15(5): 1110-1121 |
| Protat A, Zawadzki I. 1999. A variational method for real-time retrieval of three dimensional wind field from multiple-Doppler bistatic radar network data. J Atmos Ocean Technol, 16(4): 432-449 |
| Satoh S, Wurman J. 2003. Accuracy of wind fields observed by a bistatic Doppler radar network. J Atmos Ocean Technol, 20(8): 1077-1091 |
| Wurman J, Heckman S, Boccippio D. 1993. A bistatic multiple-Doppler radar network. J Appl Meteor, 32(12): 1802-1814 |
| Wurman J, Randall M, Burghart C. 2001. Bistatic radar networks//30th International Conference on Radar Meteorology. Munich, Germany: Artech House, 130-133 |
 2013, Vol. 71
2013, Vol. 71

