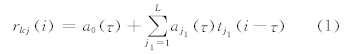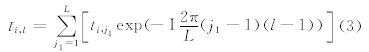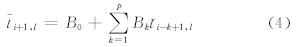中国气象学会主办。
文章信息
- 杨秋明. 2014.
- YANG Qiuming. 2014.
- 基于20—30d振荡的长江下游地区夏季低频降水延伸期预报方法研究
- Study of the method of the extended-range forecast for the low frequency rainfall over the lower reaches of the Yangtze River in summer based on the 20-30 day oscillation
- 气象学报, 72(3): 494-507
- Acta Meteorologica Sinica, 72(3): 494-507.
- http://dx.doi.org/10.11676/qxxb2014.028
-
文章历史
- 收稿日期:2013-7-18
- 改回日期:2013-12-27
10—30 d延伸期天气预报对于气象防灾、减灾和经济社会的发展具有重要意义,也是填补1—3 d短期天气预报和3—10 d中期天气预报与月气候预测之间的时间缝隙和构建完备性预报体系的必然要求。它是近20年来大气科学研究的重点领域和国际上天气气候业务发展的一个主要方向(Waliser et al,2003; Hoskins,2013),有凸出的科学价值和广泛的应用价值。
10—30 d延伸期预报的核心问题之一,即极端天气气候事件发生的预测。只要能预测出延伸期时段内的主要异常天气过程(如强降水等),则认为延伸期预报取得了成功。总体而言,延伸期天气预报的基本方法主要有动力模式和统计方法两类(Waliser et al,2003)。前者有集合数值模式(Vitart et al,2010; Fu et al,2013)和可预报分量提取法(丑纪范等,2010)以及采用数值模式预报资料的动力-统计方法(陈官军等,2012),后者有基于大气低频信号演变的统计方法(von Storch et al,1990;杨秋明,1998,2012b;Waliser et al,1999; Wheeler et al,2004; Jiang et al,2008)和采用多种观测资料的统计方法(Mo,2001; Xavier et al,2007)。此外,还有低频天气图(孙国武等,2013)、神经网络方法(Love et al,2009)、基于经验模态分解(EMD)的统计方法(Love et al,2008;梁萍等,2012)等方法正在试验之中。 Miyakoda等(1983)率先利用数值模式成功预报了未来10—30 d阻塞高压的变化,这一工作被看作是延伸期数值预报的开端。近年来,尽管数值模式的预报能力大大提高(如ECMWF中期数值预报模式),预报时效达到 10 d,但10 d之后预报技巧迅速下降,降水预报效果改进较缓慢(Miller,2010)。这是因为天气和气候预报模式存在各种不确定性,10 d以上的预报误差仍然增长较快。这些不确定性的来源以及大气混沌本质和复杂的各种耦合过程也尚待深入研究。已有的观测研究表明,在10—30 d的时间尺度内,仍然存在一些可预报的气象场的特征。数值模式的状态变量可分解为可预报的稳定分量与不可预报的混沌分量,针对10—30 d的延伸期预报,需提取和分析该时间尺度可预报的稳定分量,才能基于这些稳定分量改进现有的全球预报模式(丑纪范等,2010;王阔等,2012a,2012b;郑志海等,2013;封国林等,2013)。无疑需要更多理论上的新突破,才可能有效地做出较长预报时效的10—30 d延伸期动力预测。
从物理上来说,在延伸期尺度内,大气季节内振荡(ISO)既是大气活动的强信号(时间尺度为20—70 d),也是诱发大气环流演变的重要因子,因此,基于大气季节内振荡信号开展延伸期预报成为除数值方法之外的另一个主要研究方向(von Storch et al,1990; 杨秋明,1998,2009,2011;杨秋明等,2012a,2012b;Waliser,2003; Cassou,2008; Kikuchi K et al,2012; Krishnamurthy,2012; 梁萍等,2012)。从气候角度来说,大气季节内振荡既是高频天气变化的直接背景,又是月、季气候的主要组成分量,它是“天气对气候界面”,是连接天气和气候的直接纽带。通过对观测资料的合理处理和分解,客观分离资料中的不同时间尺度的天气变化和气候变化分量,可直接从观测资料中提取与影响天气事件密切相关的不同时间尺度的主要大气季节内振荡型。在分别研究制约这些不同的大气季节内振荡 型演变的因子和时间变化规律的基础上,利用大气低频振荡动力机制分析可传播信号(如与夏季长江下游地区强降水(暴雨)等极端事件密切相关的20—30 d大气季节内振荡型:南半球中纬度绕球遥相关(SCGT)型和热带西太平洋(TWP)型等(杨秋明,2009),其中与南北半球热带外低频环流相互作用有关的SCGT的变化(Ambrizzi et al,1995; Yadav,2009; Shimizu et al,2011)和5—8月长江下游地区、南亚地区和南非、澳大利亚、南美洲地区20—30 d低频降水均有密切联系)的放大和对预报区域的影响,建立简化统计动力学模型,能做出远高于随机判断和单纯依靠统计计算的有效延伸期天气预报。杨秋明等(2012b)对20—30 d振荡较强的年份,用多年观测的东亚850 hPa低频经向风资料,建立主振荡型(POP)预测模型(Hasselmann,1988),对东亚环流20—30 d大气季节内振荡进行预测试验,发现环流低频变化预报时效大约为20 d,能为夏季延伸期长江下游地区强降水过程预测提供重要预报信号。
如何对未来10 d以后的极端天气事件做出更为准确的预报,从观测资料中提取更多有用的信息,针对一定的时间尺度,基于关键区的低频变化建立较稳定的预报模型,并进一步延长预报时效,是需要深入研究的主要问题之一。本研究将用降水低频分量和环流低频主成分,构造一种多变量时滞回归模型(MLR)和主成分复数自回归模型(PC-CAR)的混合预报方法,对2011年夏季长江下游地区20—30 d降水低频分量进行延伸期逐日变化预报,显著延长了预报时效。同时应用于20—30 d大气季节内振荡较强年份(杨秋明等,2012b)的多年资料,进行长江下游地区低频降水预测模型的构建和预测试验研究,并分析了选择不同关键区域850 hPa低频经向风主成分为预报因子的模型对低频降水延伸期预测精度和时效的影响。
2 资 料850 hPa经向风场选用美国国家环境预测中心/美国国家大气研究中心(NCEP/NCAR)逐日再分析风场资料(Kalnay et al,1996)全球范围内的2.5°×2.5°的格点,时间为1979、1984、1987、1991、1997、1998、1999、2000、2002、2005、2007、2009和2011年的3—8月; 采用一阶Butterworth滤波器进行20—30 d带通滤波,得到全球850 hPa低频经向风场资料阵。逐日长江下游地区降水量采用区域(30.5°—32.0°N,118.0°—122.5°E)中25站平均值,时间为每年 3月15日—8月31日。长江下游地区低频降水预测试验的时间为6月1日—8月29日。此外,在相关系数检验中考虑滤波序列持续性的影响,采用有效自由度进行显著性检验。
3 方 法3.1 多变量时滞回归模型(MLR)设某区域D中气象场的M个观测样本和格点为N的滤波资料阵MSN=(sij),i=1,2,…,M;j=1,2,…,N,主成分分析(PCA)后,得到MSN=MTLLVTN,其中,T=tj1(i)为时间系数矩阵(由前L个主要分量tj1(i)组成),i=1,2,…M;j1=1,2,…,L;长江下游地区低频降水(rlcj)与时间滞后为τ的主要分量tj1满足线性方程
式中,aj1为系数,j1=0,1,2,…,L,由线性最小二乘估计,当τ=1,2,…,30 d时,长江下游地区低频降水(rlcj)的1,2,…,30 d 变化可由上式预测。式(1)称为主成分低频多变量滞后线性回归模式(MLR),反映了各个时间滞后τ主要分量tj1和低频降水相互独立的回归关系。式(1)可变为 rlcj(i+τ)=a0(τ)+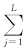 aj1(τ)tj1(i),由初始时间的i=i0的tj1(i0),可得到低频降水预测值rlcj(i0+τ),τ=1,2,…,30 d,时滞相关结构(回归系数aj1(τ)随τ变化)体现了低频降水与主要环流低频分量的相互作用;这种相互作用增强,低频降水也增强,其正位相产生强降水的概率明显增大。
3.2 主成分复数自回归模型(PC-CAR)
aj1(τ)tj1(i),由初始时间的i=i0的tj1(i0),可得到低频降水预测值rlcj(i0+τ),τ=1,2,…,30 d,时滞相关结构(回归系数aj1(τ)随τ变化)体现了低频降水与主要环流低频分量的相互作用;这种相互作用增强,低频降水也增强,其正位相产生强降水的概率明显增大。
3.2 主成分复数自回归模型(PC-CAR)
设M个观测样本和格点为N的滤波资料阵MSN=(sij),i=1,2,…,M;j=1,2,…,N。对MSN进行主成分分析
式中,MTL,NVL分别为时间系数和特征向量构成的矩阵,得到前L个主要空间模态和时间变化。对MTL=(ti,j1)的L个时间序列进行一维傅里叶变换式中,exp(-I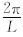 (j1-1)(l-1))=cos(
(j1-1)(l-1))=cos(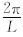 (j1-1)(l-1))-Isin(
(j1-1)(l-1))-Isin(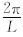 (j1-1)(l-1)),I为虚数单位,i=1,2,…,M;j1=1,2,…,L;l=1,2,…,L。因此,得到L个复时间序列i,l=ai,l+bi,lI,每一个复数表示不同的波数,对每一分量i,l建立p阶复数自回归模型(CAR)用复数最小二乘法(谷湘潜等,2006)得到参数的估计Bk,k=0,1…,p,其中p=1,2,…,由式(4)可得M+1时刻的预报值 〈 M+1,l=
(j1-1)(l-1)),I为虚数单位,i=1,2,…,M;j1=1,2,…,L;l=1,2,…,L。因此,得到L个复时间序列i,l=ai,l+bi,lI,每一个复数表示不同的波数,对每一分量i,l建立p阶复数自回归模型(CAR)用复数最小二乘法(谷湘潜等,2006)得到参数的估计Bk,k=0,1…,p,其中p=1,2,…,由式(4)可得M+1时刻的预报值 〈 M+1,l=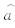 〈 M+1,l+
〈 M+1,l+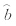 〈 M+1,lI,由一维傅里叶逆变换得到主分量的预报值t 〈 M+1,j1,再由式(2)可得预报场(
〈 M+1,lI,由一维傅里叶逆变换得到主分量的预报值t 〈 M+1,j1,再由式(2)可得预报场(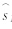 〈 M+1,j=
〈 M+1,j=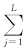
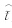 〈 M+1,j1vj,j1(NVL=(vj,j1),j=1,2,…,N)。 通过式(4)递推K步,可得第K天的预报值
〈 M+1,j1vj,j1(NVL=(vj,j1),j=1,2,…,N)。 通过式(4)递推K步,可得第K天的预报值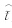 〈 M+K,j1,
〈 M+K,j1,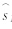 〈 M+K,j1。这种主成分复数自回归模型中采用的复数最小二乘法为实数最小二乘法的扩展,能在复平面上描述变量之间的时间变化特征,得到比实数空间中更全面的变化信息,较稳定地揭示低频变量的时间演变。
3.3 MLR和PC-CAR混合模型(MLR/PC-CAR)
〈 M+K,j1。这种主成分复数自回归模型中采用的复数最小二乘法为实数最小二乘法的扩展,能在复平面上描述变量之间的时间变化特征,得到比实数空间中更全面的变化信息,较稳定地揭示低频变量的时间演变。
3.3 MLR和PC-CAR混合模型(MLR/PC-CAR)
设初始时间为t0,由[ t-2,t-1]的历史资料Fj(滤波序列组成的气象场的主成分tj)建立MLR: rlcj(t0)=a0(τ)+ 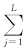 aj(τ)Fj(t0-τ),可得到各个滞后时间τ独立的线性回归方程 rlcj(t0+τ)=a0(τ)+
aj(τ)Fj(t0-τ),可得到各个滞后时间τ独立的线性回归方程 rlcj(t0+τ)=a0(τ)+ 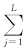 aj(τ)Fj(t0),τ=1,2,…,30,用实测值Fj(t0)预测1—30 d的低频降水
aj(τ)Fj(t0),τ=1,2,…,30,用实测值Fj(t0)预测1—30 d的低频降水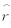 〈 lcj(t0+1),
〈 lcj(t0+1),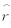 〈 lcj(t0+2),…,
〈 lcj(t0+2),…,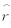 〈 lcj(t0+30)。
〈 lcj(t0+30)。
然后,由[ t-2,t-1]的资料,建立复数自回归(CAR),通过递推得到预测值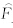 j(t0+1),…,
j(t0+1),…,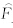 j(t0+20),用上述MLR,令τ=30,
j(t0+20),用上述MLR,令τ=30,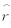 〈 lcj(t0+30+k)=a0(30)+
〈 lcj(t0+30+k)=a0(30)+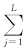 aj(30)
aj(30)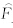 j(t0+k),用主成分的预测值
j(t0+k),用主成分的预测值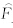 j(t0+k)(k=1,2,…,20)计算得到31—50 d的低频降水预测值:
j(t0+k)(k=1,2,…,20)计算得到31—50 d的低频降水预测值: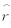 〈 lcj(t0+31),
〈 lcj(t0+31),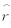 〈 lcj(t0+32),…,rlcj(t0+50);这种混合预报模型称为MLR/PC-CAR,是一组时滞回归方程和基于初值的复数自回归递推相结合的预测方案,能较好地反映超前(滞后)相关的信息(图 1)。
〈 lcj(t0+32),…,rlcj(t0+50);这种混合预报模型称为MLR/PC-CAR,是一组时滞回归方程和基于初值的复数自回归递推相结合的预测方案,能较好地反映超前(滞后)相关的信息(图 1)。
采用3月15日—8月31日(春季和夏季,样本长度N=170)的长江下游地区逐日低频降水和850 hPa 低频经向风场资料进行预测试验。由于主成分分析得到主要空间分布型与样本序列长度有关,因此采用限定记忆法,保持子序列N0不变,用MLR/PC-CAR混合预报模型滑动进行独立样本预测试验。具体方法如下:对于初始时间i0,使用i0-N0+1,i0-N0+2,…,i0-1,i0 时次的子序列资料(N0是子序列长度),对850 hPa 低频经向风场(经过20—30 d带通滤波)资料标准化处理,经过主成分分析得到主要空间分布型和逐日变化的主成分tj(i),用长江下游逐日低频降水rlcj和低频经向风主成分tj(i),建立MLR;由初始时间i=i0的tj(i0),预测未来30 d长江下游逐日低频降水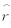 〈 lcj(i0+1),
〈 lcj(i0+1),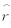 〈 lcj(i0+2),…,
〈 lcj(i0+2),…,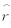 〈 lcj(i0+30);然后,由i0-N0+1,i0-N0+2,…,i0-1,i0时次的子序列资料构建PC-CAR预测模型,预测未来20 d主分量的变化:
〈 lcj(i0+30);然后,由i0-N0+1,i0-N0+2,…,i0-1,i0时次的子序列资料构建PC-CAR预测模型,预测未来20 d主分量的变化: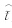 〈 j(i0+1),
〈 j(i0+1),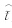 〈 j(i0+2),…,
〈 j(i0+2),…,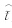 〈 j(i0+20);将这些预测值作为i0+1,i0+2,…,i0+20 的初值,用上述MLR模型中τ=30对应的时滞回归方程
〈 j(i0+20);将这些预测值作为i0+1,i0+2,…,i0+20 的初值,用上述MLR模型中τ=30对应的时滞回归方程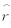 〈 lcj(i+30+i0)=a0(30)+
〈 lcj(i+30+i0)=a0(30)+ 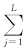 aj(30)
aj(30)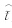 〈 j(i+i0),i=1,2,…,20,得到未来31—50 d长江下游逐日低频降水的预测值
〈 j(i+i0),i=1,2,…,20,得到未来31—50 d长江下游逐日低频降水的预测值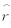 〈 lcj(i0+31),
〈 lcj(i0+31),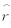 〈 lcj(i0+32),…,
〈 lcj(i0+32),…,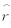 〈 lcj(i0+50)。计算中主分量个数L=4,子序列长度N0=78,复数自回归阶数p=3。从5月31日(i0=78,基于3月15日—5月31日(春季)的资料建立MLR/PC-CAR),开始每隔5 d(固定子序列长度N0=78)滑动进行独立样本预测,其中i0=78,83,…,113,118,共9次预测。当i0=118时,是基于4月24日—7月10日资料的空间模态和变量的时滞联系,基本反映了初夏5—7月期间振荡模态特征。以上建模方案有利于适应主要20—30 d振荡系统空间结构随时间的改变(从春季到夏季),在一定程度上反映20—30 d振荡型变化的非线性特征。下面对2011年夏季长江下游地区降水20—30 d低频分量进行延伸期预报试验。
〈 lcj(i0+50)。计算中主分量个数L=4,子序列长度N0=78,复数自回归阶数p=3。从5月31日(i0=78,基于3月15日—5月31日(春季)的资料建立MLR/PC-CAR),开始每隔5 d(固定子序列长度N0=78)滑动进行独立样本预测,其中i0=78,83,…,113,118,共9次预测。当i0=118时,是基于4月24日—7月10日资料的空间模态和变量的时滞联系,基本反映了初夏5—7月期间振荡模态特征。以上建模方案有利于适应主要20—30 d振荡系统空间结构随时间的改变(从春季到夏季),在一定程度上反映20—30 d振荡型变化的非线性特征。下面对2011年夏季长江下游地区降水20—30 d低频分量进行延伸期预报试验。
 |
| 图 1 MLR/PC-CAR混合模型的预测方案示意图 (Fj(t):因子; rlcj(t): 低频降水; t0:初始时间) Fig. 1 Diagrammatic sketch of the prediction scheme for the hybrid model of MLR/PC-CAR (Fj(t): factors; rlcj(t): low frequency rainfall; t0: an initial time) |
图 2a为2011年5月1日—8月31日长江下游地区20—30 d低频降水与全球850 hPa低频经向风场的相关空间分布,其中阴影区表示通过0.05的显著性检验(相关显著的格点平均有效自由度为14 d 左右,当相关系数大于0.50时,其显著性为0.05)。图中清楚表明,主要相关区域在南半球热带外地区,表现为沿纬向传播的波列结构,即SCGT的传播,主要作用区域在东南太平洋地区到南大西洋地区(绿色虚线),与过去的研究结果一致(杨秋明,2009);而中国东部地区经过北太平洋中纬度地区到北美大陆存在另一支波列,类似于东京—芝加哥“快车”或上海—堪萨斯“快车”(Lau et al,2002; 丁一汇等,2008),其中中国东部地区到北太平洋中纬度地区更显著(浅红色虚线)。此外,欧亚大陆和北美大陆中高纬度地区还存在绕球的纬向传播波列(与北半球中纬度对流层高层的绕球遥相关(CGT)型对应,紫色虚线),但显著相关区域的范围小于与南半球SCGT的相关。上述波列活动区均处于20—30 d振荡的解释方差大值区(图 2b),反映了2011年夏季长江下游地区降水 20—30 d振荡主要受到两半球热带外低频波列的影响,其中南半球SCGT的作用更明显。本研究中对2011年6—8月,每隔5 d,由MLR/PC-CAR混合模型滑动进行独立样本预报试验,做未来50 d长江下游地区20—30 d低频降水的实时预测,初始时间为5月31日、6月5、10、15、20、25、30日、7月5日和10日(即对应于i0=78,83,…,113,118),共9次预测试验。为了分析不同区域的不同低频主成分作为因子构建的预测模型预测精度的差异,分别用不同区域的主成分建立模型的2种方法进行预测试验:
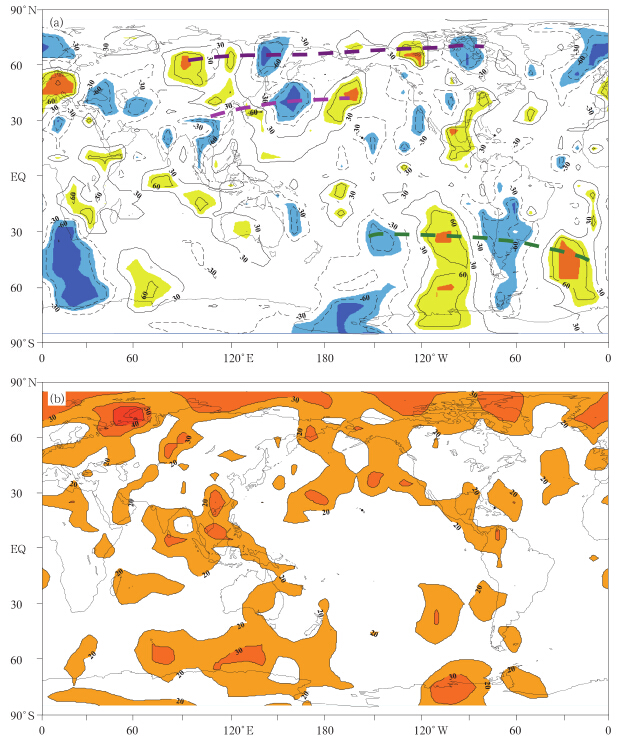 |
| 图 2 2011年5月1日—8月31日长江下游地区20—30 d低频降水与全球850 hPa低频经向风场的相关 (a,相关系数已乘100,阴影表示通过0.05 的显著性检验的区域)及全球850 hPa 高度距平20—30 d 滤波序列与原始序列标准差比值的空间分布(b,数值已乘100,单位: %,阴影区表示≥20 的区域) Fig. 2(a)Correlation between the rainfall over the lower reaches of the Yangtze River(valley)(LYRV) and the global meridional wind anomaly of 850 hPa on the time scale of the 20-30 day from 1 May to 31 August in 2011 in which values are multiplied by 100 and areas singificant at the confidence levels of 95% are shaded,and (b)the spatial distribution of the ratio of the st and ard deviation for the 20-30 day signal to the total variability,whose values(unit: %)are multiplied by 100 and the contours greater than or equal to 20 are shaded |
(1)东亚区域A(0°—45°N,90°E—180°)的前4个低频主成分PC1—PC4:图 3为前5个主要空间模态(2011年3月15日—5月31日),解释方差分别为64.1%、14.5%、9.2%、5.7%和3.1%,反映了东亚中低纬度地区各种纬向和经向波列的传播,其中第2、4模态与热带西太平洋型的传播有关(杨秋明,2009)。
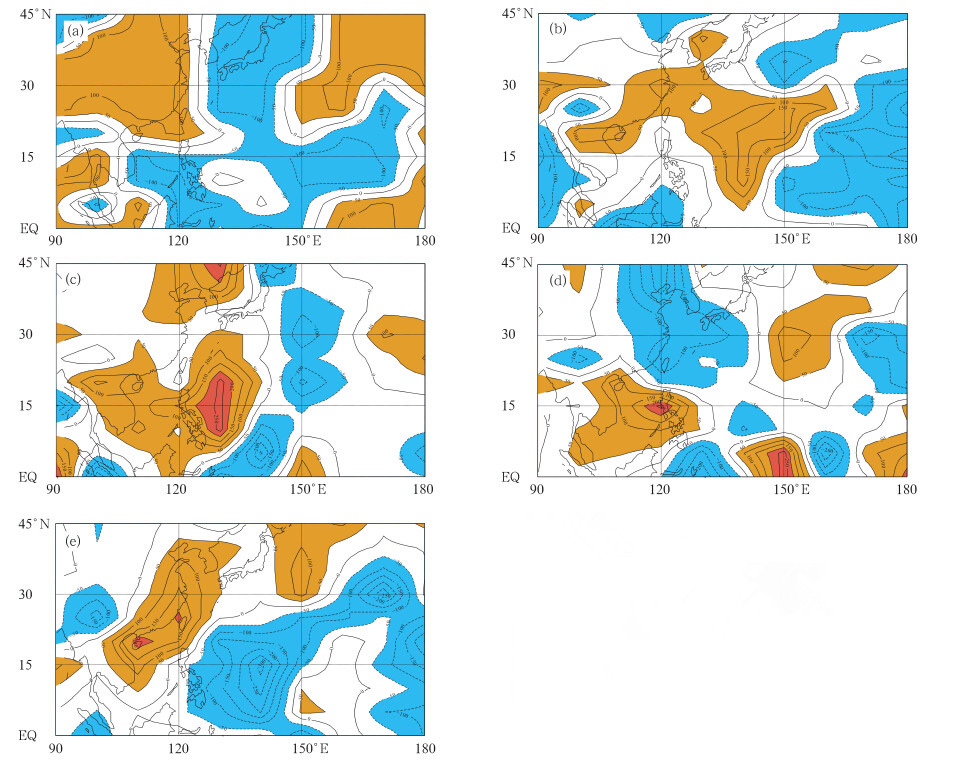 |
| 图 3 850 hPa低频经向风场的主要空间模态(区域A:(0°-45°N,90°E-180°),a-e. 对应于第1—5模态,图中虚线表示负值,数值已 乘1000,棕(蓝)色阴影表示≥50(≤-50)) Fig. 3 Principal modes of the meridional wind anomaly of 850 hPa on the time scale of the 20-30 days in the region A: 0°-45°N,90°E-180°,(a),(b),(c),(d) and (e)are for the first,second,third,fourth and fifth pattern,respectively,in which the values are multiplied by 1000 with the brown(blue)grey shaded areas representing the regions greater than 50(less than -50) |
(2)南半球中纬度地区B(10°—65°S,0°E—180°—0°W)的前4个低频主成分PC1—PC4:图 4为前5个主要空间模态(2011年3月15日—5月31日),解释方差分别为53.8%、19.5%、8.7%、7.5%和4.2%,均表现为沿纬向传播的波列结构,其中第2、3模态对应于SCGT的传播(杨秋明,2009;Matthewman et al,2012)。
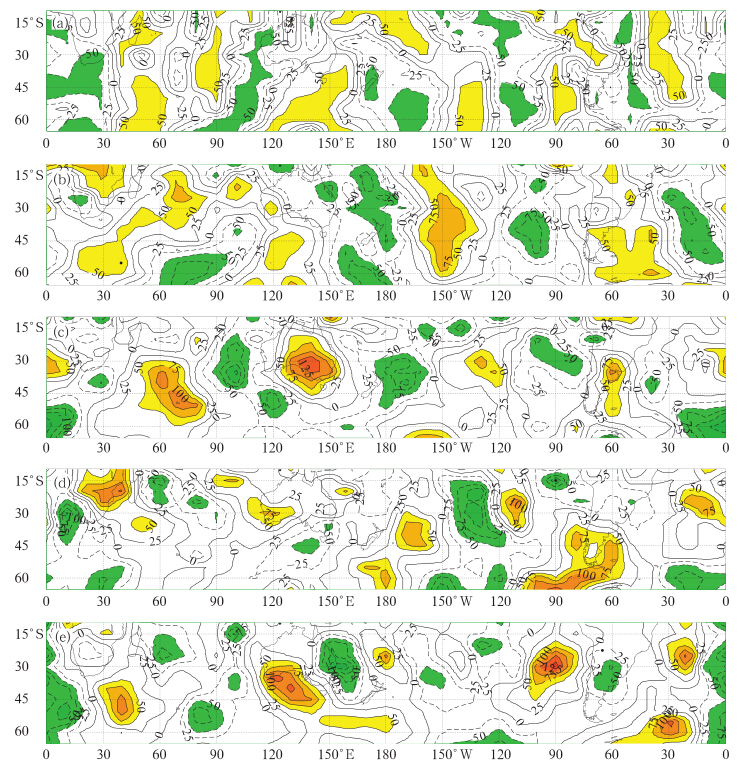 |
| 图 4 850hPa低频经向风场的主要空间模态(区域B:10°—65°S,0°E—180°—0°W),其他同图 3 Fig. 4 As in Fig. 3 but for the region B:(10°-65°S,0°E-180°-0°W) |
在每次滑动独立预报试验中,采用上述2种方法,将区域A(东亚地区)和B(南半球中纬度地区)的风场计算出的前5个主要空间模态,得到低频主成分PC1—PC5的观测值,基于PC1—PC4,分别建立MLR/PC-CAR模型作6—8月的长江下游低频降水变化的50 d预测。
表 1给出这2种方法预测技巧的相关检验,图 5、6分别给出方法1和2的9次预报中的5次预报结果(初始时间分别为5月31日、6月10、20、30日和7月10日)。从表 1中可以发现方法2的预报效果明显高于方法1,9次预报的相关预报技巧均大于0.60(考虑序列的持续性,其显著性为0.05),最好的是初始时间为5月31日的50 d预报,预报技巧达到0.92(表明长江下游地区20—30 d降水季节内振荡与SCGT存在极显著的相关),方法1最好的50 d预测都低于这一水平,以6月5日为初始时间的预报相关技巧下降到0.42。 此外,从不同日期初始场的预报效果来看,方法2在 6月25日之前的6次预测效果均较好,即能预测6月上旬开始的50 d内长江下游降水20—30 d振荡强度增强并稳定,其正位相有利于这个地区强降水过程的形成。
| 预报初始日期 | 2011年 | 2002年 | ||
| 方法1 | 方法2 | 方法1 | 方法2 | |
| 5月31日 | 0.61 | 0.92 | 0.79 | 0.80 |
| 6月5日 | 0.42 | 0.87 | 0.78 | 0.65 |
| 6月10日 | 0.54 | 0.89 | 0.54 | 0.49 |
| 6月15日 | 0.66 | 0.78 | 0.52 | 0.51 |
| 6月20日 | 0.76 | 0.81 | 0.39 | 0.60 |
| 6月25日 | 0.82 | 0.82 | 0.62 | 0.71 |
| 6月30日 | 0.56 | 0.68 | 0.59 | 0.65 |
| 7月5日 | 0.69 | 0.74 | 0.59 | 0.92 |
| 7月10日 | 0.52 | 0.78 | 0.67 | 0.83 |
| 平均 | 0.62 | 0.81 | 0.61 | 0.68 |
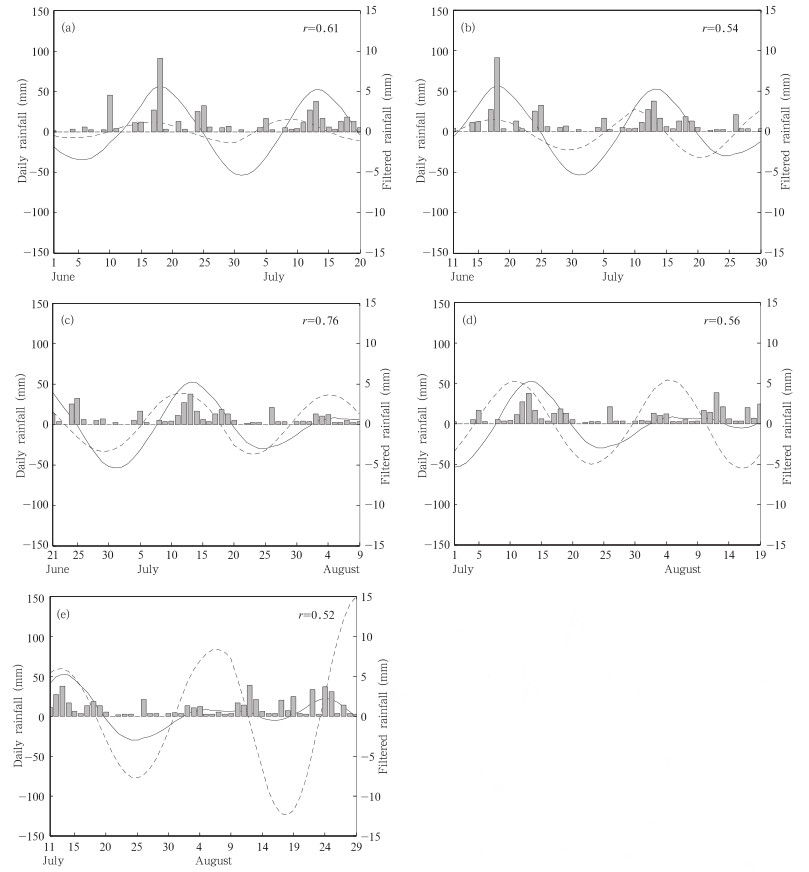 |
| 图 5 2011年夏季长江下游地区20—30 d低频降水1—50 d预报(虚线)和实况(实线), (初始场(a)5月31日,(b)6月10日,(c)6月20日,(d)6月30日,(e)7月10日,直方图表示长江下游地区逐日降水变化(基于区域A的 850 hPa低频经向风场的主成分),r为相关系数) Fig. 5 Prediction(dashed line) and observation(solid line)of the 20-30 day rainfall over the lower reaches of the Yangtze River for the period from 1 to 50 days in the summer of 2011 based on the principal components of the low frequency meridional wind anomaly of 850 hPa of the region A(0°-45°N,90°E-180°); the bar represents the time series of the daily precipitation(unit: mm),initial dates:(a)31 May,(b)10 June,(c)20 June,(d)30 June,and (e)10 July; r: correlation coefficients |
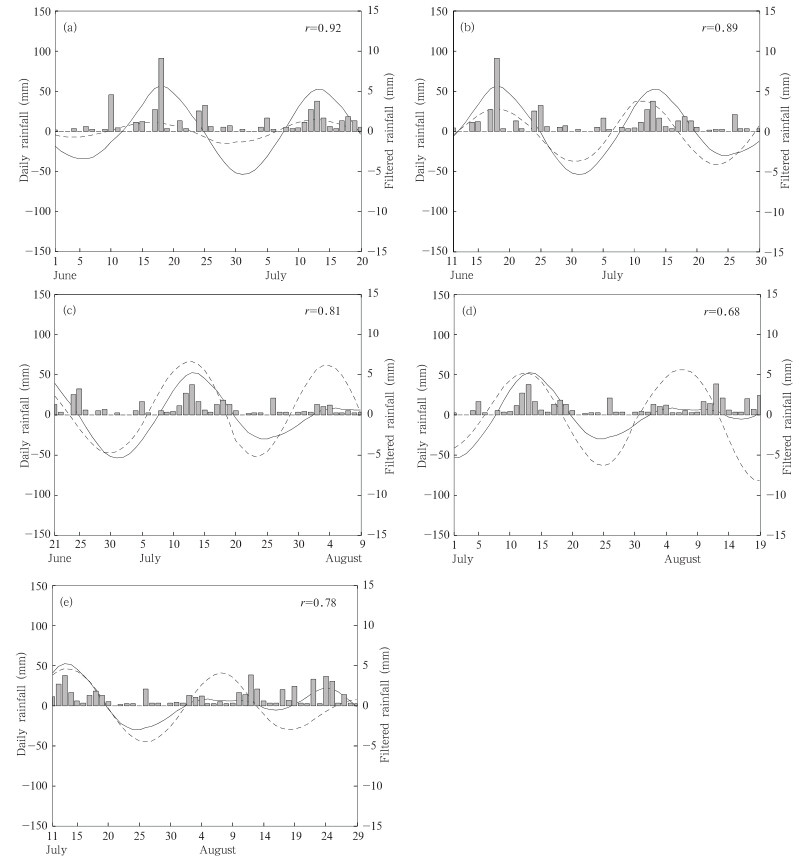 |
| 图 6 长江下游地区20—30 d低频降水1—50 d预报(基于区域B),其他同图 5 Fig. 6 As in Fig. 5 but for the region B |
从5月31日(图 6a)、6月10日(图 6b)、20日(图 6c)为初始时间的预报可以发现,方法2这3次精确地预报出了7月上旬末至中旬后期长江下游地区较明显的正位相变化,对应于7月中旬多强降水过程(预报技巧大于0.80)。它为2011年7月18日南京地区的特大暴雨过程(杨秋明,2011)的预测提供了显著的预报信号,预报时效达35—45 d。这表明SCGT对于2011年6—8月长江下游地区强降水形成起主导作用(通过南半球中纬度地区环流和东亚环流在20—30 d 时间尺度上的相互作用); 同时上述长江下游降水20—30 d振荡强度从6月初开始将持续增强的趋势预测(伴随强降水过程的显著增加),也为2011年6月上旬长江下游地区旱涝急转预测提供了重要预报信号。值得注意的是,前期春季长江下游降水 20—30 d季节内振荡与南半球SCGT变化也有较显著的相关(图 7a),与SCGT在东南太平洋至南大西洋地区传播的联系更密切(绿色虚线);20—30 d季节内振荡主要解释方差显著区域在南半球中高纬度地区和热带印度洋地区以及欧亚大陆高纬度地区和北大西洋中高纬度地区(图 7b),与北半球热带外地区环流季节内振荡的变化关系不密切(与北半球中高纬度地区的绕球遥相关型波列的相关较弱),仅与绕球遥相关型在欧亚和北美大陆北部地区的传播有较明显的关系(图 7a中紫色虚线)。因此,在2011年春季,长江下游20—30 d 低频降水与SCGT的联系已较显著,这种与SCGT关系具有较好的季节持续性也是上述方法2的预报效果更好的一个原因。此外,对于东亚地区强20—30 d振荡的2002年,进行类似的独立预测试验,也发现方法2的预报技巧好于方法1(表 1),MLR/PC-CAR模型的预报时效可达50 d(而低频变化主振荡预测模型的预报时效仅20 d左右(杨秋明等,2012b)),能有效估计未来6—7周长江下游地区强降水过程的变化。与2011年不同的是,方法2中初始时间为6月10、15、20日3次预报技巧出现较明显减小,表明2002年从春季到夏季,长江下游地区20—30 d低频降水与SCGT的相关呈增强、减弱、增强的过程;而2011年这种相关略微减弱,但仍然稳定。以上分析表明,3—5月SCGT强度变化对于6—8月长江下游降水 20—30 d振荡强度也有重要预示性。从春季到夏季持续维持较强的SCGT活动,有利于后期夏季长江下游强降水的形成,这时基于南半球中纬度低频风场主要空间模态的时间变化(主成分)建立的MLR/PC-CAR混合模型能更稳定地预测夏季长江下游地区20—30 d低频降水分量未来50 d的变化。
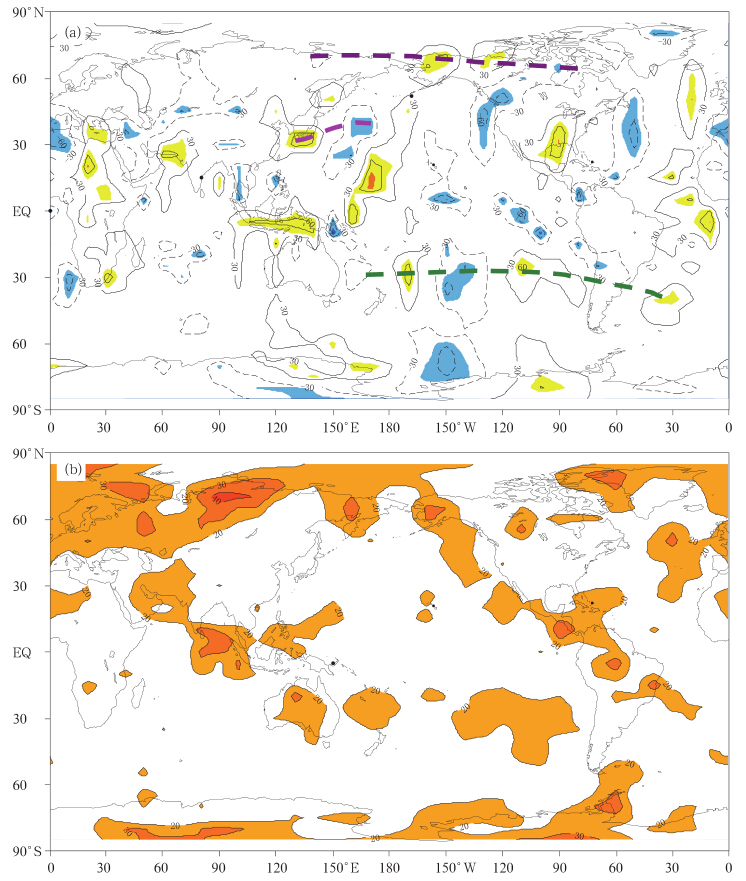 |
| 图 7 2011年3月1日—5月31日长江下游地区20—30 d低频降水与全球850 hPa低频经向风场的相关(a)及全球850 hPa 高度距平20—30 d 滤波序列与原始序列标准差比值的空间分布(b),其他同图 2 Fig. 7 As in Fig. 2 but for the period from 1 March to 31 May in 2011 |
由于MLR与PC-CAR预报模型分别采用独立回归方程组和复数自回归递推方法,所以对于大气季节内振荡型主要分量变化的预测时效也有一定差异,下面对预测方法2进行分析。图 8是基于2011年3月15日—8月31日的资料,对区域B观测的低频PC1—PC4构成的数据阵和长江下游低频降水建立的MLR,用初始时间 5月31日,6月1日,…,7月22日分别预测未来20,21,…,40 d低频降水变化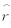 〈 lcj(t)与观测低频降水(rlcj(t)(t =1,2,…,Tl;Tl=20,21,…,40)的平均相关系数(共53次预测)。从图中可发现,预测时效达30 d左右(对应的预测时间为26—34 d,其显著性为0.05)。此外,图 9给出了用区域B观测的低频PC1—PC4构成的数据阵建立CAR模型做PC1、PC2、PC3和PC4的1—30 d预报的相关预报技巧(63次预报平均),用限定记忆法保持子序列N0 不变,滑动进行独立样本预测试验(初始时间分别为2011年5 月 31 日,6月1日,…,8月1日,预报未来 30 d),取预报时间τ=30 d,子序列长度 N0=50 d。从图 9可以看出,平均相关预报技巧达19—20 d(相关系数大于0.56,其显著性为0.05),其中对PC1、PC4的预测时效更长(黑色实线和红色实线),分别达25 d以上和23 d左右。这表明CAR能有效预测与SCGT等低频波传播有关的南半球中纬度低频环流未来20 d左右的变化。但用区域A观测的低频PC1—PC4构成的数据阵建立CAR模型的预报时效只有14—15 d(图略),即在20—30 d 时间尺度上,CAR模型对于东亚环流主要季节内振荡型的预报能力小于其对南半球中纬度环流季节内振荡型的预报能力,这可能与后者振荡的时间稳定性较好有关。
〈 lcj(t)与观测低频降水(rlcj(t)(t =1,2,…,Tl;Tl=20,21,…,40)的平均相关系数(共53次预测)。从图中可发现,预测时效达30 d左右(对应的预测时间为26—34 d,其显著性为0.05)。此外,图 9给出了用区域B观测的低频PC1—PC4构成的数据阵建立CAR模型做PC1、PC2、PC3和PC4的1—30 d预报的相关预报技巧(63次预报平均),用限定记忆法保持子序列N0 不变,滑动进行独立样本预测试验(初始时间分别为2011年5 月 31 日,6月1日,…,8月1日,预报未来 30 d),取预报时间τ=30 d,子序列长度 N0=50 d。从图 9可以看出,平均相关预报技巧达19—20 d(相关系数大于0.56,其显著性为0.05),其中对PC1、PC4的预测时效更长(黑色实线和红色实线),分别达25 d以上和23 d左右。这表明CAR能有效预测与SCGT等低频波传播有关的南半球中纬度低频环流未来20 d左右的变化。但用区域A观测的低频PC1—PC4构成的数据阵建立CAR模型的预报时效只有14—15 d(图略),即在20—30 d 时间尺度上,CAR模型对于东亚环流主要季节内振荡型的预报能力小于其对南半球中纬度环流季节内振荡型的预报能力,这可能与后者振荡的时间稳定性较好有关。
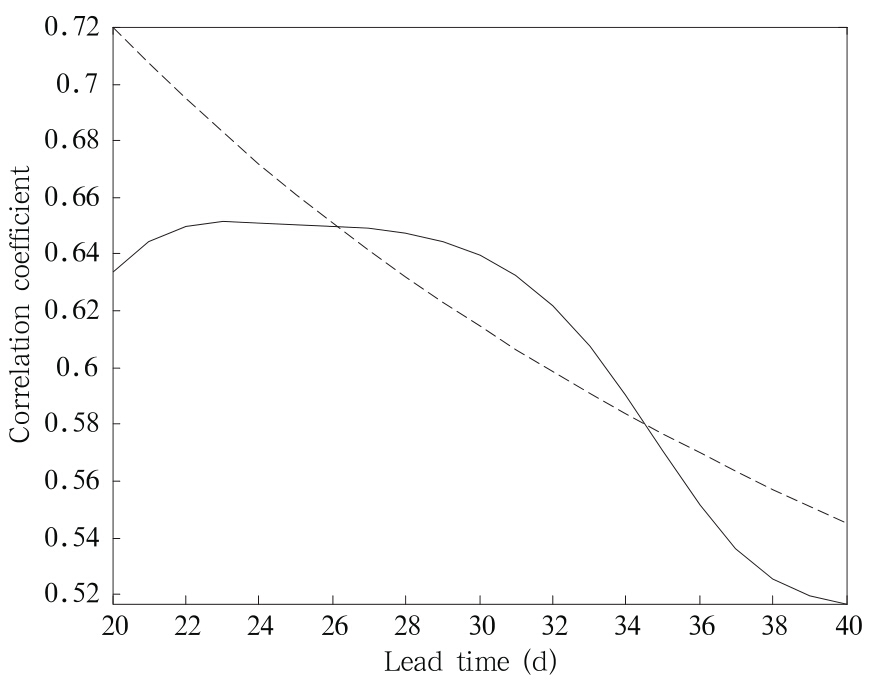 |
| 图 8 区域B的PC1—PC4构建MLR模型的低频降水20—40 d预报的相关预报技巧(虚线表示达到95%的显著性水平) Fig. 8 Forecasting skills of the low frequency rainfall for the MLR model based on the PC1-PC4 for the region B during the 20-40 days(the significant levels of 95% are represented by the dashed line) |
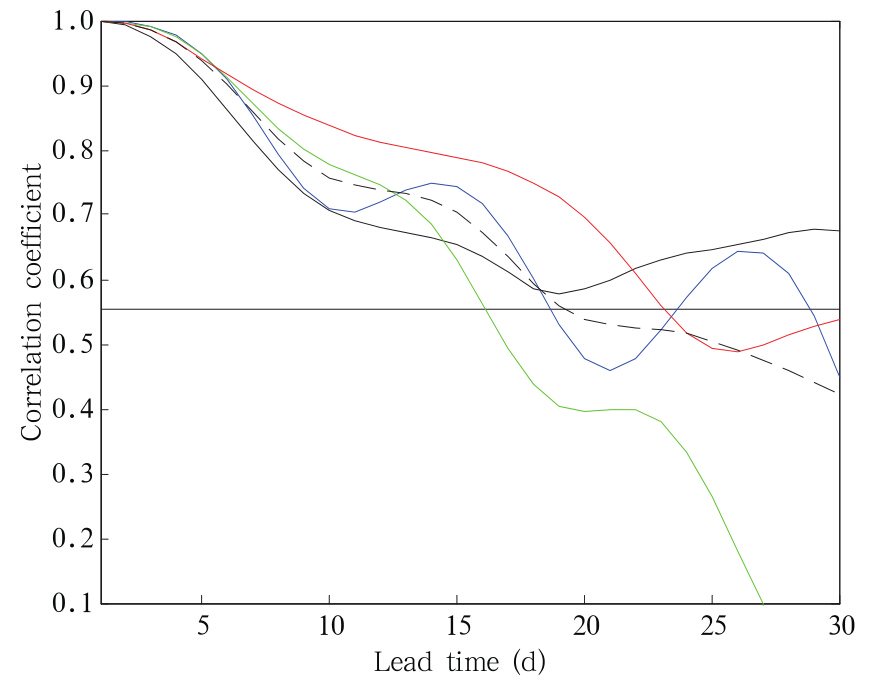 |
| 图 9 区域B的PC1—PC4的CAR模型1—30 d预报的技巧(黑、蓝、绿、红线对应于PC1、PC2、PC3、PC4;黑虚线为PC1—PC4的平均预报技巧,水平实线表示达到95%的显著性水平) Fig. 9 Forecasting skills for the CAR model based on the PC1-PC4 for the region B during the 1-30 days(the black,blue,green,red lines are corresponding to PC1,PC2,PC3,and PC4,respectively,and black dashed line is corresponding to the mean correlation forecasting skills,and the significant levels of 95% are represented by the horizontal line) |
通过上述计算结果可发现,基于南半球中纬度大气季节内振荡的变化,MLR(不同的时间滞后的一组独立线性回归方程)和PC-CAR(复数自回归递推)的预测时效分别可达30和20 d左右。因此,MLR和PC-CAR结合的混合预报方法(MLR/PC-CAR)能将长江下游低频降水的预报时效延长到50 d左右,可以更好地反映南半球中纬度环流季节内振荡的时空变化过程对长江下游降水季节内振荡的重要作用。
2011和2002年的预测试验表明,选择合适关键区的低频主分量作为因子,基于MLR/PC-CAR混合预报方法,能有效延长大气季节内振荡的预报时效。进一步对于20—30 d振荡较强的年份(1979、1984、1987、1991、1997、1998、1999、2000、2005、2007、2009年)6—8月的预测试验(区域B观测的低频PC1—PC4构成的数据阵,即方法2)结果表明,预报时效也达到50 d 左右(表 2),能很好地预测多数强降水过程的正位相的变化。从表 2可以看出,除了1997、1999、2005年夏季的9次预报的平均相关技巧较低外(分别为0.39、0.39和0.26,未达到95%的显著性水平,反映从春到夏,SCGT对长江下游低频降水的作用持续减弱或不稳定),其余年份均能有效预测长江下游地区降水20—30 d低频分量的未来50 d变化趋势,将低频降水的预测时效从30 d显著延长到50 d(尤其是1979、1984、1987、1998、2002、2007、2009、2011年,平均相关预报技巧≥0.60,达到95%的显著水平),表明上述年份南半球中纬度地区SCGT与夏季长江下游地区20—30 d低频降水存在强相互作用,是影响长江下游地区强降水形成和变化的主导因素。
因此,MLR/PC-CAR混合预报方法能使预测模型更好地体现降水和环流主要的低频时滞相关及其较长时段的变化,较准确地描述准线性的低频动力过程的演变。这种复数时间序列统计方法,能在复平面上描述低频波的传播特征,得到比实空间波动更多的信息,更稳定地揭示波动的时间演变,有利于进一步延长预测时效。需要指出的是,影响长江下游地区夏季强降水的20—30 d振荡强度存在显著的年际变化,与春季太平洋海温距平的变化有一定的联系(杨秋明等,2012b)。若春季太平洋海温距平的变化有利于后期夏季 20—30 d振荡信号减弱(长江下游地区强降水过程减少),需考虑10—20或30—50 d振荡的不同关键区低频主分量的作用,预测未来 50 d长江下游地区夏季低频降水分量的位相变化,做出较强降水过程或持续降水过程的发生时段的估计,改进延伸期强降水过程预报的精度。
| 年份 | 初始日期 | |||||||||
| 5月31日 | 6月5日 | 6月10日 | 6月15日 | 6月20日 | 6月25日 | 6月30日 | 7月5日 | 7月10日 | 平均 | |
| 1979 | 0.95 | 0.93 | 0.91 | 0.87 | 0.94 | 0.60 | 0.70 | 0.57 | 0.74 | 0.80 |
| 1984 | 0.75 | 0.79 | 0.89 | 0.89 | 0.88 | 0.77 | 0.75 | 0.57 | 0.70 | 0.78 |
| 1987 | 0.49 | 0.74 | 0.86 | 0.96 | 0.83 | 0.86 | 0.76 | 0.84 | 0.94 | 0.81 |
| 1991 | 0.89 | 0.87 | 0.71 | 0.42 | 0.24 | 0.27 | 0.21 | 0.26 | 0.34 | 0.47 |
| 1997 | 0.92 | 0.94 | 0.89 | 0.59 | 0.01 | 0.79 | -0.12 | -0.13 | -0.36 | 0.39 |
| 1998 | 0.96 | 0.87 | 0.92 | 0.66 | 0.75 | 0.42 | 0.37 | 0.32 | 0.50 | 0.64 |
| 1999 | 0.04 | 0.78 | 0.12 | 0.91 | -0.07 | 0.57 | 0.58 | 0.52 | 0.02 | 0.39 |
| 2000 | 0.84 | 0.74 | 0.71 | 0.57 | 0.54 | 0.40 | 0.33 | 0.42 | -0.12 | 0.49 |
| 2002 | 0.80 | 0.65 | 0.49 | 0.51 | 0.60 | 0.71 | 0.65 | 0.92 | 0.83 | 0.68 |
| 2005 | 0.74 | 0.22 | -0.22 | -0.17 | -0.11 | 0.19 | 0.40 | 0.71 | 0.57 | 0.26 |
| 2007 | 0.84 | 0.88 | 0.86 | 0.84 | 0.90 | 0.66 | 0.69 | 0.65 | 0.61 | 0.77 |
| 2009 | 0.62 | 0.88 | 0.96 | 0.91 | 0.78 | 0.81 | 0.64 | 0.74 | 0.69 | 0.78 |
| 2011 | 0.92 | 0.87 | 0.89 | 0.78 | 0.81 | 0.82 | 0.68 | 0.74 | 0.78 | 0.81 |
本研究通过构造多变量时滞回归模型(MLR)和主成分复数自回归模型(PC-CAR)混合预报模型(MLR/PC-CAR),对夏季长江下游地区20—30 d降水低频分量进行延伸期逐日变化预测试验,得到如下结论:
(1)在20—30 d时间尺度上,全球主要大气季节内振荡型与长江下游降水低频分量存在较显著的时滞相关,其中与SCGT型相关的主要低频分量之间的时滞相关最为显著(对应于南半球热带外地区一类准线性低频波动的传播)。基于这些时滞关系的线性预测方程(MLR)能很好地预测2011年夏季长江下游降水低频分量10—30 d延伸期的变化,提高夏季长江下游地区未来10—30 d强降水过程预报的准确率。
(2)用主成分的复数自回归模型(PC-CAR)预报与2011年6—8月SCGT型相关的南半球中纬度地区环流主要低频分量延伸期逐日变化,预报时效可达20 d左右。上述基于观测低频资料时滞关系的线性预测方程在30 d预报的基础上,用 MLR/PC-CAR模型可将预报时效进一步延长20 d,达到50 d左右。采用南半球中高纬度地区850 hPa 低频经向风的主成分作为预测因子的模型的预测精度显著高于东亚地区低频经向风作为预测因子的模型。这些低频降水分量的50 d预测,对于长江下游地区2011 年6月初旱涝急转和7 月中旬持续降水和强降水过程的预报有重要指示意义。
(3)对于较强的20—30 d振荡的多年资料预测试验也表明,SCGT是预测夏季长江下游低频降水未来50 d变化的主要信号之一。基于南半球中纬度地区环流20—30 d主要低频主成分,构建MLR/PC-CAR模型可以更有效地预测1—50 d长江下游降水低频分量的变化,估计未来 6—7周内长江下游强降水过程发生的时段,显著延长夏季长江下游强降水事件的预报时效。
10—30 d延伸期预报同时受到初始条件和大气外部强迫因子的影响。初始场的信息随着预报时效的延长而逐渐减弱,而气候系统中缓变的外强迫所起的作用则在逐渐显现。因此,它既是初值问题,也是边值问题。基于缓变外强迫与大气的耦合所形成的大气内部过程,如40—60 d振荡、绕球遥相关、SCGT等大气季节内振荡,有助于提高可预报期限。目前统计模式对季节内振荡的预报能力要比动力模式好,在动力模式进一步得到改进之前,它是一种研究季节内振荡可预报性的更加有效的途径。低频振荡作为大气内部动力过程,其可预报性本身存在一些不确定性。通过构造时滞相关和复数空间上的动力统计模型,能更客观地揭示气候系统主要的季节内低频信号的演变,基于合适的关键区域环流低频主分量构建统计预测模型,能显著延长环流和降水季节内振荡的预报时效,同时也为月时间尺度的气候距平预测提供重要预报信号。
| 陈官军, 魏凤英. 2012. 基于低频振荡特征的夏季江淮持续性降水延伸期预报方法. 大气科学, 36(3): 633-644 |
| 丑纪范, 郑志海, 孙树鹏. 2010. 10—30 d延伸期数值天气预报的策略思考:直面混沌. 气象科学, 30(5): 569-573 |
| 丁一汇, 刘芸芸. 2008. 亚洲—太平洋季风区的遥相关研究. 气象学报, 66(5): 670-682 |
| 封国林, 孙树鹏, 赵俊虎等. 2013. 基于2009年初长江中下游地区持续阴雨过程的10—30天延伸期稳定分量的提取及配置分析. 中国科学(地球科学), 43(5): 836-847 |
| 谷湘潜, 康红文, 曹鸿兴. 2006. 复数域内的最小二乘法. 自然科学进展, 16(1): 49-54 |
| 梁萍, 丁一汇. 2012. 基于季节内振荡的延伸预报试验. 大气科学, 36(1): 102-116 |
| 孙国武, 李震坤, 信飞等. 2013. 延伸期天气过程预报的一种新方法:低频天气图. 大气科学, 37(4): 945-954 |
| 王阔, 封国林, 孙树鹏等. 2012a. 基于2008年1月中国南方低温雨雪冰冻事件10—30天延伸期稳定分量的研究. 物理学报, 61(10): 520-529 |
| 王阔, 封国林, 孙树鹏等. 2012b. 2009年11月冰冻雨雪事件10—30d延伸期稳定分量提取及分析. 物理学报, 61(20): 209201 |
| 杨秋明. 1998. 西太平洋热带地区环流低频变化的主振荡型预测试验. 应用气象学报, 9(3): 345-351 |
| 杨秋明. 2009. 全球环流20—30d 振荡与长江下游强降水. 中国科学(D辑), 39(11): 1515-1529 |
| 杨秋明. 2011. 2011年7月中旬长江下游地区强降水期间低频环流延伸期预报试验. 科技导报, 29(32): 61-66 |
| 杨秋明, 宋娟, 李熠等. 2012a. 全球大气季节内振荡对长江流域持续暴雨影响的研究进展. 地球科学进展, 27(8): 876-884 |
| 杨秋明, 李熠, 宋娟等. 2012b. 2002年夏季东亚地区环流20—30 d主振荡型延伸期预报研究. 气象学报, 70(5): 1045-1054 |
| 郑志海, 黄建平, 封国林等. 2013. 延伸期可预报分量的预报方案和策略. 中国科学(地球科学), 43(4): 594-605 |
| Ambrizzi T, Hoskins B J, Hsu H H. 1995. Rossby wave propagation and teleconnection patterns in the austral winter. J Atmos Sci, 52(21): 3661-3672 |
| Cassou C. 2008. Intraseasonal interaction between the Madden-Julian Oscillation and the North Atlantic Oscillation. Nature, 455(7212): 523-527 |
| Fu X, Wang W Q, Lee J Y, et al. 2013. Intraseasonal forecasting of the Asian summer monsoon in four operational and research models. J Climate, 26(12): 4186-4203 |
| Hasselmann K. 1988. PIPs and POPs: The reduction of complex dynamical systems using principal interaction and principal oscillation patterns. J Geophys Res, 93(D9): 11015-11021 |
| Hoskins B. 2013. The potential for skill across the range of the seamless weather-climate prediction problem: A stimulus for our science. Quart J Roy Meteor Soc, 139(672): 573-584 |
| Jiang X, Waliser D E, Wheeler M C, et al. 2008. Assessing the skill of an all-season statistical forecast model for the Madden-Julian Oscillation. Mon Wea Rev, 136(6): 1940-1956 |
| Kalnay E, Kanamitsu M, Kistler R, et al. 1996. The NCEP/NCAR 40-year reanalysis project. Bull Amer Meteor Soc, 77(3): 437-471 |
| Kikuchi K, Wang B, Kajikawa Y. 2012. Bimodal representation of the tropical intraseasonal oscillation. Climate Dyn, 38(2-3): 1989-2000 |
| Krishnamurthy V, Achuthavarier D. 2012. Intraseasonal oscillations of the monsoon circulation over South Asia. Climate Dyn, 38(11-12): 2335-2353 |
| Lau K M, Weng H Y. 2002. Recurrent teleconnection patterns linking summertime precipitation variability over East Asia and North America. J Meteor Soc Japan, 80(6): 1309-1324 |
| Love B S, Matthews A J, Janacek G J. 2008. Real-time extraction of the Madden-Julian Oscillation using empirical mode decomposition and statistical forecasting with a VARMA model. J Climate, 21(20): 5318-5335 |
| Love B S, Matthews A J. 2009. Real-time localised forecasting of the Madden-Julian Oscillation using neural network models. Quart J Roy Meteor Soc, 135(643): 1471-1483 |
| Matthewman N J, Magnusdottir G. 2012. Clarifying ambiguity in intraseasonal Southern Hemisphere climate modes during austral winter. J Geophys Res, 117, D03105, doi:10.1029/2011JD016707 |
| Miller M, Buizza R, Haseler J, et al. 2010. Increased resolution in the ECMWF deterministic and ensemble prediction systems. ECMWF Newsl, 124: 10-16 |
| Miyakoda K, Gordon T, Carerly R, et al. 1983. Simulation of a blocking event in January 1977. Mon Wea Rev, 111(4): 846-849 |
| Mo K C. 2001. Adaptive filtering and prediction of intraseasonal oscillations. Mon Wea Rev, 129(4): 802-817 |
| Shimizu M H, Cavalcanti I. 2011. Variability patterns of Rossby wave source. Climate Dyn, 37(3-4): 441-454 |
| Vitart F, Molteni F. 2010. Simulation of the Madden-Julian oscillation and its teleconnections in the ECMWF forecast system. Quart J Roy Meteor Soc, 136(649): 842-855 |
| von Storch H, Xu J S. 1990. Principal oscillation pattern analysis of the 30-to 60-day oscillation in the tropical troposphere. Climate Dyn, 4(3): 175-190 |
| Waliser D E, Jones C, Schemm J K, et al. 1999. A statistical extended-range tropical forecast model based on the slow evolution of the Madden-Julian Oscillation. J Climate, 12(7): 1918-1939 |
| Waliser D E, Lau K M, Stern W, et al. 2003. Potential predictability of the Madden-Julian oscillation. Bull Amer Meteor Soc, 84(1): 33-50 |
| Wheeler M C, Hendon H H. 2004. An all-season real-time multivariate MJO index: Development of an index for monitoring and prediction. Mon Wea Rev, 132(8): 1917-1932 |
| Xavier P K, Goswami B N. 2007. An analog method for real-time forecasting of summer monsoon subseasonal variability. Mon Wea Rev, 2007, 135(12): 4149-4160 |
| Yadav R K. 2009. Role of equatorial central Pacific and northwest of North Atlantic 2-metre surface temperatures in modulating Indian summer monsoon variability. Climate Dyn, 32(4): 549-563 |
 2014, Vol. 72
2014, Vol. 72