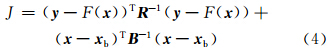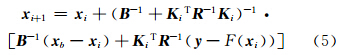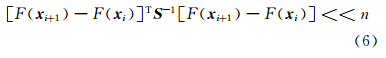中国气象学会主办。
文章信息
- 王云, 王振会, 李青, 朱雅毓. 2014.
- WANG Yun, WANG Zhenhui, LI Qing, ZHU Yayu. 2014.
- 基于一维变分算法的地基微波辐射计遥感大气温湿廓线研究
- Research of the one-dimensional variational algorithm for retrieving temperature and humidity profiles from the ground-based microwave radiometer
- 气象学报, 72(3): 570-582
- Acta Meteorologica Sinica, 72(3): 570-582.
- http://dx.doi.org/10.11676/qxxb2014.036
-
文章历史
- 收稿日期:2013-7-17
- 改回日期:2014-2-24
2. 南京信息工程大学大气物理学院, 南京, 210044
2. School of Atmospheric Physics, Nanjing University of Information Science and Technology, Nanjing 210044, China
大气温度和湿度廓线是大气环境的重要参数,获得连续的大气温、湿廓线对认识各种尺度的天气演变过程与做好临近天气预报具有重要意义。常规探空资料具有较高的代表性和可信度(伊里哈木等,2009),但其较低的时间分辨率,越发不能满足现代气象事业的发展需求。地基微波辐射计能够以分钟的时间分辨率连续给出0—10 km的大气温度和湿度的垂直分布,属于被动遥感(能耗低、保密性好),对云雾有一定的穿透能力,且远离太阳辐射干扰,所以具有较强的全天候、全天时工作能力。目前,地基微波辐射计获得的大气温、湿度廓线资料已被广泛应用于暴雨(王建等,2012)、冰雹(唐仁茂等,2012)、台风(赵兵科等,2009)等灾害性天气分析及强对流天气预报(Chan,2009; Knupp et al,2009; 王叶红等,2010)等研究。近几年来,对地基微波辐射计的关注程度越来越高,中国地基微波辐射计台数增加很快,已有近30台。
地基微波辐射计获得大气温、湿度廓线,是采用遥感的间接测量方式,需要经过“反演”(即将辐射计测量到的辐射能量,按照一定的方法,转化成为大气温、湿度廓线)。用于反演大气温、湿度廓线的技术有很多,主要有回归法(Güldne et al,2001)、神经网络(Solheim et al,1998;刘亚亚等,2010)、一维变分(Hewison,2007; Cimini et al,2010)等。Cimini等(2006)对不同反演算法的利弊进行了分析,回归算法简单清楚,但对解决非线性问题有局限性;目前大多数地基微波辐射计自带的反演软件都是运用神经网络算法,能部分解决非线性问题,回归法和神经网络算法都比较稳定,但依赖于训练样本,训练数据集需大样本且尽可能覆盖所有的天气状况,以建立较有代表性的反演模型,在实际工作中往往难以满足这样的需求。相比于前两种方法,一维变分算法不需要过多的训练数据集,能够较好地解决非线性问题,但对辐射传输模式的精度和数据定标的精度有依赖性,此外,一维变分算法的计算量较大,随着计算能力的提高,这方面的局限也在慢慢消除。对于一维变分算法的应用,较早的是在星载微波辐射计资料的反演问题上(English,1999;Deblonde et al,2003),近几年有学者开始将其运用于地基辐射计资料的反演,如Hewison(2007)用12通道地基微波辐射计资料反演,Cimini等(2010)用北极多频率扫描辐射计反演实验,结果都表明一位变分算法能够优化数值预报输出,获得的温、湿度廓线更接近探空观测结果。中国学者将一维变分算法应用于资料同化(王华荣等,2005;王叶红等,2012),但未见报道用于地基微波辐射计反演温、湿度廓线。
针对中国地基微波辐射计反演现状和需求,研究一维变分算法应用于地基微波辐射计反演温、湿度廓线,利用北京地区的地基微波辐射计、地面观测、探空和NCEP再分析等资料,讨论无云样本的提取方法,并对观测亮温进行质量控制,然后利用一维变分算法对微波辐射计观测亮温进行反演,以探空数据作为实际大气,对反演结果进行统计分析。2 资料说明及预处理
研究使用的亮温资料来自地基微波辐射计的22个通道,包括频率为22.234—27.500 GHz的 6个水汽通道(用通道序号1—6表示),28.000和30.000 GHz 的2个大气窗通道(用通道序号7—8表示)及51—59 GHz的14个氧气通道(用通道序号9—22表示),共采集了2010年1月—2011年12月2年的level1和level2数据,其中level1是观测亮温数据,level2是微波辐射计自带神经网络算法反演得到的温度和湿度廓线,0—0.5 km,每隔50 m一层;0.5—2.0 km,每隔100 m一层;2.0—10.0 km,每隔250 m一层,共58层。该辐射计在2010年12月22日进行了定标,在2011年9月29日从北京顺义搬迁到上甸子。由于地基微波观测亮温数据没有整时数据,将00和12时(世界时,下同)前后15 min的亮温平均值作为00和12时的整时值。使用1天两次的探空数据、NCEP再分析数据以及地面气象观测数据(00和12时)。对探空数据和NCEP再分析数据进行插值处理,使得与level2数据各高度层相同。地基微波辐射计、地面观测站、探空站、NCEP数据的具体位置如图 1所示,上甸子地基微波辐射计离其他数据所在位置较远。
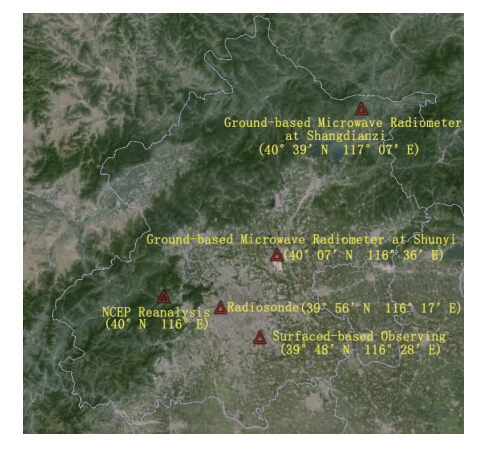 |
| 图 1 站点位置Fig. 1 Schematic map for the station position |
尽管一般认为微波辐射可以穿透云层,但是云对微波辐射的吸收和散射可以有很大差异(主要取决于云温和云中含水量)(王振会,1988),而云体高度、云内微物理量等参数有很大的不确定性,因此难以在对地基微波辐射计观测亮温数据进行大气温、湿度廓线反演时将云参数考虑进来。为了排除云的影响,使得能够准确评价反演方法的可靠性及反演效果,本研究仅使用无云样本。
对于不同的云,地基微波辐射计自带的红外温度传感器测得的红外亮温(Tir)是不一样的。为此,首先,利用地面观测的总云量(CT)和低云量(CL)将2年的样本分为无云、低云和中高云3类
分类得到343个无云样本,444个中高云样本,607个低云样本。然后,对3类样本的红外亮温进行统计(图 2a—c)。可以看出3种情况下红外亮温的频数直方图都呈峰状分布,频数峰值对应的红外亮温分别为205、230和280 K,有云比无云时的红外亮温高,且云越低红外亮温越高,这为寻找区分有云还是无云的红外亮温阈值提供了条件。从图 2d中看出,3种情况的直方图叠加后呈现3峰2谷分布,第1个谷就是区分有云还是无云的界限,其值为225 K,以此为阈值Tir_threshold得到2010和2011年地基微波辐射计上空的无云样本数目分别为202和276。  |
| 图 2 红外亮温直方图(a.无云,b.有中高云,c.有低云,d.3种情况下的叠加)Fig. 2 Histograms of infrared brightness temperature(a.cloudless,b.medium-high cloud,c.low cloud,d.the overlaid figure of the three cases) |
从图 1可以看出,探空站和微波辐射计位置相距约20 km。为了减少云的局地差异对反演的影响,需对无云样本的约束条件进一步加强。根据探空数据将各高度层上相对湿度<85%判定为无云(黄润恒等,1987)。使用以上条件得到2010和2011年的无云样本数分别为187和245,总样本数为432。 2.2 无云样本的质量控制
地基微波辐射计定标使其电压-亮温转换关系改变,而搬迁则使其观测环境改变,这都会引起观测数据不连续。需对亮温观测数据进行质量控制。
首先以地基微波辐射计的定标和搬迁为断点,将样本分成3段;然后以探空数据代入辐射传输模式(Westwater et al,1985; Liebe et al,1992;王振会等,1995)计算得到的模拟亮温(TBC)为参考值,对无云条件下的观测亮温(TBM)进行分段去“奇点”处理,即分别计算3段样本的观测亮温与模拟亮温的均方根误差(RMSE),各样本中任一个通道的观测亮温与模拟亮温的绝对误差大于所在样本的均方根误差的两倍,就将该个体作为“奇点”去除。去“奇点”后样本总数为357。图 3a和b分别为第10通道(吸收较弱的氧气通道)分段去“奇点”前后观测亮温(星线)和模拟亮温(圈线)的时间序列,可以看出亮温异常的个体已被去除。
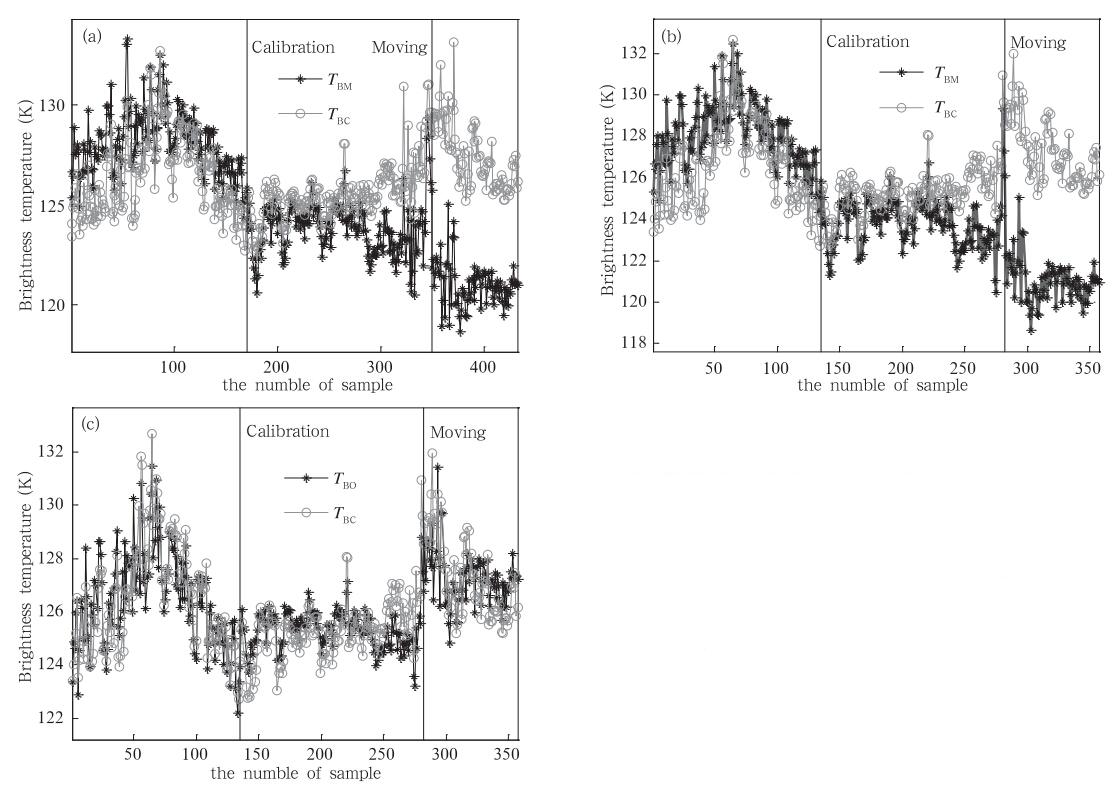 |
| 图 3 通道10的观测亮温和模拟亮温的时间序列(a.质量控制前,b.去“奇点”后,c.线性订正后)Fig. 3 Time series contrasts between the observed brightness temperatures and simulated brightness temperatures of Channel 10 (a.before quality control,b.after wiping off singularity,c.after linear correction) |
第2步是针对数据存在的不连续问题。利用李青等(2014)提出的线性拟合法对去“奇点”后的观测亮温与模拟亮温进行分段拟合,计算得到订正后的观测亮温(TBO)。图 3c为第10通道分段线性拟合订正后的观测亮温(星线)和模拟亮温(圈线)的时间序列,可以看出订正后的观测亮温与模拟亮温已经基本重合,时间变化趋势也基本一致。经上述两步订正后各通道的观测亮温与模拟亮温的一致性都明显得到改善。 3 一维变分算法3.1 算法介绍
用亮温观测向量(记为y)反演大气温、湿度廓线(记为向量x)的问题,可以用条件概率公式P(x/y)表示(Rodgers,2000),由Bayes理论可得
式中,P(y/x)为在已知x的条件下y的发生概率,包含了辐射传输模式和观测误差的信息;P(x)为大气温、湿状态廓线x的发生概率;P(y)为观测数据y的发生概率。对于反演问题,P(y)是已知的,其值为1。假设上式中各随机变量的概率密度函数都符合高斯分布,经过简化可以得到代价函数J式中,xb是背景状态矩阵;F(x)为前向模式,用来描述观测过程,是从状态场到观测场的一种映射关系,即辐射传输模式;R和B分别表示y的观测场和x的背景场的误差协方差矩阵。代价函数中包括两项,第1项表示观测场误差,第2项表示背景场误差。那么,P(x/y)最大化的问题就转换成了求解代价函数J最小值的问题。根据极值定理和牛顿迭代公式可得近似解这就是一维变分迭代公式,xi和xi+1分别是迭代前和迭代后的状态向量。Ki是雅克比矩阵,是一个描述观测向量y对大气层结向量x敏感性的权重函数。从式(5)可以看出,一维变分算法融合了观测场和背景场的信息,通过不断调整初始场来获得最可能的大气状态信息。迭代终止的条件为
式中,S=R(R+KiBKiT)-1R,n为观测向量y的维数,此处为22。本研究利用式(5),结合辐射传输模式,设计了大气温、湿度廓线反演软件。3.2 反演参数设置
2010年的无云资料,按照月份用于建立一维变分算法模型,2011年的无云资料用于反演试验,由于
2010年1—2和5—8月晴空样本较少,此外,地基微波辐射计搬迁导致2011年9—11月观测亮温数据不全,因此仅对2011年的3、4和12月共89个无云样本进行反演。
反演的状态向量x是温度T(K)和绝对湿度ρV(g/m3)廓线。绝对湿度由相对湿度U和温度T转换得到(盛裴轩等,2003)
式中,e为水汽压,es为饱和水汽压,单位均为 hPa。为了减弱湿度廓线的非线性和避免反演过程中出现负值,对绝对湿度取对数(lnρV)。反演中常使用3种背景场,即气候态资料、数值预报结果与统计反演结果,由于条件的限制,本研究将提前反演时刻12小时(t-12)的NCEP再分析数据作为一维变分算法的背景状态向量xb,以保证在反演时刻有实时的背景场资料,此外,相较于气候态资料,NCEP再分析数据更接近于真实大气。迭代计算的初始输入xi与背景状态向量xb是一致的。
考虑到误差太大会出现不收敛的问题,背景场误差协方差矩阵B是逐月计算的,分别由2010年3、4和12月同时刻无云条件下的探空和NCEP再分析数据计算而得,表示背景状态向量和真实大气状态之间的误差,其中包含了因站点与格点数据的差异而带来的额外误差。图 4为3月背景场误差协方差矩阵,可以看出温度协方差矩阵都是在对角线上误差较大,且在0.5 km以下差异尤其明显,0.5—5 km误差较小,5—8 km误差又有所增大;绝对湿度取对数后得到的误差协方差矩阵在高空处表现出较大的误差,而实际上绝对湿度在低空误差较大,经分析得知在高空绝对湿度的值都远小于1,取对数后会获得绝对值较大的负值,在低空是较接近于1的正值,取对数后只能得到绝对值较小的正值,即取对数缩小了低空的差异,放大了高空的差异。
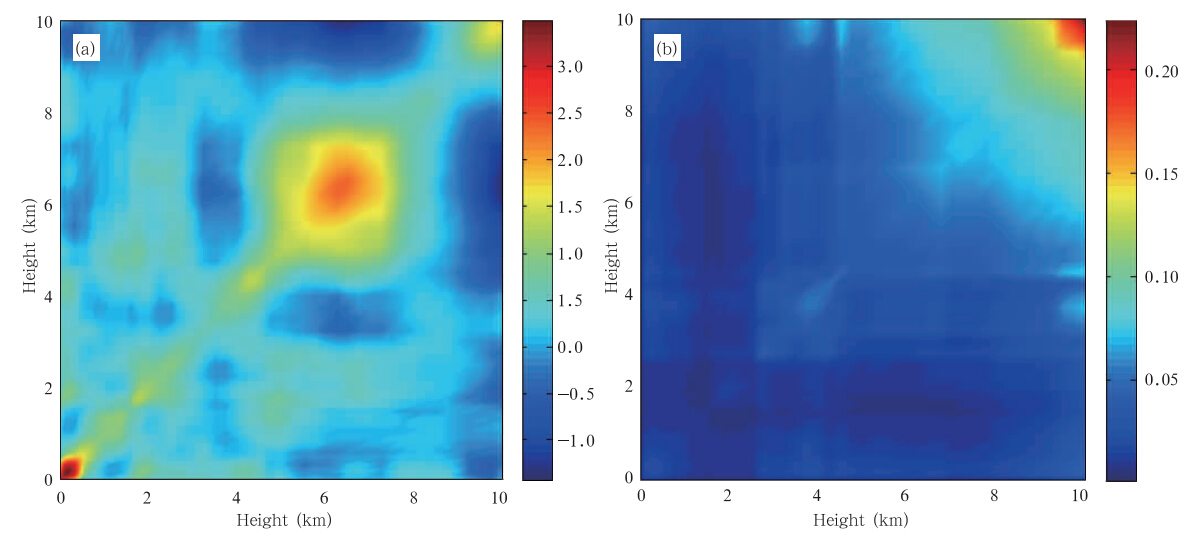 |
| 图 4 3月背景场误差协方差矩阵(a.温度,单位:K2; b.绝对湿度的对数,单位:(ln(g/m3))2)Fig. 4 Background error covariance matrixes in March(a.temperature,unit: K2; b.natural logarithm of absolute humidity,unit:(ln(g/m3))2) |
观测向量y是22通道亮温数据。观测场误差协方差矩阵R是由服从正态分布的随机误差模拟而得到的,其中随机误差的平均值都为0,标准差为1.5。雅克比矩阵K是通过大气温度层结或者湿度层结分别在初值附近以微量的变化(ΔT=1 K,ΔlnρV=0.001)(Hewison,2007; Cimini et al,2010),代入辐射传输模式计算观测向量的扰动量ΔF,再求比值(ΔF/ΔT,ΔF/ΔlnρV)而得,图 5为利用2011年3月10日00时NCEP再分析数据计算得到的雅克比矩阵。从图 5a中可以看出,1—8通道对湿度的敏感性随着吸收强度减弱而平行变小,且对6 km以下各高度层湿度变化都有不同程度的响应,在近地面响应较大。此外,可以注意到,绝对湿度的雅克比矩阵廓线不是很平滑,从地面到高空呈波浪式分布,在水汽吸收越强的通道越明显,经分析发现,该时刻大气湿度层结分布不均匀(图 6a),绝对湿度的大小与雅克比矩阵的大小呈正相关;9—22通道处于氧气吸收带,主要反映的是大气温度的信息,从图 5b可以看出,9—22通道随着吸收强度增强对温度的敏感区域由空中移向近地面,其中,19—22通道仅对0—1.5 km处的温度变化有较强的响应,13—18通道对1.5—3 km大气温度比较敏感,而9—12通道吸收强度很弱,对各层结大气温度变化的响应都不明显。温度廓线在0.8 km附近出现逆温层(图 6b),但是未在温度雅克比矩阵中表现出来。总体来看,地基微波辐射计观测亮温主要反映的是低层大气信息。
 |
| 图 5 2011年3月10日00时的雅克比矩阵(a. 绝对湿度,b. 温度)Fig. 5 Jacobians matrixes at 00:00 UTC 10 March 2011(a.absolute humidity,b.temperature) |
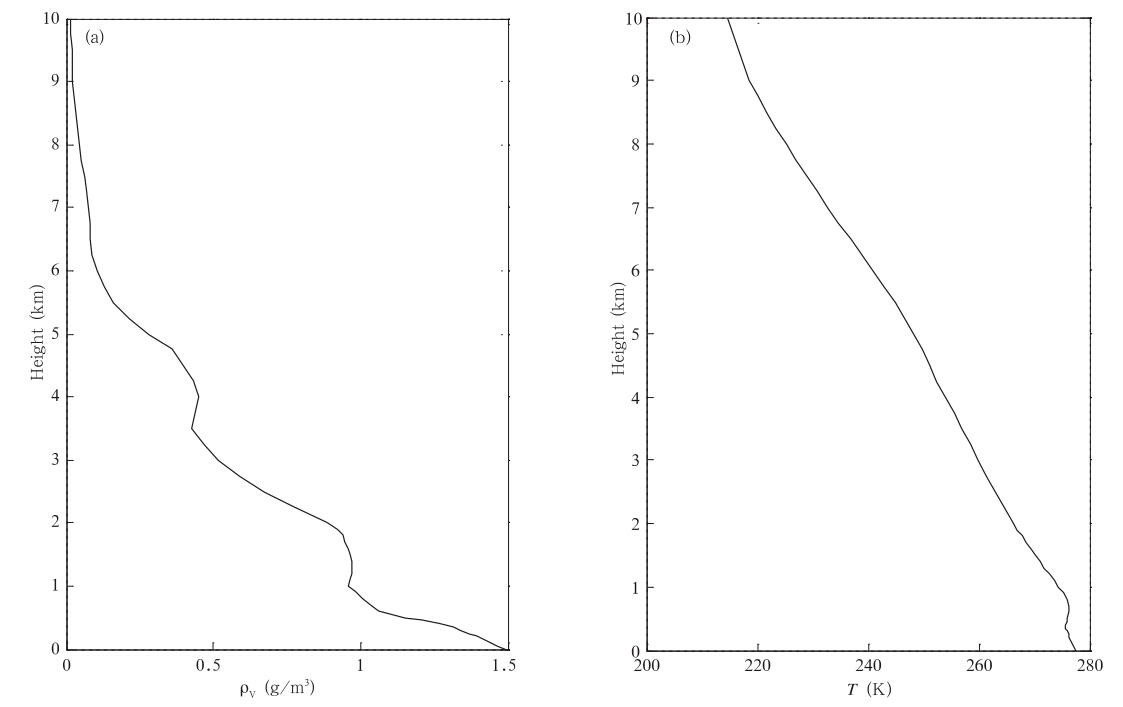 |
| 图 6 2011年3月10日00时的大气温湿廓线(a.绝对湿度,b.温度)Fig. 6 Temperature and humidity profiles at 00:00 UTC 10 March 2011(a.absolute humidity,b.temperature) |
为检验一维变分算法应用于地基微波辐射计遥感大气状态信息的可行性,利用无云条件下的探空数据进行了模拟试验。
将2011年3、4和12月无云条件下的探空数据代入到辐射传输模式计算得到的模拟亮温作为y,其他参数按照3.2节设置。图 7为2011年12月24日12时模拟试验反演结果,其中NCEP再分析数据作为背景场和初始场。对于温度廓线,可以看出NCEP再分析数据和探空数据在0—3 km相差较大,且越接近地面偏差越大,约4 K;一维变分反演的温度廓线在 0—3 km偏离NCEP数据,与探空更加一致,说明在迭代计算过程中温度廓线不断从初始场向真实大气逼近;3 km以上反演结果与NCEP温度廓线较为接近,虽有较小的调整,但没有低空明显,这是因为地基微波辐射计的观测亮温主要携带的是低空大气温度的信息(图 5b),且背景场误差协方差矩阵中低空的误差较大,因此,一维变分算法对低空的温度调整较多。对于绝对湿度廓线,NCEP数据和探空在0—10 km有较大的偏差,而反演得到的湿度廓线与探空数据较为吻合,说明一维变分算法对初始湿度廓线的各高度层都有优化,从绝对湿度的雅克比矩阵也可以看出,地基微波辐射计对不同高度处的湿度变化都有一定的敏感性。总之,一维变分算法能够不断地调整初始场,使反演结果最可能地接近真实值。
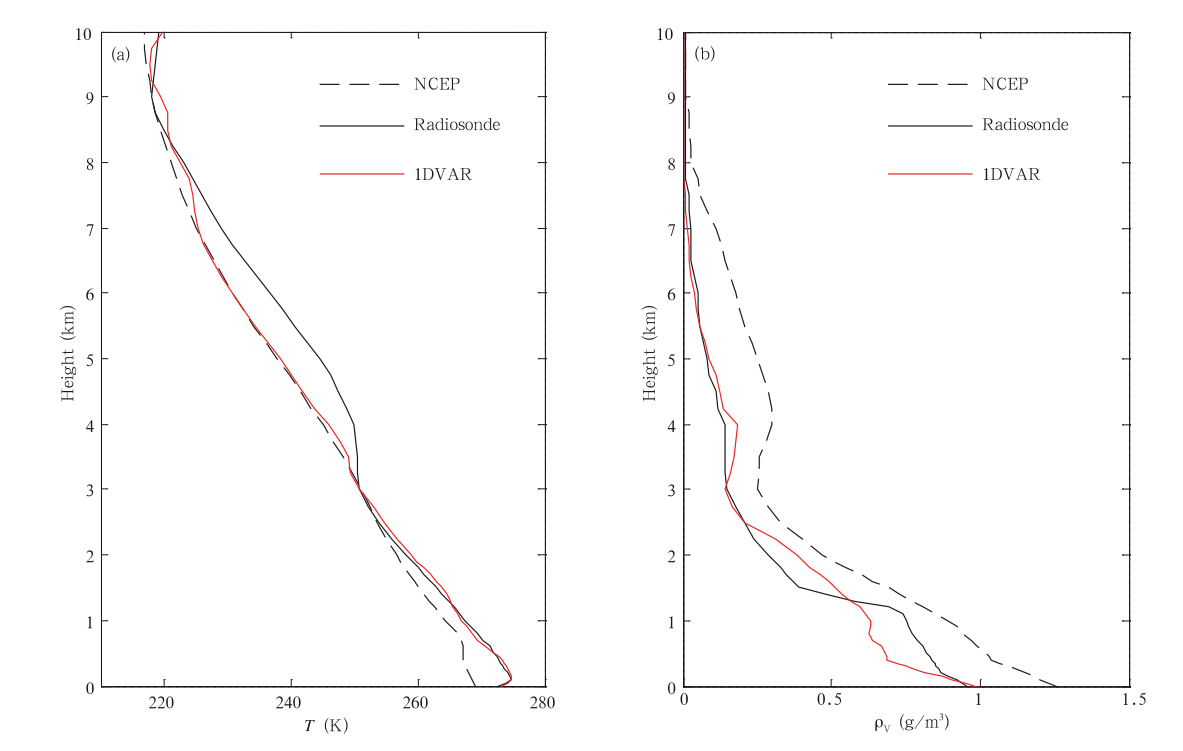 |
| 图 7 2011年12月24日12时模拟试验反演结果(a.温度廓线,b.绝对湿度廓线)Fig. 7 Retrieval results from the simulative experiment at 12:00 UTC 24 December 2011(a.temperature profiles,b.absolute humidity profiles) |
为了进一步估计一维变分算法的反演精度,对所有模拟样本的反演结果进行了统计,分别计算NCEP再分析数据、一维变分反演结果与探空数据的平均误差(ME)及均方根误差(RMSE)(图 8)。就温度廓线而言,一维变分反演的温度廓线与探空数据的平均误差和均方根误差均比NCEP数据的小,在3 km以下尤为明显,近地面误差减小了近4 K,3 km以上两者较接近,因此一维变分算法仅对0—3 km温度廓线的反演有影响,而3 km以上反演结果好坏主要依赖于初始场。0.5 km 以下,一维变分反演得到的温度廓线与探空数据的均方根误差小于1 K,0.5—3 km小于2 K,3—10 km小于2.8 K;对于湿度廓线,与温度廓线类似,在整个大气层中一维变分反演的绝对湿度廓线与探空数据的平均误差和均方根误差都比NCEP数据的小,且平均误差的绝对值小于0.15 g/m3,均方根误差小于0.4 g/m3。
通过模拟试验可知,利用一维变分算法反演大气温、湿度廓线是可行的,且反演精度在可接受的范围内,这为用实际观测资料进行温、湿度廓线反演提供了保障。
 |
| 图 8 模拟试验反演结果的误差统计(a.温度,b.绝对湿度;NCEP(黑色)和一维变分反演结果(红色)分别与探空数据的平均误差廓线(实线)和均方根误差廓线(虚线))Fig. 8 Error statistics of the retrieval results from the simulative experiment(a.temperature,b.absolute humidity; profiles of ME(solid) and RMSE(dashed)of NCEP(black) and 1DVAR retrievals(red)respectively with respect to radiosonde data) |
基于上面的模拟试验,利用一维变分算法分别对订正前的观测亮温(TBM)和订正后的观测亮温(TBO)进行温、湿度廓线的反演,关于反演参数的设置,与模拟试验不同的只有观测向量y,并将一维变分算法的反演结果和微波辐射计自带神经网络的反演结果分别与探空数据对比计算平均误差及均方根误差,以便比较两种算法的反演能力。考虑到搬迁后地基微波辐射计的位置离探空站较远,探空数据已不能代表地基微波辐射计所在位置的真实大气,因此仅对搬迁前(3、4月)52个无云样本的反演效果进行分析。
从2011年3月17日12时温度和绝对湿度廓线的反演结果(图 9)可以看出,相比神经网络反演的温、湿度廓线,一维变分的反演结果与探空数据更加一致,且分别对订正前、后的观测亮温进行反演,而得到的结果差别不大,其中温度廓线已基本重合。从图 10a可以看出,在观测亮温订正前后,一维变分反演的温度廓线的平均误差基本一致,其绝对值小于1 K,均方根误差也基本一致,小于2.9 K;而神经网络反演的温度廓线的平均误差绝对值小于2.4 K,均方根误差小于3.5 K,因此一维变分反演的温度廓线更接近探空值。从图 10b可以看出,观测亮温订正前,一维变分算法反演的湿度廓线的平均误差绝对值小于0.13 g/m3,均方根误差小于0.47 g/m3;观测亮温订正后,一维变分反演的湿度廓线误差有所减小,平均误差绝对值小于0.11 g/m3,均方根误差小于0.35 g/m3;神经网络反演的湿度廓线的平均误差绝对值小于0.15 g/m3,均方根误差小于0.56 g/m3,一维变分反演的湿度廓线也稍优于神经网络反演的湿度廓线。
 |
| 图 9 2011年3月17日12时反演结果(a.温度廓线,b.绝对湿度廓线;黑实线表示探空数据,蓝实线表示一维变分算法对订正前的观测亮温进行反演的结果,红实线表示一维变分算法对订正后的观测亮温进行反演的结果,绿实线表示辐射计自带神经网络算法的反演结果)Fig. 9 Retrieval results at 12:00 UTC 17 March 2011(a.temperature profiles,b.absolute humidity profiles; radiosonde data(black solid),1DVAR retrievals from TBM(blue solid),1DVAR retrievals from TBO(red solid),NN retrievals from TBM(green solid)) |
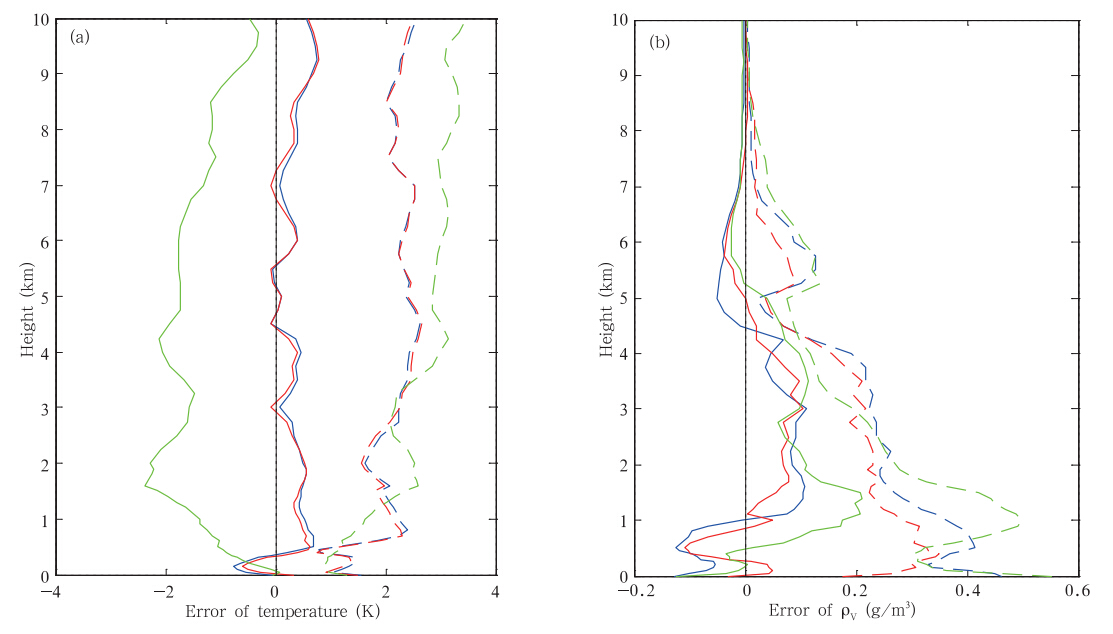 |
| 图 10 搬迁前(3、4月)反演结果误差统计(a.温度,b.绝对湿度; 一维变分算法对订正前的观测亮温进行反演的结果(蓝色)、一维变分算法对订正后的观测亮温进行反演的结果(红色)和辐射计自带神经网络的反演结果(绿色)分别与探空数据的平均误差廓线(实线)和均方根误差廓线(虚线))Fig. 10 Error statistics of retrieval results before “moving”(in March and April)(a.temperature,b.absolute humidity; profiles of ME(solid) and RMSE(dashed)of 1DVAR retrievals from TBM(blue),1DVAR retrievals from TBO(red) and NN retrievals from TBM(green)respectively with respect to radiosonde data) |
从上述结果可知,是否对搬迁前的观测亮温进行订正,对反演结果的影响并不是很大。分析其原因可能是3、4月为在液氮定标后、搬迁之前,属于地基微波辐射计的最佳工作时期,另外,由于搬迁前的地基微波辐射计离探空站较近,用探空资料模拟得到的亮温对观测亮温进行线性订正,对观测亮温的调整甚微,基本不会改变其所携带的大气状态信息。为了进一步验证,利用一维变分算法对搬迁后(12月)订正前、后的观测亮温进行了反演(图 11、12)。从图 11可以看出,一维变分对订正后的观测亮温反演得到的温度和绝对湿度廓线与探空数据较为接近,而对订正前的观测亮温反演得到的结果在低空与神经网络结果较为接近,说明是否对搬迁后的观测亮温进行订正,对反演结果的影响很大。地基微波辐射计搬迁后,探空站离其较远,以模拟亮温为参考对搬迁后观测亮温进行订正,使得订正后观测亮温携带的是探空站所在位置的大气信息,因此对其进行反演得到的结果与探空数据较为接近,而订正前的观测亮温所携带是搬迁后地基微波辐射计所在位置的大气信息,因此反演的结果与自带神经网络算法结果较为一致。从图 12的统计结果也可以看出同样的结果,另外,对观测亮温订正后,一维变分反演的温度廓线的均方根误差小于3 K,绝对湿度的均方根误差小于0.33 g/m3。
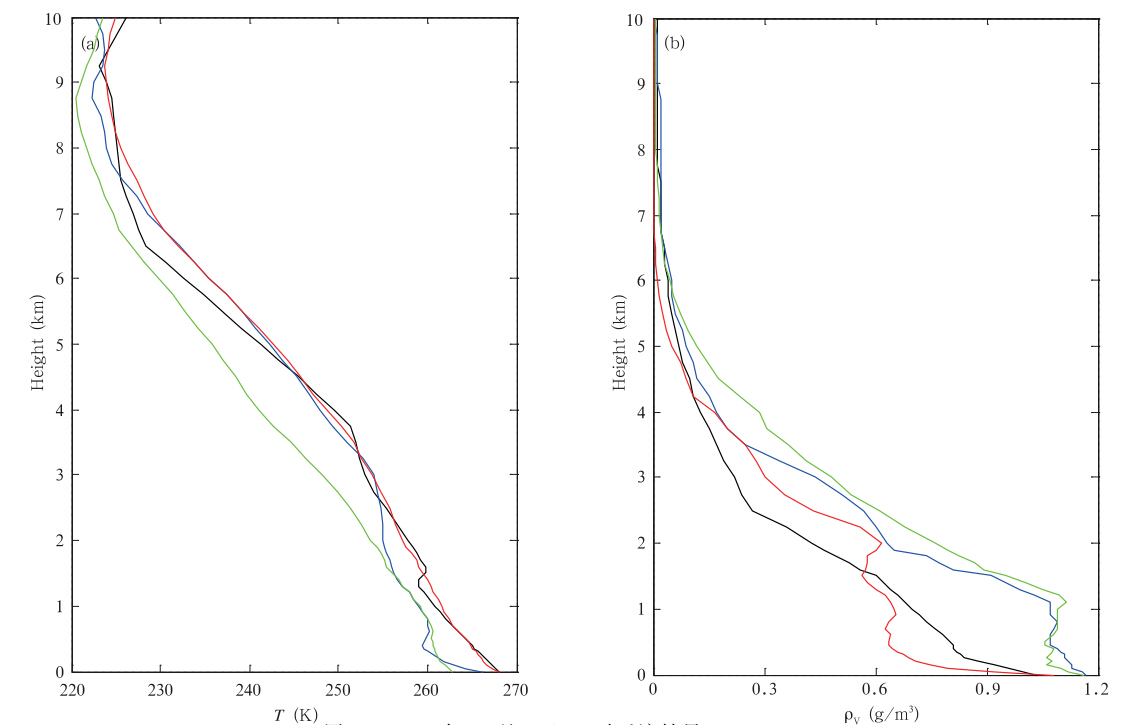 |
| 图 11 2011年12月9日00时反演结果(说明同图 9)Fig. 11 As in Fig. 9 but at 00:00 UTC 9 December 2011 |
 |
| 图 12 搬迁后(12月)反演结果误差统计(说明同图 10)Fig. 12 As in Fig. 10 but after “moving”(in December) |
通过对北京地区2010—2011年00和12时的多通道地基微波辐射的观测亮温进行提取无云样本和质量控制两步预处理,并利用一维变分反演算法对亮温进行温、湿度廓线反演,得到以下结论:
(1)可以通过寻找红外亮温阈值来确定地基微波辐射计上空是有云还是无云,针对本研究所用微波辐射计,确定红外亮温阈值为225 K,考虑到云的局地差异,利用探空数据的“相对湿度<85%”这一条件对无云样本做进一步约束,最终得到432个无云样本。
(2)以探空数据代入辐射传输模式计算得到的模拟亮温为参考,对无云条件下的地基微波辐射计观测亮温进行去“奇点”和线性订正两步质量控制,质量控制后各通道的观测亮温与模拟亮温更加一致,基本解决由于“定标”和“搬迁”引起的数据不连续的问题。
(3)利用无线电探空数据进行模拟试验,结果表明,一维变分算法能够在迭代计算过程中不断调整初始场,使得反演结果最接近于真实大气,其中,对温度廓线在0—3 km高度调整较为明显,而对绝对湿度廓线在0—10 km高度都有一定的调整;与探空数据相比,在0—10 km高度一维变分反演的温度廓线的均方根误差小于2.8 K,绝对湿度廓线的均方根误差小于0.4 g/m3。
(4)利用一维变分算法分别对2011年搬迁前、后的TBM和TBO进行温、湿度廓线的实际反演,将结果与探空进行对比分析发现:在搬迁前,是否对观测数据进行订正,对一维变分的反演结果影响不是很大,这是因为地基微波辐射计工作状态较佳且探空站离其较近;与神经网络反演结果对比发现,一维变分的反演误差小于神经网络。
值得注意的是,一维变分算法反演大气温、湿度廓线结果的好坏,很大程度上依赖于初始场,尤其是温度廓线,所以寻找较好的初始场对该算法意义重大;另外,本研究仅对无云条件下的观测亮温进行了反演,并未考察有云条件下一维变分算法的反演效果,这也是以后工作需要完善之处。
致谢:感谢中国气象局北京城市气象研究所提供2010—2011年每天00和12时的地基微波辐射计亮温观测数据,感谢该所楚艳丽、李炬、刘红燕、阮顺贤、曹晓彦和北京市气象局保障中心沈永海等老师提供的帮助。特别感谢城市所楚艳丽老师对论文的指导。
| 黄润恒, 邹寿祥. 1987. 两波段微波辐射计遥感云天大气的可降水和液态水. 大气科学, 11(4): 397-403 |
| 刘亚亚, 毛节泰, 刘钧. 2010. 地基微波辐射计遥感大气廓线的BP神经网络反演方法研究. 高原气象, 29(6): 1514-1523 |
| 李青, 胡方超, 楚艳丽等. 2014. 北京一地基微波辐射计的观测数据一致性分析和订正实验. 遥感技术与应用,29(4) |
| 盛裴轩, 毛节泰, 李建国等. 2003. 大气物理学. 北京: 北京大学出版社, 20-23 |
| 唐仁茂, 李德俊, 向玉春等. 2012. 地基微波辐射计对咸宁一次冰雹天气过程的监测分析. 气象学报, 70(4): 806-813 |
| 王华荣, 郁凡, 桂海林. 2005. GMS-5反演湿度场的一维变分质量控制实验. 气象学报, 63(3): 342-350 |
| 王建, 吕新生, 赵克朋等. 2012. 地基微波辐射计对乌鲁木齐暴雨天气过程的观测分析. 沙漠与绿洲气象, 6(3): 45-49 |
| 王叶红, 赖安伟, 赵玉春. 2010. 地基微波辐射计资料同化对一次特大暴雨过程影响的数值试验研究. 暴雨灾害, 29(3): 201-207 |
| 王叶红, 赖安伟, 赵玉春. 2012. 降水资料同化在梅雨锋特大暴雨个例模拟中的应用研究. 气象学报, 70(3): 402-417 |
| 王振会. 1988. 大气温度分布的地面微波遥感数值试验. 南京气象学院学报, 11(3): 346-355 |
| 王振会, 徐培源, 邓军等. 1995. 三通道微波辐射计遥感大气中水汽、液水和电长度增量的数值实验. 南京气象学院学报, 18(3): 396-403 |
| 伊里哈木, 王秋香, 贺晓东等. 2009. L 波段与 59-701 系统高空对比观测资料特征分析. 沙漠与绿洲气象, 3(5): 50-53 |
| 赵兵科, 邵德民, 鲁小琴等. 2009. 多通道地基微波辐射计在0713号"韦帕"台风登陆先后探测性能及特征分析. 地球科学进展, 24(9): 1001-1008 |
| Chan P W. 2009. Performance and application of a multi-wavelength, ground-based microwave radiometer in intense convective weather. Meteor Z, 18(3): 253-265 |
| Cimini D, Hewison T J, Martin T, et al. 2006. Temperature and humidity profile retrievals from ground-based microwave radiometers during TUC. Meteorol Z, 15(5): 45-56 |
| Cimini D, Westwater E R, Gasiewski A J. 2010. Temperature and humidity profiling in the Arctic using ground-based millimeter-wave radiometry and 1DVAR. IEEE Trans Geos Remote Sens, 48(3): 1381-1388 |
| Deblonde G, English S J. 2003. One-dimensional variational retrievals from SSMIS:Simulated observations. J Appl Meteor, 42(10): 1406-1420 |
| English S J. 1999. Estimation of temperature and humidity profile information from microwave radiances over different surface types. J Appl Meteor, 38(10): 1526-1541 |
| Güldner J, Spnkuch D. 2001. Remote sensing of the thermodynamic state of the atmospheric boundary layer by ground-based microwave radiometry. J Atmos Ocean Technol, 18(6): 925-933 |
| Hewison T J. 2007. 1D-VAR retrievals of temperature and humidity profiles from a ground-based microwave radiometer. IEEE Trans Geosci Remote Sens, 45(7): 2163-2168 |
| Knupp K R, Coleman T, Phillips D, et al. 2009. Ground-based passive microwave profiling during dynamic weather conditions. J Atmos Ocean Technol, 26(6): 1057-1073 |
| Liebe H J, Rosenkranz P W, Hufford G A. 1992. Atmospheric 60-GHz oxygen spectrum: New laboratory measurements and line parameters. J Quant Spectrosc Rad Transfer, 48(5-6): 629-643 |
| Rodgers C D. 2000. Inverse Methods for Atmospheric Sounding: Theory and Practice. Singapore: World Scientific, 22-97 |
| Solheim F, Godwin J R, Westwater E R, et al. 1998. Radiometric profiling of temperature, water vapor and cloud liquid water using various inversion methods. Radio Sci, 33(2): 393-404 |
| Westwater E R, Wang Z H, Grody N C, et al. 1985. Remote sensing of temperature profiles from a combination of observations from the satellite-based microwave sounding unit and the ground-based profiler. J Atmos Ocean Technol, 2(2): 97-109 |
 2014, Vol. 72
2014, Vol. 72