中国气象学会主办。
文章信息
- 周生辉, 魏鸣, 张培昌, 徐洪雄, 赵畅. 2014.
- ZHOU Shenghui, WEI Ming, ZHANG Peichang, XU Hongxiong, ZHAO Chang. 2014.
- 单多普勒天气雷达反演降水粒子垂直速度Ⅰ:算法分析
- The precipitation particles’ vertical velocity retrieval with single Doppler weather radar. PartⅠ: Retrieval method’s analysis
- 气象学报, 72(4): 760-771
- Acta Meteorologica Sinica, 72(4): 760-771.
- http://dx.doi.org/10.11676/qxxb2014.053
-
文章历史
- 收稿日期:2013-12-30
- 改回日期:2014-4-28
2. 灾害天气国家重点实验室, 中国气象科学研究院, 北京, 100081
2. State Key Laboratory of Severe Weather, Chinese Academy of Meteorological Sciences, Beijing 100081, China
多普勒雷达是探测中小尺度降水的重要手段,有助于了解降水区内的风场结构。多普勒雷达探测的径向速度包含了水平风场和垂直风场信息,由于其仅探测径向速度分布,而不能直接得到三维风场结构的信息,所以理论上直接获取大气的三维风场结构至少需要3部雷达同时探测(Armijo,1969; Miller et al,1974),但多部雷达联合探测需要同步观测区域,这种探测模式不仅耗资巨大,而且探测的范围有限。在利用单多普勒天气雷达反演风场的研究中,Lhermitte 等(1961)提出了基于均匀风场假设下的速度方位显示(VAD)方法,但VAD方法的风场模型不适用于复杂风场的反演,为了能够得到更多的风场信息和更精细的风场结构,随后相继出现了VARD(Velocity area display)(Easterbrook,1975),体积速度处理(Volum Velcaty Processing,VVP)(Waldteufel et al,1979),EVAD(Extend-VAD)(Srivastava et al,1986; Matejka et al,1991),VAP(Velocity-azimuth processing)(陶祖钰,1992),CEVAD(Concurrent extend-VAD)(Matejka,1993),涡度-散度法(姜海燕等,1997),AVAD(Airbone-VAD)(Leon et al,1998),TREC(Tracking radar echo by correlation)(Tuttle et al,1999),VPP(Velocity Plan Processing)(郎需兴等,2001),GVAD(Gao et al,2004),T-IVAP(Integrating VAP)(Liang,2007),EVPP(Extended VPP)(方德贤等,2007),TREC(Typhoon circulation TREC)(王明筠等,2010),反演热带气旋近中心风场的VAP扩展应用方法(罗昌荣等,2011),反射率因子和径向速度共同约束法(韩丰等,2013)等基于各种简单假设下的风场反演算法。
假设风场满足运动学或动力学规律而构建的三维或四维变分反演方法可以同时使用多部多普勒雷达的观测数据。在变分方法中不仅可以融合多种观测资料作为背景场,而且还可以将动力学方程或者诊断方程作为约束条件。因而部分非观测的大气参量与小尺度的大气结构都可通过反演得到(Gao et al,1999,2006; Huang et al,2010; Protat et al,1999; Qiu et al,1992; Rihan et al,2005; Shapiro et al,1995,2003,2009; Sun et al,1997; Sun,1998; Liu et al,2005; Weygandt et al,2002)。但由于观测误差与约束方程引入的模型误差等因素的影响,变分方法的泛函数在选取合适的权重系数时仍存在困难(Shapiro et al,2009)。若风场模型存在偏差,如风场结构在雷达扫描过程中不变的假设不成立时,反演的精度会大幅度降低。对于早期利用单多普勒雷达反演风场的方法,主要是基于简单风场模型假设提出的。因此在处理简单风场时,往往能得到较好的反演效果(Shapiro et al,1995)。另外,简单风场模型得到的反演结果,还可以作为变分方法的初始条件。在实际业务应用中,如变分方法等算法由于计算过程较复杂、耗时相对较多也限制了其使用(Caya et al,2002; Gao et al,2006)。另外,多普勒雷达网间距较大,能够实现多部雷达联合观测的区域有限,因而利用简单风场假设的单多普勒雷达反演方法,在实时分析天气过程中仍有优势。
由于风场模型的假设条件不同,各种反演方法的适用范围也不同,实际应用中大多数反演算法在低仰角的二维水平风场反演中,往往忽略垂直速度对反演精度的影响。相比其他反演算法,基于线性风场假设的体积速度处理(VVP)算法可以较好地描述真实风场,使用体积扫描资料能够得到较多的三维风场信息,因此在国际上被广泛应用。但VVP方法包含的待反演参量较多,反演过程中系数矩阵的病态问题会造成求解困难,使反演结果的误差较大,甚至不能直接求解。针对这种求解时遇到的困难,一般的做法是减少反演参数的个数以降低计算难度(Xin et al,1998; Holleman,2005),这样的处理不仅能求解,而且可使解更稳定。在算法求解方面的研究中,Waldteufel等(1979)根据反演参量的量级大小,选择舍弃了较小的量,简化了求解矩阵。Boccippio(1995)选取了其中6个参量,应用奇异矩阵分解的方法进行反演,同时对忽略其他变量进行了敏感试验,指出被忽略的变量在反演时会成为潜在的误差来源。魏鸣(1998)对系数矩阵的特点进行了分析,指出反演垂直速度中的病态矩阵问题,用矩阵平衡的方法减少条件数,并根据共轭梯度算法迭代求解。Li 等(2007)提出了分步计算的方法,先求出均匀风场下的反演结果,然后通过风场参量之间的假设关系进一步得出其他参量。
虽然通过VVP反演方法理论上可以得到丰富完整的三维风场信息,但反演时风场模型的完整性与系数矩阵的复杂程度会明显影响反演结果,因而也限制了对垂直速度的反演。当建立风场模型选取较多的反演参数时,虽然减小了模型误差的影响(王鹏飞等,2011),但VVP算法中由于复杂系数矩阵的条件数过多,会将计算误差与观测误差放大而影响反演精度。同样,若选取较少的反演参数,虽可避免因条件数过多引起的计算误差,但由于风场模型过于简单,也会限制其在复杂风场反演中的应用。由系数矩阵对反演精度的影响,已有研究指出系数矩阵中基函数的线性相关是造成矩阵病态的原因(Boccippio,1995; Waldteufel et al,1979),但线性相关的项及其成因并未确定。
本研究从数学上分析和论证了造成系数矩阵病态的原因,针对垂直速度的反演,提出了改进的VVP算法,并验证了求解方程。2 VVP算法及系数矩阵病态的原因2.1 VVP算法简介
VVP算法利用多普勒天气雷达多个PPI(plane position indicator)扫描资料进行反演,将径向、切向和垂直方向构成的一个三维空间作为分析体积(Waldteufel et al,1979)。由于选取的分析对象是一个三维的空间区域,因而适用于高仰角的情况。在选定的分析体积中假设:(1)风场结构呈线性分布,(2)在雷达扫描期间风场不随时间变化。
在直角坐标系中以雷达为原点,分析体积的中心坐标为(x0,y0,z0),并认为降水粒子(以下简称粒子)的水平速度等于风场的水平速度,分析体积中心的粒子速度大小为V=(u0,v0,w0),则分析体积内各点的粒子速度大小可表示为
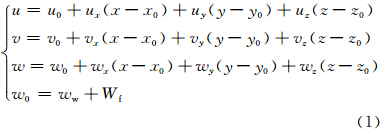
由风场在雷达径向上的投影关系,雷达观测到的径向速度为
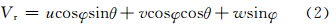
由于多普勒雷达探测到的是降水粒子的有效回波,当粒子的尺寸较小时,粒子的运动状态可认为是大气的状态。而当粒子脱离大气开始下落后,粒子的垂直速度则为大气的垂直速度与粒子下落速度之和。而在建立反演风场的算法模型时,将粒子下落末速度这一常量与垂直风速ww合并,仍将式(1)中的参量(u0,v0,w0,ux,uy,uz,vx,vy,vz,wx,wy,wz)作为风场模型的待反演参量,对应式(2)中的系数分别为
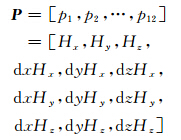
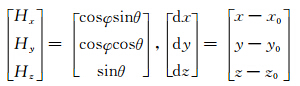


将式(3)简化,在一个分析体积内,则有


式中,A为反演算法中的系数矩阵,N为分析体积内格点数,Vri为每个格点上的径向速度值。通过求解式(4)即可得到各风场参量。2.2 误差因素对反演精度的影响
从误差分析的角度来看,在反演过程中影响结果精度的误差可概括为:(1)建立风场模型时,因数学模型不准确(忽略了次要因素)造成的误差,此为“模型误差”;(2)观测得到的模型参数(坐标值)或者初始数据(径向风速)带有的误差,此为“观测误差”;(3)在求解时,由于计算方式和计算机精度造成的误差,此为“计算误差”(王鹏飞等,2011)。
在计算机精度限制的情况下,系数矩阵的阶数越高、条件数越多、计算机字长越短,则舍入误差对解的影响越大。因而求解精度受限于矩阵的规模、矩阵的性态、选取的算法和计算机精度等因素。因此,系数矩阵运算时的复杂度越高,通过式(5)直接求解时反演结果的误差就会越大(Ward,1977; Fischer,2014)。将反演计算过程中的计算误差等因素归纳为系数矩阵的误差,并同时考虑存在观测误差,求解方程可以表示为
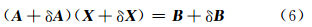
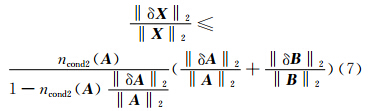
但若假设条件不成立时,利用式(7)对误差范数的估计也就不再合适。因此,将带有误差的系数矩阵作为分析对象时,令

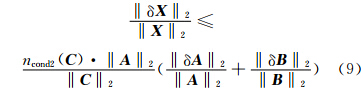
由式(6)中δA的构成可知,由于雷达探测能力的限制,雷达方位角、距离库等观测误差会引入到求解的矩阵方程中;另外,当风场模型不准确时,选取的待反演量不完整也会造成模型误差。所以,不考虑计算误差时,反演结果求解的难易程度和精度主要取决于选取的系数矩阵和雷达的探测能力两个方面。通过误差范数上界的估计可以发现,选取合适的系数矩阵(C)不仅可以提高求解的精度,而且可以降低求解难度。较大的矩阵条件数不仅使求解计算的难度增大,并且会将误差等因素的影响放大,使最终结果变差。由式(9)可知,当选取较少反演参量时,虽引入了模型误差,但在一定程度上对系数矩阵改善可以抵消模型误差造成的影响,即选取较少反演参数时,反演结果往往会比反演较多参数时的效果好。2.3 系数矩阵的条件数
为比较选取不同的风场模型时系数矩阵条件数的差异,将式(1)中的待反演参量进行分组(表 1)。根据参量量级的大小来分组(Waldteufel et al,1979),通过逐渐增加待反演参量的个数,来构建含有不同参量的系数矩阵。
| 组 | 参数 | 组 | 参数 | 组 | 参数 |
| 3P | u0,v0,w0 | 5P2 | 3P+(uy,vx) | 9P1 | 7P+(wx,wy) |
| 4P1 | u0,v0,ux,vy | 6P1 | 3P+(ux,vy,wz) | 9P2 | 7P+(uz,vz) |
| 4P2 | u0,v0,uy,vx | 6P2 | 4P1+(uy,vx) | 11P | 7P+(wx,wy,uz,vz) |
| 5P1 | 3P+(ux,vy) | 7P | 3P+(ux,vy,uy,vx) | 12P | All |
由条件数本身的特点可知,条件数是对计算难易程度的一种衡量,也代表了解对误差或是不确定度的敏感性,条件数越大,代表求解的问题越病态。同理,在VVP的反演算法中,系数矩阵的条件数越大,说明反演结果越不稳定,误差会越大。
从条件数大小的分布变化(图 1)可以看出:
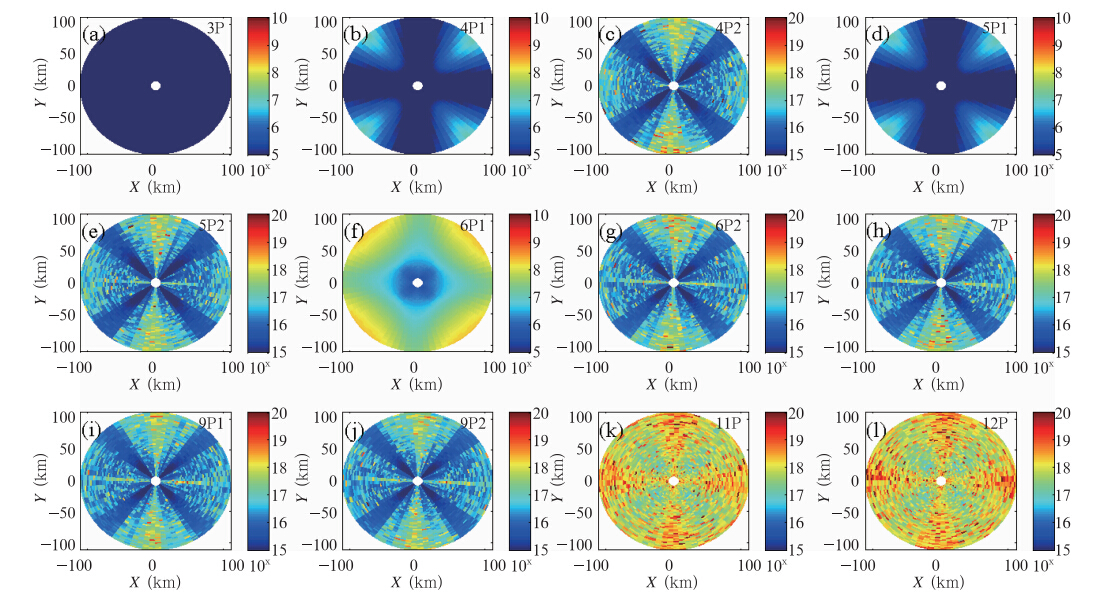 |
| 图 1 不同反演参数对应的系数矩阵的条件数(分析体积:10°×20 Gates;仰角:2.5°;a—l的系数矩阵分组见表 1) Fig. 1 Variations of coefficient matrix condition number with the different retrieved parameters. The size of analysis volume is specified as the sector gap of 10°×20 gates for each radial. The elevation is 2.5°. The grouped retrieved parameters of(a)-(l)are shown in Table 1 |
(2)当待反演参数不同时,系数矩阵条件数差别较大。通过观察4P2、5P2、6P2的条件数分布可以发现,含有uy、vx的系数矩阵的条件数远大于4P1、5P1、6P1的条件数。同样通过观察11P、12P的条件数也可以发现,加入wx、wy后的条件数比其他分组大出许多量级。由此也可说明,风场模型直接决定了反演计算的精度和求解的难易程度。
(3)在不同方位角、距离雷达不同的位置,系数矩阵的条件数亦不相同。4P1、5P1、6P1在方位角为45°、135°、225°、315°附近的条件数大于其他位置,并且随着距离雷达中心越远,半径越大处条件数越大。而4P2、5P2、6P2在上述位置的条件数相对较小,但在方位角为0°、90°、180°、270°附近的条件数相对较大。通过计算矩阵矢量的相关性发现(图略),上述位置处的相关系数大于其他方位角处。因此可以判断,矩阵矢量的线性相关,造成了系数矩阵病态。2.4 系数矩阵病态原因的分析
在已有研究成果(Boccippio,1995; Waldteufel et al,1979)中曾指出,系数矩阵中基函数的线性相关可能是造成矩阵病态的原因,但线性相关的项及其函数关系仍未确定。由图 1中系数矩阵条件数的变化可以发现,含有uy、vx与wx、wy的系数矩阵相比于其他参量组合,条件数会有较大的增加,因此需将这两组参数对应的矩阵矢量进行比较分析。
以uy、vx的系数dyHx、dxHy为例,与其他任意待反演参量Hm构成的系数矩阵为
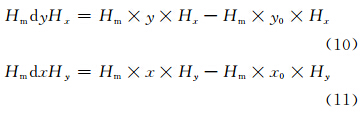
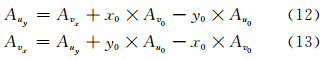
因此可知,同时含有uy与vx的矩阵矢量,其系数矩阵是奇异的。当含有部分参量时,矩阵矢量的这种线性关系会使得系数矩阵奇异,由此可以解释和证明图 1c中4P2组的条件数较大的原因。而在利用计算机计算时,由于实际反演中观测误差和计算误差的影响,系数矩阵表现出的病态只是计算的结果。
同理可知,同时含有uz、wx与vz、wy对应的矩阵矢量时,系数矩阵同样是奇异的,证明过程不再赘述。 3 舍弃参量对反演结果的敏感性
在利用VVP方法反演求解过程中,当系数矩阵A的条件数过大时,会造成求解困难,反演误差较大。为了简化求解步骤,降低求解难度,往往选取其中几个变量进行求解。Waldteufel等(1979)通过对比各反演参量的量级大小,选取了在实际风场中量值较大的参量来构成系数矩阵。Boccippio(1995)通过敏感试验计算了舍去某些反演参量后的结果误差,指出分析体积的大小、位置和待反演量的线性相关性等多种因素都会对反演结果产生影响。为了便于观察舍弃参量对求解的影响,令风场模型参量及其对应的矩阵矢量为
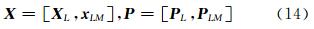
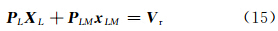
当舍弃部分反演参量后,反演结果的误差大小为
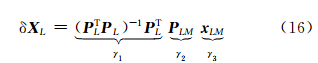
观察上式可以发现,由于求解计算中的系数矩阵为位置坐标的函数,因此当选取的反演参量不完全时,产生的误差大小取决于舍弃参量的大小xLM和其对应的系数矩阵PLM。所以,选择舍弃量级较小的参量对反演效果的影响将会相对较小。
同理可知,被忽略的量xLj对Xi造成的误差δXi,Lj可表示为
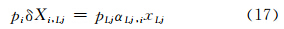
令,δXi,Lj=ξLjxLj,则有
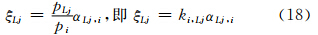
选用表 1中的5P1模型来构建模拟风场,其中径向风场共10层,每层仰角间隔1°;方位角个数为360个,间隔1°;每条径向有460个距离库,库长为250 m,分析体积大小为20°×40个距离库×两层仰角。模拟风场的参数设置如表 2所示,其中将ux与vy设置为相等大小,同时垂直速度设定为固定值,依此来观察在不同位置处舍弃参量对反演效果的影响。
| 名称 | 参量值 |
| u0,v0 | 3.0 m/s,2.0 m/s |
| ux,vy | -0.3 s-1,0.3 s-1 |
| x0,y0,z0 | 0,0,0 |
| w0 | 1.0 m/s |
如表 3所示,尽管模拟风场中ux与vy的值是相同的,但在反演中分别舍弃ux或vy时,首先可以发现反演结果在不同方位角处的不同,另外,对比两组结果还可以看到,在相同方位角处反演结果的误差也不相等。通过比较反演结果误差的大小可知,ξw的绝对值越小,则反演得到的垂直速度误差越小,如在方位角45°时的ξw在舍弃vy与ux分别为-0.06和-0.14,而垂直速度的反演结果误差45°时也为最小,由此也验证了上述的分析结果。
| 5° | 15° | 30° | 45° | 60° | 75° | 90° | ||
| vy | w(m/s) | 2.19 | 2.47 | 1.61 | 1.01 | 0.80 | 0.72 | 0.70 |
| ξw | -3.97 | -4.91 | -2.04 | -0.06 | 0.65 | 0.93 | 1.00 | |
| ux | w(m/s) | 0.70 | 0.73 | 0.81 | 1.04 | 1.67 | 2.47 | 2.09 |
| ξw | 0.99 | 0.92 | 0.62 | -0.14 | -2.25 | -4.91 | -3.65 |
由于真实的风场中大气垂直速度的量级小,对雷达径向风速的贡献也小,因而也增加了反演垂直速度的难度,风场反演中为了简化求解方程往往将其忽略(Gao et al,2004; Li et al,2007)。在垂直速度的风场反演方法中,基于动力学方程的变分反演方法,可以根据多个时次的观测资料求解出垂直速度,但变分方法所依赖大气动力学方程仍是真实风场的理想模型,并对背景场和代价函数中的权重系数较为敏感(Wei et al,1998; Gao et al,2006; Shapiro et al,2003,2009; Huang et al,2010)。相比之下,基于空间几何方法的VVP算法具有统计学特征,能够利用空间多个格点上的风场信息,并且风场模型的参量不依赖权重系数,反演结果比较客观。
在建立风场模型时为了更好地描述真实的风场,风场模型中需尽可能选择较多的参量。但由2.4节中对VVP系数矩阵病态原因的分析和论证可知,矩阵矢量之间的线性关系会造成矩阵奇异和求解困难,若舍弃部分相关的参量又会引入模型误差。由此可判断,为避免求解困难而选择舍弃部分参量的情况下,如能将反演结果再修正,即可得到准确的风场参量。4.1 对求解方程的分析
由实际风场的连续性特点,假定在一个小的分析体积内风场变化不太大,并考虑到风场模型要尽可能准确,同时尽量避免因系数矩阵矢量直接的线性关系而造成系数矩阵奇异,选择表 1中7P的风场模型进行分析。由表 1中7P模型的参量可知,该风场模型包括u0、v0、w0三个量级较大的分量与u、v在水平方向上的变化项ux、uy、vx、vy,并假设分析体积内垂直风速在水平方向上保持不变。观察式(1)不难发现,当(x0,y0,z0)为坐标原点时,即将风场的“起点”设定在坐标原点,(u0,v0,w0)则为雷达处的风场。因此,式(2)可写为

由式(19)可以看出,uy与vx此时合并为一个参量,因而其系数矩阵不再奇异,这可以降低求解的难度。同时注意,通过式(19)得到的uradar与vradar为风场模型中雷达处的值,并不是分析体积处的风场分量。因此,仍将(x0,y0,z0)选择在分析体积的中心,由第3节对系数矩阵的分析可知,同时含有uy与vx的矩阵矢量会造成系数矩阵奇异,为此只选择uy与vx其中的一个,并观察反演结果的变化。待反演参量的分组见表 4。
| 组别 | 待反演参量 |
| 6PM | u0,v0,w0,ux,vy,uy+vx |
| 6PM1 | u0,v0,w0,ux,vy,uy |
| 6PM2 | u0,v0,w0,ux,vy,vx |
通过对比表 4中6PM、6PM1和6PM2的条件数可以发现(图略),这3种风场模型的系数矩阵的条件数相比7P减小许多量级。为验证上述推断和求解方程的普适性,选择6PM1中的参量作为待反演量,并对求解方程进行分析。
由式(19)可知,当选择6PM1的参数时,式(2)可变为
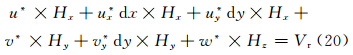
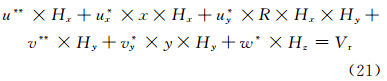
观察式(20)、(21)的系数项不难发现,两式解的形式相同,即
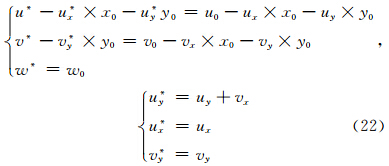
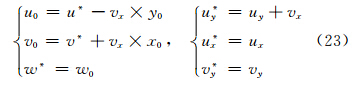
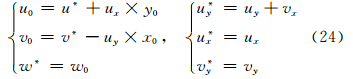
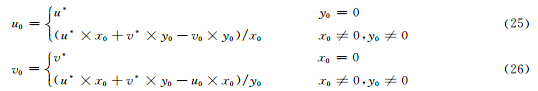
通过以上分析可知,由于系数矩阵中矩阵矢量存在线性相关,因而在选择风场模型时不能将VVP方法中的参量全部包含。但若风场模型对实际风场描述得不准确,这样又会引入模型误差。对于7P的风场模型而言,可以比较准确地描绘风场结构,符合实际的风场特征。但选择7P模型时系数矩阵却是奇异的,并且由于观测误差和计算误差的影响,使得在实际反演中看到的系数矩阵是病态的,因而反演结果的误差很大。倘若采用其他数学方法,如用奇异值分解(SVD)来求解(Boccippio,1995),计算的结果仍是通过对病态矩阵在数学上的近似处理后得到的,这种数学的近似处理方法仅避开了对病态矩阵直接求解,但待求方程中的参量因为矩阵奇异仍不能全部解出,并且还会引入计算误差。对SVD处理方法进一步分析可知,系数矩阵分解后可表示为

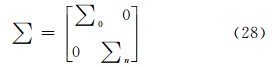
在计算中为了避免病态矩阵造成求解不稳定的问题,近似处理的方法是将∑n舍去。观察舍弃相对较小奇异值后的式(27)不难发现,舍弃奇异值只是对病态矩阵的近似处理,但对于本身就奇异的系数矩阵而言并没有实质性改变,因为被舍弃的奇异值对应的是奇异矩阵中为0的矩阵矢量。因而,这种处理方式的结果与舍弃uy或vx构建的系数矩阵等效,但后一种处理可以使用更准确的风场模型,并且避免引入新的计算误差。
由式(23)、(24)可知,由于缺少其他条件,u0与v0不能直接反演得到,但可以通过观测值或其他约束条件由式(25)或(26)解出u0或v0,从而进一步解出其他参量。另外,通过以上分析可以发现,虽然求解方程中舍弃了uy或vx,但风场模型仍为7P的模型,对求解方程的调整使反演结果中w0、ux与vy并不受影响,所以改进后的求解方程避免了系数矩阵奇异的问题,因而反演结果的精度得到提高,上述3个参量也可以得到较准确的值。4.2 模拟风场的检验
构建的模拟线性风场为:雷达探测的径向风场,共10层,每层仰角间隔1°;方位角个数为360个,间隔1°;每条径向有460个距离库,库长250 m;选取的分析体积大小为10°×20个距离库×两层仰角。7P的模拟风场中各参量的值如表 5。
| 名称 | 参量值 |
| u0,v0 | 3.0 m/s,2.0 m/s |
| ux,vy | -0.1 s-1,0.1 s-1 |
| uy,vx | -0.2 s-1,0.1 s-1 |
| x0,y0,z0 | 0,0,0 |
| w0 | 3.0 m/s |
由图 2中计算结果可以发现,当选择6PM中的参量时,反演得到的u、v、w为雷达位置处的值,这与式(22)的分析结论一致。当选择6PM1或6PM2中的参量时,反演得到的u和v带有偏差,但垂直速度w及ux、vy(图略)的结果与模拟数据相等,由此说明调整后的求解方程得到的这3个参量没有受到风场模型的影响,验证了式(23)和(24)的分析结论。
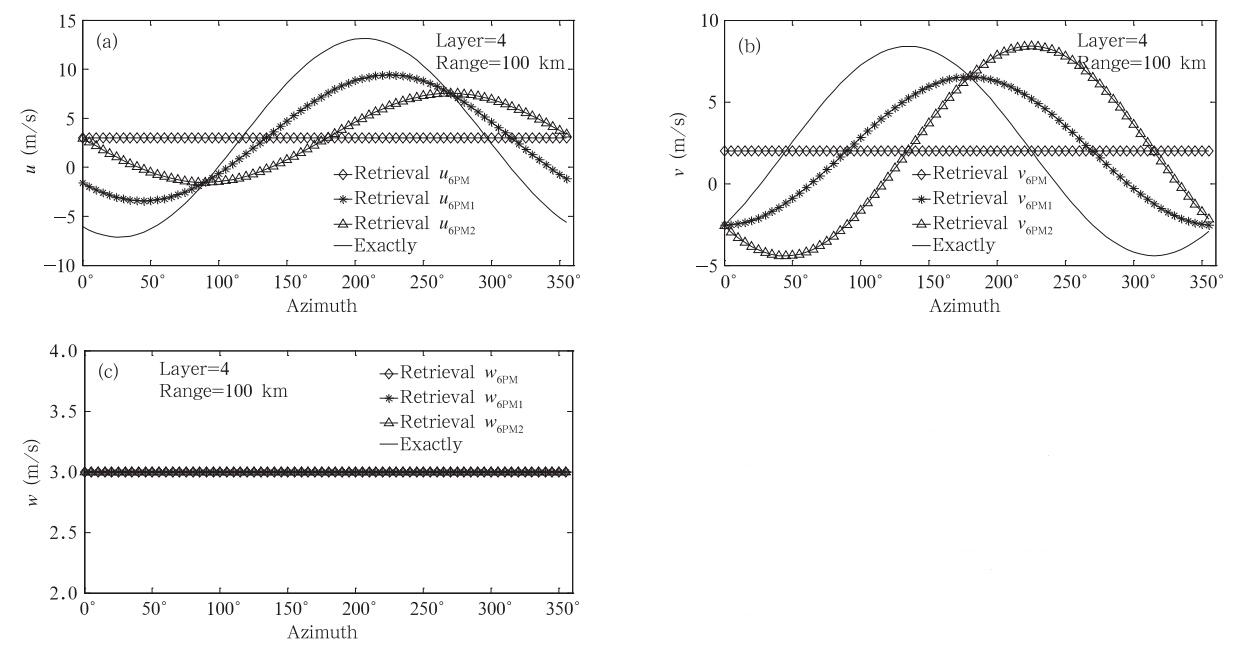 |
| 图 2 分别选择6PM、6PM1和6PM2 中的参量时u、v和w的反演结果(a.u分量,b.v分量,c.w分量; 6PM、6PM1和6PM2的参数见表 1) Fig. 2 Retrieval results of u,v and w when selecting the different parameters included in 6PM,6PM1 and 6PM2(a.u component,b.v component,c.w component; fitted parameter has shown in Table 1) |
当在求解方程中舍弃uy或vx参量时,由式(25)和(26)可知,反演得到的分析体积处的u*与v*是带有误差的,为此根据模拟风场的参量和式(23)、(24)的分析结果,分别对这两种求解方程的计算结果进行修正。如图 3所示,修正后的结果与真值完全符合,由此也验证了4.1节中的分析和结论。
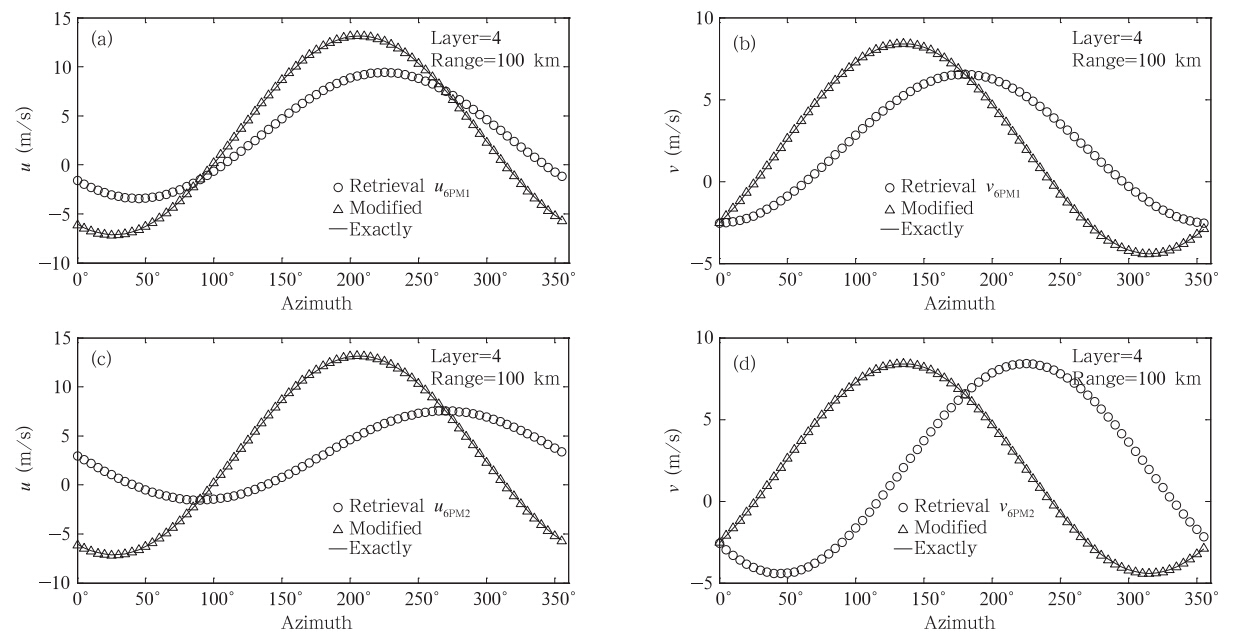 |
| 图 3 对选择6PM1(a、b)和6PM2(c、d)参数时u(a、c)和v(b、d)分量反演结果的修正(6PM1、6PM2参数见表 1) Fig. 3 Modification for u(a,c) and v(b,d)components' retrieval results when selecting the parameters of 6PM1(a,b) and 6PM2(c,d)(Fitted parameter has shown in Table 1) |
基于线性风场假设的VVP算法虽包含较多的风场信息,但其所含的待反演参量多,在实际反演中系数矩阵的病态问题会造成求解的困难,造成反演结果的误差较大,甚至不能直接求解。本研究从数学上分析和论证了造成系数矩阵病态的原因,改进并验证了针对垂直速度的求解方程,主要结论有:
(1)当选择较多的反演参量时,风场模型对实际风场的数学描述更准确,但构建的系数矩阵的条件数却呈指数增大,系数矩阵会愈加病态,以至于不可直接求解。另外,对于相等个数的反演参量,选择的风场模型不同,系数矩阵的条件数也会有较大差别。对误差范数上界的分析表明,为避免求解的困难,选取较少的反演参量时尽管会存在模型误差,但选择合适的系数矩阵能够降低求解难度和计算中的误差,反演效果好于较多参量时。
(2)VVP算法中系数矩阵矢量的线性相关造成了矩阵奇异,由于观测误差和计算误差的影响,在实际反演计算中系数矩阵则表现为病态。对比SVD分解处理的方法发现,舍弃的奇异值只是对病态矩阵的近似,而被舍弃的奇异值对应的是奇异矩阵中为0的矩阵矢量,原系数矩阵并没有实质性改变,并且还会引入新的计算误差。
(3)在VVP算法误差分析的基础上,分析并验证了舍弃部分参量时的反演误差。证明了合并或舍弃线性相关项时,其余待反演参量会受模型误差的影响,并且这种模型误差的大小并不仅与待反演参量的量级有关,而是会随着位置的不同而改变。对调整后求解方程的验证结果表明,如垂直速度等部分待参量仍然可以保持准确值。
本研究对单多普勒雷达的VVP反演算法进行了分析,改进并检验了垂直速度的求解方程,为准确反演垂直速度提供了理论基础。在实际风场反演中的应用,如对流单体、中尺度气旋和0608“桑美”台风的风场分析结果,将在本论文的第二部分“单多普勒雷达反演降水粒子垂直速度Ⅱ: 实例分析”中给出。
| 方德贤, 刘国庆, 董新宁等. 2007. 单多普勒雷达二维风场反演-ExtendedVPP方法. 气象学报, 65(2): 231-240 |
| 韩丰, 魏鸣, 李南等. 2013. 反射率因子和径向速度共同约束的单多普勒雷达风场. 遥感学报, 17(3): 584-589 |
| 姜海燕, 葛润生. 1997. 一种新的单部多普勒雷达反演技术. 应用气象学报, 8(2): 219-223 |
| 郎需兴, 魏鸣, 葛文忠等. 2001. 一种新的单多普勒雷达风场反演方法. 气象科学, 21(4): 417-424 |
| 罗昌荣, 孙照渤, 魏鸣等. 2011. 单多普勒雷达反演热带气旋近中心风场的VAP扩展应用方法. 气象学报, 69(1): 170-180 |
| 陶祖钰. 1992. 从单Doppler速度场反演风矢量场的VAP方法. 气象学报, 50(1): 81-90 |
| 王明筠, 赵坤, 吴丹. 2010. T-TREC方法反演登陆中国台风风场结构. 气象学报, 68(1): 114-124 |
| 王鹏飞, 黄荣辉, 李建平. 2011. 数值积分过程中截断误差和舍入误差的分离方法及其效果检验. 大气科学, 35(3): 403-410 |
| 魏鸣. 1998. 单多普勒天气雷达资料的变分同化三维风场反演和VVP三维风场反演[D]. 南京: 南京大学, 97-105 |
| Armijo L. 1969. A theory for the determination of wind and precipitation velocities with Doppler radars. J Atmos Sci, 26(3): 570-573 |
| Boccippio D J. 1995. A diagnostic analysis of the VVP single-Doppler retrieval technique. J Atmos Ocean Tech, 12(2): 230-248 |
| Caya A, Laroche S, Zawadzki I, et al. 2002. Using single-Doppler data to obtain a mesoscale environmental field. J Atmos Ocean Tech, 19(1): 21-36 |
| Easterbrook C C. 1975. Estimating horizontal wind fields by two-dimensional curve fitting of single Doppler radar measurements∥Preprints, 16th Conf. on Radar Meteorology. Houston: Amer Meteor Soc, 214-219 |
| Fischer T M. 2014. On the stability of some algorithms for computing the action of the matrix exponential. Linear Algebra and its Applications, 443: 1-20 |
| Gao J D, Xue M, Shapiro A, et al. 1999. A variational method for the analysis of three-dimensional wind fields from two Doppler radars. Mon Wea Rev, 127(9): 2128-2142 |
| Gao J D, Droegemeier K K, Gong J, et al. 2004. A method for retrieving mean horizontal wind profiles from single-Doppler radar observations contaminated by aliasing. Mon Wea Rev, 132(6): 1399-1409 |
| Gao J, Xue M, Lee S, et al. 2006. A three-dimensional variational single-Doppler velocity retrieval method with simple conservation equation constraint. Meteor Atmos Phys, 94(1-4): 11-26 |
| Holleman I. 2005. Quality control and verification of weather radar wind profiles. J Atmos Ocean Tech, 22(10): 1541-1550 |
| Huang S X, Cao X Q, Du H D, et al. 2010. Theoretical analyses and numerical experiments for two-dimensional wind retrievals from single-Doppler data. J Hydrod, Ser B, 22(2): 185-195 |
| Leon D, Vali G. 1998. Retrieval of three-dimensional particle velocity from airborne Doppler radar data. J Atmos Oceanic Tech, 15(4): 860-870 |
| Lhermitte R M, Atlas D. 1961. Precipitation motion by pulse Doppler radar∥Preprints, 9th Conf. on Radar Meteorology. Kansas City: Amer Meteor Soc, 218-223 |
| Li N, Wei M, Tang X W, et al. 2007. An improved velocity volume processing method. Adv Atmos Sci, 24(5): 893-906 |
| Liang X D. 2007. An integrating velocity-azimuth process single-Doppler radar wind retrieval method. J Atmos Oceanic Tech, 24(4): 658-665 |
| Liu S, Qiu C H, Xu Q, et al. 2005. An improved method for Doppler wind and thermodynamic retrievals. Adv Atmos Sci, 22(1): 90-102 |
| Matejka T, Srivastava R C. 1991. An improved version of the extended velocity-azimuth display analysis of single-Doppler radar data. J Atmos Oceanic Tech, 8(4): 453-466 |
| Matejka T. 1993. Current Extended Vertical Velocity Azimuth Display (CEVAD) analysis of single-Doppler radar data∥Preprints, 26th Int Conf. on Radar Meteorology. Norman OK: Amer Meteor Soc, 463-465 |
| Miller L J, Strauch R G. 1974. A dual Doppler radar method for the determination of wind velocities within precipitating weather systems. Remote Sens Environ, 3(4): 219-235 |
| Protat A, Zawadzki I. 1999. A variational method for real-time retrieval of three-dimensional wind field from multiple-Doppler bistatic radar network data. J Atmos Oceanic Tech, 16(4): 432-449 |
| Qiu C J, Xu Q. 1992. A simple adjoint method of wind analysis for single-Doppler data. J Atmos Oceanic Tech, 9(5): 588-598 |
| Rihan F A, Collier C G, Roulstone I. 2005. Four-dimensional variational data assimilation for Doppler radar wind data. J Comput Appl Math, 176(1): 15-34 |
| Shapiro A, Ellis S, Shaw J. 1995. Single-Doppler velocity retrievals with phoenix II data: Clear air and microburst wind retrievals in the planetary boundary layer. J Atmos Sci, 52(9): 1265-1287 |
| Shapiro A, Robinson P, Wurman J, et al. 2003. Single-Doppler velocity retrieval with rapid-scan radar data. J Atmos Oceanic Tech, 20(12): 1758-1775 |
| Shapiro A, Potvin C K, Gao J. 2009. Use of a vertical vorticity equation in variational dual-Doppler wind analysis. J Atmos Oceanic Tech, 26(10): 2089-2106 |
| Srivastava R C, Matejka T J, Lorello T J. 1986. Doppler radar study of the trailing anvil region associated with a squall line. J Aerosol Sci, 43(4): 356-377 |
| Sun J, Crook N A. 1997. Dynamical and microphysical retrieval from Doppler radar observations using a cloud model and its adjoint. Part I: Model development and simulated data experiments. J Atmos Sci, 54(12): 1642-1661 |
| Sun J. 1998. Dynamical and microphysical retrieval from Doppler radar observations using a cloud model and its adjoint. Part II: Retrieval experiments of an observed Florida convective storm. J Atmos Sci, 55(5): 835-852 |
| Tuttle J, Gall R. 1999. A single-radar technique for estimating the winds in tropical cyclones. Bull Amer Meteor Soc, 80(4): 653-668 |
| Waldteufel P, Corbin H. 1979. On the analysis of single-Doppler radar data. J Appl Meteor, 18(4): 532-542 |
| Ward R C. 1977. Numerical computation of the matrix exponential with accuracy estimate. SIAM J Numer Anal, 14(4): 600-610 |
| Wei M, Dang R Q, Ge W Z, et al. 1998. Retrieval single-Doppler radar wind with variational assimilation method-part I: Objective selection of functional weighting factors. Adv Atmos Sci, 15(4): 553-568 |
| Weygandt S S, Shapiro A, Droegemeier K K. 2002. Retrieval of model initial fields from single-Doppler observations of a supercell thunderstorm. Part I: Single-Doppler velocity retrieval. Mon Wea Rev, 130(3): 433-453 |
| Xin L, Reuter G W. 1998. VVP technique applied to an Alberta storm. J Atmos Ocean Tech, 15(2): 587-592 |
 2014, Vol. 72
2014, Vol. 72


