中国气象学会主办。
文章信息
- 李耀锟, 巢纪平. 2014.
- LI Yaokun, CHAO Jiping. 2014.
- 二维能量平衡模式对若干气候问题的研究
- Two-dimensional energy balance model and its application to some climatic issues
- 气象学报, 72(5): 880-891
- Acta Meteorologica Sinica, 72(5): 880-891.
- http://dx.doi.org/10.11676/qxxb2014.061
-
文章历史
- 收稿日期:2014-1-23
- 改回日期:2014-5-12
2. 国家海洋环境预报中心, 北京, 100081
2. National Marine Environmental Forecasting Center, Beijing 100081, China
全球变化是当今最活跃、发展最快的科学领域之一,而气候变化又是全球变化主要的研究领域之一(叶笃正等,2002)。大气中温室气体和气溶胶含量的变化,及其导致的地-气辐射平衡和地表特性的变化,都会改变气候系统的能量平衡,引起全球气候变化(秦大河等,2007)。气候变化对自然生态系统、国民经济系统和国家安全系统的负面影响远比其正面影响更受关注(秦大河,2004)。与气候变化相伴随的一系列严重的环境问题已经威胁到了人类社会的发展和进步,为了避免可能出现的环境灾难,通过科学合理的方式(有序人类活动)实现经济社会的可持续发展成为人类现实生存发展的迫切需求(叶笃正等,2001)。
尽管温室气体增加对全球变暖的贡献已经得到了公认,然而人类目前尚未真正了解不同时间尺度气候变化的驱动力以及气候系统内部各种复杂的响应和反馈过程(刘玉芝,2006),如冰芯资料分析表明大气中温室气体的浓度跟大气温度并没有直接的因果关系,甚至温度的变化可能会超前温室气体浓度的变化(崔伟宏等,2012)。又如,1999—2008年全球变暖的趋势接近于0,显著低于此前的预估(Knight et al,2009),而大气中温室气体的浓度则在逐步升高。因此,深入分析和了解气候变化的各种驱动因子及反馈过程,不仅有着重要的理论意义,也会为指导有序人类活动提供一定的实际意义。
由于气候系统极为复杂,气候模式甚至是地球系统模式成为研究的有利工具,模式可以定量分析某种驱动因子或某种反馈过程对全球气候甚至是局地气候的影响,加深人们对气候变化的认识水平,并对未来做出预估,为决策者提供决策参考。此外,通过一些简单的,但是却具有坚实物理基础的理论模式研究气候变化,有利于突出引起气候变化的因子,深入分析其影响气候变化的物理过程;有利于从理论和物理上对数值模式的结果进行补充,完善和丰富气候变化这一研究领域。最简单的做法是将地-气系统看作一个质点,利用地-气系统的能量平衡来求解平均温度的分布特征,即0维能量平衡模式,对若干参数进行订正,很容易将温室效应和冰雪反照率反馈机制引入到0维能量平衡模式中(Budyko,1969; North et al,1981)。在0维能量平衡模式的基础上,考虑温度沿纬度的分布,即得到了1维能量平衡模式,Budyko(1969)、Sellers(1969)及North(1975a)的1维气候模式正是这类研究中最具有代表性的工作,对以后的研究产生了深远的影响。若进一步在1维能量平衡模式中加入经向或垂直方向的物理过程,即可得到2维能量平衡模型(Sellers,1976; 巢纪平等,1979),还可以进一步考虑海洋的作用(石广玉等,1996)。若从垂直方向上扩展0维模式,就得到了1维辐射-对流模式(Manabe et al,1964,1967),1维辐射-对流模式已经不能用解析的方法来求解。若要求得垂直方向的解析解,需要对长波吸收谱进行简化,巢纪平等(1979)在郭晓岚1973年简化长波吸收谱工作基础上发展了一个2维能量平衡模式,并利用该模式研究了冰界和太阳常数的关系(巢纪平等,1979)、荒漠化(巢纪平等,2010a)以及二氧化碳的温室效应(巢纪平等,2010b)这些有着重要价值的问题。本研究将在他们工作基础上,进一步完善和发展2维能量平衡模式在上述3个领域内的应用。2维能量平衡模式
平均温度场的形成受到许多因子的控制,如太阳辐射的纬度分布、辐射能传播及转换过程、湍流热交换、水汽凝结和蒸发等过程造成的潜热、冷暖平流引起的热量交换。完整的温度方程可写为(叶笃正等,1958)

令kj为对波长为λj的长波辐射吸收系数,k′为对太阳辐射的平均吸收系数,Aj(Bj)表示在波长Δλi区间内向下(向上)的长波辐射,Ej为波长Δλi区间内的黑体辐射,Q表示向下的太阳辐射,则由于辐射引起的热通量可写为

根据布格-朗伯定律

由湍流引起的热通量可以表述为


 ,
, 为纬度,a为地球半径。式(7)要对整个吸收谱求积分,较为复杂,且不利于理论分析,如何用解析或半解析的方法处理辐射能传输是一个非常重要的问题,Kibel(1943)建立了严格的温度分布理论,Blinova(1947)将该理论进一步发展并精细化,他们将整个吸收谱作为一个整体考虑,并假定吸收系数为常数,这样就避免了繁杂的积分计算,最终可得到一个温度的四阶微分方程,详细介绍可参见叶笃正等(1958)。郭晓岚1973年将长波吸收谱分为强、弱吸收区两个部分(分别用下标s、w表示),两个吸收区域的平均吸收系数定义为
为纬度,a为地球半径。式(7)要对整个吸收谱求积分,较为复杂,且不利于理论分析,如何用解析或半解析的方法处理辐射能传输是一个非常重要的问题,Kibel(1943)建立了严格的温度分布理论,Blinova(1947)将该理论进一步发展并精细化,他们将整个吸收谱作为一个整体考虑,并假定吸收系数为常数,这样就避免了繁杂的积分计算,最终可得到一个温度的四阶微分方程,详细介绍可参见叶笃正等(1958)。郭晓岚1973年将长波吸收谱分为强、弱吸收区两个部分(分别用下标s、w表示),两个吸收区域的平均吸收系数定义为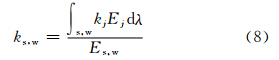
 。
。引入光学厚度




模式的上、下边界条件分别取为

 分别表示抵达大气上界的净太阳辐射及到达地面的太阳辐射。
分别表示抵达大气上界的净太阳辐射及到达地面的太阳辐射。 分别为其全球积分平均值。巢纪平等(1979)没有考虑上边界对太阳辐射的反射,即Π0=1。
分别为其全球积分平均值。巢纪平等(1979)没有考虑上边界对太阳辐射的反射,即Π0=1。利用勒让德级数给出式(10)的解,设

20世纪60年代气候处于冷期,众多科学家对冷期产生的条件进行了研究,其中最有代表性的是Budyko(1969)、Sellers(1969)及North(1975a)的工作(图 1)。1维模式中冰界纬度对太阳常数较为敏感,太阳常数只需减小2%左右即可使冰界向南推进到50°N,甚至出现全球冰封的情形;另外,1维模式在太阳常数取某些值(如取目前的观测值)时,会存在多个平衡态的冰界纬度,对应着不同的气候状态。1维模式中出现的这两个现象可归结为两个问题:一是冰界纬度对太阳常数的敏感性如何,一是不同平衡态的稳定性及是否具有物理意义。
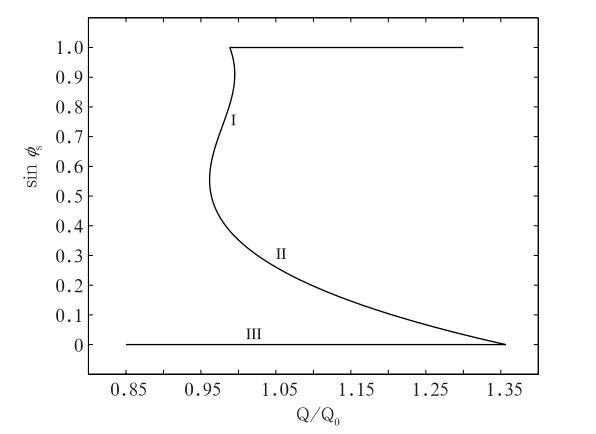 |
图 1 1维模式中冰界纬度与太阳常数的关系(North,1975a)(图中横坐标为无量纲的太阳辐射,Q0为当前的太阳常数, s为冰界纬度)Fig. 1 The ice cap latitude s为冰界纬度)Fig. 1 The ice cap latitude  s(sine of latitude)as a function of the solar constant in units of the present solar constant(Q0)(North,1975a) s(sine of latitude)as a function of the solar constant in units of the present solar constant(Q0)(North,1975a) |
Lindzen等(1977)指出,只要在模式中加入一些更为实际的热量输送过程,就可以使冰界对太阳常数的依赖性降低;Lian等(1977)发现通过修正温度和反照率的关系可以降低温度变化对太阳常数变化的敏感性;Oerlemans 等(1978)用卫星资料对长波辐射和温度的参数化关系进行了合理的修正,结果表明太阳常数要减小9%左右才能出现冰期气候。考虑到他们的结果是用1维能量平衡模式得到的,而一般来说,1维模式由于缺少垂直方向的能量调节,对太阳常数的变化较为敏感。巢纪平等(1979)应用郭晓岚-巢纪平-陈英仪模式重新研究这一问题,指出太阳常数要减小15%左右才能出现冰期气候,即在2维能量平衡模式下冰界纬度对太阳常数的敏感性会大大减低。
Budyko(1972)最早发现了简单1维模型中解的多平衡态特征,指出当平衡态所在位置满足dQ/dxs>0,则平衡态是稳定的,而当dQ/dxs<0时,平衡态是不稳定的。Chýlek等(1975)随后也分析解的分岔这一现象。North(1975a,1975b)在其所用的1维模型中发现极地附近存在两个位置很接近的平衡态,其中更靠近极地的平衡态不稳定,他认为这一平衡态不是很合理,并通过调整太阳辐射的分布去掉了这一平衡态。Held等(1974)分析了简单模型中的反照率反馈机制,他的结论支持Budyko(1972)的结果,同时他认为极地附近的两个平衡态的出现是由于引入和温度梯度有关的扩散项造成的,当扩散项足够小时,此时极地附近的两个平衡态之间不再存在显著的物理差别。Ghil(1976)发现存在间冰期、冰期和几乎全球冰封3个平衡态。Drazin等(1977)进一步分析了模式中多平衡态解产生的原因,指出如果模式中方程的特征值小于0,则其对应的平衡态是不稳定的。Lin(1978)认为给定非线性湍流交换系数可以去掉极地附近的不稳定的平衡态。Cahalan等(1979)则认为极地附近的分岔点是由于反照率取阶梯函数造成的,在冰界附近对反照率做任何形式的平滑,均可以去掉这一分岔点。Coakley(1979)也提到了采用光滑的反照率可以去掉分岔点。
由于不稳定的平衡点意味着冰界会随着太阳常数的增大而向南推进,这似乎有些不符合物理常识,因而North等(1981)在对1维模式的总结回顾中更倾向于认为分岔点可能是为了数学上处理方便引入分段阶梯反照率函数而人为导致的,实际中很有可能并不存在。然而Held等(1974)和Ghil(1976)似乎并没有这样的倾向性。实际中反照率的分布可以存在较大的不连续性,如南极极冰和其周边海水的反照率差异很大,此时取反照率为阶梯函数似乎也更合理一些,因此,分岔点的出现可能表征某些情况下地球气候的演变特征,不宜将其当作没有物理意义的计算解而简单去掉。
巢纪平等(1979)认为1维模式中没有考虑热量在垂直方向的输送,因而对太阳常数较为敏感,他们建立了一个考虑了能量垂直输送的2维模式,研究结果表明,温度对太阳常数并不是十分敏感,太阳常数要减少15%—20%才能出现冰期气候,同时,解对其他参数也并不是十分敏感,各种参数变化20%都不会对解产生显著的影响(陈英仪,1982b)。
2 维模式中反照率取与1维模式相似的分布,即

 s,
s, s为冰界所在纬度,由温度T=-10℃决定,而α1、α2分别为冰面和非冰面的反照率分布,可以取不同的形式。
s为冰界所在纬度,由温度T=-10℃决定,而α1、α2分别为冰面和非冰面的反照率分布,可以取不同的形式。图 2给出了3种反照率分布情形下冰界纬度与太阳常数的关系。图中实线中反照率分布取为α1(x)=α2(x)=a0+a2P2(x),即反照率分布为连续函数(North et al,1979),此时冰界与太阳常数的关系较为稳定,表现为随着太阳常数的增大,冰界会向北退却,直到全球无冰。若要出现全球无冰的情形,太阳常数要增大10%左右;若要出现极冰向南扩张到50°N附近,太阳常数大约要减小20%。
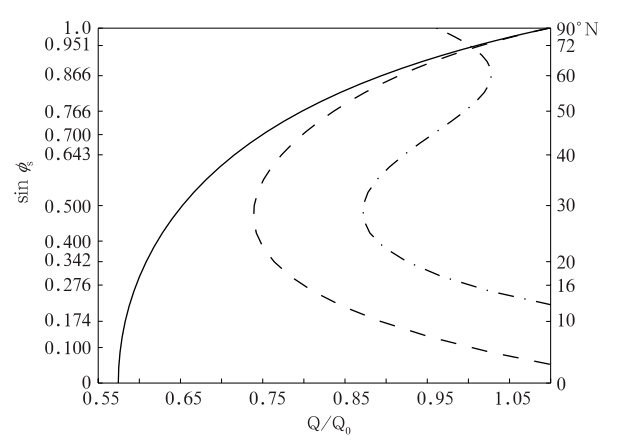 |
图 2 冰界纬度与太阳常数的关系(实线为反照率取α1(x)=α2(x)=a0+a2P2(x);虚线为反照率取α1(x)=0.62,α2(x)=a0+a2P2(x);点划线为反照率取α1(x)=0.62,α2(x)=0.132,横坐标为无量纲化的太阳常数, s为冰界纬度,右纵坐标为相应的纬度)Fig. 2 The ice cap latitude as a function of the solar constant in units of the present solar constant(The right and left y-axis coordinates are latitude and its sine. The solid,dashed,and dash-dotted lines indicate that the albedo distribution is taken as α1(x)=α2(x)=a0+a2P2(x);α1(x)=0.62,α2(x)=a0+a2P2(x); and α1(x)=0.62,α2(x)=0.132) s为冰界纬度,右纵坐标为相应的纬度)Fig. 2 The ice cap latitude as a function of the solar constant in units of the present solar constant(The right and left y-axis coordinates are latitude and its sine. The solid,dashed,and dash-dotted lines indicate that the albedo distribution is taken as α1(x)=α2(x)=a0+a2P2(x);α1(x)=0.62,α2(x)=a0+a2P2(x); and α1(x)=0.62,α2(x)=0.132) |
图 2中虚线表示反照率取为α1(x)=0.62,α2(x)=a0+a2P2(x),即将冰面的反照率固定为0.62,非冰面的反照率仍然按照观测资料给定(Coakley,1979)。在约30°N以北,冰界纬度会随着太阳常数的增大而向北退却,直到全球无冰。若要出现全球无冰的情形,太阳常数大约要增加10%;若要冰界向南发展到50°N,太阳常数要减小16%。在30°N以南,还存在一支冰界纬度随着太阳常数的增大而向南扩张的解。两支解在30°N附近汇合成一支。
图 2中点划线表示反照率取为α1(x)=0.62,α2(x)=0.132,此时冰面和非冰面的反照率均取为常数(Budyko,1969)。由图可知,存在两个分岔点,分别位于约30°N、60°N位置。从赤道到30°N及从60°N到北极,极冰范围会随着太阳常数的增大而增大,而30°—60°N,极冰范围会随着太阳常数的增大而减小。在目前的太阳常数下存在3个冰界纬度,分别在72°、50°和16°N附近。这3个冰界纬度似乎在地球演变历史中均出现过,目前冰界大约在72°N;在石炭—二叠纪冰期及第四纪冰期,冰界纬度能抵达中纬度地区;而在新元古代冰期,有证据表明冰界能够抵达低纬度地区,甚至可能出现全球冰封的情形(Sumner et al,1987; Schmidt et al,1991,1995; Sohl et al,1999)。
综上所述,当反照率分布形式变化时,冰界纬度和太阳常数的关系也会发生变化:反照率分布连续时,冰界纬度和太阳常数存在一一对应的关系,即冰界纬度随着太阳常数的增大(减小)而向北退缩(向南推进);反照率分布不连续时,冰界纬度和太阳常数一一对应的关系被破坏,太阳常数对应2个或3个冰界纬度,此时会出现某个冰界纬度随太阳常数的增大(减小)而向南推进(向北退缩)的情形,不过此种情况对应的平衡态并不稳定。冰界纬度和太阳常数的关系强烈地依赖反照率的分布,充分应用卫星资料对全球反照率分布给出更为细致的刻画将有助于加深对这一问题的认识。
由2维模式计算的地表温度分布(图 3a)可知,理论模式较好表征了地面温度的分布,在热带地区模式模拟的结果较高,这可能是由于模式中没有考虑哈得来环流对热输送的影响造成的,如果引入更接近实际的热输送(Lindzen et al,1977),会改进对热带地区温度分布的模拟情况。直接利用光学厚度定义式(9)计算得到的温度垂直分布与观测相比有较大差别,通过观测资料订正光学厚度,可算得温度的垂直分布如图 3b,可见2维模型能较好表征对流层内温度分布的主要特征,但是与观测资料相比仍然存在一定的差别,尤其是在对流层下部的热带区域及对流层上部的极地地区,由于模式没有考虑大气动力过程对温度分布的调节作用,不能苛求其计算结果与观测资料完全一致。
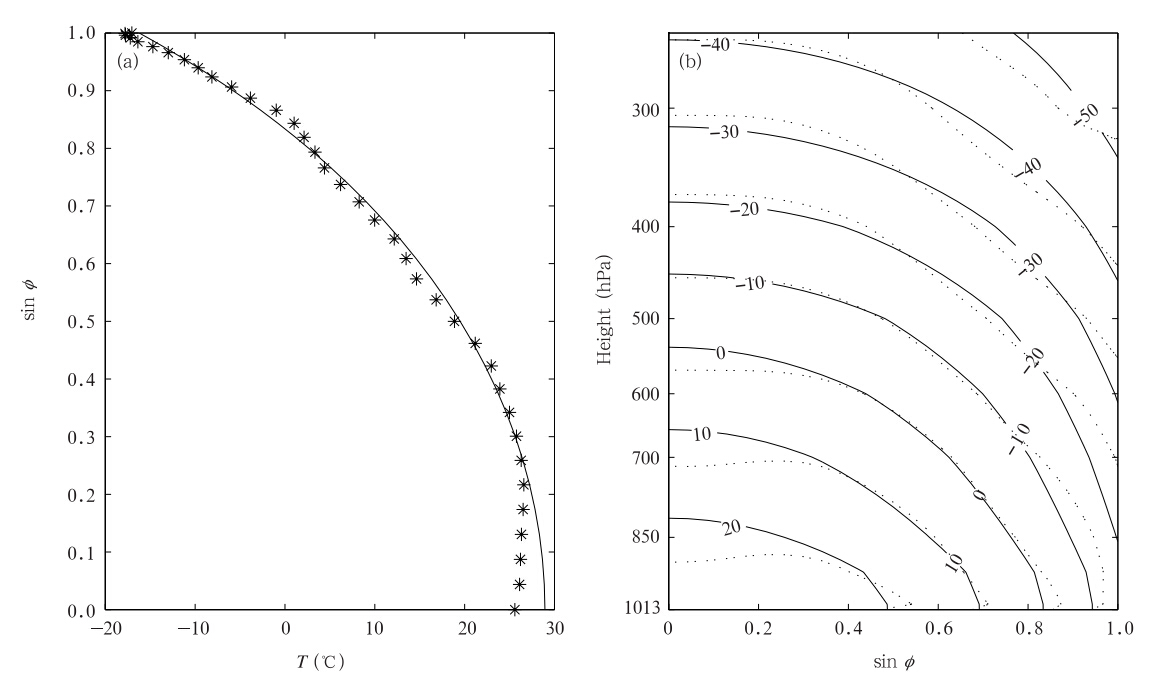 |
图 3 2维模式计算的温度分布(a.地表温度的分布,图中实线为理论计算值,星号为观测资料结果,图中纵坐标为纬度的正弦值(sin ); b. 温度随高度的分布,图中实线为理论计算结果,点线为观测资料结果)Fig. 3 Surface temperature(a) and vertical temperature(b)distributions(The solid lines represent the theoretical results. The asterisk in(a) and the dotted lines in(b)are the temperature distribution derived from observation. The x-axis is temperature in(a) and the sine of latitude in(b).The y-axis is the sine of latitude in(a) and vertical levels in(b)) ); b. 温度随高度的分布,图中实线为理论计算结果,点线为观测资料结果)Fig. 3 Surface temperature(a) and vertical temperature(b)distributions(The solid lines represent the theoretical results. The asterisk in(a) and the dotted lines in(b)are the temperature distribution derived from observation. The x-axis is temperature in(a) and the sine of latitude in(b).The y-axis is the sine of latitude in(a) and vertical levels in(b)) |
联合国防治荒漠化公约(UNCCD)将荒漠化定义为包括气候变异和人类活动在内的种种因素造成的干旱、半干旱和亚湿润干旱地区的土地退化。全球干旱陆地中(不包括极度干旱的沙漠),大约有3.6×109 hm2或70%发生了土地退化(UNCCD,2000)。中国严重缺水的华北和西北是受气候变化影响较大的气候脆弱地区(叶笃正,1986),截至2009年底,中国荒漠化土地总面积2.62×106 km2,占国土总面积的27.33%,主要分布在西北、华北地区(国家林业局,2011)。近几十年来,中国北方地区的干旱有加剧的趋势,干旱和半干旱带有向东和向南扩展的趋势,持续的干旱导致了当地荒漠化等一系列环境问题(马柱国等,2005,2006; 符淙斌等,2008),已经成为经济发展的严重障碍。北方干旱化如何形成、其发展趋势、其对经济社会的影响以及应对对策已经成为国家需求,围绕这些问题,中国科学家取得了一系列研究成果,如从3个方面分析研究北方干旱化形成和发展的驱动因子:季风系统干湿变化的自然规律;全球变化(主要是全球变暖)影响下,季风系统的异常响应;人类活动对生存环境的影响(符淙斌等,2002a,2002b)。
Charney(1975)最早从理论上分析了沙漠边缘植被变化对气候的影响,他指出植被退化会导致下垫面的反照率增大,改变地表的能量平衡,引起异常的下沉气流,从而抑制降水,而降水减少则不利于植被生长,这一正反馈过程加速了荒漠化发展。Dickinson(1984)将植被蒸腾作用引入到大气模式中。这一开创性的工作促进了陆面模式的发展和成熟,目前大多数研究都是从利用陆面模式或气候模式来研究荒漠化这一问题,而理论研究则相对匮乏。巢纪平等(2010a)根据极冰、荒漠带及植被带反照率的不同,给定分段的反照率分布,并假定植被和荒漠带的分界线可以通过温度来确定,由此探讨了荒漠化气候的演变。
由地表反照率分布(图 4)可知,虽然在不同地区反照率的分布差异较大,但是一般而言,北半球从极地开始,反照率先减小后增大而后又减小,分别对应着极冰、高纬度植被、中纬度荒漠及低纬度植被,这一点在亚洲和北美洲大陆西侧体现得最为明显。南半球陆面地面较小,整个南极大陆为冰雪所覆盖,往北依次是海洋(反照率可取为0.07)、较小的荒漠分布及热带植被。根据观测的反照率分布,将2维模型所用到的地表反照率分布给定为

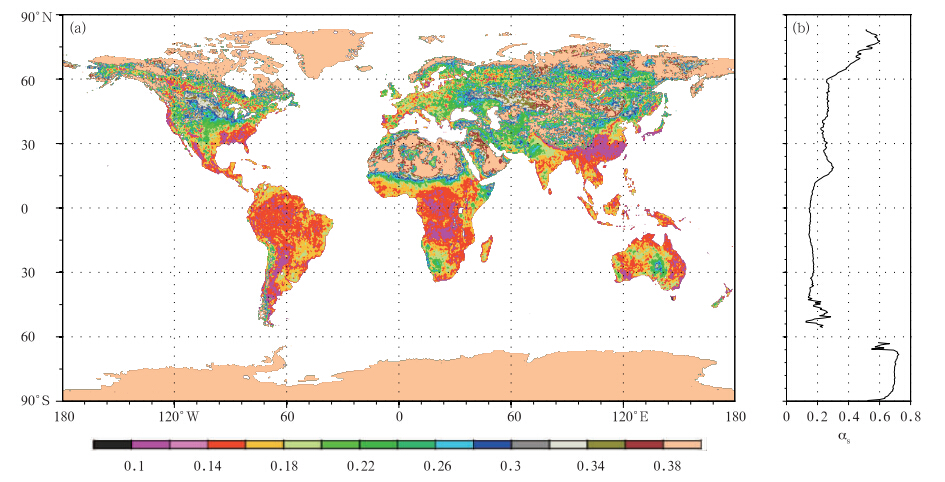 |
| 图 4 地表反照率(a)及其纬向分布(b)(反照率资料下载自ESA GlobAlbedo项目网站http://www.GlobAlbedo.org)Fig. 4 Spatial distribution of(a)the surface albedo and (b)its zonal mean values(The surface albedo data are downloaded from the ESA GlobAlbedo Project's website: http://www.GlobAlbedo.org) |
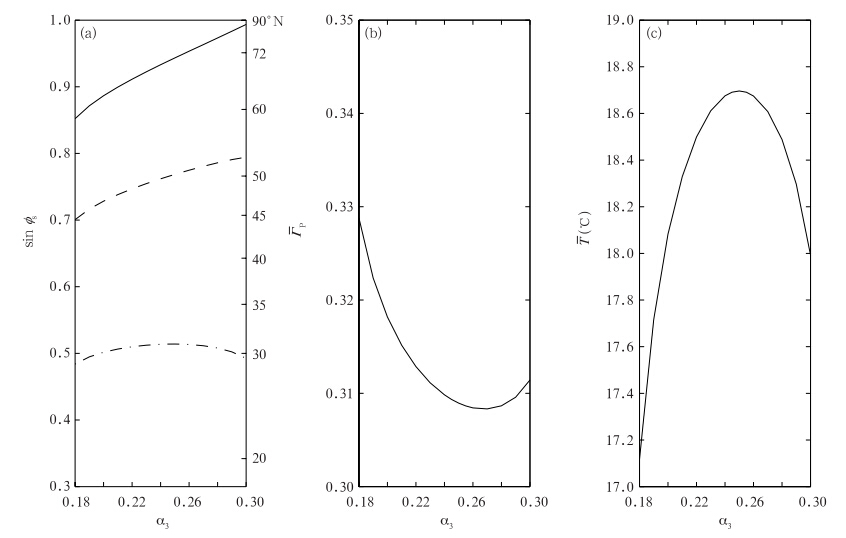 |
| 图 5(a)xs(实线)、xd(虚线)、xv(点划线)随α3的变化(纵坐标为纬度及纬度的正弦值),(b)全球积分的行星反照率随α3的变化,(c)全球积分平均的地表温度随α3的变化Fig. 5(a)The variations of xs,xd,xv(solid,dashed,and dash-dotted lines)with the desert albedo value α3(The y-axis coordinates are latitude and its sine);(b)The variation of global integrated planetary albedo Tp with desert albedo value α3;(c)The variation of global integrated surface temperature T with desert albedo value α3 |
图 6给出了不同α3时地表温度相对于当前气候状态(α3=0.25)的偏差。可见在α3较小时,由于极冰范围较大,负的温度距平可达中低纬度,只有热带地区存在一定的升温。随着α3的增大,冰界范围迅速减小,高纬度温度由负距平转为正距平,而低纬度地区则相反,为正的温度距平。高纬度的温度距平要大于中低纬度,这表明极冰-反照率反馈机制对温度的调节作用在高纬度更为明显。
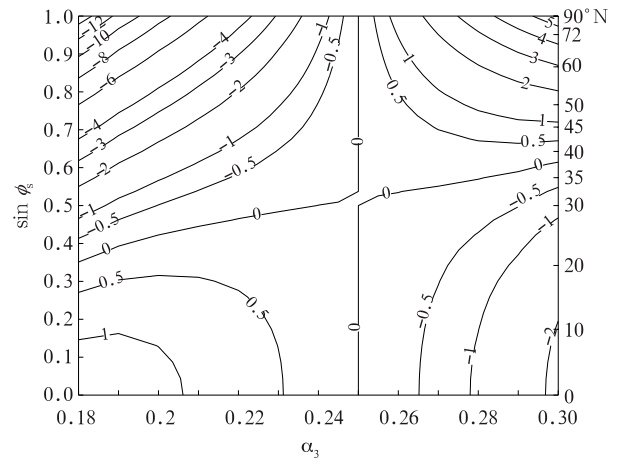 |
| 图 6 不同α3条件下的地表温度相对于当前气候状态(α3=0.25)的偏差(纵坐标为纬度和纬度的正弦值)Fig. 6 Surface temperature discrepancy with the current climate states(α3=0.25)(The y-axis coordinates are latitude and its sine) |
xd会随着α3的增大一直向北退却,这表明荒漠化的演变有利于荒漠带向北发展侵入高纬度植被带,但同时xs的位置也会北移,这表明冰界会退缩而高纬度植被则会向北推进,由此可知,荒漠化主要会使高纬度植被带整体向北推移,但是对于中纬度而言,植被带和荒漠带的北移会恶化当地的生存环境,危害当地人的生产生活。对于中低纬度而言,xv向北移动表示低纬度植被会向北迁移,这对改善当地的环境是有利的;当荒漠化发展加剧时,低纬度植被带会向南迁移,这又不利于改善当地环境。不过相比xd,xv的变化范围并不大,其大约在30°N附近几个纬度内变化。将xd、xv分别看作是荒漠带的北边界和南边界,荒漠会随着其反照率的增大而向北、向南扩张,恶化荒漠和植被交界带的生态环境,而当地的生态环境本来就是较为脆弱的,如此将更有利于荒漠化的发展。由于下垫面物理和生态状态的分布影响了反照率的分布。 因此,反照率地理位置变化影响气候的敏感性研究是值得加强的,因为这将告诉人们,有序人类活动(如灌溉、造林等)能在多大程度上改变区域性气候,使其向有利于人类社会生产、生存环境的方向可持续性发展。5 二氧化碳的温室效应
通过吸收向上的长波辐射,温室气体可以使地球保持在适当的温度区间内,过多的温室气体则会使地球温度升高。人类生产、生活活动排放的二氧化碳被认为是 全球气候变暖的一个非常重要的原因。工业革命以来,大气中二氧化碳的浓度一直在稳步升高,根据世界气象组织(WMO)的报告,2013年几个测站的二氧化碳日均浓度已经突破400 ×10-6,达到过去300万年来的最高值,按照目前的速率,二氧化碳的年均浓度很有可能在2015年到2016年突破400×10-6。人们普遍认为,随着二氧化碳浓度的不断升高,全球平均温度会继续升高,但升高的速率会有多大,目前似乎尚无定论,特别是最近十多年来,虽然大气二氧化碳浓度在一直升高,全球平均温度却表现出升温停滞的现象(Kerr,2009; Knight et al,2009)。可见大气中二氧化碳等温室气体浓度变化导致的温度变化,尚不能完全定论,仍然有必要通过多种途径来研究大气对二氧化碳温室效应的响应这一问题。
刘玉芝等(2002)讨论了二氧化碳温室效应的饱和度问题,指出虽然在15 μm这一强吸收带中心确已达到饱和,但是二氧化碳浓度变化对辐射强迫的贡献主要来自于15 μm带的两翼,其温室效应远没有达到饱和,这表明二氧化碳的增温潜力仍然存在。那么该如何表征二氧化碳浓度继续升高和温度变化的关系呢?通过气候模式来对这一问题进行分析和探讨不失为一个很好的方法,同时,采用一些简单的、具有坚实物理基础的简单模式作为补充,无疑会进一步加深对这一问题的认识和理解。如刘玉芝(2006)利用Budyko(1969)1维模型分析了近几十万年来控制冰期—间冰期气候旋回的物理机制。
巢纪平等(2010b)利用郭晓岚-巢纪平-陈英仪模式讨论了大气对二氧化碳温室效应的响应。本节在其工作的基础上进一步利用更贴合物理实际的方法来更新这一工作。大气在某一波段对辐射的吸收系数kj,可写为

图 7给出了温度为290 K,压强为一个标准大气压时二氧化碳浓度在0—1000×10-6 内强、弱吸收区吸收系数及强吸收区占总能量的比例分布。可见随着二氧化碳浓度的升高,强吸收区的吸收系数会逐步减小,到二氧化碳浓度超过400×10-6 后,变化的幅度大大减小,基本稳定在1.36 m-1附近;而弱吸收区的吸收系数变化则较为复杂,出现较为明显的波动现象,不过总的趋势也是在逐步减小,最终大约维持在1.32 mm-1附近;强吸收区占总吸收的比例则会稳步上升。巢纪平等(2010b)在研究时假定强吸收区所占比例不变(0.5),即强、弱吸收区各占一半,并对弱辐射区吸收系数给了较为简单直观的假定,虽然这么做具有一定的物理考量,但是仍显得较为粗糙,利用更为精确的HITRAN 2004分辨率光谱资料,按照式(8)来计算强、弱吸收区的吸收系数,进一步发展了巢纪平等(2010b)的工作。在不同温度、压强下计算结果虽有所不同,但是不会产生明显的变化,通过调整湍流交换系数,仍能保证在当前情况下温度分布符合观测。
 |
| 图 7 强、弱吸收区吸收系数及强吸收区占总吸收的比例随二氧化碳浓度的变化关系(T=290 K,压强为一个标准大气压)Fig. 7 The absorption coefficients in strong and weak absorptive zones and the proportion of the strong absorptive zone in the total absorption as a function of the concentration of carbon dioxide(The reference temperature and pressure are 290 K and the st and ard atmospheric pressure) |
参照前文,将地表反照率分为两段,分别取α1=0.62,α2=0.132,计算不同二氧化碳浓度下冰界温度的分布,此时的3个冰界纬度分别如图 8a—c所示。可见随着二氧化碳浓度升高,3个平衡态的演化出现不同特征,目前的气候状态下,冰界纬度会随着二氧化碳浓度的升高而缓慢向北退却,二氧化碳大约要升高到1000×10-6,才会出现全球几乎无冰的情形(图 8a)。极冰并不单调地随着二氧化碳浓度的升高而向北退却,在某些浓度区间内(如(400—500)×10-6),极冰变化很小,在某些区间内极冰甚至会增加。在冰期气候下(图 8b),极冰并不会随着二氧化碳浓度的升高而消融,反而会向南推进。注意到,在(0—120)×10-6和(180—270)×10-6两个区间段内,并没有冰界与之对应,这是由于这两支解在区间端点附近发生了融合,此时没有实数解对应着冰界纬度。在全球几乎冰封的气候状态下(图 8c),冰界纬度会随着二氧化碳浓度的升高向北退 却。图 9给出了3种气候状态下对应的全球平均的地表温度,当前气候下(图 9a)全球平均的地表温度会随着二氧化碳浓度的升高而升高,但是升高的幅度越来越小,当二氧化碳浓度超过600×10-6后,全球平均温度几乎不再随二氧化碳浓度变化,达到“饱和”的状态。在冰期气候中(图 9b),全球平均温度会随着冰界的向南推移而逐步降低;而在全球几乎冰封的气候下(图 9c),虽然冰界向北移动,但是全球平均温度仍然会降低,不过幅度不大。
 |
| 图 8 冰界纬度随二氧化碳浓度的变化(a. 当前气候,b. 冰期气候,c. 近冰封气候)Fig. 8 The variations of the three equilibrium ice cap latitudes with the concentration of carbon dioxide |
 |
| 图 9 全球平均的地表温度随二氧化碳浓度的变化(a. 当前气候,b. 冰期气候,c. 近冰封气候)Fig. 9 The variations of the global mean surface temperature in the three equilibrium states with the concentration of carbon dioxide |
系统回顾了2维能量平衡模式的发展历史及其在若干气候问题上的应用,2维能量平衡模式虽然较为简单,但具有坚实的物理基础,有助于加深对气候变化的认识,未来需要进一步通过古气候资料及气候模式来验证理论分析结果。所述气候问题都是目前人们极为关注的,也是还没有完全认识清楚的重大问题,未来对这些问题的回答很可能会取得一定突破和进展,这也在一定程度上代表了理论气候变化的研究方向。
(1) 反照率分布和冰界纬度多平衡态及平衡态稳定性的关系,平滑的反照率分布会减小平衡态的数目,不连续的反照率则会增加平衡态的数目,虽然实际情况很可能介乎二者之间,但是哪一种情况更容易出现仍然是值得研究的,此外,平衡态的稳定性如何,不稳定的平衡态是否具有物理意义,其演变趋势如何,这些都是值得进一步研究的问题。对这些问题的回答将有助于理解目前气候所处的状态及其发展的趋势。
(2) 荒漠化的发展及其对全球温度分布、大气运动的影响。目前研究主要集中下垫面反照率分布变化对荒漠化及边界层运动的影响,需要进一步将其与自由大气的运动耦合在一起,讨论荒漠化对大气环流的影响。同时,现有的反照率分布及荒漠和植被交界纬度的确定仍存在一定的简单化和人为性,荒漠化对这些参数的敏感性如何,如何设计既能体现物理本质又能便于理论计算的不同下垫面属性分布及其差异,都是需要进一步研究的问题。
(3) 二氧化碳浓度升高对全球平均温度的影响到底该如何确定。现有研究发现,对于不同的平衡态,二氧化碳浓度升高可以对应着全球温度升高或降低的情形,在目前的气候态下,二氧化碳造成的升温似乎存在逐步“饱和”的情形,这些结论的合理性及其中涉及到的物理过程如何,这些问题仍然没有定论,需要进一步分析研究。在更符合实际的下垫面属性分布下,是否仍然会存在此种现象,这些也都是需要进一步研究的问题。
(4) 除了文中详述的3个问题外,还可以将2维能量平衡模式运用到其他重要的气候问题中,如气溶胶的气候效应等。
致谢: 地表反照率资料下载自ESA GlobAlbedo项目http://www.GlobAlbedo.org。
| 巢纪平, 陈英仪. 1979. 二维能量平衡模式中极冰-反照率的反馈对气候的影响. 中国科学 A 辑, 22(12): 1198-1207 |
| 巢纪平, 李耀锟. 2010a. 热力学和动力学耦合的二维能量平衡模式中荒漠化气候的演变. 中国科学: 地球科学, 40(8): 1060-1067 |
| 巢纪平, 李耀锟. 2010b. 二维能量平衡模式中大气温度对二氧化碳增温效应的响应. 气象学报, 68(2): 147-152 |
| 陈英仪. 1982a. 二维能量平衡模式中极冰对气候的影响——解的稳定性分析(一). 气象学报, 40(1): 1-12 |
| 陈英仪. 1982b. 二维能量平衡模式中极冰对气候的影响——参数敏感性分析(二). 气象学报, 40(2): 175-184 |
| 陈英仪, 巢纪平. 1988. 对“对二维气候能量平衡模式中辐射和动力学参数化的一些看法”的回答. 大气科学, 12(1): 106-112 |
| 崔伟宏, Singer S F, Courtillot V等. 2012. 自然是气候变化的主要驱动因素. 北京: 中国科学技术出版社, 20-21 |
| 符淙斌, 安芷生. 2002a. 我国北方干旱化研究——面向国家需求的全球变化科学问题. 地学前缘, 9(2): 271-275 |
| 符淙斌, 温刚. 2002b. 中国北方干旱化的几个问题. 气候与环境研究, 7(1): 22-29 |
| 符淙斌, 马柱国. 2008. 全球变化与区域干旱化. 大气科学, 32(4): 752-760 |
| 国家林业局. 2011. 第四次中国荒漠化和沙化状况公报. 北京: 国家林业局 |
| 刘玉芝, 肖稳安, 石广玉. 2002. 论大气二氧化碳温室效应的饱和度. 地球科学进展, 17(5): 653-658 |
| 刘玉芝. 2006. 地球气候变化的自然强迫——冰芯资料分析与物理模式研究[D]. 北京: 中国科学院大气物理研究所, 98pp |
| 吕越华, 巢纪平. 1981. 行星大气温度分布的气候理论. 大气科学, 5(2): 145-156 |
| 马柱国, 符淙斌. 2005. 中国干旱和半干旱带的 10 年际演变特征. 地球物理学报, 48(3): 519-525 |
| 马柱国, 符淙斌. 2006. 1951—2004 年中国北方干旱化的基本事实. 科学通报, 51(20): 2429-2439 |
| 秦大河. 2004. 进入 21 世纪的气候变化科学——气候变化的事实、影响与对策. 科技导报, 22(7): 4-7 |
| 秦大河, 陈振林, 罗勇等. 2007. 气候变化科学的最新认知. 气候变化研究进展, 3(2): 63-73 |
| 石广玉, 郭建东, 樊小标等. 1996. 近百年全球平均气温变化的物理模式研究. 科学通报, 41(18): 1681-1684 |
| 叶笃正, 朱抱真. 1958. 大气环流的若干基本问题. 北京: 科学出版社, 73-75 |
| 叶笃正. 1986. 人类活动引起的全球性气候变化及其对我国自然、生态、经济和社会发展的可能影响. 中国科学院院刊, 1(2): 112-120 |
| 叶笃正, 符淙斌, 季劲钧等. 2001. 有序人类活动与生存环境. 地球科学进展, 16(4): 453-460 |
| 叶笃正, 符淙斌, 董文杰. 2002. 全球变化科学进展与未来趋势. 地球科学进展, 17(4): 467-469 |
| Blinova E N. 1947. On the mean annual temperature distribution in the earth's atmosphere with consideration of continents and oceans (in Russian). Izv AN USSR, Ser Geogr Geofiz, 11(1): 3-13 |
| Brunt D. 1934. Physical and Dynamical Meteorology. New York: Cambridge University Press, 411pp |
| Budyko M I. 1969. The effect of solar radiation variations on the climate of the earth. Tellus, 21(5): 611-619 |
| Budyko M I. 1972. The future climate. Eos, Transactions American Geophysical Union, 53(10): 868-874 |
| Cahalan R F, North G R. 1979. A stability theorem for energy-balance climate models. J Atmos Sci, 36(7): 1178-1188 |
| Charney J G. 1975. Dynamics of deserts and drought in the Sahel. Quart J Roy Meteor Soc, 101(428): 193-202 |
| Chýlek P, Coakley J A Jr. 1975. Analytical analysis of a Budyko-type climate model. J Atmos Sci, 32(4): 675-679 |
| Coakley J J A. 1979. A study of climate sensitivity using a simple energy balance model. J Atmos Sci, 36(2): 260-269 |
| Dickinson R E. 1984. Modeling evapotranspiration for three-dimensional global climate models. Geophys Monogr Ser, 29: 58-72 |
| Drazin P G, Griffel D H. 1977. On the branching structure of diffusive climatological models. J Atmos Sci, 34(11): 1696-1706 |
| Ghil M. 1976. Climate stability for a Sellers-type model. J Atmos Sci, 33(1): 3-20 |
| Held I M, Suarez M J. 1974. Simple albedo feedback models of the icecaps. Tellus, 26(6): 613-629 |
| Kerr R A. 2009. What happened to global warming? Scientists say just wait a bit. Science, 326(5949): 28-29 |
| Kibel A. 1943. Distribution of the temperature in the Earth's atmosphere (in Russian). DAN USSR, 39(1): 18-22 |
| Knight J, Kennedy J J, Folland C, et al. 2009. Do global temperature trends over the last decade falsify climate predictions. Bull Amer Meteor Soc, 90(8): S22-S23 |
| Lian M S, Cess R D. 1977. Energy balance climate models: a reappraisal of ice-albedo feedback. J Atmos Sci, 34(7): 1058-1062 |
| Lin C A. 1978. The effect of nonlinear diffusive heat transport in a simple climate model. J Atmos Sci, 35(2): 337-339 |
| Lindzen R S, Farrell B. 1977. Some realistic modifications of simple climate models. J Atmos Sci, 34(10): 1487-1501 |
| Manabe S, Strickler R F. 1964. Thermal equilibrium of the atmosphere with a convective adjustment. J Atmos Sci, 21(4): 361-385 |
| Manabe S, Wetherald R T. 1967. Thermal equilibrium of the atmosphere with a given distribution of relative humidity. J Atmos Sci, 24(3): 241-259 |
| North G R. 1975a. Analytical solution to a simple climate model with diffusive heat transport. J Atmos Sci, 32(7): 1301-1307 |
| North G R. 1975b. Theory of energy-balance climate models. J Atmos Sci, 32(11): 2033-2043 |
| North G R, Coakley J A. 1979. Differences between seasonal and mean annual energy balance model calculations of climate and climate sensitivity. J Atmos Sci, 36(7): 1189-1204 |
| North G R, Cahalan R F, Coakley J A. 1981. Energy balance climate models. Rev Geophys, 19(1): 91-121 |
| Oerlemans J, Van Den Dool H M. 1978. Energy balance climate models: stability experiments with a refined albedo and updated coefficients for infrared emission. J Atmos Sci, 35(3): 371-381 |
| Schmidt P W, Williams G E, Embleton B. 1991. Low palaeolatitude of Late Proterozoic glaciation: early timing of remanence in haematite of the Elatina Formation, South Australia. Earth Planet Sci Lett, 105(4): 355-367 |
| Schmidt P W, Williams G E. 1995. The Neoproterozoic climatic paradox: Equatorial palaeolatitude for Marinoan glaciation near sea level in South Australia. Earth Planet Sci Lett, 134(1): 107-124 |
| Sellers W D. 1969. A global climatic model based on the energy balance of the Earth-atmosphere system. J Appl Meteor, 8(3): 392-400 |
| Sellers W D. 1976. A two dimensional global climatic model. Mon Wea Rev, 104(3): 233-248 |
| Sohl L E, Christie-Blick N, Kent D V. 1999. Paleomagnetic polarity reversals in Marinoan (ca. 600 Ma) glacial deposits of Australia: Implications for the duration of low-latitude glaciation in Neoproterozoic time. Geol Soc Am Bull, 111(8): 1120-1139 |
| Sumner D Y, Kirschvink J L, Runnegar B N. 1987. Soft-sediment paleomagnetic fold tests of late Precambrian glaciogenic sediments. EOS, 68: 1251 |
| UNCCD. 2000. Fact Sheet 2: The Causes of Desertification. United Nations Secretariat of the Convention to Combat Desertification[2006-03-21].http://www.unccd.int/publicinfo/factsheets/showFS.php?Number=2[Geo-2-171] |
 2014, Vol. 72
2014, Vol. 72

