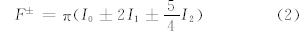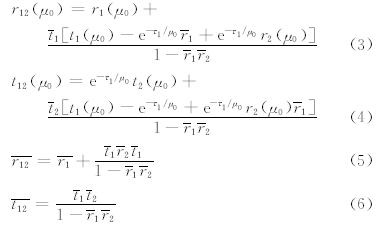中国气象学会主办。
文章信息
- 张华, 卢鹏. 2014.
- ZHANG Hua, LU Peng. 2014.
- 多层四流球谐函数算法的构建及在大气辐射传输模式中的应用
- Construction of the multi-layers four-stream spherical harmonic expansion algorithm and its application to atmospheric radiative model
- 气象学报, 72(6): 1257-1268
- Acta Meteorologica Sinica, 72(6): 1257-1268.
- http://dx.doi.org/10.11676/qxxb2014.077
-
文章历史
- 收稿日期:2013-11-19
- 改回日期:2014-06-30
2. 中国气象局气候研究开放实验室, 国家气候中心, 北京, 100081;
3. 江苏省气候中心, 南京, 210008
2. Laboratory for Climate Studies, China Meteorological Administration, National Climate Center, Beijing 100081, China;
3. Jiangsu Climate Center, Nanjing 210008, China
辐射方案的精度差异会对大气模式模拟效果产生一定影响(杨学胜等,2009;许尤福等,2011;荆现文等,2012;张梦等,2014;Zhang et al,2014)。在平行大气假设下,Stamnes等(1988)开发的离散纵标法(DISORT)程序包是目前使用最广泛的辐射传输模式之一。DISORT 32流或48流方案计算的辐射结果一般可以作为衡量其他辐射传输算法优劣的参考标准。但是高流(大于二流)DISORT程序的计算成本比较高,目前高性能计算机的运算能力尚不足以将高流DISORT算法应用于气候模式。目前大多数气候模式仍然采用二流辐射传输方法,其主要优点是计算速度快,且在晴空大气下的计算精度基本能满足气候模式的需求,但是在有云大气情况下误差较大。因此,对于有云大气情况,需要采用更为精确的辐射传输计算方法。随着高性能计算机的发展,四流辐射传输方案逐渐被应用于全球气候模式的计算。Shibata等(1992)研究表明利用四流矩阵算子法能将辐射传输计算的误差控制在10%以内。Chou(1992)利用单层四流离散坐标法结合二流累加法,计算了辐射通量和加热率,与通过求解线性方程组的传统四流离散坐标法相比,明显地节省了计算时间。Kay等(2001)比较了二流和四流离散纵坐标法以及矩阵求逆法。其结果表明在光化通量的计算中,四流离散纵坐标法略优于矩阵求逆法,而两者都要优于二流离散纵坐标法。而在辐射通量的比较中,四流离散纵坐标法要优于矩阵求逆法和二流离散纵坐标法。Ayash等(2008)在第3代加拿大气候中心大气环流模式(Scinocca et al,2008)中引入了二流-四流混合离散纵坐标法(Liou et al,1988),并比较了其与二流近似辐射传输算法对辐射通量计算结果的影响。Zhang等(2013a,2013b)分别利用四流离散纵坐标、四流球谐函数法结合四流累加法构造了多层四流离散纵坐标和多层四流球谐函数法,在有云情况下可以使得加热率和辐射通量的相对误差小于1%。
以上研究进展表明与二流辐射传输方案相比,四流方案在计算精度上有明显的优势。采用二流累加法和单层四流辐射传输方案相结合能够兼顾计算时间和精度。Li等(1996)的研究表明,对于求解单层辐射传输方程而言,四流球谐函数辐射传输算法计算的透过率和反射率精度要略优于四流离散纵标法,大幅度优于Eddington近似方法。因此,本研究利用Li等(1996)给出的单层四流球谐函数辐射传输算法的数值解析解结合累加法,构造了应用于非均匀大气辐射传输计算的四流球谐函数辐射传输算法,首先应用于北京气候中心辐射传输模式(BCC-RAD)(Zhang et al,2003,2006a,2006b;Randles et al,2013),并进行了检验。2 单层四流球谐函数结合多层二流累加法的辐射传输算法介绍2.1 单层四流球谐函数求解
一般的辐射传输方程可以写成以下形式(廖国男,2004)
式中,μ为局地天顶角,I是辐射强度,τ是光学厚度,J是源函数。Li等(1996)推导了单层四流球谐函数算法的数值解
式中,Ii为辐射强度展开式的各项,F±为向上和向下辐射通量。 2.2 多层二流累加法Coakley等(1983)给出了计算2层大气总的反射率和透射率的公式
式中,ri、ri、ti、ti分别表示第i层的反射率、漫反射率、透过率/漫射透过率;r12、r12、t12、t12分别表示总反射率、总漫反射率、总透过率、总漫射透过率;μ0是入射太阳天顶角余弦,τ1表示光学厚度。通过式(3)—(6),可以得到任意两层的反射率和透过率,从而得到每层大气的向上和向下的辐射通量。
单层四流球谐函数方法在辐射强度的计算上采用了更多的展开项,在精度上优于单层二流辐射传输方案。利用式(3)—(6)计算的任意层的反射率和透过率,采用的是二流累加法,在时间上优于多层四流辐射传输方案。因此,单层四流球谐函数和多层二流累加法的组合方式,一方面单层计算具有四流方法的精度;另一方面可以节约部分计算时间。
2.3 BCC-RAD介绍
BCC-RAD采用Zhang等(2003,2006a,2006b)研发的相关k分布算法;原短波辐射传输方案采用二流Eddington算法。波长范围10—49000 cm-1,分为17个波段(长波8个波段,短波9个波段)。共包含了8种主要温室气体(水汽、二氧化碳、臭氧、氧化亚氮、甲烷和氟氯烃等),其气体吸收系数和吸收截面数据取自HITRAN2000光谱数据库(Rothman et al,2001)。水汽、二氧化碳、臭氧和氧气的连续吸收系数数据来源于CKD_2.4(Zhang et al,2003)。水云和冰云光学性质来自Nakajima等(2000);气溶胶光学性质取自卫晓东等(2011)、Zhang等(2012)。详细介绍可参见Randles等(2013)。 3 四流球谐函数结合二流累加法在大气辐射模式中的应用 3.1 晴空大气情况
将48流DISORT算法、Eddington近似、四流球谐函数和四流离散纵坐标算法加入BCC-RAD,主要比较四流球谐函数方法与传统的Eddington近似算法对大气辐射计算的影响。由于四流离散纵坐标法被广泛应用于大气辐射传输模式中,因此,文中也将该算法加入比较。同时将48流DISORT辐射传输算法的结果作为参考标准。4种辐射传输方案的相函数展开式采用Henyey等(1941)提出的公式
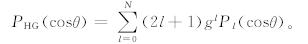
式中,PHG(cosθ)为项函数,Pl(cosθ)为勒让德函数展开式,g为非称的因子,θ为太阳天项角。
48流DISORT辐射传输算法相函数展开为48项,Eddington近似将相函数展开成两项,四流球谐函数和四流离散纵坐标法将相函数展开成4项。在进行辐射传输计算之前对光学厚度、单次散射比和相函数采用了δ函数调整(廖国男,2004)。
首先在晴空情况下比较了Eddington近似、四流球谐函数、四流离散纵坐标法与48流DISORT算法计算的辐射通量以及加热率的差别。在计算中,大气廓线采用的中纬度夏季大气廓线与张华等(2005)相同,模式的垂直分辨率为1 km,在计算中模式顶选取在70 km,因为50 km以上需要考虑非局地热力学,因此,作图时仅显示50 km以下的结果。地表反照率采用Nakajima等(2000)的方案,在短波第9、10波段分别取0.1和0.26;在短波11—17波段取为0.3。
图 1给出了晴空加热率的比较结果。与48流DISORT辐射传输方案的加热率相比,Eddington近似、四流球谐函数和四流离散纵坐标3种辐射传输方案在40 km以下高度的绝对误差都小于0.3 K/d;太阳天顶角为60°时小于0.15 K/d。20 km 以下高度,3种辐射传输方案的加热率计算结果的绝对误差都小于0.03 K/d;20 km以上高度,3种辐射传输方案计算的加热率误差有所增大,但相对误差不超过2%。
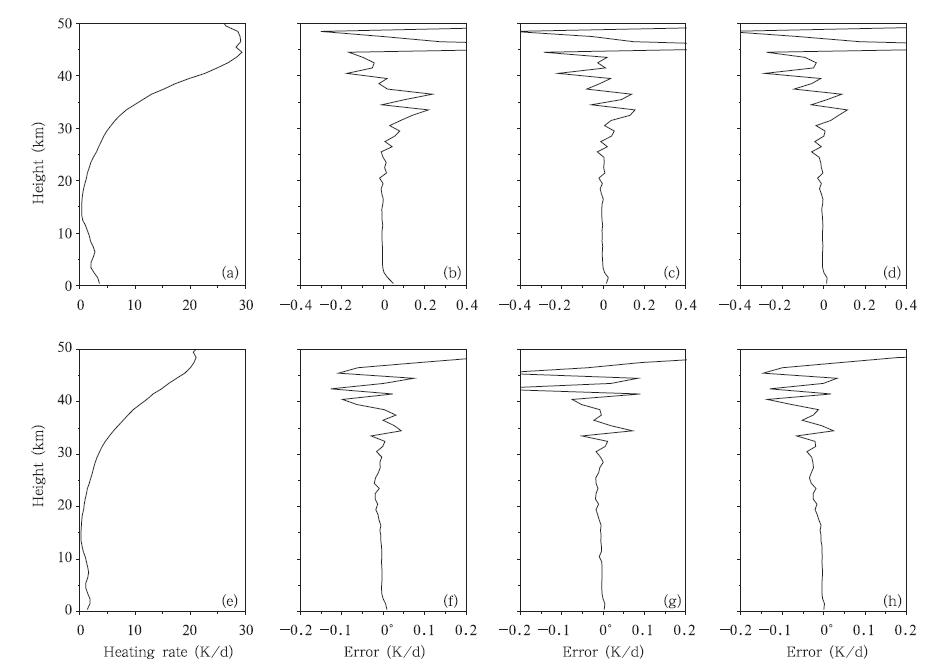 |
| 图 1 晴空短波加热率
(a、e.48流DISORT辐射传输方案的参考结果,b、f. Eddington近似,c、g.四流球谐函数,d、h.四流离散纵坐标辐射传输方案与48流DISORT辐射传输方案的差值;(a)—(d)为 太阳天顶角为0°时的结果,(e)—(h)为太阳天顶角为60°时的结果) Fig. 1 Shortwave heating rate in clear sky ((a),(e)is the results of the 48-stream discrete-ordinate approximation method,the others are the differences between the Eddington method((b),(f)),four-stream spherical harmonic expansion approximation((c),(g)),four-stream discrete-ordinate approximation((d),(h)) and 48-stream discrete-ordinate approximation method,respectively.(a)-(d)are for the solar zenith angle of 0°; and (e)-(h)are for the solar zenith angle of 60°) |
图 2给出了短波向下辐射通量的比较结果,与48流DISORT辐射传输方案的向下辐射通量结果相比,当太阳天顶角为0°时,Eddington近似、四流球谐函数、四流离散纵坐标3种辐射传输方案中,Eddington近似的最大误差为-6.3 W/m2;四流球谐函数法的最大误差为-1.5 W/m2;四流离散纵坐标法的最大误差为2.8 W/m2。太阳天顶角为60°时,Edington近似的最大误差为-1.44 W/m2;四流球谐函数法的最大误差为-1.1 W/m2;四流离散纵坐标法的最大误差为1.14 W/m2。从中可以看出,当太阳天顶角为0°时,两种四流辐射传输算法的结果要优于Eddington近似。太阳天顶角为60°时,3种辐射传输算法的误差相差不大,其中Eddington近似和四流球谐函数的误差曲线的形状相似,只是四流球谐函数的误差要略小。Eddington近似是球谐函数的二流展开。因此,与四流球谐函数的误差曲线形状相似,而由于四流球谐函数的辐射强度展开式比Eddington近似的展开式多两项,因此计算误差要略小。对于晴空向下辐射通量而言,3种辐散传输算法的误差相差不大,相对误差都在0.6%以内。
 |
| 图 2 同图 1,但为晴空向下辐射通量的结果 Fig. 2 As in Fig. 1 but for the downward radiative flux in clear sky |
图 3给出了短波向上辐射通量的比较。与48流DISORT辐射传输方案的结果相比,太阳天顶角为0°时,Eddington近似、四流球谐函数、四流离散纵坐标3种辐射传输方案中 Eddington近似的最大误差为-1.92 W/m2,四流球谐函数法的最大误差为-1.62 W/m2,四流离散纵坐标法的最大误差为2.17 W/m2。太阳天顶角为60°时,Eddington近似的最大误差为-1.11 W/m2,四流球谐函数法的最大误差为-0.92 W/m2,四流离散纵坐标法的最大误差为-0.9 W/m2。对于晴空向上辐射通量而言,3种辐散传输算法的误差相差不大,相对误差都在1%以内。
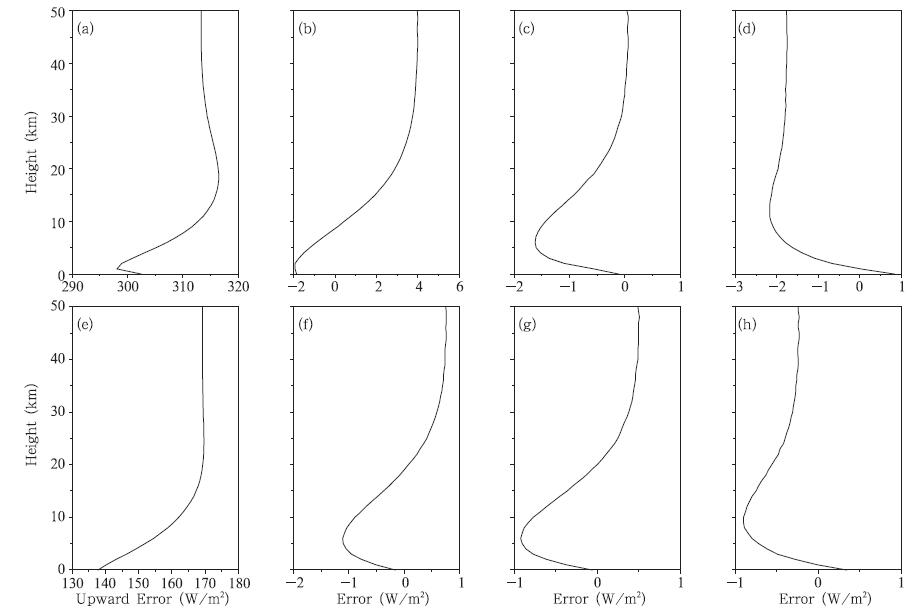 |
| 图 3 同图 1,但为晴空向上辐射通量的结果 Fig. 3 As in Fig. 1 but for the upward radiative flux in clear sky |
在有云情况下,仍然采用中纬度夏季大气廓线进行计算。云水含量和云滴有效半径的设置与Fu等(1997)中的设置一致,本文选取的低云位于1—2 km,云水含量为0.22 g/m3,云滴有效半径为5.89 μm;中云位于4—5 km,云水含量为0.28 g/m3,云滴有效半径为6.2 μm。由于着重关注云的辐射传输计算,因此在计算有云大气情况时,将模式的垂直分辨率加密到0.25 km,同时只显示16 km以下有云时的计算结果,垂直分辨率设置与Fu等(1997)一致。
图 4给出了低云情况下短波加热率的比较。可以看出,与48流DISORT辐射传输方案加热率结果相比,太阳天顶角为0°时,Eddington近似、四流球谐函数、四流离散纵坐标3种辐射传输方案中,Eddington近似在云顶的加热率最大误差为-1.57 K/d,而四流球谐函数和四流离散纵坐标方法在云顶的加热率绝对误差都在0.3 K/d以内;太阳天顶角为60°时,Eddington近似、四流球谐函数、四流离散纵坐标3种辐射传输方案计算的云顶加热率的绝对误差都小于0.2 K/d。这表明在太阳天顶角比较小时,Eddington近似引起的云顶加热率的相对误差可以达到5%,而同样情况下的四流球谐函数和四流离散纵坐标方案的相对误差小于1%。
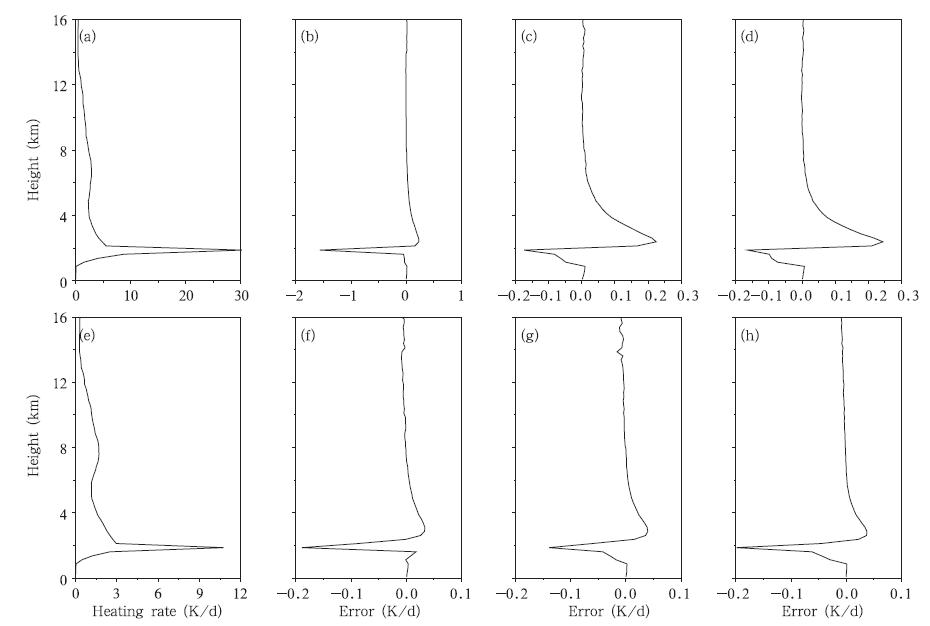 |
| 图 4 同图 1,但为有云大气短波加热率的结果 Fig. 4 As in Fig. 1 but for the shortwave heating rate in cloudy sky |
图 5给出了有云大气短波向下辐射通量的比较。可以看出,与48流DISORT辐射传输方案向下辐射通量结果相比,太阳天顶角为0°时,Eddington近似、四流球谐函数、四流离散纵坐标3种辐射传输计算方案中,Eddington近似的最大误差为-13.6 W/m2,四流球谐函数法最大误差为5.13 W/m2,四流离散纵坐标法的最大误差为40.87 W/m2。而太阳天顶角为60°时,Eddington近似的最大误差为-6.64 W/m2,四流球谐函数法的最大误差为-13.26 W/m2,四流离散纵坐标法的最大误差为9.82 W/m2。当太阳天顶角为0°时,3种辐射传输方案计算的短波向下辐射通量的最大差别都出现在云顶的下一层大气,同时Eddington方案的最大差别为负值,而两种四流辐射传输算法的最大差别为正值。出现这种差别的原因可能与相函数的展开式有关。两种四流方案都将相函数展开成4项,与Eddington二流方案相比多展开了两项,因此可能造成更多的前向散射,从而造成云顶下一层的辐射通量相对较大,而在进行辐射传输计算时由于仍然采用与二流方案相匹配的累加法,因此计算的总的辐射通量,会由于单层四流方案与多层二流累加法的不匹配造成比较大的误差。而当太阳天顶角为60°时,Eddington近似和四流球谐函数法计算的短波向下辐射通量的最大误差都出现在云顶所在层大气,最大误差为负值;而四流球谐函数算法计算的向下辐射通量的最大误差出现云顶下一层大气,最大误差为正值。
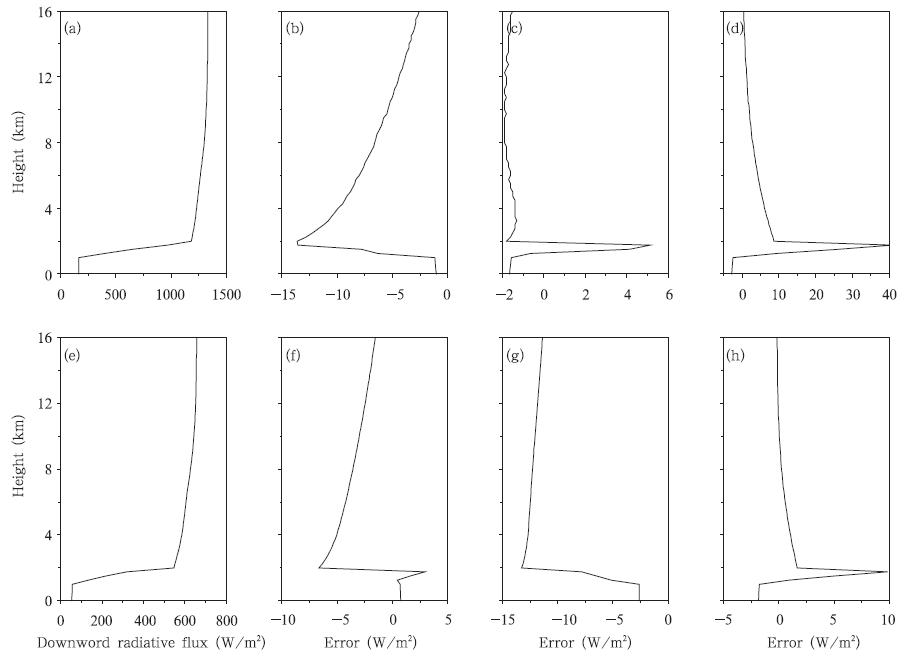 |
| 图 5 同图 1,但为有云大气短波向下辐射通量的结果 Fig. 5 As in Fig. 1 but for the downward radiative flux in cloudy sky |
图 6给出有云大气短波向上辐射通量的比较。可以看出,与48流DISORT辐射传输方案向上辐射通量结果相比,太阳天顶角为0°时,Eddington近似、四流球谐函数、四流离散纵坐标3种辐射传输方案中,Eddington近似的最大误差为-12.63 W/m2,四 流球谐函数法的最大误差为6.79 W/m2,四流离散纵坐标法的最大误差为43.57 W/m2;太阳天顶角为60°时,Eddington近似的最大误差为-6.71 W/m2,四流球谐函数法的最大误差为-10.76 W/m2,四流离散纵坐标方法的最大误差为11.53 W/m2。最大误差出现的位置与正负和短波向下辐射通量的情况一致。
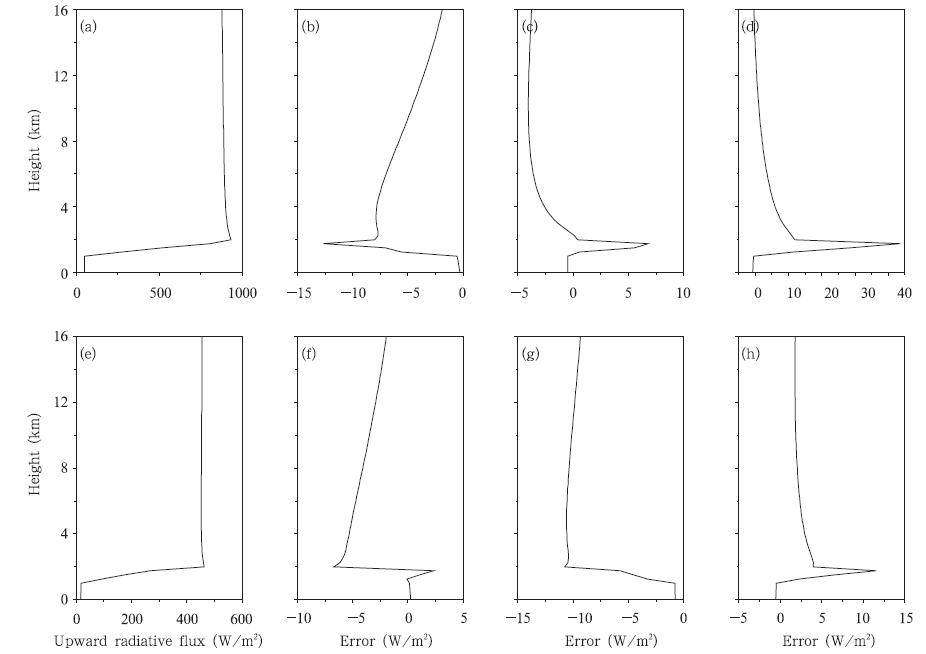 |
| 图 6 同图 1,但为有云大气短波向上辐射通量的结果 Fig. 6 As in Fig. 1 but for the upward radiative flux in cloudy sky |
从图 5和6可以看出,与48流DISORT辐射传输方案结果相比,Eddington近似、四流球谐函数、四流离散纵坐标3种辐射传输方案在云顶附近的辐射通量的误差较大,但是向上辐射通量和向下辐射通量的误差是一致的。气候模式中辐射模块的输出量主要是大气顶和地表的辐射通量以及加热率,而加热率是由相邻两层的净辐射通量决定的,因此在图 7中给出了48流DISORT算法计算的短波净辐射通量以及Eddington近似、四流球谐函数、四流离散纵坐标算法计算的短波净辐射通量分别与48流DISORT算法的差值。可以看出,以上3种辐射传输方案与48流DISORT辐射传输方案的结果相比,在太阳天顶角为0°时,Eddington近似的最大误差为-5.6 W/m2,四流球谐函数法的最大误差为-2.22 W/m2,四流离散纵坐标法的最大误差为-3.19 W/m2;太阳天顶角为60°时,Edington近似的最大误差为0.62 W/m2,四流球谐函数法的最大误差为-2.66 W/m2,四流离散纵坐标法的最大误差为-2.42 W/m2。从中可以看出,当太阳天顶角为0°时,两种四流辐射传输方案计算的净辐射通量要优于Eddington近似;而当太阳天顶角为60°时,Eddington近似计算的净辐射通量结果要优于这两种四流方案。
 |
| 图 7 同图 1,但为有云大气净辐射通量的结果 Fig. 7 As in Fig. 1 but for the net radiative flux in cloudy sky |
表 1给出了晴空大气情况大气顶和地表的净辐射通量的比较结果,大气顶取50 km。从表 1中可以看出太阳天顶角为0°时,四流球谐函数法的结果远好于其他两种方法;太阳高度角为60°时,四流球谐函数法也略好于其他两种方法。
| 晴空大气 | 太阳天顶角0° | 太阳天顶角60° | ||
| 大气顶 | 地表 | 大气顶 | 地表 | |
| DISORT | 1041.5 | 769.2 | 507.4 | 349.2 |
| Eddington | -3.7 | -4.4 | -0.1 | -0.5 |
| 四流球谐函数 | 0.3 | -0.4 | -0.1 | -0.3 |
| 四流离散纵坐标 | 1.8 | 2.0 | 0.3 | 0.8 |
表 2给出了有云大气的比较结果,可以看出,太阳天顶角为0°时,对大气顶的净辐射通量的计算,四流离散纵坐标法的结果较好,而对地表的净辐射通量的计算,Eddington方法结果较好;太阳天顶角为60°时,Eddington方法的结果要优于两种四流方法,可能是由于后两者单层辐射方程求解与多层二流累加法不匹配造成的;但两种四流方法的最大误差都小于3.3 W/m2。
| 有云大气 | 太阳天顶角0° | 太阳天顶角60° | ||
| 大气顶 | 地表 | 大气顶 | 地表 | |
| DISORT | 498.9 | 159.3 | 218.6 | 53.5 |
| Eddington | -1.6 | -0.6 | 0.9 | 0.7 |
| 四流球谐函数 | 1.6 | -1.2 | -3.3 | -1.9 |
| 四流离散纵坐标 | -0.3 | -2.8 | -2.3 | -1.5 |
图 8给出了低云和中云情况下的云顶加热率随太阳天顶角的变化。从中可以看出,随着太阳天顶角的减小(对应太阳天顶角的余弦的增大),云顶的向下辐射能量增大,因此云顶的加热率也随之增大。不论是低云还是中云情况,当太阳天顶角大于60°时,Eddington近似计算的云顶加热率略高于两种四流方案;当天顶角小于60°时,Eddington近似计算的云顶加热率开始低于两种四流方案。与48流辐射传输方案计算的云顶加热率相比,两种四流方 案计算的短波加热率在绝大多数太阳天顶角情况下都优于Eddington近似的结果。特别是在太阳天顶角小于60°时,两种四流算法要明显优于Eddington近似。由于中云的云水含量比低云高,造成的云顶加热率比低云大,因此其云顶加热率的误差比低云情况有所增大。
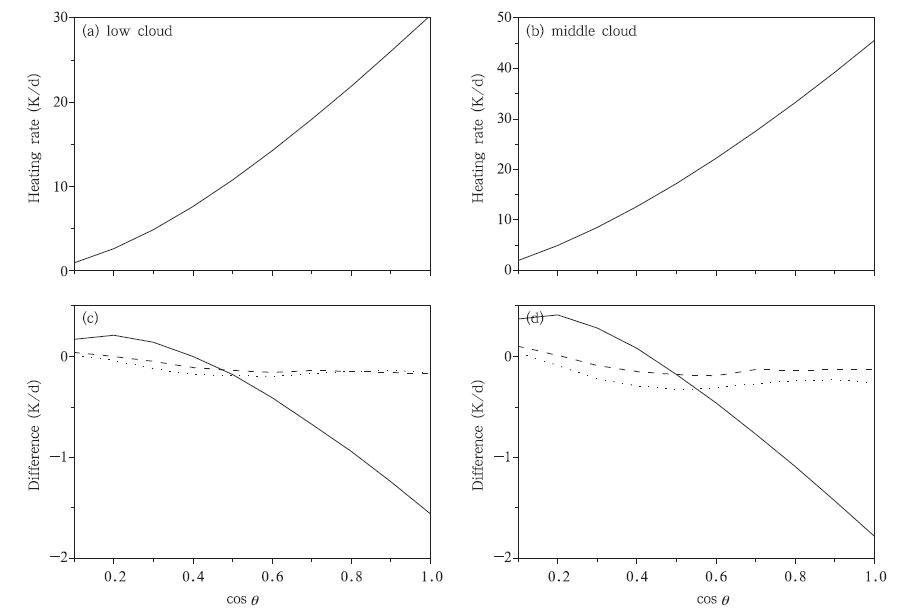 |
| 图 8 低云(a、c)和中云(b、d)情况下的云顶加热率随太阳天顶角变化
(a、b. 48流DISORT计算的云顶加热率,c、d. 实线、虚线和点线分别表示Eddington近似、 四流球谐函数法、四流离散纵坐标法计算的云顶加热率与48流DISORT结果的差值) Fig. 8 Changes in the heating rate at the top of cloud with the solar zenith angle for low(a,c) and middle(b,d)cloud cases ((a),(b)are the results of the 48-stream discrete-ordinate approximation method; and (c),(d)are the differences between the Eddington method(solid line),four-stream spherical harmonic expansion approximation(dashed line) and four-stream discrete-ordinate approximation(dotted line),and the 48-stream discrete-ordinate approximation method,respectively) |
图 9给出低云和中云情况下云顶加热率随云水含量的变化。可以看出,随着云水含量的增大,水云的光学厚度随之增大,云顶的加热率也随之增大。不论是低云还是中云情况,两种四流方案的短波云顶加热率误差都要远小于Eddington近似的误差。
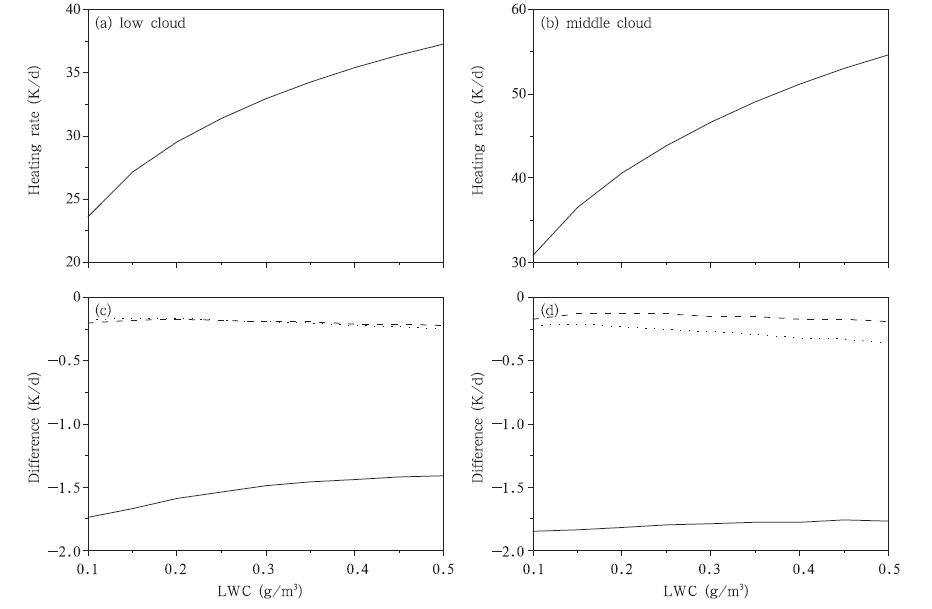 |
| 图 9 太阳天顶角0°,低云(a、c)和中云(b、d)情况下的云顶加热率随云水含量的变化
(a、b. 48流DISORT计算的云顶加热率,c、d. 实线、虚线和点线分别表示Eddington近似、 四流球谐函数法、四流离散纵坐标法计算的云顶加热率与48流DISORT结果的差值) Fig. 9 Changes in the heating rate at the top of cloud with among the liquid water content for low(a,c) and middle(b,d)cloud cases ((a),(b)are the results of the 48-stream discrete-ordinate approximation method; and (c),(d)are the differences between the Eddington method(solid line),four-stream spherical harmonic expansion approximation(dashed line) and four-stream discrete-ordinate approximation(dotted line),and the 48-stream discrete-ordinate approximation method,respectively) |
从表 3可以看出,DISORT48方法最费时,运行一次单气柱辐射传输的时间是Eddington方法的3000多倍,可以用于一般辐射传输模式计算,尚不能应用于气候模式;而四流球谐函数和四流离散纵坐标法的运行时间仅为Eddington近似的2倍左右,都在百分之一秒的量级,可以用于通常的辐射传输模式,也可以应用于全球气候模式的辐射过程计算。
|
| DISORT | Eddington | 四流球谐函数 | 四流离散纵坐标 |
| 运行时间(s) | 57.6 | 1.56×10-2 | 3.12×10-2 | 3.12×10-2 |
利用单层四流球谐函数结合二流累加法,构造了可用于多层大气的四流球谐函数算法,并将四流球谐函数应用于大气辐射模式中。结果表明:在未大幅度增加计算成本的情况下,所构造的四流球谐函数结合二流累加法方案,在晴空大气情况下,无论是对加热率的计算还是对辐射通量的计算都要优于传统的Eddington近似。在有云大气情况下,四流球谐函数和四流离散纵坐标法计算的加热率与标准结果相比优于传统的Eddington近似;对有云大气辐射通量的计算,当太阳天顶角为60°时,两种四 流方案的向上和向下辐射通量的最大误差要大于Eddington方法;当太阳天顶角为0°时,四流算法计算的向上和向下辐射通量的精度也没有传统的Eddington方法高。经分析发现这可能是由于单层精确的四流球谐函数计算与大气辐射传输二流累加法的不匹配造成的,这种不匹配使得单层计算的辐射通量的精度在逐层传输过程中损失了一部分。因此,单层精确的辐射计算也需要精确的辐射传输算法匹配才能达到提高整个辐射计算精度的目的。总体而言,本研究构建的四流球谐函数及二流累加法可以应用于大气辐射传输模式来改进晴空大气的整体辐射计算精度和有云大气的加热率计算精度,而不会大幅度增加计算成本。
| 荆现文,张华.2012.McICA云-辐射方案在国家气候中心全球气候模式中的应用与评估.大气科学,36(5):945-958 |
| 廖国男.2004.大气辐射导论.北京:气象出版社,614pp |
| 卫晓东,张华.2011.非球形沙尘气溶胶光学特性的分析.光学学报,31(5):D0501002,doi:10.3788/AOS201131.0501002 |
| 许尤福,赵凤生,闵玉秋.2011.平面平行大气中偏振辐射传输的数值计算.气象学报,69(5):912-921 |
| 杨学胜,沈元芳,徐国强.2009.辐射方案对GRAPES全球模式的影响.大气科学,33(3):593-599 |
| 张华,石广玉,刘毅.2005.两种逐线积分辐射模式大气吸收的比较研究.大气科学,29(4):581-594 |
| 张梦,王宏,黄兴友.2014.NASA/Goddard长波辐射方案在GRAPES_Meso模式中的应用研究.大气科学,38(3):603-614 |
| Ayash T, Gong S L, Jia C Q. 2008. Implementing the delta-four-stream approximation for solar radiation computations in an atmosphere general circulation model. J Atmos Sci, 65(7): 2448-2457 |
| Chou M D. 1992. A solar radiation model for use in climate studies. J Atmos Sci, 49(9): 762-772 |
| Coakley J A, Cess R D, Yurevich F B. 1983. The effect of tropospheric aerosols on the Earth's radiation budget: A parameterization for climate models. J Atmos Sci, 40(1): 116-138 |
| Fu Q, Liou K N, Cribb M C, et al. 1997. Multiple scattering parameterization in thermal infrared radiative transfer. J Atmos Sci, 54(24): 2799-2812 |
| Henyey L C, Greenstein J L. 1941. Diffuse radiation in the galaxy. Astrophys J, 93: 70-83 |
| Kay M J, Box M A, Trautmann T, et al. 2001. Actinic flux and net flux calculations in radiative transfer: A comparative study of computational efficiency. J Atmos Sci, 58(24): 3752-3761 |
| Li J, Ramaswamy V. 1996. Four-stream spherical harmonic expansion approximation for solar radiative transfer. J Atmos Sci, 53(8): 1174-1186 |
| Liou K N, Fu Q, Ackerman T P. 1988. A simple formulation of the delta-four-stream approximation for radiative transfer paramterization. J Atmos Sci, 45(13): 1940-1947 |
| Nakajima T, Tsukamoto M, Tsushima Y, et al. 2000. Modeling of the radiative process in an atmospheric general circulation model. Appl Opt, 39(27): 4869-4878 |
| Randles C A, Kinne S, Myhre G, et al. 2013. Intercomparison of shortwave radiative transfer schemes in global aerosol modeling: results from the AeroCom Radiative Transfer Experiment. Atmos Chem Phys, 13(5): 2347-2379 |
| Rothman L S, Barbe A, Benner D C, et al. 2001. The HITRAN molecular spectroscopic database: Edition of 2000 including updates of 2001. J Quant Spectrosc Radiat Transfer, 82(1): 5-44 |
| Scinocca J F, McFarlane N A, Lazare M, et al. 2008. Technical Note: The CCCma third generation AGCM and its extension into the middle atmosphere. Atmos Chem Phys, 8(23): 7055-7074 |
| Shibata K, Uchiyama A. 1992. Accuracy of the delta-four-stream approximation in inhomogeneous scattering atmospheres. J Meteor Soc Japan, 70(6): 1097-1109 |
| Stamnes K, Tsay S C, Wiscombe W, et al. 1988. A numerically stable algorithm for discrete-ordinate-method radiative transfer in multiple scattering and emitting layered media. Appl Opt, 27(12): 2502-2509 |
| Zhang F, Shen Z P, Li J G, et al. 2013a. Analytical delta-four-stream doubling-adding method for radiative transfer parameterizations. J Atmos Sci, 70(3): 794-808 |
| Zhang F, Li J. 2013b. Doubling-adding method for delta-four-stream spherical harmonic expansion approximation in radiative transfer parameterization. J Atmos Sci, 70(10): 3084-3101 |
| Zhang H, Nakajima T, Shi G Y, et al. 2003. An optimal approach to overlapping bands with correlated k-distribution method and its application to radiative calculations. J Geophy Res, 108(D20): doi: 10.1029/2002JD003358 |
| Zhang H, Shi G Y, NakajimaT, et al. 2006a. The effects of the choice of the k-interval number on radiative calculations. J Quant Spectrosc Radiat Transfer, 98(1): 31-43 |
| Zhang H, Suzuki T, Nakajima T, et al. 2006b. Effects of band division on radiative calculations. Optical Eng, 45(1): D016002, doi: 10.1117/1.2160521 |
| Zhang H, Shen Z P, Wei X D, et al. 2012. Comparison of optical properties of nitrate and sulfate aerosol and the direct radiative forcing due to nitrate in China. Atmos Res, 113: 113-125 |
| Zhang H, Jing X W, Li J. 2014. Application and evaluation of a new radiation code under McICA scheme in BCC_AGCM2.0.1. Geosci Model Dev, 7(3): 737-754 |
 2014, Vol. 72
2014, Vol. 72