中国气象学会主办。
文章信息
- 穆穆, 王强, 段晚锁, 姜智娜. 2014.
- MU Mu, WANG Qiang, DUAN Wansuo, JIANG Zhina. 2014.
- 条件非线性最优扰动法在大气与海洋目标观测研究中的应用
- Application of conditional nonlinear optimal perturbation to targeted observation studies of the atmosphere and ocean
- 气象学报, 72(5): 1001-1011
- Acta Meteorologica Sinica, 72(5): 1001-1011.
- http://dx.doi.org/10.11676/qxxb2014.081
-
文章历史
- 收稿日期:2014-3-13
- 改回日期:2014-7-11
2. 中国科学院大气物理研究所大气科学和地球流体力学数值模拟国家重点实验室, 北京, 100029;
3. 中国气象科学研究院灾害天气国家重点实验室, 北京, 100081
2. State Key Laboratory of Numerical Modeling for Atmospheric Sciences and Geophysical Fluid Dynamics (LASG), Institute of Atmospheric Physics, Chinese Academy of Sciences, Beijing 100029, China;
3. State Key Laboratory of Severe Weather (LaSW), Chinese Academy of Meteorological Sciences, Beijing 100081, China
在数值天气预报发展的初期,气象学家们注意到某一区域数值预报的技巧受限于前期某一局部区域的初值条件(Riehl et al,1956),这意味着在增加观测以改善初始条件进而提高预报效果时,只在该局部区域增加观测,可能对预报结果改进的效果不亚于进行大范围增加观测改进预报技巧的效果。上述为提高某一区域的数值预报而在前期某一局部区域增加观测的思想,在20世纪90年代中后期开始被称为“目标观测”。目标观测,又称为适应性观测,具体地,它是指为了使将来时刻(验证时刻tv)所关注的区域(验证区)内的预报更加准确,要在将来时刻(目标时刻ta, ta<tv)对验证区域预报影响较大的区域(敏感区)进行额外的加密观测,获得更多的观测资料(图 1)。这些观测资料经过资料同化系统处理后,为模式提供更接近真实状况的初始场,以期得到更加准确的预报。关于目标观测更详细的介绍参见Mu(2013)。
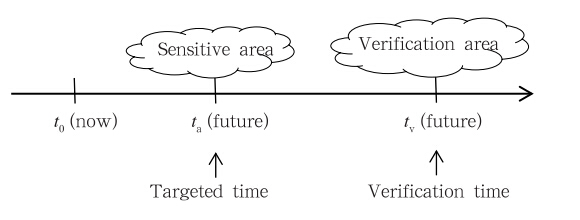 |
| 图 1 目标观测示意图(穆穆等,2012)Fig. 1 Schematic diagram of targeted observation(Mu et al,2012) |
数值天气预报和气候预测的理论与实践告诉我们,除了预报模式的性能以外,成功的预报还依赖于初始场的质量;特别地,初始场中是否含有所关注对象发生、发展的信号,以及初始误差的大小,都将影响预报的效果。仔细分析可知,目标观测的核心思路是寻找对预报技巧影响较大的初始误差敏感区(记为区域A)。另外,也应考察异常事件发生的前期征兆的敏感区(记为区域B)。目前并没有关于这两类敏感区之间关系的研究。直觉上可能认为区域A应该覆盖区域B,但是分析起来仍然有可能出现两个区域差别较大的情形。这时,虽然用区域A指导的目标观测可以较有效地降低预报误差,但是可能仍然没有很好地捕捉到信号,预报技巧可能仍然不高。另外,如果敏感区A和敏感区B大体相同,那么仅在该区域进行观测,既能发现前期征兆,又能减小初始误差,这将十分有助于提高预报的准确性,同时能够节省由观测带来的大量开支。有趣的是,穆穆等在研究厄尔尼诺-南方涛动(ENSO)、黑潮路径变异和大气的阻塞等大气与海洋异常事件的可预报性时,发现上述两个敏感区基本相同。该结果不仅揭示了前述两类敏感区之间的关系,也为上述事件的目标观测,打下了更坚实的基础。
在上述研究工作中,使用了条件非线性最优扰动(CNOP;Mu et al,2003)法。具体地,条件非线性最优扰动代表了在预报时刻具有最大非线性发展的一类初始扰动。由于不做线性近似,它充分考虑了非线性动力与物理过程的影响,是奇异向量方法在非线性领域的拓展(Duan et al,2009a)。已有研究(Mu et al,2011,2014; Wang et al,2013)将条件非线性最优扰动法应用于研究ENSO、黑潮路径变异和大气的阻塞事件可预报性中的最优前期征兆(OPR)和增长最快初始误差(OGE)问题。所谓最优前期征兆,是指在一定条件下,最容易发展成某一天气或气候事件的初始异常;增长最快初始误差则是指发展最快且导致不容忽视的预报误差的初始误差。结果发现对于这些事件,最优前期征兆和最快增长初始误差的空间结构均具有高度的相似性,另外,还发现最优前期征兆和最快增长初始误差的空间模态具有明显的局地性特征。这表明基于这种相似性和局地性特征识别的敏感区不仅能够较好地捕捉到前期征兆,还能够有效地减小初始误差,提高预报技巧。
条件非线性最优扰动法也已经被成功应用于台风和暴雨的目标观测敏感区的确定,为提高台风预报技巧提供指导,例如Mu等(2009)和Qin等(2011)用条件非线性最优扰动法确定了台风目标观测敏感区,Wang等(2009)和谭晓伟等(2011)发展了一种快速计算条件非线性最优扰动的算法并用其识别出台风目标观测的敏感区;此外,刘段灵等(2013)还将条件非线性最优扰动法用于确定长江中下游地区冬季暴雨的目标观测敏感区,关于这部分研究的成果,可参见Mu(2013),这里不再赘述。本研究重点总结近年来关于ENSO事件、黑潮路径变异事件,以及阻塞事件的最优前期征兆和最快增长初始误差的研究结果,特别关注的是最优前期征兆和最快增长初始误差的相似性及其伴随的局地性特征对确定目标观测敏感区的启发,为这些事件的目标观测研究与实施,提供科学支持。2 厄尔尼诺预测的目标观测敏感区
国际上许多文献从初始误差增长的角度研究ENSO可预报性。例如,Moore等(1996)和Xue等(1997)的研究表明了ENSO可预报性对数值模式初始误差的敏感依赖性;Chen等(2004)通过改进Zebiak-Cane数值模式(Zebiak et al,1987)的初始化程序,减弱了ENSO事件的春季预报障碍(SPB)现象,提高了该模式对ENSO的预报技巧。近来,Mu等(2007a,2007b)和Duan等(2009b)进一步研究了ENSO的可预报性,揭示了非线性不稳定性导致的初始误差的增长对ENSO可预报性的影响,而且表明了具有特定空间结构的初始误差能够导致显著的春季预报障碍现象,产生较大的预报不确定性。Duan等(2010)和Yu等(2012a)量化比较了初始误差和模式参数误差对ENSO可预报性的影响,阐明了初始误差是ENSO预报结果不确定性的主要误差来源之一。因此,对初始态的准确估计可能有助于较大程度地提高ENSO预报技巧。要提供更准确的初始场,方法之一是增加额外观测。正如引言所述,利用目标观测改进初始场,有可能为改进ENSO数值预报模式的初始场提供一条捷径(Duan et al,2009a; Yu et al,2009)。
Mu等(2007b)用Zebiak-Cane模式研究发现,条件非线性最优扰动初始误差代表了厄尔尼诺事件最快增长初始误差,且最容易导致厄尔尼诺事件显著的春季预报障碍现象,而且还发现,与条件非线性最优扰动初始误差大小相同,但空间结构不同的初始误差却不能导致大的预报误差,并且这些误差的发展也没有明显的季节依赖性,最终未能导致春季预报障碍。该结果说明厄尔尼诺事件春季预报障碍现象的发生可能依赖于初始误差的特定空间结构。Yu等(2009)进一步利用聚类分析将条件非线性最优扰动初始误差分为两类(图 2):一类误差的海表温度距平(SSTA)分量在赤道太平洋呈现偶极子模态,表现为东太平洋的正异常和中西太平洋的负异常,而斜温层深度则沿着赤道一致加深(记为type-1 最快增长初始误差);另一类误差则呈现与前者几乎相反的模态(记为type-2 最快增长初始误差)。由此可见,条件非线性最优扰动初始误差尽管存在不同的空间结构,但空间模态一致地具有局地性特征,即误差能量主要集中于某些局地区域。
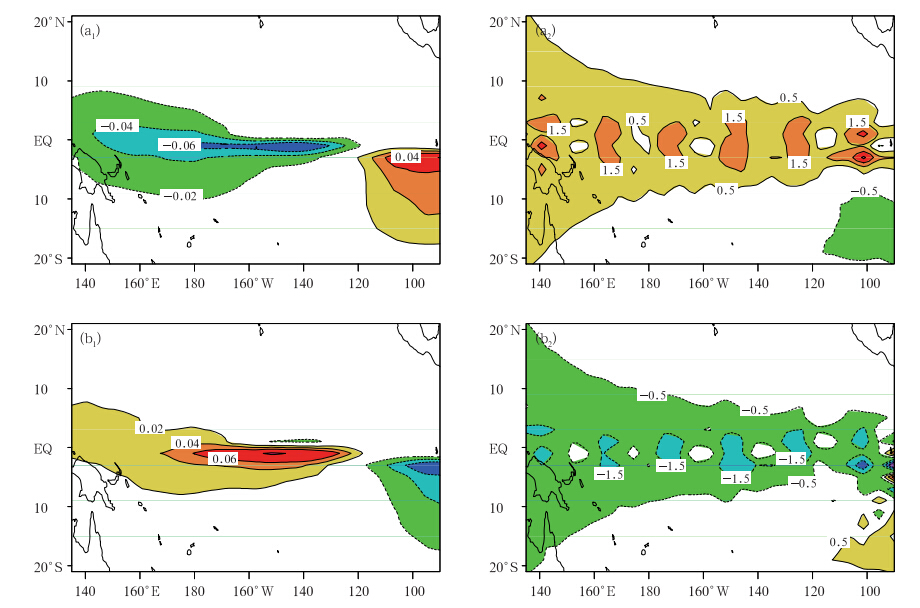 |
| 图 2 厄尔尼诺事件的type-1(a1、a2)和type-2(b1、b2)最快增长初始误差(a1、b1.海表温度距平,a2、b2.斜温层深度距平;Yu et al,2009)Fig. 2 Type-1(a) and type-2(b)OGEs for El Ni o events(a1,b1. the sea surface temperature anomaly(SSTA),a2,b2. the thermocline depth anomaly;Yu et al,2009) |
条件非线性最优扰动也扮演了最容易导致厄尔尼诺和拉尼娜事件的初始距平模态,即厄尔尼诺和拉尼娜事件的最优前期征兆(图 3)。Duan等(2013)计算的Zebiak-Cane模式条件非线性最优扰动初始距平模态表明,厄尔尼诺事件的最优前期征兆通常具有与厄尔尼诺事件的type-1 最快增长初始误差相似的模态,即海表温度距平分量在赤道东太平洋为正异常,而在中西太平洋为负异常,另外,斜温层深度沿着赤道一致加深;Mu等(2014)进一步研究表明,拉尼娜事件的最优前期征兆与type-2 最快增长初始误差的模态相似。因此,Mu等(2014)指出,厄尔尼诺事件的最优前期征兆与最快增长初始误差的空间结构具有高度的相似性和明显的局地性特征,而且它们的发展机理也高度类似,即厄尔尼诺事件的最快增长初始误差具有类似于厄尔尼诺或拉尼娜事件发展的动力学行为;这种最优前期征兆和最快增长初始误差的相似性启发人们考虑:如果在最优前期征兆和最快增长初始误差的扰动大值区增加观测,不仅可以改善数值预报的初始场,而且可能有助于加强人们对ENSO事件前期信号的识别能力,从而提高对ENSO事件的预报技巧;这样的扰动大值区可能代表了ENSO预测的敏感区。
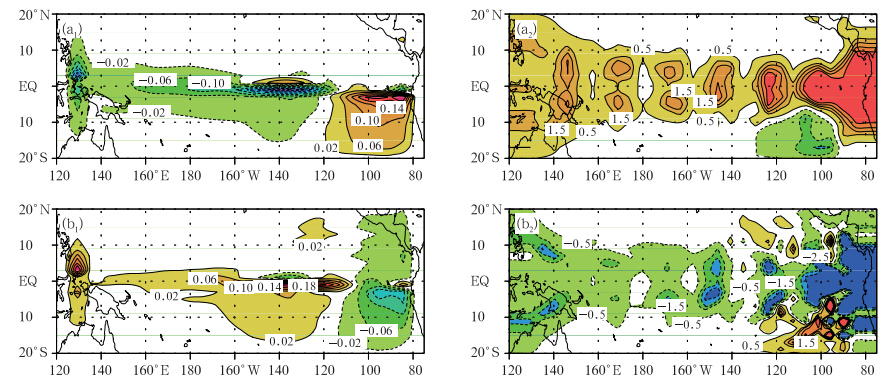 |
| 图 3 厄尔尼诺(a1、a2)和拉尼娜(b1、b2)的最优前期征兆(a1、b1.海表温度距平,a2、b2.斜温层深度距平;Mu et al,2014)Fig. 3 OPRs for El Ni o(a1,a2) and La Ni a(b1,b2)(a1,b1. the SSTA,a2,b2. the thermocline depth anomaly;Mu et al,2014) |
为了考察上述敏感区的有效性,Yu等(2012b)将热带太平洋划分为6个区域(图 4),其中区域5(赤道中东太平洋区域)是厄尔尼诺事件最优前期征兆和最快增长初始误差的扰动大值区。对于每一个区域,计算了对厄尔尼诺预报结果不确定性影响最大的条件非线性最优扰动误差,并考察了它们导致的预报误差的大小。结果表明,与其他区域相比,区域5的条件非线性最优扰动误差导致了厄尔尼诺事件最大的预报误差,说明赤道中东太平洋的海表温度初始误差可能对厄尔尼诺预报结果的影响最大,也就是说,厄尔尼诺预报结果的不确定性对赤道中东太平洋区域的海表温度初始误差最敏感。
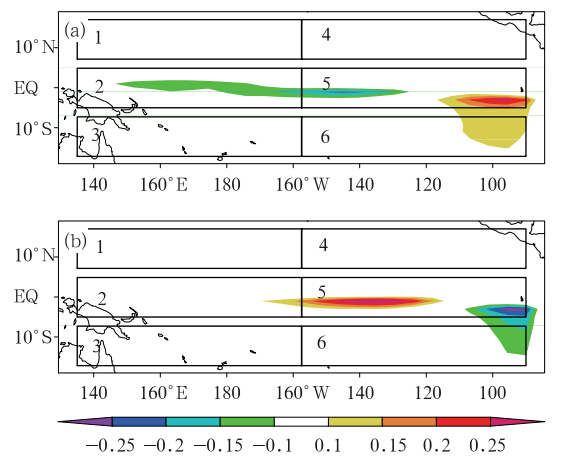 |
| 图 4 依据两类条件非线性最优扰动型初始误差,将热带太平洋区域划分为6个区域,即Domain i(i=1,…,6)(a.type-1,b.type-2;其中两类误差的大值区发生在Domain 5;Yu et al,2012b)Fig. 4 Two kinds of CNOP initial errors:(a)type-1 and (b)type-2 over the tropical Pacific divided into six regions labeled as Domain i(i=1,…,6).(large values of both kinds of errors occur mainly in Domain 5;Yu et al,2012b) |
为了在理想回报试验中进一步验证上述敏感区,Yu等(2012b)用Zebiak-Cane模式的最新版本(LDEO5;Chen et al,2004)关于1980年1月至1999年12月回报试验的240个初始分析场,考察了Zebiak-Cane模式在回报厄尔尼诺事件时上述敏感区对改进预报技巧的影响。对于这些初始分析场,Yu等(2012b)将上述6个区域中每个区域的初始分析场替换为厄尔尼诺事件的初始场,即分别消除每个区域的初始分析场误差,考察预报误差的减小程度。图 5表明,当区域5的初始分析场误差被消除后,厄尔尼诺事件的预报误差大幅度减小,其减小程度显著大于消除其他区域导致的预报误差的减小。上述结果表明,区域5,即赤道中东太平洋区域,也就是厄尔尼诺事件的最优前期征兆和最快增长初始误差的扰动大值区,可能确实代表了厄尔尼诺预测的目标观测敏感区。因此,如果在该区域增加观测改善初始场,ENSO的预报误差可能会大幅度减小,而且也有助于人们捕捉最优前期征兆刻画的厄尔尼诺事件的前期信号,进而提高对ENSO的预报技巧。
 |
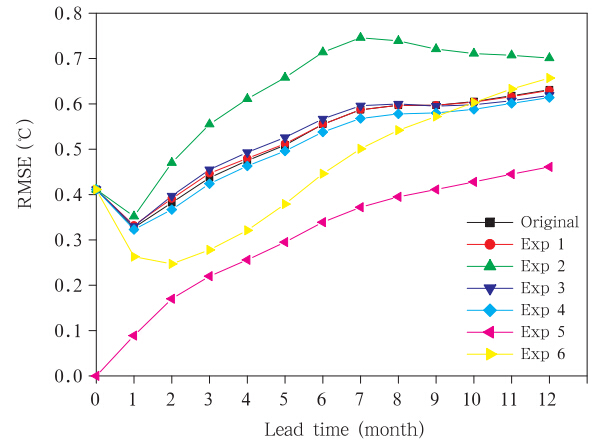
| 图 5 由初始分析误差(即original所示)和6组新的初始分析误差(即Exp i所示,i=1,2,…,6)导致的预报误差的Nino-3海温距平的均方根误差(其中每一组新初始分析误差是通过消除原初始分析误差场中图 4所示每个区域的误差所得到的;Yu et al,2012b)Fig. 5 Root-mean-square errors for Nino-3 SSTA caused by the original initial errors(black line) and six other sets of initial errors(shown by Exp i,i=1,2,…,6). Each set of new initial errors was generated by eliminating errors in one of the six domains(Fig. 4)from the original initial errors(Yu et al,2012b) |
日本南部的黑潮路径变异一直都是物理海洋学研究的一个重点,由于其对气候、海洋环境及渔业有重要影响,所以近来许多研究者考虑对它进行预报。在开展业务预报之前,许多学者开展了相关的可预报性研究(Komori et al,2003; Kamachi et al,2004; Miyazawa et al,2005; Usui et al,2006; Wang et al,2012)。特别地,类似于上述ENSO可预报性研究,Wang等(2013)利用条件非线性最优扰动方法研究了黑潮路径变异可预报性中的最优前期征兆和最快增长初始误差,发现了最优前期征兆和最快增长初始误差的空间结构具有高度的相似性和明显的局地性特征。
 |
| 图 6 黑潮大弯曲路径发生的最优前期征兆(a)及大弯曲路径预报中的type-1 最快增长 初始误差(b)和type-2最快增长初始误差(c)的上层厚度分量(单位:m)(Wang et al,2013)Fig. 6 The upper-layer thickness component of the OPR(a)for the Kuroshio large me and er,and the type-1(b) and type-2(c)OGEs in the prediction of the large me and er path(unit: m)(Wang et al,2013) |
Wang等(2013)首先利用1.5层浅水模式,用条件非线性最优扰动法考察了黑潮大弯曲路径发生的最优前期征兆。图 6a给出了该最优前期征兆的上层厚度扰动分量,可以看到其空间结构具有明显的局地性特征,并且主要位于黑潮大弯曲路径发生区域的上游,调查发现在最优前期征兆导致黑潮大弯曲路径形成过程中,位涡平流过程起主要作用。Wang等(2013)也计算了导致黑潮路径变异最大预报误差的最快增长初始误差,其包含两种类型误差:type-1最快增长初始误差和type-2最快增长初始误差(图 6b和c)。可以清楚的看到,最优前期征兆和两类最快增长初始误差的空间结构均比较相似,并且最优前期征兆和type-1最快增长初始误差的空间结构符号基本相反,相似系数为负,而和type-2最快增长初始误差的符号基本相同,相似系数为正。Wang等(2013)还发现,与最优前期征兆成负相似的type-1最快增长初始误差,其随时间的发展过程与最优前期征兆的发展过程也成负相似,并导致预报的黑潮大弯曲路径偏弱,同样,成正相似的type-2最快增长初始误差的发展过程与最优前期征兆的发展过程也成正相似,导致预报的黑潮大弯曲路径偏强,这反映了最优前期征兆和最快增长初始误差可能具有相似的发展机制。
以上揭示的最优前期征兆和最快增长初始误差的空间结构的相似性和局地性特征,引导人们进行黑潮路径变异预报的目标观测研究。为了识别目标观测敏感区,Wang等(2013)计算了type-1最快增长初始误差的总能量分布(图 7)。由于最优前期征兆和最快增长初始误差的空间结构有很高的相似性,所以它们的总能量分布与type-1最快增长初始误差的能量分布基本相同,因此这里未给出最优前期征兆和type-2最快增长初始误差的能量分布,具体可参见Wang等(2013)。从图 7可以看出,type-1最快增长初始误差的总能量的大值主要位于日本九州岛东南部。根据这一分布特征,他们将敏感区定义为一个矩形区域,使其恰好包含总能量的大值部分,该矩形区域被记为R3(如图 7所示)。
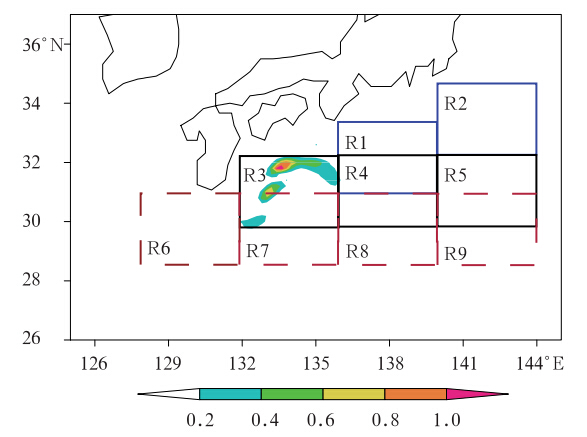 |
| 图 7 Type-1 最快增长初始误差的总能量的空间分布(阴影部分,单位:m3/s2),9个矩形区域被用于进行理想目标观测试验,其中R3区域为敏感区,这些区域的具体位置见表 1(Wang et al,2013)Fig. 7 The spatial structure of the total energy for type-1 OGE(shaded,unit: m3/s2). The nine regions were used for the ideal targeted observation experiments,where R3 was the sensitive area. The locations of these nine regions are listed in Table 1(Wang et al,2013) |
为了考察所得到的敏感区的有效性,Wang等(2013)研究了上述不同区域随机误差的发展。图 7中有9个相同大小的矩形区域,包括敏感区R3和其他8个任意选取的区域,每个区域包含240个格点。这些区域主要位于日本南部和黑潮延伸体上游,在每个区域产生40个随机误差场,每个随机误差场产生的过程如下:首先,对于每个区域生成一个服从给定方差σij的正态分布的随机序列,其中i表示模式变量(在1.5层浅水模式中共有3个模式变量),j表示格点,该随机序列记为N(0,σij),i=1,2,3;j=1,2,…,240。然后从随机序列N(0,σij)任意选取一个随机数作为变量i在格点j上的随机误差。取遍所有格点和模式变量,就能获得一个随机初始误差场。最后,为了比较随机误差场和type-1最快增长初始误差的发展,Wang等(2013)设定随机初始误差场的总能量与type-1最快增长初始误差的总能量相等,即将所得到的随机初始误差场进行尺度化,得到一个新的随机误差场,依此类推,每个区域能得到40个新的随机初始误差场。考察每个区域40个随机初始误差场的发展,得到的预报误差的平均动能列在表 1中,结果表明初始误差的发展依赖于其所在的位置,敏感区R3中的随机初始误差得到的预报误差最大,说明预报结果的不确定性对R3区域的初始误差十分敏感。
| 区域标记 | 区域位置 | 动能的平均值 (×109 m5/s2) |
| R1 | (31—33.4°N,136—140°E) | 9.6 |
| R2 | (32.2—34.6°N,140—144°E) | 3.1 |
| R3 | (29.8—32.2°N,132—136°E) | 26 |
| R4 | (29.8—32.2°N,136—140°E) | 9.6 |
| R5 | (29.8—32.2°N,140—144°E) | 4.7 |
| R6 | (28.6—31°N,128—132°E) | 1.7 |
| R7 | (28.6—31°N,132—136°E) | 7.6 |
| R8 | (28.6—31°N,136—140°E) | 6.5 |
| R9 | (28.6—31°N,140—144°E) | 2.7 |
为了考察在敏感区R3实施目标观测是否能较大程度的改进黑潮路径变异预报,Wang等(2013)进行了如下理想回报试验:首先在整个模式模拟区域生成40个随机初始误差场,这些随机初始误差场的总能量与type-1最快增长初始误差的总能量相同;考察这些随机误差场的发展,得到的预报误差的平均动能记为J1,然后,假设在9个区域中的一个区域实施目标观测,相应地,该区域内的初始随机误差被消除,而该区域以外的误差保持不变,这样对于每个区域就能得40个新的随机误差场,这些随机误差场发展得到的预报误差的平均动能记为J2,那么由于目标观测的实施而导致的预报误差相对减小程度为(J2-J1)/J1,显然负号表示预报误差减小。表 2给出了9个不同区域的预报误差相对减小程度,发现在敏感区R3区域预报误差的减小程度最大,达到43.59%。这说明在敏感区实施目标观测能够有效地减小黑潮路径变异的预报误差。综上所述,在上述敏感区进行目标观测,不仅可以显著地减小黑潮路径数值预报的预报误差,而且有利于捕捉黑潮路径变异的前期信号,从而提高对黑潮路径的预报技巧。
| 区域标记 | R1 | R2 | R3 | R4 | R5 | R6 | R7 | R8 | R9 |
| 预报误差动能的相对偏差(%) | -15.28 | -1.68 | -43.59 | -11.85 | -26.70 | -0.04 | -1.25 | -1.53 | 0.73 |
阻塞是一个典型的大尺度环流,其对区域天气和气候有着深远的影响(Rex,1950)。对阻塞预报对初始条件极端敏感,阻塞环流转型的预报技巧较低。因此,提高其预报能力是中长期数值天气预报研究的核心问题之一(Tibaldi et al,1990;Kimoto et al,1992; Frederiksen et al,2004),所以有必要开展阻塞的可预报性研究。正如在ENSO事件和黑潮路径变异事件的可预报性研究中,已经发现了最优前期征兆和最快增长初始误差的具有高度相似性且其空间模态存在显著的局地性特征,那么,这种最优前期征兆和最快增长初始误差的相似性及其伴随的局地性特征是否也在阻塞事件的预报中存在呢?
Jiang等(2010)用条件非线性最优扰动法和T21L3准地转全球谱模式(Marshall et al,1993)计算了欧洲—大西洋阻塞事件爆发的最优前期征兆。图 8显示该最优前期征兆主要呈现为北美大陆的波列结构,且随高度西倾,分布于大西洋急流的北侧,轴线沿着东北—西南方向。另外,从空间结构上看,最优前期征兆呈较强的局地性特征。考察最优前期征兆随着时间的发展演变,结果发现最优前期征兆扰动逐渐向下游传播并发展,最终在大西洋区域形成典型的偶极子阻塞结构。上述最优前期征兆扰动发展的能量主要来自于基本流的水平切变,斜压调整仅起较小的作用。
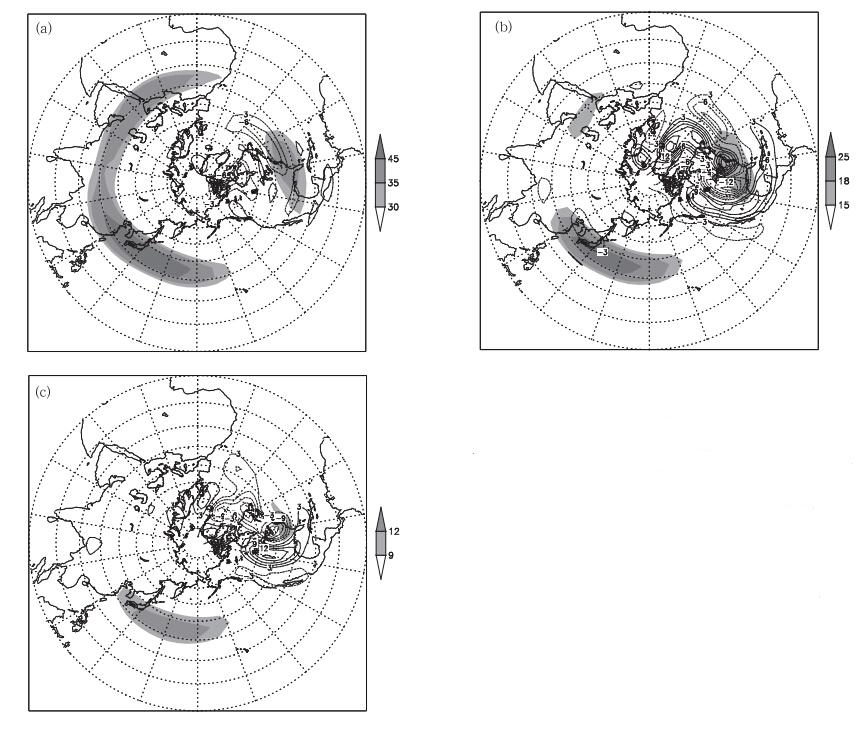 |
| 图 8 200 hPa(a)、500 hPa(b)、800 hPa(c)上优化时间为3 d激发的欧洲—大西洋阻塞发生的最优 前期征兆(等值线,单位:gpm)和从1983年12月1日 积分20年得到的气候态纬向风场(阴影,单位:m/s)(Jiang et al,2010)Fig. 8 OPR(unti: gpm)of Europe-Atlantic blocking for an optimization time of 3 d(contour),and the climatological zonal wind(unit: m/s)over a 20-year integration from 1 December 1983(shaded)at 200 hPa(a),500 hPa(b) and 800 hPa(c)(Jiang et al,2010) |
Mu等(2011)选取了欧洲—大西洋区域1985年冬至1991年冬的20个个例,进一步探讨了阻塞发生的最优前期征兆。20个个例最优初始扰动的合成演变(图 9)表明,最优前期征兆为位于阻塞上游的天气尺度波列,随着时间演变向下游传播并增长,逐渐演变为一个北正南负的偶极子结构。他们也探讨了阻塞预报的最快增长初始误差。最快增长初始误差分为两类,一类为局部条件非线性最优扰动型初始误差,记为type-1最快增长初始误差;另一类为全局条件非线性最优扰动型初始误差,记为type-2最快增长初始误差。结果发现,阻塞事件的最优前期征兆和最快增长初始误差,与ENSO事件和黑潮路径变异事件类似,其空间模态具有很高的 相似性。以优化时间3 d为例,阻塞的最优前期征兆与type-1最快增长初始误差的相似指数达到0.95,与type-2最快增长初始误差的相似指数达到-0.87;当把优化时间延长为4 d时,两者之间相似度降低,但最优前期征兆与type-1最快增长初始误差的相似指数仍然高达0.85,与type-2最快增长初始误差的相似指数达到-0.69。从随时间的发展演变来看,最优前期征兆和type-1最快增长初始误差有相似的发展行为,并且最终都发展成为大西洋区域的北正南负偶极子阻塞模态;而type-2最快增长初始误差则随时间的演变,发展成为上述偶极子阻塞的相反模态。总之,阻塞发生的最优前期征兆与最快增长初始误差不仅在空间结构上具有较高的相似性,而且它们的发展演变过程也十分相似。
 |
| 图 9 500 hPa上20个个例最优前期征兆的演变的合成(第0天(a)及其在第1天(b)、第2天(c)、第3天(d)的非线性演变的合成场;单位:gpm;Mu et al,2011)Fig. 9 Composite nonlinear evolution of the OPR(unit: gpm)for 20 cases at 500 hPa at day 0(a),day 1(b),day 2(c),and day 3(d)(Mu et al,2011) |
尽管阻塞事件是一个大气过程,但其所呈现的最优前期征兆和最快增长初始误差的相似性及其伴随的空间局地性特征与厄尔尼诺事件和黑潮路径变异事件类似。因此,如果在最快增长初始误差局地性特征描述的误差大值区实施目标观测,不仅可以消除最快增长初始误差出现的可能性,而且有助于捕捉最优前期征兆的信号,对提高阻塞事件的预报能力具有十分重要的意义。当然,这些是根据厄尔尼诺事件和黑潮路径变异事件目标观测研究结果的推理,是否确实如此,还应该进一步通过理想回报试验与观测系统模拟试验,考察阻塞事件目标观测敏感区在提高预报技巧中的有效性。5 总结和讨论
主要回顾了条件非线性最优扰动方法在ENSO事件、黑潮路径变异以及阻塞事件爆发目标观测研究方面的应用,特别关注最优前期征兆和最快增长初始误差的相似性及其伴随的局地性特征对确定上述异常事件目标观测敏感区的启发。具体地,ENSO事件、黑潮路径变异,以及阻塞事件,它们的最快增长初始误差都主要分布在少数特定区域,具有明显的局地性特征,且都导致显著的预报误差。这些事件的最快增长初始误差所呈现的局地性区域可能代表了各自的目标观测敏感区。在ENSO事件和黑潮路径变异事件的目标观测问题研究中,人们已经通过理想回报试验表明了上述敏感区在提高预报技巧中的有效性。对于阻塞事件,是否也与ENSO和黑潮路径变异事件类似,目标观测敏感区可以在预报技巧的提高中发挥有效作用,需要进一步数值试验加以验证。
另外,本研究强调了上述事件最优前期征兆和最快增长初始误差的相似性及其伴随的空间局地性特征。正如文中指出,这种相似性和空间局地性特征可以为目标观测的布控提供有用信息。也就是说,如果在最快增长初始误差确定的敏感区实施目标观测,一方面可以消除最快增长初始误差出现的可能性,改进初始场,提高预报技巧;另一方面也可以改善局地观测网,有助于捕捉最优前期征兆提供的前期信号,从而提高对上述事件的预报能力。既然最优前期征兆和最快增长初始误差的相似性和局地性特征对于目标观测有重要作用,那么在上述事件中所展现的这种相似性和局地性特征是否是大气与海洋异常事件的一个基本特征呢?如要回答该问题,需要针对不同的异常事件,探讨其最优前期征兆和最快增长初始误差,进而考察其相似性和空间局地性特征。
大气与海洋异常事件的目标观测问题是一个具有挑战性的课题,仍然有大量的科学技术问题需要解决,这不仅需要学者具备扎实的大气、海洋和气候学知识,而且需要具备坚实的数理基础和利用高性能计算机进行数值模拟的能力。随着计算机的发展,以及有效的学科交叉和来自不同领域的学者的通力合作,该领域的进展将会为提高天气和气候事件的预报技巧做出贡献。
| 刘段灵, 孙照渤, 彭世球. 2013. 条件非线性最优扰动在长江中下游地区冬季暴雨中的应用研究. 热带气象学报, 29(5): 782-792 |
| 穆穆, 秦晓昊, 周菲凡等. 2012. 加强目标观测, 服务防灾减灾. 成都信息工程学院学报, 27(1): 20-26 |
| 谭晓伟, 王斌, 王栋梁. 2011. 基于条件非线性最优扰动的目标观测中瞄准区不同引导性变量的影响试验研究. 气象学报, 69(3): 400-411 |
| Chen D, Cane M A, Kaplan A, et al. 2004. Predictability of El Niño over the past 148 years. Nature, 428(6984): 733-736 |
| Duan W S, Mu M. 2009a. Conditional nonlinear optimal perturbation: Applications to stability, sensitivity, and predictability. Sci China (Ser D: Earth Sci), 52(7): 883-906 |
| Duan W S, Liu X C, Zhu K Y, et al. 2009b. Exploring the initial errors that cause a significant "spring predictability barrier" for El Niño events. J Geophys Res, 114: C04022, doi:10.1029/2008JC004925 |
| Duan W S, Zhang R. 2010. Is model parameter error related to a significant spring predictability barrier for El-Niño event? Result from theoretical model. Adv Atmos Sci, 27(5): 1003-1013 |
| Duan W S, Yu Y S, Xu H, et al. 2013. Behaviors of nonlinearities modulating the El Niño events induced by optimal precursory disturbances. Climate Dyn, 40(5-6): 1399-1413 |
| Frederiksen J S, Collier M A, Watkins A B. 2004. Ensemble prediction of blocking regime transitions. Tellus A, 56(5): 485-500 |
| Jiang Z N, Wang D H.2010. A study on precursors to blocking anomalies in climatological flows by using conditional nonlinear optimal perturbations. Quart J Roy Meteor Soc, 136(650): 1170-1180 |
| Kamachi M, Kuragano T, Sugimoto S, et al. 2004. Short-range prediction experiments with operational data assimilation system for the Kuroshio south of Japan. J Oceanogr, 60(2): 269-282 |
| Kimoto M, Mukougawa H, Yoden S. 1992. Medium-range forecast skill variation and blocking transition: A case study. Mon Wea Rev, 120(8): 1616-1627 |
| Komori N, Awaji T, Ishikawa Y, et al. 2003. Short-range forecast experiments of the Kuroshio path variabilities south of Japan using TOPEX/Poseidon altimetric data. J Geophys Res, 108(C1), doi: 10.1029/2001JC001282 |
| Marshall J, Molteni F. 1993. Toward a dynamical understanding of planetary-scale flow regimes. J Atmos Sci, 50(12): 1792-1818 |
| Miyazawa Y, Yamane S, Guo X, et al. 2005. Ensemble forecast of the Kuroshio meandering. J Geophys Res, 110(C10), doi: 10.1029/2004JC002426 |
| Moore A M, Kleeman R. 1996. The dynamics of error growth and predictability in a coupled model of ENSO. Quart J Roy Meteor Soc, 122(534): 1405-1446 |
| Mu M, Duan W S, Wang B. 2003. Conditional nonlinear optimal perturbation and its applications. Nonlin Processes Geophys, 10(6): 493-501 |
| Mu M, Duan W S, Wang B. 2007a. Season-dependent dynamics of nonlinear optimal error growth and El Niño-Southern Oscillation predictability in a theoretical model. J Geophys Res, 112: D10113, doi: 10.1029/2005JD006981 |
| Mu M, Xu H, Duan W S. 2007b. A kind of initial errors related to "spring predictability barrier" for El Niño events in Zebiak-Cane model. Geophys Res Lett, 34(3): L03709, doi:10.1029/2006GL027412 |
| Mu M, Zhou F F, Wang H L. 2009. A method for identifying the sensitive areas in targeted observations for tropical cyclone prediction: Conditional nonlinear optimal perturbation. Mon Wea Rev, 137(5): 1623-1639 |
| Mu M, Jiang Z N. 2011. Similarities between optimal precursors that trigger the onset of blocking events and optimally growing initial errors in onset prediction. J Atmos Sci, 68(12): 2860-2877 |
| Mu M. 2013. Methods, current status, and prospect of targeted observation. Sci China(Ser D: Earth Sci), 56(12): 1997-2005 |
| Mu M, Yan Y S, Xu H, et al. 2014. Similarities between optimal precursors for ENSO events and optimally growing initial errors in El Niño predictions. Theoretical and Applied Climatology, 115(3-4): 461-469 |
| Qin X H, Mu M. 2011. A study on the reduction of forecast error variance by three adaptive observation approaches for tropical cyclone prediction. Mon Wea Rev, 139(7): 2218-2232 |
| Rex D F. 1950. Blocking action in the middle troposphere and its effects upon regional climate. I: An aerological study of blocking action. Tellus, 2(3): 196-211 |
| Riehl H, Haggard W H, Sanborn R W. 1956. On the prediction of 24-hour hurricane motion. J Meteor, 13(5): 415-420 |
| Tibaldi S, Molteni F. 1990. On the operational predictability of blocking. Tellus A, 42(3): 343-365 |
| Usui N, Tsujino H, Fujii Y, et al. 2006. Short-range prediction experiments of the Kuroshio path variabilities south of Japan. Ocean Dyn, 56(5-6): 607-623 |
| Wang B, Tan X W. 2009. A fast algorithm for solving CNOP and associated target observation tests. Acta Meteor Sinica, 23(4): 387-402 |
| Wang Q, Mu M, Dijkstra H A. 2012. Application of the conditional nonlinear optimal perturbation method to the predictability study of the Kuroshio large meander. Adv Atmos Sci, 29(1): 118-134 |
| Wang Q, Mu M, Dijkstra H A. 2013. The similarity between optimal precursor and optimally growing initial error in prediction of Kuroshio large meander and its application to targeted observation. J Geophys Res, 118(2): 869-884 |
| Xue Y, Cane M A, Zebiak S E. 1997. Predictability of a coupled model of ENSO using singular vector analysis. Part I: Optimal growth in seasonal background and ENSO cycles. Mon Wea Rev, 125(9): 2043-2056 |
| Yu Y S, Duan W S, Xu H, et al. 2009. Dynamics of nonlinear error growth and season-dependent predictability of El Niño events in the Zebiak-Cane model. Quart J Roy Meteor Soc, 135(645): 2146-2160 |
| Yu Y S, Mu M, Duan W S. 2012a. Does model parameter error cause a significant spring predictability barrier for El Niño events in the Zebiak-Cane model? J Climate, 25(4): 1263-1277 |
| Yu Y S, Mu M, Duan W S, et al. 2012b. Contribution of the location and spatial pattern of initial error to uncertainties in El Niño predictions. J Geophys Res, 117: C06018, doi:10.1029/2011JC007758 |
| Zebiak S E, Cane M A. 1987. A model El Niño southern oscillation. Mon Wea Rev, 115(10): 2262-2278 |
 2014, Vol. 72
2014, Vol. 72


