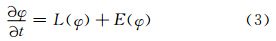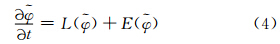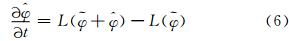中国气象学会主办。
文章信息
- 于海鹏, 黄建平, 李维京, 封国林. 2014.
- YU Haipeng, HUANG Jianping, LI Weijing, FENG Guolin. 2014.
- 数值预报误差订正技术中相似-动力方法的发展
- Development of the analogue-dynamical method for error correction of numerical forecasts
- 气象学报, 72(5): 1012-1022
- Acta Meteorologica Sinica, 72(5): 1012-1022.
- http://dx.doi.org/10.11676/qxxb2014.082
-
文章历史
- 收稿日期:2014-3-31
- 改回日期:2014-7-14
2. 中国人民解放军93811部队86分队, 兰州, 730020;
3. 国家气候中心, 中国气象局气候研究开放实验室, 北京, 100081
2. Unit 86 of No. 93811 PLA, Lanzhou 730020, China;
3. Laboratory for Climate Studies, National Climate Center, Chinese Meteorological Administration, Beijing 100081, China
在《国家中长期科学和技术发展规划纲要(2006—2020年)》的“公共安全”重点领域及其优先主题“重大自然灾害监测与防御”中明确指出:“重点研究开发地震、台风、暴雨、洪水、地质灾害等监测、预警和应急处置关键技术,森林火灾、溃坝、决堤险情等重大灾害的监测预警技术以及重大自然灾害综合风险分析评估技术。”而就各种灾害性天气的预报而言,其关键技术是数值天气预报技术。自从Charney等(1950)第一次成功实现数值预报以来,经过60年的发展,数值预报水平取得了很大进步(陈德辉等,2004),但预报误差仍然显著地存在,对重大天气灾害的预测准确率仍然很低(伍荣生等,2007),需要进一步提高预报能力。制约数值天气预报准确率的两个基本因素是初值误差和模式误差(钟剑等,2011),因此提高初值场质量和减小模式误差自然成为提高预报水平的两个努力方向。近年来数值预报也一直朝着数值模式精细化、初始条件准确化的方向发展,在此发展趋势下,观测资料更加密集,同化技术更加完善,数值模式更加精密,参数化方案更加合理,这些努力大大提高了数值预报的准确率,但经济社会和国防建设的发展对业务预报的要求越来越高(伍荣生等,2007),而目前的预报水平还不能满足人们日益增长的需求。
无论是何等精细的模式,误差总是不可避免,在现有的预报水平上做出改进需要付出的努力也会越来越大。同时,中国业务预报水平与发达国家相比仍有一定差距,因此,在提高中国模式精度和改进资料同化技术的同时,要进一步提高预报水平,一个有效且可行的方向是在现有数值模式基础上针对预报误差开展订正技术。这样既能依靠模式本身,利用现有模式的发展成果;又不对模式本身做过多改动,实施时简便可行。中外在发展订正技术方面已开展了大量工作,值得一提的是,中国学者在这方面的研究中,将统计和动力相结合(丑纪范,1986),取得了一系列创新性的理论和方法(顾震潮,1958a,1958b; 丑纪范,1974; 郑庆林等,1973; 邱崇践等,1990; 黄建平等,1991b; 张邦林等,1991; 曹鸿兴,1993; 张培群等,1997; 谷湘潜,1998)。特别是将大气的相似演变规律和动力模式相结合,突破国际上统计相似预报的局限性,提出了相似-动力方法(丑纪范,1979),并开展了大量探索性的工作,在创新预报理论和提高实际预报水平等方面发挥了重要作用。如今,在相似-动力方法基础上发展起来的预报订正技术已经在中短期预报、延伸期预报、短期气候预测等各个时间尺度上有效提高了预报技巧,展现出了较好的应用前景。2 误差订正技术研究进展
一般预报误差可以分为系统性误差和非系统性误差两种(邵爱梅等,2009),前者是不随时间变化的部分,常由大量预报误差的时间平均得到,表征了模式平衡态相对于实际气候态的漂移;后者则是随流型变化的部分,即依赖于大气状态变量,又包含随机误差。针对不同的误差,订正方法也可相应地分为两类:系统订正和依流型订正(Dalcher et al,1987)。2.1 系统订正
系统订正的订正量不依赖于模式变量,常用的方法是计算大量回报误差的平均值(考虑季节变化和日变化),将其叠加到对应预报时效的当前输出结果上。曾庆存等(1990)在短期气候预测中采取了一种简便有效的方法去除模式的气候漂移,即将预报场的气候平均用实况的气候平均代替,将预报场的距平叠加到实况的气候平均上作为预测值。之后又提出了一系列误差订正方案(Zeng,1994),如最大似然、最小偏差、经验正交函数分解(EOF)订正法等,并在中国科学院大气物理研究所两层大气环流模式中取得了订正效果(林朝晖等,1998; 赵彦等,1999; 周广庆等,1999; 王会军等,2000; 李芳等,2006)。此外,根据大量回报和历史实况资料建立统计关系的方法在预报中也较为常用,例如早期发展的PP法和MOS法(Klein et al,1959; Klein,1971; Glahn et al,1972),利用历史观测或预报结果建立环流场与天气实况之间的统计关系进行预报。这些方法均是在预报完成后对结果的后处理,一般称之为事后订正(Danforth et al,2007)。因其操作简便,得到了广泛的应用,但缺点是没有考虑模式积分过程中内部误差和外部误差的非线性相互作用(Danforth et al,2007)。
与之不同的是过程订正,即在模式积分过程中加入强迫项以抵消倾向误差,从而抑制误差的非线性增长(Danforth et al,2008a)。由于订正的是模式变量在积分过程中的变化倾向,因此又叫倾向误差订正。这其中最为常用的是张弛逼近技术,它来源于资料同化,通过在预报方程中增加一个强迫项使预报接近观测值(Hoke et al,1976; Jeuken et al,1996)。有学者将张弛逼近技术和事后订正方法进行了对比,表明二者均能有效提高预报技巧,但在二者效果的优劣上存在不确定性。Danforth等(2008a)的研究表明在1天后张弛逼近技术相对于事后订正表现出更好的订正效果;Saha(1992)结果表明张弛逼近技术在预报技巧上并没有体现出优势;而Johansson等(1989)的结果表明,张弛逼近技术对小尺度有更好的改进效果,但可能会破坏瞬变能量的守恒性。这些差异说明二者的订正性能很大程度上依赖于所采用的模式,而过程订正中强迫项的量级过大易破坏模式变量间的协调性(Danforth et al,2008a)。
为了对强迫项给出合理估计,Klinker等(1992)利用一步积分的平均结果估计倾向误差,通过依次关闭每个独立的参数化方案以得到各项的贡献,并发现重力波参数化过程起主导作用;Kaas等(1999)将几个低分辨率的大气环流模式向一个高分辨率的大气环流模式进行张弛逼近以得到水平扩散的经验作用函数,从而使得动能谱和观测更加接近,并减小了大尺度系统误差。以上两种方法操作上较为复杂,对实际预报模式而言一般采取经验估计的方式,即将大量预报误差和对应预报时间的比值进行集合平均作为强迫项。这类方法实际上是假设预报误差随时间线性增长(Yang et al,2008),这就要求预报时效不宜过长。对于预报时效的取法,不同研究有差异。Danforth等(2007)将其设为与分析资料间隔一致的6 h,将近5年内相同月份的所有6 h预报误差进行平均;Saha(1992)将预报起始时刻前1个月内所有24 h预报误差进行平均,以避免日变化的影响;Yang等(2008)则是将多年的6、12、18和24 h的预报误差进行平均,从而避免了倾向误差在不同预报时段内变化的影响。
上述经验性订正易于实现,但并不能保证所加入的强迫项是最优的。最优往往和变分方法相联系,在传统的四维变分同化(4DVar)中假定模式是准确的,无法考虑模式误差的作用;Bennett等(1992,1996,1997)发展的弱约束四维变分同化考虑了模式误差的存在,通过在目标函数中加入模式倾向误差项达到同时减小初值误差和模式误差的目的。该类方法通过一些简单模式和复杂模式的试验取得了显著的订正效果(Derber,1989; Zupanski,1993; Trémolet,2007; Akella et al,2009),但该方法需要先验地给定倾向误差的形式,在应用中需要针对模式反复试验进行确定。另外,四维变分同化的求解受到伴随模式的限制,而模式误差项的加入更增加了计算量,这无疑增大了该方法的推广难度。2.2 依流型订正
有部分研究(Saha,1992; DelSole et al,1999,2008)表明,系统订正仅能有效减小系统误差,对非系统误差作用较小,这意味着发展依流型订正是非常必要的。
Leith(1978)利用统计方法建立了倾向误差和模式状态变量距平的关系,即将强迫项表达为状态变量的线性函数,通过大量样本给出了统计模型。虽然是在线性假设下进行的推导,但试验表明对非线性模式的误差也有改进效果。这一著名工作被后续进行了深入研究,Delsole等(1999)将该方法应用到一个准地转模式中,有效提高了预报效果,但误差协方差矩阵的计算对计算量要求很高。Danforth等(2007,2008a,2008b)通过奇异值分解对该方法进行了降维处理,从而大大降低了计算量。在准地转模式上进行的6 h预报试验结果表明,该方法能够在误差大值区有效减少误差,但全球的提高量相对较小。上述方法的共同点是需要一个训练样本序列以建立误差协方差矩阵,这意味着所建立的统计模型严重依赖于所选取的样本,其稳定性难以保证;一旦模式有了改进或者变动,误差协方差矩阵的重建需要重新进行大量计算和调试,不便于移植(郑志海,2013)。
对于线性系统而言,建立统计关系是一个有效的解决方案,并且样本量越大,其可靠性越高;但对于非线性系统,改进效果和样本之间的关系变得不稳定,也并非样本量越大效果越好,因此,样本的选取非常重要(丑纪范等,2006)。在大气和海洋的演变中广泛存在相似现象(赵宗慈等,1982; 王绍武等,1983),对于相似的两个大气状态,其演变规律往往相似,这种现象为订正样本的选取提供了参考。例如,陈伯民等(2003,2004a,2004b)基于相空间重构理论和非线性时空序列预测方法,寻找历史相似状态的信息预报当前状态,构建了纬向平均月尺度逐候非线性动力学区域预报模型,并用非线性预报结果在模式积分过程中实施过程订正。试验表明不仅减少了纬向平均误差,对部分波分量也有明显改进,这表明相似现象对提高预报效果具有参考价值。
基于上述考虑,中国学者将相似现象与动力模式相结合,发展出一套用于误差订正的相似-动力方法。下面将对该方法的基本原理和演化过程进行系统介绍,并重点讨论其在不同预报领域中的发展。3 相似-动力方法的发展3.1 相似现象与相似预报
大气和海洋中广泛存在相似现象,基于这种现象进行的相似预报方法很早就已经形成并被广泛采用。该方法的依据是对于两个相似的初始状态,当大气处于稳定流型时,由于大气的连续演变性,这种相似性可以在天气时间尺度内得以维持。而在月和季节尺度中,也存在明显的相似韵律现象,即大气环流在长期演变中存在相似—不相似—相似的交替过程,这种现象的成因与上述天气尺度的规律不同。对于其形成的动力学机制,黄建平等(1989a,1990a,1991)通过海-气耦合模式进行了研究,认为这种现象的产生是由于在月平均环流季节变化的强迫下,海-气系统非线性反馈造成的相似离差扰动的不均匀振荡,这种不均匀振荡和大气环流的不均匀变化密切相关。首次发现相似现象不是大气或海洋自身的演变形成的,海-气耦合作用在相似形成中起了关键作用,而月平均环流季节变化显著增大了离差扰动的振幅。该研究表明海洋和季节变化是相似选取时需要考虑的重要因素,对相似预报具有实际指导意义。
相似预报被广泛应用于天气和气候预测。Lorenz(1969)曾用自然相似样本来研究预报误差增长的可预报性,其结果同时表明,找到较严格的相似样本是非常困难的,这一结论被Van den Dool(1994)证实。但这并不意味着相似性在天气预报中无用武之地,Van den Dool(1989,1991)相继提出了区域相似、构造相似(Van den Dool et al,2003)等概念,而Barnett等(1978)通过经验正交分解对多维状态空间进行降维,提取出描述气候系统演变的“相似气候状态向量”进行相似选取。相似预报的不断发展使其在NCEP实现了业务化(Livezey et al,1988)。
将未来状态看作过去状态的重复再现,这种考虑过于简化(任宏利等,2007a)。在相似预报基础上发展起来的相似-动力方法,将相似方法与动力模式相结合,成为提高数值预报技巧的一个途径。3.2 相似-动力方法的提出
相似-动力方法最早于1979年提出,其基本思想是“把要预报的场视为叠加在历史相似上的一个小扰动,就可以把天气学的预报经验吸收到数值预报中来”(丑纪范,1979)。相对于经典的数值预报而言,该方法承认了倾向误差的存在,并通过历史相似对倾向误差进行估计。
数值预报是作为偏微分方程的初值问题提出来的,可以表示为
式中,ψ为模式状态变量,L为数值模式算子,t0为预报初始时刻,ψ0为模式初值。由于模式误差的存在,模式大气与实际大气的状态演变不同。将模式倾向误差算子表示为E,则实际大气的状态变量φ的演变可描述如下这里将E视为状态变量的函数,这与Leith(1978)的观点是一致的。对比式(1)和(3)发现,假定模式倾向误差可以得到,将其加入模式中可以在每一时间步对模式倾向进行强迫,使模式状态向实际状态接近。从历史资料中选择一个相似参考态,将当前状态变量视为叠加在历史相似上的一个扰动,即φ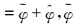 为相似状态变量,
为相似状态变量,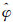 为相似离差。相似参考态作为大气的历史演变,满足以下关系将式(3)和(4)相减,可以得到离差方程
为相似离差。相似参考态作为大气的历史演变,满足以下关系将式(3)和(4)相减,可以得到离差方程求解倾向误差本身是非常困难的,为了避免倾向误差的计算,相似-动力方法做了如下近似,将当前的倾向误差项用历史相似对应的倾向误差近似代替,即得到相似-动力模式
该方程的控制变量不再是预报变量本身,而是当前变量相对于相似状态变量的扰动。根据该方程求解得到扰动变量的演变规律后,叠加到相似状态变量上即得到当前预报场。将式(1)和(6)与(4)对比可以发现,该方法与原预报的差别在于,原预报式(1)将整个倾向误差项全部省略,而该方法式(6)省去的仅仅是当前倾向误差和相似参考态倾向误差之间的差别,考虑了环流异常相似演变的作用,因此在理论上有更高的精度。这同时对相似的选取提出了要求,在初值相似的同时,尽量保证气候环境和边界状况相近(邱崇践等,1989)。3.3 相似-动力方法的早期发展
方法提出后,首先考察了参考态在多高的相似度下,新方法会优于原预报。邱崇践等(1989)在一个准地转正压涡度方程中分别引入强迫源误差、地形高度误差和次网格误差,试验表明相似-动力方法均能有效减少预报的均方差。通过定义一个相似指标发现该方法对参考态与预报量之间的相似度要求不高,但对相似度有依赖性,提高量随相似度的提高而增大,随预报时效的延长而增大。
环流异常在长期演变过程中具有正压性(周琴芳等,1989; 杨成彬等,1990; 黄建平等,1988; 1990b)、驻波性(衣育红等,1990)和相似性等特点,黄建平等(1990)将其引入到长期数值模式中,发展了一套准地转斜压海-气耦合模式(黄建平等,1992,1993),并建立了对应的相似离差方程,首次采用相似-动力方法进行了季节预测试验(Huang et al,1993)、月预报试验(Huang et al,1991)和汛期洪涝预测(黄建平等,1993b)。采用预报与实况的距平同号率作为评分,结果显示能够较准确地反映500 hPa主要距平中心。冬季(1月)报夏季(8月)的8年平均预测结果(黄建平等,1991a)表明,500 hPa平均准确率达56.8%,地表温度达55.4%;夏季(7月)报冬季(2月)的8年平均预测结果(黄建平等,1993a)表明,500 hPa平均准确率达57%,地表温度达55.7%。预报效果明显优于传统的相似预报,且随着预报时效的延长,优势更明显。该工作为预报技巧较低的季节预测提供了新思路。
简单模式的试验成功表明了相似-动力方法的有效性。为考察该方法在复杂模式中的可行性和提高月尺度业务预报水平,鲍名等(2004)将该方法应用到中国国家气候中心T63L16月动力延伸业务预报模式(李维京等,2005)中,以该模式为动力核建立了相似-动力月预报模式。突破了选取单个相似成员的局限,从历史资料中选取了多个样本进行相似-动力预报,并将预报结果进行集合平均。将2002年12个月作为试验对象,结果显示引入集合平均后效果优于单个相似成员预报,全球距平相关系数(ACC)平均提高0.2,均方根误差(RMSE)减少12 gpm。从不同区域和不同尺度的对比发现,热带、副热带地区改进最为明显;行星尺度波的改进效果在预报15日以后较控制预报有所改善,但天气尺度波预报技巧没有改进。这表明,该方法对预报技巧的提高主要体现在延伸期。3.4 方法的简化——相似预报误差订正
在中国学者发展相似-动力方法之后,D’Andrea等(2000)独立提出了一种利用历史相似估计倾向误差的方法。该方法使用四维变分同化技术得到历史相似样本的倾向误差的最优估计,将其作为当前预报的强迫项加入到模式中。可见其思想是和相似-动力方法等价的,都是将当前倾向误差用相似参考态对应的倾向误差近似代替。不同之处在于该方法利用变分技术求解式(4)得到E()后代入式(3)中进行预报;而相似-动力方法将式(3)和(4)作差,并建立了新的方程。这也同时表明相似-动力方法是一种合理并有效的误差订正技术,中国学者较早地领先其他国家开展了这方面的研究(任宏利,2006)。
四维变分同化技术巨大的计算量使得D'Andrea的方法仅仅在准地转斜压模式上进行了试验,难以应用到复杂业务模式。而上述相似-动力方法虽然避免了编写伴随模式来求解强迫项,但需要重新建立相似离差方程,这很大程度上限制了在复杂模式中的应用。
针对此问题,Ren等(2009)对原有的相似-动力方法进行了简化,由原有的倾向误差相似简化为预报误差相似,即认为相似样本具有相似的预报误差,进而利用若干相似样本对应的预报误差估计当前预报误差,以避免求解倾向误差。预报过程中将预报时段分为若干订正间隔,在每个间隔处用对应相似样本的预报误差的集合平均叠加到当前预报结果上。不再是在每个时间步长上进行强迫,而是每隔若干时间步长进行一次事后订正。考虑到相似持续时间有限,每隔一定时间后重新选取相似。这些改进避免了重新建立数值模式,增强了方法的可操作性和可移植性。选取24个个例在中国国家气候中心T63L16模式上进行了月平均预报试验(任宏利等,2006),全球距平相关系数平均提高0.1,均方根误差降低了7.49 gpm,对热带地区的改善最为明显。从预报不同时段看,对逐日预报技巧的提高主要在一周以后,且主要集中在行星尺度波部分,对天气尺度波几乎无提高。此外,通过 NCC/IAP T63海-气耦合模式进行了夏季降水的预测试验(任宏利等,2007b),23个个例平均结果表明对夏季降水的全球距平相关系数提高0.092,对东亚地区提高0.124。3.5 延伸期预报中的发展——基于可预报分量的相似-动力方法
对相似-动力方法以及传统的相似预报而言,相似场的选取始终是核心问题。一方面,数值模式对初值敏感,难以保证相似初值之间预报误差演变规律的一致性;另一方面,数值模式具有很大自由度,选取理想的相似初值很困难(郑志海等,2013)。
丑纪范等(2010)针对大气系统的混沌特性,从误差增长的角度给出了分离延伸期可预报分量(对初值误差不敏感的分量,可用数值模式预报)和不可预报的随机分量的方法。郑志海等(2009,2010)基于此理论,通过将历史资料作经验正交函数分解提取出气候吸引子(汪守宏等,1989; 黄建平等,1989b)基底,对模式变量以此基底展开后滤除随机分量,保留可预报分量,针对可预报分量进行数值预报,并发展了基于可预报分量的相似-动力方法。避免了小尺度分量预报误差快速增长的影响,更能针对可预报分量进行确定性预报。由于可预报分量对初值不敏感且自由度小,用它进行相似选取避免了上述两方面的困难。在T63L16模式上进行了6—15 d中期预报试验(郑志海等,2013),将基于可预报分量的相似-动力方法和可预报分量数值模拟结果进行了对比,结果表明相似-动力方法对10 d以后预报技巧有提高作用。但其具体表现与上述研究结果不同:第一,对环流场的距平相关系数提高最明显的区域在南半球热带外,而并非在热带地区;第二,对天气尺度波预报效果略有提高,这表明基于可预报分量的相似-动力方法可能在一定程度上抑制小尺度分量预报误差的增长,也可能是由于行星波尺度的改善通过高低频相互作用部分制约了天气尺度波误差的增长。而对于不可预报的随机分量,利用历史资料中相似的强迫给出可能的概率分布。针对两种分量的不同特性,采用历史相似分别估计可预报分量的预报误差,并将历史相似对应的随机分量相加形成集合预报。与中国国家气候中心的业务动力延伸集合预报系统的对比(郑志海等,2012)表明,6—15 d平均的距平相关系数评分提高了0.12,均方根误差减少了12.36 gpm。
上述研究从历史实况资料中提取气候吸引子作为基底,这种方法易于操作。但实际上模式大气与实况大气之间存在气候漂移,其气候吸引子也不相同;而且将气候吸引子基底固定,不能考虑大气流型的特殊性和时间演变(王启光等,2014)。因此,利用历史资料确定的大尺度分量,与数值模式中误差增长较慢的分量并不能保证对应。为解决此问题,王启光等(2012a,2012b)基于条件非线性最优扰动(CNOP)方法(Mu et al,1999; 王斌等,2009)提取出数值模式在给定初值下误差增长较慢的可预报分量基底,对数值模式中可预报分量进行了相似-动力订正,并将历史相似对应的随机分量进行了集合平均,将二者相加形成延伸期预报结果。基于T63L16模式对10—30 d 500 hPa平均环流场的预报效果进行了比较(王启光等,2014),全球平均距平相关系数由0.06提高到0.32,对不同区域也都有一定提高,其中北半球热带外和热带地区提高明显,南半球热带外改进较小,这可能与所选取的个例为北半球冬季(1月)有关。从不同尺度波的预报效果看,各尺度均有改进效果,行星尺度波最为明显。3.6 相似-动力方法在短期气候预测中的发展
夏季降水预测是短期气候预测的重点和难点,直接关系到国家防灾、减灾的重大需求,而相似-动力方法在提高汛期预测技巧方面发挥了重要作用。与上述月平均预报和延伸期预报不同,汛期预测是边值问题,主要受外源强迫作用,体现出低频信号特征。因此,在选取相似因子时,不宜仅以初始场为指标,而应综合考虑外源强迫和海-气低频变化。封国林等(2013)基于中国国家气候中心业务模式——BCC-CGCM,利用相似年的预报误差信息对预报年的预报误差进行估计和订正,发展了汛期降水动力-统计客观定量化预测方法。该方法的核心为相似预报因子的筛选和组合配置,在正常年份选取最优多因子组合进行订正,当预报年前期因子出现异常时,采用异常因子订正方案。针对不同区域影响因素的差异,王启光等(2011,2012b)、熊开国等(2012a,2012b)、Xiong等(2011)和杨杰等(2011,2012)从不同角度分别建立了针对长江中下游地区、东北地区和华北地区的动力-统计集成预测方案、最优多因子动态预测方案和动态多因子组合预测方案。该方法自2009年开始参加中国夏季汛期会商以来,连续5年较好地把握了中国夏季的主雨带特征。其中2009—2012年PS评分平均为73分,距平相关系数平均为0.16,相比BCC_CGCM模式系统订正的预测结果(PS平均分63分,距平相关系数平均0.01)有较大的提高(封国林等,2013)。基于该方法研发的动力-统计集成的季节气候预测系统1.0版本(FODAS1.0)于2012年投入业务运行(封国林等,2013),并在多个地区进行了推广。在2013年的汛期预测中,该系统预测结果的PS平均分74分,距平相关系数平均0.20(赵俊虎等,2014a),对夏季旱涝分布的大体形势预测基本正确。在每年的汛期结束之后,对该方法的预测结果进行了检验和总结,并对气候异常成因进行了诊断分析(赵俊虎等,2011,2013a,2013b,2014a,2014b)。除上述汛期预测外,该方法也被应用到关键区域高度场的跨季度预测中,一定程度上减小了预报误差(赵俊虎等,2013a,2013b)。
ENSO循环作为年际气候变化中最强信号之一,与大气环流异常变化有关,对中国气候有重要指示意义。孙丞虎等(2006)将相似-动力方法应用到ENSO预测中,以中国国家气候中心的简化海-气耦合模式为平台对Nino3指数进行了12个月的预报试验。在选取相似时,考虑了ENSO预测的特殊性,将部分相似(仅考虑海表温度)和全相似(考虑海表温度和风场)进行了对比,结果表明全相似比部分相似更能反映海-气耦合系统的相似程度,且在相似样本个数为5个、海洋相似更新周期设为20 d 、大气更新周期设为10 d时,预报效果最佳。通过对1980—2003年Nino3指数的回报试验发现,相似-动力方法的预报效果在整个预报时段均好于控制预报,12个月内控制预报的平均距平相关系数和累计绝对误差分别为0.29和13.78℃,而相似-动力方法对应的预报技巧分别为0.45和10.69℃。3.7 相似-动力方法在中短期预报中的发展
通过以上讨论可以发现,相似-动力方法在提高短期气候预测、月平均预报和延伸期预报领域有效提高了预报水平,但对中短期预报改进效果不明显(任宏利等,2006)。这归因于相似-动力方法的理论基础,即考虑了环流异常相似演变的动力过程。这种过程时间尺度大,初始场作用相对较小,低频变化特征明显,其相似演变规律易于把握。而对于中短期预报,对初值极为敏感,且存在内部误差的非线性增长,要通过相似方法进行依流型订正的难度很大,实现此方法显得尤为迫切。发展中短期预报的相似-动力方法,将能拓展应用领域,是对该方法的补充和完善。
针对这一问题,Yu等(2014)发展了用于改进中短期天气业务预报模式的相似-动力方法。首先,上述简化后的相似-动力方法认为相似样本具有相似的预报误差,这与早期的相似-动力方法相比无疑是更大程度的近似,其合理性需要从理论上进行检验。通过引入预报误差的连续性定理,在一些假定条件下,证明了当历史资料足够多时,预报误差可以构成超空间的连续曲面,当前预报误差可以由曲面上某邻域内若干点(即相似样本对应的预报误差)插值得到,从而证明了近似的合理性,并指明了相似-动力订正可以蜕化为控制预报和系统订正。在其实施过程中,根据中短期天气预报对初值敏感和全球模式对海温强迫依赖的特点,从季节变化、日变化、大气环流型和海温类型等方面对相似选取作了严格要求;同时为避免误差非线性增长对相似性的破坏,通过敏感性试验确定出中短期预报中最优相似更新周期为5 d。选取了冬季和夏季的40个个例在中国自主研发的GRAPES全球中期预报系统(陈德辉等,2009)上进行了回报试验(Yu et al,2014),结果表明相似-动力方法将500 hPa全球可用预报时效延长了0.8 d,最为显著的热带地区延长了1.25 d,且随着预报时效的延长,提高效果逐渐增强。通过各层高度场的距平相关系数和均方根误差的对比发现,相似-动力方法在垂直各层均有稳定的改进效果,预报第10天各层平均距平相关系数相对于控制预报提高0.07,而系统订正相对于控制预报的平均提高量为0.03。除了高度场,对温度场和风场动能也进行了对比分析,发现相似-动力方法能够准确识别各物理量误差的高值区,并能够削弱误差量级。这充分表明了相似-动力方法在中短期预报中的有效性。4 总 结
数值模式的发展与误差订正技术的发展并不矛盾,反而相辅相成。一方面,预报误差不仅仅是内部误差(初始误差)和外部误差(模式误差)的简单叠加,而是二者非线性相互作用的结果(陈明行等,1989),要从预报结果中确定误差根源以针对性地正面改进是非常困难的,因此改变观点很有必要,即承认预报误差的客观存在,总结其演变规律,建立经验关系对预报误差进行估计和订正;另一方面,作为动力方法的数值预报将大气视为一个确定论系统(丑纪范,2007),即未来状态是由现在状态和满足的物理规律所决定的,但数值模式和初值实际上都是大气真实状态的近似描述,本身存在很大的不确定性,预报得到的未来状态也必然存在很大的不确定性,与动力方法不同,统计方法承认未来的不确定性,依据历史资料和现在状态中所包含的信息对未来状态进行概率推断,但缺点是没有考虑应满足的物理规律。可见,动力方法和统计方法各有长短,将动力与统计相结合(丑纪范,1986),发展误差订正技术是十分必要的。
在误差订正技术研究方面,中国学者将统计方法与动力模式有机结合,开展了一系列独具特色的工作,发展了一种基于相似误差订正的预测方法,实现了在动力预报中有效运用历史资料的相似信息。本研究回顾了该方法的提出和发展过程,讨论了针对不同时间尺度预报时需要解决的问题、对应的技术思路,以及预报技巧改进情况。
通过回顾和讨论可以看到,相似-动力方法经过几十年的努力,逐步发展完善,形成了一套有中国特色的预报技术方法。从理论提出,到简单模式的试验成功,再到复杂模式上取得改进效果,最后在中短期预报、延伸期预报、月平均环流预报和短期气候预测等各个时间尺度的业务模式上均有效提高了预报技巧,展现出广阔的应用前景。该方法利用历史相似提供的预报误差对预报误差进行预报,不但考虑了模式的系统性误差,还包含了与相似初值相近流型的模式误差演变信息,且避免了建立预报误差与模式变量统计关系的困难,具有良好的可操作性和可移植性(李维京等,2013)。
同时,对比近期和早期的相似-动力方法可以发现,为了便于在复杂模式上应用和推广,近期的方法对早期的方法做了简化,用预报误差取代了倾向误差,用事后订正取代了过程订正。这样虽然使得方法能够移植到任意复杂模式,但也带来了问题,即无法考虑内部误差和外部误差的非线性相互作用(Danforth et al,2008a)。因此,一个有意义的发展方向是,吸取近期方法和早期方法的优势,发展既简便易行,又能够抑制误差非线性增长的相似-动力方法,进一步提高模式预报水平,为中国数值预报业务发挥更大作用。
致谢: 感谢丑纪范院士细致地审阅了初稿并提出了很有意义的修改意见。
| 鲍名, 倪允琪, 丑纪范. 2004. 相似-动力模式的月平均环流预报试验. 科学通报, 49(11): 1112-1115 |
| 曹鸿兴. 1993. 大气运动的自忆性方程. 中国科学(B辑), 23(1): 104-112 |
| 陈伯民, 纪立人. 2003. 改善月动力延伸预报水平的一种新途径. 科学通报, 48(5): 513-520 |
| 陈伯民, 纪立人, 杨培才等. 2004a.与非线性区域预测方法结合的月延伸预报试验I: 纬向平均环流的预报. 气象学报, 62(1): 1-10 |
| 陈伯民, 纪立人, 杨培才等. 2004b.与非线性区域预测方法结合的月延伸预报试验II: 对波动分量预报的改进. 气象学报, 62(1): 11-19 |
| 陈德辉, 薛纪善. 2004. 数值天气预报业务模式现状与展望. 气象学报, 62(5): 623-633 |
| 陈德辉, 薛纪善, 杨学胜等. 2009. GRAPES 新一代全球/区域多尺度统一数值预报模式总体设计研究. 科学通报, 53(20): 2396-2407 |
| 陈明行, 纪立人. 1989. 数值天气预报中的误差增长及大气的可预报性. 气象学报, 47(2): 147-155 |
| 丑纪范. 1974. 天气数值预报中使用过去资料的问题. 中国科学, (6): 635-644 |
| 丑纪范. 1979. 长期数值天气预报的若干问题//中长期水文气象预报文集. 北京: 水利电力出版社, 216-221 |
| 丑纪范. 1986. 为什么要动力-统计相结合?——兼论如何结合. 高原气象, 5(4): 367-372 |
| 丑纪范, 任宏利. 2006. 数值天气预报——另类途径的必要性和可行性. 应用气象学报, 17(2): 240-244 |
| 丑纪范. 2007. 数值天气预报的创新之路——从初值问题到反问题. 气象学报, 65(5): 673-682 |
| 丑纪范, 郑志海, 孙树鹏. 2010. 10-30 d延伸期数值天气预报的策略思考——直面混沌. 气象科学, 30(5): 569-573 |
| 封国林, 赵俊虎, 支蓉等. 2013. 动力-统计客观定量化汛期降水预测研究新进展. 应用气象学报, 24(6): 656-665 |
| 谷湘潜. 1998. 一个基于大气自忆原理的谱模式. 科学通报, 43(9): 909-917 |
| 顾震潮. 1958a. 作为初值问题的天气形势数值预报与由地面天气历史演变作预报的等值性.气象学报, 29(2): 93-98 |
| 顾震潮. 1958b. 天气数值预报中过去资料的使用问题.气象学报, 29(3): 176-184 |
| 黄建平, 丑纪范. 1988. 北半球中高纬月平均环流正压斜压动能的年变化特征. 高原气象, 7(3): 264-268 |
| 黄建平, 丑纪范. 1989a. 海气耦合系统相似韵律现象的研究.中国科学(B辑), 19(9): 1001-1008 |
| 黄建平, 丑纪范, 衣育红. 1989b. 500 hPa月平均距平场演变的宏观描述.气象学报, 47(4): 484-487 |
| 黄建平. 1990. 环流异常的时空特征与长期数值预报模式设计. 气象科技, (3): 27-32 |
| 黄建平, 郜吉东. 1990a. 北半球月平均环流异常演变的相似韵律现象. 高原气象, 9(1): 88-92 |
| 黄建平, 郭学良, 丑纪范. 1990b. 北半球月平均环流正压斜压动能的比重以及各自特点的动力统计分析//长期天气预报论文集. 北京:气象出版社, 53-62 |
| 黄建平. 1991. 环流异常相似性演变的动力学机制. 北京大学学报(自然科学版), (1): 99-108 |
| 黄建平, 王绍武. 1991a. 相似-动力模式的季节预报试验.中国科学(B辑), (2): 216-224 |
| 黄建平, 衣育红. 1991b. 利用观测资料反演非线性动力模型. 中国科学(B辑), (3): 331-336 |
| 黄建平. 1992. 理论气候模式.北京: 气象出版社, 152-178 |
| 黄建平, 衣育红, 王绍武. 1993a. 相似-动力模式的由夏季报冬季的季节预报试验.气象学报, 51(1): 118-121 |
| 黄建平, 衣育红, 王绍武等. 1993b.1991年江淮大涝环流形势的季节预报//王绍武等.长江黄河旱涝灾害发生规律及其经济影响的诊断研究.北京: 气象出版社,228pp |
| 黄建平. 1993.相似-动力季节数值预报模式//王绍武等.气候预测与模拟研究.北京: 气象出版社, 99-147 |
| 李芳, 林中达, 左瑞亭等. 2006. 基于经验正交函数和奇异值分解对东亚季风区跨季度夏季降水距平的订正方法. 气候与环境研究, 10(3): 658-668 |
| 李维京, 张培群, 李清泉等. 2005. 动力气候模式预测系统业务化及其应用. 应用气象学报, 16(1): 1-11 |
| 李维京, 郑志海, 孙丞虎. 2013. 近年来我国短期气候预测中动力相似预测方法研究与应用进展. 大气科学, 37(2): 341-350 |
| 林朝晖, 李旭, 赵彦等. 1998. 中国科学院大气物理研究所短期气候预测系统的改进及其对1998年全国汛期旱涝形势的预测. 气候与环境研究, 3(4): 339-348 |
| 邱崇践, 丑纪范. 1989. 天气预报的相似-动力方法. 大气科学, 13(1): 22-28 |
| 邱崇践, 丑纪范. 1990. 预报模式的参数优化方法. 中国科学(B辑), 20(2): 218-224 |
| 任宏利. 2006. 动力相似预报的策略和方法[D]. 兰州: 兰州大学, 52pp |
| 任宏利, 张培群, 李维京等. 2006. 基于多个参考态更新的动力相似预报方法及应用. 物理学报, 55(8): 4388-4396 |
| 任宏利, 丑纪范. 2007a. 数值模式的预报策略和方法研究进展.地球科学进展, 22(4): 376-385 |
| 任宏利, 丑纪范. 2007b. 动力相似预报的策略和方法研究.中国科学(D辑), 37(8): 1101-1109 |
| 邵爱梅, 希爽, 邱崇践. 2009. 修正数值天气预报的非系统性误差的变分方法. 中国科学(D辑), 39(2): 235-244 |
| 王斌, 谭晓伟. 2009. 一种求解条件非线性最优扰动的快速算法及其在台风目标观测中的初步检验. 气象学报, 67(2): 175-188 |
| 王会军, 周广庆, 赵彦. 2000. 降水和大气环流距平年际预测的一个高效的修正方案. 应用气象学报, 11(A06): 40-50 |
| 王启光, 封国林, 郑志海等. 2011. 长江中下游汛期降水优化多因子组合客观定量化预测研究. 大气科学, 35(2): 287-297 |
| 王启光, 封国林, 郑志海等. 2012a. 基于 Lorenz 系统提取数值模式可预报分量的初步试验.大气科学, 36(3): 539-550 |
| 王启光, 封国林, 支蓉等. 2012b. 长江中下游汛期降水数值预报业务模式误差场预报研究.气象学报, 70(4): 789-796 |
| 王启光, 丑纪范, 封国林. 2014. 数值模式延伸期可预报分量提取及预报技术研究. 中国科学(D辑), 44(2): 343-354 |
| 汪守宏, 黄建平, 丑纪范. 1989. 大尺度大气运动方程组解的一些性质: 定常外源强迫下的非线性适应. 中国科学(B辑), (3): 328-336 |
| 王绍武, 赵宗慈, 陈振华. 1983. 月平均环流异常的持续性与韵律性和海气相互作用. 气象学报, 41(1): 33-42 |
| 伍荣生, 谈哲敏, 王元. 2007. 我国业务天气预报发展的若干问题思考. 气象科学, 27(1): 112-118 |
| 熊开国, 封国林, 黄建平等. 2012a. 最优多因子动态配置的东北汛期降水相似动力预报试验.气象学报, 70(2): 213-221 |
| 熊开国, 赵俊虎, 封国林等. 2012b. 汛期降水相似动力预报:模式误差主分量相似预报方法. 物理学报, 61(14): 149204,doi:10.7498/aps.61.149204 |
| 孙丞虎, 李维京, 任宏利等. 2006. 一个ENSO动力-相似误差订正模式及其后报初检验. 大气科学, 30(5): 965-976 |
| 杨成彬, 黄建平, 周琴芳. 1990. 月平均大气环流异常的垂直结构//长期天气预报论文集.北京: 气象出版社, 99-106 |
| 杨杰,王启光,支蓉等. 2011. 动态最优多因子组合的华北汛期降水模式误差估计及预报. 物理学报, 60(2): 029204,doi:10.7498/aps.61.029204 |
| 杨杰, 赵俊虎, 郑志海等. 2012. 华北汛期降水多因子相似订正方案与预报试验. 大气科学, 36(1): 11-21 |
| 衣育红, 潘桃, 黄建平等. 1990. 北半球1月和7月纬偏场遥相关结构分析.高原气象, 9(1):43-52 |
| 曾庆存, 袁重光, 王万秋等. 1990. 跨季度气候距平数值预测试验. 大气科学, 14(1): 10-25 |
| 张邦林, 丑纪范. 1991. 经验正交函数在气候数值模拟中的应用. 中国科学(B辑), 21(4): 442-448 |
| 张培群, 丑纪范. 1997. 改进月延伸预报的一种方法. 高原气象, 16(4): 376-388 |
| 赵俊虎, 封国林, 王启光等. 2011. 2010年我国夏季降水异常气候成因分析及预测. 大气科学, 35(6): 1069-1078 |
| 赵俊虎, 杨杰, 封国林等. 2013a. 2011年我国夏季降水动力统计预测与异常成因.应用气象学报, 24(1): 43-54 |
| 赵俊虎, 杨杰, 龚志强等. 2013b. 欧亚中高纬阻塞高压关键区高度场动力-统计跨季度预测试验.物理学报, 62(9): 099206,doi:10.7498/aps.62.099206 |
| 赵俊虎, 封国林, 杨杰. 2014a. 2013年中国夏季降水动力-统计预测回顾及存在问题探讨.气象科技进展, 录用待刊 |
| 赵俊虎, 支蓉, 申茜等. 2014b. 2012年我国夏季降水预测与异常成因分析.大气科学, 38(2): 237-250 |
| 赵彦, 李旭, 袁重光等. 1999. IAP短期气候距平预测系统的定量评估及订正技术的改进研究. 气候与环境研究, 4(4): 353-364 |
| 赵宗慈, 王绍武, 陈振华. 1982. 韵律与长期天气预报. 气象学报, 40(4): 464-474 |
| 郑庆林, 杜行远. 1973. 使用多时刻观测资料的数值天气预报新模式. 中国科学, 16: 289-297 |
| 郑志海, 任宏利, 黄建平. 2009. 基于季节气候可预报分量的相似误差订正方法和数值实验. 物理学报, 58(10): 7359-7367 |
| 郑志海, 封国林, 丑纪范等. 2010. 数值预报中自由度的压缩及误差相似性规律. 应用气象学报, 21(2): 139-148 |
| 郑志海, 封国林, 黄建平等. 2012. 基于延伸期可预报性的集合预报方法和数值试验. 物理学报, 61(19): 199203,doi:10.7498/aps.61.199203 |
| 郑志海. 2013. 月动力延伸预报研究进展回顾. 气象科技进展, 3(1): 25-30 |
| 郑志海, 黄建平, 封国林等. 2013. 延伸期可预报分量的预报方案和策略. 中国科学(D辑), 43(4): 594-605 |
| 钟剑, 黄思训, 费建芳等. 2011. 模式误差动力特征: 模式参数误差和物理过程描绘缺失误差. 大气科学, 35(6): 1169-1176 |
| 周广庆, 曾庆存, 张荣华. 1999. 一个改进的海气耦合模式及其数值模拟. 自然科学进展, 9(6): 542-551 |
| 周琴芳, 黄建平, 杨成彬. 1989. 北半球冬季环流异常的垂直结构特征. 气象学报, 47(2): 173-179 |
| Akella S, Navon I M. 2009.Different approaches to model error formulation in 4D-Var: A study with high-resolution advection schemes. Tellus A, 61(1): 112-128 |
| Barnett T, Preisendorfer R W. 1978. Multifield analog prediction of short-term climate fluctuations using a climate state vector.J Atmos Sci, 35(10):1771-1787 |
| Bennett A F. 1992. Inverse Methods in Physical Oceanography.Cambridge:Cambridge University Press |
| Bennett A F, Chua B S, Leslie L M. 1996. Generalized inversion of a global numerical weather prediction model.Meteor Atmos Phys, 60(1-3): 165-178 |
| Bennett A F, Chua B S, Leslie L M. 1997. Generalized inversion of a global numerical weather prediction model, II: Analysis and implementation.Meteor Atmos Phys, 62(3-4): 129-140 |
| Charney J G, Fjörtoft R, Neumann J. 1950. Numerical integration of the barotropic vorticity equation.Tellus, 2(4): 237-254 |
| Dalcher A, Kalnay E. 1987. Error growth and predictability in operational ECMWF forecasts.Tellus A, 39(5):474-491 |
| D'andrea F, Vautard R. 2000. Reducing systematic errors by empirically correcting model errors.Tellus A, 52(1):21-41 |
| Danforth C M, Kalnay E, Miyoshi T. 2007. Estimating and correcting global weather model error. Mon Wea Rev, 135(2):281-299 |
| Danforth C M, Kalnay E. 2008a. Impact of online empirical model correction on nonlinear error growth.Geophys Res Lett, 35: L24805, doi: 10.1029/2008GL036239 |
| Danforth C M, Kalnay E. 2008b. Using singular value decomposition to parameterize state-dependent model errors.J Atmos Sci, 65(4):1467-1478 |
| DelSole T, Hou A Y. 1999. Empirical correction of a dynamical model.Part I: Fundamental issues. Mon Wea Rev, 127(11):2533-2545 |
| DelSole T, Zhao M, Dirmeyer P A, et al. 2008. Empirical correction of a coupled land-atmosphere model.Mon Wea Rev, 136(11):4063-4076 |
| Derber J C. 1989. A variational continuous assimilation technique. Mon Wea Rev, 117(11): 2437-2446 |
| Glahn H R, Lowry D A. 1972. The use of model output statistics (MOS) in objective weather forecasting. J Appl Meteor, 11(8):1203-1211 |
| Hoke J E, Anthes R A. 1976. The initialization of numerical models by a dynamic-initialization technique. Mon Wea Rev, 104(12): 1551-1556 |
| Huang J P, Wang S W. 1991. The monthly prediction experiments using a coupled analogy-dynamical model. Acta Meteor Sinica, 5(1):8-15 |
| Huang J P, Yi Y H, Wang S W, et al. 1993. An analogue-dynamical long-range numerical weather prediction system incorporating historical evolution. Quart J Roy Meteor Soc, 119(511): 547-565 |
| Jeuken A B M, Siegmund P C, Heijboer L C, et al. 1996. On the potential of assimilating meteorological analyses in a global climate model for the purpose of model validation. J Geophys Res, 101(D12): 16939-16950 |
| Johansson A, Saha S. 1989. Simulation of systematic error effects and their reduction in a simple model of the atmosphere. Mon Wea Rev, 117(8):1658-1675 |
| Kaas E, Guldberg A, May W, et al. 1999. Using tendency errors to tune the parameterization of unresolved dynamical scale interactions in atmospheric general circulation models.Tellus A, 51(5):612-629 |
| Klein W H, Lewins B M, Enger I. 1959.Objective prediction of five-day mean temperatures during winter.J Meteor, 16(6):672-682 |
| Klein W H.1971.Computer prediction of precipitation probability in the United States.J Appl Meteor, 10(5):903-915 |
| Klinker E, Sardeshmukh P D. 1992. The diagnosis of mechanical dissipation in the atmosphere from large-scale balance requirements.J Atmos Sci, 49(7):608-627 |
| Leith C. 1978.Objective methods for weather prediction.Annu Rev Fluid Mech, 10(1):107-128 |
| Livezey R E, Barnston A G. 1988. An operational multifield analog/antianalog prediction system for United States seasonal temperatures: 1. System design and winter experiments. J Geophys Res, 93(D9):10953-10974 |
| Lorenz E N. 1969.Atmospheric predictability as revealed by naturally occurring analogues. J Atmos Sci, 26(4):636-646 |
| Mu M, Duan W S, Wang B. 1999.Conditional nonlinear optimal perturbation and its applications.Nonlinear Proc Geoph, 10(6): 493-501 |
| Ren H L, Chou J F, Huang J P, et al. 2009. Theoretical basis and application of an analogue-dynamical model in the Lorenz system. Adv Atmos Sci, 26(1): 67-77 |
| Saha S. 1992. Response of the NMC MRF model to systematic-error correction within integration.Mon Wea Rev, 120(2):345-360 |
| Trémolet Y. 2007. Model-error estimation in 4D-Var. Quart J Roy Meteor Soc, 133(626): 1267-1280 |
| Van den Dool H M. 1989. A new look at weather forecasting through analogues. Mon Wea Rev, 117(10): 2230-2247 |
| Van den Dool H M. 1991. Mirror images of atmospheric flow.Mon Wea Rev, 119(9): 2095-2106 |
| Van den Dool H M. 1994. Searching for analogues, how long must we wait? Tellus A, 46(3):314-324 |
| Van den Dool H M, Huang J, Fan Y. 2003. Performance and analysis of the constructed analogue method applied to US soil moisture over 1981-2001. J Geophys Res, 108(D16), doi: 10.1029/2002JD003114 |
| Xiong K G, Feng G L, Huang J P, et al. 2011. Analogue-dynamical prediction of monsoon precipitation in Northeast China based on dynamic and optimal configuration of multiple predictors. Acta Meteor Sinica, 25(3): 316-326 |
| Yang X, DelSole T, Pan H L. 2008.Empirical correction of the NCEP global forecast system. Mon Wea Rev, 136(12):5224-5233 |
| Yu H, Huang J, Chou J. 2014. Improvement of medium-range forecasts using the analogue-dynamical method. Mon Wea Rev, 142(4): 1570-1587 |
| Zeng Q C, Zhang B L, Yuan C G, et al. 1994. A note on some methods suitable for verifying and correcting the prediction of climatic anomal.Adv Atmos Sci, 11(2): 121-127 |
| Zupanski M. 1993. Regional four-dimensional variational data assimilation in a quasi-operational forecasting environment. Mon Wea Rev, 121(8): 2396-2408 |
 2014, Vol. 72
2014, Vol. 72