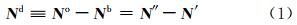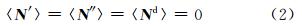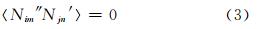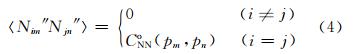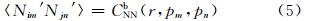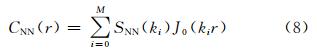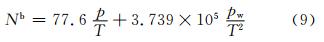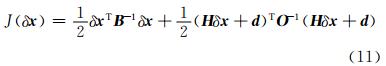中国气象学会主办。
文章信息
- 王金成, 龚建东, 赵滨. 2015.
- WANG Jincheng, GONG Jiandong, ZHAO Bin. 2015.
- 一种新的COSMIC大气折射率资料观测误差估计方法及在GRAPES全球三维变分同化中的应用
- A new method for estimating observation error of the COSMIC refractivity data and its impacts on GRAPES-GFS model weather forecasts
- 气象学报, 73(1): 142-158
- Acta Meteorologica Sinica, 73(1): 142-158.
- http://dx.doi.org/10.11676/qxxb2015.005
-
文章历史
- 收稿日期:2014-02-26
- 改回日期:2014-08-20
1995年开始的GPS/MET计划(Ware et al,1996)验证了无线电掩星技术观测地球大气参量的概念和方法,开启了利用全球定位系统(GPS)无线电掩星技术观测地球大气的序幕。目前为止,世界上已经发射了携带GPS无线电接收机的卫星有美国-阿根廷的SAC-C、德国-美国的CHAMP(CHAllenging Mini-satellite Payload)、美国-德国的GRACE-A(Gravity Recovery And Climate Experiment)、欧洲的METOP-A/GRAS(METeorological Operational satellite-A,GNSS Receiver for Atmospheric Sounding)、台湾地区-美国的FORMOSAT-3/COSMIC(FORMOsa SATellite mission-3/Constellation Observing System for Meteorology,Ionosphere and Climate)、德国的TerraSAR-X(雷达成像仪地球观测卫星)、美国的C/NOFS(Communications/Navigation Outage Forecasting System)、欧洲的Metop-B/GRAS(Meteorological Operational satellite-B,GNSS Receiver for Atmospheric Sounding)等(Wickert et al,2008)。2006年美国大学大气科学联合会(UCAR)和台湾地区空间计划局等机构联合开发的气象、电离层及气候星座观测系统(COSMIC)(Rocken et al,2000; Anthes et al,2008)和欧洲气象卫星局(EUMETSAT)发射的METOP-A/GRAS卫星对地球大气的掩星观测已实现业务化。COSMIC资料的分析和存储中心(CDAAC)收集并分析存储了大部分GPS无线电掩星观测资料。因GPS无线电掩星观测资料具有观测精度高、不受云雨等天气影响、高垂直分辨率、观测覆盖全球,以及成本低廉等优点(Kursinski et al,1996; Zou et al,2006; Anthes et al,2008),已经在数值天气预报中得到了广泛研究和应用(Zou et al,1995,2004; Kuo et al,2000; Liu et al,2001; Chen et al,2009; Ma et al,2009,2011; Huang et al,2010; 成巍等,2012)。
GPS无线电掩星观测资料在数值天气预报中的应用主要是通过资料同化系统对其进行同化实现的,CDAAC提供了两种级别和多种形式的GPS无线电掩星资料产品:一级产品(L1)包括原始观测的位相、振幅及卫星轨道和地面基站数据;二级产品(L2)主要包括弯角、折射率、反演的大气气压、温度和水汽(Kuo et al,2004; 郭鹏,2005)。为了使用较小计算量获得较高精度的分析结果,同化的资料越是原始观测资料越好,而需要的观测算子越简单越好,因此选择何种级别的产品进行同化,需要综合考虑:(1)资料处理过程中是否加入了带有误差的额外信息;(2)观测误差特征是否能够容易准确估计;(3)观测算子是线性的还是非线性的;(4)观测算子的代表性;(5)观测算子的代表性误差是否能容易准确估计;(6)观测算子及其伴随的计算量等(Syndergaard et al,2006)。Kuo等(2000)和Syndergaard等(2006)详细分析了同化GPS掩星观测各级别产品的优缺点,认为弯角和折射率是最适宜同化的产品:弯角产品仍然是比较原始的观测资料,观测算子不要求精确的卫星轨道信息,也不需要电离层模式,重要的是能够相对容易和准确地估计其观测误差;折射率产品的优点是其观测算子简单,不需要精确的卫星轨道信息,不需要电离层模式和大气模式层顶以上的大气变量,计算量小。
变分同化的目标是通过极小化目标函数,最大限度地提取观测信息,最大可能改进模式初始场的精度(Lorenc,1986)。在已有变分同化系统中,要同化一种新的观测资料,主要有两个方面的工作:(1)建立一个简单、精确、高效的观测算子,(2)准确估计观测误差方差等统计参数。弯角和折射率都不是大气变量的直接观测,因此,建立简单、精确和高效观测算子是同化弯角和折射率的关键和主要研究内容,目前已经发展了若干同化弯角(Zou et al,1999,2000,2002,2004;Liu et al,2001,2003; Shao et al,2002; Palmer et al,2000; Poli,2003,2004)和同化折射率(Poli,2003,2004; Ahmad et al,1998; Syndergaard et al,2005; Sokolovskiy et al,2005a,2005b; Shao et al,2009; Smith et al,1953; 毕研盟等,2013)的观测算子。由于折射率局地观测算子简单,具有计算量小等优点,目前主要业务中心都采用局地观测算子来同化折射率资料(Cucurull,2008; Poli et al,2010; Rennie,2010)。成功同化弯角和折射率资料的另一个关键是观测误差的准确估计。在变分同化(Lorenc,1986)中,观测误差包括测量误差与观测算子的代表性误差两部分。观测算子代表性误差主要来源于两个方面,一是数值天气预报(NWP)模式的有限分辨率,二是观测算子不能够将完美的模式状态计算出完美的观测,即观测算子本身的误差。所以,即使相同观测产品,采用不同观测算子,代表性误差不同,造成的观测误差也不同。Zou等(2002)针对二维射线积分算子统计估计了弯角的观测误差并应用于弯角同化中。由于折射率资料是数值天气预报中应用最广泛的GPS无线电掩星产品,其观测误差的准确估计就显得尤为重要。针对局地观测算子,已经有许多学者研究了折射率观测误差。Steiner等(2006)采用观测与模拟对比的方法,估计了CHAMP折射率在2002/2003年北半球冬季和夏季的南北半球高、中、低纬度带上折射率的观测误差方差及其垂直相关性,这个研究主要针对的是CHAMP观测的折射率,并且采用的是观测与分析对比的方法,其中,欧洲中心分析场模拟的折射率误差是经验获得的,且被主观经验地乘以2倍因子;Scherllin-Pirscher等(2011)利用与Steiner等(2006)同样的经验分析方法,估计了CHAMP、GRACE-A和COSMIC卫星观测的弯角、折射率、反演的干大气气压和温度等变量在4—50 km的观测误差,发现了不同卫星观测误差具有很强的一致性,并且在20 km以上,观测误差具有明显的季节变化,在各半球冬季的观测误差最大,但是Scherllin-Pirscher等(2011)并未对4 km以下的观测资料进行估计,且其对观测误差的估计也存在与Steiner等(2006)相同的问题,同时这个研究所估计的观测误差相比Kursinski等(1996)估计的值偏大,特别是在10—20 km高度。Kuo等(2004)针对折射率局地观测算子,用CHAMP和SAC-C卫星2001年12月的折射率资料,估计了折射率在1000—10 hPa的观测误差,分析了低纬度(30°S—30°N)和中纬度(30°—60°N)两个纬度带上折射率观测误差,并与Kursinski等(1996)估计的观测误差进行了比较。Kuo等(2004)采用从观测折射率与背景场(模式预报场)模拟的折射率的总误差中扣除预报误差的方法,其中,采用美国气象中心(NMC)和新息增量法(H-L法)(Hollingsworth et al,1986; Xu et al,2001)两种方法对所使用的背景场的误差进行估计。NMC方法估计背景误差的缺点是经常低估背景误差,而H-L法局限在探空观测稠密的大陆地区。Kuo等(2004)认为H-L法只能应用于具有稠密固定观测站点且有长时间的观测时间的地区使用,不能直接使用GPS无线电掩星观测来估计背景误差,而背景误差不因观测系统和观测资料不同而不同,他们使用探空观测资料估计其中使用的背景误差。这样估计的背景误差局限在探空资料集中的大陆地区,对南半球、热带、广大海洋和两极等探空观测稀少地区的估计只能用探空观测稠密的北半球大陆地区的估计结果代替。而研究表明,背景误差随着纬度有显著变化(Wu et al,2002)。Chen等(2011)采用与Kuo等(2004)相似的方法,用WRF模式预报作为背景场,采用AVN模式分析作为另外一种观测资料用以估计WRF背景误差。他们使用东亚和西太平洋地区的COSMIC折射率资料,估计该区域冬季(2007年1月15日—2月15日)和夏季(2007年8月15日—9月15日)针对局地观测算子的折射率观测误差标准差,和针对线性非局地观测算子(Sokolovskiy et al,2005a)的过剩相位的观测误差方差,探讨了折射率误差与过剩相位观测误差对纬度带的依赖性,同时也比较了冬季和夏季观测误差的差异,分析了非局地观测算子与局地观测算子观测误差的区别。Chen等(2011)的不足在于其仅对东亚和西太平洋地区20 km以下的观测误差进行了估计,具有区域局限性,仅分析了冬季1个月及夏季1个月的观测,并未研究折射率在春季和秋季的观测误差。
因观测误差的估计精度直接影响变分同化分析和预报效果,因此,提高折射率观测误差的估算精度是改进和提高其同化效果的重要途径。为了提高折射率观测误差的估计精度,本研究从理论上分析了H-L法对GPS无线电掩星这类覆盖全球但观测位置不固定观测系统适用的必要条件,并提出了可行的实施方案;针对局地观测算子,在H-L法中使用COSMIC折射率资料直接估计所使用的背景误差,分季节统计了南北纬度高(60°—90°)、中(30°—60°)、低(0°—30°)共6个纬度带1000—10 hPa折射率的观测误差。同时,将统计的夏季结果应用于GRAPES全球变分同化系统中,做了26 d的同化循环预报试验,分析了使用新统计的观测误差相比原来使用的全球平均的单一观测误差对分析和预报的影响。
本研究第1次给出了H-L法使用COSMIC折射率这类全球覆盖且观测位置不固定的GPS无线电掩星资料,估计背景误差协方差以及对应的观测误差方差的适用条件,并设计了实施方案;针对局地观测算子,统计估计了COSMIC折射率的观测误差,并分析了其季节变化;同时将新估计的观测误差应用于GRAPES全球变分同化系统,提高了折射率同化效果,提高了GRAPES全球同化预报系统的预报技巧。本研究有两个方面的意义,一是实现了H-L法应用GPS无线电掩星观测系统更准确的估计观测误差,二是通过更新折射率的观测误差提高了GRAPES全球同化预报系统的预报技巧。2 H-L法对GPS无线电掩星资料的适用条件2.1 基本假设
Hollingsworth等(1986)提出了一种利用观测和模式模拟之差(新息增量)来统计背景误差协方差和观测误差协方差的方法,称为新息增量法(简称H-L法),其优点是可以同时估计出背景误差协方差和观测误差,且结果精度较高,代表性较好。用H-L法估计的观测误差包含了测量误差与代表性误差,可以直接应用于变分同化系统。H-L法被广泛用来估计背景误差协方差三维结构(Xu et al,2001; 龚建东等,2006)和观测误差(Kuo et al,2004)。
设Nb和No分别为背景场(模式6 h预报场)模拟的折射率和观测折射率向量,N′=Nb-Nt和N″=No-Nt分别为折射率背景误差和观测误差,Nt为空间和时间四维空间中的大气折射率真值。一般情况下,No和N″被认为是离散的数组,而Nb和N′是模式空间中连续的向量,设模式空间坐标系为(x,y,p),新息增量Nd为在观测空间中观测折射率与模拟折射率之差,则
为了采用新息增量来估计背景误差协方差和观测误差,H-L法要求观测误差和背景误差满足4个假设:
(1)假设N′和N″满足无偏(或是经过偏差订正后的背景误差和观测误差)高斯分布
这里〈·〉表示(·)所有可能实现的集合平均。(2)假设折射率观测误差和背景模拟误差相互独立,对任意i,j,m,n
式中,Nim″为N″在点(xi,yi,pm)(垂直坐标是气压坐标系)的值,Njn′为N′在(xj,yj,pn)的值。(3)假设在水平面上,不同水平位置的折射率的观测误差不相关,对任意m,n
式中,CNNo(pm,pn)为观测误差的垂直相关函数。(4)假设在有限的区域内,背景误差在水平方向是同质、各向同性的,因此背景误差的自相关
在探空这类观测点固定的大气观测过程中,同一时间同一观测点仅有一次观测实现,根据各态遍历性理论,集合平均可以用时间样本平均代替(Hollingsworth et al,1986; Xu et al,2001)。但GPS无线电掩星的观测点的位置不固定,是随时间变化的,对同一观测点若没有足够多的时间样本,则不能直接采用时间样本平均代替集合平均。在一定水平区域内,如果将不同空间点的观测误差和背景误差看作是同一随机变量的不同实现,或假设所有观测点的观测误差和背景误差是具有相同统计特性的随机变量的各自不同的实现,那么集合平均就可以用所有空间和时间的样本点的平均来代替,即〈·〉等于(·)所有空间和时间点数值的平均。因观测误差和背景满足假设条件(1)—(4),即观测误差和背景误差都是无偏高斯分布(假设(1)),不同观测点的观测误差在水平上满足不相关(假设(2)),背景误差水平相关也是同质和各项同性的(假设(4))。在满足假设条件(4)情况下,即可以认为在一定水平区域内,不同位置的观测误差和背景误差是具有相同正态分布的随机变量,其统计特性是相同的。因此,集合平均就可以用所有空间和时间的样本点的平均来代替,即〈·〉等于(·)所有空间和时间点对数值的平均来近似。
在原H-L法中,是固定的观测点对之间,从时间上取样,而GPS的观测点对是变化的,相同的站点对之间不可能有长时间的观测系列。H-L法做探空资料误差估计和背景误差估计时,也用了有限区域内背景误差协方差是均匀(假设(3))(Xu et al,2001)的假设。因为H-L法假设观测误差之间不相关,这只是观测误差方差在有限区域内是均匀的(假设(4))假设中的一种情况。严格来讲,观测误差方差在一定纬度上是均匀的假设是一个非常近似的假设,因为GPS观测误差是随纬度变化的(Chen et al,2011),其原因主要有两个方面:一是对流层低层的GPS观测误差,其随纬度变化主要是由于随纬度变化的水汽产生了随纬度变化的局地观测算子的代表性误差;二是高层20 km以上的平流层中,GPS观测资料在转化为折射率过程中,大气高层(80 km以上)引入了不精确的气候场作为Abel反演的背景场(Kuo et al,2004)。由于对流层低层观测误差在高、中、低3个纬度带具有显著的纬度带变化,而在这些纬度带内变化相对较小(Chen et al,2011),本研究旨在估计具有显著纬度变化的高、中、低几个纬度带的观测误差,用于实际的资料同化。
掩星观测与探空观测的另一个巨大不同是掩星观测不是一个局地观测,而是无线电射线穿越大气路径上大气折射率的平均,其水平特征距离约为350 km,这使得在观测站点较为接近且两个掩星事件射线方向接近的情况下,观测误差可能存在较强的相关。因此在站点对距离小于350 km情况下,假设条件(3)很难得到满足,会对观测误差的估计结果产生影响。另外,掩星观测本身不是局地观测也是局地观测算子主要的代表性误差的主要原因。通过统计分析发现,在所使用的所有观测样本中,站点对距离小于350 km且射线路径相近(二射线路径夹角小于30°)的样本很少,这说明掩星折射率观测误差的水平相关较小且对观测误差估计的影响也很小。2.2 观测误差和背景误差分离
根据式(1)—(6),对任意m、n,新息增量Nd的协方差
式中,新息增量的协方差函数CNN(r,pm,pn)=〈NdimNjnd〉可用相同距离的新息增量样本计算得到,进而推算得到CNN(0,pm,pn)。从新息增量在距离为0的协方差中,扣除CNN(0,pm,pn),即可以获得观测误差协方差CNNo(pm,pn)。因为主要是估计观测误差方差,因此仅考虑在单一垂直层上分析,不考虑观测误差的垂直相关。当pm=pn时,CNNo(pm,pn)表示观测误差方差βNNo,CNN(0,pm,pn)表示背景误差方差βNNb,CNN(r,pm,pn)表示单层水平空间中的背景误差方差(不同位置的观测误差在水平空间上相互独立,假设(2)),用CNN(r,pm)表示,或者直接表示为CNN(r)。
同Xu等(2001)采用的分析方法一样,将背景误差协方差CNN(r)在区域r≤D=3000 km范围进行谱展开
式中,k0=0,ki(i=1,2,L,M)为J0′(kD)=0的解,即J1(kD)=0的解。这里的J0′(·)为J0(·)对(·)的一阶偏导数,J1(·)是一阶贝塞尔函数。选取合适的谱截断阶数M,以保证SNN(ki)≥0,进而保证背景误差协方差的半正定性。截断阶数可以根据实际情况进行微小的调整。文中设定M=6。3 资料和计算实施方案3.1 资 料采用CDAAC提供的2010年3月1日00时—2011年2月28日18时(世界时,下同)共1年的COSMIC的二级产品(L2,wetPrf)的折射率资料。采用相同时段美国大气研究中心全球模式GFS的6 h预报场作为背景场,垂直方向有26层等压面,水平分辨率是1°×1°。使用的观测算子为折射率的局地观测算子
式中,Nb为模拟的大气折射率(单位:N),p为气压(单位:hPa),T为大气温度(单位:K),pw为大气中的水汽压(单位:hPa)。3.2 计算实施方案
在2.1节中已经探讨了H-L法对GPS无线电掩星资料误差估计的适用条件,在此再简述针对COSMIC观测资料观测误差估计的实施方案。将全球分为6个纬度带,分别为90°—60°S,60°—30°S,30°S—0°,0°—30°N,30°—60°N,60°—90°N。针对每个纬度带计算:
(1) 读取观测:从COSMIC的二级产品(L2,wetPrf)中读取时间、经度、纬度、高度、气压和折射率。将获得的100 m分辨率的折射率廓线采用3次样条插值方法插值到GFS背景场的26层等压面上。
(2) 计算折射率的新息增量:读取某一时刻的GFS大气背景场,用局地观测算子计算模式空间的三维大气折射率。在背景场时间±3 h时间窗内寻找匹配的折射率的观测廓线。用双线性插值方法将模式空间中三维折射率插值到匹配的所有观测点上,计算出观测点上的背景折射率与观测折射率的差,即折射率的新息向量,将背景场的时间作为新息向量时间。
(3) 空间配对:在给定水平范围内(本研究中采用30°间隔的纬度带),计算具有相同背景场时间的任意两个观测点的距离,并按照距离将观测点对进行分类,采用200 km作为分类间隔,最大距离为3000 km,共有16个类别,将距离偏移量设定为±100 km,认为处在同一分类的点对之间的距离相同。按照此方法,将所有给定时间范围(本研究中为3个月)内所有的观测点对分类。分类后的所有观测点作为H-L法的统计样本。图 1为2010年夏季850和500 hPa不同纬度带上每个距离分类中的样本个数(观测点对数)。
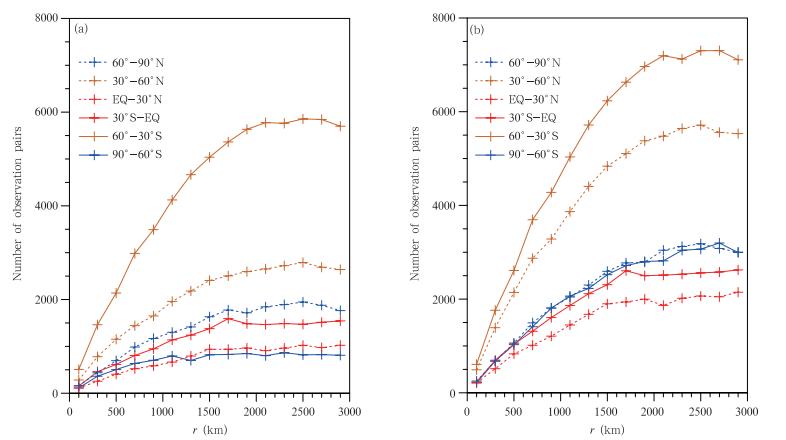 |
| 图 1 2010年6月1日00时—8月31日23时850 hPa(a)、500 hPa(b)不同纬度带、不同距离分类的COSMIC观测点对数(样本个数) (距离r=0时的总观测数未在图中给出) Fig. 1 Number of the available COSMIC observation pairs within each bin of fixed r interval(Δr=200 km)for the range of 0 < r ≤ 3000 at 850 hPa(a) and 500 hPa(b)in the different latitude b and s in the boreal summer(JJA)of 2010 (The total numbers of observations at r=0 are not showed) |
(4) 新息增量协方差的计算:对0—3000 km的所有分类中的观测点对进行统计,针对每个等压面,计算每个距离类别的所有观测点对新息增量样本的协方差CNN(r)。图 2中的圆点代表统计折射率新息向量不同距离的协方差,实线为采用式(8)的拟合结果,时间和空间范围同图 1。
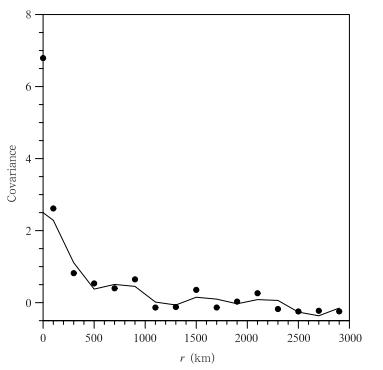 |
| 图 2 2010年6月1日00时—8月31日23时在0°—30°N 500 hPa统计的新息增量的协方差(圆点)和拟合的背景误差协方差(实线) Fig. 2 Binned innovation covariance(closed circle) and fitted forecast covariance function(solid line)for the single level analyses at 500 hPa in the latitude b and (0°-30°N)in the boreal summer(JJA)of 2010 |
(5) 观测误差方差和背景误差的分离:将第(4)步中计算的每个等压面层的协方差函数进行谱展开(式(8)),并计算拟合的协方差函数CNN(r)(图 2),其中,使用每个距离分类内的样本数作为权重。根据式(6)和(7),计算背景误差方差和观测误差方差。4 COSMIC折射率资料观测误差估计结果分析
由于折射率绝对观测误差垂直变化非常大,为了分析方便,将使用H-L法估计的绝对误差转化为相对误差,即将绝对误差除以同层次相对应区域的平均折射率
式中,δo为由H-L法估计的折射率绝对观测误差标准差,No为观测折射率的区域平均值。如无特别说明,文中所称的观测误差均指式(10)定义的折射率相对观测误差。图 3给出了春、夏、秋、冬四季在不同纬度带上COSMIC折射率观测误差。春季(图 3a),观测误差随纬度升高而减小;各纬度带的观测误差在600—850 hPa达到最大值,300—50 hPa观测误差随高度变化较小,50—10 hPa观测误差随着高度升高而增大。对于低纬度地区,在200 hPa相对误差最小,约为0.35%。其他季节(图 3b、c、d)折射率观测误差的垂直变化特征与春季结果一致。同时,图 3给出的折射率相对观测误差随高度的变化特征与已有研究结果(Kuo et al,2004; Chen et al,2011; Scherllin-Pirscher et al,2011)非常一致。在50 hPa以上,相对观测误差随高度增大的原因在于COSMIC折射率资料反演过程中所使用的高层气候背景场误差随高度而增大,大气平均折射率减小,因而导致气候背景误差产生的相对观测误差增大(Kursinski et al,1996; Kuo et al,2004)。在300 hPa以下的对流层低层,所有纬度带上的观测误差均达到最大值,造成这种变化的原因在于大气水汽水平分布不均匀、超折射以及多路径现象(Foelsche et al,2004; Kuo et al,2004)。
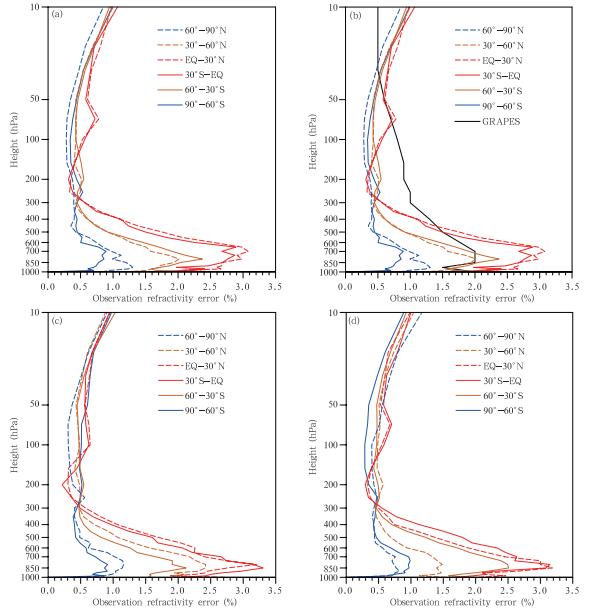 |
| 图 3 春(a)、夏(b,黑实线为GRAPES变分同化系统中采用的全球平均的折射率相对观测误差)、秋(c)、冬季(d)不同纬度带COSMIC折射率的相对观测误差 Fig. 3 Fractional observation error of the refractivity of COSMIC for the seasons of(a)MAM,(b)JJA,(c)SON,and (d)DJF in the different latitude b and s(The fractional observation error of the refractivity in the GRAPES 3DVAR is represented by black solid line in(b)) |
春季(图 3a),300 hPa以下的对流层低层,观测误差随纬度的增高而减小。高纬度地区相对观测误差较小,最大值仅为0.9%,而低纬度地区相对观测误差较大,最大值出现在低纬度地区700 hPa附近,达3%。造成折射率相对观测误差纬度变化的原因是从高纬度到低纬度,大气水汽含量逐渐增大,水平梯度逐渐增大,同时折射率水平尺度增大,使得局地观测算子的代表性误差增大。对春季而言,南、北半球相同纬度带上的相对观测误差基本相同,春季COSMIC折射率的相对观测误差具有很好的赤道对称性。
夏季(图 3b),300 hPa以下的对流层低层,北半球中高纬度带的相对观测误差明显比南半球相同纬度带的相对误差大,北半球高纬度带的相对观测误差与南半球中纬度的相对观测误差基本相当,而北半球中纬度带的相对误差与南半球低纬度带的相对观测误差相当。结果显示了南、北半球的相对观测误差的不对称性。这种不对称性的可能原因是:夏季北半球的水汽丰富,天气变化剧烈,使得局地观测算子的代表性误差增大。秋季(图 3c),300 hPa以下的相对观测误差南、北半球的不对称性介于春季和夏季之间,北半球中高纬度带的相对观测误差都略高于南半球相同纬度带的相对观测误差。冬季结果与夏季正好相反,即南半球中高纬度相对观测误差比北半球相对观测误差大,南北半球的相对观测误差也有显著的不对称性。
用冬季结果与文献(Kuo et al,2004)中相同纬度带的观测误差对比,对低纬度地区,300—50 hPa的相对误差大小与Kuo等(2004)使用的H-L法基本一致,最小值约为0.3%,而在50 hPa以上,与Kuo等(2004)中使用NMC方法估计的结果相似,在10 hPa最大值都达到1%;在300 hPa以下对流层低层,最大值与Kuo结果相同,达3%,但相对观测误差最大值的高度层不同,Kuo结果最大值在模式最底层(1000 hPa),而本研究结果最大值出现在850—700 hPa。对北半球中纬度地区而言,本研究估计的300—50 hPa相对观测误差大小介于Kuo等(2004)中两种方法估计的相对误差之间,而在10 hPa的相对观测误差比Kuo等(2004)两种方法估计值都小,为1%;而在300 hPa以下,本研究估计的相对观测误差大小比Kursinski(1996)的结果略大,但是相对观测误差随高度变化规律与Kursinski(1996)以及Chen等(2011)结果一致,在850 hPa附近有最大值,约1.5%。
为了更清晰地分析各纬度带折射率相对观测误差的季节变化,将每个纬度带四季的相对观测误差整合在一起(图 4)。为了更加客观地分析COSMIC掩星折射率观测误差方差的季节变化(图 5),定义显著的季节变化为:假设相对观测误差满足高斯分布,对四季中相对观测误差最大值和最小值具有显著不同的假设进行统计检验,如果通过检验则说明具有显著的季节变化,反之说明观测误差不具有显著的季节变化。图 5c蓝色阴影区表示通过显著季节变化检验的区域。
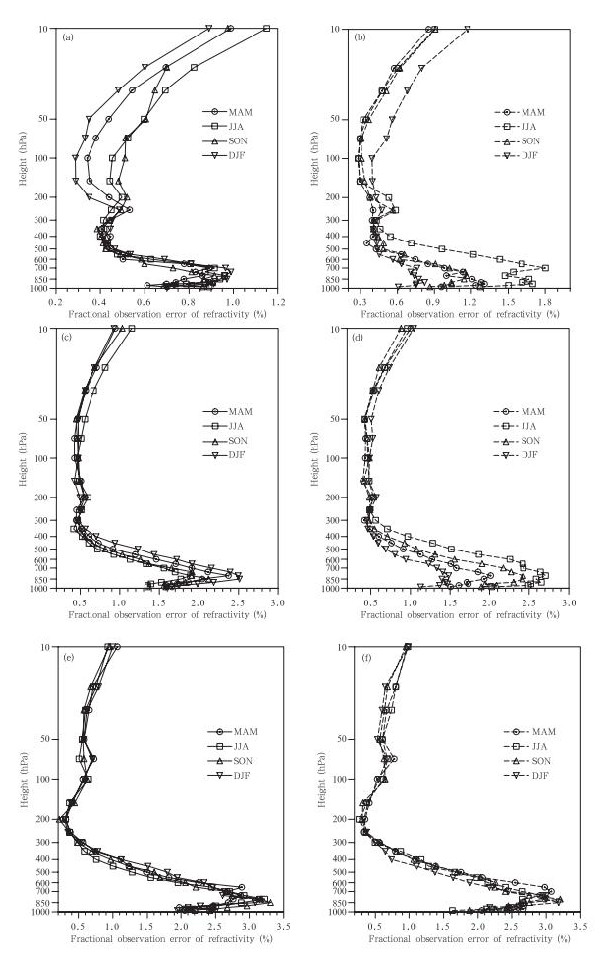 |
| 图 4 不同纬度带COSMIC折射率四季相对观测误差 (a.90°—60°S,b.60°—90°N,c.60°—30°S,d.30°—60°N,e.30°S—EQ,f.EQ—30°N) Fig. 4 Fractional observation error of the refractivity of COSMIC in the four seasons in (a),(b)high latitudes,(c),(d)mid-latitude,and (e),(f)low latitudes of both(a),(c),(e)south(solid) and (b),(d),(f)north(dashed)hemisphere respectively |
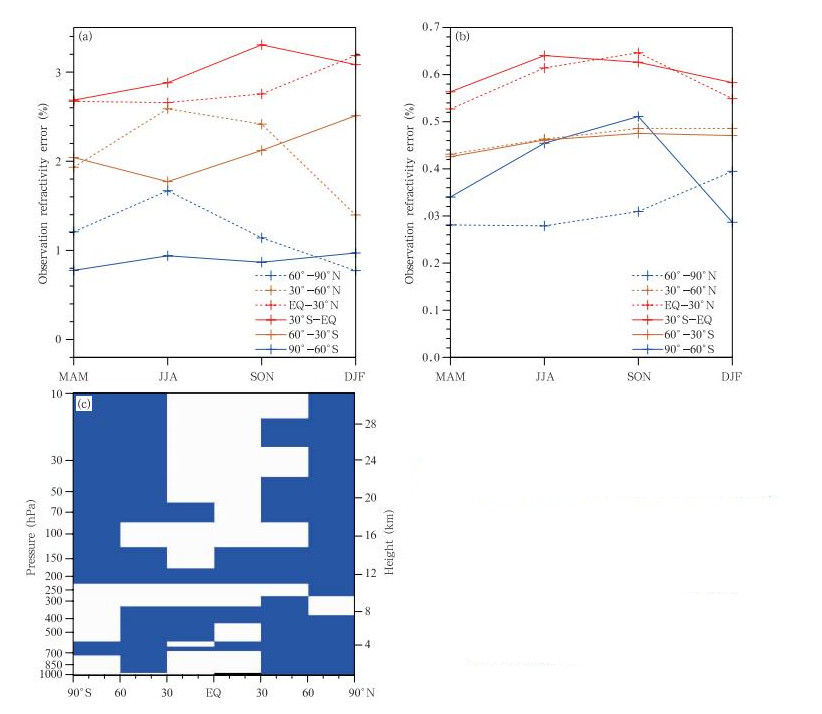 |
| 图 5 850 hPa(a)、100 hPa(b)上不同纬度带的折射率观测误差方差的季节变化及(c)观测误差方差具有显著季节变化的区域(阴影表示通过99%信度检验的区域) Fig. 5 Seasonal variation of the fractional refractivity observation error on 850 hPa(a) and 100 hPa(b)in the different latitude b and s,and (c)domains and levels(blue shaded)in which the seasonal variation of the fractional refractivity observation error is significant(The significance level of F-test is at α=0.01) |
北半球高纬度地区(图 4b),对流层低层相对观测误差夏季最大,冬季最小,春、秋季居中;夏季相对观测误差最大值(1.8%)是冬季最大值(0.9%)的两倍;同时不同季节相对观测误差最大值出现的层次也不同,夏季最大值在700 hPa附近,而冬季则在925 hPa附近。相对观测误差明显的季节变化可能是大气中水汽含量随季节变化造成的。 200 hPa 以上,春、夏和秋季的相对观测误差基本相同,只有冬季的相对观测误差较其他3个季节大,差值达0.3%。这可能是由于在COSMIC弯角反演过程中,使用的高层大气背景场冬季误差比其他季节大造成的。图 5c表明北半球高纬度地区,除了400—300 hPa没有通过季节变化显著性检验,其他高度层都通过了季节变化显著性检验,即北半球高纬度地区除400—300 hPa以外的所有高度层上折射率观测误差都具有显著的季节变化。
北半球中纬度地区(图 4d、5c),300 hPa以下的对流层低层,相对观测误差具有明显的季节变化,夏季最大,秋季较大,春季较小,冬季最小。相对观测误差在夏季850 hPa最大,为2.7%,冬季最大值在850 hPa附近,仅为1.5%。在250 hPa以上,相对观测误差冬季最大,夏季最小,差别约为0.1%,这可能是由于在COSMIC弯角反演过程中使用的大气背景场误差在不同季节不同引起的。从图 5c可知,在北半球中纬度地区除了250、100和30 hPa层次的折射率观测误差方差没有通过显著的季节性变化以外,其他层次均具有显著的季节变化。
在南半球高纬度地区(图 4a、5c),250 hPa以下的对流层,相对观测误差没有明显的季节变化,而在250 hPa至模式层顶的10 hPa,相对观测误差具有明显的季节变化,冬季最小,夏季最大,约相差0.3%,200—50 hPa夏季的相对观测误差是冬季值的2倍。目前,尚无研究指出南半球高纬度对流层高层和平流层低层折射率观测误差的季节变化,其原因亦需要进一步研究。
南半球中纬度地区(图 4c、5c),折射率相对观测误差除300—250和100 hPa层外均具有显著的季节变化,在对流层低层不同季节最大值冬季和夏季相差为0.4%,相比北半球中纬度的季节变化要小得多(但也通过了季节变化显著性检验),造成这一现象的原因可能是南半球中纬度地区大面积的海洋,其天气变化和水汽含量随季节变化相比北半球中纬度要小,水汽含量大时其分布各向异性及不均匀性较强,Abel反演过程中大气状态球对称近似误差较大,使得局地观测算子的代表性误差较大。
在北半球低纬度地区(图 4f、5c),折射率相对观测误差除了650、350和200—150 hPa以外其他层次不存在明显的季节变化特征。同时在南半球低纬度地区(图 4e、5c),折射率相对误差除了550—350 hPa以及200、70 hPa以外也都不存在显著的季节变化特征。因此,在低纬度地区折射率相对误差的季节变化不明显。5 新观测误差在GRAPES全球三维变分同化系统中的应用
GRAPES变分同化系统采用增量分析方案(庄世宇等,2005; 薛纪善等,2008),其目标函数表达式为
式中,δx=x-xb为分析变量x的增量,xb为背景场,H为观测算子H的切线性近似,B是背景误差协方差矩阵,O是观测误差协方差矩阵,d=H(xb)-yo为观测余差,其中yo为观测。目前,GRAPES全球变分同化系统已经实现了对GPS无线电掩星折射率资料的同化,采用的是局地观测算子式(9)。在同化GPS无线电掩星折射率之前,对其进行必要的预处理:首先将GPS无线电掩星折射率资料的几何高度坐标转化为GRAPES模式的位势高度坐标;其次,对GPS无线电掩星折射率资料进行质量控制和垂直方向的稀疏化(Liu et al,2014)。质量控制的好坏直接决定了观测资料同化效果,GRAPES全球三维变分同化系统中对GPS无线电掩星折射率资料进行了严格的质量控制,具体质量控制方案见文献(Liu et al,2014)。研究结果表明,相比不同化COSMIC折射率,同化COSMIC折射率显著提高了GRAPES全球同化预报系统的预报技巧(唐细坝等,2009; Liu et al,2014)。
本研究第4部分结果已表明,COSMIC折射率观测误差随纬度有显著变化,同时也有显著的季节变化。但在目前GRAPES同化系统中,折射率的观测误差采用全球平均的单一观测误差廓线(图 3b中黑实线,以下用δNg表示)(Rennie,2010)。将δNg与本研究第4部分估计的夏季所有纬度带的折射率观测误差(图 3b彩色线条)比较发现,400 hPa以下,δNg比估计的南北半球高纬度和南半球低纬度地区的观测误差大,而比低纬度地区和北半球中纬度地区的观测误差小;400—100 hPa,δgN大于估计的所有纬度带的观测误差;100 hPa以上δNg则小于估计的所有纬度带的观测误差。通过第4部分的分析及与其他研究的对比发现,本研究估计的折射率观测误差更合理。为了提高GPAPES全球变分同化系统同化折射率的效果,提高GPAPES全球变分同化系统的预报技巧,可用文中估计的折射率观测误差取代GRAPES中原有的全球平均不随季节变化的观测误差。
为了验证估计的折射率相对观测误差对GRAPES全球同化预报系统的影响,设计了如下2个同化预报循环试验:
(1) CTRL:使用GRAPES原有的折射率相对观测误差;
(2) NEWOE:使用文中第4部分估计的夏季的随纬度带变化的折射率相对观测误差。
上述2个试验的起报时间均为2009年7月5日00时,循环同化积分至2009年7月31日12时。2个试验所同化的观测资料完全一致,同化的观测资料有常规观测资料(GTS),卫星微波温度计观测资料(NOAA-16、NOAA-17、NOAA-18、Metop-A)以及COSMIC折射率资料。试验结果采用中国气象局数值预报中心开发的GRAPES诊断分析工具GET进行诊断分析。
从观测与分析场模拟折射率之差(O-A)的均值和标准差(图 6)可以发现,相比旧的折射率观测误差,采用新统计的折射率观测误差,O-A的均值和标准差都减小了(除10、30 hPa外)。说明采用新的折射率观测误差方差后,分析场模拟的折射率更接近观测折射率。因此,统计的折射率观测误差方差更合理,提高了分析场的分析精度。
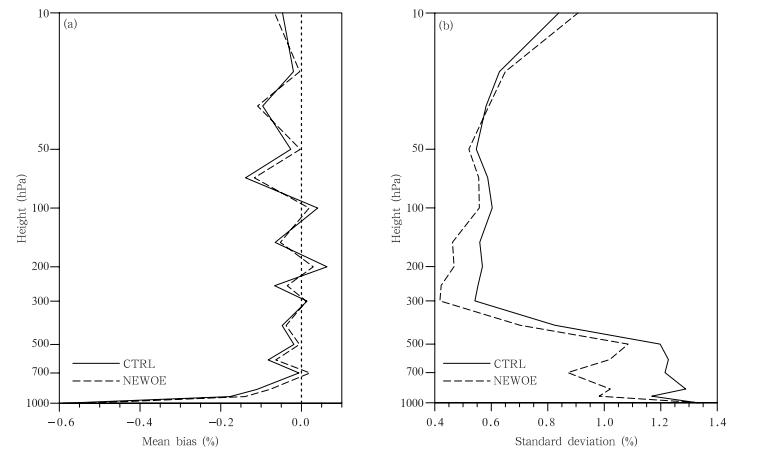 |
| 图 6 观测与分析场模拟折射率差的均值(a)和标准差(b) Fig. 6 Mean(a) and st and ard deviation(b)of the fractional refractivity difference between the observation and the analysis from the experiments |
图 7给出了北半球(20°—90°N)、南半球(90°—20°S)和热带(20°S—20°N)3个区域CTRL试验各等压面平均的温度预报场的均方根误差,以及NEWOE试验平均的温度预报场的均方根误差与CTRL试验平均的温度预报场均方根误差的差值(NEWOE-CTRL)。相比控制试验(CTRL),采用新的折射率观测误差后,北半球温度场平均预报均方根误差在模式层顶(20 hPa以上)有明显减小,其他高度变化不大。南半球,除了1000—700和20—10 hPa平均的温度预报场均方根误差略有增大外,其他所有层次的均方根误差都有明显减小;热带地区,300—50 hPa温度预报误差都减小了,特别是对流层顶100 hPa附近,第3天以后的预报误差显著减小。总体上采用新估计的随纬度和季节变化的折射率观测误差,对温度场的预报技巧有正效果。同时,位势高度场和风场的预报结果与温度场相同。总体上平均的温度预报场的均方根误差减少了2%—3%。所以,采用新统计的折射率观测误差,减小了温度预报场的均方根误差。
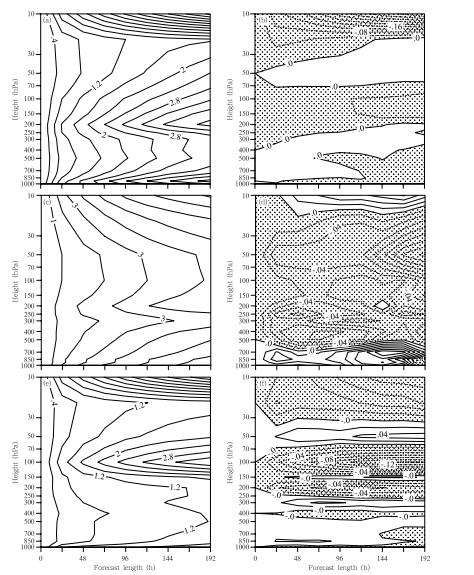 |
| 图 7(a、c、e)CTRL试验平均的各层温度预报场的均方根误差及(b、d、f)NEWOE与CTRL试验平均的温度预报场的均方根误差之差值(NEWOE-CTRL,负值用点阴影填充) (a、b.北半球(20°—90°N),c、d.南半球(90°—20°S),e、f.热带(20°S—20°N)) Fig. 7(a),(c) and (e)Forecast hour-pressure cross section of the averaged forecast temperature anomaly root-mean-squared error(RMSE)of experiment CTRL,and (b),(d),and (f)RMSE differences between experiment NEWOE and CTRL over (a),(b)the northern hemisphere(20°-90°N),(c),(d)the southern hemisphere(90°-20°S),and (e),(f)the tropics(20°S-20°N)(Negative values are shaded by dots) |
图 8a、b为平均的北半球、南半球700 hPa位势高度预报场的距平相关系数。从图 8a中可以看出,相比CTRL试验,采用新统计的折射率观测误差的NEWOE平均的高度预报场的距平相关系数都增大了。因此,相比原折射率观测误差,新统计的折射率观测误差的使用提高了北半球700 hPa位势高度预报场预报技巧。图 8b表明,相比CTRL试验,NEWOE试验平均的南半球700 hPa高度预报场距平相关系数增大(除第2天预报)。所以相比原折射率观测误差,新统计的折射率观测误差的使用提高了南半球700 hPa位势高度预报场预报技巧。从图 8b可以看出,相比CTRL试验,NEWOE试验平均的热带700 hPa高度预报场距平相关系数增大(除第6天预报)。相比原折射率观测误差,新统计的折射率观测误差的使用提高了热带700 hPa位势高度场预报技巧。风场的结果与高度场的结果相同。图 8c、d为平均的北半球和南半球500 hPa位势高度预报场的距平相关系数。比较图 8c、d与图 8a、b,NEWOE与CTRL试验平均的500 hPa高度预报场的距平相关系数与700 hPa结果相同,即相比原折射率观测误差,新统计的折射率观测误差的使用提高了500 hPa位势高度场的预报技巧。其他层次上的结论也与700和500 hPa结论一致。所以,总体上讲,新折射率观测误差提高了GRAPES全球变分同化系统的预报技巧。但并不是十分显著,其原因可能是在GRAPES全球变分同化系统中已经同化了大量的观测资料,特别是大量的卫星资料,使得这一部分的改进对预报的影响不是十分显著。
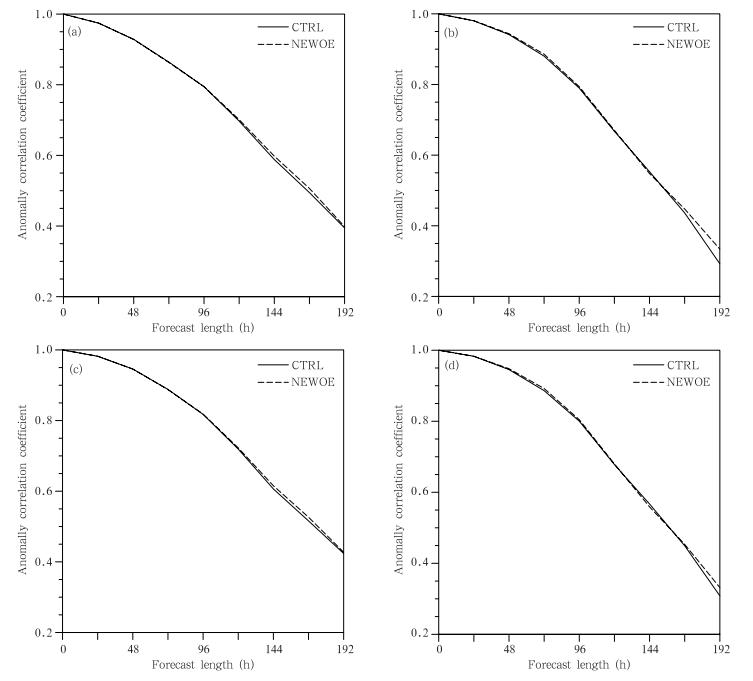 |
| 图 8 CTRL与NEWOE试验700 hPa(a、b)及500 hPa(c、d)1个月平均的位势高度预报场距平相关系数 (a、c.北半球(20°—90°N),b、d.南半球(90°—0°S)) Fig. 8 Averaged anomaly correlation coefficients of the forecast geopotential height for experiment CTRL and NEWOE over (a),(c)the north hemisphere(20°-90°N) and (b),(d)the south hemisphere(90°-0°S)on(a),(b)700 hPa and (c),(d)500 hPa |
详细分析了新息增量法(H-L法)直接估计GPS无线电掩星资料这类观测位置不固定的观测误差的适用条件,设计了实施方案,并用1年的COSMIC折射率资料,针对局地观测算子估计了折射率资料在南、北半球高、中、低6个纬度带的四季观测误差,并将估计的夏季的观测误差应用于GRAPES全球三维变分同化系统,做了2009年7月5—31日的同化循环预报对比试验。主要结论如下:
(1) 对局地观测算子,COSMIC折射率观测相对误差随高度而变化:折射率的相对观测误差在对流层低层850—700 hPa附近达到最大,高纬度500—50 hPa与中纬度300—50 hPa观测误差达到最小且随高度变化较小,而在50 hPa以上随高度升高而增大。
(2) 不同纬度带折射率相对观测误差显著不同,特别是在对流层低层。不同纬度带的COSMIC折射率资料的观测误差有显著差异,在对流层低层,低纬度地区的折射率观测误差的最大值是高纬度地区最大值的3倍。
(3) 中高纬度的折射率观测误差具有显著的季节变化。折射率观测误差在北半球中高纬度地区以及南半球中纬度地区和高纬度地区平流层具有显著的季节变化。北半球中高纬度,夏季的观测误差约是冬季的2倍。
(4) 采用新统计的随纬度和季节变化的折射率观测误差后GRAPES全球变分预报系统的预报技巧略有提高。
本研究提出了直接采用H-L法估计GPS掩星这类观测点不固定但全球分布的观测资料观测误差的实施方案,针对局地观测算子对COSMIC折射率的观测误差进行了估计和分析,提高了GRAPES全球变分同化系统对折射率资料的同化效果。但采用精度更高的线性非局地观测算子是未来提高GPS掩星折射率资料同化效果的必然途径。原因是随着观测技术的提高,测量误差不断减小,当代表性误差与测量误差相近或者更大的时候,代表性误差就显得尤为重要,有理由相信,未来掩星观测资料的代表性误差将是对流层低层的主要误差。而线性非局地观测算子的代表性误差相比局地观测算子,减小了由大气水平梯度造成的代表性误差和系统性偏差。因此,采用本研究提出的估计方案,更精确的估计针对非局地观测算子的折射率观测误差是非常值得进一步研究的内容。
致谢:感谢俄克拉荷马大学许秦教授在H-L法方面给予的指导。
| 毕研盟, 廖蜜, 张鹏等. 2013. 应用一维变分法反演GPS掩星大气温湿廓线. 物理学报, 62(15): 159301, doi: 10. 7498/as. 62. 159301. Bi Y M, Liao M, Zhang P, et al. 2013. 1DVAR retrieval method for GPS radio occultation measurements of atmospheric temperature and humidity profiles. Acta Phys Sin, 62(15): 159301, doi: 10. 7498/as. 62.159301 (in Chinese) |
| 成巍, 王斌, 徐幼平. 2012. 基于局地和非局地观测算子的GPS掩星资料后向映射四维变分同化研究. 中国科学: 数学, 42(5): 377-387. Cheng W, Wang B, Xu Y P. 2012. Assimilation of GPS radio occultation data with the local and non-local operators using Backward-4DVar approach. Sci Sinica Math, 42(5): 377-387, doi: 10.1360/012012-17 (in Chinese) |
| 龚建东, 魏丽, 陶士伟等. 2006. 全球资料同化中误差协方差三维结构的准确估计与应用I: 观测空间协方差的准确估计. 气象学报, 64(6): 669-684. Gong J D, Wei L, Tao S W. 2006. Accurate estimation and application of 3-D error covariance structures in global data assimilation Part I: Accurate estimation of error covariance in observation space. Acta Meteor Sinica, 64(6): 669-684 (in Chinese) |
| 郭鹏. 2005. 无线电掩星技术与CHAMP掩星资料反演[D]. 上海: 中国科学院上海天文台, 1-133. Guo P. 2005. GPS Radio Occultation Technique and CHAMP Occultation Data Retrieval[D]. Shanghai: Shanghai Astronomical Observatory, Chinese Academy of Sciences,1-133 (in Chinese) |
| 唐细坝, 薛纪善. 2009. COSMIC资料在GRAPES全球三维变分同化系统的初步研究. 热带气象学报, 25(5): 521-531. Tang X B, Xue J S. 2009. Preliminary study of the use of COSMIC data in the global 3-Dimensional variance assimilation system of GRAPES. J Trop Meteor, 25(5):521-531 (in Chinese) |
| 薛纪善, 陈德辉等. 2008. 数值预报系统GRAPES的科学设计与应用. 北京: 科学出版社, 1-61. Xue J S, Chen D H, et al. 2008. Scientific Design and Application of Numerical Prediction System GRAPES. Beijing: Science Press, 1-61 (in Chinse) |
| 赵德显, 郁红弟, 沈桐立. 2011. GPS折射率资料在梅雨锋暴雨数值模拟中的应用. 气象, 39(12): 1511-1518. Zhao D X, Yu H D, Shen T L. 2011. The application of GPS refractive index data to numerical simulation of Meiyu front. Meteor Mon, 39(12): 1511-1518 (in Chinese) |
| 庄世宇, 薛纪善, 朱国富等. 2005. GRAPES全球三维变分同化系统:基本设计方案与理想试验. 大气科学, 29(6): 872-884. Zhuang S Y, Xue J S, Zhu G F, et al. 2005. GRAPES Global 3D-Var System:Basic scheme design and single observation test. Chinese J Atmos Sci, 29(6): 872-884 (in Chinese) |
| Ahmad B, Tyler G L. 1998. The two-dimensional resolution kernel associated with retrieval of ionospheric and atmospheric refractivity profiles by Abelian inversion of radio occultation phase data. Radio Sci, 33(1): 129-142 |
| Anthes R A, Bernhardt P A, Chen Y, et al. 2008. The COSMIC/FORMOSAT-3 mission: Early results. Bull Amer Meteor Soc, 89(3): 313-333, doi: 10.1175/BAMS-89-3-313 |
| Chen S Y, Huang C Y, Kuo Y H, et al. 2009. Assimilation of GPS refractivity from FORMOSAT-3/COSMIC using a nonlocal operator with WRF 3DVAR and its impact on the prediction of a typhoon event. Terr Atmos Ocean Sci, 20(1): 133-154, doi: 10.3319/TAO.2007.11.29.01(F3C) |
| Chen S Y, Huang C Y, Kuo Y H, et al. 2011. Observational error estimation of FORMOSAT-3/COSMIC GPS radio occultation Data. Mon Wea Rev, 139(3): 853-865, doi: 10.1175/2010MWR3260.1 |
| Cucurull L, Derber J C. 2008. Operational Implementation of COSMIC observations into NCEP's global data assimilation system. Wea Forecasting, 23(4): 702-711 |
| Foelsche U, Kirchengast G, 2004. Sensitivity of GNSS occultation profiles to horizontal variability in the troposphere: A simulation study//Kirchengast G, Foelsche U, Steiner A K. Occultations for Proving Atmosphere and Climate. Berlin-Heidelberg: Springer, 127-136 |
| Hollingsworth A, Lönnberg P. 1986. The statistical structure of short-range forecast errors as determined from radiosonde data. Part Ⅰ: The wind field. Tellus, 38A(2): 111-136 |
| Huang C Y, Kuo Y H, Chen S Y, et al. 2010. Impact of GPS radio occultation data assimilation on regional weather predictions. GPS Solut, 14(1): 35-49, doi: 10.1007/s10291-009-0144-1 |
| Kuo Y H, Sokolovskiy S, Anthes R A, et al. 2000. Assimilation of GPS radio occultation data for numerical weather prediction. TAO, 11(1): 157-186 |
| Kuo Y H, Wee T K, Sokolovskiy S, et al. 2004. Inversion and error estimation of GPS radio occultation data. J Meteor Soc Japan, 82(1B): 507-531 |
| Kursinski E R, Hajj G A, Bertiger W I, et al. 1996. Initial results of radio occultation observations of Earth's atmosphere using the Global Positioning System. Science, 271(5252): 1107-1110, doi: 10.1126/science.271.5252.1107 |
| Liu H, Zou X, Shao H, et al. 2001. Impact of 837 GPS/MET bending angle profiles on assimilation and forecasts for the period June 20-30, 1995. J Geophys Res, 106(D23): 31771-31786 |
| Liu H, Zou X. 2003. Improvements to a GPS radio occultation ray-tracing model and their impacts on assimilation of bending angle. J Geophys Res, 108(D17): 4548, doi: 10.1029/2002JD003160 |
| Liu Y, Xue J S. 2014. Operational implementation of the assimilation of global navigation satellite radio occultation observations into GRAPES data assimilation system. J Meteor Res, 28, doi: 10. 1007/s13351-014-4028-0 |
| Lorenc A C. 1986. Analysis methods for numerical weather prediction. Quart J Roy Meteor Soc, 112(474): 1177-1194 |
| Ma Z Z, Kuo Y H, Wang B, et al. 2009. Comparison of local and nonlocal observation operators for the assimilation of GPS RO data with the NCEP GSI system: An OSSE study. Mon Wea Rev, 137(10): 3575-3587, doi: 10.1175/2009MWR2809.1 |
| Ma Z Z, Kuo Y H, Ralph F M, et al. 2011. Assimilation of GPS radio occultation data for an intense atmospheric river with the NCEP regional GSI system. Mon Wea Rev, 139(7): 2170-2183, doi: 10.1175/2011MWR3342.1 |
| Palmer P I, Barnett J J, Eyre J R, et al. 2000. A nonlinear optimal, estimation inverse method for radio occultation measurements of temperature, humidity, and surface pressure. J Geophys Res, 105(D13): 17513-17526 |
| Poli P. 2003. A fast forward model for simulating GPS radio occultation bending angles and refractivity in a two dimensional plane: Implementation and simulations//SAF Training Workshop: 2nd GRAS SAF User Workshop, EUMETSAT, Darmstadt, Germany, 38-48 |
| Poli P. 2004. Effects of horizontal gradients on GPS radio occultation observation operators. Ⅱ: A fast atmospheric refractivity gradient operator (FARGO). Quart J Roy Meteor Soc, 130(603): 2807-2825 |
| Poli P, Healy S B, Dee D P. 2010. Assimilation of Global Positioning System radio occultation data in the ECMWF ERA-Interim reanalysis. Quart J Roy Meteor Soc, 136(653): 1972-1990 |
| Rennie M P. 2010. The impact of GPS radio occultation assimilation at the Met Office. Quart J Roy Meteor Soc, 136(646): 116-131 |
| Rocken C, Kuo Y H, Schreiner W S, et al. 2000. COSMIC system description. TAO, 11(1): 21-52 |
| Scherllin-Pirscher B, Steiner A K, Kirchengast G, et al. 2011. Empirical analysis and modeling of errors of atmospheric profiles from GPS radio occultation. Atmos Meas Tech, 4: 1875-1890, doi: 10. 5194/amt-4-1875-2011 |
| Shao H, Zou X. 2002. The impact of observational weighting on the assimilation of GPS/MET bending angle. J Geophys Res, 107(D23): ACL 19-1-ACL 19-28, doi: 10. 1029/2001JD001552 |
| Shao H, Zou X L, Hajj G A. 2009. Test of a non-local excess phase delay operator for GPS radio occultation data assimilation. J Applied Remote Sensing, 3(1): 033508, doi: 10. 1117/1. 3094060 |
| Smith E K, Weintraub S. 1953. The constants in the equation for atmospheric refractive index at radio frequencies. Proceeding of the IRE, 41(8): 1035-1037, doi: 10.1109/JRPROC.1953.274297 |
| Sokolovskiy S, Kuo Y H, Wang W. 2005a. Assessing the accuracy of a linearized observation operator for assimilation of radio occultation data: Case simulations with a high-resolution weather model. Mon Wea Rev, 133(8): 2200-2212, doi: 10.1175/MWR2948.1 |
| Sokolovskiy S, Kuo Y H, Wang W. 2005b. Evaluation of a linear phase observation operator with CHAMP radio occultation data and high-resolution regional analysis. Mon Wea Rev, 133(10): 3053-3059, doi: 10.1175/MWR3006.1 |
| Steiner A K, Löscher A, Kirchengast G. 2006. Error characteristics of refractivity profiles retrieved from CHAMP radio occultation data//Atmosphere and Climate: Studies by Occultation Methods. Berlin-Heidelberg: Springer, 27-36 |
| Syndergaard S, Kursinski E R, Herman B M, et al. 2005. A refractivity index mapping operator for assimilation of occultation data. Mon Wea Rev, 133(9): 2650-2668 |
| Syndergaard S, Kuo Y H, Lohmann M S. 2006. Observation operators for the assimilation of occultation data into atmospheric models: A review//Atmosphere and Climate. Berlin Heidelberg: Springer, 205-224, doi: 10.1007/3-540-34121-8_18 |
| Ware R, Rocken C, Solheim F, et al. 1996. GPS sounding of the atmosphere from low earth orbit: Preliminary results. Bull Amer Meteor Soc, 77(1): 19-40 |
| Wickert J, Arras C, Ao C O, et al. 2008. CHAMP, GRACE, SAC-C, TerraSAR-X/TanDEM-X: Science results, status and future prospects. GRAS SAF Workshop on Applications of GPSRO Measurements, 43-52 |
| Wu W S, Rurser R J, Parrish D F. 2002. Three-dimensional variational analysis with spatially inhomogeneous covariances. Mon Wea Rev, 130(12): 2905-2916 |
| Xu Q, Wei L, Van Tuyl A, et al. 2001. Estimation of three-dimensional error covariances. Part Ⅰ: Analysis of height innovation vectors. Mon Wea Rev, 129(8): 2126-2135 |
| Zou X, Kuo Y H, Guo Y R. 1995. Assimilation of atmospheric radio refractivity using a nonhydrostatic adjoint model. Mon Wea Rev, 123(7): 2229-2250 |
| Zou X, Vandenberghe F, Wang B, et al. 1999. A ray-tracing operator and its adjoint for the use of GPS/MET refraction angle measurements. J Geophys Res, 104(D18): 22301-22318 |
| Zou X, Wang B, Liu H, et al. 2000. Use of GPS/MET refraction angles in three-dimensional variational analysis. Quart J Roy Meteor Soc, 126(570): 3013-3040 |
| Zou X, Liu H, Anthes R A. 2002. A statistical estimate of errors in the calculation of radio-occultation bending angles caused by a 2D approximation of ray tracing and the assumption of spherical symmetry of the atmosphere. J Atmos Ocean Technol, 19(1):51-64 |
| Zou X, Liu H, Anthes R A, et al. 2004. Impact of CHAMP radio occultation observations on global analysis and forecasts in the absence of AMSU radiance data. J Meteor Soc Japan, 82(1B): 533-549 |
| Zou X, Zeng Z. 2006. A quality control procedure for GPS radio occultation data. J Geophys Res, 111(D2): D02112, doi: 10. 1029/2005JD005846 |
 2015, Vol. 73
2015, Vol. 73