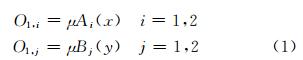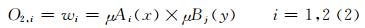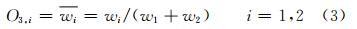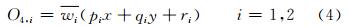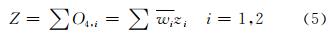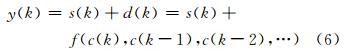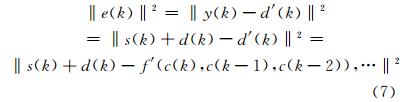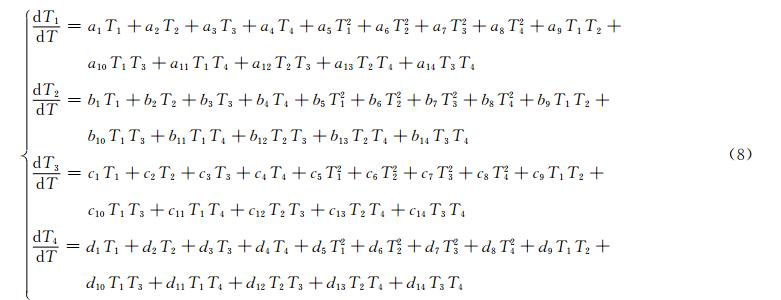中国气象学会主办。
文章信息
- 洪梅, 陈希, 张韧, 曾文华, 毛科峰, 郝志男. 2015.
- HONG Mei, CHEN Xi, ZHANG Ren, ZEN Wenhua, MAO Kefeng, HAO Zhinan. 2015.
- 基于模糊系统的西太平洋副热带高压异常年份的影响因子检测分析和动力预报模型反演
- Analysis of the impact factors of abnormal Western Pacific subtropical high years based on the fuzzy systems and the dynamical forecast model inversion
- 气象学报, 73(2): 355-367
- Acta Meteorologica Sinica, 73(2): 355-367.
- http://dx.doi.org/10.11676/qxxb2015.017
-
文章历史
- 收稿日期:2014-07-22
- 改回日期:2014-10-16
2. 中国科学院大气物理研究所大气科学和地球流体力学数值模拟国家重点实验室, 北京, 100029
2. State Key Laboratory of Atmospheric Sciences and Geophysical Fluid Dynamics, Institute of Atmospheric Physics, Chinese Academy of Sciences, Beijing 100029, China
西太平洋副热带高压作为东亚夏季风系统中的一个重要成员,与其他季风环流成员共存于一个非线性系统中,彼此之间相互影响、相互作用,其异常活动往往会导致中国淮河流域洪涝和干旱灾害现象。如副热带高压异常南落正是导致长江流域1998年8月特大洪涝灾害的原因,2006年盛夏重庆、川东地区出现的持续高温伏旱天气以及2007年7月淮河流域普降暴雨也是由于季节内副热带高压的持续偏北偏西的结果,2008年1月10日以来发生在中国南方的大范围持续性低温雨雪冰冻极端天气灾害也与副热带高压异常偏强偏北,并多次向西伸展的反常行为有关。副热带高压是高度非线性动力系统,而季风系统中其他众多因子会通过非线性过程共同制约其演变发展和异常(黄露等,2012)。时至今日,副热带高压天气和气候系统比较复杂,它的影响因子、因子间的非线性关系以及不同因子对副热带高压系统的影响程度仍然难以准确确定。傅立叶变换和低(带)通滤波等各种统计平滑法(祝从文等,2004;李勋等,2010;孙长等,2009)可以过滤掉系统快波,从而得出其基础波动特征,并且凸出其天气和气候趋势的主要特征。然而,这些方法也存在着缺点,比如仅处理信号的频率结构本身,并不能清楚地辨认噪声的滤波究竟如何产生,从哪里产生,所以该滤波处理方法一般不能有效地诊断出天气气候异常的观测信号中的主要因素。如何将观测资料中隐含的映射关系和定性的经验规则进行提练归纳,升华为定量的控制系统和诊断预测模式,模糊系统方法为人们提供了一条简捷有效的途径(顾秀萍,2010;Soyguder et al,2009)。
模糊理论是Lotfi Zadeh 1965年创立的,他发表的“模糊集合”论文,将模糊概念首次提出,对每一个对象的集合,详细描述了凸分离论(Zadeh,1965)如何将一套完整的模糊集系统扩展为模式识别。模糊系统的核心是通过专家经验或者实践感知可以将自然描述的语言转化成为定量计算机算法及控制系统,而这种算法和控制系统可以用模糊规则和模糊集合表示。曹鸿兴等(1980,1988)最早将模糊集理论引入到气象学中,并且对季节天气预报进行了实例分析。而魏凤英等(1993)建立了模糊均生函数模型,并将其用于淮河、长江流域夏季长期降水预报,取得了较好的效果。
自适应网络模糊推理系统(Adaptive-Netwook-Based Fuzzy Inference System,ANFIS)是模糊系统的一种。由于ANFIS系统具有容错性、自适应学习和非线性等特性,因此适宜于研究和模拟副热带高压等动力学不易准确描述的问题。本研究将用模糊系统ANFIS模型讨论副热带高压异常的2010年夏季风主要成员对副热带高压异常的贡献和影响,找出2010年夏季风系统主要成员中对副热带高压异常影响最显著的因子。
通过对副热带高压与季风系统的诊断分析,可以发现每年的副热带高压季节性转换有不同的特点,副热带高压的异常进退和形态突变又是一个极其复杂的过程,因此,问题的困难之处在于如何从实际观测资料反演出副热带高压动力学模型并且建立一个“精确”的副热带高压及其影响因子的动力学模型,这些可以扩展副热带高压形态变异的动力机制研究和探索动力延伸预报方法。目前,传统的动力模型参数反演方法和时延相空间重构方法是较为常用的动力模型重建方法。遗传算法是近年来被广泛使用于优化算法,其优点是全局搜索和良好的参数优化能力(黄建平等,1991;王凌,2001)。
为此,将遗传算法引入动力系统反演和模型参数优化的研究之中,通过与传统建模方法的有机结合,对模型反演及模型参数的搜索优选过程进行改进。首先基于前面所揭示的关于副热带高压与季风系统的诊断事实,选取副热带高压以及与之相关密切的季风系统成员的特征指数,运用遗传算法和动力模型反演相结合的方法对副热带高压及其影响因子的非线性动力模型反演和模型参数优化,其后进一步进行动力延伸预报试验。 2 资料与方法 2.1 资 料
利用美国国家大气研究中心(NCAR)和美国国家环境预报中心(NCEP)提供的2010年5—10月逐日的再分析资料,包括:(1)850 、200 hPa水平风场和位势高度场,500 hPa位势高度场,海平面气压场资料,分辨率均为2.5°×2.5°;(2)地表感热和对流降水率资料的高斯网格资料;(3)NOAA 卫星观测的射出长波辐射(OLR)资料。 2.2 ANFIS模糊推理系统
ANFIS模糊推理系统最初由Sugeno等(1983)提出,通过训练与自适应,依靠经验隶属函数的调整来提高逼近效率和减小误差的工作。
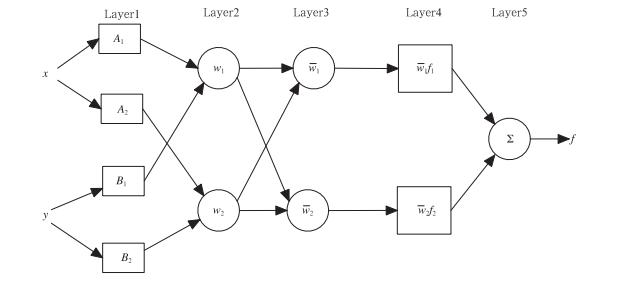
Sugeno等(1988)其实提出的是Sugeno型的ANFIS模糊系统。以一阶Sugeno型为例,x和y为双输入,z为单输出,其具有下面两个如果-则规则:
规则1: 如果x是A1和y是B1,则h1=p1x+q1y+r1
规则2:如果x是A2和y是B2,则h2=p2x+q2y+r2 式中,Ai、Bi为输入信号对应的映射值;x,y为模糊推理系统的训练输入;pi、qi、ri为模糊推理的隶属度参数或常数,zi为规则1与规则2的输出信号,i=1,2。
Sugeno型的模糊系统的等效ANFIS结构如图 1所示,其结构和计算原理可以分为如下5层:
|
| 图 1 一阶Sugeno型的ANFIS模糊系统结构 Fig. 1 Schematic chart for the ANFIS architecture for a two rule Sugeno system |
(1)第1层:输入层。将输入变量映射到模糊集合中
式中,x、y是节点的输入数据,μAi(x)和μBj(y)分别是x、y输入的隶属度函数,其参数都是非线性参 数。O1,i、O1,j为第一层对应节点的输出数据。本层每个节点都是具有节点函数的自适应节点。(2) 第2层:规则层。用乘法来计算每条规则适用度
式中,O2,i为第3层对应节点的输出数据。本层的每个节点都是被标记为Ⅱ固定的节点。(3) 第3层:正规化层。将适用度归一化
式中,O3,i为第3层对应节点的输出数据。本层的每个节点都是被标记为N固定的节点。(4) 第4层:结论推论层。可以计算每条规则的输出:
式中,O4,i为第4层对应节点的输出数据;pi、qi、ri是隶属度参数或常数,一般被称为结论参数。本层节点都是自适应的节点。(5) 第5层:输出层。模糊系统的总输出可以通过下式计算出
用某种特定算法来训练ANFIS,得到参数值,达到模糊建模的目的。
对于多阶的Sugeno型ANFIS模糊系统的建立和计算原理也与上面的类似,
具体可见 Sugeno等(1988)。ANFIS为放射性的网络,并且其前提和结论的参数都已经解耦,这样使其具有一定的优势,学习效率要高于神经网络。 2.3 模糊自适应信号去噪原理
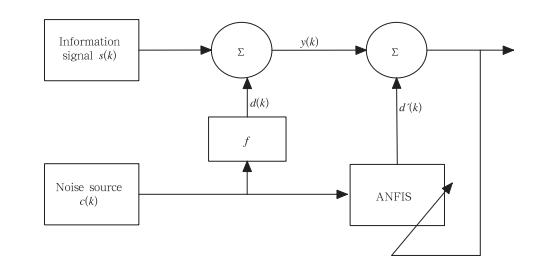
图 2显示了模糊自适应在理想状况下的噪声消除原理。图中的畸变噪声是由噪声源通过未知非线性动态特性f(·)产生的,并且被加入到形成可测的输出信号。任务就是将信息信号s(k)从可测的输出信号y(k)中恢复出来,而y(k)则由c(k)的畸变信号和信息信号s(k)以及相对应的延迟信号所组成。
|
| 图 2 ANFIS噪声消除原理示意图 Fig. 2 Schematic chart for the noise elimination by ANFIS |
被测的输出信号用符号可以表示为
由于函数f(·)未知,并不能直接从y(k)中减去d(k)而达到恢复原始信息的目的。所以需要取得独立于信息信号的清晰噪声源信号c(k)而达到对畸变的噪声信号d(k)估计的目的。因此只要噪声源信号c(k)与信息信号s(k)不相关,信号y(k)作为ANFIS训练的期望输出就可以被检测出。
通过以下的ANFIS学习规则误差可以被极小化
式中,ANFIS实现的函数是f′。在数据的拟合过程中被当作不相关噪声成分的是信息信号s(k),所以ANFIS对s(k)并没有有效方法,除非s(k)的表态趋势可以取得。相反,ANFIS则擅长于极小化和d(k)相关的误差分量,即‖d(k)-f′(c(k),c(k-1),c(k-2)),…‖2,而这正是所期望的误差测量。关于ANFIS的进一步去噪计算步骤可以参见相关文献(刘宇等,2012;王文涛等,2009),这里不再详述。并且张韧等(2002)也专门研究过基于ANFIS方法的混沌动力系统的去噪试验,其研究成果表明基于ANFIS建立的模糊系统模式比较简单,但在复杂混沌动力系统中的识别结果基本正确,恢复出来的信号与信息信号相关系数约为0.955,由此证明了用类似的模糊推理方法来研究实际天气气候问题是可行的。 3 异常活动年份的副热带高压强度的影响因子检测分析 3.1 2010年夏季副热带高压活动的基本事实
不同年份的副热带高压季节内变化与平均状况相比会有很大出入,特别是一些年份出现的副热带高压“异常”活动往往造成东亚地区副热带环流异常和中国的极端天气事件。基于此,先对典型副热带高压活动个例进行筛选和分析。2010年是副热带高压活动异常较为凸出的年份,该年从5月开始到9月,副热带高压面积指数均在均值以上,且在7—8月达到近10年来的最大峰值。正是由于副热带高压强度的这种异常,造成了2010年中国气候严重异常,全年气温偏高,降水偏多,极端高温和强降水事件发生之频繁、强度之强、范围之广历史罕见。特别是6—8月出现的有气象记录以来最为强大的西太平洋副热带高压,直接造成了华南、江南、江淮、东北和西北东部出现罕见的暴雨洪涝灾害;特别是5—7月华南、江南遭受14轮暴雨袭击,7月中旬至9月上旬北方和西部地区遭受10轮暴雨袭击。因此,选取2010年夏季副热带高压异常变化过程作为典型案例来分析其副热带高压增强与季风系统成员的关联性。 3.2 时滞相关分析
为了进一步揭示2010年的亚洲夏季风系统成员和副热带高压的相关特征,本研究对象采用中国中央气象台(1976)定义的,表征副热带高压范围和强度形态的副热带高压面积指数(SI):即在2.5°×2.5°网格的500 hPa位势高度图上,10°N以北,110°E—180°范围内,平均位势高度大于588 dagpm网格点数。其值越大,代表副热带高压的范围越广或者强度越大。
夏季风系统成员较多,根据有关文献(王会军等,2003;余丹丹等,2007),与副热带高压关系密切的因子主要有21个。考虑到复杂性,首先将这21个因子与副热带高压面积指数进行时滞相关分析,样本取样时间为2010年5月1日—10月31日,总共为184 d,即每个样本的容量是184(相关分析表略)。筛选出其中相关性最强的3个因子进一步研究。其分别是
马斯克林冷高压强度指数(MH):(25°—35°S,40°—60°E)区域内的海平面气压格点平均值;
索马里低空急流(SJ):(5°S—5°N,40°—50°E)区域内850 hPa经向风格点平均值;
印度季风潜热通量(FLH):(10°—20°N,70°—85°E)区域内的潜热通量。
其与副热带高压面积指数(SI)的时滞相关结果如表 1。从表中可以看出,相关性最强的3个因子与副热带高压面积指数的相关系数均能超过0.85。南半球马斯克林高压(MH)在早期就对副热带高压增强产生影响,两者关系十分密切,而且是正相关,这与已有研究结果基本一致(薛峰等,2003)。索马里低空急流指标(SJ)、印度季风潜热通量(FLH)与副热带高压强度关系密切也是与已有研究结果基本相符的(王会军等,2003;余丹丹等,2007)。
| 序号 | 夏季风系统主要成员 | 最大相关系数(时间) |
| 1 | 马斯克林高压(MH) | 0.85(8 d) |
| 2 | 索马里低空急流指标(SJ) | 0.90(6 d) |
| 3 | 印度季风潜热通量(FLH) | 0.87(3 d) |
| *注: 时延天数中正数表示季风成员变化超前副热带高压面积指数变化;负数表示滞后 | ||
根据2.2节的原理,ANFIS可以用一个由2N个规则的Sugeno型模糊系统来适应训练的数据,其中N一般指输入数据的维数(通常N<7)。训练后的模糊系统以一个模糊推理系统(FIS)形式的矩阵返回。本研究采用由3个输入和1个输出网络来构建ANFIS模糊推理系统。
设P和T分别是ANFIS模糊系统模型的输入因子与目标输出,即
P=[MH(t-10),MH(t-9),MH(t-8),T=SI(t)]
即每个时次的数据集合为: [MH(t-10),MH(t-9),MH(t-8),SI(t)]
式中,MH(t-10)代表的是超前10天的马斯可林高压指数序列;MH(t-9)代表的是超前9天的马斯可林高压指数序列;MH(t-8)代表的是超前8天的马斯可林高压指数序列;SI(t)代表的是副热带高压面积指数序列。以SI(t)为例,其有效数据样本时段为2010年5月1日—10月31日共184个,分为训练与校验两个部分,其中150个数据用于训练,其余的34个样本用于校验。数据样本的长度都是一样,但是不同输入因子的起始和终止时间是不同的。
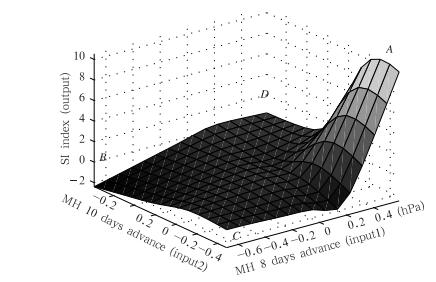
根据2.2节的原理,此处所用的ANFIS模型系统采用高斯隶属函数,通过减法聚类可以得到初始的模糊推理系统,适当隶属函数可以通过最小二乘法和后传梯度下降法结合的学习算法来调配出,所需要的模糊系统的输入、输出关系便可以被满足。模型的训练、建立与推理仿真都采用Mathlab语言编程,并在模糊工具箱仿真环境中实现。经过200次的训练迭代后,可以达到指定的误差量级(10-3),这样就建立起马斯克林高压同滞后的副热带高压的模糊推理系统与模糊映射关系。选取的几个因子和副热带高压指数的量级差别较大,为了在同一指标中各变量的量级相当,可以使画出的映射图像显示得更加匹配,物理意义更加直观明了,所以在计算中的马斯克林冷高压强度指数(MH)取距平值且统一除以1000,而副热带高压面积指数(SI)距平值已统一除以200。图 3和4分别是超前不同天数的MH与SI的输入、输出映射关系,图中输入1、输入2分别是超前8、10(9)天的MH输入,输出为滞后的SI输出。
|
| 图 3 超前8天(输入1)和超前10天(输入2)的马斯克林高压(MH)与副热带高压面积指数(SI)(输出)的三维映射曲面 Fig. 3 Fuzzy reasoning map of MH 8 days in advance(input1),MH 10 days in advance(input2) and SI(output) |
由图 3可见,若10天之前马斯克林冷高压指数为强的负距平(输入2<0),而在8天之前时转为强的正距平(输入1>0),则对应出现副热带高压面积指数的异常正距平(图 3中A点)。这就代表当马斯克林高压的突然增强爆发(负距平转变为正距平),滞后8天后的副热带高压面积指数也会发生突变(忽然增强),两者成明显正相关。从图 3还可以看出,若超前10天的马斯克林冷高压指数忽然由强的正距平(输入2>0)变成了超前8天的强的负距平(输入1<0),则对应的副热带高压面积指数也会产生负距平(图 3中B点),但减少程度很小。这代表马斯克林高压的忽然减弱,对于滞后的副热带高压减弱也会产生一定影响,但影响程度较小。而10天之前到8天之前的马斯克林高压均维持正常的偏强或偏弱(输入1及 输入2同时为正或者负),没有突变,则对应的副热带高压面积指数则也没有什么突变(图 3中C、D点)。
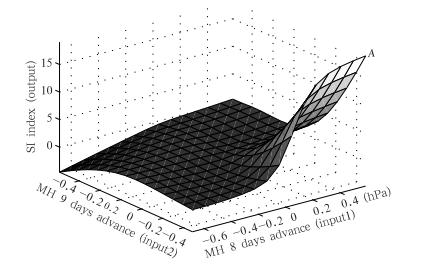
图 4与图 3比较类似,但比较可以发现如果马斯克林高压从9天之前的负距平(输入2<0)突变成8天之前的正距平(输入1>0)(也就是马斯克林高压爆发的更加剧烈,图 4中的A),可见副热带高压面积指数发生突变(增强)也更为剧烈。
|
| 图 4 超前8天(输入1)和超前9天(输入2)的马斯克林高压(MH)与副热带高压面积指数(SI)(输出)的三维映射曲面 Fig. 4 Fuzzy reasoning map of MH 8 days in advance(input1),MH 9 days in advance(input2) and SI(output) |
上述推理映射特征大体反映了副热带高压与马斯克林高压对应关系的基本事实和主要特征。从上面两幅图的分析可以看出,超前8天的马斯克林高压突然增强爆发,会引起副热带高压面积指数的增强爆发,而稳定的马斯克林高压并不能引起副热带高压的异常变化,这与前面3.2节的时滞相关分析结果也是吻合的。3.2节的时滞相关分析结果是从线性角度分析的,具有很强的局限性,而ANFIS是从非线性角度进行分析,特别是对于不确定性问题和复杂的天气系统,ANFIS的分析结果更合理和令人信服。并且此模糊推理系统的建立是完全基于马斯克林冷高压强度指数与副热带高压面积指数对应的时间序列数据集合,因而也是比较客观可信的。
为了进一步说明模糊推理系统结果的真实可信性,将模糊推理的映射特征与2010年的实际天气情况结合分析。从前面的分析可知,对马斯克林高压的迅速爆发,副热带高压会在8—10 d出现增强响应,响应幅度随时间由大渐小,如2010年8月7日(15°—25°S,40°—60°E)范围内的海平面气压格点平均值为1007.9 hPa)到8月11日(海平面气压格点平均值为1028.1 hPa)马斯克林高压出现一次明显增强爆发,随后副热带高压在8 d之后的2010年8月15日(副热带高压面积指数是301)—8月18日(副热带高压面积指数是422)出现一次显著增强。
若马斯克林高压稳定少变,则马斯克林高压的偏强、偏弱基本状况对副热带高压没有明显影响,即副热带高压强度的显著变化主要发生在马斯克林高压突变的情况下,稳定的马斯克林高压状况一般不易导致副热带高压异常。
其他的2个因子(索马里低空急流指数和印度季风潜热通量)与副热带高压的模糊映射特征与马斯克林高压类似,这里不再赘述。 3.4 模型仿真和推理结果讨论
根据2.3节介绍的基于ANFIS模糊自适应信号去噪原理,采用2-输入自适应网络模糊推论系统ANFIS(即对于每个输入,指定2个隶属函数,
激活4条模糊规则)对超前8 d和9 d的马斯克林高压和副热带高压面积指数的数据集合进行聚类分析和训练识别。考虑到马斯克林高压和副热带高压面积指数的量级相差较大,为了方便训练识别和比较画图,将训练数据先用公式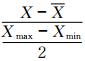 归一化到-1至1,一共有184对如下的训练数据:[c(k),c(k-1);y(k)];其中c(k)用的是超前9 d的马斯克林高压指数数据,c(k-1)是超前8 d的马斯克林高压指数数据,而y(k)则用的是副热带高压面积指数数据。式中k是从1到184,训练数据通过4条ANFIS规则拟合,其中每个输入都被赋予2个一般的钟型隶属函数(王文涛等,2009)。 前20步的均方根误差曲线如图 5所示。
归一化到-1至1,一共有184对如下的训练数据:[c(k),c(k-1);y(k)];其中c(k)用的是超前9 d的马斯克林高压指数数据,c(k-1)是超前8 d的马斯克林高压指数数据,而y(k)则用的是副热带高压面积指数数据。式中k是从1到184,训练数据通过4条ANFIS规则拟合,其中每个输入都被赋予2个一般的钟型隶属函数(王文涛等,2009)。 前20步的均方根误差曲线如图 5所示。
|
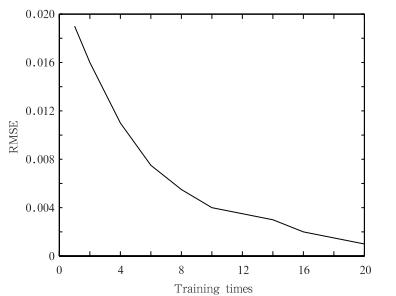
| 图 5 均方根误差曲线 Fig. 5 RMSE vs.training time |
均方根误差曲线的起点显示了仅用最小二乘法识别线性参数时的误差。最终,系统仿真和模糊去噪的结果可以用来揭示马斯克林高压对副热带高压演变所做的扰动贡献(图 6),不同时段的副热带高压大致有以下特点:
|
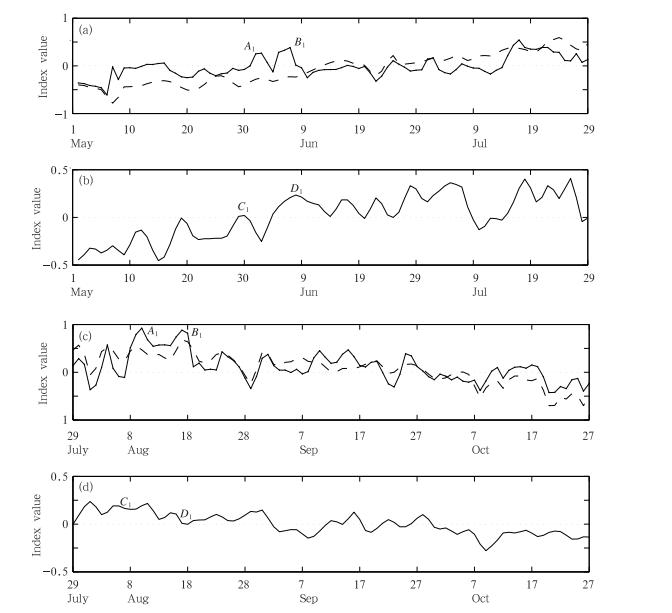
| 图 6 不同时段的实测SI(实线)、滤除8天前MH干扰后的SI(虚线)(a、c)和超前8天的MH(b、d) Fig. 6 Temporal evolution in the SI(solid line),SI after filtering the MH disturbance before 8 d(dashed line)(a,c) and MH 8 d in advance(b,d) |
从图 6中可以看出,5月30日—6月10日(图中A1点到B1点)若不考虑前期的马斯克林高压的作用,则此期间副热带高压异常减弱过程的低谷将被填平,说明8月10—18日(副热带高压异常减弱过程的主要原因之一是前期的马斯克林高压异常减弱(图中C1点到D1点)所致;而发生在7月底到8月中旬(图中A2点到B2点)的一次副热带高压异常增强则是由于前期的马斯克林高压异常增强(图中C2点到D2点)所致(滤除马斯克林高压影响后,副热带高压异常增强的高峰被挫平)。其余幅度较小的SI正距平时段,若滤除MH影响,则副热带高压的增强幅度均有不同程度的减弱,而较小的负距平时段,滤除MH影响后,对副热带高压并没有太大影响。 4 异常活动年份的副热带高压及其相关因子的非线性动力模型反演
从观测资料重构非线性动力系统的基本思想在Takens(1981)的相空间重构的理论中有着严格的阐述与证明。因此,系统演变的非线性动力学模型可以从有限的观测数据中重构出来。基于前面对于异常年份副热带高压及其影响因子的检测分析基础,拟用副热带高压面积指数、马斯克林冷高压强度指数、索马里低空急流指数和印度季风潜热通量这4个时间序列,通过动力系统反演的思想和模型参 数优化等途径,异常活动年份的副热带高压及其相关因子的动力预报模型可以被反演重构出来。
动力模型重构的基本思想在以前的研究(洪梅等,2010)中已经有了详细的证明和介绍,这里不再赘述。
基于动力模型重构的基本思想,拟以T1、T2、T3、T4表征3.2节选定的副热带高压面积指数、马斯克林冷高压强度指数、索马里低空急流指数、印度季风潜热通量指数的时间序列,引入遗传算法进行模型参数优化和动力模型重构。
基于动力模型重构的基本思想金星模型反演途径,约束条件是残差平方和S=(D-GP)T(D-GP)的最小值,在参数空间中以模型参数的种群(多解)与并行方式来做参数的最优搜索。设拟重构反演的非线性动力学模型具有如下形式的广义二阶非线性常微方程组形式,副热带高压面积指数选择的时间是2010年5月1日—7月31日;马斯克林冷高压强度指数由前面的分析可知,提前8 d相关最强,所以选择2010年4月23日—7月23日;同样索马里低空急流由于提前6 d相关最强,选择2010年4月25日—7月25日;印度季风潜热通量选择2010年4月27日—7月27日;但4个时间序列的总长都是92 d。将这4个时间序列作为模型输出的“期望数据”,用来进行模型未知参数的优化反演。
设上述方程组中的未知参数矩阵 P =[a1,a2,…a14;b1,b2,…b14;c1,c2…c14,d1,d2…d14]为种群,而残差平方和S=(D-GP)T(D-GP)为目标函数值,遗传个体适应值取为li= 1/S,总的适应值为L=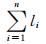 ,
,
具体的遗传操作步骤和详细说明均可参阅王小平等(2003)。计算中将取迭代步长为1 d,约 40次的优化搜索和遗传操作之后,目标的适应值可迅速收敛,非线性动力学方程组各项的优化参数可反演获得。量级系数极小的弱项被剔除之后,如下副热带高压面积指数及其相关因子指数时间序列的非线性动力模型可以反演得到。具体反演方程组为
对其进行拟合检验,其中副热带高压面积指数和索马里低空急流指数的时间序列拟合效果比较好,相关系数达到0.9138和0.8891,而马斯克林冷高压强度指数和印度季风潜热通量的时间序列拟合效果稍微差一些,相关系数是0.8159和0.8546,但也超过了0.8。 5 副热带高压及其相关因子的非线性建模预报试验 5.1 2010年副热带高压面积指数预报试验
为检验上述模型的实际预测效果,未参加反演建模时段(2010年8月1日—9月5日)的副热带高压面积指数、马斯克林冷高压强度指数、索马里低空急流指数和印度潜热通量指数的时间序列被选用来检验模型的预报效果。取2010年8月1日的副热带高压面积指数、7月24日的马斯克林冷高压强度指数(超前8 d)、7月26日的索马里低空急流指数(超前6 d)和7月28日的印度潜热通量指数(超前4 d)的值作为初值,将其代入以上非线性动力模型方程组,进行数值积分运算,得到2010年8月1日至9月5日共35 d的副热带高压面积指数数值积分预测结果,如图 7a所示。而其他3个因子的35 d数值积分预测结果如图 7b—d所示。为节省篇幅,在一幅图中集中显示15、25、35 d的短、中、长期预报效果。
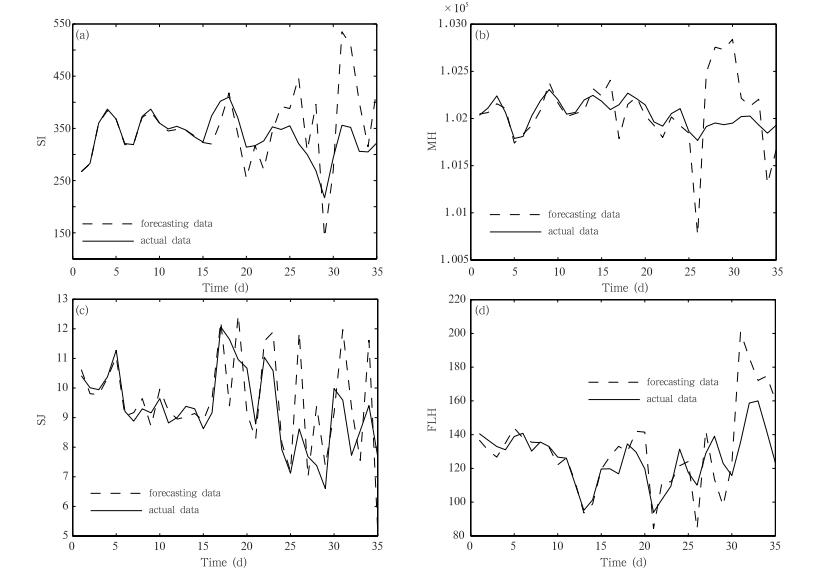
|
| 图 7 副热带高压面积指数(a)、马斯克林冷高压强度指数(b)、索马里低空急流指数(c)和印度季风潜热通量指数(d)的35 d预报 Fig. 7 35 days forecast results of SI(a),MH(b),SJ(c) and FLH(d) |
从图 7a可以看出,副热带高压面积指数的预报效果还是很好的,在前15天,不仅趋势预报得准确,相关系数达到0.9542,而且预报值与真实值的相对误差也很小,只有2.45%。15—25天,也是一样,趋势预报准确,相关系数达到0.9254,误差也不大(6.37%)。但是在接近25天的时候,误差已经开始增大。25—35天,趋势预报还算准确,高峰和低谷都预报出来了,相关系数为0.8136,但预报发散厉害,这与数值积分后期易发散的特性有关,特别是32天以后,误差也增大到19.18%。而从图 7b—d也可以看出,马斯克林冷高压强度指数、索马里低空急流指数和印度季风潜热通量指数与副热带高压面积指数类似,预报效果在25 d之内,趋势预报很好,相关系数都在0.8以上,预报值与真实值的相对误差也都控制在9%以内。但是25天以后,其发散程度增大,误差也增大,基本都在15%—20%。特别是马斯克林冷高压指数在25天之后发散更为明显,这可能是与其量级较其他几个指数比较大有关。
从图 7的4幅图综合可以看出,副热带高压面积指数、马斯克林冷高压强度指数、索马里低空急流和印度潜热通量指数虽然长期预报会有发散现象,但是25 d以内的中短期预报效果还是很好的,误差基本不超过10%,也很好地将指数的变化趋势给预报出来了。 5.2 更多对于副热带高压面积指数异常年份的预报试验
为了进一步检验模型的预报能力,需要进行更多试验。选择4个副热带高压面积指数异常增强年份(1998、2006、2003和1983年)和5个副热带高压面积指数异常减弱年份(1984、2000、1994、1999和1985年),用前面的2010年的模型来进行预报检验。预报结果根据不同的时段(1—15天是短期,16—25天是中期,26—35天是长期)与真实天气情况进行对比。结果如表 2。
| 预报案例 | 短期(1—15天) | 中期(16—25 天) | 长期(26—35 天) | |||
| 相关系数 | 最小均方根误差 | 相关系数 | 最小均方根误差 | 相关系数 | 最小均方根误差 | |
| 副热带高压面积指数较
大年份1(1998年6月21日作为 初始值进行预报) | 0.933 | 3.32% | 0.804 | 5.77% | 0.714 | 10.91% |
| 副热带高压面积指数较
大年份2(2006年7月18日作为 初始值进行预报) | 0.912 | 3.88% | 0.825 | 5.96% | 0.796 | 11.49% |
| 副热带高压面积指数较
大年份3(2003年 7月8日作为 初始值进行预报) | 0.902 | 3.96% | 0.866 | 4.88% | 0.722 | 12.70% |
| 副热带高压面积指数较
大年份4(1983年8月5日作为 初始值进行预报) | 0.896 | 5.10% | 0.839 | 7.97% | 0.756 | 12.88% |
| 副热带高压面积指数较
小年份1(1984年7月28日作为 初始值进行预报) | 0.917 | 4.81% | 0.821 | 8.17% | 0.689 | 14.55% |
| 副热带高压面积指数较
小年份2(2000年6月29日作为 初始值进行预报) | 0.880 | 4.22% | 0.842 | 6.97% | 0.612 | 13.48% |
| 副热带高压面积指数较
小年份3(1994年8月17日作为 初始值进行预报) | 0.923 | 4.76% | 0.787 | 7.98% | 0.677 | 10.76% |
| 副热带高压面积指数较
小年份4(1999年6月12日作为 初始值进行预报) | 0.812 | 3.86% | 0.837 | 6.95% | 0.754 | 11.71% |
| 副热带高压面积指数较
小年份5(1985年7月11日作为 初始值进行预报) | 0.942 | 3.16% | 0.853 | 7.81% | 0.712 | 12.65% |
| 平均 | 0.902 | 4.12% | 0.830 | 6.94% | 0.715 | 12.35% |
由表 2可以看出,副热带高压面积指数的短期和中期预报效果比较好,长期的预报效果(26—35天)也在可以接受的范围。异常年份的马斯克林冷高压强度指数、索马里低空急流和印度潜热通量指数预报结果也与副热带高压面积指数比较类似。 6 总 结
基于模糊系统的检测分析和通常的基于频率结构的滤波方法不同,它是用模糊推理逼近和识别具 体影响因子产生的扰动或贡献,从而有针对性地滤去其产生的干扰。因此,这种方法能够有针对性地检测和分析出不同因子对大气海洋系统变化或异常所起的作用大小或影响程度。本研究正是利用模糊系统的非线性、容错性和自适应学习等优越性,讨论副热带高压异常的2010年夏季风主要成员对副热带高压异常的贡献和影响,找出了对2010年副热带高压异常作用最显著的3个因子:马斯克林高压、索马里低空急流和印度季风潜热通量。
基于上述分析,针对东亚夏季风环流演变与副热带高压活动极为复杂,难以准确建立其动力模型的情况,从2010年实际观测资料中用遗传算法反演重构出副热带高压面积指数与3个显著因子动力模型的方法途径,将副热带高压面积指数与东亚夏季风环流因子的非线性动力模型客观合理地反演重构出来,并做了进一步动力延伸预报试验。经过了多个异常年份的试验,结果标明:副热带高压面积指数、马斯克林冷高压强度指数、索马里低空急流和印度潜热通量指数虽然长期预报会有发散现象,但是在25 d以内的中短期预报效果较好,误差基本不超过10%,也很好预报出了指数的变化趋势。通过对比可以看出,反演模型的可操作性和预报时效要明显优于常规的统计预报方法(包括神经网络等)(李勋等,2010),为复杂天气系统(特别是其动力模型无法准确获取)的诊断预测和动力学研究探索了新途径。
过拟合现象是一般统计预报和机器学习方法共性的问题,其原因大致为:(1)建模学习训练样本偏少、拟合率过高,(2)预报因子选择不够准确,(3)模型参数选择不够合理(Tetko et al,1995)。本研究首先利用ANFIS进行预报因子诊断和建模,正是希望利用ANFIS的非线性特征映射和自适应模糊参数调整的特性来减少过拟合现象,当然该方法不可能完全消除过拟合现象,所以用ANFIS进行预报,发现其中长期预报效果并不是很好。考虑在ANFIS挑选预报因子的基础上,引入动力重构预报方法,此方法的预报准确率主要取决于是否能够有效刻画副热带高压动力系统,预报效果与初值和预报积分时效有关,并不存在过拟合问题,所以中长期预报效果会更好一些。
此外,模型在预报过程中,无需像神经网络和统计回归预报等方法要提供众多的预报因子,而只需提供动力方程组初值即可;模型也无需像传统统计方法那样分别建立多个时效预报模型,而直接可以提供多个时效的预报。因此,反演动力统计模型的预报方法同时兼备了传统的统计预报和数值预报方法的优点。当然,模型的预报准确率对初值和预报积分时效有强依赖性,这样就会限制长期(>25天)的预报效果,如何克服这个问题,是以后研究的重点。本文仅讨论了副热带高压面积指数,事实上,副热带高压的强度指数、脊线指数和西脊点指数也很重要,要实现副热带高压的整体预报,此方法是否适用于其他3种指数的预报,这也是下一步要考虑的工作。
| 曹鸿兴, 陈国范. 1980. 天气过程的模糊划分. 科学通报, 25(10): 457-460. Cao H X,Chen G F.1980.Fuzzy Partition of weather process. Chinese Sci Bull, 25(10):457-460 (in Chinese) |
| 曹鸿兴, 陈国范. 1988. 模糊集方法及其在气象中的应用. 北京: 气象出版社, 14-20. Cao H X,Chen G F.1988. Fuzzy Sets and Its Application in Meteorology. Beijing: China Meteorological Press, 14-20 (in Chinese) |
| 顾秀萍. 2010. 自适应神经模糊推理系统(ANFIS)及其仿真. 火力与指挥控制, 35(2): 48-49. Gu X P.2010. Study on the adaptive network-based fuzzy inference system and its simulation. Fire Control & Command Control, 35(2):48-49 (in Chinese) |
| 洪梅, 张韧, 万齐林等. 2010. EOF分解与GA优化的热带太平洋海温场动力预报模型反演. 气象学报, 68(5): 731-739. Hong M, Zhang R, Wan K L,et al.2010. Retrieving the parameters of the dynamic forecast model of tropical Pacific ocean SST field based on the EOF technique and GA optimization. Acta Meteor Sinica, 68(5): 731-739 (in Chinese) |
| 黄建平, 衣育红. 1991. 利用观测资料反演非线性动力模型. 中国科学(B辑), (3): 331-336. Huang J P, Yi Y H.1991. The use of observational data inversion nonlinear dynamic model.Sci China B, (3): 331-336 (in Chinese) |
| 黄露, 何金海, 卢楚翰. 2012. 关于西太平洋副热带高压研究的回顾与展望. 干旱气象, 30(2): 255-260. Huang L,He J H, Lu C H.2012. Review and outlook of researches about Western Pacific subtropical high. J Arid Meteor, 30(2): 255-260 (in Chinese) |
| 李勋, 李泽椿, 赵声蓉等. 2010. 强台风Chanchu(0601)的数值研究:转向前后内核结构和强度变化. 气象学报, 68(5): 598-611. Li X, Li C Z, Zhao S R, et al.2010. A numerical study of Typhoon Chanchu(0601); The inner core structure evolution and intensity changes around its northward turn. Acta Meteor Sinica,68(5): 598-611 (in Chinese) |
| 刘宇, 曾燎燎, 路永乐等. 2012. 粒子滤波和ANFIS级联滤波的去噪技术. 重庆大学学报, 35(4): 19-26. Liu Y, Zeng L L, Lu Y L, et al.2012. Denoising technique based on cascaded filtering of particle filter and ANFIS. J Chongqing Univ (Natural Sci Edition),35 (4): 19-26 (in Chinese) |
| 孙长, 毛江玉, 吴国雄. 2009. 大气季节内振荡对夏季西北太平洋热带气旋群发性的影响. 大气科学, 33(5): 950-958. Sun Z, Mao J Y, Wu G X. 2009.Influences of intraseasonal oscillations on the clustering of tropical cyclone activities over the western North Pacific during boreal summer. Chinese J Atmos Sci,33(5): 950-958 (in Chinese) |
| 王会军, 薛峰. 2003. 索马里急流的年际变化及其对半球间水汽输送和东亚夏季降水的影响. 地球物理学报, 46(1): 18-25. Wang H J, Xue F.2003. Interannual variability of Somali jet and its influences on the inter-hemispheric water vapor transport and on the East Asian summer rainfall. Chinese J Geophys,46(1): 18-25 (in Chinese) |
| 王凌. 2001. 智能优化算法及其应用. 北京: 清华大学出版社, 132-133. Wang L.2001. Intelligent Optimization Algorithm and Its Application. Beijng: Tsinghua Univ Press,132-133 (in Chinese) |
| 王文涛, 李天娟, 2009. ANFIS网络在噪声消除中的应用研究. 长春工程学院学报:自然科学版, 10(1): 56-58. Wang W T, Li T J.2009. Study on application of ANFIS network in noise cancellation. J Changchun Insti Technol (Natural Sci Edition),10(1): 56-58 (in Chinese) |
| 王小平, 曹立明. 2003. 遗传算法: 理论、应用与软件实现. 西安: 西安交通大学出版社, 176-177. Wang X P, Cao L M.2003. Genetic algorithms: Theory, application and software. Xi'an: Xi'an Jiaotong Univ Press,176-177 (in Chinese) |
| 魏凤英, 曹鸿兴. 1993. 模糊均生函数模型及其应用. 气象, 19(2): 7-11. Wei.F Y, Cao H X.1993. Fuzzy mean generating function model and its application. Meteor Mon,19(2):7-11 (in Chinese) |
| 薛峰, 王会军, 何金海. 2003. 马斯克林高压和澳大利亚高压的年际变化及其对东亚夏季风降水的影响. 科学通报, 48(3): 287-291. Xue F, Wang H J ,He J H.2003. Mascarene high interannual variability and its impact on Australian High East Asian summer monsoon rainfall. Chinese Sci Bull,48(3): 287-291 (in Chinese) |
| 余丹丹, 张韧, 洪梅等. 2007. 亚洲夏季风系统成员与西太平洋副高的相关特征分析. 热带气象学报, 23(1): 78-84. Yu D D, Zhang R, Hong M, et al.2007. A characteristic correlation analysis between the asia summer monsoon memberships and West Pacific subtropical high. J Tropical Meteor, 23(1): 78-84 (in Chinese) |
| 张韧, 王继光, 蒋国荣等. 2002. 非线性模糊识别及其在海温异常检测中的应用. 地球科学进展, 17(4): 470-476. Zhang R,Wang J G,Jiang G R, et al. 2002. Non-linear fuzzy recognition and its application in identifying SST abnormality. Adv Earth Sci, 17(4): 470-476 (in Chinese) |
| 中央气象台长期预报组. 1976. 长期天气预报技术经验总结(附录). 北京: 中央气象台, 5-6. Central Meteorological Station Long-term Forecasting Group. 1976. The Technology Experience of the Long Term Weather Forecast (Appendix). Beijing:Central Meteorological Observatory,15-17 (in Chinese) |
| 祝从文, Tetsuo N, 李建平.2004. 大气季节内振荡对印度洋—西太平洋地区热带低压/气旋生成的影响. 气象学报, 62(1): 42-50. Zhu C W, Tetsuo N, Li J P.2004. Modulation of tropical depression/cyclone over the Indian-western Pacific oceans by Madden-Julian oscillation. Acta Meteor Sinica, 62(1): 42-50 (in Chinese) |
| Soyguder S, Alli H. 2009. An expert system for the humidity and temperature control in HVAC systems using ANFIS and optimization with Fuzzy. Energy Buildings, 41(8): 814-822 |
| Sugeno M, Takgi H. 1983. Derivation of fuzzy control rules from human operator's control actions//Proceedings of IFAC Sympesium on Fuzzy Information, Knowledge Representation and Decision Analysis. Hsinchu: Chiao Tung University, 55-60 |
| Sugeno M, Kang G T. 1988. Structure identification of fuzzy model. Fuzzy Sets Syst, 28(1): 15-33 |
| Takens F. 1981. Detecting strange attractors in fluid turbulence. Lecture Notes Mathem, 898(2): 366-381 |
| Tetko I V, Livingstone D J, Luik A I. 1995. Neural network studies. 1: Comparison of overfitting and overtraining. J Chem Inf Comput Sci, 35(5): 826-833 |
| Zadeh L A. 1965. Fuzzy sets. Inform Control, 8(3): 338-353 |
 2015, Vol. 73
2015, Vol. 73