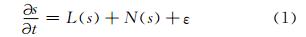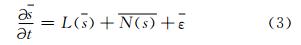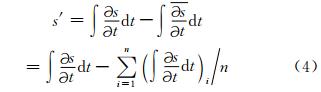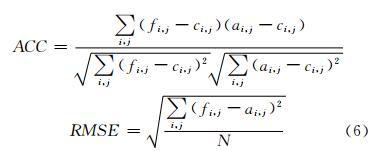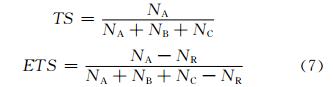中国气象学会主办。
文章信息
- 常俊, 彭新东, 范广洲, 车玉章. 2015.
- CHANG Jun, PENG Xindong, FAN Guangzhou, CHE Yuzhang. 2015.
- 结合历史资料的数值天气预报误差订正
- Error Calibration of Numerical Weather Prediction with Historical Data
- 气象学报, 73(2): 341-354
- Acta Meteorologica Sinica, 73(2): 341-354.
- http://dx.doi.org/10.11676/qxxb2015.021
-
文章历史
- 收稿日期:2014-07-21
- 改回日期:2014-11-04
2. 中国气象科学研究院灾害天气国家重点实验室, 北京, 100081;
3. 中国气象局北京城市气象研究所, 北京, 100089
2. State Key Laboratory of Severe Weather, Chinese Academy of Meteorological Sciences, Beijing 100081, China;
3. Institute of Urban Meteorology, China Meteorological Administration, Beijing 100089, China
Bjerknes(1904)对数值天气预报理论首次作出明确论述,得益于计算数学、计算机硬件和大气动力学理论的进步,数值天气预报快速发展,已经成为当今天气预报不可替代的主要手段。尤其近15年,随着计算机的进步和大规模计算能力的提高,高分辨率数值天气预报取得了令人瞩目的成就,预报精度不断提高,预报时效不断延长。但不可否认,无论什么样的精细数值预报都是对真实大气的数学物理近似,并通过计算机离散计算获得的数值解,存在系统误差和随机误差。数值预报系统误差主要来源于初始误差和模式误差,其中,初始误差包括了观测误差和资料客观分析误差;模式误差(穆穆等,2011)则包括模式动力过程误差、物理过程误差和数值计算误差及计算机舍入误差,这些误差导致数值预报结果的系统偏差。因此,为了提高数值天气预报的质量,通常采取各种措施来改进模式初始场、采用更完整的非静力完全可压缩方程和高精度的计算方法构建动力框架、开发精细的次网格物理过程和参数化计算方案来改进确定性预报。
然而,无论是初始场还是模式动力过程或物理过程的描述,都不可能是实际大气复杂过程的精确反映,而只能是一个近似。通过努力只能在一定程度上提高预报精度,减小模式预报误差,并不能完全消除误差。另外,迄今已有大量观测和再分析资料的积累,这些观测资料应是大气实际运动状态的最真实描述,使数值预报结果的统计订正成为可能,如模式输出统计(MOS)线性回归方法、卡尔曼滤波及变分修正方法等,从而改进数值预报结果。
顾震潮(1958a、1958b)针对已有丰富的大气演变资料的应用,提出将数值天气预报由初值问题看作历史演变问题,大量的历史观测资料是对真实大气最客观的反映。丑纪范(1974)提出了在数值天气预报中使用历史资料来考虑物理场演变的时间连续性问题,在1986年又进一步论述了动力数值天气预报方法和统计方法都有预报能力,又各有困难和问题的观点,提出了应探索二者结合的新方法——动力-统计方法(丑纪范,1986)。邱崇践等(1987)和丑纪范(2007)认为,观测可看作模式方程足够精确的解,可以通过求解反问题的方法来修正模式参数,从而改进模式预报结果。Huang等(1993)率先利用相似-动力方法来缩减模式预报误差,任宏利等(2005)则根据大气相似性原理,提出了利用历史资料的相似信息估计模式误差的反问题,并发展了一种统计和动力方法有机结合的相似性误差订正方法。这些工作,推动了数值天气预报的动力-统计方法的结合和发展。
另外,从大气观测资料的利用和代表性考虑,钱维宏(2012)提出利用大气连续变量物理分解思想进行中期-延伸期天气预报的方法,从而将观测变量的变化在数学和物理上统一起来。在此基础上,Peng等(2013)提出了基于历史资料的模式距平积分预报订正(Anomaly Numerical-correction with Observations,ANO)方法,并采用CAM3.0(T42)模式,ERA-interim资料作为初值分别对冬季不同个例进行了大量的订正试验。应用ANO方法对2008年1月雨雪冰冻灾害天气过程的预报订正,充分显示出该方法的有效性、实用性和灵活性,利用已有观测资料可有效提高环流场的数值预报精度,特别是CAM3.0模式的温度预报场改进最大。Peng等(2013)将ANO方法与Xu等(2012)考虑气候变化趋势的新订正方法进行了比较,ANO方法表现出了一定的优势。同时,由于采用离线的距平积分订正,不影响模式本身的计算稳定性。在实际业务应用中,附加计算负担极小,但会增加模式结果存储需求。就灾害性天气预报而言,自然更关心高分辨率区域模式结果,特别是降水预报的改进。由于降水存在时空不连续性,能否采用ANO方法获得满意的订正效果,正是本研究想回答的问题。此外,数值模式质量会影响模式订正,模式分辨率的提高在显著改善数值预报质量的同时,也降低了预报量的可订正范围,那么对于高分辨率模式结果而言,ANO订正能否获得明显的预报改进也是备受关注的问题。
本研究将结合2013年7月中国四川的一次暴雨过程,同时兼顾2008—2012年同期四川地区降水过程和1983—2012年的同期环流场预报,运用ANO方法对高分辨率WRF非静力模式的数值预报结果进行订正试验,以检验ANO方法对区域高分辨率数值模拟环流场和区域性暴雨天气的降水预报改进效果,给出环流场和降水订正的独立样本检验和分析结果,以期获得适用的中短期数值天气预报订正方法。 2 暴雨个例和资料 2.1 个例简介
2013年7月8—13日,四川盆地在西太平洋副热带高压、欧亚冷槽、台风“苏力”外围环流和地面冷锋、高空切变线、高原槽和低涡、低空急流等多重高低空天气系统,以及地形的共同作用下发生了持续时间较长的暴雨过程,这次过程强降水中心在四川盆地从西向东移动,对流强、降水强度大,且持续时间长,雨带稳定维持,在四川盆地内造成了严重的水害和次生地质灾害。
由于本研究重点在于灾害天气数值预报的订正,本次过程的天气环流形势和降水机理分析不作为讨论内容,而是着重研究采用ANO方法对该暴雨过程的高分辨数值模拟订正改进,尝试对模式降水预报的优化,探讨灾害性天气数值预报的改进方法。首先采用WRF模式,针对2013年7月8日00时(世界时,下同)—13日00时的大气环流和降水进行模拟,并采用历史资料对模拟结果进行ANO订正和讨论。 2.2 资料选取
采用欧洲中期天气预报中心(ECMWF)的ERA-interim再分析资料作为实施ANO预报订正的历史数据和模式的初值。ERA-interim资料水平分辨率为0.75°×0.75°,全球480×241个水平格点,垂直方向1000—1 hPa共分31层,时间间隔6 h,每日4次。相对2013年7月个例,还选用1983—2012年的ERA-interim再分析资料作为环流场的历史资料,对预报场进行订正。
关于降水实况格点数据,采用中国国家气象信息中心制做的中国地面观测与CMORPH逐时融合降水产品(V1.0),该资料从2008年1月1日开始,时间间隔为1 h,空间分辨率0.1°×0.1°,水平范围(60°—15°N,70°—140°E)。地面降水融合资料为2008—2012年7月的降水融合资料,评估区域位于四川盆地,地面站相对稠密,资料可信。 3 模式介绍和试验设计
使用的WRF3.5.1模式是一个非静力完全可压模式,采用通量型控制方程组,水平方向采用Arakawa-C网格,对快波和慢波的积分采用时间分离方案,垂直方向采用地形追随坐标洛伦兹跳层分布,时间积分为3阶Runge-Kutta多步计算,对水平方向声波项小步长显式时间积分,垂直方向隐式计算。模式对于不同的物理过程(包括云微物理过程、积云参数化、辐射参数化、行星边界层、陆面过程等)均有多种选择,方便针对性研究应用。
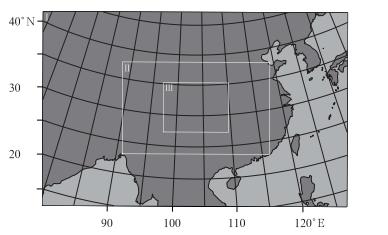
模拟区域中心选在(31.073°N,103.438°E),采用三重嵌套网格(图 1),水平网格格点数分别为154×98、223×139和295×223,相应的水平网格距为36、12和4 km,模式层顶选在50 hPa,垂直方向分为30层。首先对物理过程进行简单对比试验,最终选定模式的主要物理参数化方案,即Lin云微物理过程方案、RRTMG长、短波辐射方案、YSU行星边界层过程方案和莫宁-奥布霍夫近地面层湍流计算方案,陆面过程选用5层热量扩散模式,在粗网格区域(Ⅰ)采用Grell-Freitas积云对流参数化方案,12 km网格区域(Ⅱ)采用简化Arakawa-Schubert方案,4 km细网格(Ⅲ)则关闭积云对流参数化。在固定计算区域和模式物理过程的情况下,对1983—2013年31 a的7月8日00时—13日00时分别进行连续5 d的模拟积分,将其中某一年个例作为检验样本时,而其余30 a则作为统计样本用于建模,并首先重点对2013年的模拟进行了订正检验。
|
| 图 1 模式计算区域定义和嵌套设计 Fig. 1 Definition of the computational domains and the design of nesting areas |
大气运动具有高度非线性特征,是一个有边界强迫的复杂流体系统。大气运动不仅受其内在动力过程的约束,还受到地表(海面)动力、热力过程和太阳辐射等外源的强迫作用,对其状态变化的预知具有很大的难度。从物理上讲,大气中的任一变量s随时间的变化都遵循牛顿第二定律、热力学第一定律和连续方程,这些动力方程与大气状态方程一起构成了可预报大气变化的数值模式。遗憾的是该模式是一组偏微分方程,无法求得准确的解析解,只能通过数值方法近似求解,所以,可将该方程概括为
式中,L(s)和N(s)分别表示预报变量s的线性和非线性部分,ε代表模式误差。s在某一时段上可以分解为气候态s和相对于气候态的天气扰动量(或距平量)对式(1)关于时间求平均并结合式(2),考虑到线性项L(s) =L(s),可得可见气候态变量并不是数值天气预报模式的解,但气候态变量的预报可以通过数值天气预报结果的平均获得。式(3)也阐释了模式系统误差增长机制,如果时间平均的时段足够长,ε 即表现为数值预报的系统误差,也表示预报与实际气候场的差异。同样,误差ε=ε+ε′则表示误差可利用气候平均表示为系统误差和随机误差。因此,可利用模式和实际气候态的差异订正预报模式结果,消除系统误差,从而减小预报误差增长。由式(1)和(3)积分可得天气扰动量
式中,n一般取为30(即取为30 a)。由此获得模式对天气扰动(距平)场的预报,而去除模式气候场,从而避免气候场s的误差的影响。气候场是天气变化的多年(一般取30 a)平均,即每时每刻的天气状态是在对应时刻气候场上的天气扰动,由于不同年份的相同时刻对应相同的太阳高度角,大气具有相同的辐射外源,所以,这种分解更具物理意义。对天气预报而言,可认为气候场是已知、不变的,因此,可以充分利用历史资料,得到大气真实的气候态s a,并与天气扰动预报量s′相加得到最终的预报量用已有的观测资料求得的sa是大气最真实演变的刻画,用其代替模式气候态s 可以提高数值预报技巧(Peng et al,2013),上述气候态的替代过程实际上消除了模式气候态的误差。这样利用历史观测资料和天气扰动距平积分思想,部分消除了模式系统误差,使预报场sp更加接近真实。对于模式的系统误差,会在每一次数值预报结果中体现,那么,这些系统误差就会在s 值体现,而随机误差则在平均值中消失,用s a代替s 就实现了预报场系统误差的订正。对于区域模式而言,模式预报量的系统误差受到边条件的影响,边条件误差在非静力模式中对气压、温度场影响会以声速传播,误差表现与全球模式不同。对中短期预报而言,区域高分辨率模式也具有更高的精度,统计订正效果与低分辨率的全球模式也不同。本研究对环流场的订正采用1983—2012年ERA-interim再分析资料,首先插值到模式格点上,然后计算模式离散点的历史分析资料气候态s a,而模式气候态则通过对1983—2012年同时段的模式积分平均得到。对于降水量的气候态观测结果,由于所采用的地面观测和CMORPH卫星产品融合资料从2008年开始发布,无法获得30 a的气候平均值,这里仅采用2008—2012年5 a分析资料构建气候态,这无疑给降水的订正带来一些不确定性。 4.2 预报结果检验指标 4.2.1 距平相关系数和均方根误差
对高分辨率数值预报结果的检验,将与观测或再分析结果对比,且对环流场和降水场采用不同的方法进行评估。对大气环流场(如温、高、湿、风)主要从环流特征的型相似和值相似两个方面评估,分别采用距平相关系数(Anomaly Correlation Coefficient,ACC)和均方根误差(RMSE)(Jolliffe et al,2012)来计算和评价数值预报结果与观测的相似程度
式中,f为预报场,a为分析场,c为分析气候场,i、j为经纬格点序号,N为空间上总格点数。 4.2.2 TS和ETS评分对模式预报降水结果的评价,除了应用均方根误差指标评价降水预报误差外,还进一步考虑降水的不连续性,采用常用的统计评分标准,包括TS(Threat Score)评分和ETS(Equitable Threat Score)评分标准进行预报结果评价,其定义为
式中,NA为有效命中率,NB为空报率,NC为漏报率,其中,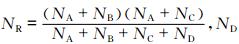 为无效命中率。
5 四川暴雨个例的ANO方法预报订正和检验
5.1 环流场预报订正
为无效命中率。
5 四川暴雨个例的ANO方法预报订正和检验
5.1 环流场预报订正
中尺度暴雨过程一般是由大尺度环流场和其中发展的中尺度对流系统共同作用的产物。2013年7月7日开始,在强烈的东南低空急流作用下,来自孟加拉湾和中国南海的水汽向四川盆地输送,遭遇南北走向的龙门山脉阻挡,在地形抬升作用和地面冷锋、高空切变线不稳定环境下激发对流。由于东南低空急流稳定作用和两支水汽通道的不 断输送,造成龙门山一带的广元、成都、绵阳、德阳、雅安等地的强降水持续不断,其中,成都都江堰市幸福镇7月9日的24 h最大降水量达到创历史记录的751.6 mm,9—11日的72 h降水量同样达到创历史纪录的1108.9 mm,整个降水过程表现出典型的持续性区域暴雨天气特征。
选取7月8日00时—7月13日00时作为暴雨后报试验时段,在三重嵌套WRF高分辨率模拟基础上检验模式的环流场和降水预报,利用ANO方法对WRF计算结果进行订正分析,以检验ANO方法对灾害性天气、尤其持续性强降水的预报订正效果。 5.1.1 位势高度
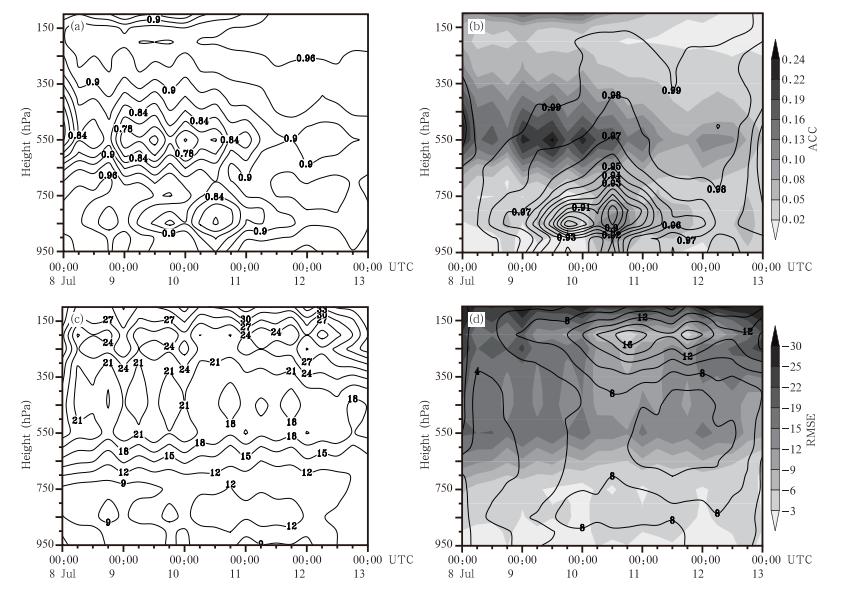
位势高度场虽然不是模式的直接预报量,但常被用来分析环流形势,在模式中也综合反映了气压、温度和空气密度的分布。为了显示大范围的模式环流场特征,这里分析模式粗网格区域(Ⅰ)的结果。图 2为粗网格位势高度场模拟结果和ANO方法订正结果与再分析资料的距平相关系数和均方根误差时间-高度分布。可见在本次过程中,WRF模式在850、550和200 hPa层上的位势高度预报偏差较大,环流型与实况的相似性较差,其中在550 hPa层上距平相关系数出现极小值(0.75)。经过ANO方法的订正,预报结果大为改善,在整个预报时段的所有层次上的位势高度距平相关系数和均方根误差相对于模拟结果均有显著的提高和降低,订正之后位势高度距平相关系数(图 2b)在绝大部分层次都在0.95以上,整个预报时段所有层次的距平相关系数提高0.02—0.24,平均提高7.8%,尤其在中层600—450 hPa 距平相关系数约提高0.15,提高幅度达15%左右。 从图 2c来看,模拟位势高度场的均方根误差为9—33 gpm,从低层到高层逐渐增大。与距平相关系数分布对应,分别在850、550和200 hPa层上存在均方根误差峰值。而订正后的位势高度均方根误差(图 2d)为4—15 gpm,绝大部分层次上都在10 gpm以下,最多减小25 gpm以上,整个预报时段所有层次的均方根误差平均降低了55.7%,尤其在对流层中层550 hPa处出现了均方根误差订正幅度约为20 gpm的峰值,效果尤为显著。模式位势高度的预报误差反映了模式动力、物理、地形和地表过程的综合结果,模式陆面过程、边界层过程和地形处理对近地层位势高度影响较大,而青藏高原动力作用计算偏差对四川盆地500 hPa高度预报有极大负面影响,对流层高层200 hPa的主要误差来源可能来自平流层过程的缺失。这些误差大多是模式定常的系统误差,正如4.1节所述,利用观测资料对数值结果的订正可以改进预报效果。
|
| 图 2 WRF模式预报(a、c)和ANO订正(b、d)的等压面位势高度场与ERA-interim资料的距平相关系数(a、b)和均方根误差(c、d,单位:gpm)(等值线)时间-高度分布(灰阶为ANO和WRF模式结果对应量的差) Fig. 2 Temporal-vertical distribution of ACC(a,b) and RMSE(c,d ; gpm)of geopotential height from the WRF simulation(a,c) and ANO correction(b,d)(contour lines)with regarding to the ERA-interim reanalysis,where the shaded shows the difference between the ANO correction and the WRF model simulation |
从位势高度距平相关系数和均方根误差在订正前后的变化可以看出,采用ANO方法的预报订正效果明显,在所有层次和整个预报时段内环流形势更趋近于再分析场的分布,在全球预报(Peng,et al,2013)的基础上进一步说明了ANO订正方法对区域模式环流形势预报的作用。 5.1.2 比 湿
比湿的分布具有随高度迅速递减的分层特点,因此,预报误差的分布也会表现出随高度递减的特征。图 3给出了WRF模式预报比湿以及结合历史分析资料的ANO订正结果与ERA-interim再分析资料的距平相关系数和均方根误差时间-高度分布。总体来看,WRF模式预报900—150 hPa的比湿距平相关系数在0.7以上,仅有对流层顶300 hPa附近在48 h后距平相关系数在0.5左右。对流层低层的850—550 hPa的预报比湿型相关最好,出现了上下层间的极大值区,而在近地层和对流层顶预报比湿相关较差。比湿均方根误差基本呈现自下而上的递减分布,且随时间减小。
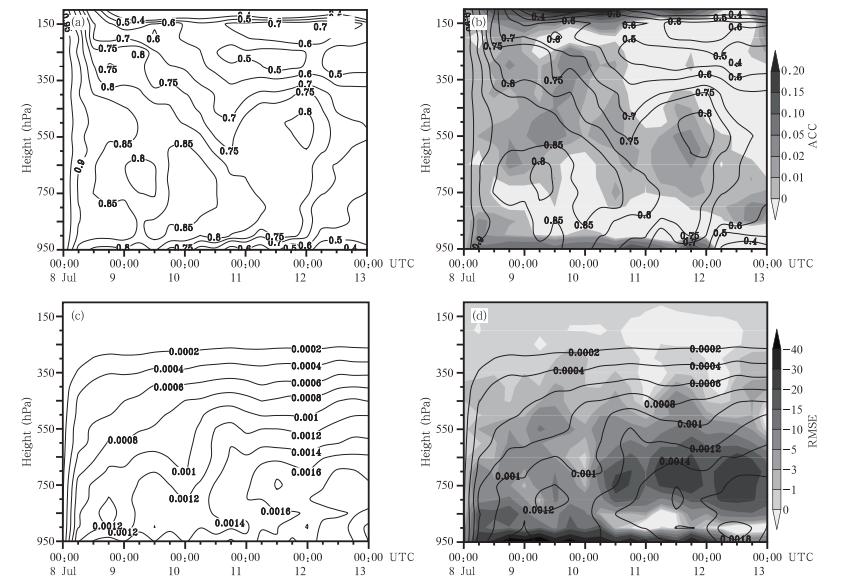
|
| 图 3 WRF模式预报(a、c)和ANO订正(b、d)比湿与ERA-interim资料的距平相关系数(a、b)和均方根误差(c、d,单位:10-5 g/g)(等值线)的时间-高度分布(灰阶为ANO和WRF模式结果对应量的差) Fig. 3 Temporal-vertical distribution of ACC(a,b) and RMSE(c,d,10-5 g/g)of specific humidity from the WRF simulation(a,c) and ANO correction(b,d)(counters)with regarding to the ERA-interim reanalysis,where the shaded shows the difference between the ANO correction and the WRF model simulation |
在结合历史再分析资料和ANO方法对比湿预报场订正之后,比湿的距平相关系数(均方根误差)均有明显的提高(减小),特别是900 hPa以下近地层,距平相关系数和均方根误差都有明显改善。总体而言,图 3a中比湿距平相关系数随预报时间不断变小的事实没有改变,但900 hPa以下近地层和150 hPa以上对流层顶的水汽距平相关系数预报得到较大改善,对流层中层也出现了一个以550 hPa层为中心、随时间自上而下的距平相关系数改进层,改进了水汽分布预报,这为改进模拟降水分布提供较好的基础条件。
就比湿的均方根误差(图 3d)来看,订正后均方根误差仍然呈从低层至高层随模拟时间增加而增大的变化趋势,与WRF的直接预报误差分布相似,但订正后的均方根误差在整个计算空间和预报时间内都明显减小,整个预报时段所有层次的均方根误差平均减小6.9%。尤其在900 hPa以下的近地层和850—550 hPa的对流层中下层,出现了均方根误差改善(阴影)的极值区,均方根误差的减小幅度为6.5%—21%,ANO方法的订正效果明显。同时,也说明了数值模式存在对近地层和对流层中下层水汽预报的系统性偏差,这不仅牵涉到陆面过程、边界层垂直输送,还可能与青藏高原复杂地形边坡地区的地形动力(如摩擦和拖曳)有关,通过对应时刻观测资料的应用可部分消除模式误差影响。从图 3d还可以发现,对流层中下层(如750 hPa)均方根误差的改善具有明显的夜间极值特点,四川盆地在这一时段具有明显的夜间增湿特点,数值模式对这一特点描述不充分,提供了统计订正的空间。 5.1.3 温度场
WRF中尺度模式对本次个例温度场的预报在对流层中上层500—-250 hPa明显表现出较高的预报技巧(图 4),绝大部分层次和时次的距平相关系数均在0.8以上,但在500 hPa以下层次,温度距平相关系数随积分时间不断减小,650 hPa以下预报温度距平相关系数相对均匀,在72 h以后的预报距平相关系数的值偏低。与温度场距平相关系数相对应,均方根误差在450 hPa出现了该预报时段极小值,在0.8℃以下;在800 hPa层则出现了温度极大均方根误差。从图 4b和d可见,结合历史再分析资料的ANO方法订正之后,温度场距平相关系数和均方根误差在大多层次和时次都有明显改善,特别是在低层750—-550 hPa的距平相关系数和均方根误差改善幅度较大,大部分层次和时次距平相关系数均在0.85以上,平均约提高1.6%。均方根误差在大多层次和时次均有明显减小,平均减小0.09℃(约9.1%),但在850 hPa的一些时次以及36 h积分之后的500—-100 hPa,订正距平相关系数和均方根误差反而变得更差,特别是对流层顶150 hPa附近的距平相关系数订正负效果明显,均方根误差约增大0.2℃,可能与本次过程的对流层顶环流异常有关。从950 hPa附近温度的距平相关系数和均方根误差分布可以看出,WRF模式模拟的气温日变化误差较大,尤其06—14时的模拟温度距平相关系数出现低谷,均方根误差增大,订正结果在该模拟时段改善了距平相关系数和均方根误差值,从而改善了近地层温度日变化模拟。
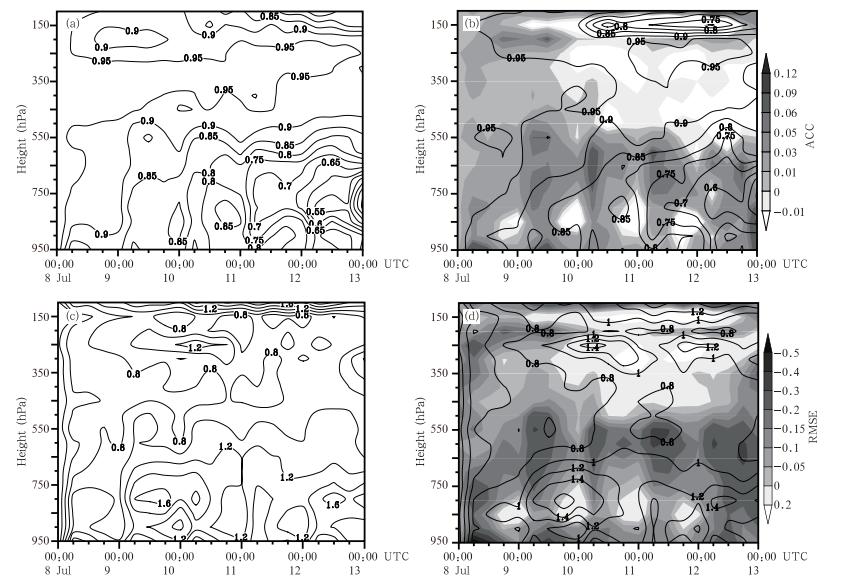
|
| 图 4 WRF模式预报(a、c)和ANO订正(b、d)温度场与ERA-interim资料的距平相关系数(a、b)和均方根误差(c、d,单位: ℃)(等值线)时间-高度分布(灰阶为ANO和WRF模式结果对应量的差) Fig. 4 Temporal-vertical variation of ACC(a,b) and RMSE(c,d. ℃)of temperature from the WRF simulation(a,c) and ANO correction(b,d)(counter lines)with regarding to the ERA-interim reanalysis,where the shaded shows the difference between the ANO correction and the WRF model simulation |
湿度和温度场是WRF模式的热力学直接预报量,其短期预报受模式数值解法、初值条件和辐射、下垫面强迫等外源共同作用。在本研究采用的三重嵌套模拟中,高分辨率和详细的云微物理过程应用基本成功模拟了强降水过程,但误差分布显示了四川盆地中低层和近地层大气温、湿度场偏差,可能与陆面过程和边界层过程有关。而ANO方法基于相同太阳高度角情况下的气候态偏差进行订正,充分利用观测资料中相同外源强迫的物理信息,对不同 层次的水汽和温度有效订正,既反映了预报量变化的物理本质,也反映了温度和水汽时间变化的统计特征,这是本研究方法区别于其他(如MOS)统计方法的重要方面。另外,高分辨率模式性能的提高,压缩了统计订正的空间,但由于区域高分辨率模式仍然存在系统误差,既使模式前3天预报温度场0.8以上的距平相关系数,ANO方法仍有正订正效果。从图 4d不难看出,温度均方根误差订正量在白天午后的对流层中层出现极大值,这与湿度场极大误差订正量出现时间不同,也恰是地面和大气升温最强的时刻,说明模式中水汽、辐射、云微物理和对流等过程及其相互作用的偏差,仍然有待改进。 5.1.4 水平风场
从图 5给出的风场u、v的模式模拟结果及ANO方法订正结果与ERA-interim再分析资料的距平相关系数和均方根误差时间-高度分布可以看出,WRF模式模拟纬向风的距平相关系数(图 5a)高于经向风的模拟结果(图 5e),预报时段内纬向风所有层距平相关系数平均为0.88,经向风距平相关系数平均为0.74。WRF模式在350 hPa以上高层很好地模拟了纬向风的形势分布,距平相关系数要高于中低层,其次在850 hPa模式也可较好地预报出纬向环流,而中层550 hPa相对较差。经向风的低层距平相关系数普遍高于中高层的值,其中,500—200 hPa的预报经向风距平相关最差。

|
| 图 5 WRF模式预报(a、c、e、g)和ANO订正(b、d、f、h)的风场分量u(a、b、c、d)和v(e、f、g、h)与ERA-interim资料的距平相关系数(a、b和e、f)和均方根误差(c、d和g、h,单位:m/s)(等值线)时间-高度分布(灰阶为ANO和WRF模式结果对应量的差) Fig. 5 Temporal-vertical distribution of ACC(a,b and e,f) and RMSE(c,d and g,h,m/s)of u(a,b,c,d) and v(e,f,g,h)from the WRF simulation(a,c,e,g) and the ANO correction(b,d,f,h)(counter lines)with regarding to the ERA-interim reanalysis,where the shaded shows the difference between the ANO correction and the WRF model simulation |
经过ANO方法订正后的纬向风距平相关系数(图 5b)和经向风距平相关系数(图 5f)都比原模拟结果有明显提高,纬向风和经向风距平相关系数平均分别提高1.4%和11.5%,其分别在低层850 hPa和高层200 hPa提高最为显著,可能与模式地形拖曳、边界层动量混合计算、区域模式缺少平流层过程和与对流层相互作用的描述有关。另外,纬向风订正结果的距平相关系数在48小时预报后的高层及950 hPa部分时次有所降低,经向风普遍改善明显。整体而言,经向风的距平相关系数订正效果要好于纬向风。而对于风场均方根误差,WRF模式模拟纬向风在预报时段的所有层平均误差为3.5 m/s,中低层纬向风(图 5c)与经向风误差(图 5g)接近,但高层经向风误差较大。ANO方法的经向风订正明显优于纬向风订正效果(图 5f与h),订正后经向风误差平均减小18.1%,纬向风平均减小6.3%。均方根误差的分布同样反映出纬向风和经向风分别在低层850 hPa和高层200 hPa附近订正较多。
从风分量误差订正量(图 5d和h)可见,低层850 hPa的极大订正值也出现在夜间的稳定边界层内,反映出模式自身对四川盆地夜间边界参数化的不足。此外,由于四川盆地的特殊地形,纬向风和经向风的误差订正极值出现时间也有差异。 5.1.5 ANO方法与其他模式误差订正方法的对比
为了进一步了解ANO方法的表现,将之与其他模式误差订正方法的比较是最为直接的。模式输出统计(MOS)方法最为常用,但由于MOS方法一般针对某一点建立预报变量与其他模式变量的线性回归方程,对高分辨率模式每一个格点的线性回归计算量巨大;同时由于MOS方法在建模中采取相关因子显著性更新法筛选预报因子,不同格点的预报因子可能不同,所以,这里将不与MOS方法进行对比,而是与Xu和Yang提出的考虑了气候变化因素的气候模拟订正新方法(后称XY方法)(Xu et al,2012)进行对比,更能体现最新模式订正研究成果间的相对效果。
ANO和XY方法都利用了已有的大量历史资料信息来订正模式的预报结果,XY方法主要针对气候变化的降尺度预测问题研究,考虑了气候长期变化的影响,将30 a基本气候态的变化幅度引入订正结果。为了反映区域天气预报环流场的差异,着重对500 hPa位势高度场和温度场的订正结果进行比较。图 6给出了ANO方法、XY方法订正结果和WRF模式输出结果分别与ERA-interim再分析资料的距平相关系数和均方根误差的时间演变。从位势高度场的距平相关系数(图 6a)和均方根误差(图 6b)可以明显看出,ANO和XY方法订正结果的距平相关系数和均方根误差随时间的变化趋势保持一致,相对原模式结果均有较为明显的改善。在整个预报时段ANO方法订正结果的距平相关系数较XY方法结果略高,相应的均方根误差则略低,ANO方法整体改善效果要好于XY方法。分析温度场的距平相关系数(图 6c)和均方根误差(图 6d)可以看出,ANO方法对500 hPa温度场的改善效果并不如位势高度场那么明显,距平相关系数的改善在48 h预报中较为明显,整个预报时段的21个时次中有10个时次有所提高,但XY方法的订正距平相关系数仅有两个时次有所改善。尽管如此,两种方法对温度均方根误差的改善仍然非常明显,其中,ANO 方法订正结果在整个预报时段的均方根误差明显减小,缩小了模式预报温度场的误差范围,而XY方法在其中6个时次的温度误差有减小。
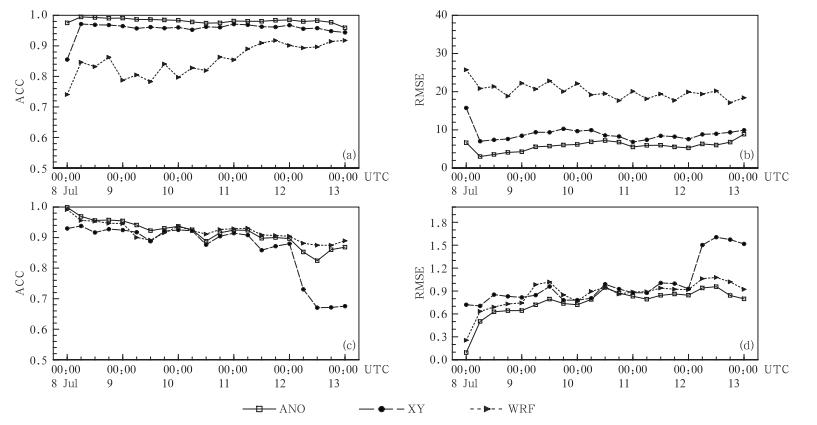
|
| 图 6 WRF模式预报、ANO订正及XY订正的500 hPa位势高度与ERA-interim再分析资料的距平相关系数(a)、均方根误差(b,单位:gpm)以及500 hPa温度与ERA-interim再分析资料的距平相关系数(c)、均方根误差(d,单位:℃)的时间演变 Fig. 6 Temporal variation of ACC(a) and RMSE(b,gpm)of the geopotential height,and ACC(c) and RMSE(d,℃)of the temperature at 500 hPa with regarding to the ERA-interim reanalysis |
2013年7月四川强降水个例为极端天气过程,具有特殊性,那么对于更多独立样本订正检验的结果如何?以1983—2013年中前30年任意一年7月8—13日00时的WRF模拟结果作为独立研究样本,其余30 a作为气候态统计对象建模,30个例环流场预报订正前后 所有等压面和全部时次的距平相关系数和均方根误差平均值(表 1)显示均有较大改进,5个预报量距平相关系数明显提高,均方根误差大幅下降,除v风分量外的其他变量平均订正效果均好于2013年个例。该结果显示ANO方法对极端天气过程的订正效果欠佳,不及其他30个例的平均情况。正是由于极端事件的特殊性,历史样本缺少对其统计代表性,削弱了订正效果,但仍有明显正效果。
| 订正增量(%) | 个例 | 位势高度 | 温度 | 纬向风分量 | 径向风分量 | 比湿 | |
| 距平相关系数 | 2013年 | 7.81 | 1.60 | 1.40 | 11.47 | 0.20 | |
| 1983—2012年平均 | 12.33 | 3.96 | 2.30 | 5.88 | 3.88 | ||
| 均方根误差 | 2013年 | -55.67 | -9.08 | -6.30 | -18.07 | -6.88 | |
| 1983—2012年平均 | -76.49 | -14.07 | -6.74 | -14.64 | -7.36 |
区别于环流变量,由于降水在空间和时间上的不连续性,预报难度较大,对局地偶发性的强对流降水统计特性薄弱,给统计订正也增加了难度。正是由于对流暴雨的偶发性,历来的暴雨和大暴雨数值预报评分较低,这也为改进暴雨以上量级降水的预报效果提供了机会。利用ANO方法对本次灾害性强降水过程的降水预报进行订正评估,采用中国国家气象信息中心的2008—2012年中国地面与CMORPH融合逐时降水产品作为历史分析数据,对四川盆地2013年7月8日00时—13日00时的强降水过程进行预报订正,通过均方根误差、TS评分和ETS评分分析降水预报和订正效果。模拟降水的分析以及均方根误差、TS和ETS统计量的计算均在高分辨率模式区域Ⅲ上进行。
图 7给出了WRF模式模拟6 h累积雨量与 ANO方法订正结果对于融合分析降水的均方根误差随时间演变。可以看到,订正前后的降水均方根误差变化趋势基本一致,且整个预报过程中的均方根误差存在着显著的日变化,06时降水预报误差为最小,18时误差最大。全部预报时段内的18个时次中,ANO方法订正的均方根误差减小的为16次,显示了 ANO方法在大多时次对降水预报的均方根误差有改善,最大降低8.4%,整个过程中降水量预报误差平均降低3.4%。尽管这里仅用了5 a的观测降水资料来构建降水气候分布,订正结果仍然显示出了ANO方法的效果,这主要体现出5 a历史资料对模式降水系统误差仍有一定的表达能力。
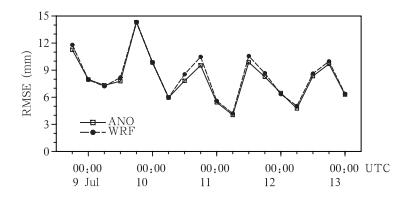
|
| 图 7 WRF模式预报和ANO订正降水均方根误差的时间演变 Fig. 7 Temporal variations of RMSE of the rainfall prediction from the WRF model and the ANO correction |
为了对本次暴雨过程的模拟降水和ANO方法订正效果进行详细分析,首先按照中国中央气象台对降水量级的划分(表 2),定义6 h降水量不小于60.0 mm为大暴雨、[25.0 mm,60.0 mm)为暴雨、[13.0 mm,25.0 mm)为大雨。在计算TS和ETS评分时,严格按照此分段分级的方法,即大雨的TS评分仅为6 h降水量在[13.0 mm,25.0 mm)的格点统计值,而非向上包容的降水量不小于13.0 mm所有格点的统计结果。由于TS计算结果与ETS有很大的相似性,这里仅给出ETS的评分分析。
| 等级 | 大暴雨 | 暴雨 | 大雨 | 中雨 | 小雨 |
| p | 60≤p | 25≤p<60 | 13≤p<25 | 4≤p<13 | 0.1≤p<4 |
图 8给出了模拟降水和ANO方法订正结果的大暴雨、暴雨及大雨的ETS评分随时间变化。总体而言,对于大雨以上降水量级的ETS评分在绝大多数时次都有提高,虽然改进幅度不大,在个别时次效果变差,这除了所用5 a历史降水资料的气候代表性问题之外,还与该区域降水气候值的大小有关。从大暴雨的ETS评分(图 8a)来看,在5 d预报时段的前24小时中ETS评分逐渐升高,其中,第6和第12小时模拟大暴雨不足,ETS评分为-0.0005,显然与模拟开始时段模式调整和冷启动降水有关,ANO方法的订正也没有明显效果。在随后4 d的17个时次中,大暴雨ETS评分值随预报时间的延长呈下降趋势,ANO方法订正之后的大暴雨ETS评分较模式结果均有提高,最小提高0.8%,最大提高5.7%,整个时段平均提高3.1%。对应的大暴雨TS评分(图略)类似,最小提高0.6%,最大提高5.4%,平均提高2.8%。
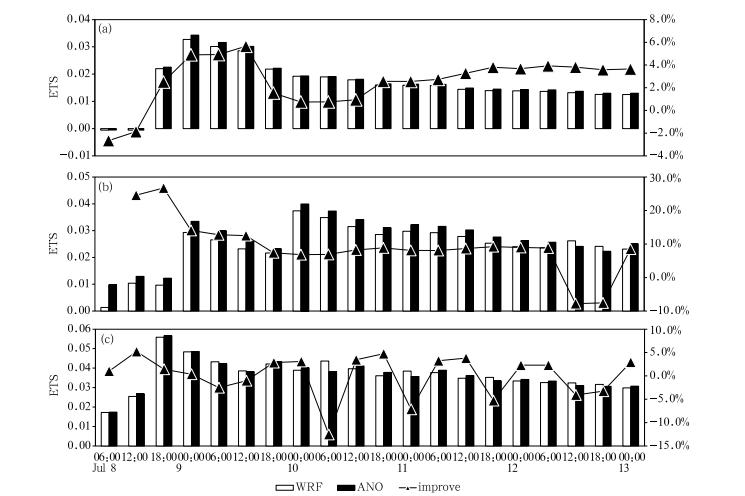
|
| 图 8 WRF模式预报和ANO订正后的大暴雨(a)、暴雨(b)和大雨(c)预报的ETS评分 Fig. 8 ETS scores for heavy rainstorm(a),rainstorm(b) and heavy rainfall(c)from the WRF simulation and the ANO correction |
暴雨量级的ETS评分(图 8b)在整个预报时段内有18个时次ANO方法订正有明显正效果,ETS评分的订正提高幅度随预报时间延长呈下降趋势,订正后的暴雨ETS评分最小提高7.4%,最大提高26.7%,全时段平均提高9.2%,但有两个时次TS评分在订正后下降。而TS评分(图略)最小提高3.7%,最大提高11.8%,全时段暴雨ETS评分平均提高6.1%。
相对于大暴雨和暴雨,ANO方法对本个例大雨、中雨和小雨评分的改善并不显著。从大雨的ETS评分(图 8c)来看,整个预报时段内20个时次有15个时次的ETS评分在订正后有所提高,其余5个时次有不同程度的降低,就出现订正ETS评分降低的时次看,没有明显规律。
在表 3中给出了2008—2012年同期5个个例作为独立样本的5 d(20个时次)预报降水订正后的ETS平均增量,发现在5个独立样本降水预报中2009、2010和2012年ETS评分订正效果较好,均好于2013年订正效果,其中,2009年各量级降水预报评分大幅度提高。2008年降水订正变差,与该年四川盆地降水较少,模拟结果异常,严重偏离气候分布有关。可见,采用ANO订正方法对模式降水预报的订正有明显正效果,但不及环流场改善效果好。如果采用时间序列更长的降水分析资料作为历史观测场,模式降水的系统误差可能得到更好地纠正,可以期望更好的订正效果。虽然仅为一个个例试验结果,该方法的应用前景仍是可以期待的。
| 个例 | ETS评分提高(%) | ||||
| 小雨 | 中雨 | 大雨 | 暴雨 | 大暴雨 | |
| 2008年 | -16.07 | -27.90 | 21.56 | -15.98 | N |
| 2009年 | 29.83 | 43.77 | 5.82 | 4.49 | 25.30 |
| 2010年 | 20.72 | 37.19 | 2.02 | 13.96 | 0.99 |
| 2011年 | -25.51 | -22.12 | -1.89 | 38.85 | N |
| 2012年 | 20.60 | 14.72 | -4.34 | 4.19 | 14.55 |
| 注: N表示无此量级降水 | |||||
以ERA-interim再分析资料作为初值和侧边界条件,在利用高分辨率WRF非静力模式对2013年7月8—13日四川暴雨过程模拟的基础上,以ERA-interim再分析资料和地面观测与CMORPH卫星资料融合降水产品为历史分析资料,检验ANO预报订正技术对本次四川暴雨的订正效果。不仅确认了该方法对高分辨率数值模式的环流预报场的显著改进作用,还首次证实了ANO方法订正可减小暴雨过程降水预报误差,提高预报评分。
ANO方法对高分辨率模式预报环流场具有显著的改善效果。位势高度、比湿、温度和风场在整个预报时段的绝大多数层次表现为距平相关系数明显提高,其中纬向风(经向风)平均提高1.4%(10.8%),均方根误差平均降低5.7%(17.3%);位势高度场的订正改进更为明显,距平相关系数平均提高7.8%,均方根误差平均降低55.7%。多年的同期独立样本检验证实这一结论的正确性。虽然降水在空间和时间上存在很强的不连续性,预报难度大,但结合5 a历史数据的预报降水ANO订正仍显正效果,对本个例5 d模拟中降水均方根误差大多都有改善,误差降低在0.04%—8.4%。对大暴雨和暴雨的订正较明显,ETS评分提高在0.8%—26.7%。2008—2012年的降水预报订正显示了ANO方法对不同量级降水的订正正效果。
ANO方法可以显著提高环流场预报精度,可有效消除环流场预报误差,并改进降水预报,提高数值预报水平,可见该方法具有实际业务预报应用价值。另外,由于本研究降水历史资料样本不足,影响了订正效果,将开展台站降水资料应用的相关研究来进一步提高模式降水预报订正效果。
致谢: 感谢丑纪范先生对本研究在完善订正方法、资料应用方面给予的热心指导和讨论。
| 丑纪范. 1974. 天气数值预报中使用过去资料的问题[J]. 中国科学,17(6):635-644 |
| 丑纪范. 1986. 为什么要动力-统计相结合——兼论如何结合[J]. 高原气象,5(4):367-372 |
| 丑纪范. 2007. 数值天气预报的创新之路——从初值问题到反问题[J]. 气象学报,65(5):673-682 |
| 顾震潮. 1958a. 天气数值预报中过去资料的使用问题[J]. 气象学报,29(3):176-184 |
| 顾震潮. 1958b. 作为初值问题的天气形势数值预报与由地面天气历史演变作预报的等值性[J]. 气象学报,29(2):93-98 |
| 穆穆,陈博宇,周菲凡等. 2011. 气象预报的方法与不确定性[J]. 气象,37(1):1-13 |
| 钱维宏. 2012. 如何提高天气预报和气候预测的技巧[J]. 地球物理学报,55(5):1532-1540 |
| 邱崇践,丑纪范. 1987. 改进数值天气预报的一个新途径[J]. 中国科学:B辑,17(8): 903-910 |
| 任宏利,丑纪范. 2005. 统计-动力相结合的相似误差订正法[J]. 气象学报,63(6):988-993 |
| Huang J P, Y H Yi, S-W Wang, et al. 1993. An analogue-dynamical long‐range numerical weather prediction system incorporating historical evolution[J]. Q. J. Roy. Meteoro. Soc., 119: 547-565 |
| Jolliffe, I T and D B Stephenson eds. 2012. Forecast verification: a practitioner's guide in atmospheric science. John Wiley & Sons, 292pp |
| Peng X D, Che Y Z, Chang J. 2013. A novel approach to improve numerical weather prediction skills by using anomaly integration and historical data[J]. J. Geophy. Res., 118(16): 8814-8826 |
| Xu, Z F and Z-L Yang. 2012. An Improved Dynamical Downscaling Method with GCM Bias Corrections and Its Validation with 30 Years of Climate Simulations[J]. J. Climate., 25: 6271-6286 |
 2015, Vol. 73
2015, Vol. 73