中国气象学会主办。
文章信息
- 张旭, 黄伟, 陈葆德. 2015.
- ZHANG Xu, HUANG Wei, CHEN Baode. 2015.
- 二阶精度半隐式半拉格朗日轨迹计算和时间积分方案在GRAPES区域模式中的应用
- Implementation of a 2nd order semi-implicit semi-Lagrangian trajectory algorithm and time integration scheme in the GRAPES regional model
- 气象学报, 73(3): 557-565
- Acta Meteorologica Sinica, 73(3): 557-565.
- http://dx.doi.org/10.11676/qxxb2015.023
-
文章历史
- 收稿日期:2014-04-10
- 改回日期:2014-12-04
2. 中国气象局上海台风研究所, 上海, 200030
2. Shanghai Typhoon Institute of China Meteorological Administration, Shanghai 200030, China
半隐式半拉格朗日(Semi-Implicit Semi-Lagrangian,以下简称SISL)时间积分方案具有绝对稳定性,即理论上时间步长的选取只取决于方案的计算精度,而不用考虑时间稳定性(Gravel et al,1993),时间步长可以取得比显式的欧拉方案长得多,自从SISL时间积分方案提出以来在大气模式中得到了广泛应用。在应用SISL时间积分方案时,空气质点的轨迹计算对方案的精度和稳定性有重要影响,实际上轨迹计算的精度在很大程度上决定了模式计算的精度和稳定性(Staniforth et al,1991)。Ritche等(1994)假定空气质点在拉格朗日轨迹上是等速运动,采取中点近似,使轨迹中间点的速度近似等于半时间步时(t+Δt/2)的速度,再利用t和t-Δt时刻格点上的速度进行外插,得到网格点上t+Δt/2时刻的速度,然后进行空间插值迭代求解出上游点的位置。由于Ritche-Beaudoin上游点方案中引入了时间外插,因而会给SISL时间积分方案带来不稳定性。如果质点速度随轨迹变化,即不再是等速运动,当CFL(Coutant-Friedrichs-Lewy)计算稳定性判据大于1时,SISL方案就会不稳定(Durran,1999)。为了解决不稳定的问题,Hortal(2002)提出了两时间层稳定外插方案(Stable Extrapolation Two-Time-Level Scheme,以下简称SETTLS),该方案假定质点沿拉格朗日轨迹做匀加速运动,这时轨迹时间中间点的位置不再是上游点与到达点的平均,从而改善了方案的稳定性。因为在SISL时间积分方案中对非线性项的处理也要涉及时间外插,因此,也可以将SETTLS方案用于处理非线性项,使得非线性项的计算在等权重时达到二阶精度。
在SISL时间积分方案中对线性项的处理也要慎重考虑。在半隐式时间积分方案中,线性项是对模式方程依照参考大气廓线进行线性化而得到的(Robert et al,1972),一般对线性项进行非中央权重的时间平均,其能够有效地抑制虚假的半拉格朗日地形共振(Rivest et al,1994),但同时也使得时间差分的精度由二阶变为一阶,而且,对大气真实的低波数波动振幅产生了较强的衰减(McDonald et al,1993; Bates et al,1993)。Simmons等(1978)也指出,线性化模式方程时参考大气廓线不能任意选择,否则可能造成时间积分不稳定。
中国气象局的全球和区域同化预报多尺度统一模式(GRAPES)采用了SISL时间积分方案,其轨迹计算使用Ritche等(1994)方案。模式积分有时会发生计算不稳定,模式同时又在时间积分方案上使用了较大的非中央权重系数处理相关项,这时模式时间积分方案只有一阶精度且对波动有显著的衰减。本研究拟将SETTLS时间积分方案引入GRAPES区域模式拉格朗日轨迹和非线性项的计算,同时对参考大气和线性项进行处理,将线性项的时间离散精度由一阶提高至二阶,并减小对波动的衰减作用。 2 上游点的SETTLS计算方案
按照Hortal(2002)提出的SETTLS,考虑到上游点在拉格朗日轨迹上可以通过求解拉格朗日轨迹方程得到。拉格朗日轨迹方程

为了获得二阶精度的方案,将n+1时刻到达点的位置矢量 R n+1A在上游点附近做泰勒展开,保留二次项

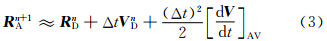
平均加速度可取为
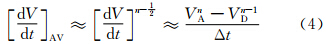
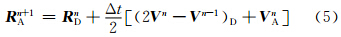
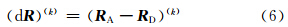
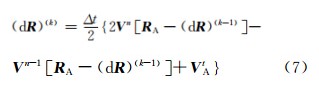
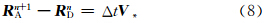
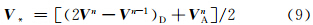
考虑球面上的算法,上游点可由以下迭代方案进行计算
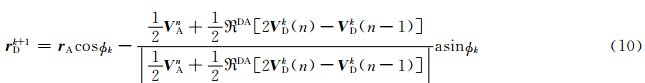
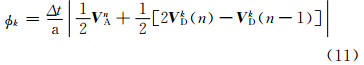
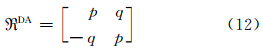
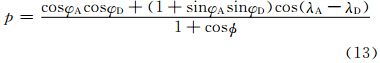
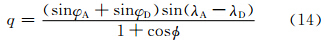
如果φ是小角度近似,则有
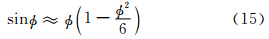
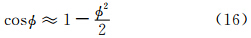
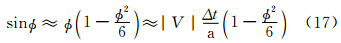
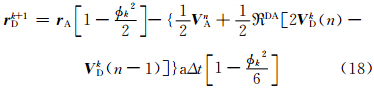
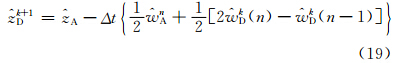
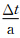 | V nA|,下一步迭代,将(2 V(n)- V(n-1))和(2
| V nA|,下一步迭代,将(2 V(n)- V(n-1))和(2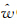 (n)-
(n)-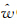 (n-1))插到第1步计算出的D(φ(1)D,λ(1)D,
(n-1))插到第1步计算出的D(φ(1)D,λ(1)D,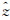 (1)D)点,如此循环,一般进行3次迭代就能够达到收敛精度。
(1)D)点,如此循环,一般进行3次迭代就能够达到收敛精度。
可将 V (u,v)写为一般形式  V nA+
V nA+  [2 VDk(n)- V kD(n-1)]。模式实际计算中是将矢量写成分量形式
[2 VDk(n)- V kD(n-1)]。模式实际计算中是将矢量写成分量形式
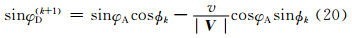
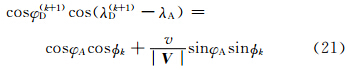
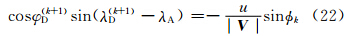
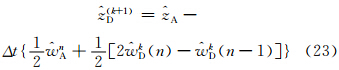
目前GRAPES区域模式的SISL时间积分方案为
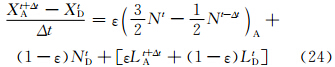
如上所述,SISL时间积分方案中对线性项采取的是隐式处理,这样可以抑制快波项对时间步长的限制,使得SISL时间积分方案无条件稳定,但对非线性项仍然需要进行时间外插,因此,可将稳定外插方案SETTLS用于非线性项的计算。同时为了构建二阶精度的SISL时间积分方案,减小衰减作用,拟对线性项进行二阶精度非中央权重计算。
二时间层SISL方案的一般离散形式为
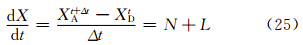
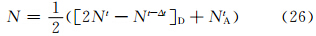
Simmons等(1997)根据稳定性分析提出了一种线性项的二阶精度非中央权重计算方案,将该方案应用于线性项,则有

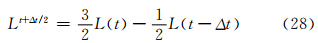
在采用半隐式时间积分方案时,首先须对模式方程使用参考大气廓线进行线性化。一般参考大气可有两种选择,一种为等温大气(Tr=常数),另一种是等熵大气(θr=常数),GRAPES模式取等温大气作为参考大气。
关于等温参考大气的选择,Simmons等(1997)指出,等温参考大气的温度要高于实际大气平均温度才能保证半隐式方案的稳定(中纬度地区的实际平均大气温度一般低于300 K)。Bénard(2003)利用简单的一维浅水波方程分析了二时间层SISL方案中参考大气与模式稳定性的关系,同样得到等温参考大气温度要高于实际平均大气温度才能保持稳定的结论。Temperton等(2001)将线性项的二阶精度非中央权重方案应用于欧洲中期天气预报中心(ECMWF)的二时间层全球预报模式中,其中,等温参考大气取Tr=300 K,ξ取为0.05。本研究参考ECMWF模式,在方案中采用Simmons等(1997)和Bénard(2003)的结论,取高于实际大气平均温度的等温参考大气温度(300 K),以保证模式计算方案的稳定性。
Simmons等(1997)指出,线性项的一阶非中央权重系数与参考大气温度对稳定性具有等同的影响,增加非中央权重系数(即采用一阶非中央权重方案式(24))就不需要取较高的参考大气温度,这可能是GRAPES原SISL时间积分方案可以取较低的等温参考大气(Tr= 257.93 K)的原因。但是较大的非中央权重系数会对低波数波动产生较强的衰减作用。
由于使用SETTLS方案和新的SISL离散形式后上游点的计算方案和时间积分形式均发生了变化,因此,要对标量场和矢量的时间离散形式进行修改。将t时间层表示为n,t+Δt时间层表示为n+1,t+Δt/2时间层为n+1/2,标量场的SISL时间离散形式,对于热力学方程,可写为
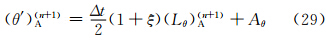
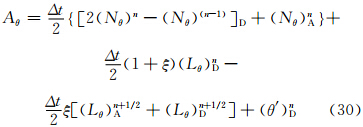
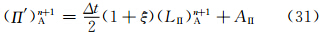
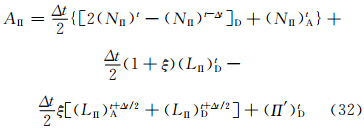
计算上游点采用SETTLS方案后,不需要首先计算上游点与到达点的中间点,而是直接计算出上游点,因此需对矢量场的时间离散形式做一定的修改。设上游点D和到达点A其坐标分别为(λD,φD,zD)和(λA,φA,zA),所对应的局地单位矢量分别为(i *,j *,k *)和(i,j,k),球面上D和A点的单位矢量之间的转换关系为
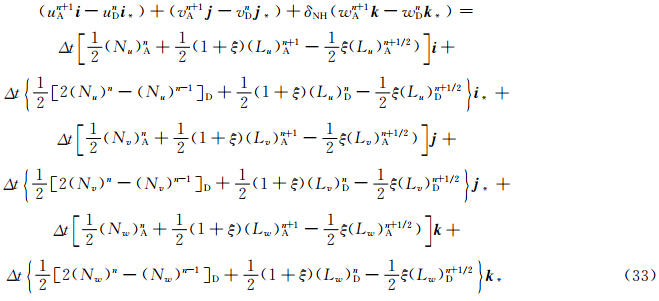
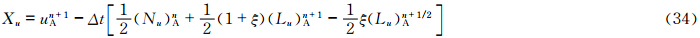
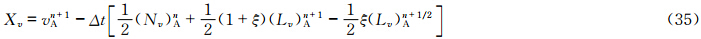
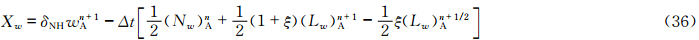
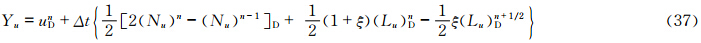
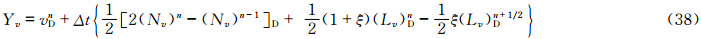
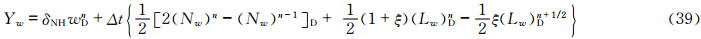
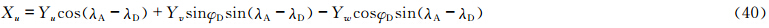
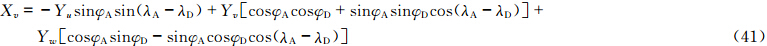
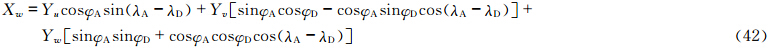
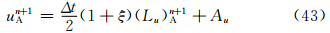
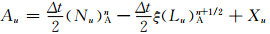

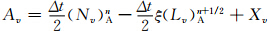
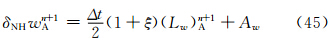

值得注意的是,新SISL的时间离散形式仅改变了赫姆霍兹方程相应的系数,赫姆霍兹方程在形式上并没有发生变化。 4 理想试验 4.1 平衡流试验
对于SISL模式来说,拉格朗日轨迹的计算是整个模式动力框架的基础,关系到平流过程计算的合理性和正确性。由于本研究采用了新的上游点SETTLS计算方案,所以,需进行平衡流试验来验证上游点计算的正确性。参考薛纪善等(2008)设计的平衡流试验,初始水平风分量场u与气压场满足地转平衡关系,并呈平行的东西向的直线,详细的试验设计不再赘述。特别需要指出的是,试验初始场地面气温取为T0=288 K,等温参考大气Tr=300 K,ξ取为0.05。
从新方案积分的结果(图 1)可以看到,模式积分15 d后水平风u(图 1b)仍然保持初始时刻理想场(图 1a)所具有的东西向平行结构,初始场的平行结构不随模式积分时间而改变。对于气压变量场Π同样保持初始场的平行结构而不随时间变化(图略)。平衡流试验的结果表明新的时间积分方案和拉格朗日轨迹计算是稳定和正确的。
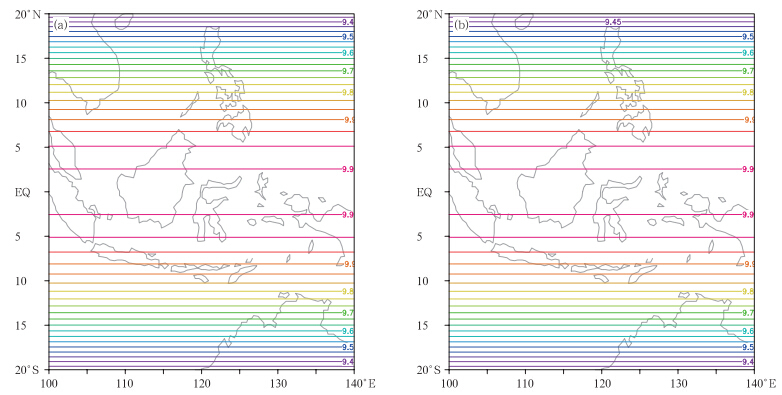 |
| 图 1 GRAPES区域模式平衡流试验u风速分量(m/s)的(a)初始场(t = 0)和(b)积分15 d后的结果(t=15 d)Fig. 1 Zonal wind u(m/s)from the balance flow experiment of the GRAPES model at(a)initial time(t=0) and (b)15 days(t=15 d) |
从平衡流试验全区域内总动能((u2+v2+w2)/2)的时间序列(图 2)可以看出,原SISL时间积分方案的总动能随积分时间而减少,新SISL时间积分方案总能量虽也有很小的增加,但在16 d的积分时间内,总能量大体保持稳定。相比原SISL方案,新SISL时间积分方案总动能没有明显的衰减。可以看出新SISL积分方案有效地抑制了总能量的衰减。
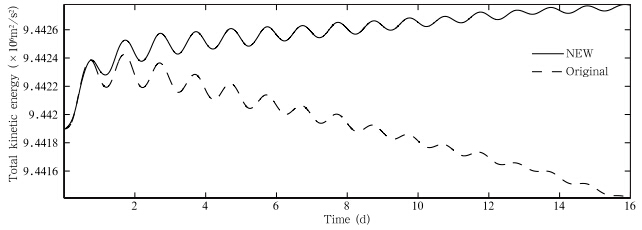 |
| 图 2 平衡流试验全区域内总动能((u2+v2+w2)/2)的时间序列(实线代表新SISL时间积分方案(式(26)、(27),Tr=300 K),虚线为原SISL时间积分方案(式(24),Tr=257.93 K,ε=0.7))Fig. 2 Time series of the total kinetic energy((u2+v2+w2)/2)from the balance flow experiment(Solid line is from the new SISL scheme(equation(26),(27),Tr=300 K),and dashed line from the original SISL scheme(equation(24),Tr=257.93 K,ε=0.7)) |
为了评估新SISL时间积分方案对重力波衰减作用的影响,设计了非静力重力波试验,采用孤立圆形山作为理想地形,地形廓线取为
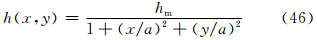
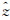 = 400 m,垂直取64层。假定初始时刻大气满足静力平衡关系,过山气流速度u为20 m/s,地面气温取为290 K,浮力频率N=0.01 s-1,原SISL时间积分方案的参考大气温度Tr= 257.93 K,新SISL时间积分方案(式(26)、(27))参考大气取为等温大气Tr= 300 K。在模式顶部4 km对垂直速度进行隐式瑞利衰减(Klemp et al,2008),消除重力波在刚性上边界反射对结果的影响。这时无量纲量Na/u=0.5<1,根据Smith(1980)线性理论分析,气流经过山体时地形激发的重力波为非静力重力波。非静力重力波的结构特征是垂直倾斜向上传播,而静力重力波结构特征是垂直向上传播。
= 400 m,垂直取64层。假定初始时刻大气满足静力平衡关系,过山气流速度u为20 m/s,地面气温取为290 K,浮力频率N=0.01 s-1,原SISL时间积分方案的参考大气温度Tr= 257.93 K,新SISL时间积分方案(式(26)、(27))参考大气取为等温大气Tr= 300 K。在模式顶部4 km对垂直速度进行隐式瑞利衰减(Klemp et al,2008),消除重力波在刚性上边界反射对结果的影响。这时无量纲量Na/u=0.5<1,根据Smith(1980)线性理论分析,气流经过山体时地形激发的重力波为非静力重力波。非静力重力波的结构特征是垂直倾斜向上传播,而静力重力波结构特征是垂直向上传播。
模式积分2 h后基本平衡,图 3给出了其重力波结构(垂直速度)分布。相比全球非静力模式如Model for Prediction Across Scales(MPAS)、Non-hydrostatic Icosahedral Model(NIM)(见Dynamical Core Model Intercomparison Project,DCMIP,https://earthsystemcog.org/projects/dcmip-2012/)模拟的非静力重力波结果,沿赤道一周大概有10个模左右闭合重力波数。本研究的GRAPES是有限区域模式,未使用周期边界条件,采用新SISL时间积分方案(式(26)、(27))后,闭合重力波数同样有10个左右(图 3b),且在下游重力波呈明显的垂直倾斜结构,表现出了更多非静力重力波分量,这些特征均与全球非静力模式(如NIM,MPAS)的结果相近。而原GRAPES模式采用的SISL时间积分方案(式(24)),由于非中央权重系数ε=0.7,对重力波有较强的衰减作用,闭合重力波数明显减少,垂直倾斜度也明显减小(图 3a),波动在下游被逐渐衰减,非静力重力波的分量并不明显,且总体上波动振幅明显弱于新SISL时间积分方案。
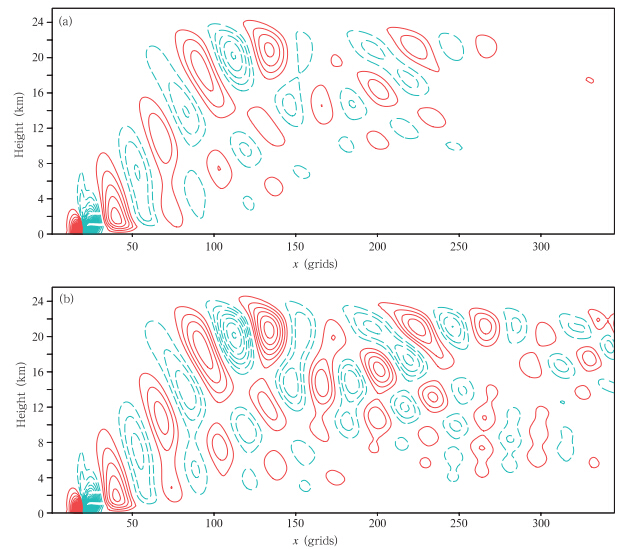 |
| 图 3 积分2 h后非静力重力波试验垂直速度场的垂直剖面(a.GRAPES原SISL时间积分方案(式(24),其中ε=0.7),b.新SISL时间积分方案(式(26)、(27));实线表示垂直向上的速度,虚线表示垂直向下的速度;等值线间隔为0.008 m/s)Fig. 3 Vertical cross section of vertical velocity from the non-hydrostatic gravity wave experiment after 2 h integration:(a)original SISL scheme(equation(24)),and (b)new SISL scheme(equation(26),(27))(Contour interval is 0.008 m/s,the downward(upward)motion is shown in dashed(solid)line) |
同样的结果亦可从垂直速度的水平分布上看出(图 4),新SISL时间积分方案的重力波垂直速度扰动一直传播至格点340(图 4b),而原SISL方案垂直速度的扰动仅传播至格点250附近(图 4a)。
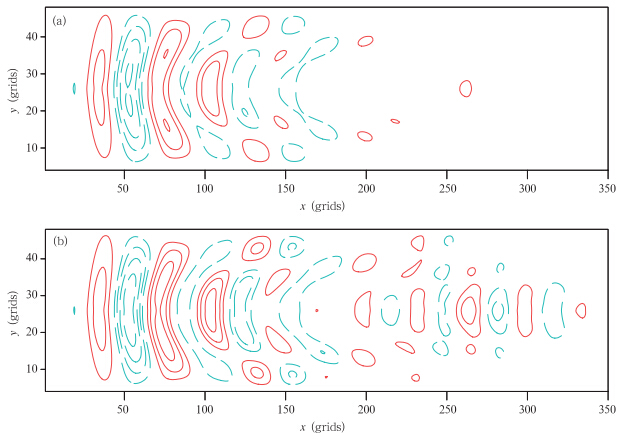 |
| 图 4 积分2 h后非静力重力波试验8000 m高度上的垂直速度场(a.GRAPES原 SISL时间积分方案(式(24),其中ε=0.7),b.新SISL时间积分方案(式(26,27))实线表示垂直向上的速度,虚线表示垂直向下的速度,等值线间隔为0.006 m/s)Fig. 4 Horizontal distribution of vertical velocity at the height of 8000 m from the non-hydrostatic gravity wave experiment after 2 h integration:(a)original SISL scheme(24),and (b)new SISL scheme(26,27).(Contour interval is 0.006 m/s,and downward(upward)motion is shown in dashed(solid)line) |
将两时间层稳定外插方案(SETTLS)引入GRAPES区域模式,并将其用于计算上游点和非线性项的时间外插计算,计算精度均为二阶。使用SETTLS方案计算上游点时,可直接计算出上游点的位置,而无需先计算出中间点。同时对于线性项采用了二阶精度的非中央权重计算方案,通过平衡流和非静力重力波等理想试验对新SISL时间积分方案进行评估,并与GRAPES原 SISL时间积分方案进行比较,得到如下结论:
(1)对线性项采用二阶精度的计算,要求等温参考大气温度必须大于实际大气温度,才能保证半隐式时间积分方案的稳定性。
(2)线性项的一阶非中央权重平均虽然对参考大气的温度没有要求(不要求取高于实际平均大气温度的参考大气),但较大的非中央权重系数对低波数波动具有较强的衰减作用。对线性项采用二阶精度的非中央权重计算方案,同时取较高的参考大气温度(一般取为300 K),使得线性项的计算具有二阶精度,对重力波的衰减明显减弱。
对于式(4)中ξ的选取,一系列的平衡流敏感性试验结果表明,在积分25 d以后选择较大的ξ能够增加模式的稳定性,但在短期天气预报中(一周以内)的选取对结果并无太大的影响,因此,对于一周以内的天气预报而言,倾向于取较小的ξ值,如0.05或0.1。
以上的结果均基于理想试验,在真实大气数值模式中尤其在应用于GRAPES区域模式后的预报效果需要做进一步的检验。
| 薛纪善, 陈德辉. 2008. 数值预报系统GRAPES的科学设计与应用. 北京: 科学出版社, 383pp. Xue J S, Chen D H. 2008. Scientific Design and Application of GRAPES. Beijing: Science Press, 383pp (in Chinese) |
| Bates J R, Moorthi S, Higgins R W. 1993. A global multilevel atmospheric model using a vector semi-Lagrangian finite-difference scheme. Part Ⅰ: Adiabatic formulation. Mon Wea Rev, 121(1): 244-263 |
| Bénard P. 2003. Stability of semi-implicit and iterative centered-implicit time discretizations for various equation systems used in NWP. Mon Wea Rev, 131(10): 2479-2491 |
| Côté J, Gravel S, Staniforth A. 1995. A generalized family of schemes that eliminate the spurious resonant response of semi-Lagrangian schemes to orographic forcing. Mon Wea Rev, 123(12): 3605-3613 |
| Durran D R. 1999. Numerical Methods for Wave Equations in Geophysical Fluid Dynamics. New York: Springer-Verlag |
| Durran D R, Reinecke P A. 2004. Instability in a class of explicit two-time-level semi-Lagrangian schemes. Quart J Roy Meteor Soc, 130(596): 365-369 |
| Gravel S, Staniforth A, Côté J. 1993. A stability analysis of a family of baroclinic semi-Lagrangian forecast models. Mon Wea Rev, 121(3): 815-824 |
| Hortal M. 2002. The development and testing of a new two-time-level semi-Lagrangian scheme (SETTLS) in the ECMWF forecast model. Quart J Roy Meteor Soc, 128(583): 1671-1687 |
| Klemp J B, Dudhia J, Hassiotis A D. 2008. An upper gravity-wave absorbing layer for NWP applications. Mon Wea Rev, 136(10): 3987-4004 |
| McDonald A, Haugen J E. 1993. A two time-level, three-dimensional, semi-Lagrangian, semi-implicit, limited-area gridpoint model of the primitive equations. Part Ⅱ: Extension to hybrid vertical coordinates. Mon Wea Rev, 121(7): 2077-2087 |
| Ritche H, Beaudoin C. 1994. Approximations and sensitivity experiments with a baroclinic semi-Lagrangian spectral model. Mon Wea Rev, 122(10): 2391-2399 |
| Rivest C, Staniforth A, Robert A. 1994. Spurious resonant response of semi-Lagrangian discretizations to orographic forcing: Diagnosis and solution. Mon Wea Rev, 122(2): 366-376 |
| Robert A, Henderson J, Turnbull C. 1972. An implicit time integration scheme for baroclinic models of the atmosphere. Mon Wea Rev, 100(5): 329-335 |
| Simmons A J, Hoskins B J, Burridge D M. 1978. Stability of the semi-implicit method of time integration. Mon Wea Rev, 106(3): 405-412 |
| Simmons A J, Temperton C. 1997. Stability of a two-time-level semi-implicit integration scheme for gravity wave motion. Mon Wea Rev, 125(4): 600-615 |
| Smith R B. 1980. Linear theory of stratified hydrostatic flow past an isolated mountain. Tellus, 32(4): 348-364 |
| Staniforth A, Côté J. 1991. Semi-Lagrangian integration schemes for atmospheric models-A review. Mon Wea Rev, 119(9): 2206-2223 |
| Temperton C, Hortal M, Simmons A J. 2001. A two-time-level semi-Lagrangian global spectral model. Quart J Roy Meteor Soc, 127(571): 111-127 |
 2015, Vol. 73
2015, Vol. 73


