中国气象学会主办。
文章信息
- 袁招洪. 2015.
- YUAN Zhaohong. 2015.
- 不同分辨率和微物理方案对飑线阵风锋模拟的影响
- Study of the influence of the different horizontal resolutions and microphysical setups on the idealized simulation of a squall line
- 气象学报,73(4):648-666
- Acta Meteorologica Sinica, 73(4): 648-666.
- http://dx.doi.org/10.11676/qxxb2015.049
-
文章历史
- 收稿日期:2014-06-19
- 改回日期:2015-03-19
阵风锋是对流风暴中的下沉气流到达地面形成冷堆,并向四周扩展流出在风暴移动方向形成强风的前沿(张培昌等,2001),其产生的地面强风常常造成重大人员伤亡和财产损失。阵风锋常与飑线存在相互作用和影响,特别是飑线产生的阵风锋具有突发性、局地性、强度大、持续时间短等特点,因此,研究阵风锋对日常天气预报和气象防灾、减灾有重要意义。
利用数值预报模式模拟飑线系统是阵风锋日常预报和研究的重要手段。近年来,已有许多利用数值模式成功模拟飑线过程的个例,如慕熙昱等(2007)利用MM5模式模拟了2003年4月12日一次飑线过程,并发现飑线内存在中涡旋族的现象。夏文梅等(2011)利用ARPS模式对2006年6月29日发生在南京的一次飑线过程进行了数值模拟,成功地模拟出雷暴单体前侧的下沉出流、冷出流与环境气流形成的辐合上升气流,以及辐合上升气流处对应阵风锋发生的位置。沈杭锋等(2010a)使用WRF(Weather Research and Forecasting)模式模拟了2006年6月10日严重影响浙江的一次强飑线演变过程,分析了浙江沿海中尺度辐合线和阵风锋相互作用对飑线爆发的作用。在提高模式模拟飑线能力方面也取得了明显的研究进展。张入财等(2009)研究表明,地面资料同化能提高模式对飑线的模拟效果。沈杭锋等(2010b)开展了应用云迹风资料同化的江南飑线模拟试验,认为云迹风资料的使用能使模式模拟的主降水强度和落区与实际降水分布更加接近,大风预报质量也能得到改善。肖现等(2013)基于雷达资料四维变分同化技术成功模拟和分析了北京地区一次下山突发性增强风暴的热动力机制,并分析了阵风锋在风暴发生过程中的作用。陈明轩等(2012)利用变分多普勒雷达分析系统(VDRAS)对2009年7月23日发生在华北的一次飑线也进行了成功的模拟,分析了低层环境垂直风切变与冷池在飑线发展和维持中的相互作用机制。此外,张进等(2008)进行了启动对流的初始扰动对热带飑线模拟的影响研究,结果表明,初始扰动的结构、形态分布及其与环境场的不同配置对具有深对流的飑线生命史存在重要影响。然而,正如Bryan等(2012)研究所指出的,飑线过程的数值模拟对模式分辨率和微物理方案很敏感。一般认为,模式水平分辨率达到1 km就能有效模拟出深的湿对流系统,但Bryan等(2003)通过比较分辨率为1 km、0.5 km、250 m、150 m的模拟结果认为,1 km分辨率所模拟的飑线与更高分辨率模拟的飑线的结构和发展并不相同。随分辨率的提高,模式模拟的降水量、系统移动速度、云厚、雷暴单体的大小等也随之增大。Weisman等(1997)利用不同分辨率模式进行了准三维飑线数值模拟,发现4 km分辨率能模拟出1 km分辨率所能模拟出飑线的大部分特征。粗分辨率模式模拟的飑线发展慢,但成熟时飑线的环流特征要强于1 km分辨率模式模拟的结果,并且发现粗分辨率模式模拟飑线发展慢的原因主要是由于冷池加强滞后了。因此,对由飑线产生的阵风锋的模拟需要关注模式分辨率的影响。
微物理方案是飑线模拟研究关注的另一个重点。目前,业务数值预报模式通常采用的整体微物理方案可以分为一阶矩和多阶矩两种类型。一阶矩微物理方案仅预报水凝物的混合比,而二阶矩微物理方案不仅预报水凝物的混合比,还预报水凝物的数浓度。尽管多阶矩微物理方案需要花费更多的计算资源,但这是业务模式发展的趋势。因此,已有很多研究关注一阶矩与多阶矩微物理方案的区别,如Morrison等(2009)利用WRF二维模式进行了飑线理想试验,研究发现,由于蒸发小的原因,二阶矩方案比一阶矩方案在飑线的层云区域产生更多的降水。Dawson等(2010)对一次龙卷过程进行了模拟,与一阶矩微物理方案相比,尽管多阶矩微物理方案模拟的冷池更小、更弱,但与实际观测更为接近,模拟的反射率因子结构也更加合理。对于不同的二阶矩微物理方案对飑线模拟的影响,Morrison等(2011)进行了WRF理想模式中Morrison和Milbr and t二阶矩微物理方案比较试验,结果表明,Morrison二阶矩方案产生更高的地面降水率,产生的冷池也更强。董昊等(2012)对不同云微物理参数化方案做了对比研究,分析云凝结核浓度对WRF模式模拟飑线降水的影响。总体来说,目前的研究主要集中在飑线整体结构的模拟和分析比较方面,对模式的不同分辨率、不同的微物理方案对飑线阵风锋模拟及其增强作用机制的影响研究尚少。
本研究以2009年6月5日发生的一次飑线过程为试验对象,选用WRF模式为试验模式,研究模式不同分辨率、不同微物理过程对飑线产生阵风锋的模拟差异,重点探讨WRF模式不同试验方案对飑线结构、冷池、冷池前沿最大风速、雨水蒸发率和飑线发展维持机制等方面的模拟差异,并与多普勒天气雷达和地面自动站观测资料进行比较分析,评估各试验方案对飑线阵风锋的模拟能力,为业务数值预报模式模拟飑线阵风锋采用何种水平分辨率和微物理方案的选择提供依据。
2 天气过程描述2009年6月5日发生在长三角地区的天气过程是一次典型的飑线过程。系统发生前,东北地区有一冷性低涡维持,其西南侧不断有冷平流从华北向华东东部输送。该飑线过程是在东北冷涡后部的高空强冷平流与低空暖平流形成的强不稳定层结的背景下产生的,其发生、发展在暖区中,经过由“热岛效应”和海陆风锋共同形成的低空辐合线时明显加强发展(戴建华等,2012)。5日下午先后影响江苏、上海,出现了强降水、雷电、大风、龙卷和冰雹天气。该系统影响上海期间,降下了上海多年罕见的大冰雹,其中,徐家汇冰雹直径25—30 mm(15时35分,北京时,下同),大部分地区出现了超过8级的大风,局部达10级。此次飑线过程给上海造成了较严重影响:部分路段交通出现拥堵,30余航班受影响,轮渡停航,浦东一塔吊倒塌,多处工棚和两处简陋房屋阳台倒塌,多辆轿车被冰雹砸坏,有市民因冰雹击中受伤。
图 1为2009年6月5日14时上海宝山站探空曲线。该探空站位于飑线东南方约50 km,探空在飑线到达前2 h施放。因此,该探空曲线可代表飑线的环境大气层结状况。由探空资料计算可得,SI指数-3.9℃,K指数38.4℃,对流有效位能(CAPE)1165 J/kg,对流抑制能量(CIN)为-211 J/kg,自由对流高度748 hPa,抬升凝结高度826 hPa,对流温度为31.4℃。因此,大气层结处于不稳定的状态,有利于对流的发生、发展,特别是在500—400 hPa明显存在西北急流并伴有相对湿度较低的干层。该干层由东北冷涡后部的高空强冷平流产生,这种上干下湿的配置和中高空的急流有利于强对流天气的发生和维持。
 |
| 图 1 2009年6月5日14时上海宝山站探空曲线Fig. 1 Sounding profile from Baoshan station at 14:00 BT 5 June 2009 |
本理想试验选用由美国国家大气研究中心(NCAR)开发的完全可压缩、非静力、三维中尺度模式WRF-ARW(V3.4)(Skamarock et al,2007)作为试验模式。WRF模式将理想模式技术与实时业务模式技术融合,使得理想模式采用实时业务模式的框架,有更多的物理过程方案可以选择,也使模拟的结果与实际模拟更加接近,更有利于将理想试验的研究成果应用于实时业务模式。
试验模式采用无积云对流参数化方案,微物理方案选用Morrison方案(Morrison et al,2009),水平和垂直湍流扩散采用1.5阶湍流动能方案(TKE)(Skamarock et al,2007)。水平和垂直平流分别采用5阶和3阶离散方案,上下边界垂直速度为0。侧边界条件采用周期边界,模式顶高度为20 km,垂直51层,垂直分辨率为400 m。文中所有模拟试验的积分步长5 s。为简化起见,地面通量设置为0,同时忽略了长波和短波辐射传输过程。
3.2 试验方案设计采用2009年6月5日14时上海宝山站探空资料作为输入探空(图 1),构建水平均匀的三维初始场。在模式初始场中加入水平半径15 km、垂直1.5 km、扰动位温4 K的暖泡以触发对流。为了试验不同的模式水平分辨率和微物理方案对飑线阵风锋模拟的影响,试验中选用3、1和0.5 km共3种水平分辨率和Morrison方案(Morrison et al,2009),分别进行一、二阶矩微物理参数化方案模拟试验(表 1)。
| 名称 | 模式描述 |
| 3 km-sm | 水平分辨率3 km,一阶矩微物理方案,格点400×400 |
| 3 km-dm | 水平分辨率3 km,二阶矩微物理方案,格点400×400 |
| 1 km-sm | 水平分辨率1 km,一阶矩微物理方案,格点800×800 |
| 1 km-dm | 水平分辨率1 km,二阶矩微物理方案,格点800×800 |
| 0.5 km-sm | 水平分辨率0.5 km,一阶矩微物理方案,格点950×950 |
| 0.5 km-dm | 水平分辨率0.5 km,二阶矩微物理方案,格点950×950 |
采用的二阶矩整体云微物理方案能预报5种水凝物:云水、云冰、雪、雨水、软雹或冰雹。该方案由Morrison等(2005)开发,移植入WRF模式并进行了改进。水凝物的体积分布N(D)可由Γ函数表示
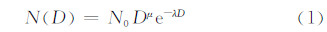
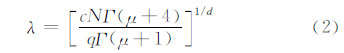
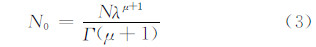
一阶矩微物理方案中除降水(雨水、雪、软雹)的数密度由诊断而不是预报得到外,方案的其他方面与二阶矩微物理方案完全一致。这样,雨水、雪、软雹的N0设为常数,N、λ由式(1)、(2)计算得到。对于不同的一阶矩微物理方案,N0的取值略有不同。有一些微物理方案中N0的取值随模式预报量的变化而变化,如在WRF模式的WSM3、WSM5、WSM6等方案中N0就随雪预报量值的大小而改变。文中,雪、雨水、软雹对应的N0取值分别为2.0×107、1.0×107、4.0×106m-4。
5 结果分析5.1 模拟飑线的结构与移速 5.1.1 飑线结构试验结果表明,3种水平分辨率模式都能模拟出飑线的弓状特征(图 2),但由于模式水平分辨率不同,模拟飑线细微结构的能力存在差异。很明显,0.5和1 km分辨率比3 km分辨率能更仔细刻画出飑线的结构,前者能分辨出弓状回波前沿细小的回波单体,后者则连成了一片而无法分辨出独立的回波小单体。特别是3 km分辨率的试验,模式积分6 h后,回波前沿与回波主体出现了“分离”。0.5和1 km分辨率模拟飑线的弓状形态基本一致,但模拟的飑线在细微结构上却存在一些差异,如0.5 km分辨率模式模拟的回波前沿中的小单体比1 km更精细,1 km分辨率模式模拟的回波前沿小单体回波的强度要大于0.5 km分辨率模式的模拟结果,此外,弓状回波后部强回波的分布也存在不同。这说明模式的分辨率不仅对模式模拟飑线的形态有影响,对飑线细微结构的描述也存在差异。
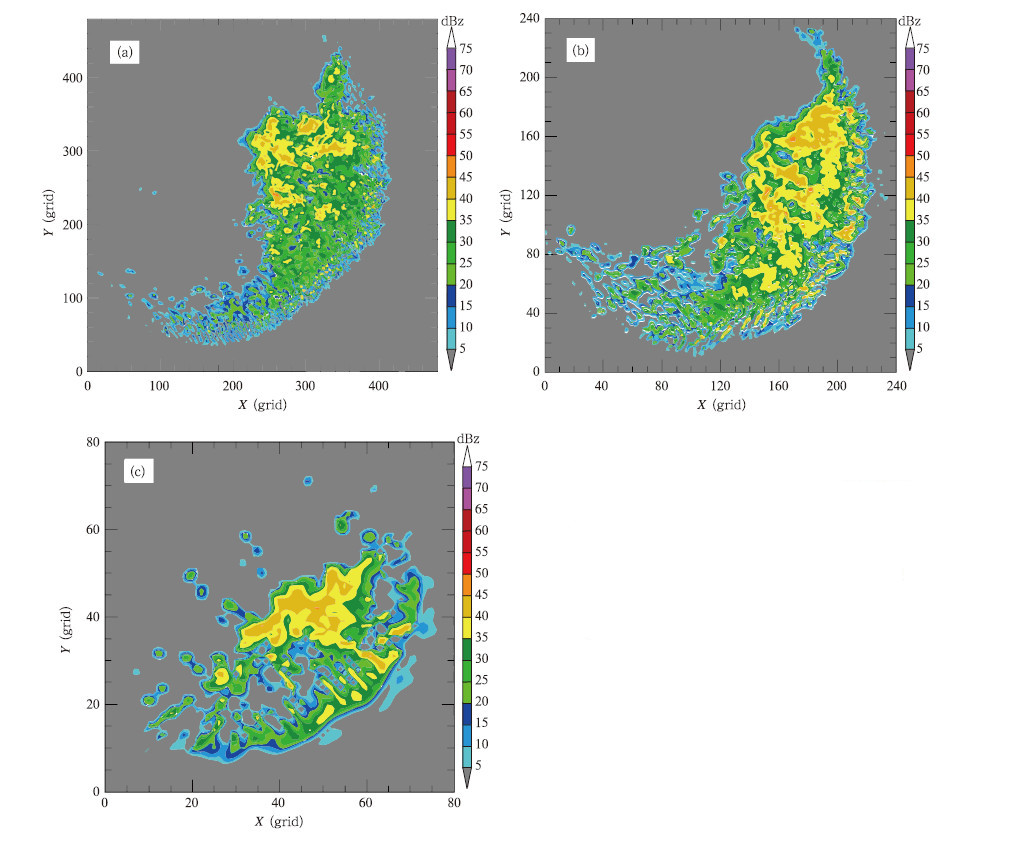 |
| 图 2 3种水平分辨率一阶矩微物理方案模式积分 6 h模拟的2 km高度的雷达反射率因子(a.0.5 km,b.1 km,c.3 km)Fig. 2 2 km CAPPI ( constant altitude plan position indicator) of the reflectivity simulated by (a) 0.5 km, (b) 1 km and (c) 3 km at the 6 h prediction |
不同微物理方案对飑线结构的模拟也存在差异。图 3为1 km分辨率模式分别选用一、二阶矩微物理方案,模式积分10 h模拟的雷达反射率因子水平和垂直剖面,其中,模拟的雷达反射率因子剖面为沿图 3a、b中红线按弓状回波走向左右各50 km雷达反射率因子的平均值。可以看出,1 km分辨率模式一、二阶矩微物理方案均很好地模拟出了飑线的弓状回波特征。二阶矩微物理方案模拟出了飑线弓状回波前部强回波区域、后部弱回波区的特征,且回波强度变化比较连续。一阶矩微物理方案尽管模拟出了弓状回波特征,却没能模拟出弓状回波前沿回波强、后部回波弱的特征,且模拟的雷达回波结构相对松散。这与Houze等(1990)、 Morrison等(2009)、Bryan等(2012)的模拟结果一致。由图 3c、d也可以发现同样的现象,即二阶矩微物理方案模拟的弓状回波前部强、后部弱,强回波区到后部弱回波区是逐步过渡的,而一阶矩微物理方案却模拟不出这种强弱回波连续过渡的特征。出现这种现象的原因可能是因为一阶矩微物理方案软雹、雪、雨水的截断参数N0值是固定值,即模式模拟飑线中的软雹区、雪区、雨水区之间N0值是跳跃的,而不是连续的,这使得一阶矩微物理方案模拟的软雹区、雪区、雨水区之间存在不连续,从而导致了一阶矩微物理方案不能很好模拟出飑线弓状回波前部回波强、后部回波弱的特征。
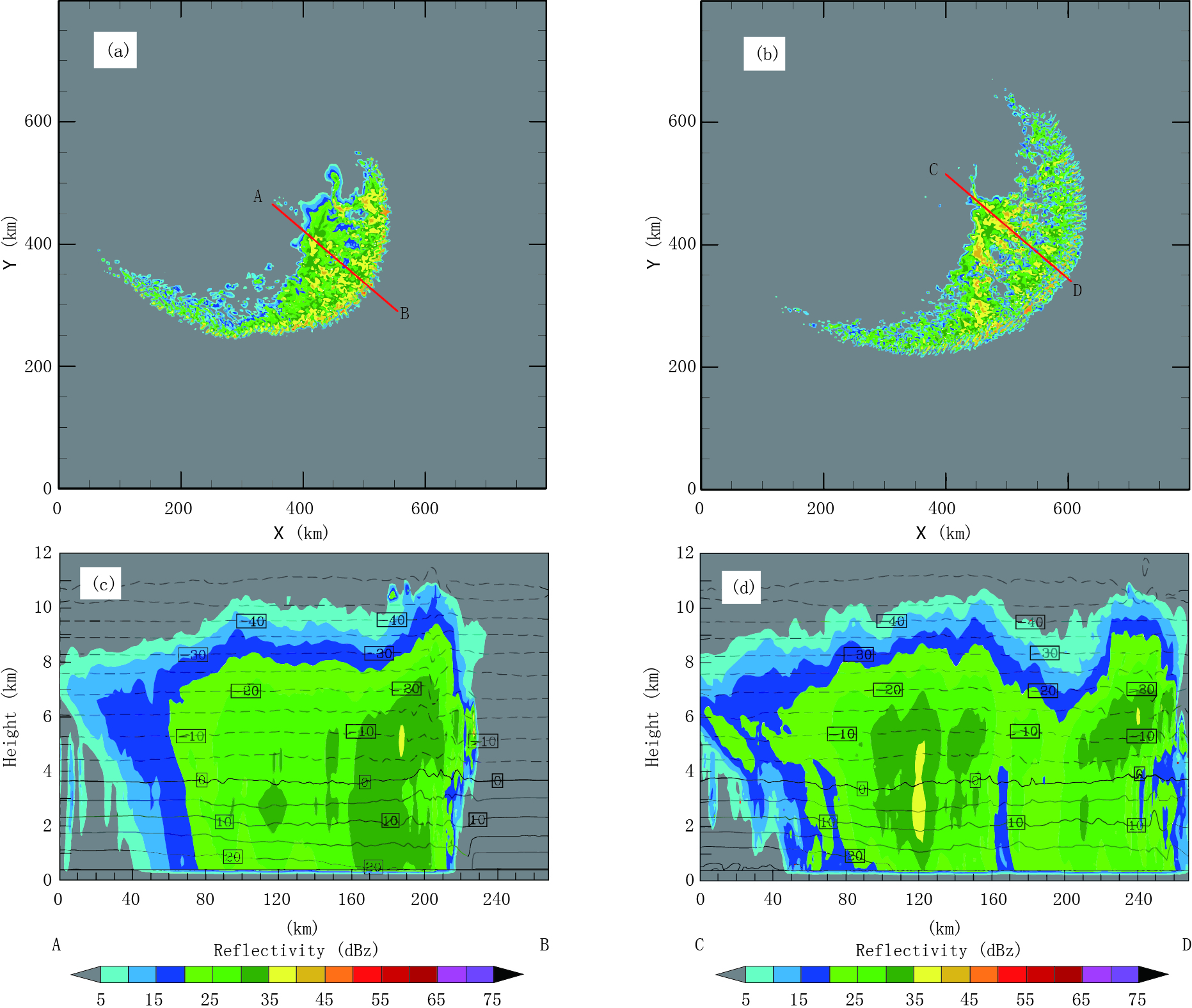 |
| 图 3 1 km分辨率模式积分10 h时模拟的雷达反射率因子水平和垂直剖面 (a.1 km-dm 方案2 km高度(二阶矩微物理),b.1 km-sm方案2 km高度(一阶矩微物理), c.沿(a)中红线AB剖面,d.沿(b)红线CD剖面)Fig. 3 Line-averaged cross sections of the reflectivity simulated by (a) 1 km-dm (2 km CAPPI) and (b) 1 km-sm (2 km CAPPI) at the 10 h prediction. Cross sections (c) and (d) are made along red lines in (a) and (b), respectively |
由图 3c、d还可以看到,一、二阶矩微物理方案模拟的平均雷达回波强度也存在差异。二阶矩微物理方案弓状回波前部4—6 km高度处平均反射率因子强度大于35 dBz,并且在0℃线以下,平均反射率因子最大值也达到35 dBz。与之对应的一阶矩微物理方案模拟的平均反射率因子明显较弱,而在弓状回波的后部区域,其平均回波范围和强度要大于二阶矩微物理方案。0.5 km分辨率模式模拟的结果与1 km分辨率模式类似(图略)。3 km分辨率模式能模拟出飑线前部弓状特征,但无论是一阶矩还是二阶矩微物理方案都不能模拟出飑线弓状回波前部回波强、后部弱的特征,并且回波整体结构松散(图略)。综上所述,与一阶矩微物理方案相比,二阶矩微物理方案更能模拟出飑线的形态特征。
图 4为2009年6月5日16时14分飑线上海WSR-88D多普勒天气雷达2 km高度的反射率因子等高平面位置显示和反射率因子垂直剖面。可以看出,飑线在雷达反射率因子图上呈现出明显的弓状特征,在弓状回波的前部存在明显的强回波带,其后是相对弱回波区域(图 4a);在雷达反射率因子垂直剖面上也同样反映出了前强后弱的特征(图 4b)。这与典型的飑线雷达回波特征一致。
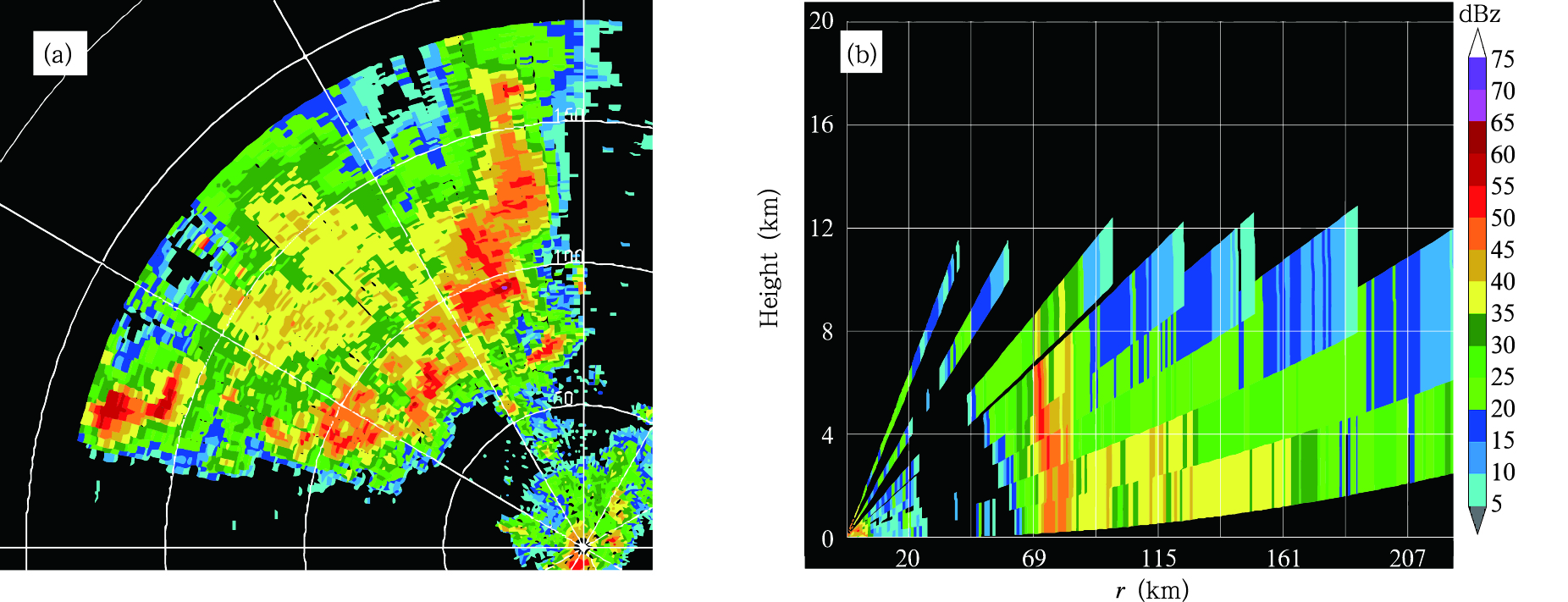 |
| 图 4 2009年6月5日16时14分WSR-88D多普勒天气雷达反射率因子 (a.2 km高度CAPPI,b.垂直剖面,方位角321°)Fig. 4 Reflectivity of WSR-88D at 16:14 BT 5 June 2009 (a. CAPPI at 2 km, b. cross section of the reflectivity at the azimuth angle of 321°) |
比较图 2和4a可以看出,0.5和1 km分辨率模式一阶矩微物理方案模拟的飑线其弓状回波特征明显,结构比较完整,3 km分辨率模式一阶矩微物理方案模拟的飑线结构松散,相比而言,前者模拟的飑线结构与WSR-88D多普勒天气雷达观测的实况更接近。通过比较还可发现,模拟的反射率因子强度与雷达实际探测存在差异。实际探测的飑线弓状回波带上雷达回波强度达55—60 dBz,而模拟的雷达反射率因子最大为40—45 dBz,这说明模拟的雷达反射率因子要弱于雷达实际观测值。比较图 3和4b可以发现,与一阶矩微物理方案相比,1 km分辨率模式二阶矩微物理方案模拟的飑线前强后弱的结构特征与雷达观测更接近,这说明采用二阶矩微物理方案的业务数值预报模式更能模拟出飑线前强后弱的回波特征,并且模式的水平分辨率需达到1 km。
5.1.2 飑线移动速度试验中,模拟的飑线移动速度是由沿其移动方向2 km高度弓状前沿大于20 dBz反射率因子的平均移动距离计算得到的。采用1 h平均移动距离计算飑线的移动速度,即用某时刻前后30 min的模拟飑线的移动距离差来计算该时刻模拟飑线的移动速度。实际观测的飑线移动采用2 km高度CAPPI弓状回波前沿大于20 dBz反射率因子移动30 min移动距离计算得到。
各试验方案模拟和观测的飑线移动速度如图 5所示。可以看出,模拟的飑线在发展过程中移动速度存在变化,在模拟前6 h,移动速度由最初平均35 km/h增至平均67 km/h,其后各试验方案模拟的风暴移动速度趋于基本稳定(图 5a),这表明飑线在发展过程中其移动速度有一个加速的过程。多普勒天气雷达也探测到了飑线移动的加速过程,13时31分—15时31分飑线的移动速度由40.0 km/h增至66.6 km/h(图 5b)。各试验模拟的飑线移动速度存在一定的差异,其中,1 km与0.5 km分辨率模式模拟的飑线速度平均大于3 km分辨率模式模拟的飑线速度,与前两者相比,平均相差约10 km/h。说明模式分辨率对飑线移动速度模拟有影响,低分辨率模式模拟飑线速度要慢于高分辨率模式。这与Bryan等(2003)的研究结果基本一致。此外,在模式模拟过程中,各试验不同时刻飑线移动速度存在“起伏”。分析模拟雷达反射率因子的演变可以发现,在飑线移动的过程中,飑线回波的前沿不断有新的单体生成,而这些新生单体的产生和发展是不连续的,这是导致飑线在不同时刻移动速度存在“起伏”的重要原因。比较图 5a、b可见,与实际雷达观测相比,除0.5 km分辨率模式二阶矩微物理方案外,理想试验没能很好地模拟出实际飑线在移动速度达到最大值后移动变慢的过程。
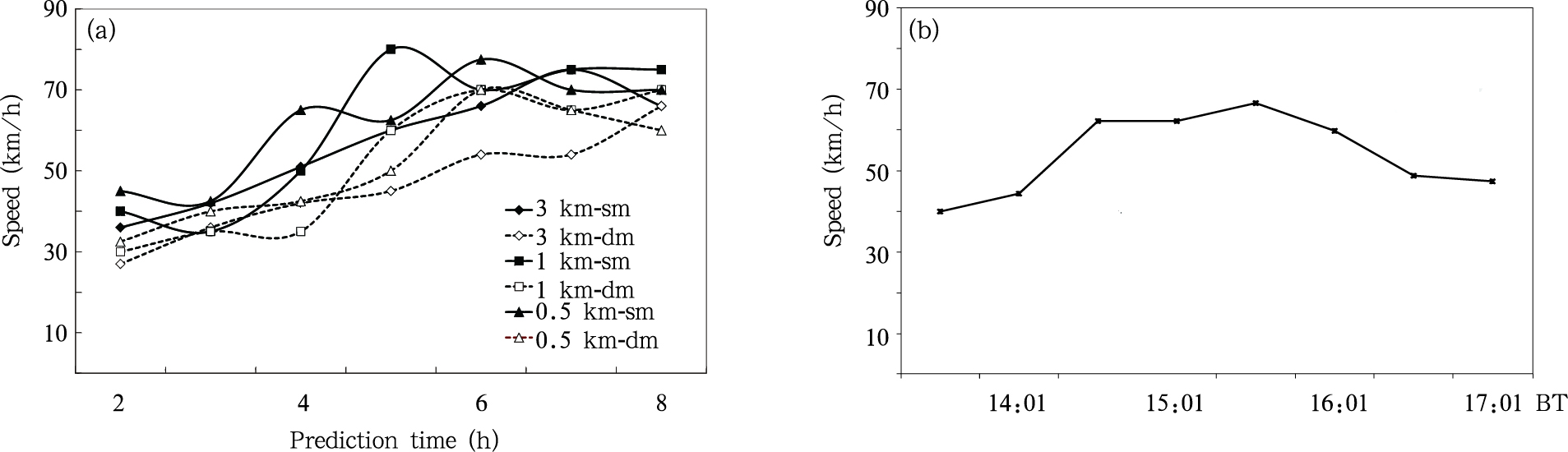 |
| 图 5 各试验模拟和观测的飑线移动速度随时间的变化(a.模拟值, b.观测值)Fig. 5 Time series of the (a) simulated and (b) observed squall line speed of movement |
模拟飑线的移动速度除与模式分辨率有关外,不同的模式微物理方案对模拟飑线的速度也有一定影响。如图 5所示,3、1和0.5 km分辨率模式一、二阶矩微物理方案模拟的飑线移动速度存在差异,其中,一阶矩微物理方案模拟的飑线移动速度总体上要大于二阶矩微物理方案,模式模拟2—8 h飑线的平均速度两者分别相差10.3、8.6、10.3 km/h。表明一阶矩微微物理方案模式模拟飑线的移动速度要快于二阶矩微物理方案。在各试验方案中,1和0.5 km分辨率二阶矩微物理方案模拟的飑线最大移动速度为70.0 km/h,与观测的飑线66.6 km/h最大移动速度较为接近。
5.2 冷 池5.2.1 冷池的面积和强度、冷池是飑线重要的边界层特征,与阵风锋和锋前新生单体密切相关,在飑线的生命史中起关键作用。冷池常常用扰动温度、扰动位温、扰动假相当位温等多种定义来表示。文中采用扰动位温(θ′)低于-1 K作为判定冷池的标准,即θ′≤-1 K。
从各试验模拟的冷池面积随模式积分时间的变化(图 6)可以看出,1和0.5 km分辨率模式均是积分30 min后出现冷池,而3 km分辨率模式在积分40 min后才出现冷池,尽管如此,3 km分辨率模式模拟冷池面积的扩大速度要快于1和0.5 km分辨率模式。这说明粗分辨率模式冷池的出现有滞后现象,但其后的发展速度要快于高分辨率模式,这与Weisman等(1997)的研究结论是一致的。各试验冷池面积随模式积分时间的延长而增大,其中,3 km分辨率模式冷池面积最大,1与0.5 km分辨率模式冷池面积较为接近。模式微物理方案对冷池的面积亦有影响,3种分辨率一阶矩微物理方案模拟的冷池面积要大于二阶矩微物理方案模拟的冷池面积,在模式模拟的3—8 h,3、1和0.5 km分辨率模式二阶矩微物理方案模拟的冷池面积与一阶矩微物理方案模拟冷池的面积比平均分别为63.2%、62.0%和61.3%,说明一阶矩微物理方案模拟的冷池面积要明显大于二阶矩微物理方案模拟的冷池面积,并且微物理方案对模拟冷池面积的影响要大于模式分辨率对其的影响。
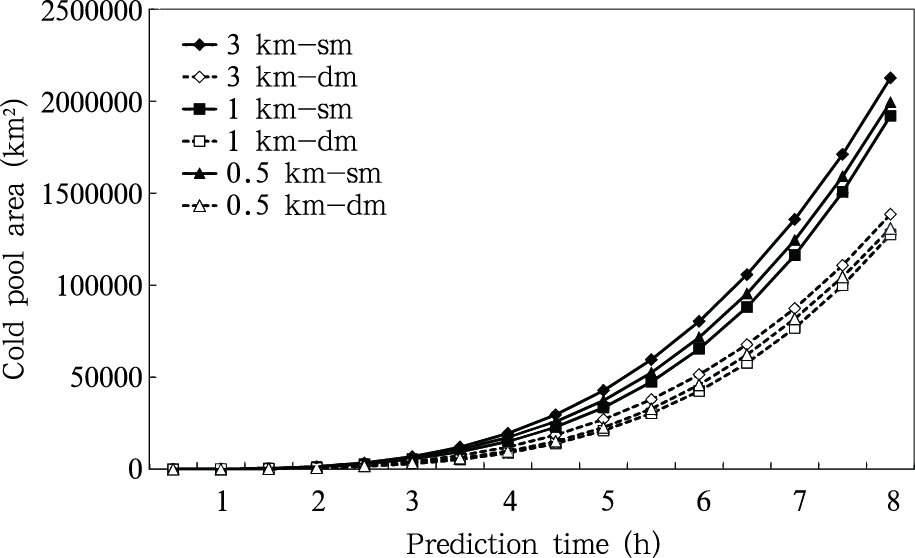 |
| 图 6 各试验模拟的冷池面积随模式积分时间的变化Fig. 6 Time series of the simulated cold pool area |
各试验方案除模拟的冷池面积存在差异外,模拟的冷池强度也不同。文中,冷池强度(C)采用Bryan等(2006)的定义
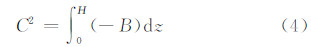
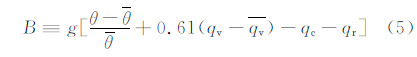
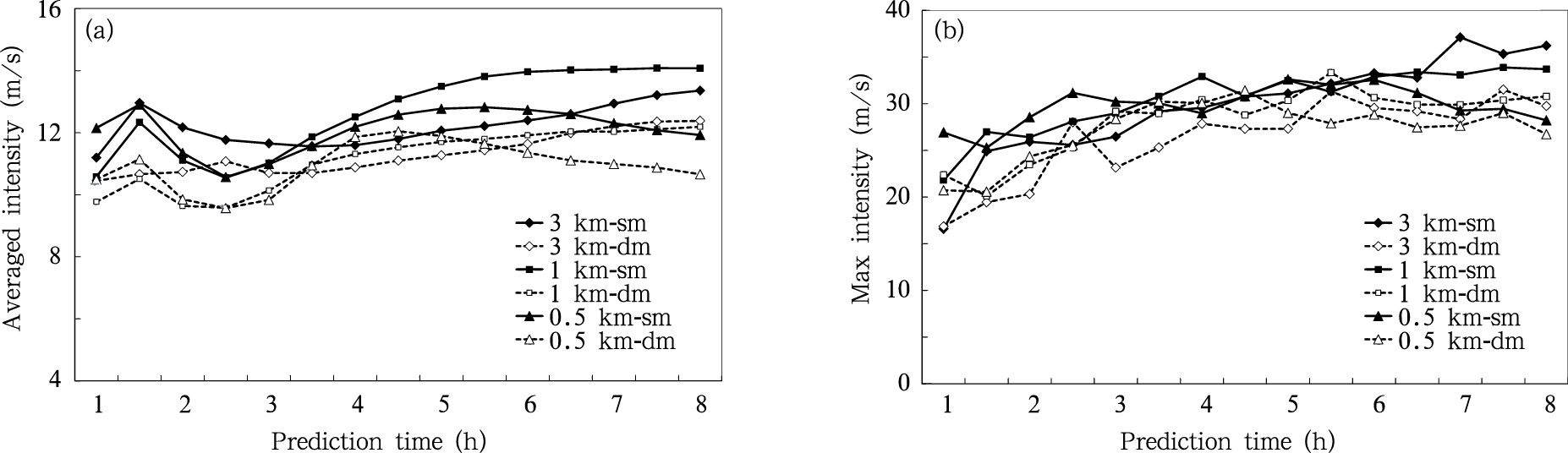 |
| 图 7 冷池(a)平均和(b)最大强度随模式积分时间的演变Fig. 7 Time series of the (a) averaged cold pool intensity and (b) max cold pool intensity |
由图 7a可以看出,各试验方案在模式积分1.5—2.5 h冷池平均强度均有一个减弱的过程,表明模式模拟的初始冷池有一个崩塌的过程。其后,随模式积分时间延长,冷池平均强度逐步增大,在模式积分约4.5 h时,增大的趋势逐步放缓,其中,0.5 km分辨率模式模拟的冷池平均强度还略有减小。产生这种现象的原因与雨水蒸发有直接的关系,后面将做具体分析。尽管平均冷池强度有一个减小再加强的过程,但如图 7b所示,冷池最大强度随模式积分时间却呈现了逐步增大的过程。与冷池平均强度一样,模式分辨率对冷池最大强度的模拟有影响。1 km分辨率模式模拟的冷池平均强度最强,0.5 km分辨率模式在积分6 h后呈现下降趋势,冷池的最大强度也呈现相同的趋势。在模式积分6.5 h后,3 km分辨率一阶矩微物理方案模拟的最大冷池强度大于其他试验方案,这与Bryan等(2012)1 km分辨率模式模拟的冷池面积最大、强度最大的结论不一致。与图 5比较可以发现,冷池强度增强的过程与飑线移动速度加快的过程相对应,这说明冷池增强与飑线移动加速可能有直接的联系,但如何从动力学的角度定量分析两者的关系尚待进一步分析。
通过图 7a还可以看到,一阶矩微物理方案模拟的冷池强度要大于二阶矩微物理方案模拟的冷池强度。在模式积分3.5 h前,无论是一阶矩还是二阶矩微物理方案,3 km分辨率模式模拟的冷池强度均大于1和0.5 km分辨率模式的模拟,其后则相反。尽管模式积分3.5 h前,1和0.5 km分辨率模式模拟的冷池强度基本一致,但其后0.5 km分辨率二阶矩微物理方案模拟的冷池平均强度要大于1 km分辨率二阶矩微物理方案模拟的冷池平均强度,而1 km分辨率模式一阶矩微物理方案模拟的冷池平均强度要大于0.5 km分辨率模式一阶矩微物理方案模拟的冷池平均强度。
5.2.2 冷池的垂直结构各试验方案模式积分3 h时沿飑线移动方向的冷池顶端的垂直剖面如图 8所示,其中,冷池为位温扰动减小超过1 K的区域。可以看出,尽管模拟的反射率因子的高度均在10 km左右,但不同分辨率、不同微物理方案模拟的飑线和冷池的垂直结构存在一定的差异。很明显,除3 km分辨率模式外,二阶矩微物理方案能模拟出飑线前部回波强、后部回波弱的特征。相比而言,0.5和1 km分辨率模式能很好模拟出飑线后部下沉气流和前部的上升气流,并且,0.5 km分辨率模式模拟的飑线前部上升气流要强于1 km分辨率模式,而3 km分辨率模式模拟的飑线无论是其后部下沉气流,还是前部的上升气流均不明显。同样,3 km分辨率模式不能很好地模拟飑线底层完整的冷池结构,而1和0.5 km分辨率模式模拟的冷池垂直结构与经典的冷池结构基本一致,与下沉气流和冷池前部上升气流对应较好。这表明模式分辨率的增加有利于提高模式对飑线的模拟能力,并且模拟出合理的飑线风场垂直结构,模式的分辨率可能需要达到1 km。
 |
| 图 8 各试验方案模式积分3 h时风矢量、反射率因子(dBz,等值线)和位温扰动(K,色阶)的沿飑线
移动方向的冷池顶端的垂直剖面 (a.0.5 km-dm,b.0.5 km-sm,c.1 km-dm, d.1 km-sm,e.3 km-dm, f.3 km-sm)Fig. 8 Vertical cross sections of wind (vector ), reflectivity (dBz, contour) and potential temperature perturbation (K, shaded), simulated by (a) 0.5 km-dm, (b) 0.5 km-sm, (c) 1 km-dm, (d) 1 km-sm, (e) 3 km-dm and (f) 3 km-sm, at the top of the cold pool along the moving direction of the squall line |
由图 8可以看出,一、二阶矩微物理方案模拟的冷池垂直剖面结构有明显的差异,尽管两者模拟的冷池高度基本接近,但在2—3 km,由于模拟的飑线后部下沉气流位置的不同,导致了模拟的冷池强度和范围不同。一阶矩微物理方案模拟的明显下沉气流出现在飑线的后部,中层(3 km以下)冷空气从飑线后部就开始下传至地面,使得在飑线的下方出现了位温扰动的大值区,也即出现了“冷堆”。“冷堆”中的冷空气以密度流的方式向飑线移动的方向扩散,在飑线前方15 km处与暖空气达到平衡,冷空气向上移动,达到2—3 km的高度,并且飑线前方低层出现了垂直环流,从而形成了冷池的“头部”。与一阶矩微物理方案相比,二阶矩方案模拟的明显下沉气流主要集中在飑线的前部,在飑线的底层并没有出现明显的“冷堆”,由于二阶矩微物理方案模拟的冷池相对较弱,飑线底层的冷空气只到达其前方10 km处,前方低层也没明显出现垂直环流。 5.3 冷池的地面特征
图 9为1 km分辨率模式积分6 h时模式底层风场和气压场分布,可见无论是一阶矩还是二阶矩微物理方案,模拟的飑线后部均有风场的辐散区域,在辐散区域与飑线前沿之间存在高压区,飑线移动方向右侧大风区域面积要大于左侧。比较图 9a、b可见,一阶矩微物理方案模拟的高压区域和大风区域面积要大于二阶矩微物理方案,产生这种现象的原因是由于前者模拟的冷池要强于后者。尽管辐散区和高压区的相对位置略有差异,但3和0.5 km分辨率模式模拟的模式底层风场和气压场分布也呈现了同样的特征(图略)。这表明不同的模式分辨率和微物理方案模拟的风场和气压场总体分布特征是一致的。
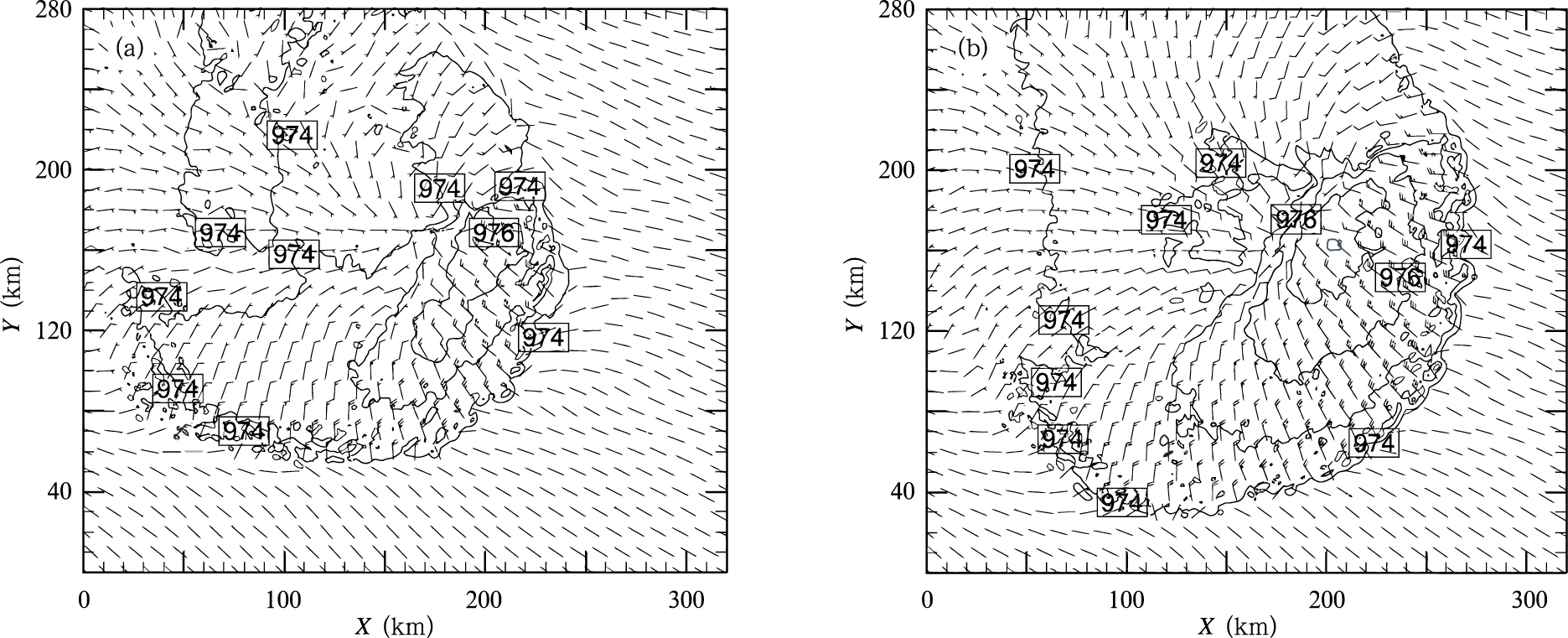 |
| 图 9 1 km分辨率模式积分6 h时模式底层风场(风矢)和气压场(hPa,等值线)分布 (a.1 km-dm,b.1 km-sm)Fig. 9 Surface wind (barbed arrow) and pressure pattern (hPa, contour) output after 6 h integration by (a) 1 km-dm, and (b) 1 km-sm |
图 10为飑线经过上海时地面风场和WSR-88D多普勒天气雷达观测的径向速度场。可以看出,飑线过境上海时,飑线大风主要出现在上海的中南部区域,即飑线移动方向的右侧(图 10a)。随飑线向东南方向移动,17时38分在上海的北部出现地面风场辐散区(图 10b),并且在辐散区与飑线前沿之间出现了高压区域,其中上海浦东站(58370)地面气压最高(图中红色圆圈),为1002.9 hPa。飑线后部低层风场辐散区在位于上海南汇的WSR-88D多普勒天气雷达的径向速度图上也能反映出来(图 10c),尽管飑线已移到海上,强度减弱,但在雷达站东部还存在明显的风场辐散区。比较图 9和10可以看出,模拟的模式底层风场和气压场分布与实际观测基本吻合,说明各试验方案都具备模拟飑线地面风场和气压场分布的能力。
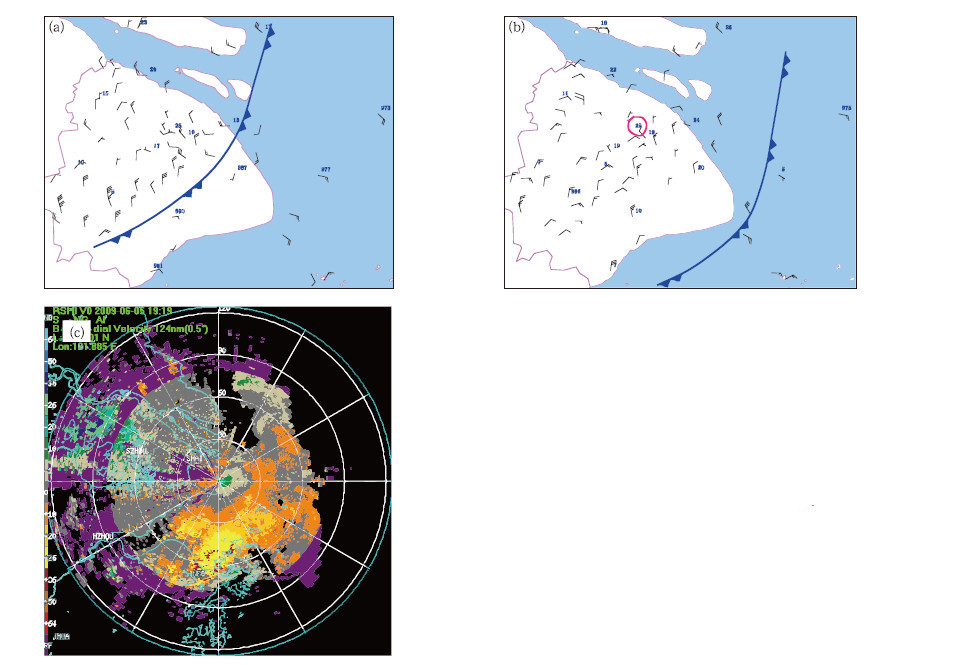 |
| 图 10 飑线经过上海时地面风场的变化
(a.17时地面风场,b. 17时38分地面风场,c.19时19分0.5°仰角雷达径向风速)Fig. 10 Surface wind patterns at (a) 17:00 BT and (b) 17:38 BT with (c) the base radial velocity (0.5°) of WSR-88D at 19:19 BT when the squall line goes across Shanghai |
图 11为各试验方案模式底层气压变化与地面气压变化的时间序列。文中取各试验方案模式积分6 h时模式底层气压最高值所在的格点作为比较点,参考的地面观测站为上海浦东站(58370)。该站是一般气象站,如前所述,飑线经过上海时该站为地面气压最高的测站。可以看出,飑线经过时各试验方案模式底层气压都经历一个上升而后下降的过程,但气压变化的幅度和快慢存在差异。3种分辨率一阶矩微物理方案模拟的最高气压变化要大于二阶矩微物理方案的模拟值,两者平均相差1.03 hPa。二阶矩微物理方案模拟气压变化达到最高值要快于一阶矩微物理方案,其中,0.5 km分辨率模式一阶矩微物理方案最长为90 min,1 km分辨率模式二阶矩微物理方案最短为40 min。与浦东站实际观测相比,各试验方案尽管均模拟出了飑线过境时气压的变化过程,但浦东站在16时40—50分实测气压上升了2.9 hPa,各试验方案模拟的气压上升速度要低于实际观测。此外,飑线过后,模拟的气压下降速度要快于实际观测。相比而言,1 km分辨率模式二阶矩微物理方案气压上升的速度与实际观测较为接近。
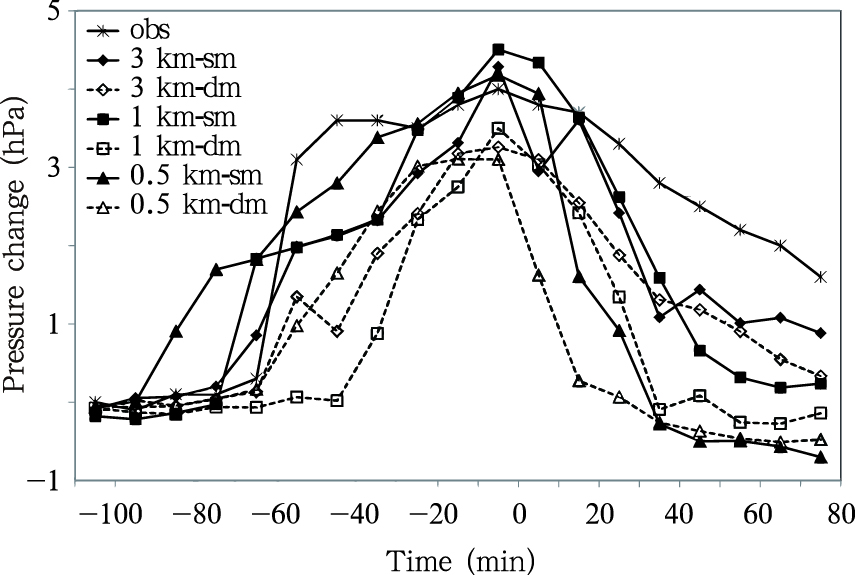 |
| 图 11 各试验方案模拟的模式底层气压变化与实际观测的比较Fig. 11 Time series of the simulated pressure change and observation at Pudong station for the various schemes |
冷池前沿最大风速和模式底层温度扰动随模式积分时间的演变如图 12所示,温度扰动T′=Tt-T0,T下标t为模式积分时间,下标0为模式初始时间。可以看出,冷池前沿最大风速呈现了随模式积分时间延长逐步增大的趋势,特别是在模式积分的前3.5 h,各试验方案模式冷池前沿最大风速增大较快,由平均7.2 m/s迅速增至平均30.8 m/s,其后冷池前沿最大风速增大趋势变缓。在模式积分的1—2 h,一阶矩微物理方案3种分辨率模式模拟的冷池前沿最大风速基本一致,其后随模式积分时间的延长,不同分辨率模式模拟的冷池前沿最大风速出现了差异,其中,1和0.5 km分辨率模式模拟的冷池前沿最大风速要大于3 km分辨率模式模拟的冷池前沿最大风速(图 12a)。模式积分6 h后,1 km分辨率模式一阶矩微物理方案模拟的冷池前沿最大风速最大,这与Bryan等(2012)模式分辨率越高,模式底层最大风速越大的结论存在差异。总体上,一阶矩微物理方案模拟的冷池前沿最大风速要大于二阶矩微物理方案,1 km分辨率模式一、二阶矩微物理方案模拟的冷池前沿最大风速相差最大,模式积分1—8 h平均相差约达到4 m/s。模式底层温度扰动最大值呈现了与冷池前沿最大风速类似的变化趋势,在各试验随模式积分1—5 h,模式底层温度扰动随模式积分时间的延长逐步下降,其后温度扰动最大值的变化趋缓。3种分辨率模式一阶矩微物理方案模拟的模式底层的温度扰动最大值要大于二阶矩微物理方案,模式积分的1—8 h两者平均相差2.4℃(图 12b)。
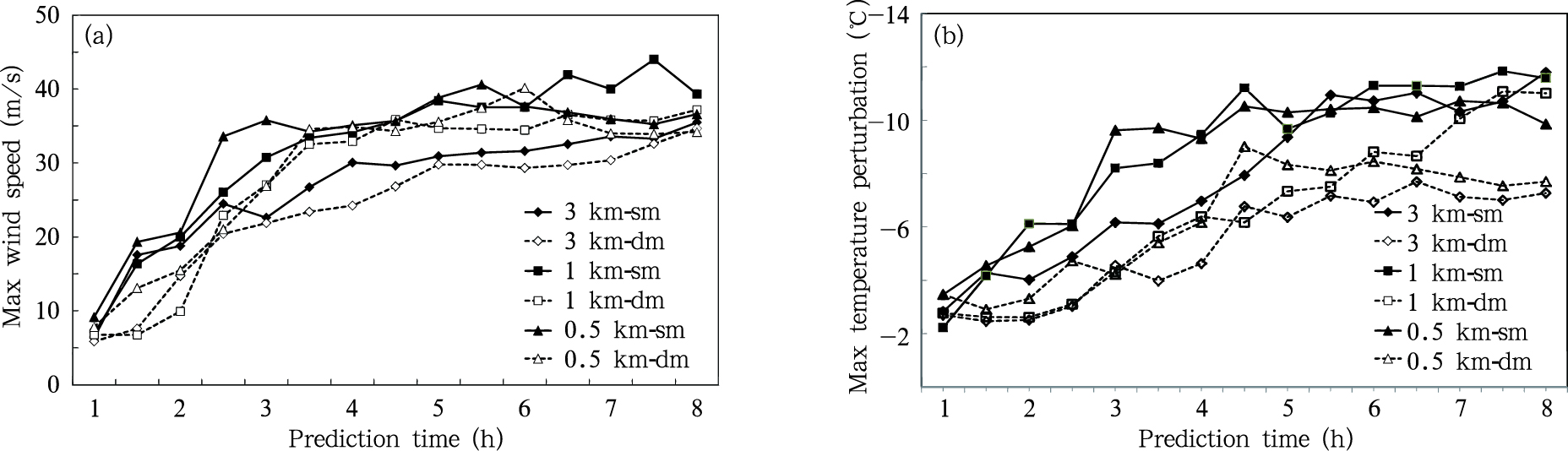 |
| 图 12 各试验方案(a)冷池前沿最大风速和(b)模式底层温度扰动最大值随模式积分时间的演变Fig. 12 Time series of the (a) max velocity in the front of the cold pool and (b) max temperature perturbation at the bottom of model |
与图 5a比较可以发现,冷池前沿最大风速增大及模式底层温度扰动幅度增大,与飑线系统移动加速的时间基本对应,即随飑线移动速度的加快,地面最大风速和地面降温幅度也随之增大,期间冷池的强度也经历一个增强的过程(图 7)。而当飑线移动速度达到最大并趋于“匀速”时,冷池前沿最大风速和模式底层温度扰动幅度也达到最大。
图 13a为模式积分6.5 h时各试验方案模式底层降温最大值与地面降温的时间序列。试验中将模式底层的温度变化作为模拟地面温度的变化。参考的地面观测站为上海松江站(58462),该站是一般站,也是飑线经过上海时地面温度下降最大的测站。可以看出,所有的试验方案地面降温在10 min内达到最大值,其后,随模式积分时间的延长降温幅度逐步减小,而地面测站的实际观测气温呈现了逐步下降的过程,松江站在飑线经过测站的40 min内地面气温每10 min分别下降4、2.1、2.1和0.8℃。图 13b中的其他地面自动站测得的气温也同样经历类似的过程。这说明模式各试验方案模拟的地面降温幅度与实况基本接近,但降温过程与实际观测存在一些差异。造成这种差异的主要原因是理想试验方案没有考虑陆面过程,忽略了下垫面对近地面温度的加热作用。此外,二阶矩微物理方案温度回归要快于实际观测,这是因为模拟试验初始场为水平均匀场,模拟的飑线系统移动过后,气象要素场很快就趋于模式初始场。由于二阶矩微物理方案模拟的飑线范围小于一阶矩微物理方案,因此,二阶矩微物理方案试验气温回归速度快于一阶矩微物理方案。
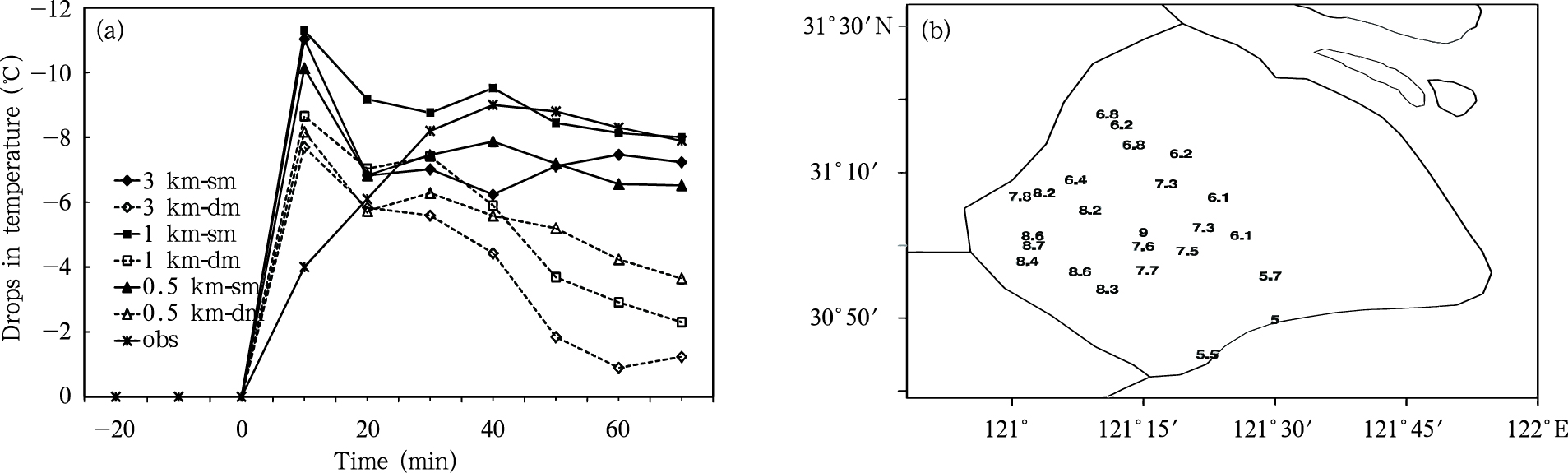 |
| 图 13 模拟的模式底层降温与实际观测的比较 (a.模式积分6.5 h时各试验方案模式底层降温与松江站地面观测随时间变化,b.飑线过境时地面测站最大降温幅度分布,℃)Fig. 13 Simulated drops in temperature comparing with observations (a. Time series of the simulated temperature change and observed temperature change at Songjiang station, b. distribution of max observed drops in temperature) |
图 13b为2009年6月5日飑线过境上海期间24个地面自动气象站测得的最大降温幅度。该24个测站位于飑线过境范围的南部区域。可以看出,不同地面自动气象站测得的最大降温幅度存在差异,最大值为9℃,最小值为5℃,平均降温为7.3℃。比较图 12b,模式积分6—8 h对应飑线发展成熟期各试验方案模式底层最大温度扰动,其中,3种分辨率模式一、二阶矩微物理方案模式底层平均降温分别为10.9和8.4℃。相比而言,二阶矩微物理方案模拟的气温变化与实际观测更接近一些。
很显然,模式水平分辨率和微物理方案对模拟飑线的结构和速度、冷池和冷池前沿最大风速以及模式底层最大降温有影响。表 2为模拟飑线的平均移动速度和平均强度,其中,平均移动速度为模式积分2—8 h的平均值,飑线强度用最大冷池强度、模式底层最大降温和最大风速来表征,各表征量的平均值为模式积分1—8 h的平均值。可以看出,1和0.5 km分辨率模式模拟的平均移动速度和平均冷池强度基本接近。总体而言,模式微物理方案对模拟飑线移动速度和强度的影响要大于模式水平分辨率。这与Bryan等(2012)认为模式分辨率的改变对模拟飑线强度的影响要大于微物理方案的结论存在差异。产生这种差异的原因可能是由于Bryan等(2012)研究选用了CM1模式且采用了4、1和0.25 km水平分辨率,与文中使用WRF模式进行3、1和0.5 km水平分辨率模拟存在一定的差异,此外,Bryan等(2012)仅使用6—9 h模拟的结果,没关注模拟飑线发展过程,选择的个例不同也可能是产生差异的原因。相对模式水平分辨率而言,模式模拟飑线强度对微物理方案更敏感,这说明在进行飑线强度的模拟研究时需更关注模式微物理方案的选择。
| 模式分辨率(km) | 平均移动速度(km/h) | 平均最大冷池强度(m/s) | 平均模式底层最大降温(℃) | 平均模式底层最大风速(m/s) | ||||
| sm | dm | sm | dm | sm | dm | sm | dm | |
| 3 | 56.6 | 46.3 | 12.2 | 11.3 | -10.9 | -7.2 | 27.0 | 24.1 |
| 1 | 60.7 | 52.1 | 12.7 | 11.2 | -11.5 | -9.9 | 32.1 | 28.3 |
| 0.5 | 61.8 | 51.4 | 12.1 | 11.0 | -10.4 | -8.0 | 32.4 | 29.3 |
| 注:sm、dm分别表示一、二阶矩微物理方案。 | ||||||||
尽管理想试验没考虑下垫面等因素对模式模拟飑线阵风锋的影响,理想试验与实际情况存在一定的差异,但模拟的结果仍给实际飑线阵风锋的预报提供了一些需要关注的信息,即飑线的移动速度与地面大风和降温直接相关。在实际预报中,当天气雷达监测到飑线移动速度增大时,可能预示着地面降温幅度和最大风速可能随之增大,而监测到飑线移动速度达到最大并趋于“匀速”时,可能意味着地面风速和地面降温也将达到最大。
5.4 雨水蒸发雨水蒸发与冷池有直接的关系。WRF模式中Morrison微物理方案(Morrison et al,2009)雨水蒸发率的计算式为
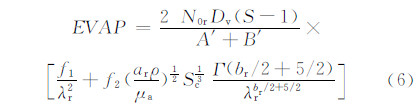
各试验4 km以下平均雨水蒸发率随模式积分时间的变化(图 14)显示,除3 km分辨率模式一阶矩微物理方案在模式积分至3 h时有异常增大外,在模式积分的前8 h,各试验雨水蒸发率呈现先增大、后减小、再趋稳的演变过程。模式分辨率的不同,雨水蒸发率达到最大值的时间也不同。无论是一阶矩还是二阶矩微物理方案,0.5 km分辨率模式模拟的雨水蒸发率均最先达到最大值。在实际模拟中,0.5 km分辨率一、二阶矩微物理方案雨水蒸发率分别在200和230 min达到最大值0.252×10-3和0.147×10-3 g·s/kg。1 km分辨率模式对应的分别是在250和270 min,其最大值分别为0.209×10-3和0.107×10-3 g·s/kg。这表明,一阶矩微物理方案要先于二阶矩微物理方案的雨水蒸发率达到最大值。
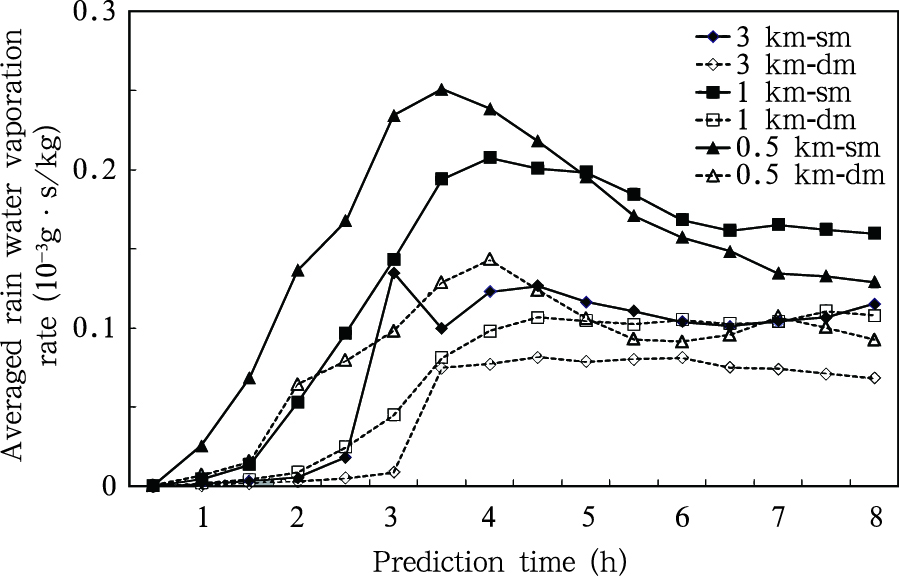 |
| 图 14 各试验4 km以下平均雨水蒸发率随模式积分时间的变化Fig. 14 Time series of the averaged rain water evaporation rate under 4 km for the various schemes |
由图 14也可以看出,在模式积分的前5 h,无论是一阶矩还是二阶矩微物理方案,0.5 km分辨率模式平均雨水蒸发率最大,其次是1 km模式,这说明模式分辨率的提高,雨水蒸发率是增大的。产生这种现象的原因是:随模式分辨率的提高,模式能更精细地模拟降水,使得降水总的表面积增大(如图 2),这样更有利于模拟降水的蒸发。同时,也可明显看出,不同分辨率模式一、二阶矩微物理方案模拟的平均雨水蒸发率存在明显的差异,其中3 km分辨率模式一、二阶矩微物理方案平均雨水蒸发率相差最小,为0.0298×10-3 g·s/kg,1和0.5 km分辨率试验相差接近,分别为0.0634×10-3和0.0669×10-3g·s/kg。总体上,无论分辨率高低,一阶矩微物理方案模拟的平均雨水蒸发率要大于二阶矩微物理方案,这与Bryan等(2012)的研究结论一致。
比较图 5、7、12、14可以发现,模拟飑线的移动速度、冷池强度、冷池前沿最大风速和平均雨水蒸发率之间存在明显的相关。在对流触发的初始阶段,即模式约积分1.5 h,虽然出现了冷池(图 7),但由于雨水蒸发率很小,随雨水下沉至模式底层的冷空气不强,使得冷池难以为继,出现了减弱的现象。其后,模式积分至3.5—4 h,各试验方案的雨水蒸发率不断增大,直至达到最大值(图 14)。在此过程中冷池平均强度、冷池前沿最大风速和飑线的移动速度均呈现出增大的过程。随后,各试验方案雨水蒸发率相继出现了减小并趋稳过程,与之相对应,冷池平均强度、冷池前沿最大风速和飑线的移动速度也经历了增大至最大值后逐步趋稳的过程。
通过比较分析可知,在模式积分的各个阶段,由于一阶矩微物理方案雨水蒸发率大于二阶矩微物理方案,而使得其对应的冷池平均强度、冷池前沿最大风速和飑线的移动速度都要大于后者。这表明雨水蒸发率与模式模拟的冷池平均强度、冷池前沿最大风速和飑线的移动速度有直接的关系,而这些也与飑线阵风锋有密切的关系,因此,在关注数值预报模式的水平分辨率和微物理方案对飑线阵风锋影响的同时,提高模式对雨水蒸发率的模拟能力也是实际业务数值预报模式预报阵风锋时需重点关注的内容。
5.5 发展维持机制为了评估各试验方案对飑线发展维持机制的模拟能力,利用经典的“RKW”理论进行分析比较。“RKW”理论由Rotunno等(1988)和Weisman等(1988)首次提出,认为飑线的强度和维持对垂直与飑线移动方向的低层(0—3 km)环境风切变最敏感,飑线冷池产生的环流与环境风垂直切变产生的环流的相互作用是飑线结构和发展维持最重要的机制。Weisman等(2004)利用简单的二维涡度流函数模式和分辨率更高、环境切变条件范围更大的三维模拟再次评估和确认了“RKW”理论。该理论可以概述为:当冷池强度(C)大于中、低层环境风切变(ΔU),即C/ΔU<1时,飑线系统向移动方向的上游倾斜,对应飑线处于发展阶段。反之,即C/ΔU>1时,飑线系统向移动方向的下游倾斜,对应飑线处于消亡阶段。当两者作用相当、处于平衡状态,即C/ΔU≈1时,飑线处于“最优”状态,此时飑线“直立”并伴有地面阵风锋。
由对冷池的垂直结构分析可知,各试验方案模拟的冷池高度为2—3 km(图 8),因此,文中重点分析0—3 km风垂直切变与冷池强度的关系。沿飑线移动方向0—3和0—6 km的风垂直切变分别为11.3和12.4 m/s,表明该飑线是在中等强度垂直切变环境中发生的。冷池强度由式(4)计算,并且沿飑线顶端左右各15 km及冷池前沿向后30 km范围内的冷池强度进行平均后获得。从各试验方案冷池前沿平均C/ΔU随模式积分时间的演变(图 15)可见,在模式积分的1—4 h,各试验方案平均C/ΔU由0.44逐步增大至1.9,在4.5—6.5 h各试验方案平均C/ΔU基本接近,其后出现了差异。这种变化趋势与雨水蒸发的变化有直接的关系。如图 14所示,在模式积分的前3.5—4 h,各试验方案雨水蒸发率均呈现增大的过程。由于雨水蒸发率的增大,导致了地面冷池强度的增大,也使得平均C/ΔU随之增大。并且,由于一阶矩微物理方案的雨水蒸发率大于二阶矩微物理方案,使得一阶矩微物理方案的平均C/ΔU要大于二阶矩微物理方案,两者平均相差约0.3。试验中,3、1和0.5 km分辨率模式一阶矩微物理方案平均C/ΔU≈1的模式积分时间约为75、100、100 min,3种分辨率模式二阶矩微物理方案对应的模式积分时间分别为135、140、150 min。根据“RKW”理论,各试验方案飑线达到“最优”状态的时间存在差异,其中,3 km分辨率模式模拟的飑线最早处于这种状态,1和0.5 km分辨率模式模拟飑线达到“最优”状态的时间基本接近,并且,3种分辨率模式二阶矩微物理方案模拟飑线处于“最优”状态的时间比一阶矩微物理方案分别晚60、40、50 min。
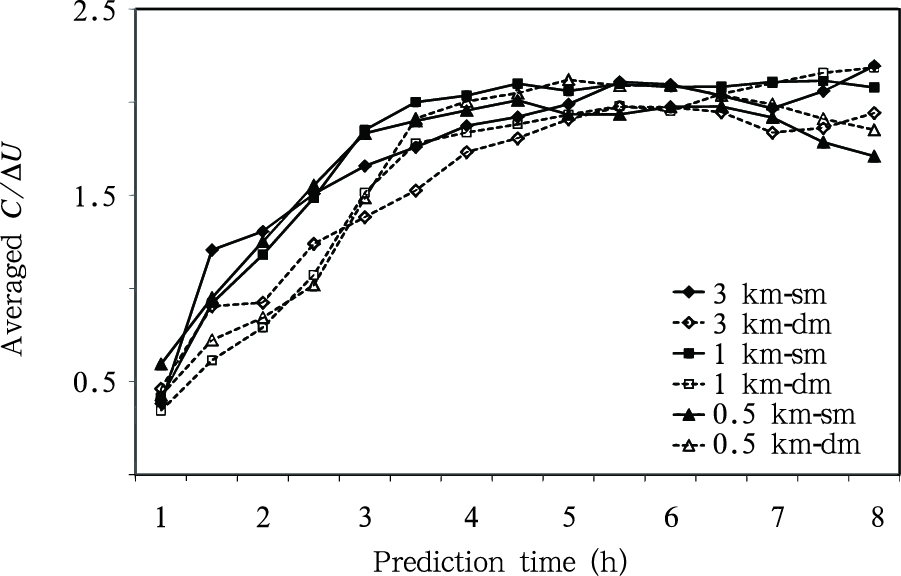 |
| 图 15 各试验方案冷池前沿平均C/ΔU随模式积分时间的变化Fig. 15 Time series of the averaged C/ΔU at the leading edge of the cold pool for the various schemes |
比较图 12可以看出,各试验方案模拟飑线冷池前沿最大风速出现在3.5—4 h,对应的C/ΔU为1.5—2,即在C/ΔU≈1时,模拟的飑线强度并没有达到最大,这与Morrison等(2012)研究结论一致。Bryan等(2006)认为,这可能与得出“RKW”结论所用模式的微物理方案中缺少冰相过程有关。由于模式没有冰相微物理过程而忽略了层云区域后部入流急流对冷池的增强作用。图 16为各试验方案模式积分3 h时平均垂直速度沿飑线移动方向的垂直剖面。其中平均垂直速度是沿剖面垂直方向(平行飑线方向)左右各15 km垂直速度的平均值,图中等值线间隔为0.5 m/s。可以看出,各试验方案飑线的后部均有明显的下沉气流。该下沉气流将中低空冷空气带入地面,而使得冷池得到加强。很明显,各试验方案模拟的飑线处于不同的“状态”,模式分辨率越高,模拟的飑线越“直立”,即C/ΔU越接近1,按“RKW”理论,越有利于飑线的维持。与一阶矩微物理方案相比,二阶矩微物理方案模拟的飑线向移动下游方向倾斜的程度要小,模拟的飑线处于更“优”的发展状态。相比而言,0.5 km分辨率模式二阶矩微物理方案模拟的飑线最“直立”(图 16a),而3 km分辨率模式一阶矩微物理方案模拟的飑线明显向飑线移动的下游方向倾斜(图 16f),特别是在冷池前沿和飑线主体之间出现了下沉气流,将飑线“分割”成了两部分。造成这种现象的原因主要是由于在模式积分1—3 h,3 km分辨率模式模拟一直维持较强的冷池(图 7a),使得冷池前沿的移动快于飑线主体的移动。这种结构切断了飑线前部的底层入流,不利于飑线的维持和发展,如图 2c所示,3 km分辨率模式一阶矩微物理方案积分6 h时模拟的雷达反射率因子已不能很好地反映飑线弓状回波的特征。因此,模式分辨率的提高和采用二阶矩微物理方案将有利于模拟飑线的维持。
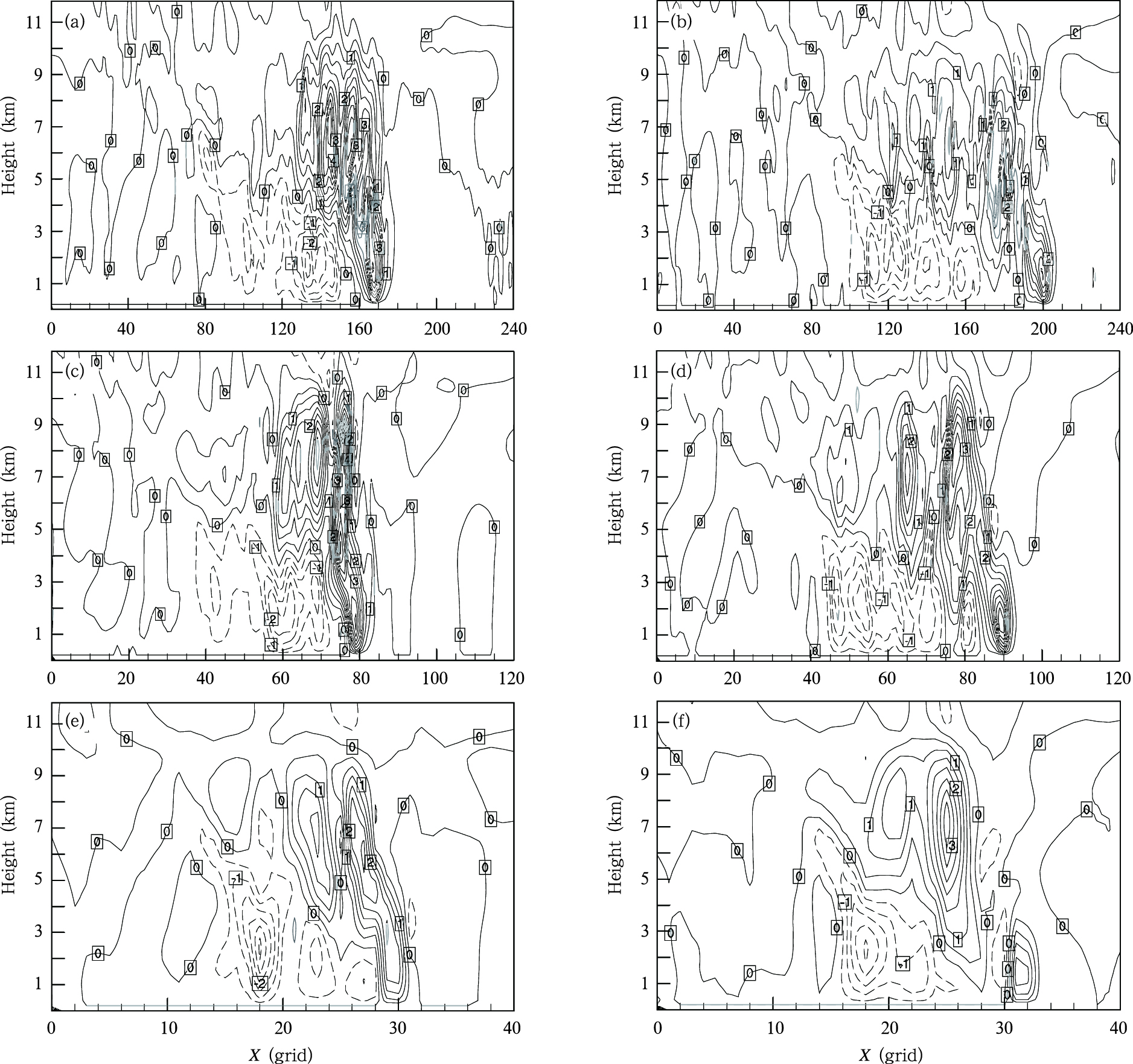 |
| 图 16 各试验方案模式积分3 h时平均垂直速度(m/s)沿飑线移动方向的垂直剖面 (a.0.5 km-dm, b.0.5 km-sm, c.1 km-dm, d.1 km-sm, e.3 km-dm, f.3 km-sm)Fig. 16 Vertical cross sections of the along-line averaged vertical velocity (m/s) , simulated by (a) 0.5 km-dm, (b) 0.5 km-sm, (c) 1 km-dm, (d)1 km-sm, (e) 3 km-dm and (f) 3 km-sm, at the 3 h prediction |
利用WRF中尺度数值预报模式,对2009年6月5日发生在上海的飑线过程进行了理想试验,对模式分辨率和微物理过程对阵风锋的模拟进行了比较分析。试验结果表明,数值预报模式的水平分辨率和微物理过程对飑线阵风锋的模拟有明显影响,这种影响主要表现在飑线结构、冷池强度、冷池前沿最大风速、雨水蒸发率和发展维持机制等方面的差别上。主要结论如下:
(1)随模式水平分辨率的提高,模式能更细致模拟出飑线的精细结构。0.5和1 km分辨率模式能很好地模拟出飑线的弓状回波特征。与一阶矩微物理方案相比,二阶矩微物理方案更能模拟出飑线回波前强后弱的结构特征。模拟飑线有一个加速移动的过程,总体上,一阶矩微物理方案模拟飑线的移动速度要快于二阶矩微物理方案。
(2)不同分辨率模式模拟出现冷池的时间略有差异,一阶矩微物理方案模拟的冷池面积和强度要明显大于二阶矩微物理方案。冷池增强的过程与飑线加速移动的过程基本一致。0.5和1 km分辨率模式能很好模拟出飑线后部的下沉气流和前部的上升气流,而3 km分辨率模式不能很好地模拟飑线底层完整的冷池结构,其模拟的飑线后部下沉气流和前部的上升气流都不明显。
(3)各试验方案能模拟出冷池地面风场和气压场的分布。冷池前沿最大风速呈现出随模式积分时间延长逐步增大的趋势,特别是在模式积分的前3.5—4 h,各试验方案冷池前沿最大风速增大较快,其后增大趋势趋缓。0.5和1 km分辨率模式模拟的冷池前沿最大风速比较接近,要大于3 km分辨率模式模拟的冷池前沿最大风速。总体上,一阶矩微物理方案模拟的冷池前沿最大风速要大于二阶矩微物理方案。冷池前沿最大风速和模式底层温度扰动幅度增大与飑线系统移动加速的过程相对应。
(4)模式分辨率的提高有利于模拟平均雨水蒸发率的增大,一阶矩微物理方案模拟的雨水蒸发率要大于二阶矩微物理方案。模式的雨水蒸发率随模式积分时间呈现了先增大、后减小、再逐步趋稳的过程。这个过程与冷池平均强度、冷池前沿最大风速和飑线移动速度的变化趋势基本一致。
(5)模式不同分辨率和微物理方案模拟飑线达到“最优”状态的时间存在差异,模式分辨率的提高和采用二阶矩微物理方案将有利于模拟飑线的维持。
综上所述,模式水平分辨率和微物理方案对飑线阵风锋模拟有明显的影响,因此,业务数值预报模式模拟飑线阵风锋时需要选择合适的水平分辨率和微物理方案。尽管模拟的雷达反射率因子略小于实际多普勒天气雷达观测的雷达回波强度,但1 km分辨率模式二阶矩微物理方案模拟的飑线结构特征与实际观测更为接近。与飑线过境时地面自动站观测降温幅度和气压升高速度相近,说明业务数值预报模式采用二阶矩微物理方案是必要的。由于雨水蒸发与冷池强度和阵风锋有直接的关系,为改善数值模式对飑线阵风锋预报性能应关注数值模式对雨水蒸发率的模拟能力。此外,文中一些结论对飑线阵风锋的预报也有启示,如在实际预报中,要特别关注飑线移动速度的变化,如飑线移动速度加快,预示着地面降温幅度和最大风速可能随之增大,而当飑线移动速度达到最大并趋于“匀速”时,可能意味着地面风速和地面降温也达到最大的程度。
各试验方案模拟结果存在差异,说明飑线过程模拟的难度和复杂性。依然有一些问题需要关注,例如图 1所示的探空资料700、500和400 hPa的平均风速为12.3 m/s,这基本可以代表飑线引导流的速度,而模拟的飑线发展成熟后其移动速度接近20 m/s(图 5),对应的冷池前沿最大风速约为35 m/s,这说明除引导气流作用外,还存在着飑线移动速度和冷池前沿最大风速增大的作用机制。“RKW”理论通过冷池与环境风切变相互作用解释了飑线发展维持机制,并且认为飑线后部入流急流对该机制有影响(Bryan et al,2006),如何定量分析这些关系,是否可以用Mahoney等(2009)提出的动量传输分析方法来定量分析这些问题尚待深入研究。此外,本试验仅仅是针对一次发生在中纬度、中等不稳定和中等风垂直切变条件下发生的飑线过程,不同的飑线过程对模拟结果可能会有一些影响,如低纬度和高纬度不同环境条件和软雹、粒子谱分布等微物理参数对飑线阵风锋模拟的影响还需进一步试验。针对模拟的不确定性,如何利用集合预报技术提高飑线阵风锋的模拟能力也是一个值得研究的问题,上述这些问题将在后续的研究中深入探讨。
致谢:上海中心气象台戴建华博士为本研究提供了WSR-88D雷达探测资料和显示软件,并提出了很多有益建议。美国NCAR的Hugh Morrison博士在微物理方案试验中给予了帮助。谨此致谢。
| 陈明轩, 王迎春. 2012. 低层垂直风切变和冷池相互作用影响华北地区一次飑线过程发展维持的数值模拟. 气象学报, 70(3): 371-386. Chen M X, Wang Y C. 2012. Numerical simulation study of interactional effects of the low-level vertical wind shear with the cold pool on a squall line evolution in North China. Acta Meteor Sinica, 70(3): 371-386 (in Chinese) |
| 戴建华, 陶岚, 丁杨等. 2012. 一次罕见飑前强降雹超级单体风暴特征分析. 气象学报, 70(4): 609-627. Dai J H, Tao L, Ding Y, et al. 2012. Case analysis of a large hail-producing severe supercell ahead of a squall line. Acta Meteor Sinica, 70(4): 609-627 (in Chinese) |
| 董昊, 徐海明, 罗亚丽. 2012. 云凝结核浓度对WRF模式模拟飑线降水的影响: 不同云微物理参数化方案的对比研究. 大气科学, 36(1): 145-169. Dong H, Xu H M, Luo Y L. 2012. Effects of cloud condensation nuclei concentration on precipitation in convection permitting simulations of a squall line using WRF model: Sensitivity to cloud microphysical schemes. Chinese J Atmos Sci, 36(1): 145-169 (in Chinese) |
| 慕熙昱, 党人庆, 陈秋萍等. 2007. 一次飑线过程的雷达回波分析与数值模拟. 应用气象学报, 18(1): 42-49. Mu X Y, Dang R Q, Chen Q P, et al. Radar data analysis and numerical simulation of a squall line. J Appl Meteor Sci, 18(1): 42-49 (in Chinese) |
| 沈杭锋, 翟国庆, 朱补全等. 2010a. 浙江沿海中尺度辐合线对飑线发展影响的数值试验. 大气科学, 34(6): 1127-1140. Shen H F, Zhai G Q, Zhu B Q, et al. 2010a. A model study of impact of coastal mesoscale convergence line on development of squall line over Zhejiang Province. Chinese J Atmos Sci, 34(6): 1127-1140 (in Chinese) |
| 沈杭锋, 翟国庆, 章元直等. 2010b. 应用云迹风资料同化的江南飑线模拟试验. 浙江大学学报(理学版), 37(6): 705-712+721. Shen H F, Zhai G Q, Zhang Y Z, et al. 2010b. Assimilation study of squall line in the south of Yangtze River using cloud motion wind data. J Zhejiang Univ (Sci Ed), 37(6): 705-712+721 (in Chinese) |
| 夏文梅, 慕熙昱, 徐琪等. 2011. 一次阵风锋过程的数值模拟与分析. 高原气象, 30(4): 1087-1095. Xia W M, Mu X Y, Xu Q, et al. 2011. Simulation and analysis of a gust front process. Plateau Meteor, 30(4): 1087-1095 (in Chinese) |
| 肖现, 王迎春, 陈明轩等. 2013. 基于雷达资料四维变分同化技术对北京地区一次下山突发性增强风暴热动力机制的模拟分析. 气象学报, 71(5): 797-816. Xiao X, Wang Y C, Chen M X, et al. 2013. A mechanism analysis of the thermo-dynamical field of a suddenly intensifying storm from mountains in the Beijing area with the radar 4DVar. Acta Meteor Sinica, 71(5): 797-816 (in Chinese) |
| 张进, 谈哲敏. 2008. 启动对流的初始扰动对热带飑线模拟的影响. 大气科学, 32(2): 309-322. Zhang J, Tan Z M. 2008. Impacts of initial convection-triggering perturbations on numerical simulation of a tropical squall line. Chinese J Atmos Sci, 32(2): 309-322 (in Chinese) |
| 张培昌, 杜秉玉, 戴铁丕. 2001. 雷达气象学. 北京: 气象出报社, 305-307. Zhang P C, Du B Y, Dai T P. 2001. Radar Meteorology. Beijing: China Meteorological Press, 305-307 (in Chinese) |
| 张入财, 陆汉城, 付伟基等. 2009. 地面资料同化的飑线数值模拟及中尺度特征分析. 大气科学, 29(1): 39-45. Zhang R C, Lu H C, Fu W J, et al. 2009. Assimilation of surface observation data in numerical simulation of a squall line and mesoscale characteristics analysis. Chinese J Atmos Sci, 29(1): 39-45 (in Chinese) |
| Bryan G H, Wyngaard J C, Fritsch J M. 2003. Resolution requirements for the simulation of deep moist convection. Mon Wea Rev, 131(10): 2394-2416 |
| Bryan G H, Knievel J C, Parker M D. 2006. A multimodel assessment of RKW theory's relevance to squall-line characteristics. Mon Wea Rev, 134(10): 2772-2792 |
| Bryan G H, Morrison H. 2012. Sensitivity of a simulated squall line to horizontal resolution and parameterization of microphysics. Mon Wea Rev, 140(1): 202-225 |
| Dawson D T, Xue M, Milbrandt J A, et al. 2010. Comparison of evaporation and cold pool development between single-moment and multimoment bulk microphysice schemes in idealized simulations of tornadic thunderstorms. Mon Wea Rev, 138(4):1152-1171 |
| Houze R A, Smull B F, Dodge P. 1990. Mesoscale organization of springtime rainstorms in Oklahoma. Mon Wea Rev, 118(3): 613-654 |
| Mahoney K M, Lackmann G M, Parker M D. 2009. The role of momentum transport in the motion of a quasi-idealized mesoscale convective system. Mon Wea Rev, 137(10): 3316-3338 |
| Martin G M, Johnson D W, Spice A. 1994. The measurement and parameterization of effective radius of droplets in warm stratocumulus clouds. J Atmos Sci, 51(13): 1823-1842 |
| Morrison H, Curry J A, Khvorostyanov V I. 2005. A new double-moment microphysics parameterization for application in cloud and climate models. Part Ⅰ: Description. J Atmos Sci, 62(6):1665-1677 |
| Morrison H, Thompson G, Tatarskii V. 2009. Impact of cloud microphysics on the development of trailing stratiform precipitation in a simulated squall line: Comparison of one-and two-moment schemes. Mon Wea Rev, 137(3): 991-1007 |
| Morrison H, Milbrandt J. 2011. Comparison of two-moment bulk microphysics schemes in idealized supercell thunderstorm simulations. Mon Wea Rev, 139(4): 1103-1130 |
| Morrison H, Tessendorf S A, Ikeda K. 2012. Sensitivity of a simulated midlatitude squall line to parameterization of raindrop breakup. Mon Wea Rev, 140(8): 2437-2460 |
| Rotunno R, Klemp J B, Weisman M L. 1988. A theory for strong, long-lived squall lines. J Atmos Sci, 45(3): 463-485 |
| Skamarock W C, Klemp J B, Dudhia J. 2007. A Description of the Advanced Research WRF version 2. NCAR Tech. Note NCAR/TN-4681STR, 1-63 |
| Weisman M L, Klemp J B, Rotunno R. 1988. Structure and evolution of numerically simulated squall lines. J Atmos Sci, 45(14): 1990-2013 |
| Weisman M L, Skamarock W C, Kiemp J B. 1997. The resolution dependence of explicitly modeled convective systems. Mon Wea Rev, 125(4): 527-548 |
| Weisman M L, Rotunno R. 2004. "A theory for strong long-lived squall lines" revisited. J Atmos Sci, 61(4): 361-382 |
 2015, Vol. 73
2015, Vol. 73

