中国气象学会主办。
文章信息
- 王亚华, 臧增亮, 潘晓滨, 何宏让, 韩威. 2015.
- WANG Yahua, ZANG Zengliang, PAN Xiaobin, HE Hongrang, HAN Wei. 2015.
- 高分辨率GRAPES-GFS的动能谱及其转折特征分析
- The kinetic energy spectrum and its transition characteristics analysis of the high-resolution GRAPES-GFS
- 气象学报, 73(5): 965-974
- Acta Meteorologica Sinica, 73(5): 965-974.
- http://dx.doi.org/10.11676/qxxb2015.051
-
文章历史
- 收稿日期: 2014-12-09
- 改回日期: 2015-03-23
2. 中国洛阳电子装备试验中心, 洛阳, 471003;
3. 中国气象局数值预报中心, 北京, 100081
2. Chinese Luoyang Electronic Equipment Test Center, Luoyang 471003, China;
3. Numerical Weather Prediction Center of China Meteorological Administration, Beijing 100081, China
大量的观测事实表明在对流层高层和平流层低层,大气动能随波数衰减的曲线在大尺度区域近似满足E ∝ k-3关系,过渡到中尺度区域近似为E ∝ k-5/3关系(Nastrom et al,1985; Bacmeister et al,1996)。大气动能谱在大尺度k-3的斜率特征可以由地转平衡的二维湍流理论解释(Gage et al,1986; Boer et al,1983; Lindborg,1999)。但对于中尺度k-5/3斜率特征的理论解释则有两类不同的观点,一类解释是基于二维湍流理论(Kraichnan,1967)的升尺度能量串级(Gage,1979; Lilly,1983; Falkovich,1992),其认为由于在更小尺度的能量强迫如湿对流等引起动能升尺度串级输送使得中尺度动能谱呈现k-5/3的斜率分布;另一类是基于三维湍流理论的降尺度能量串级(Kolmogorov,1941; Lindborg,2006),其认为由于大尺度的辐散运动激发出惯性重力波,惯性重力波能量在中尺度区域叠加使得动能谱斜率变为k-5/3。近几年,另有学者提出中尺度物理过程也具有源汇效应(Waite et al,2009,2013),中尺度运动的增强造成了动能谱在中尺度区域由k-3到k-5/3的转折。
很多研究表明,动能谱的这种斜率特征随纬度、高度和季节变化不大,可以作为大气运动的基本统计特征,并作为模式评估的参考。Laursen等(1989)使用大气的动能谱特征来检验不同的侧边界耗散参数化方案的影响,发现平均流对侧边界耗散公式选择和强度大小十分敏感。Koshyk等(2001)检验了NOAA地球物理流体动力学实验室(GFDL)SKYHI大气环流模式的模式动能谱。Skamarock(2004)应用动能谱评估了WRF模式的动力框架。郑永骏等(2008)分析GRAPES-MESO的动能谱,结果显示模式动能谱能够近似描述出大尺度E ∝ k-3、中尺度E ∝ k-5/3的斜率特征,并利用动能谱特征评估了模式的最大有效时间步长、最高有效分辨尺度等。龚建东(2007)依据大气的动能谱特征分析了特征长度与分辨率的相关关系。
虽然观测和模拟结果都能揭示大气动能谱由k-3到k-5/3的转折特征,但很少有文献对转折的具体位置做定量计算,大多是粗略描述过渡区或大致估计分界点。如Nastrom等(1985)对飞机观测资料的动能谱分析表明在波长为1000—3000 km范围内动能谱呈现出k-3的斜率特征,波长在400 km以下的动能谱表现出k-5/3的斜率特征,其认为过渡区在波长为400—1000 km的范围内。Koshyk等(2001)依据SKYHI大气环流模式的模式动能谱曲线,估计在对流层高层,动能谱曲线从k-3过渡到k-5/3约在波长为500 km的位置;平流层斜率转折的过渡大约在2000 km的位置。Hamilton等(2008)估计出AFES(Atmospheric GCM For the Earth Simulator)模式动能谱在对流层顶附近约在波数为80(波长近似为500 km)的位置出现斜率转折。如果对动能谱曲线进行分段直线拟合,那么两条线的交点必定在过渡区内,将该交点称之为“拐点”,即Burgess等(2013)提到的“Changepoint”,表示大尺度动能谱和中尺度动能谱的分界点。Burgess等(2013)基于欧洲中期天气预报中心(ECMWF)的T799模式再分析资料第1次定量计算了动能谱的拐点位置,他们对动能谱曲线进行分段直线拟合,利用Levenberg-Marquardt(L-M)方法搜索拐点位置,结果表明该方法能够较好地计算出动能谱斜率的转折点,并提出拐点不仅标志着大气动能谱的斜率变化,同时也是大气平衡运动(大尺度)和非平衡运动(中尺度)的转折点。
GRAPES(Global and Regional Assimilation and Prediction System)模式是中国自主研发的新一代同化预报系统,包括有限区域中尺度预报(GRAPES-MESO)和全球中期天气预报(GRAPES-GFS)两套系统(陈德辉等,2008;薛纪善等,2008;张人禾等,2008;杨学胜等,2008)。这两套系统是一体化发展的统一模式,具有通用的模式动力框架、资料同化框架以及统一的基础软件架构,近年来许多科技工作者在GRAPES模式的改进和发展方面做了大量工作(胡江林等,2007;王光辉等,2009;王金成等,2014;庄照荣等,2010;Zheng et al,2012; Huang et al,2013,朱国富等,2008),使得模式更加完善,预报效果有了显著提高。但是,目前还没有人从动能谱的角度对GRAPES-GFS进行检验评估,本研究针对GRAPES-GFS模式结果进行动能谱的计算和分析研究,并提出一种计算拐点的新方法,重点分析不同层次上拐点的变化特征,以及辐散和旋转分量对总动能谱斜率和拐点的贡献,为将来模式的改进发展提供参考。
2 数据和计算方案 2.1 数 据本研究的资料为GRAPES-GFS模式输出的2013年5月的预报结果,对于全球模式的谱分析而言,1个月的资料统计就能够体现大气波动的谱特性(Trenberth et al,1993; Straus et al,1999)。GRAPES-GFS全球中期预报模式的预报时效是192 h预报,每6 h输出一次预报结果,但是考虑到模式起转时间的影响,在此只对模式积分24—192 h的结果进行分析。计算每天预报24—192 h每6 h一次的输出结果的动能谱,然后再取所有结果的平均值。模式的水平分辨率为0.25°×0.25°,垂直方向29层。需要说明的是,大多数的全球模式(如ECMWF、 AFES)都是谱模式,GRAPES-GFS是格点模式,只有格点上的变量值,没有可以直接利用的谱系数,因此必须将格点数据转换成谱系数,然后再进行谱分析。
2.2 二维谐波谱计算方案采用谱展开的方法计算全球大气动能谱,通过对水平速度分量进行三角形截断的球谐函数展开,动能谱可看作是一个关于总球面谐波波数的函数(Koshyk et al,1999,2001)。
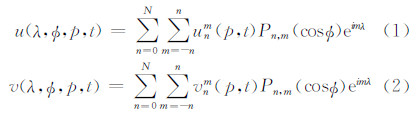
式中,m表示纬向波数,n表示总波数,N表示截断波数,unm 、vnm为u、v的谱系数,Pn,m表示自由度为n的勒让德多项式。
单位质量的动能谱可以通过u、v的谱系数来计算。

动能谱的另外一种表达式就是将水平风场分为旋转风分量和辐散风分量两部分:
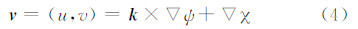
式中,ψ表示流函数,χ表示速度势。将ψ和χ进行球谐函数展开,且涡度ζ=▽2ψ,散度δ=▽2χ,那么单位质量的动能谱Enm(p,t)可写为
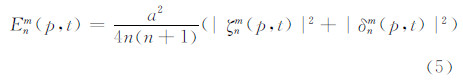
式中,a表示地球半径。
将动能谱对纬向波数m求和,从而将动能谱看作是只与总波数n有关的函数。
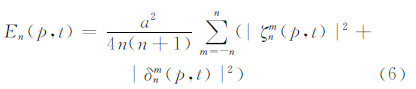
动能谱方程(6)可看做是涡度项与散度项之和,其中涡度项可看作是动能谱的旋转分量,散度项可看作动能谱的辐散分量。
2.3 波谱斜率拐点的计算方案拐点表示两段直线的转折点,可以用分段函数进行描述,假定分段函数在分界点处连续但不可导,采用分段直线回归模型(Hinkley,1969)
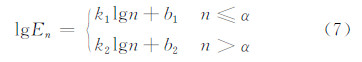
式中,En是由分段直线回归模型估计得到的波数为n的动能谱值,k1和k2为拐点两侧的斜率值,α表示拐点的位置,即拐点处的波数: α=ncp。Burgess等(2013)基于L-M算法的最小二乘法估计计算参数k1、k2及拐点α,L-M算法是高斯-牛顿法和最速下降法的结合,具有很好的收敛特性。但是在L-M算法的计算过程中,初值是一个很重要的因素,如果初值接近真值,则可快速收敛并得到全局最优,如果初值远离真解,迭代结果易陷入局部最优解从而偏离真解。
文中提出一种无需设置初值的全局搜索算法计算拐点。所谓全局搜索,就是在所有可能的拐点位置上均进行计算;然后,针对每个可能的拐点位置进行分段函数拟合,求得参数值和目标函数值;最后,利用比较目标函数值的大小,最小目标函数对应的各变量值即为全局搜索的解。假设拐点的位置为α,将波数和动能谱数据取对数,令
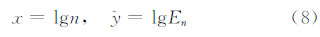
然后分为两段,第1段记为(x1t,y1t),t=1,…,m1,第2段记为(x2t,y2t),t=1,…,m2 。考虑到分段函数的连续性,则(x1m1,y1m1)与(x21,y21)为同一个点,即第1段数据的终点同时也是第2段数据的起点,这个点也就是转折点。如果要把两段数据看成独立的样本,则可分别建立一元线性回归方程
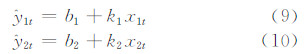
对上述两个方程分别求解则可以求出各自的回归系数k1,b1(或k2,b2)。但考虑到这两个回归直线在拐点处的连续条件,可以构建一个条件极值问题进行求解(具体求解方法见附录)。由于动能谱曲线有可能近似线性递减而不表现出斜率的转折,即也有可能不存在拐点,所以还需对拐点的真实性做进一步判断。在此设定拐点任意一侧至少有5个点,即m1≥5,m2≥5;并且拐点左侧(大尺度范围)的斜率绝对值大于拐点右侧(中小尺度范围)的斜率绝对值,即|k1|>|k2|,那么就认为拐点存在,否则拐点不存在。
3 模式动能谱计算结果分析 3.1 二维谐波谱对流层中层(500 hPa)到平流层中层(10 hPa)不同高度层的动能谱计算结果(图 1)表明,在6—60的波数范围内,250 hPa的动能谱值最大,即大尺度的波动在对流层顶附近最为剧烈;当波数大于100时,动能谱值随高度的增高而减小,说明中小尺度波动能量也随高度增高而减小。在10—100的波数范围内,100和50 hPa高度的动能谱随波数的变化曲线有明显的斜率变化,但是当波数大于200以后,动能谱的值随波数的增大迅速衰减,这可能是由模式的耗散作用造成的。Burgess等(2013)针对T799数据计算得到的动能谱也是在100 hPa及以上的高度转折特征比较明显。图 1中10 hPa高度层的动能谱曲线的谱转折特征已经不明显了,而Burgess等(2013)计算结果中10 hPa高度的动能谱曲线仍然保持着明显的斜率转折特征。这可能是由于T799的模式层可以达到0.01 hPa,而GRAPES-GFS模式的上边界只到10 hPa,前者的垂直层次延展高度更高,10 hPa高度层大气的描述更准确。同时由于模式层顶存在不真实的计算噪音,没有物理意义,因此后面的分析只讨论50 hPa及其以下的高度层。
 |
| 图 1 500—10 hPa所选高度层的模式动能谱曲线 Fig. 1 Kinetic energy spectra at the selected levels spanning 500 to 10 hPa (Lines with the slopes of -3 and -5/3 have been added for comparison) |
下面按照2.3节提到的拐点全局搜索算法计算10—100的波数范围内的拐点。计算表明,在超过225 hPa(包括225 hPa)的高度层才存在拐点(图 2a),即225 hPa为拐点出现的下限高度,在这一高度层上,拐点两侧的斜率分别是k1=-3.4和k2=-3.0,拐点的位置在ncp=60波数处,在225 hPa以下波谱的斜率近似为常数。Burgess等(2013)检测到拐点的下限高度是226 hPa,拐点位置ncp≈60,与本研究结果十分一致。此外,Nastrom等(1985)对飞机飞行高度在9—14 km的飞机报资料计算得到的动能谱分析后估计动能谱曲线斜率转折大概出现在波数40—100的位置,也与本研究计算的拐点位置一致。由图 2a可以清楚地看出,拐点的位置由225 hPa的ncp=60随着高度的增高逐渐向大尺度(小波数)移动,到100 hPa时ncp=21。高度超过100 hPa后,拐点的位置基本稳定在20—25的波数范围。Burgess等(2013)针对T799数据计算得到226—100 hPa的拐点位置波数随高度增高而减小,高度大于100 hPa后,拐点位置波数稳定在20左右,与本研究结果的变化趋势相同。
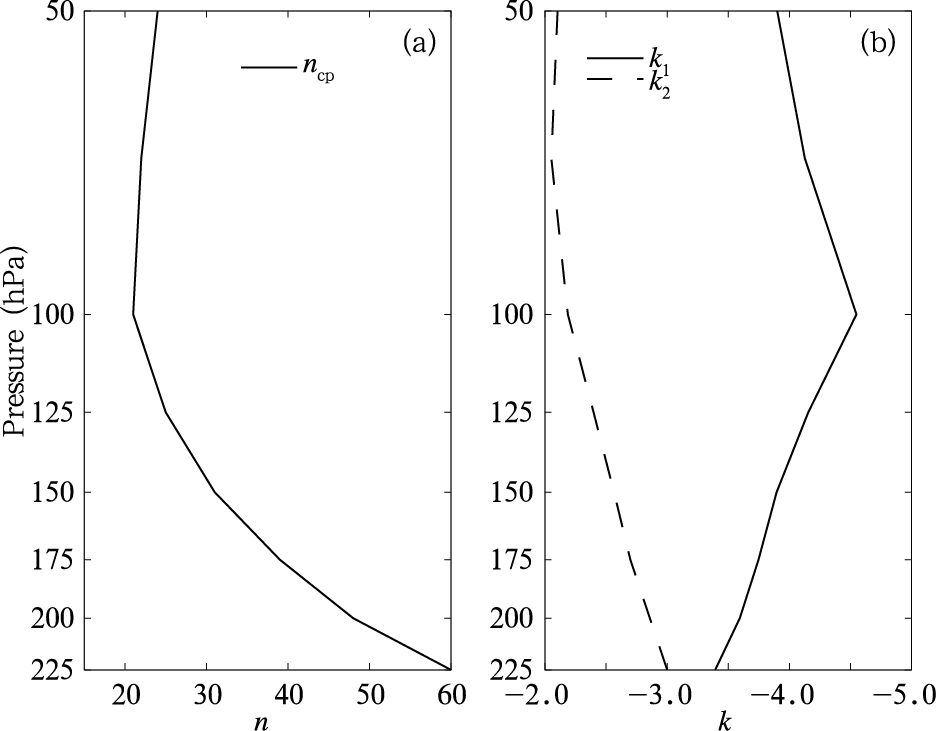 |
| 图 2 拐点位置波数(a)和拐点两侧线性拟合 得到的斜率(k1、k2)(b)随高度的变化Fig. 2 Changepoint wavenumber ncp(a) and the slope of the two changepoint segments (k1,k2) (b) as functions of the altitude |
由于拐点处的波长一般在300—1000 km,即波长大于2000 km的大尺度范围均在拐点的左侧,在拐点右侧并大于模式的最小有效分辨波长(约为140 km)的尺度范围属于中尺度范围,因此在本研究中近似将拐点左侧的尺度范围称为大尺度范围,而将拐点右侧的尺度范围称为中尺度范围。
从拐点两侧的斜率(k1和k2)随高度的变化(图 2b)可以看出,从225 hPa向上,k1减小,k2增大,两者在100 hPa附近的差值达到最大,随后又趋于减小,这也解释了图 1中斜率转折在100 hPa最明显,而在225 hPa以下由于k1和k2趋于相同,故不能检测到拐点。值得注意的是,k1的范围为-3.4—-4.5,k2为-2.1—-3.0,均比前述文献中观测得到的-3和-5/3的绝对值偏大,即使是在典型的200 hPa,k1和k2的值也分别达到了-3.5和-2.9,特别是k2的数值与观测结果相差较大。实际上Burgess等(2013)对T799数据计算的斜率绝对值也偏大,其在200 hPa的k1为-3.4,k2为-2.7,二者都是中尺度范围的斜率,同样是k2的偏差更大,这可能是全球模式动能谱计算中的普遍问题。而Peng等(2014)采用中尺度模式WRF对成熟时期的梅雨锋系统的动能谱的计算表明:在对流层高层,400—1000 km的较大尺度动能谱斜率(相当于k1)约为-3.5,而过渡到40—400 km的中尺度时动能谱斜率(相当于k2)约为-1.7,与-5/3的观测结果十分接近,这可能是因为其采用的是区域模式,分辨率较高,并且是针对梅雨期间的强降水过程,大量潜热的释放将会增加中尺度范围的动能谱值。本研究基于Burgess等(2013)所采用的L-M算法计算拐点进行对照检验(图略),结果表明L-M算法只在150—50 hPa的高度层检测到拐点,拐点位置与本研究的计算结果差异很小,波数差异均在9以下,斜率差异均在0.6以下。而且初值的选取对L-M计算结果有一定的影响。
3.2 二维谐波谱的辐散分量和旋转分量从200、150和100 hPa高度层上的总动能谱以及旋转分量和辐散分量的分布(图 3)可以看出,在这3个高度层上,在小波数(大尺度)范围动能谱都是以旋转分量为主,其与总动能谱曲线基本重合,比辐散分量要大一个量级以上,随着波数的增大,辐散分量的量级逐渐与旋转分量接近甚至超过旋转分量。图 3中的圆圈表示辐散动能谱曲线与旋转动能谱曲线的交点,对比3个高度层上的交点可以发现,200—100 hPa高度层,交叉点的位置是向小波数(大尺度)方向移动的。从200、150和100 hPa这3个高度层的旋转和辐散动能谱的变化曲线及交点的位置(图 4)可以看出,在7—200的波数范围内,旋转动能谱随着高度的增高有明显的减小,而辐散动能谱随高度的变化较小,特别在40—200的波数范围内基本重合,所以旋转动能谱和辐散动能谱曲线的交点主要受旋转分量的曲线影响,旋转分量的量级越小,交点的位置越趋向于大波数。
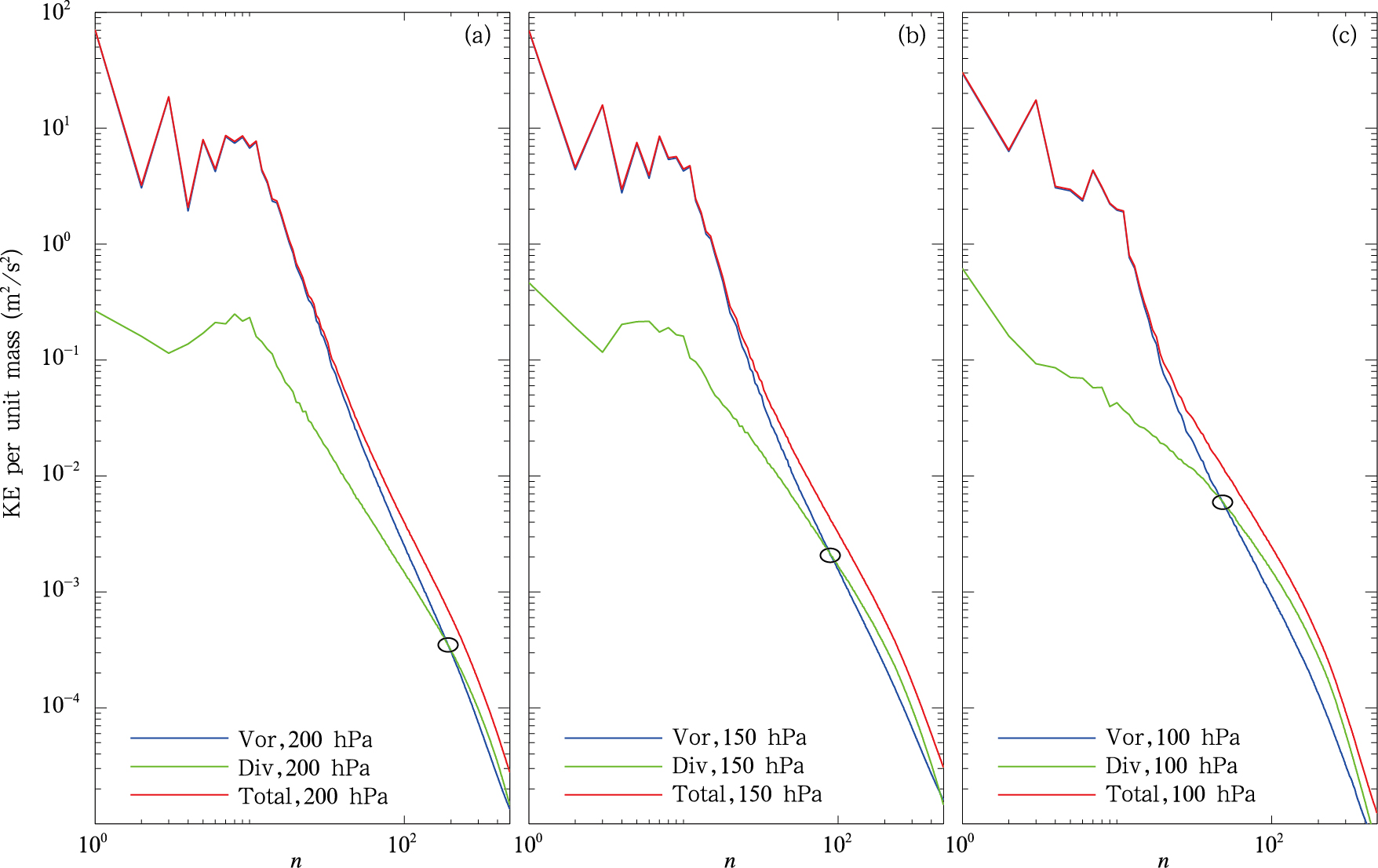 |
| 图 3 200 (a)、150 (b) 和100 hPa (c) 高度上的旋转、辐散和总动能谱 (黑色圆圈表示各个高度层上旋转和辐散动能谱的交点)Fig. 3 Rotational, divergent, and total compondents of the kenitic energy spectrum at (a) 200 hPa, (b) 150 hPa and (c) 100 hPa (circle represents the intersection of the rotational and divergent components) |
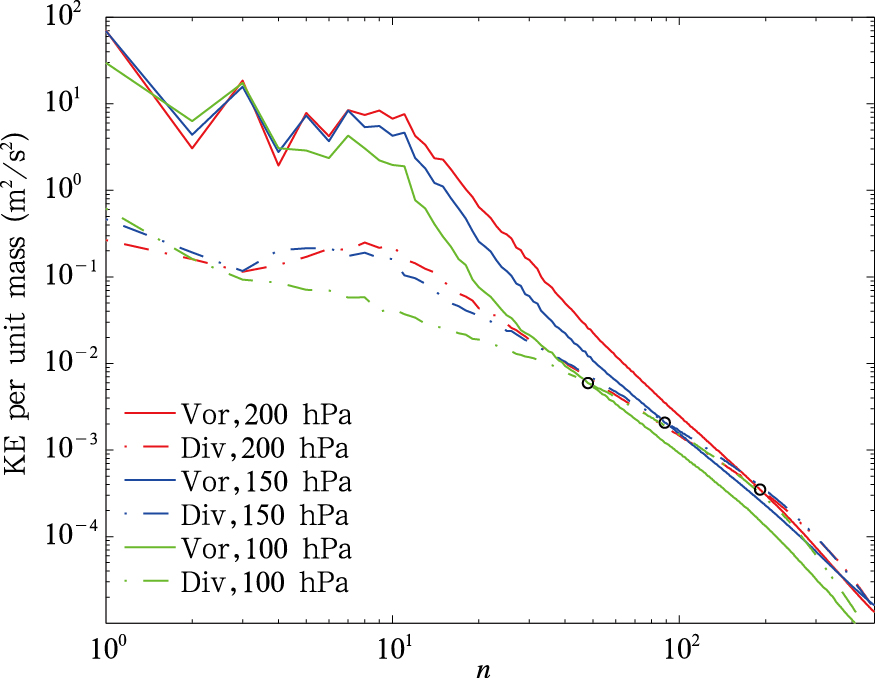 |
| 图 4 200、150和100 hPa高度上的旋转和辐散动能谱 (黑色圆圈表示各层旋转与辐散动能谱的交点)Fig. 4 Rotational and divergent compondents of the kenitic energy spectrum at 200, 150 and 100 hPa (circle represents the intersection of the rotational and divergent components) |
从辐散动能谱与旋转动能谱交点的位置(即图 3、4中圆圈)随高度的变化曲线(图 5)可以看出,225—100 hPa,交点的位置随高度增高向小波数方向移动,100—50 hPa,交点的位置稳定在波数50附近。交点的变化趋势与拐点位置随高度的变化(图 2a)具有较好的一致性,即总动能谱的拐点与旋转和辐散动能谱的交点之间存在显著的相关,但是交点的位置波数要略大于拐点的位置波数。Bartello(2010)模拟了理想状态下的旋转层结湍流,并且在总的辐散效应大于地转平衡效应时发现了中尺度动能谱斜率绝对值变小的特征。中尺度运动的一个特征就是辐散与旋转作用相当,那么辐散动能谱与旋转动能谱的交点位置随高度向小波数移动,说明随着高度的增高,中尺度波动的尺度向大尺度方向延伸。由此可以推断,动能谱斜率拐点的存在是由中尺度范围内辐散动能在总动能中作用增强造成的。通常认为,在对流层中的大尺度平衡运动条件下,辐散运动的量级应远小于旋转运动的量级,但在对流层顶和平流层下层,辐散运动和旋转运动却可能达到同一量级,这种大气运动应是非平衡的(Saujani et al,2006)。本研究中,225—100 hPa,拐点位置向大尺度区移动主要是由于动能谱的旋转分量随高度增高而减小了(图 4),同时旋转分量与辐散分量的交点向大尺度方向移动(图 5),这种旋转与辐散作用相当的中尺度波动向大尺度方向扩展,也可以理解为拐点反映了大尺度平衡运动向中尺度非平衡运动的过渡。
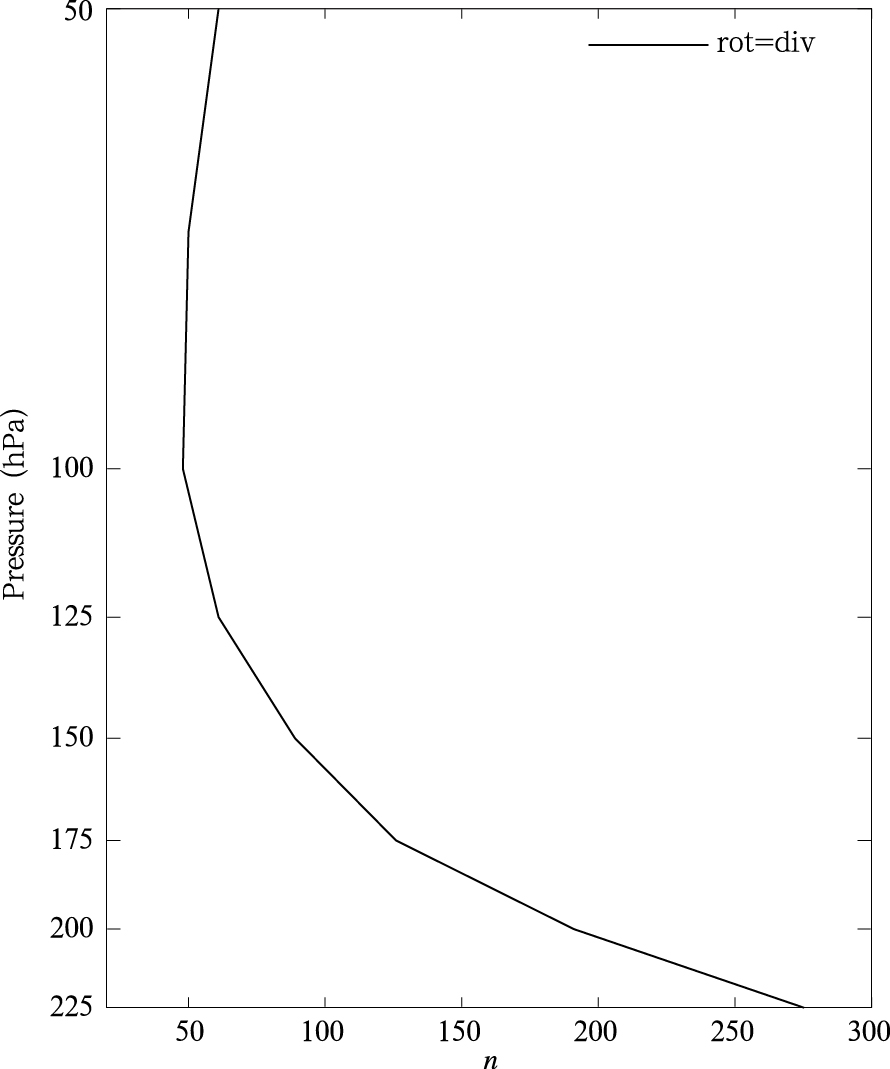 |
| 图 5 辐散动能谱与旋转动能谱交点位置波数随高度的变化Fig. 5 Wave number at which the rotational and divergent components intersect as a function of the altitude |
本研究还计算了拐点到100波数范围内辐散动能谱的斜率值(图 6),在200 hPa,辐散动能谱斜率值为-1.8,与-5/3非常接近,而且在200—50 hPa高度层内,辐散动能谱斜率值在-1.4 —-1.9,与-5/3的观测结果一致。Burgess等(2013)认为,大气动能谱在中尺度范围出现谱转折主要因为变化平缓的辐散动能谱在总动能谱中的作用增大造成的,他们计算的辐散动能谱的斜率随高度在-5/3左右变化,变化趋势也与本研究的计算结果吻合,说明GRAPES-GFS模式对于中尺度辐散动能谱的描述较为准确。前面提到模式动能谱值无论在大尺度范围内还是中尺度范围内的斜率绝对值都偏大,在大尺度范围模式动能谱以旋转分量为主,辐散分量的影响很小,可以忽略,模式动能谱的误差主要由旋转分量造成;在中尺度范围旋转分量和辐散分量相当,但模式对辐散分量的描述较为准确,因此,误差也主要由旋转分量引起。
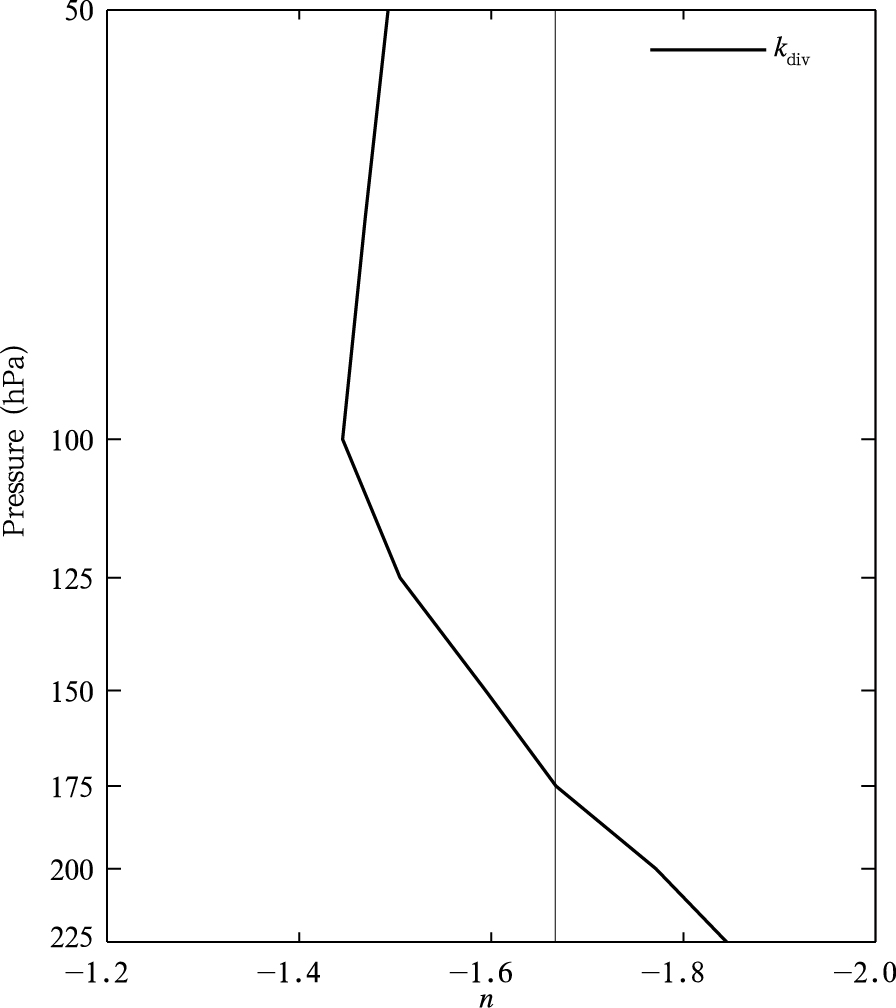 |
| 图 6 辐散动能谱斜率随高度的变化 (垂线为-5/3的参考线)Fig. 6 Divergent kinetic energy spectral slope as function of the altitude (the line of k=-5/3 has been added for comparison) |
利用高分辨率GRAPES-GFS模式资料,计算了其预报场的动能谱分布,并对动能谱中不同高度层的拐点、辐散分量、旋转分量等的关系进行了深入分析,主要结论如下:
(1)在225—50 hPa高度层,模式动能谱能较好地模拟出大气动能谱由大尺度过渡到中尺度时动能谱的斜率转折特征,但模式模拟的动能谱斜率绝对值要比观测结果偏大,其他文献中的模式结果也存在这一问题。
(2)基于条件极值的思想,提出了一种新的分段回归计算方法,可以实现拐点的全局搜索,采用该方法在10—100的波数范围内进行波数分析,在225 hPa及以上的高度层检测到拐点,该方法计算得到的拐点结果与Burgess(2013)所用的L-M算法结果一致,但本研究所提出的新方法无需提供初值,稳定性和准确性更高。
(3)分别计算模式动能谱的旋转分量和辐散分量,发现在225—100 hPa,辐散动能谱与旋转动能谱的交点位置随高度的变化与拐点位置随高度的变化一致,都是随着高度的增高向小波数方向移动。旋转分量与辐散分量交点的这种变化主要是由于旋转分量随高度降低较快、而辐散分量随高度变化不大引起的。在大尺度范围内,辐散分量远小于旋转分量,而在中尺度范围,辐散分量与旋转分量作用相当并逐渐超过旋转分量,出现交点。
(4)对动能谱的辐散分量在中尺度范围内进行线性拟合,发现225—50 hPa内的斜率均在-5/3左右变化,证实了Burgess(2013)的推断:中尺度动能谱-5/3的斜率主要是由动能谱的辐散分量决定的。同时也说明GRAPES-GFS模式对辐散运动的描述较好,模式动能谱斜率偏差主要是由模式对旋转分量的描述不准确所造成。
GRAPE-GFS能够描述出大气动能谱由大尺度过渡到中尺度时斜率转折的特征,但是模式模拟的中尺度范围动能谱斜率值较其他模式结果绝对值偏大,说明GRAPS-GFS对中尺度波动的描述能力存在较大误差,提高GRAPES-GFS对中小尺度波动的模拟能力将是下一步工作的重点,如提高模式分辨率,将更多更准确的观测资料引入同化系统,提供更为准确的初始场,改进模式耗散项和各种参数化方案,以及尝试进行多尺度同化等。
| 陈德辉, 薛纪善, 杨学胜等. 2008. GRAPES新一代全球/区域多尺度统一数值预报模式总体设计研究. 科学通报, 53(20): 2396-2407. Chen D H, Xue J S, Yang X S, et al. 2008. The overall design research about the new generational global/regional unified numerical forecast model GRAPES. Chin Sci Bull, 53(20): 2396-2407 (in Chinese) |
| 龚建东. 2007. 资料同化中二维特征长度随模式分辨率变化的分析研究. 大气科学, 31(3):459-467. Gong J D. 2007. The analysis on variation of horizontal de-correlation length with model resolution in data assimilation system. Chinese J Atmos Sci, 31(3): 459-467 (in Chinese) |
| 胡江林, 沈学顺, 张红亮等. 2007. GRAPES模式动力框架的长期积分特征. 应用气象学报, 18(3): 276-284. Hu J L, Shen X S, Zhang H L, et al. 2007. Characteristics of GRAPES dynamical core in long term integration. J Appl Meteor Sci, 18(3): 276-284 (in Chinese) |
| 王光辉, 沈学顺, 胡江林等. 2009. GRAPES全球非静力大气模式的正规模分析. 地球物理学报, 52(12):2964-2972. Wang G H, Shen X S, Hu J L, et al. 2009. Normal mode analysis of the GRAPES global non-hydrostatic atmospheric model. Chinese J Geophys, 52(12): 2964-2972 (in Chinese) |
| 王金成, 庄照荣, 韩威等. 2014. GRAPES全球变分同化背景误差协方差的改进及其对分析预报的影响: 背景误差协方差三维结构的估计. 气象学报, 72(1):62-78. Wang J C, Zhuang Z R, Han W, et al. 2014. An improvement of background error covariance in the global GRAPES variational data assimilation and its impact on the analysis and prediction: Statistics of the three-dimensional structure of background error covariance. Acta Meteor Sinica, 72(1): 62-78 (in Chinese) |
| 薛纪善, 陈德辉. 2008. 数值预报系统GRAPES的科学设计与应用. 北京: 科学出版社, 230-298. Xue J S, Chen D H. 2008. The Scientific Design and Application of GRAPES Numerical Forecast System. Beijing: Science Press, 230-298 (in Chinese) |
| 杨学胜, 胡江林, 陈德辉等. 2008. 全球有限区域数值预报模式动力框架的试验验证. 科学通报, 53(20): 2418-2423. Yang X S, Hu J L, Chen D H, et al. 2008. The experimental verification about the dynamic framework GRAPES global limit regional numerical forecast model. Chin Sci Bull, 53(20): 2418-2423 (in Chinese) |
| 张人禾, 沈学顺. 2008. 中国国家级新一代业务数值预报系统GRAPES的发展. 科学通报, 53(20): 2393-2395. Zhang R H, Shen X S. 2008. The development of China national new generationa operate numerical forecast system GRAPES. Chin Sci Bull, 53(20): 2393-2395 (in Chinese) |
| 郑永骏, 金之雁, 陈德辉. 2008. 半隐式半拉格朗日动力框架的动能谱分析. 气象学报, 66(2): 143-157. Zheng Y J, Jin Z Y, Chen D H. 2008. Kinetic energy spectrum analysis in a semi-implicit semi-Lagrangian dynamical framework. Acta Meteor Sinica, 66(2): 143-157 (in Chinese) |
| 朱国富, 薛纪善, 张华等. 2008. GRAPES变分同化系统中卫星辐射率资料的直接同化. 科学通报, 53(20): 2424-2427. Zhu G F, Xue J S, Zhang H, et al. 2008. Direct assimilation of satellite radiance data in GRAPES variational assimilation system. Chin Sci Bull, 53(22): 3465-3469 |
| 庄照荣, 薛纪善, 李兴良等. 2010. GRAPES全球模式的模式误差估计. 大气科学, 34(3):591-598. Zhuang Z R, Xue J S, Li X L, et al. 2010. Estimation of model error for the global GRAPES model. Chinese J Atmos Sci, 34(3): 591-598 (in Chinese) |
| Bacmeister J T, Eckermannn S D, Newman P A, et al. 1996. Stratospheric horizontal wavenumber spectra of winds, potential temperature, and atmospheric tracers observed by high-altitude aircraft. J Geophys Res, 101(D5): 9441-9470 |
| Bartello P. 2010. Quasi-geostrophic and Stratified Turbulence in the Atmosphere // Proc. IUTAM Symp. On Turbulence in the Atmosphere and Oceans. Cambridge, United Kingdom: Springer, 28: 117-130 |
| Boer G J, Shepherd T G. 1983. Large-scale two-dimensional turbulence in the atmosphere. J Atmos Sci, 40(1): 164-184 |
| Burgess B H, Erler A R, Shepherd T G. 2013. The troposphere-to-stratosphere transition in kinetic energy spectra and nonlinear spectral fluxes as seen in ECMWF analyses. J Atmos Sci, 70(2): 669-687 |
| Falkovich G. 1992. Inverse cascade and wave condensate in mesoscale atmospheric turbulence. Phys Rev Lett, 69(22): 3173-3176 |
| Gage K S. 1979. Evidence for a k to the -5/3 law inertial range in mesoscale two-dimensional turbulence. J Atmos Sci, 36: 1950-1954 |
| Gage K S, Nastrom G D. 1986. Thoeretical interpretation of atmospheric wavenumber spectra of wind and temperature observed by commercial aircraft during GASP. J Atmos Sci, 43(7): 729-740 |
| Hamilton K, Takahashi Y O, Ohfuchi W. 2008. Mesoscale spectrum of atmospheric motions investigated in a very fine resolution global general circulation model. J Geophys Res, 113: D18110, doi: 10. 1029/2008JD009785 |
| Hinkley D V. 1969. Inference about the intersection in two-phase regression. Biometrika, 56(3): 495-504 |
| Huang Y Y, Xue J S, Wan Q L, et al. 2013.Improvement of the surface pressure operator in GRAPES and its application in precipitation forecasting in South China. Adv Atmos Sci, 30(2): 354-366 |
| Kolmogorov A N. 1941. The local structure of turbulence in incompressible viscous fluid for very large Reynolds number. Dokl Akad Nauk SSSR, 30: 301-305 |
| Koshyk J N, Boville B A, Hamilton K, et al. 1999. Kinetic energy spectrum of horizontal motions in middle-atmosphere models. J Geophys Res, 104: 27177-27190 |
| Koshyk J N, Hamilton K. 2001. The horizontal kinetic energy spectrum and spectral budget simulated by a high-resolution troposphere-stratosphere-mesosphere GCM. J Atmos Sci, 58(4): 329-348 |
| Kraichnan R H. 1967. Inertial ranges in two-dimensional turbulence. Phys Fluids, 10(7): 1417-1423 |
| Laursen L, Eliasen E. 1989. On the effects of the damping mechanisms in an atmospheric general circulation model. Tellus A, 41A(5): 385-400 |
| Lilly D K. 1983. Stratified turbulence and the mesoscale variability of the atmosphere. J Atmos Sci, 40(3): 749-761 |
| Lindborg E. 1999. Can the atmospheric kinetic energy spectrum be explained by two-dimensional turbulence? J Fluid Mech, 388: 259-288 |
| Lindborg E. 2006. The energy cascade in a strongly stratified fluid. J Fluid Mech, 550: 207-242 |
| Nastrom G D, Gage K S. 1985. A climatology of atmospheric wave number spectra of wind and temperature observed by commercial aircraft. J Atmos Sci, 42(9): 950-960 |
| Peng J, Zhang L F, Luo Y, et al. 2014. Mesoscale energy spectra of the Mei-Yu front system. Part I: Kinetic energy spectra. J Atmos Sci, 71(1): 37-55 |
| Saujani S, Shepherd T G. 2006. A unified theory of balance in the extratropics. J Fluid Mech, 569: 447-464 |
| Skamarock W C. 2004. Evaluating mesoscale NWP models using kinetic energy spectra. Mon Wea Rev, 132(12): 3019-3032 |
| Straus D M, Ditlevsen P. 1999. Two-dimensional turbulence properties of the ECMWF reanalyses. Tellus, 51(5): 749-772 |
| Trenberth K E, Solomon A. 1993. Implications of global Atmospheric spectra for processing and displaying data. J Climate, 6(3): 531-545 |
| Waite M L, Snyder C. 2009. The mesoscale kinetic energy spectrum of a baroclinic life cycle. J Atmos Sci, 66(4): 883-901 |
| Waite M L, Snyder C. 2013. The mesoscale energy spectra of moist baroclinic waves. J Atmos Sci, 70(4): 1242-1256 |
| Zheng Z Y, Zhang W C, Xu J W, et al. 2012. Numerical simulation and evaluation of a new hydrological model coupled with GRAPES. Acta Meteor Sinica, 26(5): 653-663 |
 2015, Vol. 73
2015, Vol. 73


