中国气象学会主办。
文章信息
- 万超, 石爱丽, 周毓荃, 杨绍忠, 彭冲, 蒋元华. 2015.
- WAN Chao, SHI Aili, ZHOU Yuquan, YANG Shaozhong, PENG Chong, JIANG Yuanhua. 2015.
- 降温速率对三种类型水滴冻结过程影响的实验研究
- Experimental study of the impact of cooling rate on the freezing process of three kinds of water drops
- 气象学报, 73(5): 985-997
- Acta Meteorologica Sinica, 73(5): 985-997.
- http://dx.doi.org/10.11676/qxxb2015.068
-
文章历史
- 收稿日期:2014-11-26
- 改回日期:2015-05-26
2. 中国气象科学研究院, 北京, 100081;
3. 河南省气象局人工影响天气中心, 郑州, 450003;
4. 湖南省气象局气候中心, 长沙, 410118
2. Chinese Academy of Meteorological Sciences, Beijing 100081, China;
3. Weather Modification Center, Henan Meteorology Administration, Zhengzhou 450003, China;
4. Climate Center, Hunan Meteorology Administration, Changsha 410118, China
冻结核化有两种机制:一是同质核化,指纯净无任何杂质的过冷水通过自身水分子的随机碰撞形成冰胚的冻结过程;另一种是异质核化,当水中含有杂质时,外来粒子在某一温度下可作为形成冰胚的核心,最终导致水滴冻结。大气中一部分气溶胶粒子可充当冰核,他们能在远高于-40℃温度下在云中产生冰晶,故在较低层大气中成冰过程以异质核化为主,在温度低于-33℃的高空,则以同质核化为主(Hobbs,1974)。
目前,关于水滴冻结原理有两种解释,即随机假设和奇点假设。Bigg(1953)第一次提出随机过程的理论

式中,P(T)为温度在T时的冻结几率,Nu为比温度T高dTs时的未冻结液滴数,dN/dTs是在单位温度变化中的冻结液滴数,B、a为常数,V是液滴的体积,γ为降温速率,Ts为过冷却温度(Ts=0-T)。
Carte(1959)、Dufour等(1963)给了该理论一个更为通用的形式。式(1)指出,在任何时刻,只要温度相同,所有液滴都有相同的冻结几率。该假设对于完全纯净的水来说是合理的(同质核化),但是要对含有固体杂质的水(异质核化)有效的话,除非所有液滴有相同的核含量。Vonnegut等(1984)、Wang等(1984)通过实验研究得出了与随机假设一致的结论。
对异质冻结情况的另一种解释由Levine提出,Langham等(1958)给出了以下形式
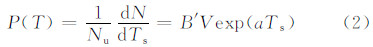
式中,B′为常数,其他物理量同式(1)。
该假设为奇点假设,认为每个杂质都有一个特征温度,达到这个温度肯定能使含有它的液滴核化冻结。在此假设下,每个水滴的冻结温度为其中最有效杂质的个体特征温度。该假设也得到了与之吻合的实验结果(Levkov,et al,1966;Salt,1966;Vali,et al,1966)。
大量液滴实验已经表明对于以恒定速率降温的样本,冻结几率随过冷却温度升高呈指数增长。式(1)和(2)都和此发现一致,不能确定是哪一种假设,因此要在不同实验中改变降温速率γ来检测。根据随机假设,降温速率每增加1倍,指数前的系数会减小一半;而根据奇点假设,降温速率的变化不会影响冻结几率和过冷却温度的关系,因为只要达到了特征温度水滴就会冻结,而与降温的快慢无关。本研究针对这两种不同的现象对雨水和瓶装饮用水做了5种不同的降温速率实验来检验。
两种假设在恒温情况下的现象也是很直接的。根据奇点假设,在固定温度下没有冻结事件发生,因为只有在液滴温度低于杂质的特征温度时冻结才发生。而随机假设有如下关系
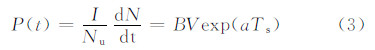
它表明冻结事件在恒温时将持续发生,也就是在一定温度下,只要时间足够长,最后都会形成冻滴,且温度越低几率越高。介于两种不同的现象,需要恒温实验进行检验。
所以在水滴冻结研究中最大的不确定性在于随机假设和奇点假设在水滴冻结过程中如何起作用以及他们的相对作用怎样,针对这个问题,Vali等(1966)对蒸馏水、冰雹融化水、雪融化水做了不同降温速率和恒温实验。该实验和大量其他实验表明,水滴冻结既与所含冰核有关,又包含一定的随机过程,水滴冻结过程是两种假设的共同作用。Vali(1994)根据实验和观测结果总结出冻结核化的时间相关冻结模式(TDFM),强调了浸入冻结机制中外来核在冰胚形成中的位置和作用,也考虑了随机冻结理论中对时间的依赖。
已有成果在平均与中值冻结温度跟降温速率的关系上所选择的水样和降温速率不多。他们没有在不同降温速率实验当中给出冻结几率与过冷却温度的定量关系,也没有在恒温实验中给出冻结几率与时间的定量关系,并且对恒温实验中出现的冻结现象解释还存在不足。云物理冻结是一个重要的基本过程,目前的模式在过冷水滴异质冻结项上大多采用随机理论,如Milbrandt等(2005)、洪延超(1996)等,这就假设了在恒温时段会一直有液滴冻结,所以深入细致地研究不同降温速率及恒温对冻结的影响不仅可以丰富水滴冻结的基础理论,也能对模式当中的相关项进行改进。
本研究在此基础上对雨水、纯净水、瓶装饮用水做了一系列不同降温速率和雨水恒温的冻结实验,旨在进一步研究降温速率对水滴冻结的影响,检验冻结过程中随机假设和奇点假设的关系,并且取得定量的结果。
2 实验仪器及实验方法 2.1 均匀水滴冻结实验装置使用中国气象科学研究院的均匀水滴冻结实验装置(杨绍忠等,2007),该装置是在Vali(1971)用于均匀水滴冻结实验检测水中冻结核含量的基础上研制的。如图 1a所示,线性降温铜板上分布着相互隔开并产生水滴冻结信号的49个热敏感应元件,其中有47个用于承放均匀水滴,水滴温度随铜板以设定的速率线性降低,在降温过程中水滴随机发生冻结。水滴冻结的同时释放冻结潜热,热敏感应元件可以探测到这一信号并送到计算机中,记录下这个水滴冻结的温度。在专用数据处理软件环境中,实时显示、处理和存储数据。
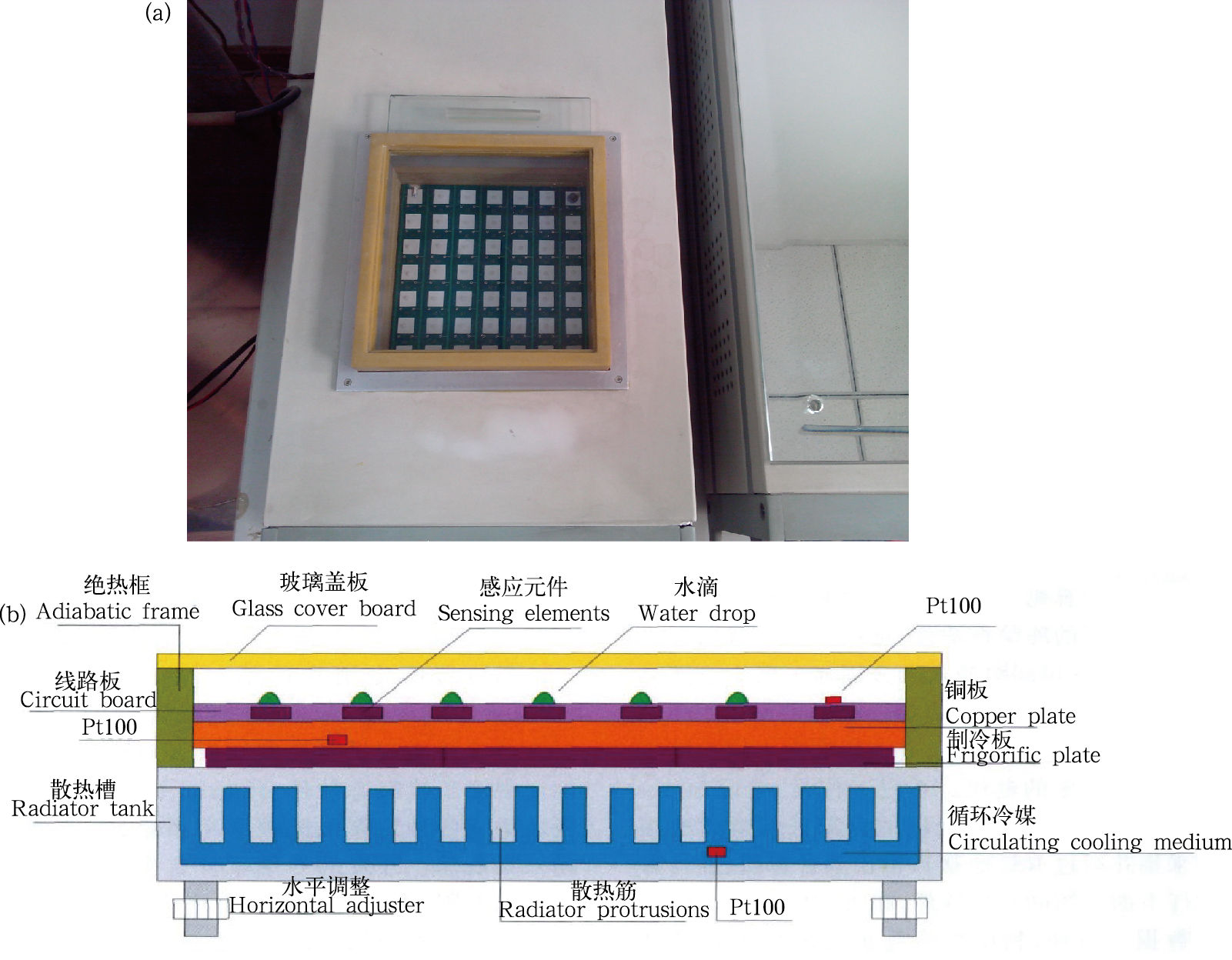 |
| 图 1 均匀水滴冻结实验装置(a)和实验装置结构示意(b)Fig. 1 Device for the uniform drops freezing experiment (a) and structure schematic diagram for the experimental device (b) |
实验装置结构如图 1b所示,该装置由制冷板、铜板、感应元件、绝热框、玻璃盖板、散热槽、电路板等组成。将尺寸为140 mm×140 mm×5 mm的铜板表面镀铬,用导热硅脂粘贴在制冷板冷面上,旁边包围绝热边框,顶上是推拉式玻璃盖板,这样构成一个高50 mm,并且能与外界隔热、防尘的封闭小室,同时玻璃盖板也便于观察。铜板上均匀分布着49个10 mm×10 mm,中心间距为18 mm的感应元件,在线性降温过程中水滴冻结释放的潜热被各自的感应元件吸收,对其他水滴的随机冻结不会产生影响。制冷板热面贴在漩涡式散热槽上,与一个装满冷媒(乙二醇水溶液)的容器相连,由另一个独立的制冷机组冷却。在水泵推动下,冷媒循环流动,不断地将制冷板热面产生的热量带走。
水滴的线性降温由欧陆818P4型控温仪控制完成。在左上角的感应元件表面粘贴一微型铂膜Pt100热电阻,用于模拟测量水滴的实际温度。另外在铜板下表面的凹槽内也用导热硅脂嵌入一个微型铂膜Pt100电阻,用于温度控制回路的温度感应。为了保证水滴温度能线性降低,需将控温仪控温程序分段设定功能,分别设定每段的控温参数,并事先进行多次试验,才能得到一条能使水滴线性降温的控温程序。此外,也可设定程序使水滴处于某一恒温值。
2.2 实验方法
实验选用3种水样,分别为:2013年7月一次中雨过程中收集的雨水,在化学试剂厂购买的纯净水,以及瓶装饮用水(农夫山泉),选此3种水样是因为它们所含杂质种类和数量不同导致纯度不同,具有一定的代表性(但因购买的纯净水杂质较多,以致和瓶装饮用水差异不大)。采用6号针头微型注射器,产生均匀水滴。具体做法是,用针管取一定量体积水样,在憎水膜上滴至水样用完,用总体积/水滴数得到每个水滴的体积,再通过 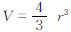 得到半径从而求得直径约2.6 mm。每一组实验47颗均匀水滴,设计了不同恒定降温速率和恒温两类实验。由于实验设备只能做直径为毫米量级的中滴冻结实验,此直径范围的水滴已是很大的雨滴,所以与云中实际冻结过程有差异。
得到半径从而求得直径约2.6 mm。每一组实验47颗均匀水滴,设计了不同恒定降温速率和恒温两类实验。由于实验设备只能做直径为毫米量级的中滴冻结实验,此直径范围的水滴已是很大的雨滴,所以与云中实际冻结过程有差异。
实验开始前,首先在每个感应元件上滴上憎水膜(维持统一的本底),等其干后将控制温度降到5℃,此时铜板的实际温度在6.2℃左右(±0.1℃),开始滴水滴。然后盖上玻璃盖板,用之前设定的程序段开始线性降温(每隔5℃为一个程序段)。一组实验完成后需将冷台升温,在高于0℃温度段用滤纸吸附小水滴并用丙酮清洗每个感应元件表面(防止前一组水滴污染后一组水滴),再开始下一组实验。
在雨水实验的事先测试中发现,每次实验最后冻结的两个滴都处在右上角两个铜板热敏感应元件,所以估计是因为装置老化导致那两个铜板的温度高于其他铜板,故每组实验取45颗水滴。其中0.2、0.4℃/min做5组共225颗水滴;1、2、4℃/min做10组共450颗水滴。这一系列的实验在2周之内完成。雨水第1次恒温实验的水滴总数为1175颗,第2次恒温实验的水滴总数为675颗。纯净水两种降温速率的实验水滴数各为690颗,瓶装饮用水5种降温速率实验的水滴数为230颗,实验各自均在1周之内完成。
3 纯净水恒定降温速率实验结果分析为了研究纯净水在恒定降温速率下的水滴冻结特征,在化学试剂厂购买纯净水(含有杂质,并不是蒸馏水),于均匀水滴冻结实验装置上完成1和2℃/min两种降温速率的实验,得到纯净水冻结随温度的分布情况。
3.1 纯净水不同降温速率累加冻结比例和温度的关系从两种降温速率的累加冻结比例(至该温度时液滴冻结数/液滴总数)(图 2)可见,纯净水在相同温度下,总体上降温速率慢的累加冻结比例大于降温速率快的,只在温度高于-14℃前2℃/min的累加冻结比例略大一点。
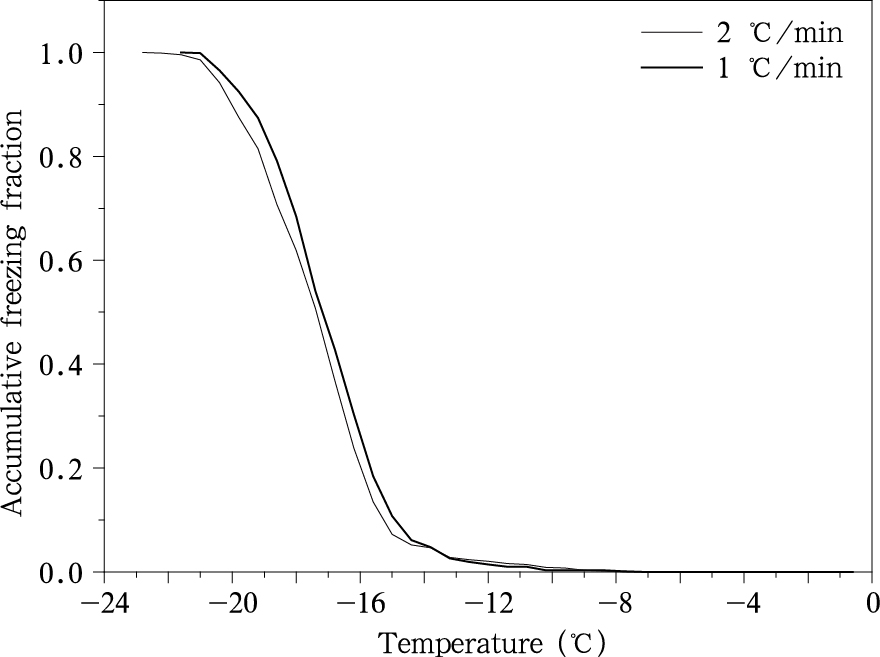 |
| 图 2 纯净水累加冻结比例与温度的关系Fig. 2 Relationship between the accumulative freezing fraction and temperature of the pure water |
从两种降温速率与冻结温度的关系(表 1)可以看出,无论是平均冻结温度还是中值冻结温度,降温速率越大其值越低,且平均冻结温度都低于中值冻结温度。
| 冷却速率(℃/min) | Ta(℃) | s(℃) | Tm(℃) |
| 1 | -17.20 | 1.88 | -17.13 |
| 2 | -17.53 | 2.03 | -17.40 |
| 注: Ta、Tm 分别为平均冻结温度和中值冻结温度,s为平均冻结温度的标准差。 Ta, Tm are the average freezing temperature and median freezing temperature, respectively, s is standard deviation of the average freezing temperature. |
|||
计算两种不同降温速率下对温度的液滴冻结几率(P=(1/Nu)(dN/dTs),Nu为比温度T高dT时的未冻结液滴数,dN/dTs 是在单位温度变化中的冻结液滴数),得到图 3,发现纯净水的液滴冻结几率随温度的降低呈指数增大。
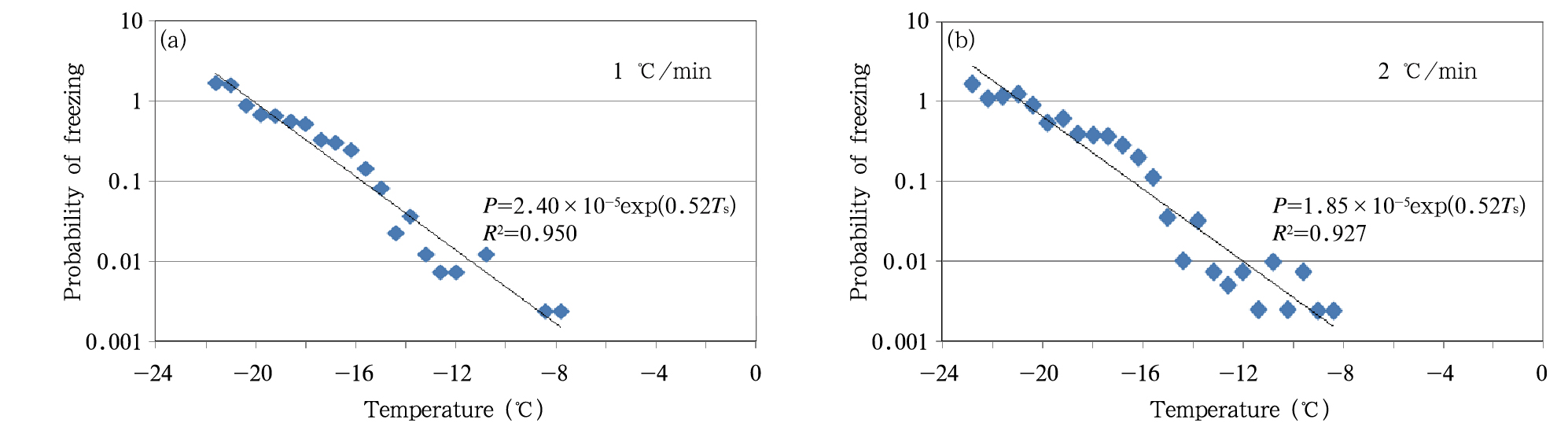 |
| 图 3 纯净水冻结几率与温度的关系Fig. 3 Relationship between the probability of freezing and temperature of the pure water |
通过拟合得到当降温速率为1℃/min时,冻结几率与温度的关系为:P=2.40×10-5exp(0.52Ts);当降温速率为2℃/min时,冻结几率与温度的关系为:P=1.85×10-5exp(0.52Ts)。可以发现两种情况的斜率相同(0.52),且当降温速率增大时,指数函数的系数会减小,这与奇点理论的公式不符,但系数的改变也不像随机理论那样减半。
4 雨水恒定降温速率实验结果分析为研究更多不同的降温速率对自然降水水滴冻结的影响,取用2013年7月一次中雨过程中收集到的雨水,分别以0.2、0.4、1、2、4℃/min的降温速率使冷台降温,得到不同降温速率下冻结随温度的变化特征。
4.1 不同降温速率下累加冻结比例和温度的关系为了得到不同降温速率下水滴的总体冻结情况,将5种降温速率实验的液滴冻结比例做累加进行对比(图 4)。由图 4可知,温度高于-13℃时,除0.2℃/min降温速率的累加冻结比例最高外,4和2℃/min的累加冻结比例都高于0.4和1℃/min的比例。当温度降到-13℃以下时,在同温度,降温速率越慢的,累加冻结比例越高;反之降温速率越快的累加冻结比例
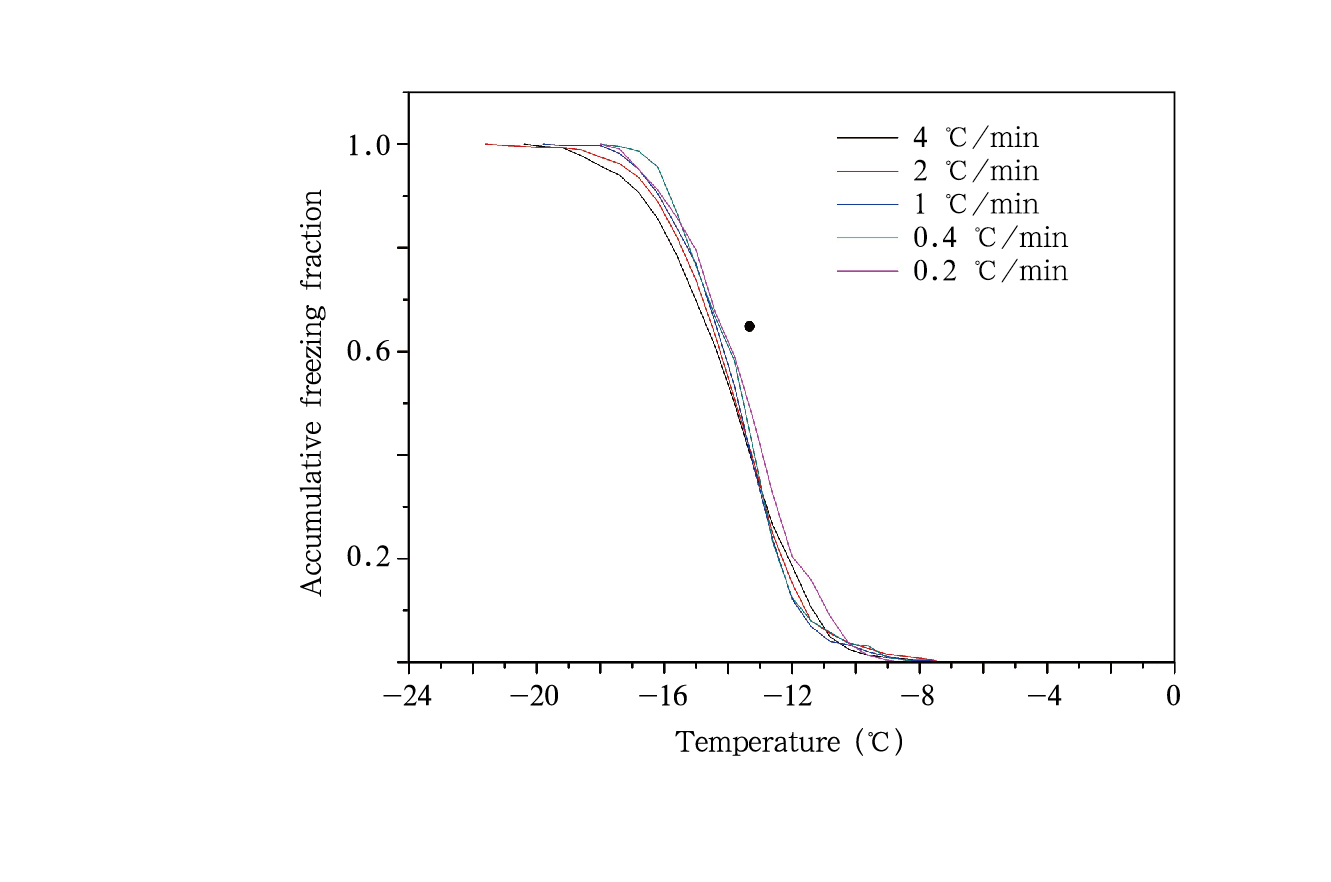 |
| 图 4 雨水5种降温速率的累加冻结比例与温度的关系Fig. 4 Relationship between the accumulative freezing fraction and temperature in the 5 kinds of cooling rate of the rainwater |
就相对越低,除了在-16—-17℃范围内0.4℃/min的冻结比例短暂超过了0.2℃/min的组。总体来看,降温速率慢的实验随温度降低时,累加的冻结比例高于降温速率快的实验,但没有纯净水那么明显。
4.2 雨水降温速率和冻结温度的关系进一步分析降温速率和冻结温度的关系,给出每组平均冻结温度(Ta)、标准差以及中值冻结温度(Tm)(表 2),可以看出,不同降温速率的平均冻结温度标准差相差不大,最大的是4℃/min时的2.11℃,最小为0.4℃/min时的1.63℃。
| 冷却速率(℃/min) | ||||||||||||||
| 0.2 | 0.4 | 1 | 2 | 4 | ||||||||||
| Ta | s | Tm | Ta | s | Tm | Ta | s | Tm | Ta | s | Tm | Ta | s | Tm |
| -13.62 | 1.90 | -13.7 | -13.09 | 1.72 | -13.2 | -13.68 | 1.72 | -13.5 | -13.70 | 1.62 | -13.5 | -13.79 | 2.34 | -13.8 |
| -12.90 | 1.83 | -12.7 | -14.35 | 1.63 | -14.6 | -14.13 | 1.71 | -13.9 | -13.64 | 1.78 | -13.7 | -14.36 | 1.98 | -14.0 |
| -13.29 | 1.86 | -13.2 | -13.48 | 1.45 | -13.4 | -14.13 | 1.61 | -14.3 | -14.11 | 2.16 | -13.9 | -14.28 | 2.33 | -13.9 |
| -14.10 | 1.95 | -14.0 | -13.84 | 1.75 | -13.6 | -13.47 | 1.91 | -13.4 | -15.02 | 1.74 | -14.6 | -13.88 | 1.88 | -13.8 |
| -13.92 | 1.71 | -13.9 | -13.82 | 1.61 | -13.6 | -13.95 | 1.43 | -13.8 | -13.98 | 1.64 | -14.1 | -13.96 | 1.93 | -14.1 |
| -14.12 | 2.11 | -14.1 | -13.58 | 2.06 | -13.2 | -14.31 | 2.04 | -14.1 | ||||||
| -13.64 | 1.78 | -13.4 | -14.18 | 1.69 | -14.1 | -13.92 | 2.03 | -13.6 | ||||||
| -14.00 | 1.87 | -13.7 | -13.33 | 2.33 | -13.1 | -13.80 | 1.94 | -13.6 | ||||||
| -14.11 | 1.83 | -14.0 | -14.09 | 2.07 | -14.0 | -13.87 | 2.22 | -13.9 | ||||||
| -13.58 | 1.67 | -13.3 | -14.02 | 2.55 | -14.2 | 14.16 | 2.40 | -14.0 | ||||||
| Ta=-13.57℃ | Ta=-13.72℃ | Ta=-13.88℃ | Ta=-13.97℃ | Ta=-14.03℃ | ||||||||||
| s=1.85℃ | s=1.63℃ | s=1.76℃ | s=1.96℃ | s=2.11℃ | ||||||||||
| Tm=-13.50℃ | Tm=-13.68℃ | Tm=-13.74℃ | Tm=-13.84℃ | Tm=-13.88℃ | ||||||||||
由表 2可见,降温速率越快,平均冻结温度越低(图 5),平均冻结温度与降温速率成对数函数关系,其关系可表达为Ta=-0.15ln(γ)-13.48。降温速率每增大1倍,平均冻结温度约降低0.12℃。这一趋势与Vali等(1966)对蒸馏水研究得到的结果相似,计算出他们的关系式为Ta=-0.245ln(γ)-20.54,平均冻结温度随降温速率增大而减小的幅度大于此次雨水实验,他们发现每当降温速率增大1倍时,平均冻结温度降低0.2℃。Bigg(1953)也曾发现降温速率为0.05℃/min时平均冻结温度比0.5℃/min时高2℃。Salt(1966)在对生物质核的研究中,也发现了当降温速率为原来的2倍时,平均冻结温度约降低0.24℃。
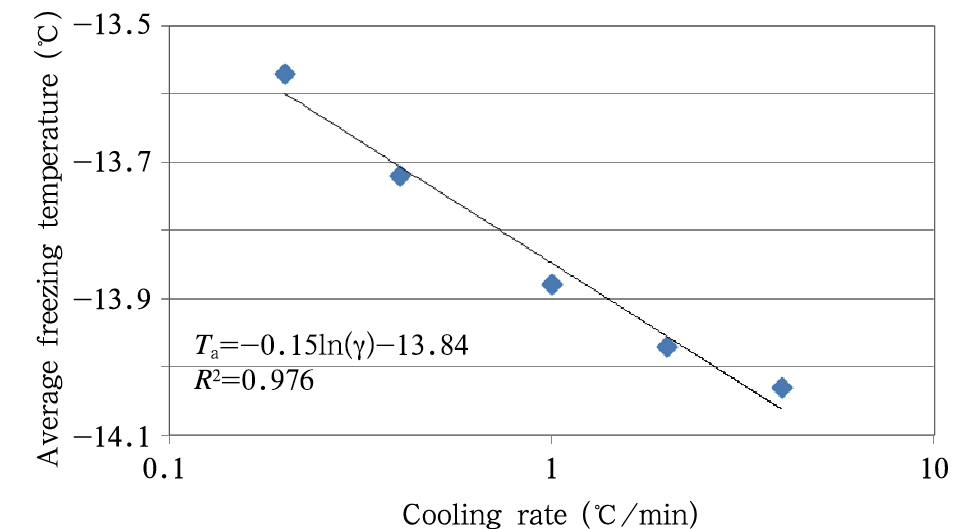 |
| 图 5 平均冻结温度和降温速率的关系Fig. 5 Relationship between the average freezing temperature and the cooling rate |
从表 2还可看出,中值冻结温度与降温速率也呈对数函数关系,拟合关系式为Tm=-0.12 ln(γ)-13.73(图 6)。降温速率每增大1倍,中值冻结温度平均约降低0.1℃。
 |
| 图 6 中值冻结温度和降温速率的关系Fig. 6 elationship between the median freezing temperature and the cooling rate |
通过数据还可发现,平均冻结温度普遍比中值冻结温度略低。
4.3 不同降温速率下雨水冻结几率和温度的关系为进一步研究在不同降温速率下,液滴冻结和温度的关系,计算5种不同降温速率情况下,液滴对温度的冻结几率,P=(1/Nu)(dN/dTs),同样发现冻结几率随温度降低呈指数增大的形式,与随机假设和奇点假设都相当吻合,与已有的分布趋势也相同。
设指数前的系数为C,斜率为a,现根据5种降温速率下最佳拟合的斜率a值,选择一个中间值0.5,对5种情况的冻结几率与温度的关系做拟合(图 7)。可以发现,除降温速率为2和4℃/min的系数分别为1.1×10-4和1.2×10-4外,指数函数前的系数是随降温速率的增大而减小的,但系数的减小也不像随机假设那样,降温速率增大1倍,系数减小一半。
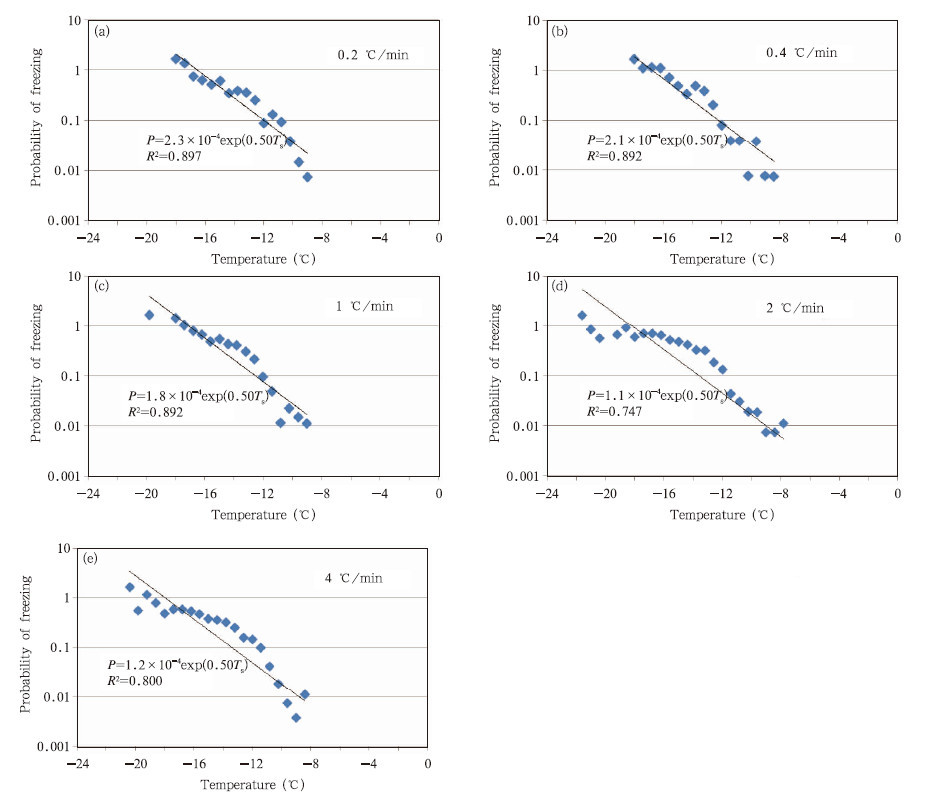 |
| 图 7 固定斜率值拟合的雨水冻结几率与温度的关系Fig. 7 Relationship between the probability of freezing and temperature of the rainwater under the fixed slope |
通过随机假设公式指数前的系数C=BV/γ,算出5种降温速率下的B值分别为0.83×10-4、1.52×10-4、 3.26×10-4、 4×10-4、 8.7×10-4cm-3s-1,平均值为3.66×10-4cm-3s-1。之前Barklie和Gokhale得到的自来水B=2.5×10-4cm-3s-1,雨水B=2.0×10-4cm-3s-1,与本次雨水实验的平均B值相差不大。但他们得到的a值在0.57—0.75,平均值为0.65,比本实验的平均斜率要大。
5 瓶装饮用水恒定降温速率实验结果分析为了进一步研究降温速率与水滴冻结的关系,取瓶装饮用水,补充做了线性降温速率分别为1、2、3、4和5℃/min的冻滴实验。
5.1 瓶装饮用水不同降温速率累加冻结比例和温度的关系从5种降温速率的累加冻结比例(图 8)可见,除在温度低于-21℃时5℃/min的累加冻结比例略大于4℃/min的以外,其他时候在相同温度下,有明显的降温速率慢的累加冻结比例大于降温速率快的这一现象。
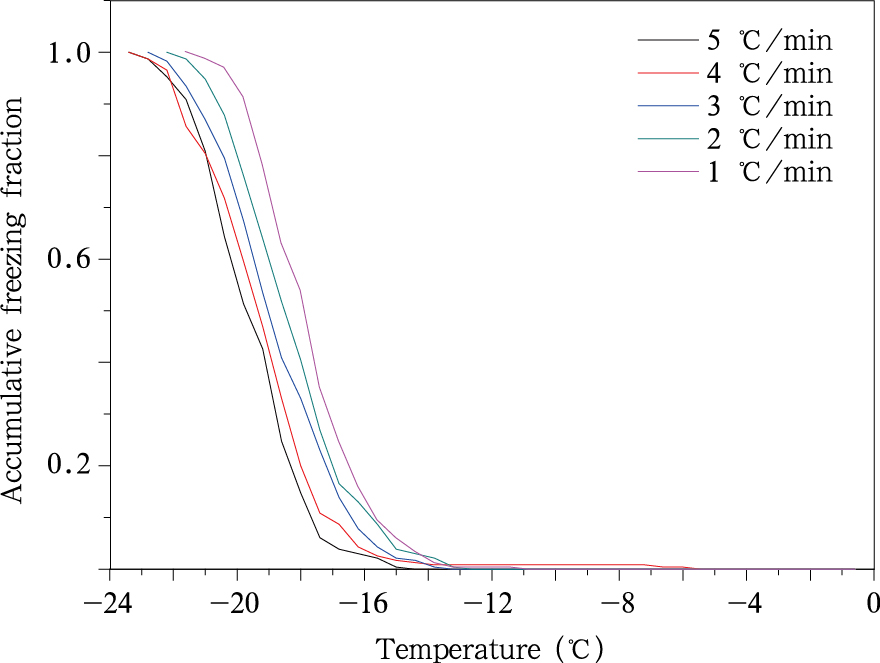 |
| 图 8 瓶装饮用水5种降温速率累加冻结比例与温度的关系Fig. 8 Relationship between the accumulative freezing fraction and temperature in the 5 kinds of cooling rate of the bottled water |
从5种不同降温速率下液滴的平均和中值冻结温度(表 3)可见,瓶装饮用水的平均、中值冻结温度与降温速率成线性关系(图 9),回归关系式分别为Ta=-0.46γ-17.49和Tm=-0.44γ-17.54 。降温速率每增加1℃/min,平均冻结温度和中值冻结温度下降0.46℃和0.44℃。虽然下降的函数不同,但冻结温度随降温速率的增大而减小这一趋势与雨水实验得到的结果一致。
| 降温速率(℃/min) | 1 | 2 | 3 | 4 | 5 | |
| 平均冻结温度(℃) | -17.89 | -18.45 | -18.95 | -19.39 | -19.74 | |
| 中值冻结温度(℃) | -17.9 | -18.5 | -18.9 | -19.3 | -19.7 |
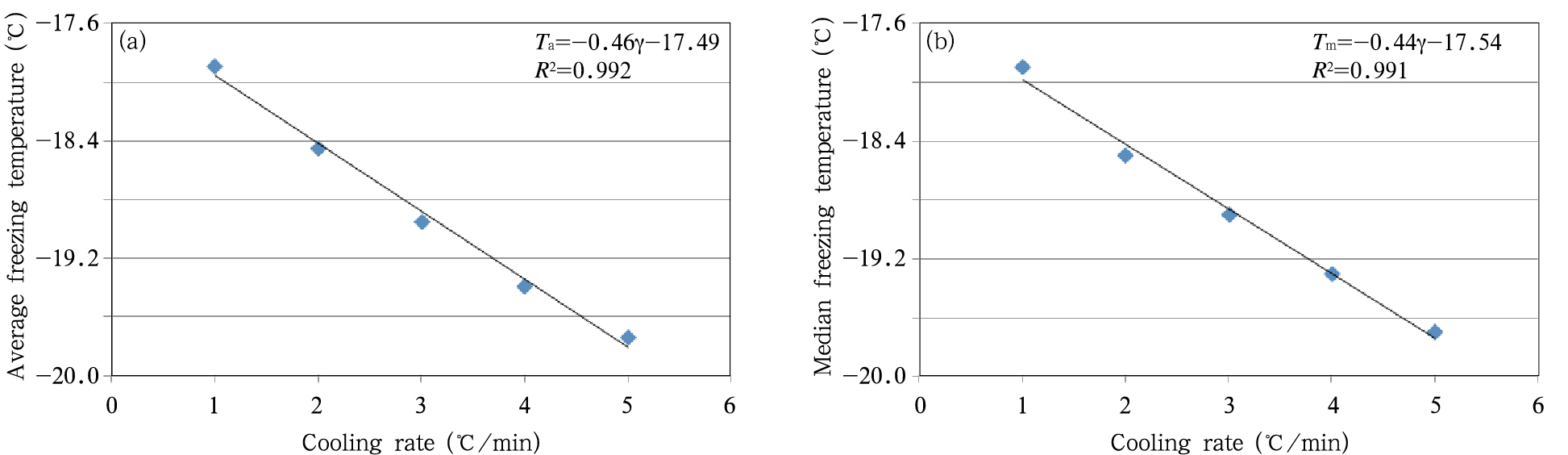 |
| 图 9 瓶装饮用水平均(a)与中值(b)冻结温度和降温速率的关系Fig. 9 Relationships of the average freezing temperature (a) and median freezing temperature (b) with the cooling rate of the bottled water |
计算5种情况对温度的液滴冻结几率(图 10),对其与温度的关系做拟合,得到降温速率为1、2、3、4、5℃/min的关系式分别为
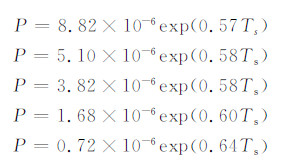
 |
| 图 10 瓶装饮用水冻结几率与温度的关系 Fig. 10 Relationship between the probability of freezing and temperature of the bottled water |
同样通过随机假设公式指数前的系数  得到瓶装饮用水的B值分别为:1.60×10-5、 1.85×10-5、 2.08×10-5、 1.22×10-5、 0.65×10-5 cm-3s-1,平均值1.48×10-5cm-3s-1。Barklie和Gokhale发现纯度比较低的蒸馏水B=2.0×10-6cm-3s-1,本实验得到的B值在雨水和纯度比较低的蒸馏水之间。
得到瓶装饮用水的B值分别为:1.60×10-5、 1.85×10-5、 2.08×10-5、 1.22×10-5、 0.65×10-5 cm-3s-1,平均值1.48×10-5cm-3s-1。Barklie和Gokhale发现纯度比较低的蒸馏水B=2.0×10-6cm-3s-1,本实验得到的B值在雨水和纯度比较低的蒸馏水之间。
将5条拟合曲线在一张图上对比(图 11),发现在相同温度下,降温速率越慢的实验,冻结几率越高;反之降温速率快的冻结几率就越低。
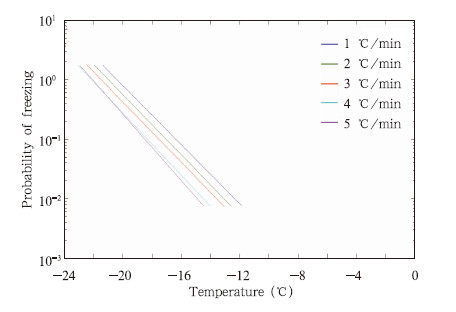 |
| 图 11 瓶装饮用水5种降温速率下冻结几率与温度关系的拟合曲线Fig. 11 Fitting curve of the probability of freezing and temperature in the 5 kinds of cooling rate of the bottled water |
设指数前的系数为C,可以发现C和降温速率γ有如下指数关系(图 12)
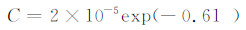
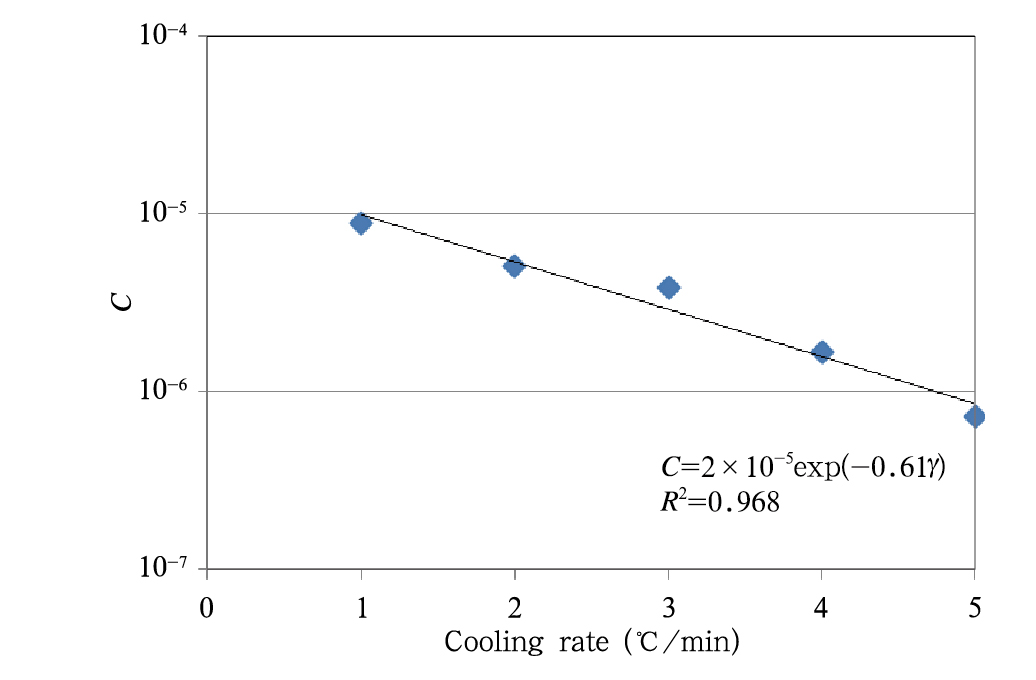 |
| 图 12 C与降温速率γ的关系Fig. 12 Relationship between C and the cooling rate γ |
从5种降温速率的冻结几率与温度关系来看,斜率a与降温速率γ有如下线性关系(图略)
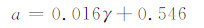
a的取值在0.57—0.64,且降温速率越大,a值越大,但相差不大,平均值为0.594。
Vali等(1966)用蒸馏水在降温速率为0.5和2℃/min时计算出了冻结几率与温度的关系(图 13),通过对他们的数据拟合得到关系式分别为
 |
| 图 13 Vali实验的蒸馏水在两种降温速率(a. 0.5℃/min, b. 2.0℃/min)下冻结几率与温度的关系Fig. 13 Relationship between the probability of freezing and temperature in the two kinds of cooling rate of the distilled water experiment by Vali (a. 0.5℃/min, b. 2.0℃/min) |
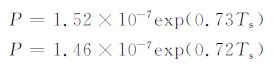
可以看出指数前的系数C也随降温速率的增大而减小,但是没有本实验对纯净水和瓶装饮用水的实验那样明显。
6 雨水恒定温度实验结果分析为研究水滴的冻结过程,在水滴冻结几率比较高的温度下维持恒温(降温速率为0或者极慢),观察水滴是否冻结以及冻结的个数,检验随机假设和奇点假设的关系。
6.1 第1次恒温实验取与恒定降温速率实验相同的雨水,以 2℃/min的降温速率使冷台温度降低到-13℃,然后维持30 min(约1 min左右控制住温度,其后的恒温时间有±0.1℃的波动),之后恢复2℃/min的降温速率,直到一组水滴全部冻结为止。
6.1.1 雨水恒温实验冻结几率和时间的关系整个过程对时间的液滴冻结几率用下式得出
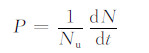
式中,Nu为未冻结的液滴数,dN/dt是单位时间里的冻结液滴数。
当样本达到0℃时开始计时,开始计时后6.5—36.5 min在-13℃维持恒温30 min。6.5 min之前和36.5 min之后的两部分是以2℃/min速率的降温阶段。从冻结几率与时间和温度的关系(图 14)可见,冻结几率是时间和温度的函数。在中间恒温部分,冻结几率随时间成指数衰减,约15 min以后,冻结现象不再发生。该现象既不按随机假设那样保持一恒定值,也不像奇点假设那样为0。在两边的恒定降温速率部分,冻结几率随温度的降低仍然成指数增大。恒温结束恢复恒定降温时,前30 s的冻结几率比恒温之前小,30 s以后,冻结几率恢复到恒温前并随温度的降低指数增大。这一结果同Vali等(1966)发现的结果有很好的一致性,他们的实验水样为蒸馏水,恒定温度为-20℃,恒温时间15 min,虽然水样、恒定温度及恒温时间都不相同,但是在线性降温过程以及恒温过程中,冻结几率随时间的变化趋势却很相似,且都有在刚恢复降温时,冻结几率没有持续降温时的冻结几率大这一现象。
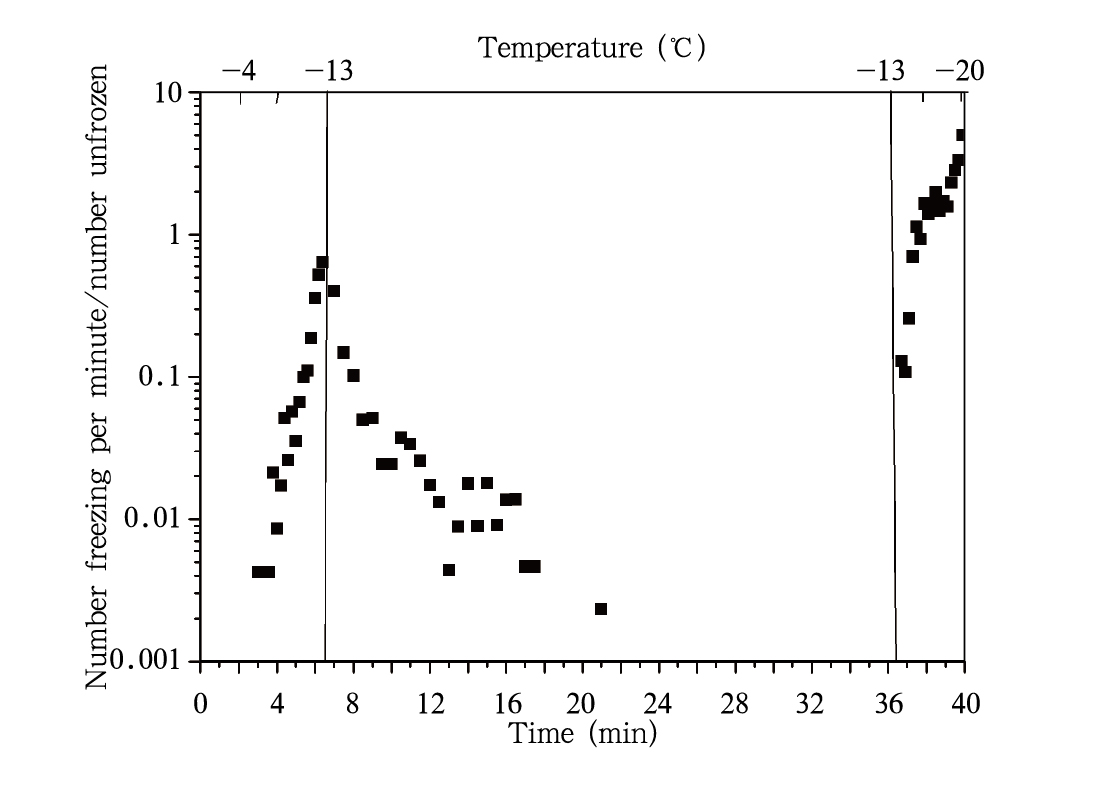 |
| 图 14 液滴冻结几率随时间的变化Fig. 14 Changes in the probability of freezing of the water drops with time |
图 15给出恒温实验的液滴累加冻结比例和温度及时间的关系,其中黑实线为累加冻结比例,红实线为温度。可以发现,刚开始两分钟的恒温阶段累加冻结比例的增长相对较快,两分钟后累加冻结比例增长明显减缓。到大约15 min后累加冻结比例不再增长。结合之前图 4累加冻结比例与温度的关系,可见在-13℃恒温30 min后,累加的液滴冻结比例高于在任何一种降温速率下的值。这也从另一方面说明了在随温度降低时,降温速率慢的(这里可看做特别慢的降温速率)累加冻结比例高于降温速率快的实验。假设温度刚降低到-13℃时的时间t为0,此后30 min恒温时间内,累加冻结比例(Nf/N0)和时间t有如下指数关系
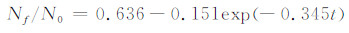
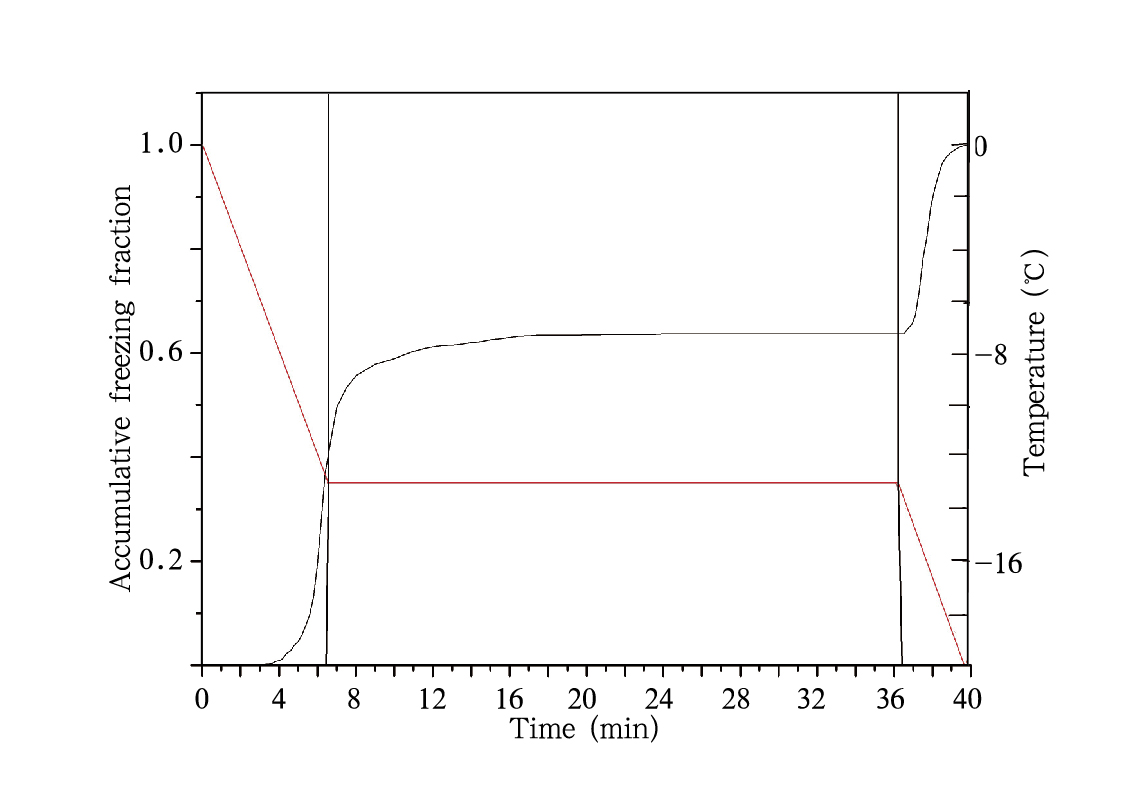 |
| 图 15 液滴累加冻结比例、温度与时间的关系Fig. 15 Relationship between the accumulative freezing fraction of the water drops and temperature and time |
对于这一现象,进一步做了补充实验:首先,以2℃/min的降温速率使冷台降温到-13℃,维持2 min,再以2℃/min降温速率使冷台温度降低到-14.5℃,保持恒温2 min,再继续以相同的速率降温,直到一组水滴完全冻结为止。
6.2.1 雨水恒温实验冻结几率和时间的关系采用同上述实验相同的公式,计算整个过程对时间的液滴冻结几率。得到冻结几率与时间和温度的关系(图 16)。当样本在温度下降到0℃时开始计时,其中,6.5—8.5 min时段在-13℃保持恒温2 min,9.1—11.1 min时段温度在-14.5℃保持恒温2 min,其余时段以2℃/min的速率降温,其中8.5—9.1 min温度由-13℃降低到-14.5℃(降温速率约2℃/min)。
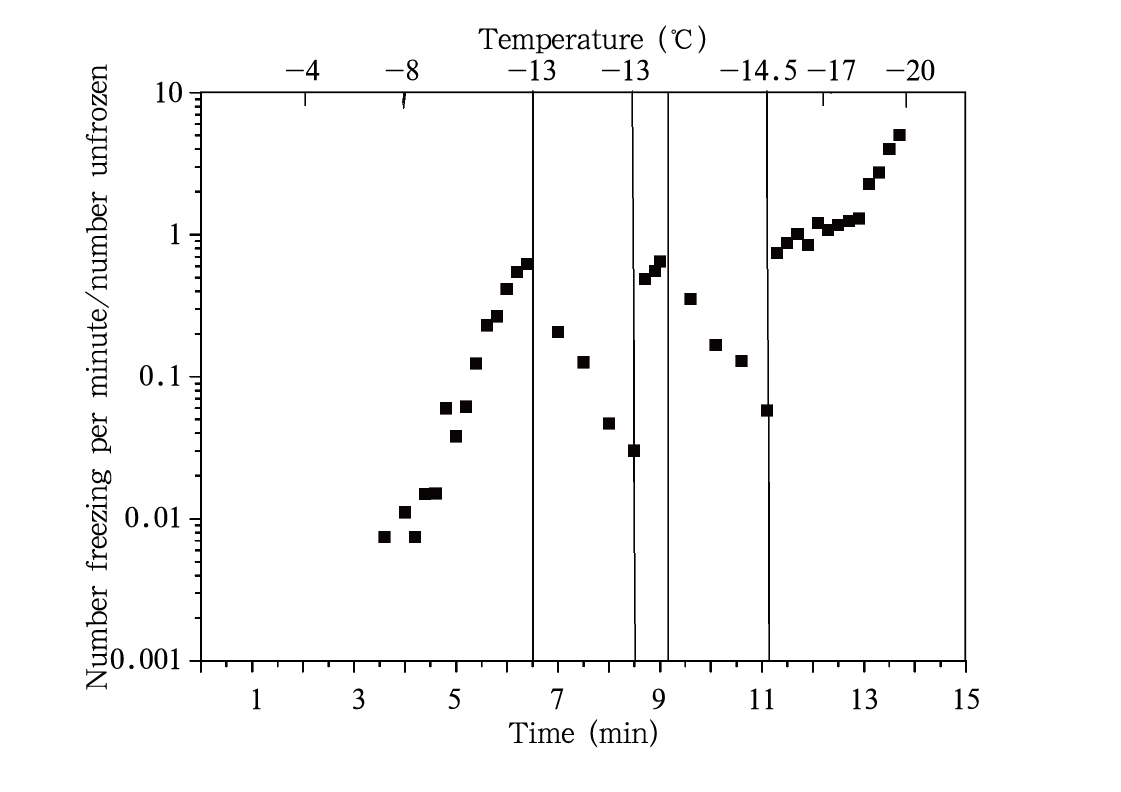 |
| 图 16 液滴冻结几率随时间和温度的变化Fig. 16 Changes in the probability of freezing of the water drops with time and temperature |
由图 16可见,冻结几率仍是时间和温度的函数。在两段恒温期,冻结几率仍然随时间呈指数衰减。在第3部分恢复恒定降温时,也出现了冻结几率没有持续降温时的冻结几率大这一现象,但是刚恢复时的冻结几率比上一个实验刚恢复降温时的大。在第5部分恢复恒定降温时,冻结几率跟恒温前的相差不大,并且随时间指数增大。
6.2.2 雨水恒温实验累加冻结比例和温度及时间的关系从液滴累加冻结比例和温度与时间的关系(图 17,黑实线为累加冻结比例,红实线为温度)可见,累加冻结比例在线性降温阶段的增长明显快于在恒温阶段的增长。
 |
| 图 17 液滴累加冻结比例、温度与时间的关系Fig. 17 Relationships between the accumulative freezing fraction of the water drops and temperature and time |
通过上述两个恒温实验的累加冻结比例(图 15和图 17)发现,水滴在恒温阶段内有一个冻结的“总量”。而当这个“总量”全部冻结完成后,水滴冻结现象不再发生。该现象可以用随机假设和奇点假设结合起来解释,当温度达到或低于特征温度时,液滴冻结,但是水分子在冻结核上的聚合需要一定的时间,所以液滴的冻结就在恒温阶段出现了,此现象在恒定降温速率实验当中容易被忽略,本来在某一温度下冻结的液滴因为需要时间冻结,出现了在下一温度段冻结的现象。
对两次实验在-13℃恒温段冻结几率与时间的关系做拟合,刚开始恒温时间t取0,可以得到,在前2 min内两次实验的公式分别为
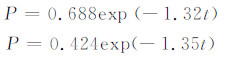
虽然指数前的系数有差别,但斜率相差不大,可见在恒温段的前2 min内,液滴的冻结几率随时间成指数降低的速率几乎一致。但对第1次实验的15 min内做拟合,发现公式:P=0.122exp(-0.29t),斜率明显减小。可见,在恒温2 min后,液滴的冻结几率随时间的衰减会变慢。从累加冻结的比例(图 15)也可看出,2 min以后新的冻结液滴很少。
为了验证在更长的恒温时间中液滴不再冻结这一现象,补充做了5组实验,共235颗液滴,同样以2℃/min的降温速率降温,在-13℃时保持恒温,但将恒温时间延长至120 min,发现在恒温15 min以后的105 min内,也仅有两颗液滴冻结,一颗是第33分钟时冻结,冻结几率4.5×10-4min-1,一颗是第57.5分钟时冻结,冻结几率3.7×10-4min-1,这可能是随机现象,且之后60多分钟再没有冻结发生,冻结几率为0。而Vali等(1966)得到冻结几率在10 min以后保持3×10-3min-1,并且100 min以后仍保持这个值。
7 结 语利用均匀水滴冻结实验装置,通过不同降温速率和恒温实验,对雨水、纯净水和瓶装饮用水等不同水样进行实验研究,进一步研究了降温速率对水滴冻结的影响,验证水滴冻结过程中随机假设和奇点假设的关系。结果如下:
(1)雨水、纯净水和瓶装饮用水3种液滴的累加冻结比例总体来看,在相同温度时,降温速率慢的累加冻结比例要大于降温速率快的,此现象在纯净水和瓶装饮用水实验中更明显。
(2)通过雨水在5种不同降温速率下的液滴冻结实验,发现平均冻结温度、中值冻结温度与降温速率成对数函数关系,降温速率越大,他们的值越小。关系式分别为:Ta=-0.15ln(γ)-13.48和Tm=-0.12ln(γ)-13.73。降温速率每增大1倍,平均冻结温度和中值冻结温度约降低0.12和0.1℃。而瓶装饮用水中值冻结温度与降温速率成线性关系,回归关系式为Tm=-0.44γ-17.54,降温速率增大1℃/min,中值冻结温度下降0.44℃。
(3)雨水、纯净水和瓶装饮用水对温度的液滴冻结几率随温度降低成指数增大,同随机假设和奇点假设的公式相似,与已有对蒸馏水的研究变化趋势相同。拟合得到瓶装饮用水在恒定降温速率下冻结几率与温度有如下关系:P=Cexp(aTs),其中C为降温速率γ的指数函数,C=2×10-5exp(-0.61γ);a为γ的线性函数,a=0.016γ+0.546,实验中a取值为0.57—0.64,随降温速率加快而缓慢增大。
(4)雨水恒温实验表明:在-13℃保持恒温时,液滴的冻结几率既不随时间保持一恒定值(随机假设),也不一直为0(奇点假设),而是随时间成指数衰减。这一现象与已有对蒸馏水做的恒温实验类似。通过对两次恒温实验拟合发现在恒温前2分钟,液滴冻结几率随温度减小较快,之后减小放缓。
(5)通过两次恒温实验的累加冻结比例发现,水滴在恒定温度段内的冻结有一个“总量”,当这一“总量”全部完成冻结以后,冻结现象不再发生(除个别随机冻结)。该现象可以看做是随机假设和奇点假设结合起来的结果,当温度达到或低于特征温度时,液滴冻结,但是水分子在冻结核上的聚合需要一定的时间,所以液滴的冻结就在恒温阶段出现了,这种现象在恒定降温速率实验中容易被忽略,原来在某一温度下冻结的液滴因为需要时间冻结,出现了在下一温度段冻结的现象。
本研究在实验水样的多样性和降温速率的变化上还有欠缺,希望以后还有更多实验和研究来证实本文所得到的结论,在此基础上加强和丰富水滴冻结机制的理论。
致 谢:感谢胡志晋教授对本研究给予的指导和提出的宝贵意见与建议。
| 洪延超. 1996. 积层混合云数值模拟研究Ⅰ:模式及其微物理过程参数化. 气象学报, 54(5): 544-557. Hong Y C. 1996.The numerical simulation study of convective-stratiform mixed cloud, PartⅠ:The model and parameterization of microphysical processes. Acta Meteor Sinica, 54(5): 544-557 (in Chinese) |
| 杨绍忠, 酆大雄. 2007. 一个检测水中冻结核含量的新装置. 气象学报, 65(6): 976-982. Yang S Z, Feng D X. 2007.A new apparatus for detecting the concentration of freezing nuclei in water. Acta Meteor Sinica, 65(6): 976-982 (in Chinese) |
| Bigg E K. 1953. The super cooling of water. Proc Phys Soc B, 66(8): 688-694 |
| Carte A E. 1959. The freezing of water droplets. Proc Phys Soc B, 69(10): 1028 |
| Dufour L, Defay R. 1963. Thermodynamics of Clouds. New York: Academic Press,255 |
| Hobbs P V. 1974. Ice Physics. Clarendon London: Oxford University Press, 461-523 |
| Milbrandt J A, Yau M K. 2005. A multi-moment bulk microphysics parameterization. PartⅡ: A proposed three-moment closure and scheme description. J Atmos Sci, 62(9): 3065-3081 |
| Langham E J, Mason B J. 1958. The heterogeneous and homogeneous nucleation of supercooled water. Proc Roy Soc A, 247(1251): 493-504 |
| Levkov L, Genadiev N.1966. Relation between freezing temperature of supercooled water drops and cooling rate. C R Acad Bulgare Sci, 19: 1139-1142 |
| Salt R W. 1966. Effect of cooling rate on the freezing temperatures of supercooled insects. Canadian J Zoo, 44(4): 655-659 |
| Vali G. 1971. Quantitative evaluation of experimental results on the heterogeneous freezing nucleation of supercooled liquids. J Atmos Sci, 28(3): 402-409 |
| Vali G. 1994. Freezing rate due to heterogeneous nucleation. J Atmos Sci, 51(13): 1843-1856 |
| Vali G, Stansbury E J. 1966. Time-dependent characteristics of the heterogeneous nucleation of ice. Canadian J Physics, 44(3): 477-502 |
| Vonnegut B, Baldwin M. 1984.Repeated nucleation of a supercooled water sample that contains silver iodide particles. J Climate Appl Meteor, 23(3): 486-490 |
| Wang M K, Vonnegut B. 1984. Repeated nucleation of supercooled water sample. J Rech Atmos, 18: 23-29 |
 2015, Vol. 73
2015, Vol. 73


