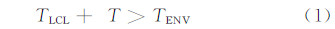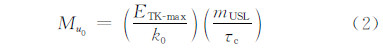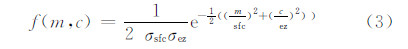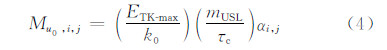中国气象学会主办。
文章信息
- 万子为, 王建捷, 黄丽萍, 康家琦. 2015.
- WAN Ziwei, WANG Jianjie, HUANG Liping, KANG Jiaqi. 2015.
- GRAPES-MESO模式浅对流参数化的改进与试验
- An improvement of the shallow convection parameterization scheme in the GRAPES-Meso
- 气象学报, 73(6): 1066-1079
- Acta Meteorologica Sinica, 73(6): 1066-1079.
- http://dx.doi.org/10.11676/qxxb2015.071
-
文章历史
- 收稿日期: 2015-02-15
- 改回日期: 2015-06-07
2. 国家气象中心, 北京, 100081
2. National Meteorological Center, Beijing 100081, China
浅对流云常常大面积发生在海洋和陆地上,是热带云中最常见的一种(Johnson et al,1999)。与深对流相比,浅对流水平尺度较大、垂直发展不够旺盛、云内质量通量相对较小,不足以产生降水或是大量降水,同时其对环境的热动力反馈也比不上深对流。但是,浅对流具有不可忽略的重要意义,它通过将近地层混合空气带到自由大气中,进而影响低层温度、湿度、云覆盖量以及风的垂直分布(Tiedtke,1989;陈德辉,1997;Bretherton et al,2004;Berg et al,2013;Nie et al,2012; Rio et al,2010)。浅对流的形成对整个温度场、湿度场所产生的影响会导致热带、副热带区域重要的热力和动力反馈(Stevens et al,2001; Brown et al,2002;刘屹岷等,2007;Dorrestijn et al,2012)。此外,浅对流在全球辐射收支平衡中也起着重要作用,这一点已形成广泛共识(Siebesma et al,2004; Soares et al,2004),Berg等(2011)通过估算与浅对流相关的短波辐射强迫,表明了浅对流对于区域气候模拟以及其他预报模式的重要性。
在大尺度模式中,浅对流的参数化主要是通过有效的湍流扩散(Tiedtke et al,1988)或是水汽调整方案(Betts,1986)来实现。在中尺度模式中,一些积云对流参数化方案中也相继考虑了浅对流过程。其积云对流参数化主要包括3个关键部分:对流触发函数、云与环境场的质量交换关系(反映质量卷入、卷出)及描述云底质量通量的闭合假设。Tiedtke(1989)提出,在考虑略厚一点的浅积云与环境场的质量交换时,应当考虑浅积云的上冲效应,即浅积云的一部分在云顶层卷出到环境中,而另一部分则冲入到上一层次,在那里卷出到环境中。Bretherton等(2004)提出了一个新的浅对流参数化方案,用基于浮力分类机制、一维卷入-卷出云模式的质量通量方案,与1阶半的湍流闭合模式相耦合。Kain(2004)在其改进的KF方案(KF eta)中引入了浅对流过程,其将浅对流视为满足对流发生条件、但云厚度达不到深对流最小云厚度临界值的云,并且将云底质量通量与云下边界层的湍流扰动动能联系起来。Berg等(2005)考虑非均匀地表的影响,对次网格浅积云的形成进行统计参数化,用一组温、湿度有差异的气块来触发对流,基于边界层温、湿度联合概率密度函数(JPDF)分布,使浅积云的发生与对流边界层气块群的对流潜在可能性差异联系起来,Berg等(2013)在中尺度模式中对此方法进行了试验评估。
中国有关积云对流参数化的研究,主要集中在参数化方案的评估和应用上,发展和改进积云对流参数化方案的工作很少。刘一鸣等(2001)在NCAR区域气候模式RegCM2中植入了一个修正的质量通量参数化方案,用总体云模式来描述积云与环境的相互作用,并同时考虑了深、浅对流;徐道生等(2014)在SAS(Simplified Arakawa Schubert)对流参数化方案中引入了对流云和层云的相互耦合机制并开展了初步试验。针对积云对流参数化方案的评估研究和分析,多是采用数值试验方法,包括使用完整的数值模型(陈静等,2003;王建捷等,2001,2005;丁一汇等,2006;屠妮妮等,2011;廖镜彪等,2012)或单柱模式(杨军丽等,2012;王德立等,2013)。而针对浅对流的研究十分缺乏,目前仅有少量理论研究(陆汉城等,2002)和模式试验(刘屹岷等,2007)。
GRAPES-Meso模式是中国自主研发的中尺度数值预报模式,优化和完善其物理过程是改进该模式的重要内容之一。目前,该模式中可选用的积云对流参数化方案有Kain-Fritsch Eta(KF eta)方案、Betts-Millers-Janic(BMJ)方案以及Simplified Arakawa Schubert(SAS)方案等。其中,KF eta方案是GRAPES-Meso 4.0的业务选项。邓华等(2008)用GRAPES-Meso对华南2005年6月17—25日的降水过程进行了15 km×15 km分辨率的数值模拟,发现在使用KF eta方案时模拟出的降水具有明显的局地性,会漏报出现的小雨,且只在实况有强降水时才会激发对流。王德立等(2013)利用GRAPES单柱模式对KF eta方案进行个例模拟,发现该方案中浅对流激发频率较低,会造成低层偏冷偏湿。此外,GRAPES-Meso模式中还存在格点尺度降水与次网格尺度降水比例不协调(格点尺度降水偏少)、地面2 m气温偏高等与深、浅对流过程相联系的其他问题。
本研究拟参考Berg等(2005,2013)提出的扰动对流触发函数方法,即对近地层温、湿度进行一组扰动,将原有的基于单一气块温、湿度条件的浅对流触发变为基于一组温、湿度扰动后气块群的温、湿度条件的浅对流触发,并用与该组扰动相关的边界层温、湿度分布确定的联合概率密度函数来表征浅对流云特征参量和对流触发函数及计算浅对流强度的方法,通过对该方法的技术方案设计及参数试验和选择,尝试在GRAPES-Meso中实现对KF eta浅对流激发和计算的改进,探讨该方法的有效性和可行性,以期提高浅对流的激发频率和浅积云的预报能力,进而一定程度影响模式低层的温、湿度场,并期望低层温、湿环境的改变有利于模式格点尺度降水与次网格尺度降水分配比的协调与改善,为该方法在GRAPES-Meso中的业务应用提供先期预研和依据。
2 GRAPES-Meso浅对流激发的改进设计2.1 KF eta方案简介KF eta方案是KF方案的改进方案。KF方案(Kain et al,1990,1993)基于FC方案(Fritsch et al,1980)发展而来,其闭合假设将次网格积云对流与格点对流有效位能相关联,在给定的对流时间内,对流的发生须使格点上绝大部分对流有效位能(约90%)被消耗掉。采用一维卷入-卷出的云模式,通过浮力分类机制来调整每一层环境与云的质量双向交换,云中考虑了湿上升流、湿下沉流,以及一些简单的云中水物质的形成过程。其触发函数为
式中,TLCL和TENV分别为抬升凝结高度层的气块温度和环境场温度,δT为一个温度扰动量,其大小与抬升凝结高度处的环境场垂直上升强弱有关。
式(1)所表达的物理意义是:在抬升凝结高度加一温度扰动,可使该处的温度高于环境温度,则对流能被触发;否则,对流不能被触发。
KF eta方案是Kain(2004)对KF方案的进一步改进,包括在上升气流中加入一个最小卷入率,将云半径定义为垂直速度的函数,基于观测将最小云厚阈值定义为温度的函数。此外,还在方案中首次加入浅对流过程,将浅对流定义为其余条件均满足深对流,但云厚低于最小云厚阈值的对流。对浅对流改用与深对流不同的闭合假设,将云底质量通量Mu0(kg/s)假定为边界层湍流扰动动能的函数
式中,ETK-max为边界层湍流扰动动能的最大值(m2/s2);k0=10 m2/s2,mUSL为云下混合层的总质量(kg),τc为对流时间,在1800—3600 s间变化。
2.2 浅对流激发的改进设计将原方案中由单一边界层温、湿度条件影响下的对流触发,变为由温、湿度联合概率密度函数确定的一组边界层温、湿度分布影响下的对流触发,并使联合概率密度函数与浅对流云的特征参量表征、浅对流的强度计算相联系。
采用Berg等(2004)提出的新温、湿度联合概率密度函数的参数化方法——混合图表法,该方法是基于这样的物理内涵:对流边界层的空气可以看作是由来自地表的空气、自由大气层中卷入的空气和停留在边界层内的空气混合形成的。其联合概率密度函数计算公式为
式中,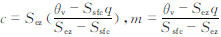 ,c和m分别为θv和q的转换坐标,Ssfc被定义为一个新的鲍恩比(Bz)、蒸发潜热(Lv)和空气定压比热(cp)的函数:
,c和m分别为θv和q的转换坐标,Ssfc被定义为一个新的鲍恩比(Bz)、蒸发潜热(Lv)和空气定压比热(cp)的函数: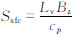 。Sez被定义为自由大气卷入层与边界层平均的θv和q差值之比:Sez=(θv,ez-θv—)/(qez-q-)。σsfc和σez的值均根据实验数据(Berg et al,2004)采用最小二乘法来拟合σsfc/q*、σez/θ*曲线得到:σsfc/q*=2.3+1.1×10-2(z/zi)-1.6,σez/θ*=2.0+8.2×10-4(z/zi)-1.8,其中,zi为边界层高度。
。Sez被定义为自由大气卷入层与边界层平均的θv和q差值之比:Sez=(θv,ez-θv—)/(qez-q-)。σsfc和σez的值均根据实验数据(Berg et al,2004)采用最小二乘法来拟合σsfc/q*、σez/θ*曲线得到:σsfc/q*=2.3+1.1×10-2(z/zi)-1.6,σez/θ*=2.0+8.2×10-4(z/zi)-1.8,其中,zi为边界层高度。
θ*和q*为边界层的相似尺度,根据Stull(1988)提出的关于边界层相似尺度的取值,在静力不稳定的边界层中,局地自由对流相似的θ*取值为0—2 K,q*取值为0—5 g/kg。
2.3 方案在GRAPES-Meso程序中的实现和有关参数的确定将文中设计的浅对流触发改进方案(简称KF eta MD)进行程序实现时,要发展相关程序模块,其中有两个关键模块:一是边界层温、湿度联合概率密度函数计算模块,二是云参数计算模块(图 1)。联合概率密度函数计算模块主要是根据模式地表、边界层混合特性等,实现式(3)的计算;而云参数模块,则是基于一组温、湿度扰动和相关的温、湿度联合概率密度函数,实现对对流触发函数、云中各参数等计算的修改。在修改方案KF eta MD中,深对流的算法与原方案保持一致。当一组温、湿度扰动触发多个浅对流,则每一个温度、湿度扰动对都按照浅对流的算法计算出相对应的云参数特性值(云底、云高、上升卷出的液态云水、云冰比率等参量),由此产生出上述各云参数的一组特性值,将每一对温度、湿度值的联合概率密度函数作为该扰动对的权重,即可对各云参数的一组特性值求得加权平均值,用于浅对流方案的相关计算。
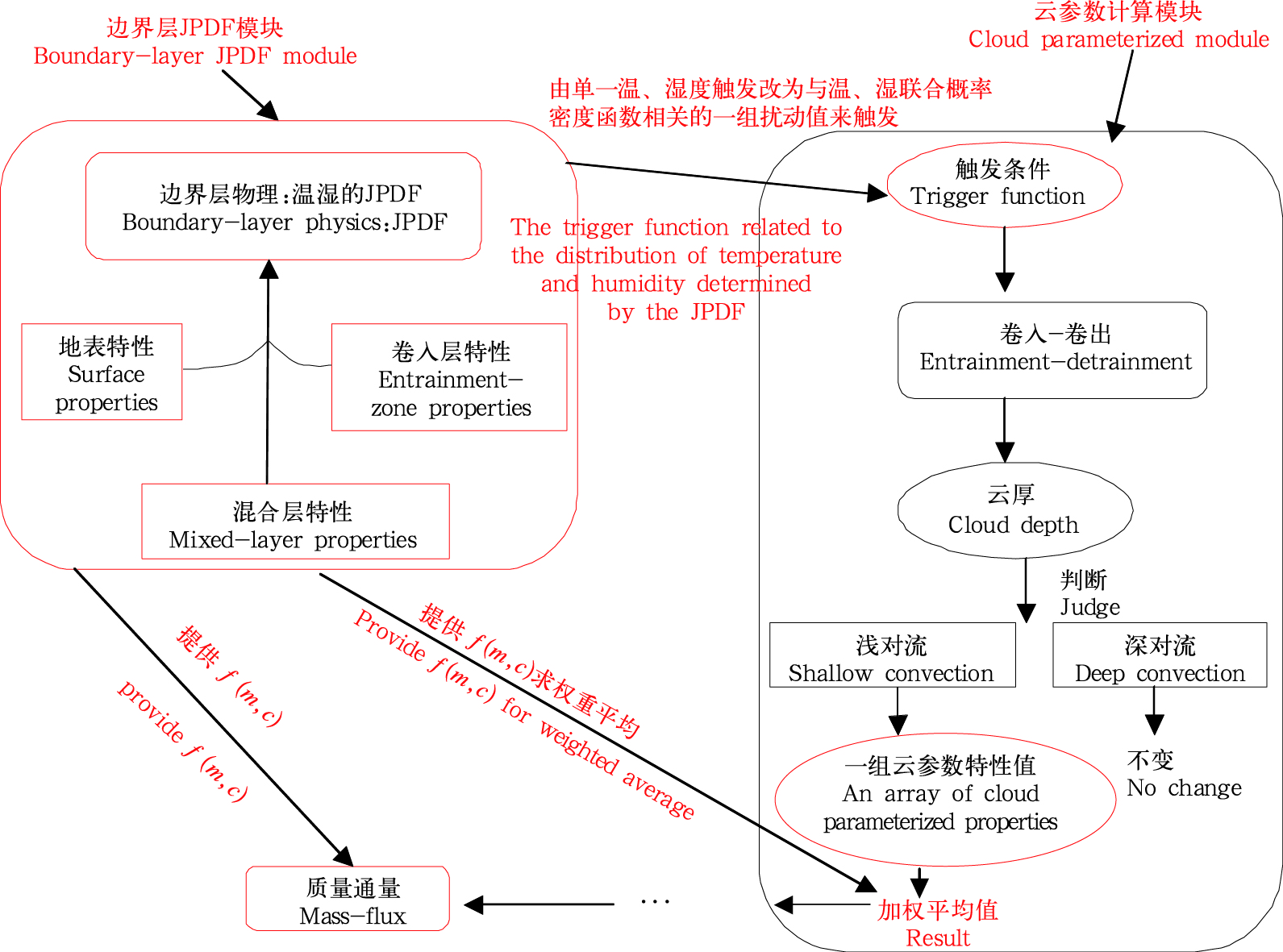 |
| 图 1 KF eta MD 方案的示意模型Fig. 1 A schematic chart for the KF eta MD scheme |
当对流激发由单一值变为与温、湿度联合概率密度函数相关的一组值时(如温度扰动有i=1,2,3,…,I个,湿度扰动有j=1,2,3,…,J个,共有I×J对扰动),将KF eta方案中浅对流质量通量原式(2)改为
式中,αi,j即为能触发浅对流的一对温、湿度扰动(第i,j个扰动对)对应的联合概率密度函数(即fi,j(m,c))与所有扰动对的联合概率密度函数总和之比。i、j分别代表温、湿度扰动的序号。总的质量通量为每一对能触发浅对流的扰动对质量通量的总和。由于并非每一对温、湿度扰动组合都能触发对流形成云,因此,有效的αi,j的总和小于1。KF eta MD方案模型见图 1。
有4个与扰动相关的新参数需要给定,分别为联合概率密度函数单元条的总数量(即扰动对的总数I×J)、联合概率密度函数单元条的宽度、浅对流的最小频率及深对流的最小频率(表 1)。温度、湿度的扰动极值范围由单元条的总数量与宽度来共同决定,例如:11×0.1 K=1 K,11×0.1 g/kg=1 g/kg。表 1给出了联合概率密度函数计算中需要确定的4个新参数敏感性试验的相关信息和结果。在模拟试验中选用5组值,前4组单元条的总数量分别为121(11×11)、256(16×16)、441(21×21)、676(26×26),单元条宽度均为0.1 K和0.1 g/kg;第5组单元条总数量为1681(41×41),单元条宽度为0.05 K和0.05 g/kg。给出深、浅对流的最小频率是考虑略去联合概率密度函数分布中的末端低概率(激发浅对流可能性小)部分,同时也可以缩短计算耗时,当一对温、湿度扰动计算得出的联合概率密度函数小于深(浅)对流最小频率时,则认为该对温、湿度扰动对触发对流无贡献。
| 参数 | 试验数值 | 选用值 |
| 联合概率密度函数单元条的总数量 | 121,256,441,676,1681 | 441 |
| 联合概率密度函数单元条的宽度 | 0.1 K, 0.1 g/kg; 0.05 K,0.05 g/kg | 0.1 K, 0.1 g/kg |
| 浅对流的最小频率 | 0.01,0.001,0.0001,0.00001 | 0.0001 |
| 深对流的最小频率 | 0.3 | 0.3 |
从参数试验结果看,单元条的宽度从0.1减至0.05时,即减小每一对扰动的幅度时,触发的浅对流有一些微弱变化,但所耗机时明显延长;保持单元条的宽度不变,增大单元条总数量,即增加温、湿度扰动的极值范围时,产生了更多的扰动对,浅对流触发有增多但同时耗时延长;浅对流的最小频率取值为0.01—0.001时,浅对流的激发增加较快,但取值继续减至0.0001后,浅对流的激发增加不明显。综合考虑浅对流触发和机时消耗情况、并参考Berg等(2013)对深对流最小频率的选择(文中对深对流未作改进),确立了改进方案中这4个参数的选用值(表 1)。
3 数值试验设计 3.1 模式与试验方案选用GRAPES-Meso(薛纪善等,2008)2014年3.3.2 .5 版,该模式为非静力平衡经纬度格点中尺度模式,采用了半隐式半拉格朗日时间积分/平流方案,水平分辨率为0.15°×0.15°,模式垂直层为31层;模式包含全物理过程的描述:积云对流、云微物理、边界层、辐射、陆面等(表 2)。
| 物理过程 | 对照试验 | 改进试验 |
| 积云对流参数化方案 | KF eta方案 | KF eta MD 方案 |
| 云微物理过程 | WSM6类方案 | WSM6类方案 |
| 长波辐射方案 | RRTM方案 | RRTM方案 |
| 短波辐射方案 | Dudhia方案 | Dudhia方案 |
| 近地面层方案 | Monin-Obukhov方案 | Monin-Obukhov方案 |
| 陆面过程 | Noah方案 | Noah方案 |
| 边界层方案 | MRF方案 | MRF方案 |
设计了两类试验:个例试验和批量试验。两类试验都包括对照试验和改进试验2组,对照试验与改进试验的唯一差别就是浅对流激发方案不同。对照试验的对流参数化方案为KF eta 方案,改进试验的对流参数化方案即为改进的方案(KF eta MD)。个例试验的目的是通过选择一个恰当的个例,通过较为深入的剖析,具体考察和分析改进方案对浅对流激发的改变、相应的浅对流过程对环境温、湿度和云水的反馈情况,以及浅对流激发的变化引起的近地面相关要素的响应等。批量试验的目的是通过连续的大量试验,进一步考察浅对流激发的改进,是否可以对模式预报(如降水和一些其他地面要素预报)产生统计意义上的正效应,即改进对GRAPES-Meso系统具有潜在的应用价值。
中国东部为对流多发区域、夏半年为对流频发时段,故模拟试验区域为(15°—55°N,100°—135°E)。批量试验的预报时段为2014年5月13日—7月13日共计62 d,起报时间为每日00时(世界时,下同),积分时长为24 h。个例试验的模拟区域为(25°—35°N,105°—125°E),起报时间与天气过程发生相联系,将在3.3节中与天气过程一同具体说明。
3.2 资 料美国NCEP每日4次、水平分辨率为1°×1°、垂直1000—10 hPa的26个等压面的分析场资料,用来作为模式的初始场和侧边界条件。观测资料用来验证和分析模拟结果,主要包括:(1)中国加密站逐时降水资料;(2)中国加密站逐时地面2 m气温资料;(3)逐3 h地面填图站点低云云底资料;(4)FY-2E卫星0.5°×0.5°分辨率的逐时黑体亮度温度(TBB)资料。
3.3 试验个例选择针对试验的需要,选择了2014年5月13—14日发生在江南的一次暴雨过程。这是一次青藏高原东部南支小槽东移、得到河西走廊弱冷空气补充而发展造成的降水过程,5月12日,河套地区有一小槽向东南方向移动,500 hPa上西藏与四川交界处有一个弱南支槽,中国北方主要受偏西气流控制,对应850 hPa四川东部有弱低压环流出现;之后,500 hPa南支槽在东移过程中得到河西走廊弱冷空气补充有所加强,于13日移经川鄂皖,至14日00时经长江口出海,在这个过程中,华南、江南有低空西南急流发展和急流核的东移、且低层比较暖湿,850 hPa沿长江中下游出现弱切变线、12日位于四川东部的弱低压环流沿切变线东移南压至湖北(图略)。
在上述天气形势和天气系统影响下,地面降水主要发生在低层切变线南侧,暴雨遍及江西北部、安徽南部以及浙江中东部地区,其中,江西与安徽交界处出现大暴雨,累积降水量达到120.1 mm(图 2a)。从暴雨中心降水量随时间的演变(图 2b)可以看出,强降水集中发生在6—7 h里,即13日14—21时,存在两个明显峰值,最大雨强约为28 mm/h,说明这个降水过程中具有明显的对流活动。同时注意到,处于暴雨中心区的江西、安徽及浙江三省交界地带,在降水发生前的13日00—06时,卫星云图显示这里天空出现部分低云且无降水发生(图 2c—f),这一带低层比较暖湿,推测低云中淡积云存在的可能性较大,故这个时段可以用来研究和分析暴雨发生前浅对流的活动。因此,文中所选的这样一个对流活动明显且前期出现淡积云的个例,便于将深、浅对流独立分开分析,对于研究浅对流激发以及对后续降水等的影响是适宜的。
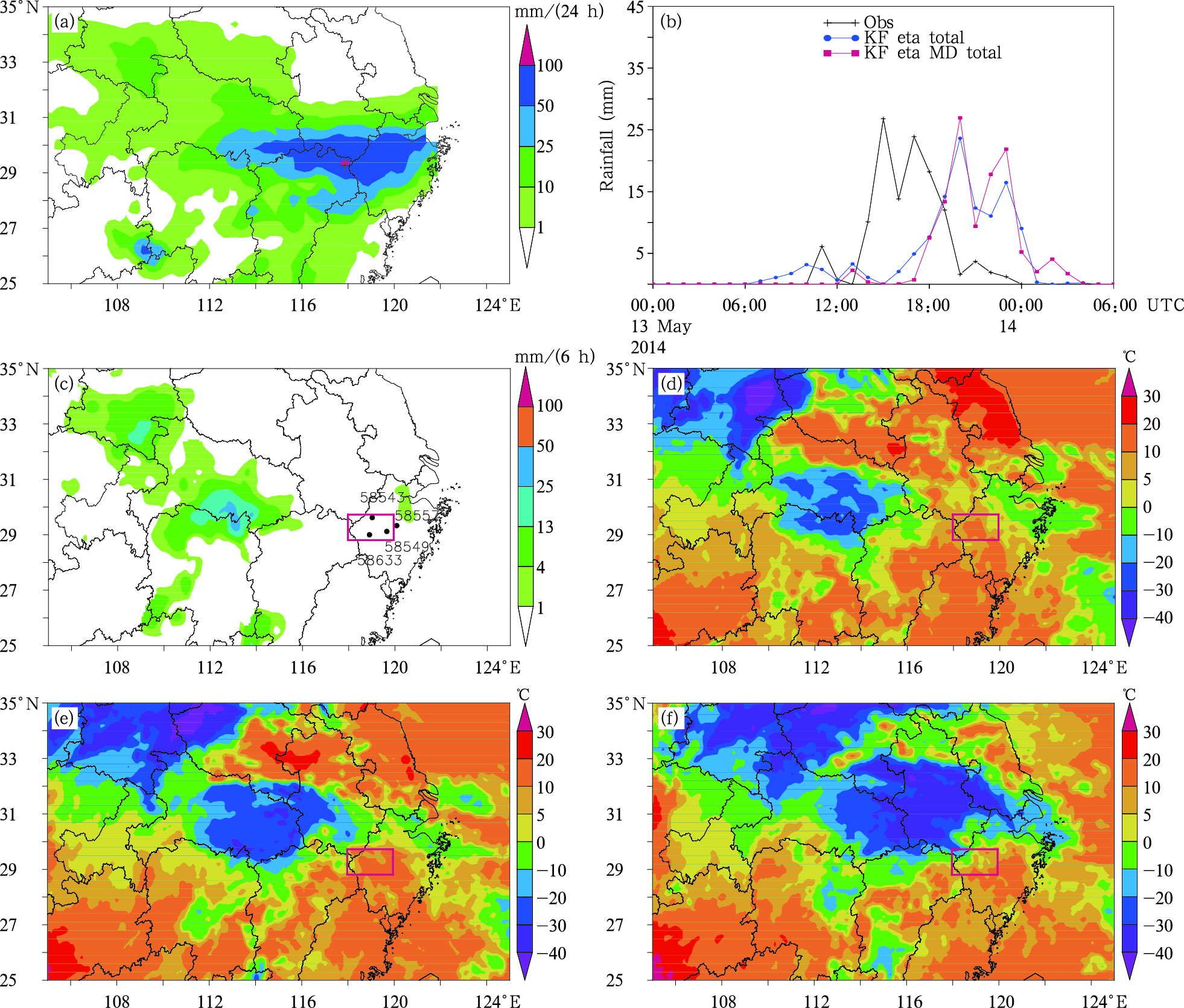 |
| 图 2 2014年5月13日00时—14日06时降水和卫星TBB观测 (a.13日00时—14日00时地面24 h累积降水观测, b.暴雨区最强降水站点总降水观测时间序列 (最强降水点在图2a、3a、c中以十字符表示), c.13日00—06时地面6 h累积降水观测, d—f.13日02、04、06时卫星TBB观测)Fig. 2 Observed precipitation and satellite TBB from 00: 00 UTC 13 May to 00: 06 UTC 14 May 2014 (a. observed 24 h accumulative precipitation from 00: 00 UTC 13 May to 00: 00 UTC 14 May 2014, b. a time series of observed precipitation at the point with maximum rainfall (marked by cross symbols in Fig. 2a, 3a, 3c), c. observed 6 h accumulative precipitation from 00: 00 to 06: 00 UTC 13 May, and d-f. satellite TBB at 02: 00, 04: 00, 06: 00 UTC 13 May) |
根据该个例天气系统影响的情况,将模拟起始时间定在2014年5月13日00时,积分36 h。
4 结果分析 4.1 模拟结果的基础验证与观测对比可知,对照试验的模拟结果合理再现了高、中、低空环流形势在2014年5月13—14日的发展演变(图略)和地面24 h累积降水,由图 3a可以看出,模式对这次暴雨的覆盖范围、不同强度降水的主要分布、大—暴雨主要落区等总体特征,都模拟得较为合理,只是特大暴雨中心的位置与实况存在一些偏差,模拟结果有两个特大暴雨中心,东西相距约300 km,而实况只有一个特大暴雨中心,其位置介于模拟的两个暴雨中心之间。观测与模拟的暴雨最强点降水的时间序列(图 2b)显示,模拟结果捕捉到了实况强降水主要集中出现在6—7 h里、存在两个明显峰值、最强雨强超过20 mm/h、两个强降水峰值出现后降水明显减弱等重要特征(尽管模拟的强降水峰值与观测存在约6 h的滞后)表明模拟结果不仅在降水的总体特征上,而且在降水的时间演变上也比较合理的。此外,在积分的第一个6 h时段,即文中拟用于研究浅对流激发问题的时段,观测到在暴雨区大暴雨中心附近并没有降水发生,模拟结果也是如此(图 3b)。
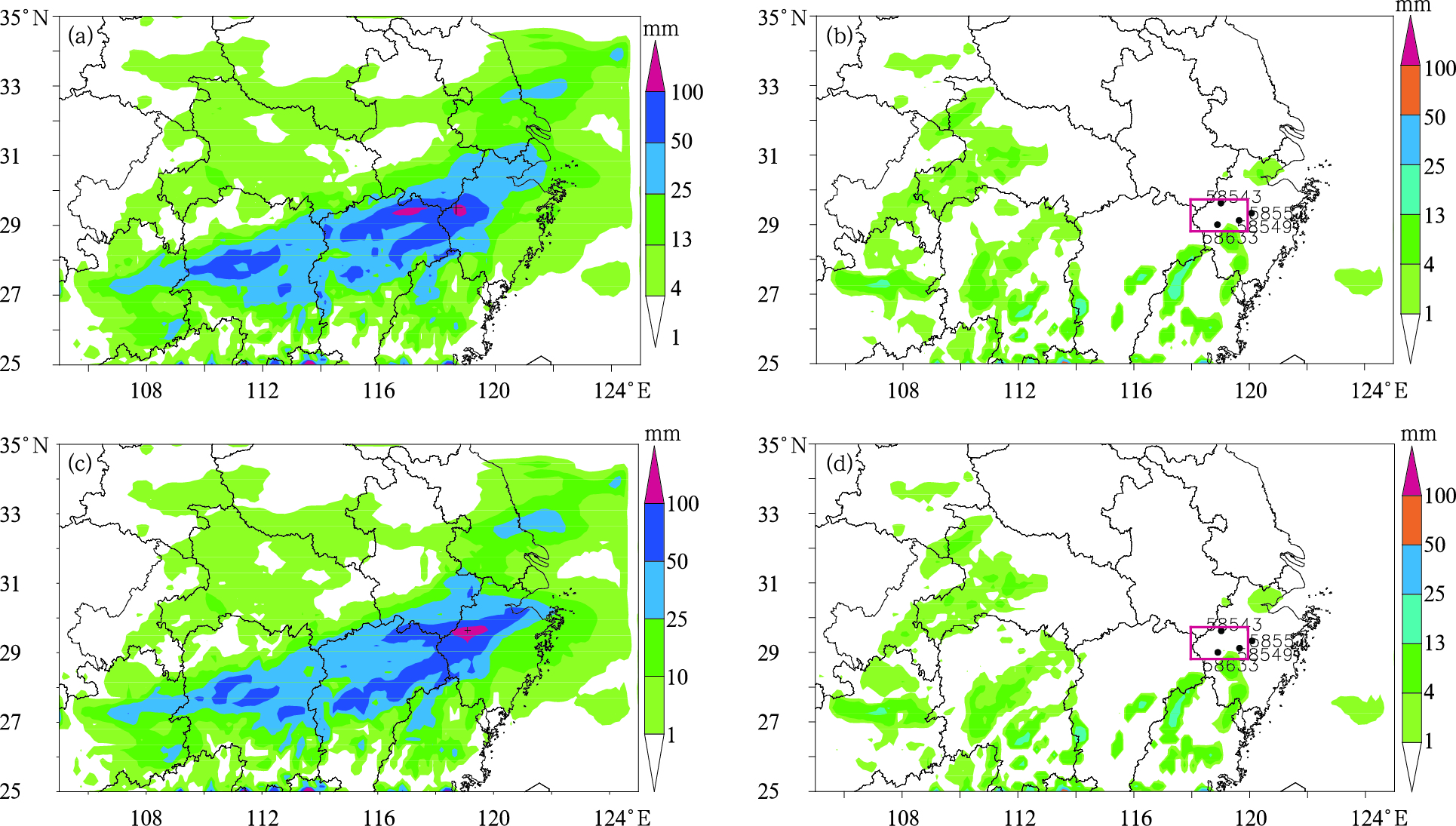 |
| 图 3 2014年5月13日00时—14日00时两种方案模拟的地面降水 (a.KF eta试验模拟的地面24 h累积降水,b.KF eta试验模拟的13日00—06时地面6 h累积降水, c.KF eta MD试验模拟的地面24 h累积降水,d.KF eta MD试验模拟的13日00—06时地面6 h累积降水)Fig. 3 Simulated precipitation initiated at 00:00 UTC 13 May 2014 by KF eta experiment and KF eta MD experiment (a. Simulated 24 h accumulative precipitation by KF eta experiment, b. Simulated 6 h accumulative precipitation by KF eta experiment from 00:00 UTC to 06:00 UTC 13 May, c. same as a, but by KF eta MD experiment, d. simulated 6 h accumulative precipitation same as b, but by KF eta MD experiment from 00:00 to 06:00 UTC 13 May) |
图 3c、d为改进试验(KF eta MD方案)的0—24和0—6 h累积降水模拟结果,与对照试验相比(图 3a、b),总体看来,对流激发方案的改进对降水总分布特征未产生明显影响,但使暴雨模拟结果的一些细节特征更接近实况(图 2a、c),一是表现在暴雨中心位置和大—暴雨范围上,例如暴雨中心只有一个,暴雨区向东延伸至浙江东北部地区,而对照试验(原KF eta方案)模拟的暴雨中心有两个,暴雨区在浙江中北部偏弱偏西而大雨范围又较实况偏大等;二是表现在暴雨中心降水随时间的演变细节上,如主雨峰的强度和主雨峰前后的弱降水特征(图 2b)。
由此可以认为,文中得到了合理的数值试验模拟结果,可以用于诊断分析与试验对比。为了深入分析对流的激发情况,选择同时覆盖观测和模拟的暴雨中心的区域作为重点分析区((29°—30°N,118°—120°E),图 2、3中以红色方框标示出的范围)。
4.2 浅对流的激发及浅对流云依据模式中深、浅对流的判断标准,统计每45 min输出的重点分析区(即暴雨中心区)内深对流云和浅对流云发生的格点数并除以分析区域总格点数,将其作为深、浅对流的激发频率,以前述的暴雨过程降水发生前出现低云的时段,即13日00—06时(模式0—6 h积分时段)来研究浅对流的激发。由图 4a可以看出如下特点:一是改进方案能早于原方案激发出浅对流,改进方案在积分3 h后开始有浅对流被激发,而原方案在积分约5 h时才有浅对流被激发;二是改进方案的浅对流激发频率明显大于原方案,改进方案在积分4—9 h时段浅对流激发频率超过50%,特别是积分5—6 h浅对流激发频率最高,而原方案浅对流激发一直未超过10%;三是改进方案在积分5 h后深对流开始出现,但深对流激发频率很小,当深对流激发频率有所增大后(积分10 h)浅对流激发频率明显减少,而原方案浅对流激发晚且1 h之后(大约在积分6 h时)就开始激发深对流,同时深对流激发频率很快就超过了浅对流激发频率,说明原方案下浅对流不易维持,这也暗示原方案存在对浅对流激发偏弱和对浅对流描述能力偏低之不足。
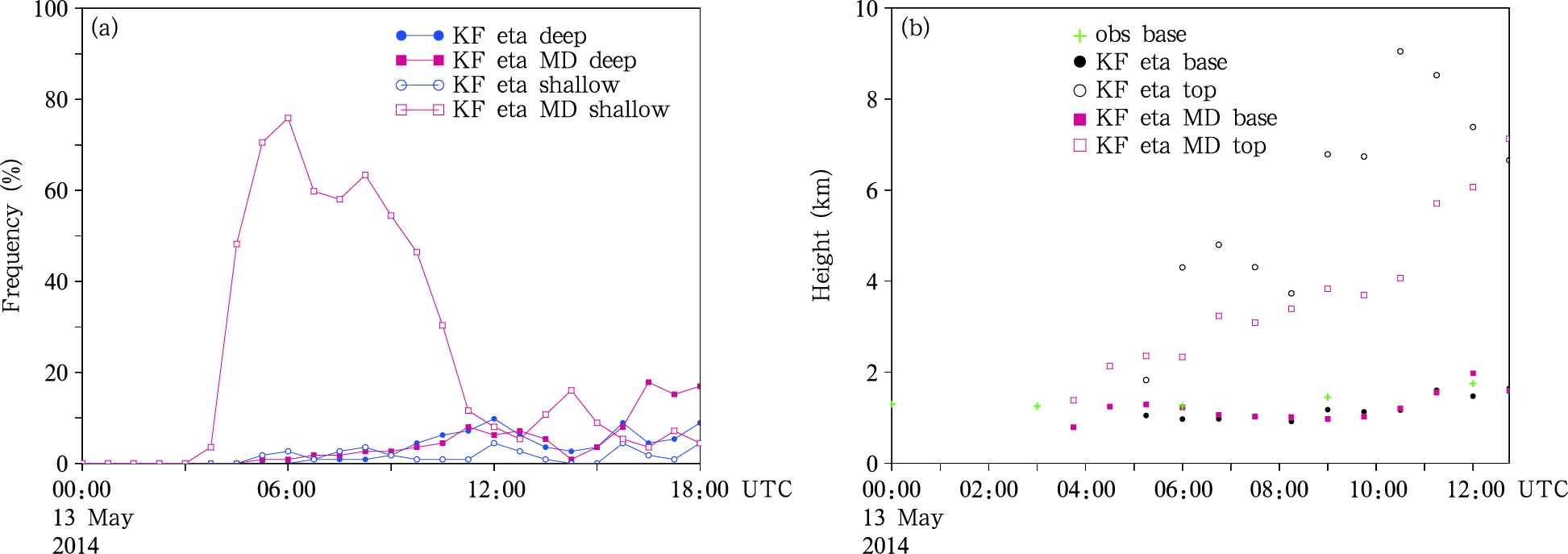 |
| 图 4 重点分析区两种方案深浅对流激发频率对比(a),平均云底、云高与观测对比(b)Fig. 4 Trigger frequencies of deep and shallow convection (a), observed and simulated average cloud-base and cloud-top heights (b) in the key zone of study |
进行全场统计可知,改进后的方案对浅对流激发的提高,在整个模拟区域也是可见的。值得一提的是,改进方案下,浅对流激发增多的同时深对流的激发略有减少,这可能对模式格点尺度和次网格尺度降水分配比的改变产生正面影响,关于这一点将在后面讨论。
进一步从对流云云底和云顶来做一些对比分析,将积分0—12 h、重点分析区内的地面气象观测站(58543、58549、58557、58633)的平均云底高度作为观测值,与模拟的云底和云顶高度在暴雨中心区内的平均值点绘于图 4b进行对比(其中,观测为3 h间隔,模拟结果为45 min间隔的输出)。可见改进方案较早地(积分3 h后)模拟出了浅对流云,浅对流云连续数小时存在,直至积分10 h,其云底高约为1 km,云顶由2 km逐渐升高至4 km,这与图 4a给出的浅对流激发频率信息是一致和对应的;而原方案不仅浅对流云出现的晚——在积分5 h时才出现,而且浅对流云维持的时间也短,1 h后云顶就从开始的约2 km抬升至4 km,数小时后进一步升至7—9 km,表明深对流云已经发展,此时云顶信息不再是浅对流云的信息。与仅有的3 h间隔云底观测值对比,改进方案和原方案模拟的云底高度偏差均较小,但呈略低于观测值的趋势。
综上分析可知,在观测到明显浅对流云特征的时段(积分0—6 h),改进方案比原方案能较早地激发出浅对流且浅对流的激发频次高,且对浅对流云一些特征(如云底和云顶)和浅对流云维持等的模拟亦更合理。
4.3 浅对流过程对环境温、湿度和云水的反馈将模拟对流造成的温、湿度倾向信息进行提取,可以清楚地看到改进方案浅对流激发后对模式环境温、湿度场形成了合理的反馈。主要在距地几百米至2 km的浅薄层内,有正的温度倾向和负的湿度倾向,即使环境产生升温和减湿现象,温、湿度倾向发生的时间和层次与浅对流激发时间和浅对流云层(图 4)相对应,这在深对流没有被明显激发的时段(如积分4—6 h)看得非常清楚(图 5)。由图 5还可以看到,原方案(KF eta方案)直到05时低层2 km内才开始产生温、湿度倾向贡献,并且温、湿度倾向都明显小于改进方案的中浅对流产生的温、湿度倾向。这进一步表明改进方案(KF eta MD方案)较原方案可提早激发出浅对流,并且由于其浅对流激发频率的增加,在低层对环境场的升温、减湿贡献亦更显著。
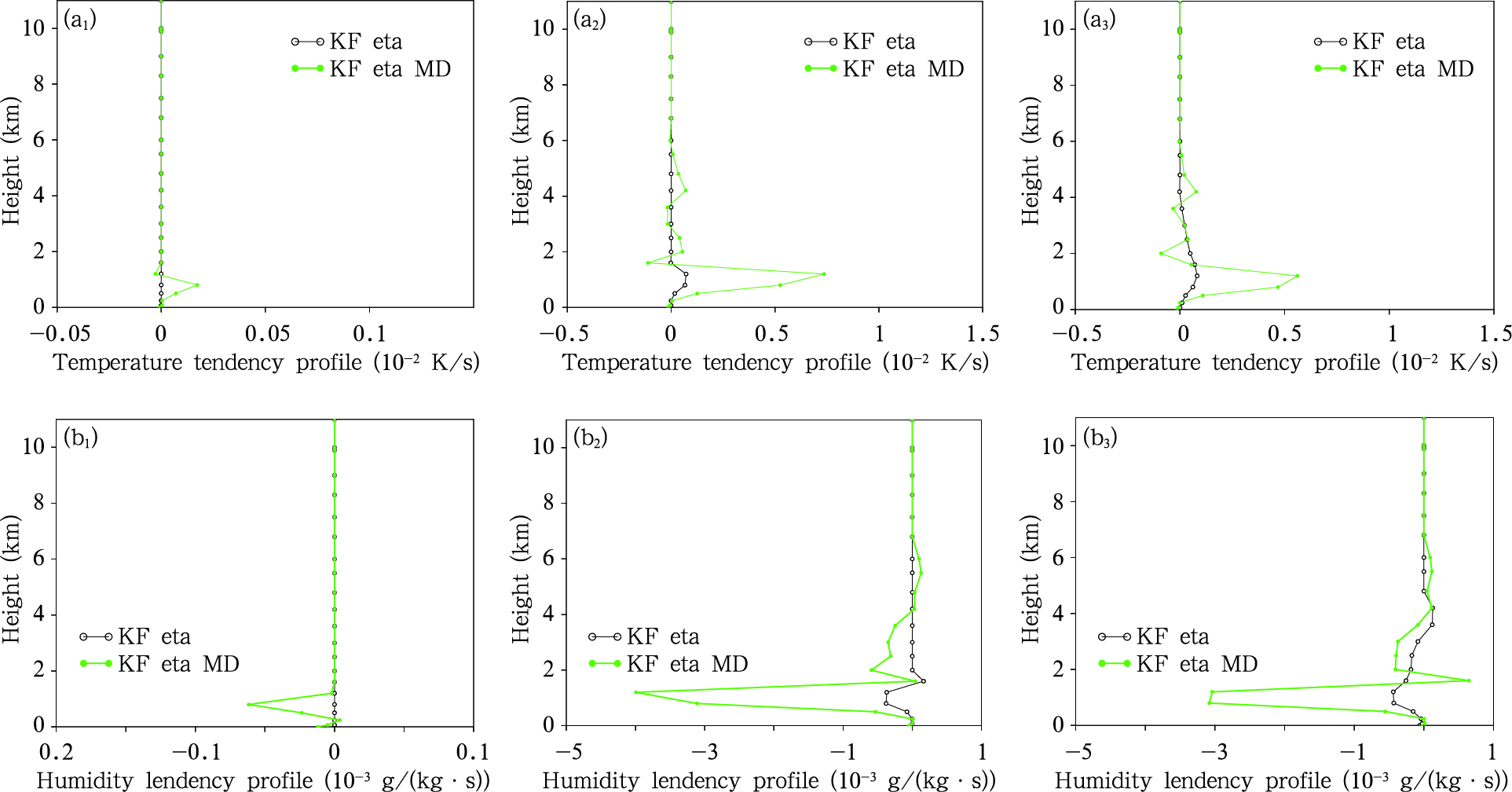 |
| 图 5 重点分析区(a1—a3)温度、(b1—b3)湿度倾向总和廓线对比 (a1、b1.04时,a2、b2.05时,a3、b3.06时)Fig. 5 Total tendency profiles of temperature (a1-a3) and humidity (b1-b3) in the key zone of study (a1, b1. 04:00 UTC, a2, b2. 05:00 UTC, a3,b3.06:00 UTC 13 May) |
KF eta方案在对流云中考虑了两类云中水凝物(云水/云冰、雨水/雪)的形成过程,并将次网格计算出的云中水凝物反馈给格点尺度。对于深对流,考虑上升气流中过饱和的水汽一部分转化为云中水凝物,一部分(不超过60%)通过下沉蒸发过程最终成为地面降水;对于浅对流,不考虑降水,只考虑云中水凝物。对重点分析区两组试验浅对流过程产生的云水分别进行纬度平均(29°—30°N)后沿经向做出剖面(图 6),可见由于浅对流垂直发展有限、对流不旺盛,两组试验浅对流过程产生的云水都主要分布在距地面数百米至2.5 km层次内,且云水含量较低(10-2 g/kg量级)。尽管浅对流发生的层次类似,但改进方案(KF eta MD方案)浅对流云水形成的时间比原方案要早,发生的范围也明显大于原方案,产生的云水量值数倍于原方案,即改进方案反馈给格点尺度的云水较原方案早且有明显增多,这与前述的分析结果——改进方案比原方案浅对流激发早激发频率高,是一致和吻合的。
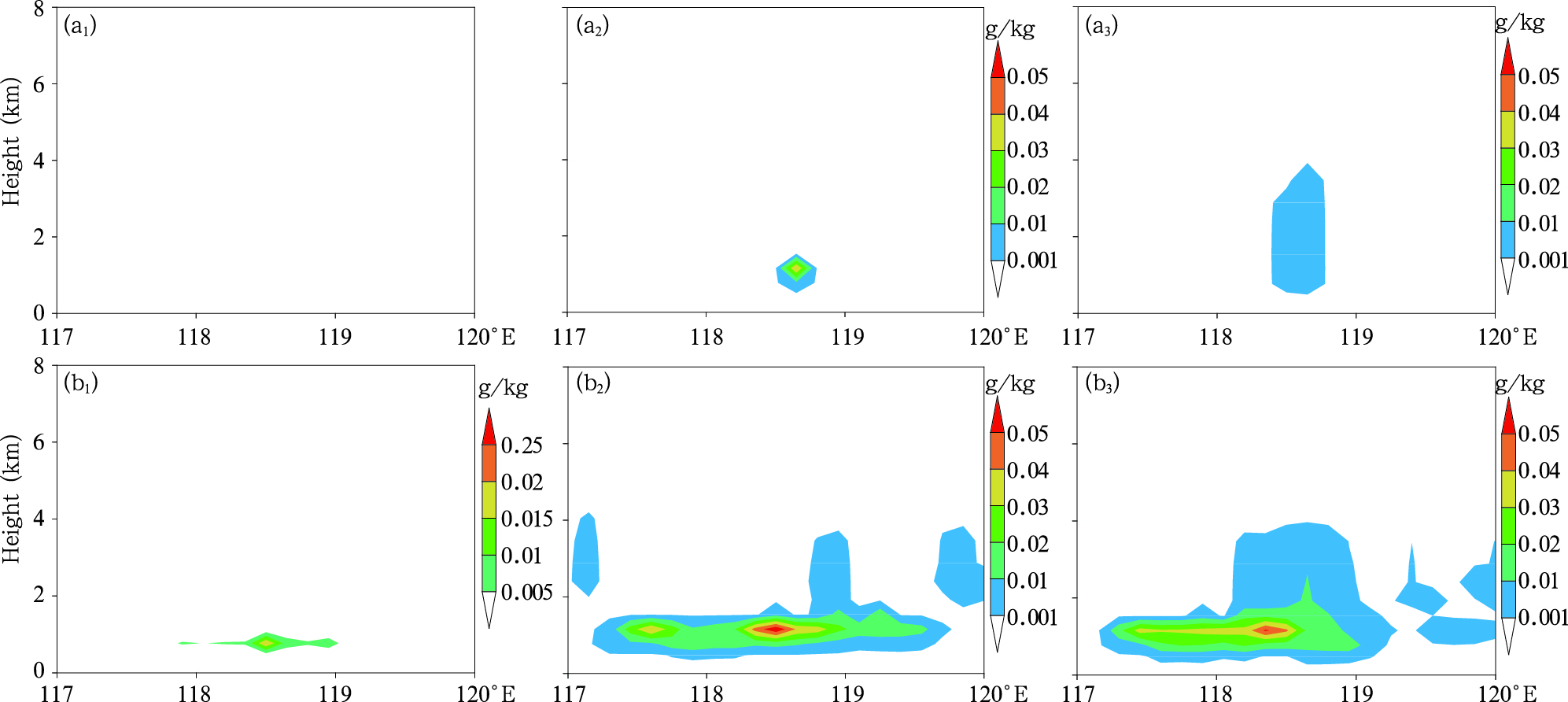 |
| 图 6 重点分析区KF eta试验(a1—a3)、KF eta MD试验(b1—b3)纬向平均的浅对流云云水剖面 (a1、b1.04时,a2、b2.05时,a3、b3.06时)Fig. 6 Cross-section of the zonal mean of subgrid cloud water in the key zone of study by KF eta experiment (a1-a3) and by KF eta MD experiment (b1-b3) (a1, b1. 04:00 UTC, a2, b2. 05:00 UTC and a3, b3.06:00 UTC 13 May) |
由4.1节的对比分析可知,对流激发方案的改进虽对降水总分布特征未产生明显影响,但可使暴雨中心位置和大—暴雨范围及暴雨中心降水随时间的演变等模拟结果的细节特征更接近实况。
进一步统计两种方案在预报区域全场逐6 h对流降水量与格点尺度降水占总降水的百分比,可以看出,在逐6 h里,改进方案(KF eta MD方案)预报的对流降水均有所减小,同时格点尺度降水略有增大。在整个24 h积分中(图略),改进方案的格点尺度降水占总降水的比例均提高2%—3%,最后一个6 h积分时段格点尺度降水占总降水的比例提高了近4个百分点(表 3),浅对流激发的改进对格点尺度降水与对流降水(次网格尺度降水)的分配产生了弱的正贡献(GRAPE-Meso模式一直存在对流降水占总降水比例偏高的问题)。这一改进作用,可能是由于改进方案总体上增大了浅对流的激发,即加大了对格点不稳定能量的消耗和对低层环境升温、减湿的贡献,从而一定程度地对深对流的发展环境产生了不利因素,导致深对流总体有减少;而深对流的减弱,可减小对格点水汽的消耗,加之改进方案浅对流对格点云雨水的反馈亦有所增大,这两方面都对成云致雨的云微物理过程(格点尺度降水)有促进作用的缘故。这也表明,改进GRAPES-Meso浅对流对活跃其格点尺度降水物理过程可产生一定程度的正效应,从而使格点尺度降水占比提高。
| 降水百分比(%) | 00—06时 | 06—12时 | 12—18时 | 18—00时 | 24 h | |
| KF eta | 对流降水 | 82.8 | 90.3 | 81.2 | 55.2 | 71.3 |
| 格点降水 | 17.2 | 9.7 | 18.8 | 46.8 | 28.7 | |
| KF eta MD | 对流降水 | 80.6 | 88.9 | 79.6 | 49.4 | 68.8 |
| 格点降水 | 19.4 | 11.1 | 20.4 | 50.6 | 31.2 |
浅对流的激发对低层环境场可直接产生升温、减湿的反馈作用并影响模式后续结果,同时浅对流产生的空中云雨水/云量也会与其他物理过程(如云微物理和辐射过程等)作用而对模式积分结果产生影响,这些影响过程都是非线性的。再考察一下地面2 m气温对浅对流激发改进所产生的响应,将改进方案与原方案模拟的逐时2 m气温通过双线性插值到位于重点分析区内的12个区域自动站站点上,并进行站点平均后与观测站点平均随时间的变化对比(图 7a),可看到,两个试验模拟结果对2 m气温的日变化趋势特征捕捉得基本合理,但均存在明显的正偏差,正偏差主要出现在中午之后,夜间尤其明显;然而改进方案与原方案相比,从积分5 h开始,改进方案(KF eta MD方案)预报出的2 m气温低于原方案、略向观测值方向靠近,即模拟的暖偏差平均约有0.5℃的减小,表明2 m气温模拟结果对浅对流激发的增加有微弱正响应。从积分区域空间分布特征的角度看两种方案2 m气温模拟结果并与观测对比,可见就全场而言,两种方案下2 m气温的总体分布是相似的,但在一些区域改进方案预报的2 m气温低于原方案2 m气温而与观测值接近度高(图略)。对改进方案与原方案逐时2 m气温之差的空间分布进行分析,发现两方案2 m气温之差仅仅在某些区域存在且表现为以负值为主的分布特点(正值少量存在),即对2 m气温正偏差减小有正影响,差值普遍为-0.5—-2℃,最大中心可达到-3—-4℃;与改进方案逐时降水模拟结果分布对比,可见两方案2 m气温之差为负值的分布区域与天气系统的移动变化相联系,一般分布在强降水外围的弱降水区(以积分12 h为例,图 7b、c)。也就是说改进方案对减小模式2 m气温偏高有一定正效应,不过这样的正效应因与天气系统及其演变相联系,仅在一些天气区可以被清楚地体现。
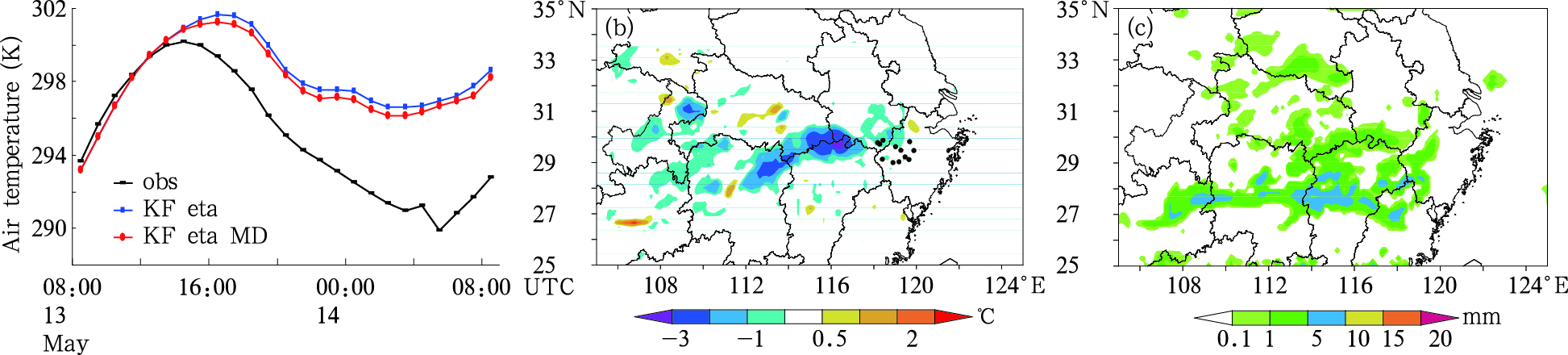 |
| 图 7 观测和两种方案模拟的2 m气温 (a.重点分析区平均2 m气温模拟结果与观测的时间序列,b.积分12 h时(即13日12 时) 2个试验模拟的2 m气温之差(KF eta MD—KF eta),c.KF eta MD试验积分11—12 h时的地面1 h累积降水)Fig. 7 Observed and simulated 2 m air temperature (a. a time series of observed and simulated 2 m air temperature averaged in the key zone of study, b. distribution of simulated 2 m temperature difference (KF eta MD-KF eta) at 12:00 UTC 13 May, c. simulated 1 h accumulative precipitation by KF eta MD experiment from 11:00—12:00 UTC 13 May) |
从上述个例的分析中可见,文中对GRAPES-Meso浅对流激发的改进,可使浅对流激发略提早,浅对流的激发频次增大和浅对流云一些发展特征(云底、云高、持续性等)的模拟更合理,这对改进GRAPES-Meso模式存在的浅对流激发偏少、偏晚问题有正贡献。浅对流激发后对低层环境温、湿度和云雨水形成合理的反馈,通过模式积分过程(即模式动力与物理过程的相互作用以及模式物理过程之间的联系与影响)对模式格点尺度和次网格尺度地面降水的分配比以及2 m气温结果均产生了一些正效应。为了进一步在更大范围、更长时间里考察文中浅对流激发的改进对模式预报的综合影响和改进作用,进行了为期2个月(2014年5月13日—7月13日)的批量试验,一组为对照试验、一组为改进试验,两组试验的唯一差别是所用的浅对流激发方案不同。
批量试验统计结果显示,在24 h累积降水预报总量相当的情况下,改进方案(KF eta MD方案)对流降水占比有所下降而格点尺度降水占比上升,改进方案比原方案格点尺度降水占总降水的比例提高了近2个百分点(图 8a),这与个例试验的结论是一致的,即GRAPES-Meso模式浅对流激发的加强可对其次网格尺度降水占比偏大产生少许改善作用。
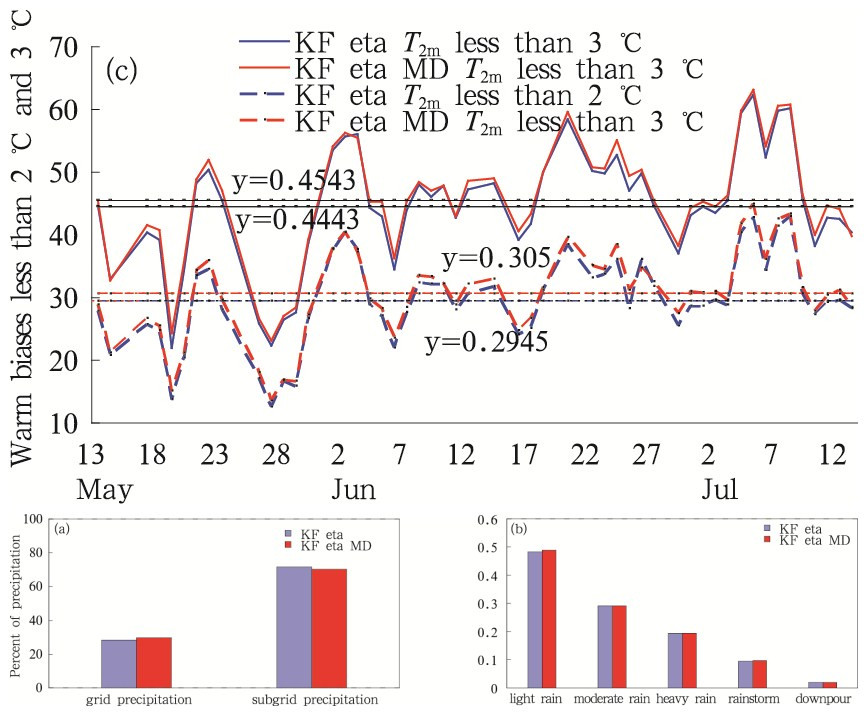 |
| 图 8 两种方案批量(2014年5月13日—7月13日)检验结果 (a.对流降水与格点尺度降水百分比,b.24 h累积降水TS 评分,c.2 m气温误差小于2和3℃的准确率)Fig. 8 Verifications to the two experiment with KF eta and KF eta MD from 13 May to 13 July 2014 (a. percentages of simulated subgrid and grid-scale precipitation, b. TS of 24 h accumulated precipitation, c. accuracy with biases less than 2℃ and 3℃ of 2 m temperature) |
以预报区域地面观测作为真值对两组模拟试验进行24 h累积降水预报评分和2 m气温预报准确率检验,由结果可知改进方案比原方案24 h各量级降水预报TS评分略有提高或持平,预报技巧的提高主要表现在小量级降水方面(图 8b);在整个批量试验期间,改进方案2 m气温的24 h预报准确率(误差小于2和3℃的逐日准确率)高于原方案,少量情况持平,积分区域平均的2 m气温预报准确率较原方案的提高率在0—3个百分点之间变化,整个批量试验平均提高了1个百分点(图 8c)。从批量试验统计平均结果看,浅对流激发的改进对降水和2 m气温的影响程度小于个例试验结果,这是可以理解也是合理的,因为浅对流的发生与环流条件和天气系统相联系,并不是时时处处都发生。尽管总体平均而言,浅对流激发改进对预报结果带来的改进幅度较小,但批量试验结果佐证了文中浅对流激发改进方案对GRAPES-Meso近地面要素(降水和2 m气温)预报的综合影响是正面的,同时改进效果在时间和空间上的变化与差异也表明这一改进对精细化预报更有价值和意义。
5 结 论在GRAPES-MESO模式中,改变KF eta方案中单一温度触发条件,对边界层温、湿度进行一组扰动触发,并且用与该组扰动相关的边界层温、湿度分布确定的联合概率密度函数来表征浅对流云的特征参量,以及计算浅对流的强度。经过个例深入分析和批量试验检验,得到以下结论:
(1)改进方案的浅对流激发和浅对流云模拟结果比原方案有一定优势。改进方案能相对早地激发出浅对流,且浅对流的发生具有一定持续性,提高了GRAPES-MESO模式浅对流的激发频率。相应地,使用改进方案时模拟出的浅对流云底、云高和云持续时间也比较合理,模拟的云底高度与观测更接近。
(2)改进方案浅对流激发后对模式环境温、湿度场产生合理反馈。由于浅对流激发频率的增大,改进方案比原方案对低层距地数百米至2—3 km环境场的升温减湿贡献更显著、浅对流云发生范围更大、反馈给格点尺度的云雨水明显增多。
(3)浅对流激发的改进,使GRAPES-Meso模式格点尺度降水占比平均提高2个百分点,对模式格点尺度降水与次网格尺度降水的分配比可产生一些改善作用。
(4)浅对流激发的改进,对GRAPES-Meso近地面要素(如:地面降水和2 m气温)预报总体上产生了正面影响效果。即:对降水预报技巧略有提高,主要表现为小量级降水预报TS评分的提高和降水细节特征预报的少许改善;对减小模式2 m气温预报偏高有正效应,这样的正效应在相关天气发生地区和时段里表现为清楚的改进作用、而在统计平均上表现为弱的正效果。这种特点,恰恰反映了其对精细化预报而言是更有价值的。
通过本研究发现一些问题值得进一步探讨,一是文中温、湿度扰动浅对流激发方案中联合概率密度函数计算涉及的相关参数(单元条的总数量、单元条的宽度、深/浅对流的最小频率),还可以做取值范围许可内的进一步敏感性试验和优化;二是本试验结果显示,浅对流激发的改进,有益于GRAPES-Meso模式格点尺度降水占比偏小问题的改善,但改进幅度较小,说明模式浅对流过程的描述不是影响GRAPES-Meso模式格点尺度降水和次网格尺度降水分配比协调性的主因,该问题的进一步研究可能还需要从改进模式深对流过程及其与云微物理过程相互作用的描述展开;三是浅对流改进方案能够激发出更多的浅对流,增加浅对流云/雨水对格点的反馈,但对2 m气温预报的总体改进不大,这可能与浅对流反馈给格点尺度的云雨水含量较小、层次浅薄,在模式后续调用的云微物理方案计算中很容易被蒸发掉,未能对模式辐射过程产生应有影响有关(Hannay et al,2009;Berg et al,2013),从而造成模式“空云效应”。这些问题在以后的研究中可以逐一探讨和深入研究。
致 谢:感谢陈德辉、孙健、徐国强等对相关问题的讨论与启发,以及王雨、孙靖等为本次试验和检验数据的收集与下载所提供的帮助。
| 陈德辉. 1997. 积云对流参数化技术. 应用气象学报, 8(Sup): 69-77. Chen D H. 1997. A review on the cumulus convective parameterization. J App Meteor Sci, 8(S): 69-77 (in Chinese) |
| 陈静, 薛纪善, 颜宏. 2003. 物理过程参数化方案对中尺度暴雨数值预报模拟影响的研究. 气象学报, 61(2): 203-218. Chen J, Xue J S, Yan H. 2003. The impact of physics parameterization schemes on mesoscale heavy rainfall simulation. Acta Meteor Sinica, 61(2): 203-218 (in Chinese) |
| 邓华, 薛纪善, 徐海明等. 2008. GRAPES中尺度模式中不同对流参数化方案模拟对流激发的研究. 热带气象学报, 24(4): 327-334. Deng H, Xue J S, Xu H M, et al. 2008. Study of different cumulus parameterization schemes of GRAPES-MESO model in simulation of convection provocation. J Trop Meteor, 24(4): 327-334 (in Chinese) |
| 丁一汇, 柳艳菊. 2006. 南海夏季风爆发的数值模拟. 应用气象学报, 17(5): 526-537. Ding Y H, Liu Y J. 2006. Simulation of the South China Sea summer monsoon onset. J App Meteor Sci, 17(5): 526-537 (in Chinese) |
| 廖镜彪, 王雪梅, 夏北成等. 2012. WRF模式中微物理和积云参数化方案的对比试验. 热带气象学报, 28(4): 461-470. Liao J B, Wang X M, Xia B C, et al. 2012. The effects of different physics and cumulus parameterization schemes in WRF on heavy rainfall simulation in PRD. J Trop Meteor, 28(4): 461-470 (in Chinese) |
| 陆汉城, 康建伟, 王力维等. 2002. 非均匀粘性基流中带状浅对流单体的发展. 南京大学学报(自然科学), 38(3): 346-353. Lu H C, Kang J W, Wang L W, et al. 2002. The development of the shallow band convection cell in nonuniform viscous basic flow. J Nanjing Univ (Nat Sci), 38(3): 346-353 (in Chinese) |
| 刘一鸣, 丁一汇. 2001. 修正的质量通量积云对流方案及其模拟试验研究Ⅰ: 方案介绍及对1991年洪涝过程的模拟. 气象学报, 59(1): 10-22. Liu Y M, Ding Y H. 2001. Modified mass flux cumulus parameterization scheme and its simulation experiment. part Ⅰ: Mass flux scheme and it simulation of the flooding in 1991. Acta Meteor Sinica, 59(1): 10-22 (in Chinese) |
| 刘屹岷, 刘琨, 吴国雄. 2007. 积云对流参数化方案对大气含水量及降水的影响. 大气科学, 31(6): 1201-1211. Liu Y M, Liu K, Wu G X. 2007. The impacts of cumulus convective parameterization on the atmospheric water-content and rainfall simulation in SAMIL. J Atmos Sci, 31(6): 1201-1211 (in Chinese) |
| 屠妮妮, 何光碧, 张利红. 2011. WRF模式中不同积云对流参数化方案对比试验. 高原山地气象研究, 31(2): 18-25. Tu N N, He G B, Zhang L H. 2011. Simulation test on the effects of various cumulus parameterization schemes in WRF model. Plat Mount Meteor Res, 31(2): 18-25 (in Chinese) |
| 王德立, 徐国强, 贾丽红. 2013. GRAPES的积云对流参数化方案性能评估及其改进试验. 气象, 39(2): 166-179. Wang D L, Xu G Q, Jia L H. 2013. The evaluation of cumulus parameterization schemes in GRAPES model and its improved experiments. Meteor Mon, 39(2): 166-179 (in Chinese) |
| 王建捷, 胡欣, 郭肖容. 2001. MM5模式中不同对流参数化方案的比较试验. 应用气象学报, 12(1): 41-53. Wang J J, Hu X, Guo X R. 2001. Comparison experiments on cumulus parameterization schemes of the MM5. Quart J App Meteor, 12(1): 41-53 (in Chinese) |
| 王建捷, 周斌, 郭肖容. 2005. 不同对流参数化方案试验中凝结加热的特征及对暴雨中尺度模拟结果的影响. 气象学报, 63(4): 405-417. Wang J J, Zhou B, Guo X R. 2005. Numerical study on characteristics of condensational heating rates and their impacts on mesoscale structures of torrential rain simulations. Acta Meteor Sinica, 63(4): 405-417 (in Chinese) |
| 徐道生, 陈子通, 钟水新等. 2014. 对流参数化与微物理过程的耦合及其对台风预报的影响研究. 气象学报, 72(2): 337-349. Xu D S, Chen Z T, Zhong S X, et al. 2014. Study of the coupling of cumulus convection parameterization with cloud microphysics and its influence on forecast of typhoon. Acta Meteor Sinica, 72(2): 337-349 (in Chinese) |
| 薛纪善, 陈德辉. 2008. 数值预报系统GRAPES的科学设计与应用. 北京: 科学出版社, 383pp. Xue J S, Chen D H. 2008. Scientific Design and Application of GRAPES. Beijing: Science Press, 383pp (in Chinese) |
| 杨军丽, 沈学顺. 2012. GRAPES单柱模式的试验研究. 气象学报, 70(2): 275-290. Yang J L, Shen X S. 2012. A case study of the GRAPES single column model. Acta Meteor Sinica, 70(2): 275-290 (in Chinese) |
| Berg L K, Stull R B. 2004. Parameterization of joint frequency distributions of potential temperature and water vapor mixing ratio in the daytime convective boundary layer. J Atmos Sci, 61(7): 813-828 |
| Berg L K, Stull R B. 2005. A simple parameterization coupling the convective daytime boundary layer and fair-weather cumuli. J Atmos Sci, 62(6): 1976-1988 |
| Berg L K, Kassianov E I, Long C N, et al. 2011. Surface summertime radiative forcing by shallow cumuli at the Atmospheric Radiation Measurement Southern Great Plains site. J Geophys Res, 116(D1): D01202, doi: 10.1029/2010JD014593 |
| Berg L K, Gustafson W I, Kassianov E I, et al. 2013. Evaluation of a modified scheme for shallow convection: Implementation of CuP and case studies. Mon Wea Rev, 141(1): 134-147 |
| Betts A K. 1986. A new convective adjustment scheme. Part I: Observational and theoretical basis. Quart J Roy Meteor Soc, 112(473): 677-691 |
| Bretherton C S, McCaa J R, Grenier H. 2004. A new parameterization for shallow cumulus convection and its application to marine subtropical cloud-topped boundary layers. PartⅠ: Description and 1D results. Mon Wea Rev, 132(4): 864-882 |
| Brown A R, Cederwall R T, Chlond A, et al. 2002. Large-eddy simulation of the diurnal cycle of shallow cumulus convection over land. Quart J Roy Meteor Soc, 128(582): 1075-1093 |
| Dorrestijn J, Crommelin D T, Siebesma A P, et al. 2012. Stochastic parameterization of shallow cumulus convection estimated from high-resolution model data. Theor Comp Fluid Dyn, 27(1-2): 133-148 |
| Fritsch J M, Chappell C F. 1980. Numerical prediction of convectively driven Mesoscale pressure systems. PartⅠ: Convective parameterization. J Atmos Sci, 37(8): 1722-1733 |
| Hannay C, Williamson D L, Hack J J, et al. 2009. Evaluation of forecasted southeast Pacific stratocumulus in the NCAR, GFDL, and ECMWF models. J Climate, 22(11): 2871-2889 |
| Johnson R H, Rickenbach T M, Rutledge S A, et al. 1999. Trimodal characteristics of tropical convection. J Climate, 12(8): 2397-2418 |
| Kain J S, Fritsch J M. 1990. A one-dimensional entraining/detraining plume model and its application in convective parameterization. J Atmos Sci, 47(23): 2784-2802 |
| Kain J S, Fritsch J M. 1993. Convective parameterization for Mesoscale models: The Kain-Fritsch scheme//Emanuel K A, Raymond D J. The Representation of Cumulus Convection in Numerical Models. New York: Ameri Meteor Soc, 165-170 |
| Kain J S. 2004. The Kain-Fritsch convective parameterization: An update. J Appl Meteor, 43(1): 170-181 |
| Nie J, Kuang Z M. 2012. Responses of shallow cumulus convection to large-scale temperature and moisture perturbations: A comparison of large-eddy simulations and a convective parameterization based on stochastically entraining parcels. J Atmos Sci, 69(6): 1936-1956 |
| Rio C, Hourdin F, Couvreux F, et al. 2010. Resolved versus parametrized boundary-layer plumes. Part II: continuous formulations of mixing rates for mass-flux schemes. Bound Layer Meteor, 135(3): 469-483 |
| Siebesma A P, Jakob C, Lenderink G, et al. 2004. Cloud representation in general-circulation models over the northern Pacific Ocean: A EUROCS intercomparison study. Quart J Roy Meteor Soc, 130(604): 3245-3267 |
| Soares P M M, Miranda P M A, Siebesma A P, et al. 2004. An eddy-diffusivity/mass-flux parametrization for dry and shallow cumulus convection. Quart J Roy Meteor Soc, 130(604): 3365-3383 |
| Stevens B, Ackerman A S, Albrecht B A, et al. 2001. Simulations of trade wind cumuli under a strong inversion. J Atmos Sci, 58(14): 1870-1891 |
| Stull R B. 1988. An Introduction to Boundary Layer Meteorology. Boston: Kluwer Academic Publishers |
| Tiedtke M, Heckley W A, Slingo J. 1988. Tropical forecasting at ECMWF: The influence of physical parametrization on the mean structure of forecasts and analyses. Quart J Roy Meteor Soc, 114(481): 639-644 |
| Tiedtke M. 1989. A comprehensive mass flux scheme for cumulus parameterization in large-scale models. Mon Wea Rev, 117(8): 1779-1800 |
 2015, Vol. 73
2015, Vol. 73