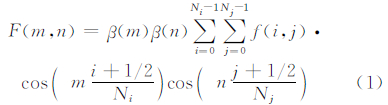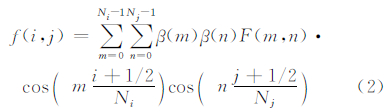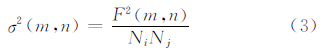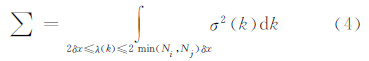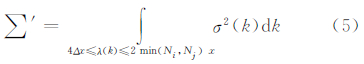中国气象学会主办。
文章信息
- 黄永杰, 崔晓鹏. 2016.
- HUANG Yongjie, CUI Xiaopeng. 2016.
- 四川地形谱特征及中尺度模式水平网格分辨率选取
- Spectral characteristics of terrain in the Sichuan basin and the horizontal grid size selection for a mesoscale model
- 气象学报, 74(1): 114-126
- Acta Meteorologica Sinica, 74(1): 114-126.
- http://dx.doi.org/10.11676/qxxb2016.010
-
文章历史
- 2015-08-24 收稿
- 2015-12-24 改回
2. 中国科学院大学, 北京, 100049;
3. 南京信息工程大学气象灾害预报预警与评估协同创新中心, 南京, 210044
2. University of Chinese Academy of Sciences, Beijing 100049, China;
3. Collaborative Innovation Center on Forecast and Evaluation of Meteorological Disasters, Nanjing University of Information Science and Technology, Nanjing 210044, China
强降水(如暴雨)对中国的经济发展和人民生活有着重要的影响,特别是在四川,经过2008年汶川和2013年雅安大地震后地质更加疏松,强降水易诱发洪涝、山体滑坡和泥石流等灾害,对人民的生命财产将造成极大的威胁。众所周知,地形对于强降水的发生有着重要的影响,会影响降水的时空分布(Smith,2006;赵玉春等,2011;李唐棣等,2012),地形的强迫抬升作用对于降水的发生和加强起着重要作用(盛春岩等,2012)。四川盆地位于青藏高原以东,云贵高原以北,秦岭高地以南,地形复杂多样。因此,研究该区域的地形以及如何用中尺度模式更好地表征其特征,对认识暴雨的发生、发展具有重要的意义。
Pielke等(1980)提出在频谱空间,地形特征能得到恰当的表征,但由于当时计算机计算能力的限制,对地形的谱分解多使用一维傅里叶变换(Young et al,1984)。在处理二维地形高度场时,Young等(1983)提出在地形变化剧烈的区域分成多个剖面并使用一维傅里叶变换进行谱分解,从而确定中尺度模式水平网格分辨率,而Steyn等(1985)使用二维的傅里叶变换对不同的区域进行研究,提出不同的区域各向同性的性质存在差异,对于用一维地形高度谱来确定中尺度气象模式网格距时要谨慎使用。Salvador等(1999)使用二维谱分析研究了数值模式模拟西班牙东海岸天气过程所需要的空间分辨率。王宛亭等(2004)利用纬向加权平均地形扰动谱,研究了青藏高原地区地形扰动特征及地形强迫对大气受迫运动的机制。舒守娟等(2006)使用纬向和经向加权平均的方法计算一维谱分解,研究了西藏高原地形扰动对其降水分布的影响。但以上提到的一维或二维谱分析采用的都是传统的离散傅里叶变换,Denis等(2002)提出,离散傅里叶变换在研究全球大气中很合适,因为离散傅里叶变换的基函数与沿着纬圈分布的大气场一样都是周期的,所以离散傅里叶变换在研究全球大气中被广泛使用。但是,在有限区域格点场的研究中,傅里叶变换并没有那么流行,因为这些格点是非周期的,而且多数情况下受到波长比研究区域大的大尺度因素的控制,容易出现大尺度方差向小尺度方差的混淆现象。Denis等(2002)把最早用于图像压缩且广泛应用于图像和信号处理的离散余弦变换(Discrete Cosine Transform,以下简记为DCT)引进大气科学领域的谱分析中,有效地克服了离散傅里叶变换在有限区域谱分析中的局限性。随后离散余弦变换在大气科学的有限区域谱分析中得到广泛应用,郑永骏等(2008)利用离散余弦变换研究了半隐式半拉格朗日格点区域模式的动能谱特征及其行为特征;江川等(2013)将离散余弦变换应用到二维有限区域湍流能谱的研究中,较真实地反映了实际湍流能谱的信息; Prein等(2013)利用离散余弦变换的方法探讨了区域气候模式网格距对模拟科罗拉多河源地区强降水的重要性。
本研究使用二维离散余弦变换(2D-DCT)对四川地区的地形和降水进行谱分解,讨论在谱空间中,四川地区地形和降水所表现出的特征,而且利用地形谱方差,定量讨论了在使用中尺度模式研究某个复杂地形地区的天气过程时,如何选择较为合适的模式水平网格分辨率,才能使模式能较大程度地抓住地形对大气的影响。
2 资料与方法 2.1 资 料对于地形资料的选择,与真实地形越接近(地形分辨率越高)越好,所以,文中使用的地形高度资料是美国国家航空航天局(NASA)提供的SRTM(Shuttle Radar Topographic Mission)3″(约90 m分辨率)的数字高程数据(http://srtm.csi.cgiar.org)(Jarvis et al,2008),降水资料为中国自动气象站与CMORPH融合的0.1°×0.1°空间分辨率2008—2014年逐时降水量数据(潘旸等,2012;沈艳等,2013)。
2.2 空间场谱分解使用2D-DCT来对地形高度场和暴雨分布场进行谱分解,计算方差谱能。离散余弦变换是首次被 Denis等(2002)应用到大气谱分析中,随后在大气科学领域得到广泛应用(郑永骏等,2008; 江川等,2013; Prein et al,2013; Ricard et al,2013; Li et al,2014; Peng et al,2014; Surcel et al,2015)。该变换对有限区域的谱分解尤其有效,能克服有限区域的非周期边界问题,与传统的离散傅里叶变换不同,离散余弦变换不需要对物理场进行周期化、去倾等处理,而且能克服大尺度方差混淆到小尺度方差的现象。对于Ni × Nj网格的物理空间场f(i,j),其离散余弦变换和逆变换分别为
和 式中,F(m,n)为波数m,n对应的谱系数。其中,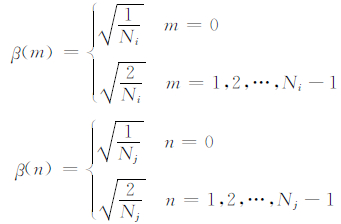
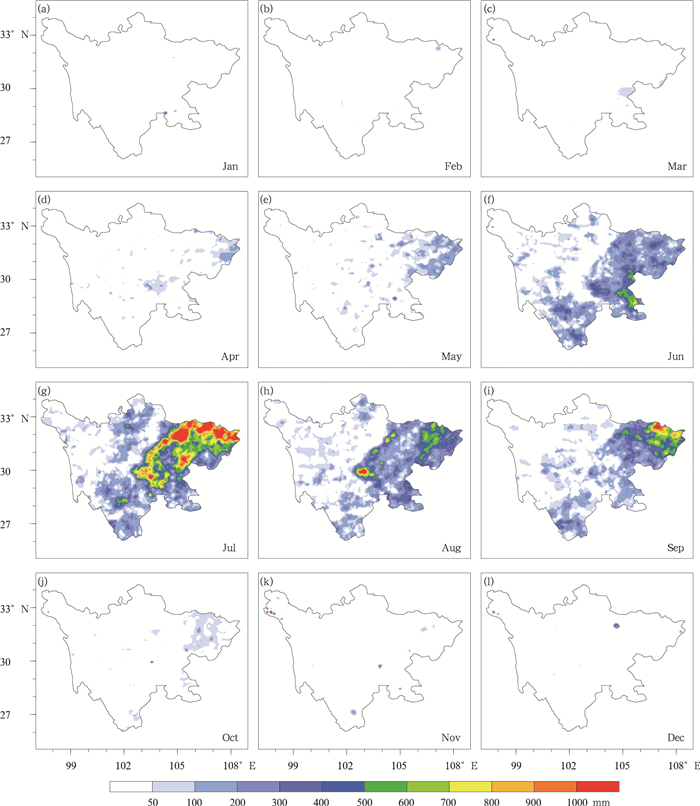
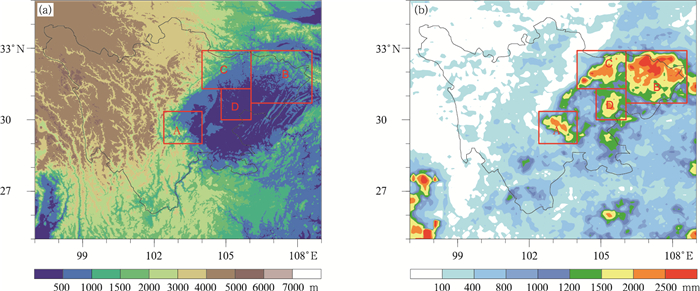
在对地形高度场和降水场进行谱分解之前,首先对四川的暴雨进行统计。图 1给出了四川地区2008—2014年暴雨(24 h降水量≥50 mm)总量月分布。可见四川暴雨主要发生在6—9月,特别是7月,且暴雨主要分布在四川盆地。为了更好地看出降水的空间分布与四川地形的关系,图 2给出了四川地形高度分布(图 2a)及2008—2014年6—9月暴雨总量的空间分布(图 2b)。可见四川暴雨分布主要存在4个大值中心,分别位于四川盆地西南部的雅安地区(图 2中的区域A)、四川盆地东北部大巴山地区(图 2中的区域B)、四川盆地西北部(图 2中的区域C)及四川盆地中部(图 2中的区域D)。其中,区域A、B、C的暴雨大值中心都分布在四川盆地的边缘陡峭地形地带。根据暴雨的分布特征,选取了本研究的4个区域,即图 2中用红色矩形圈出的区域A、B、C和D。
|
| 图 1 四川2008—2014年暴雨总量月(a-l)分布 Fig. 1 Monthly distribution (a-l) of the total torrential rainfall with the 24 h accumulative precipitation ≥ 50 mm averaged over 2008-2014 in Sichuan |
|
| 图 2 a)四川地形高度及(b)2008—2014年6—9月暴雨总量的空间分布 (图中A、B、C、D红色矩形框为文中选取的4个研究区域) Fig. 2 (a) Terrain height in Sichuan; (b) distribution of the total torrential rainfall from June to September averaged over 2008-2014 in Sichuan (Red rectangles indicate the 4 study areas (A, B, C, and D) in this study) |
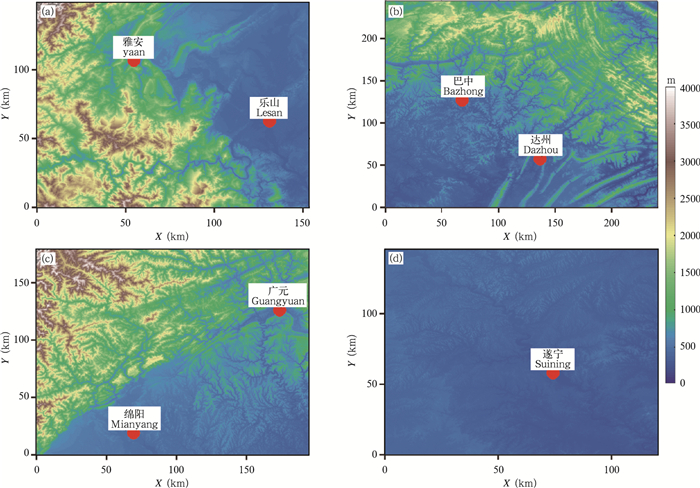
从上述4个研究区域的地形高度分布(图 3)可以看出,除了区域D(四川盆地中部)地势比较低洼外,其余区域的地形高度高且比较复杂,沟壑纵横。区域A(雅安地区)主要呈现喇叭口地形,西部地势高且复杂多样,东部较为低洼平坦,此类地形对水汽的聚集和抬升起到重要作用;区域B(四川盆地东北部)主要为西北—东南向的复杂地形带;区域C(四川盆地西北部)复杂地形主要在西北部,南部和东南部较为平坦;区域D位于盆地中部,属于盆地中的平原地带,相对其他区域,该区地形相对平坦,但也存在不少沟壑。
|
| 图 3 研究区域A、B、C、D(a—d)的地形高度分布(区域位置见图 2所示) Fig. 3 Terrain height fields in the study area A,B,C,D(a-d,area location is shown as in Fig. 2) |
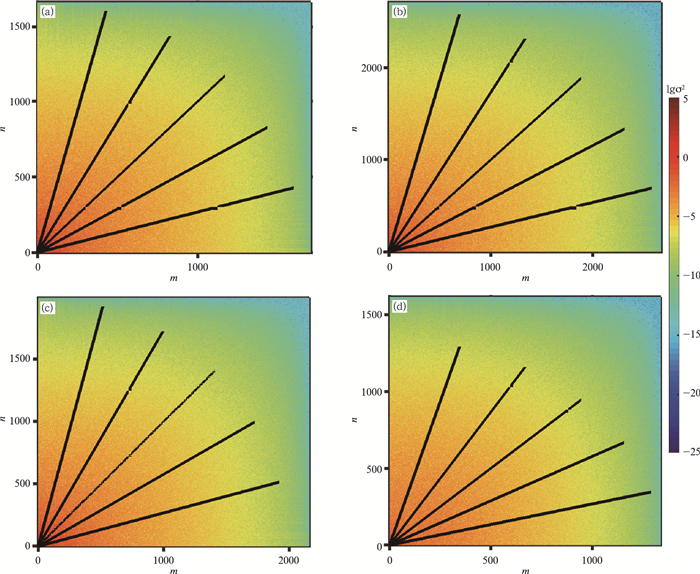
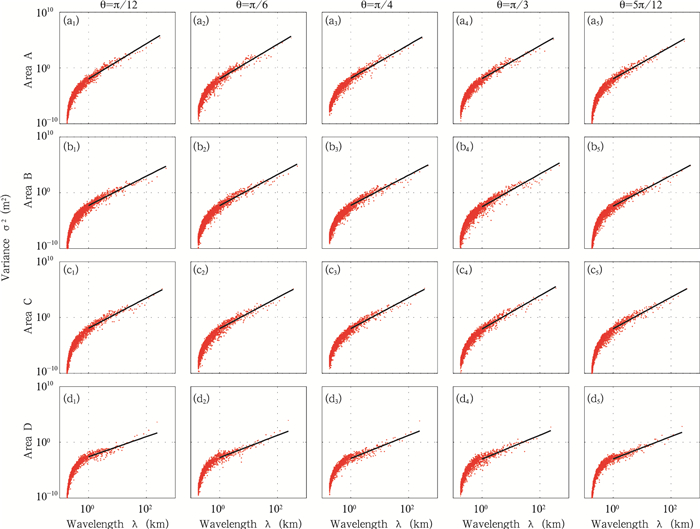
根据四川暴雨和地形的空间分布特征选取了4个研究区域,对各研究区域的地形高度场分别进行二维离散余弦变换。图 4给出了4个研究区域的二维地形高度谱方差σ2分布。总体而言,各个区域的地形高度方差随着波数减小(波长增大)而增大,为了更好看出各研究区域是否存在各向同性的特征,图 5给出了各个区域在以波数(0,0)为起点,与m轴夹角分别为π/12、π/6、π/4、π/3和5π/12的射线上的地形高度方差与波长λ的分布,同时表 1给出了分布图中波长λ在1 km以上部分,对地形高度谱方差与波长的关系 σ2 = aλb 取对数后得lnσ2 = lna + blnλ,进行lnσ2对lnλ的最小二乘拟合(图 5中的直线)得到的拟合系数a、b以及相关系数r。由此可知,参数a表示波长λ为1 km时所具有的方差,参数b表示对数坐标下拟合曲线的斜率,参数b较小,则说明波长较短处具有显著的地形方差,即小尺度地形扰动特征显著。4个研究区域的指数参数b的平均值分别为3.0129、2.7537、2.8012和1.9972,各区域不尽相同,区域A(雅安地区)最大,区域B(盆地东北部)和区域C(盆地西北部)较为接近,区域D(盆地中部)最小,说明区域A的较大尺度地形扰动明显,而区域D的小尺度地形扰动显著,因此四川盆地地区地形复杂,不同区域地形特征存在较大差异;对于每个区域来说,指数参数b的极差(最 大值与最小值之差)与指数b平均值的比值分别为8.50%、11.04%、9.64%和16.99%,参数a的极差与平均值的比值分别为28.13%、53.54%、31.57%和101.88%,从中发现,虽然盆地中部地区(区域D)地势比较平坦,但该区域的各个方向的差异是最大的,其余区域各向差异较小,其中雅安地区(区域A)的各向差异最小,但该区域的指数b的极差已经占平均值的8.50%。这再次说明四川盆地地区的地形复杂,而且各向异性特征明显,所以仅仅用一维的地形谱并不能较好表现出该区域的整体特征,而用二维离散余弦变化方法得到的地形高度谱方差则可很好地表现出各个有限区域的地形各向异性的复杂特征。
|
| 图 4 研究区域A、B、C、D(a—d)的二维地形高度谱方差σ2的常用对数 lgσ2 分布(m,n分别为纬向波数和经向波数) Fig. 4 Two-dimensional terrain height variance spectrum common logarithm (lgσ2) distribution of the study area A, B, C, and D (a-d, m and n represent zonal wave number and meridional wave number, respectively) |
|
| 图 5 研究区域A、B、C、D(a—d)在以波数(0,0)为起点,与m轴夹角分别为π/12 (a1—d1)、π/6 (a2—d2)、π/4 (a3—d3)、π/3 (a4—d4)和5π/12 (a5—d5)的射线 (图4中射线) 上的地形高度谱方差σ2与波长λ在对数坐标下的分布 Fig. 5 Terrain height variance σ2 vs wavelength λ distribution with the wave number (0, 0) as the starting point, and the angle between the rays (show in Fig.4) and the m-axis, being respectively π/12 (a1-d1), π/6 (a2-d2), π/4 (a3-d3), π/3 (a4-d3) and 5π/12 (a5-d5) for the study area A, B, C, D (a-d) |
| π/12 | π/6 | π/4 | π/3 | 5π/12 | 平均 | ||
| 区域A | a | 0.0108 | 0.0106 | 0.0139 | 0.012 | 0.0114 | 0.0117 |
| b | 3.1464 | 3.0911 | 2.9916 | 2.9449 | 2.8904 | 3.0129 | |
| r | 0.9451 | 0.9257 | 0.9341 | 0.9295 | 0.9359 | ||
| 区域B | a | 0.0050 | 0.0048 | 0.0054 | 0.0030 | 0.0040 | 0.0044 |
| b | 2.6251 | 2.777 | 2.7008 | 2.9290 | 2.7367 | 2.7537 | |
| r | 0.9227 | 0.9283 | 0.9221 | 0.9006 | 0.9333 | ||
| 区域C | a | 0.0118 | 0.0102 | 0.0105 | 0.0085 | 0.0098 | 0.0102 |
| b | 2.7065 | 2.7596 | 2.7547 | 2.9764 | 2.8088 | 2.8012 | |
| r | 0.9245 | 0.9072 | 0.9212 | 0.9333 | 0.9156 | ||
| 区域D | a | 0.0025 | 0.0017 | 0.0013 | 0.0010 | 0.0011 | 0.0015 |
| b | 1.7992 | 1.9931 | 2.0575 | 2.1385 | 1.9976 | 1.9972 | |
| r | 0.8473 | 0.8571 | 0.8818 | 0.8573 | 0.9048 | ||
| r为相关系数。 | |||||||
为了分析地形高度谱方差与暴雨总量谱方差的关系,对二维谱系数进行加法合成得到方差与总波长的关系,即利用距离权重系数将位于k和k+1波数之间的谱方差分到波数k和k+1,具体做法参见Ricard等(2013)。
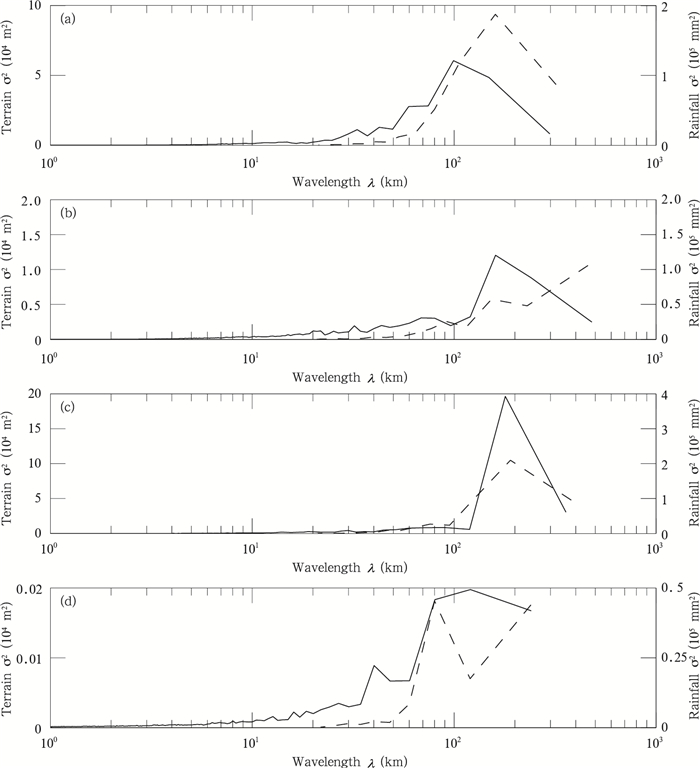
图 6给出了4个研究区域的加法合成后的地形高度谱方差σ2和2008—2014年6—9月暴雨总量谱方差σ2关于波长λ的变化曲线。可以看出,地形高度方差大部分分布在波长较大尺度范围内,其中,盆地中部(区域D)最大地形方差接近200 m2,比其他区域的明显要低,结合图 3可定性看出盆地中部的地形高度分布较其他区域平坦,较大尺度的地形扰动较弱,而其中地形扰动特征最明显的区域为盆地西北部(区域C),其地形方差相对较高。在所研究的范围内,4个区域的最大地形方差在波长100—200 km,区域A、B和C的地形方差波动有相似性,而区域D在波长小于100 km尺度的地形方差波动也较为明显,这与前文计算得到的区域D的指数参数b较小(即小尺度地形扰动特征显著)有关。对于暴雨总量谱方差,不同的区域谱方差也不尽相同,但总体来看都是随着波长的增大而增大的趋势。结合每个区域地形谱与降水谱来分析,可很清楚地看到地形谱和降水谱有较强的相关性,特别是区域A(雅安地区)和区域C(盆地西北部),地形谱方差的波动与降水谱方差的波动很一致,说明在这些区域,地形 对大气的抬升作用对暴雨的发生发展起到重要作用;而区域B(盆地东北部)和区域D(盆地中部)的地形谱与降水谱在波长较大处出现反相的关系,说明这些地区暴雨发生的因素比其他区域更加复杂,地形所起到的作用被其他因子所削弱;特别是区域D(盆地中部),从谱方差分布看出,当波长大于80 km时,地形和降水谱方差波动几乎是反相的,从图 3区域D的地形高度分布也可以定性看出,此区域的地形较为平坦,较大尺度地形扰动较弱,但此处的暴雨总量并不小,因此,盆地中部的暴雨可能以其他因素为主导,受地形抬升作用偏弱,以至于地形谱与降水谱出现反相关系。
|
| 图 6 研究区域A、B、C、D(a—d)的地形高度方差σ2 (实线) 和暴雨总量方差σ2 (虚线) 对于波长λ的分布曲线 Fig. 6 Terrain height spectral variance σ2 (solid line) and total torrential rainfall spectral variance σ2 (broken line) vs wavelength λ for the study area A, B, C, D (a-d) |
由于数值模式使用的是离散网格,因此模式网格分辨率的选取,对于模式能否很好地体现所研究区域地形特征对大气运动的作用是很重要的,如果次网格尺度的地形方差很大,则模式中必须考虑其作用,要么提高网格分辨率,要么采用次网格地形参数化的方法(王元等,2007;Jiménez et al,2012;Lee et al,2015)。因此,文中从地形作用的角度出发,对于如何选取较为合适的中尺度模式水平分辨率进行定量讨论。
Young等(1983)提出使用传统的一维快速傅里叶变换的方法计算地形谱能,并确定较为合适的中尺度模式网格分辨率。但是,如果所研究的区域地形具有各向异性的特征,则一维的谱分析并不能很好地表征二维区域的地形特征信息,所以Salvador等(1999)则在Young等(1983)的基础上,使用传统的二维快速傅里叶谱分解计算地形谱,讨论中尺度模式网格距的选取及其对模式模拟效果的影响,文中是基于Young等(1983)和Salvador等(1999)的思想,使用对于研究有限区域更为有效的2D-DCT方法计算得到的二维地形谱方差分布,确定研究某有限区域合适的中尺度模式网格距。所研究区域包含的地形方差定义为
式中,波数k = 1,2,3,…,min(Ni-1,Nj-1),波长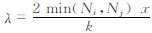 x为地形数据的分辨率。假定数值模式完全不能分辨波长小于2Δx(Δx为模式网格距)的地形方差,而要比较满意的表现可能需要4Δx波长尺度(Uliasz et al,1996),所以中尺度模式能分辨的地形方差定义为
x为地形数据的分辨率。假定数值模式完全不能分辨波长小于2Δx(Δx为模式网格距)的地形方差,而要比较满意的表现可能需要4Δx波长尺度(Uliasz et al,1996),所以中尺度模式能分辨的地形方差定义为
因此,给定一个Ni×Nj水平区域,地形数据分辨率为δx,则使用网格分辨率为Δx的中尺度模式能考虑到的方差与原始地形数据所包含的总方差的比值为
表 2给出了4个研究区域针对不同模式网格距,模式能分辨的地形方差与总地形方差的比值。可见如果模式使用3 km分辨率的网格,4个研究区域能分辨出的地形方差均达不到90%,即模式网格分辨率低于3 km时,模式并不能较好地表达地形的作用;当模式使用1 km网格分辨率时,模式能分辨出区域A(雅安地区)、区域B(盆地东北部)和区域C(盆地西北部)3个区域的90%以上地形方差,此时区域A和C已经超过95%;而对于区域D(盆地中部),整体的地形方差相比其他区域小,在较小波长处的地形方差占总方差的比例也不小,若要考虑这些较小尺度地形的作用,根据表 2可知,当模式分辨率为200 m时,模式才能分辨出该区域超过90%的地形方差。需要注意的是,这里所说的包含了90%的地形谱方差并不能保证模式能正确模拟所有的现象,只能说模式能抓住地形对大气流场90%的影响。此外,在研究某个区域时,需要先评估该区域的地形对天气系统的影响有多大,地形方差是否足够大,以至于不能忽略,然后再考虑模式网格距对地形方差的刻画问题。比如,文中的区域D地势较为平坦,地形方差量级相对于其他区域小得多,而且地形谱方差与降水谱方差有反相关系,因此该区域地形对于降水系统的影响可能并不大,在考虑模式网格距选取时应更多考虑对降水系统有较大作用的其他因素。同时,以往的研究分析发现,模式的网格分辨率并不是越高越好,应该有一个极值,当超过这个值后,无论如何再提高模式网格分辨率,模拟的效果都不会有太大的变化,而且分辨率还要和模式的各个方面协调才能有好的效果。由于影响模式网格分辨率选取的因素众多,文中主要从地形的角度进行探讨,并以模式能抓住90%以上的地形方差为标准来讨论模式网格分辨率的选取问题。
| Δx | 区域A | 区域B | 区域C | 区域D |
| 27 km | 0.2678 | 0.2661 | 0.5955 | 0.2373 |
| 18 km | 0.4624 | 0.3181 | 0.6044 | 0.2823 |
| 9 km | 0.6402 | 0.4567 | 0.7011 | 0.3737 |
| 3 km | 0.8189 | 0.7001 | 0.8468 | 0.5256 |
| 1 km | 0.9584 | 0.9016 | 0.9523 | 0.6554 |
| 333 m | 0.9945 | 0.9844 | 0.9940 | 0.8157 |
| 200 m | 0.9984 | 0.9954 | 0.9984 | 0.9147 |
| 90 m | 0.9999 | 0.9998 | 0.9999 | 0.9961 |
为了单纯地分析使用不同模式网格分辨率描述的地形对大气流场的作用,下面利用干的大气探空垂直廓线和真实地形进行理想数值试验。利用美国国家大气研究中心(NCAR)开发的天气研究和预报模式WRF V3.7进行数值试验,模拟中使用非静力方案及WRF官方提供的地形理想试验的探空廓线驱动模式,该廓线忽略了水汽,采用U=10 m/s的均匀西风。为了主要分析地形对大气的动力效应,模式积分中不考虑云微物理和积云对流参数化,忽略近地面、边界层、辐射等物理过程。为了避免扰动返回模式区域影响模拟结果,模拟中侧边界采用开放侧边界条件,并忽略了旋转效应(f= 0)的作用。将3″分辨率的地形资料引入WRF模式中,模拟区域选择具有典型复杂地形特征的区域A(雅安地区)为例,垂直方向设置为41层,模式层顶高度为30 km,模式水平分辨率分别为常用的6、3、1.5和1 km,这4种模式网格分辨率能抓住的地形方差百分比分别为72.92%、81.89%、92.41%和95.84%。
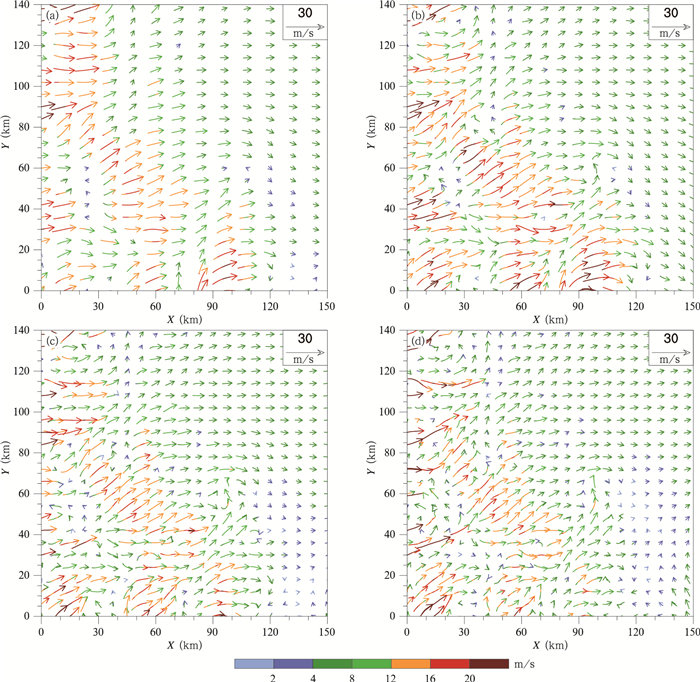
模式积分1 h的地面矢量风场(图 7)显示,4种不同模式水平分辨率模拟的主要流场形态基本一致,东北部都呈现比较均匀的偏西风,而西南部由于地形比较复杂,存在很多山沟,流场形态也较为复 杂,但4个试验的结果总体来看比较相似。当然,四者也存在些差异,如区域东南部(X方向120—140 km,Y方向0—60 km),分辨率较高的试验(图 7c、d)的风场明显要比分辨率较粗的试验(图 7a、b)偏小,而且方向差异也较大。由于大气运动是复杂的非线性过程,小的差异也会对之后的结果造成很大的不同。当模式积分至3 h(图 8),各试验的流场形态出现较大差异,如6 km分辨率试验东北部以偏北风为主,风速较小;而3 km 分辨率试验同样也是偏北风为主,风速却较大;1.5和1 km分辨率试验相似,较为一致的东南风,风速大小也较接近。对于区域的西部地区,3 km分辨率试验(图 8b)模拟的地面风速最大,1.5和1 km分辨率试验(图 8c、d)结果基本一致。因此,通过理想的数值试验可知,对于区域A,选择1.5 km或者更高分辨率的模式网格,能较好地抓住地形对大气流场的动力作用。此外,从图 8可见3 km分辨率的试验结果与其他分辨率的试验结果差异较大,通过大量的敏感性试验发现,约3 km分辨率的试验结果确实存在这样的差异,猜测这种现象的出现,可能与模式本身以及此 区域的地形特征尺度有一定关系,未来将进一步采用尺度分解结合大量的数值模拟与敏感性试验等办法,针对这一有趣的问题开展专门的研究和分析。
|
| 图 7 模式积分1 h的地面矢量风场 (填色矢线)(a.Δx=6 km, b.Δx=3 km, c. Δx=1.5 km, d. Δx=1 km) Fig. 7 Surface wind vectors (shaded vector) at the model integration of 1 hour(a.Δx=6 km, b.Δx=3 km, c. Δx=1.5 km, d. Δx=1 km) |

|
| 图 8 模式积分3 h的地面矢量风场 (填色矢线)(a. Δx=6 km, b. Δx=3 km, c. Δx=1.5 km, d. Δx=1 km) Fig. 8 As in Fig.7 but for 3 hours |
综上所述,使用中尺度模式研究某个区域的天气现象时,如果要考虑该区域地形对模式的作用,可以先通过地形谱方差的分析,判断地形是否对天气系统起到不可忽视的作用,然后计算对于该区域模式采用不同网格分辨率能分辨的地形方差,最终可确定合适的中尺度模式水平分辨率(模式能抓住90%以上地形方差较好),因此,从地形的角度,该方法给中尺度模式网格分辨率的选取提供了定量依据。
4 结论与讨论主要通过二维离散余弦变换,对四川地区地形高度场和降水场进行谱分解,讨论了四川盆地地形特征,暴雨分布特征及地形谱与降水谱的关系,同时利用地形谱方差和数值试验定量讨论了中尺度模式水平网格分辨率的选取问题,得到了如下主要结论:
(1)四川地区强降水(暴雨)主要分布在盆地边缘陡峭地形带及盆地中部,主要发生在6—9月,且以7月最为集中。 根据暴雨分布特征,选取了4个研究区域,通过对其地形高度场和暴雨总量分布场进行二维谱分解得出,盆地中部地区地形各向差异最大,雅安地区地形各向差异四者中最小,但4个区域都具有明显的各向异性复杂特征,说明仅仅使用一维的谱分解并不能很好地表征四川地区的复杂地形特征,而二维离散余弦变换则能较好地表现出其空间各向异性特征。
(2)通过对地形高度谱和降水谱方差关于波长的分布曲线分析得出,地形方差和降水方差随着波长的增大都有增大的趋势;盆地中部地区地形方差相对于其他区域偏小,这也是由于该区域的地形比较平坦造成的;雅安地区和盆地西北部地区的地形谱与降水谱方差变化较为一致,说明对于这些区域,地形的抬升作用对强降水的发生起到重要作用,而对于盆地东北部和盆地中部地区,两者的同相关系较弱,在波长较长处出现反相关系,说明这些地区暴雨发生的因素比其他区域更加复杂,地形所起到的作用被其他因子所削弱。
(3)从地形的角度出发,利用地形谱方差,对中尺度区域模式水平网格分辨率的选取建立定量的判断。在选取的4个研究区域中,基于3″分辨率的地形资料,当模式使用1 km 网格分辨率时,对于雅安地区、盆地东北部和盆地西北部地区,模式能解释超过90% 的地形方差,即模式能抓住这些区域超过90% 地形对大气流场的影响;而对于盆地中部地区,当模式分辨率为200 m时,模式才分辨出超过90%的地形方差,但通过谱方差可知,该区域的地形方差量级比其他区域都小,地形对大气流场并不起重要作用。因此,通过地形谱方差的分析,可以针对某个特定区域的地形特征,判断地形是否对天气系统起到不可忽视的作用,进而利用地形谱进行定量分析,选取合适的中尺度模式水平网格距(模式能抓住90%以上地形方差较好)。
| 江川, 沈学顺. 2013. 基于大涡模拟评估GRAPES模式对对流边界层的模拟性能. 气象学报, 71(5):879-890. Jiang C, Shen X S. 2013. Assessment of the simulative performance of the GRAPES model on the convective boundary layer based on the large eddy simulations. Acta Meteor Sinica, 71(5):879-890 (in Chinese) |
| 李唐棣, 谈哲敏. 2012. 条件不稳定大气中二维小尺度双脊地形上空对流及降水特征. 气象学报, 70(3):536-548. Li T D, Tan Z M. 2012. Characteristics of the orographiclly induced convection and precipitation over an idealized two-dimensional small scale two ridge orography in the conditionally unstable atmosphere. Acta Meteor Sinica, 70(3):536-548 (in Chinese) |
| 潘旸, 沈艳, 宇婧婧等. 2012. 基于最优插值方法分析的中国区域地面观测与卫星反演逐时降水融合试验. 气象学报, 70(6):1381-1389. Pan Y, Shen Y, Yu J J, et al. 2012. Analysis of the combined gauge-satellite hourly precipitation over China based on the OI technique. Acta Meteor Sinica, 70(6):1381-1389 (in Chinese) |
| 沈艳, 潘旸, 宇婧婧等. 2013. 中国区域小时降水量融合产品的质量评估. 大气科学学报, 36(1):37-46. Shen Y, Pan Y, Yu J J, et al. 2013. Quality assessment of hourly merged precipitation product over China. Trans Atmos Sci, 36(1):37-46 (in Chinese) |
| 盛春岩, 高守亭, 史玉光. 2012. 地形对门头沟一次大暴雨动力作用的数值研究. 气象学报, 70(1):65-77. Sheng C Y, Gao S T, Shi Y G. 2012. Numerical simulation of the dynamic effect of the orography on a Mentougou severe torrential rain event. Acta Meteor Sinica, 70(1):65-77 (in Chinese) |
| 舒守娟, 王元, 李艳. 2006. 西藏高原地形扰动对其降水分布影响的研究. 水科学进展, 17(5):585-591. Shu S J, Wang Y, Li Y. 2006. Effect of topographic perturbation on the precipitation distribution in Tibetan Plateau. Adv Water Sci, 17(5):585-591 (in Chinese) |
| 王宛亭, 王元. 2004. 卫星遥测纬向剖面地形谱分析——青藏高原背风侧地区地形扰动与西风扰动的耦合模态. 南京大学学报(自然科学), 40(3):304-318. Wang W T, Wang Y. 2004. A spectral analysis of satellite topographic profile:A coincident pattern between latitudinal topographic and westerly perturbation on the lee side of Qinghai-Tibet Plateau. J Nanjing Univ (Nat Sci), 40(3):304-318 (in Chinese) |
| 王元, 唐锦赟, 伍荣生. 2007. 一个双波地形重力波拖曳参数化方案. 气象学报, 65(5):733-743. Wang Y, Tang J Y, Wu R S. 2007. A two-wave scheme for orographic gravity wave drag parameterization. Acta Meteor Sinica, 65(5):733-743 (in Chinese) |
| 赵玉春, 王叶红, 崔春光. 2011. 大对流有效位能和条件不稳定下地形降水的三维理想数值研究. 气象学报, 69(5):782-798. Zhao Y C, Wang Y H, Cui C G. 2011. An idealized three-dimensional numerical study of the topographic precipitation under air flow of large CAPE and conditionally unstable stratification. Acta Meteor Sinica, 69(5):782-798 (in Chinese) |
| 郑永骏, 金之雁, 陈德辉. 2008. 半隐式半拉格朗日动力框架的动能谱分析. 气象学报, 66(2):143-157. Zheng Y J, Jin Z Y, Chen D H. 2008. Kinetic energy spectrum analysis in a semi-implicit semi-Lagrangian dynamical framework. Acta Meteor Sinica, 66(2):143-157 (in Chinese) |
| Denis B, Côté J, Laprise R. 2002. Spectral decomposition of two-dimensional atmospheric fields on limited-area domains using the discrete cosine transform (DCT). Mon Wea Rev, 130(7):1812-1829 |
| Jarvis A, Reuter H I, Nelson A, et al. 2008. Hole-filled SRTM for the Globe Version 4, available from the CGIAR-CSI SRTM 90 m Database. http://srtm.csi.cgiar.org |
| Jiménez P A, Dudhia J. 2012. Improving the representation of resolved and unresolved topographic effects on surface wind in the WRF model. J Appl Meteor Clim, 51(2):300-316 |
| Lee J, Shin H H, Hong S Y, et al. 2015. Impacts of subgrid-scale orography parameterization on simulated surface layer wind and monsoonal precipitation in the high-resolution WRF model. J Geophys Res, 120(2):644-653 |
| Li L F, Li W H, Jin J M. 2014. Improvements in WRF simulation skills of southeastern United States summer rainfall:Physical parameterization and horizontal resolution. Climate Dyn, 43(7):2077-2091 |
| Peng J, Zhang L F, Luo Y, et al. 2014. Mesoscale energy spectra of the Mei-Yu front system. Part Ⅰ:Kinetic energy spectra. J Atmos Sci, 71(1):37-55 |
| Pielke R A, Kennedy E. 1980. Mesoscale Terrain Features. Report UVA-ENV SCI-MESO-1980-1, University of Virginia |
| Prein A F, Holland G J, Rasmussen R M, et al. 2013. Importance of regional climate model grid spacing for the simulation of heavy precipitation in the Colorado Headwaters. J Climate, 26(13):4848-4857 |
| Ricard D, Lac C, Riette S, et al. 2013. Kinetic energy spectra characteristics of two convection-permitting limited-area models AROME and Meso-NH. Quart J Roy Meteor Soc, 139(674):1327-1341 |
| Salvador R, Calbó J, Millán M M. 1999. Horizontal grid size selection and its influence on mesoscale model simulations. J Appl Meteor, 38(9):1311-1329 |
| Smith R B. 2006. Progress on the theory of orographic precipitation. Geolog Soc Amer Spec Papers, 398:1-16 |
| Steyn D G, Ayotte K W. 1985. Application of two-dimensional terrain height spectra to mesoscale modeling. J Atmos Sci, 42(24):2884-2887 |
| Surcel M, Zawadzki I, Yau M K. 2015. A study on the scale dependence of the predictability of precipitation patterns. J Atmos Sci, 72(1):216-235 |
| Uliasz M, Stocker R A, Pielke R A. 1996. Regional modeling of air pollution transport in the southwestern United States//Environmental Modeling (Volume Three). Southampton Boston:Computational Mechanics Publications, 145-182 |
| Young G S, Pielke R A. 1983. Application of terrain height variance spectra to mesoscale modeling. J Atmos Sci, 40(10):2555-2560 |
| Young G S, Pielke R A, Kessler R C. 1984. A comparison of the terrain height variance spectra of the front range with that of a hypothetical mountain. J Atmos Sci, 41(7):1249-1250 |
 2016, Vol. 74
2016, Vol. 74