中国气象学会主办。
文章信息
- 王洪, 万齐林, 尹金方, 丁伟钰. 2016.
- Wang Hong, Wan Qilin, Yin Jinfang, Ding Weiyu. 2016.
- 双线偏振雷达资料在数值模式中的应用:模拟器的构建
- Application of the dual-polarization radar data in numerical modeling studies: Construction of the simulator
- 气象学报, 74(2): 229-243
- Acta Meteorologica Sinica, 74(2): 229-243.
- http://dx.doi.org/10.11676/qxxb2016.017
-
文章历史
- 收稿日期: 2015-09-15
- 改回日期: 2016-01-21
2. 中国气象科学研究院灾害天气国家重点实验室, 北京, 100081
2. State Key Laboratory of Severe Weather (LaSW), Chinese Academy of Meteorological Sciences, China Meteorological Administration, Beijing 100081, China
天气雷达是进行云、降水物理研究及短时临近预报的重要手段之一。许多国家和地区(如美国、中国等)先后完成了常规多普勒雷达的布网,实现了风暴监测、短时临近预警信号发布及定量降水估计的全面业务化(俞小鼎等,2006)。但常规多普勒雷达只能发射单一线偏振电磁波,其回波强度也只能提供云、降水粒子的位置、数量等一般信息。双线偏振雷达则可以发射水平/垂直偏振状态的电磁波,可得到差分反射率、比差分相位、线性退偏振比等偏振量观测值。从这些偏振量中可以获得粒子的尺度谱、二维形状、排列取向等信息(梁海河等,2005;王致君等,2004)。正是由于偏振雷达在探测云、降水粒子方面的诸多优点,许多气象组织及气象学者在偏振雷达的相关应用领域进行了大量的研究,并取得了一系列丰硕的成果,尤其是在定量降水估计(Hall et al,1980;Ryzhkov et al,2003;刘黎平等,2007)、水凝物分类(Chandrasekar et al,2013;Straka et al,2000;Vivekanandan et al,1999;曹俊武等,2005;郭凤霞等,2014)和强风暴的偏振特征描述(Bluestein et al,2007;Kumjian et al,2008;刘黎平等,1996)等领域。目前美国已经将其现有多普勒雷达升级为双线偏振雷达,中国也计划在近期内开始在业务多普勒雷达上加装双偏振功能。因此,有必要加强针对双线偏振雷达的研究,促使其在定量降水预报中发挥更大的作用。
近年来随着WRF(Michalakes et al,2004)、GRAPES(陈德辉等,2008)及COSMO-DE(Baldauf et al,2011)等中尺度数值模式在业务上的广泛使用,改进发展高分辨率数值模式逐渐成为提高定量降水预报水平的主要途径。而云、降水物理过程是影响模式定量降水预报能力的关键因素之一(王洪等,2014;尹金方等,2014)。因此,如何在数值模式中将表征云、降水粒子宏、微观特征的偏振量有效地利用起来是偏振雷达应用研究的新兴重要方向之一。
偏振量在数值模式中的作用主要体现在两个方面:一是用于资料同化;二是用于评估数值模式预报效果。但偏振量并不是模式变量,必须通过一定方式将两者联系起来。这种联系方式就是同化系统中常用的观测算子。Wu等(2000)尝试从差分反射率中获取混合相态下的雨水和云冰混合比信息,并采用四维变分同化系统同化这些反演得到的水凝物混合比。Li等(2010,2012)在WRF三维变分同化系统中,以差分反射率-雨水混合比(Ulbrich et al,1984)和比差分相位-雨水混合比关系(Bringi et al,2001)构造了相应的观测算子,实现了差分反射率、比差分相位等偏振量的间接同化。此时恰逢美国多普勒雷达探测网的双偏振升级,Li等(2010,2012)的工作对于如何将偏振雷达探测资料应用到数值模式中具有良好的指示意义。但差分反射率等偏振量并不是雨水这一种水凝物的测量值,而是云水、云冰、霰等多种粒子对探测波的综合散射结果。尤其是混合相粒子对偏振量的贡献更为显著。所以在构造偏振量观测算子时,必须以复杂云、降水物理过程为基础,区别处理云水、云冰、雨、雪及霰等多种水凝物粒子。
中外在这方面已有一些研究成果。Smith等(1975)利用云模式的体积水方案输出量计算了雷达反射率,并重点分析了雨水、冰雹的不同粒子谱描述方法对计算结果的影响。Liu等(2005)利用APRS模式Lin方案中雨、雪、雹的混合比,基于众多观测统计结论计算了反射率、差分反射率及比差分相位等偏振量。Huang等(2005)提出了一个较完备的偏振雷达模拟器,该模拟器采用T矩阵雷达散射模型,以RAMS(Regional Atmospheric Modeling System)的云微物理方案输出为输入量,模拟了相关偏振量。Caumont等(2006)开发了一个与模式云微物理参数化方案完全耦合在一起的雷达模拟器,该模拟器可基于Rayleigh、Rayleigh-Gans、米散射及T矩阵等不同散射方法模拟计算X、C和S波段的偏振雷达变量。随后为了能够将偏振雷达探测资料直接应用于模式评估或资料同化,Pfeifer等(2008)和Jung等(2008a,2008b)先后发展了各自的偏振雷达模拟器。在设计过程,Pfeifer和Jung均考虑冰相粒子对偏振量的贡献,同时前者还考虑了波束衰减效应,而后者则着重考虑了冰相粒子融化对偏振量的重要影响。
虽然中外学者已建立了多个偏振雷达模拟器,但目前中国关于如何将偏振量应用于数值模式的研究还相对较少。而且近年来众多气象学者在数值模式的云微物理过程和云降水粒子特征统计方面取得了较大进展(Yin et al,2011,2013,2014)。这也为更加全面合理地构造模拟器提供了坚实的基础。
相对于只预报水凝物混合比的单参量方案(Hong et al,2004),同时预报水凝物混合比和数浓度的双参量方案(Morrison et al,2005)对云微物理过程描述更加细致。因此,双参量方案逐步成为云微物理参数化方案的主流选择。另外,基于观测的云降水粒子统计特征也有一些新进展,比如雨滴粒子轴比(Thurai et al,2005)与粒径的关系函数、描述水凝物粒子下落倾角(Huang et al,2008)及0℃层附近的雪/雹融化模型等方面。
因此,基于中外最新研究成果,以Rayleigh-Gans散射为基本原理,采用云微物理参数化方案输出量及云降水粒子的统计结果作为输入值,构造一个S波段双线偏振雷达模拟器,将数值模式和双线偏振雷达有机地结合起来。
2 双线偏振雷达模拟器不同于早期的模拟器(Smith et al,1975; Liu et al,2005)仅考虑了粒子谱对计算偏振量的影响,文中的双线偏振雷达模拟器(以下简称模拟器)以数值模式输出量为基础,加上一些云降水粒子的统计结果,模拟计算双线偏振雷达的主要偏振量,如水平反射率、垂直反射率、差分反射率及线性退偏振比等(图 1)。首先基于Rayleigh-Gans散射推导了电磁波在水凝物粒子群中的后向散射值(2.1节)。推导结果表明,后向散射值与粒子形状、介电常数、下落倾角及一些雷达参数有关(Vivekanandan et al,1993)。这些影响散射值的参数可大致分为两类:一类是模式输出量决定或由其推导出的导出参数,如粒子的类型、含水量、轴比等;另一类是从云降水粒子的统计结论中得到的经验参数,如下落倾角、雷达参数等。
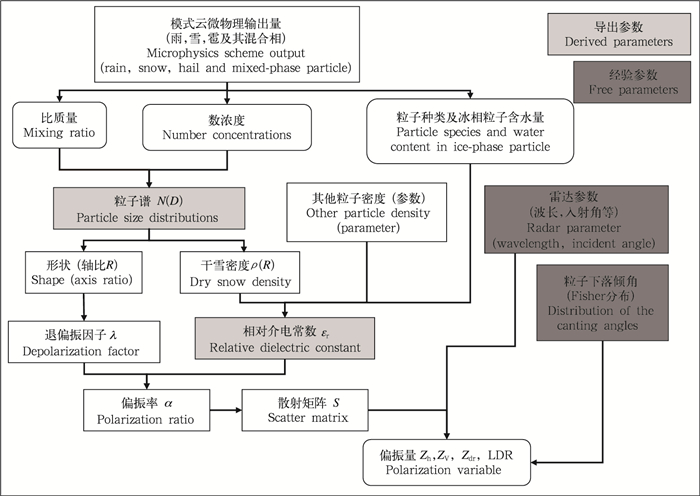 |
| 图 1 双线偏振雷达模拟器计算流程 Fig. 1 Schematic diagram of the dual-linear polarization radar simulator |
在线偏振雷达观测中,一般定义入射波为Ei,散射波Es。Ei和Es可表示为两个正交极化矢量的线性组合,该线性组合方式又被称为后向散射矩阵S。
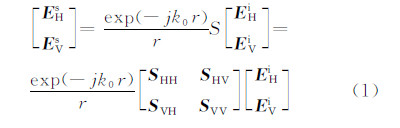
在给定粒子谱分布N(D)的前提下,采用Bringi等(2001)给出的粒子群的反射率因子各分量计算公式,这与Jung等(2008a,2008b)采用的粒子群散射方式是一致的。
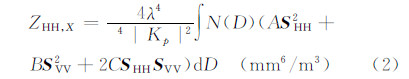

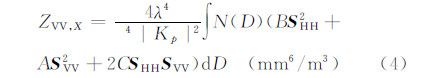


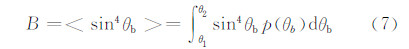
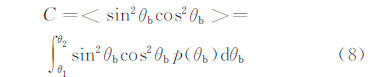
以散射矩阵为基础,进一步计算即可得到偏振雷达观测到的重要偏振量:水平偏振反射率因子(Zh,dBz)、垂直偏振反射率因子(Zv,dBz)、差分反射率(Zdr,dB)、线性退偏振比(LDR,dB)和差分反射率因子(Zdp,mm6/m3),比差分相位(Kdp,°/km)。
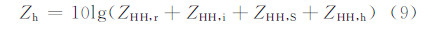
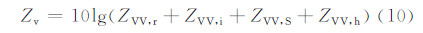
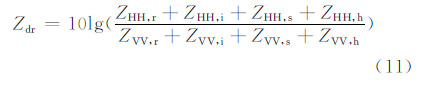
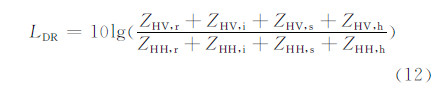
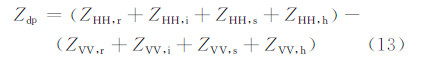
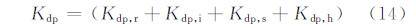
上述推导及附录表明,偏振量的计算与粒子的谱分布、轴比、相对介电常数和下落倾角有直接关系。因而下面将分别讨论相关因素的取法。
2.2 粒子谱分布无论是数值模式中的云微物理参数化方案,还是观测事实均采用粒子谱描述水凝物粒子的大小及其数浓度分布。Morrison双参量方案(Morrison et al,2009)同时预报云滴、雨、雪、雹的数浓度和混合比,这样能够更全面地描述粒子谱分布及其相关物理过程。本研究基于Morrison双参量方案发展双线偏振雷达模拟器,以该方案的混合比和数浓度预报量反算粒子谱的截距和斜率,然后确定粒子谱分布。由于云水粒径较小,其外形基本为球形,不具备偏振观测意义。因此模拟器将考虑云冰、雨、雪和雹4种水凝物。
2.3 轴 比在影响双线偏振雷达观测量的众多因素中,粒子形状是关键因子之一。对于一个水凝物粒子,一般采用轴比(R=b/a,b为半短轴长,a为半长轴长)描述其平衡态形状。但在目前的数值模式中,轴比并不是一个预报量,因而必须引入其他假定关系计算轴比。
首先考虑形状较为规则的雨滴。早期Green(1975)根据一个简单的流体静力学模型,得到了雨滴轴比与同体积圆球等效直径的函数解析式。随后有人从理论(Beard et al,1987)或实验室观测结果(Andsager et al,1999;Pruppacher et al,1970;Thurai et al,2005)中得到了多种轴比与有效直径的拟合函数。由于Andsager等(1999)考虑雨滴的振荡效应后的拟合标准差仅为0.01 mm。因此本研究中雨滴轴比计算采用Andsager等(1999)的结论:当1 mm≤D≤4 mm时,
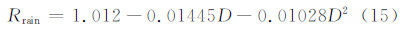
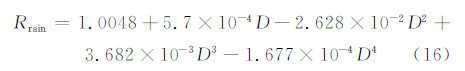
雹的形状多种多样,有球形、椭球形、锥形、扁圆形和无规则形状等。有观测表明地面附近的雹和典型湿雹的轴比约为0.8,含水量较高的雹的轴比在0.6—0.8。根据List(1986)的建议,模拟器取直径在10 mm以下的雹粒子轴比为1;当雹粒子直径为10—50 mm时,取其轴比为0.75;认为直径50 mm以上的雹会出现翻滚现象,其轴比取为1。这点与Jung等(2008a,2008b)将雹的轴比取为固定值有所不同。
当云内温度低于0℃时可以形成冰晶,冰晶长大到一定程度(一般以线性尺度0.3 mm为分界线)即成为雪晶,而雪晶聚集体则常称为雪花。冰晶的形状十分复杂多变,很难对其模型化处理。基于Straka等(2000)的工作,统一将冰晶、雪晶和雪的轴比取为0.75。
2.4 雪/雹融化模型在0℃层附近,冰相粒子处于融化过程中,融化的水会在雪/雹粒子的表面形成一层水膜,或渗入粒子的缝隙之中,进而形成冰水共存的混合相粒子。图 2显示了在给定粒子谱的情况下,不同含水量的雪和雹的偏振量分布形态。随着含水量升高,雪和雹的Zh、Kdp、Zdr均有明显升高。其中雪的升幅更明显,当含水量升高至65%,相应偏振量值提高一倍以上。因此混合相粒子在偏振量模拟中是一个需要重点考虑的对象。由于云微物理方案的预报量十分有限,因此,模拟器(Jung et al,2008a)一般采用冰/水的混合比比例表征雹/雪的融化程度。但不同的模拟器采用了不同的计算公式。
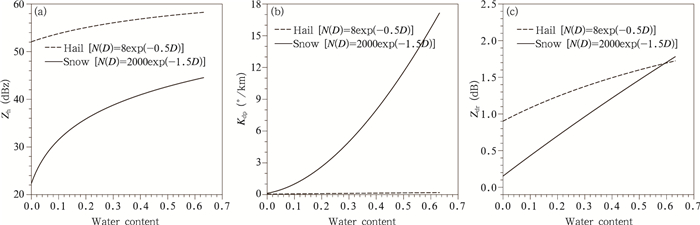 |
| 图 2 雪、雹的偏振量(a.Zh, b.Kdp, c.Zdr)随含水量的演变 Fig. 2 Changes of (a) Zh, (b) Kdp, (c) Zdr of snow and hail with different water content |
在Morrison方案中,冰相粒子有云冰、雪和雹3类,但该方案假定云冰一旦降落到0℃层高度以下,就立即融化并全部转化为云水,因而只有雪和雹存在冰水混合相状态。本研究通过以下流程考虑雪-雨和雹-雨的混合相过程。首先假定只有雨水混合比及冰相粒子混合比大于指定阈值(10-9kg/kg),才存在混合相粒子,并且只存在0℃层高度以下区域。然后确定冰相粒子开始融化的高度层ks,再计算融化层以下各层冰相粒子含水量
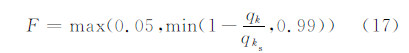
εr定义为物质的介电常数(ε)与真空绝对介电常数(ε0)的比值。随着水凝物粒子的种类、密度、含水量以及温度等环境因素的变化,εr的取值也会发生剧烈变化。同时差分反射率等偏振量对εr的取值十分敏感。对于单个相同轴比的雪和雨滴,其差分反射率值最大可相差10倍以上(图 3)。因此,准确地给出不同水凝物粒子的εr值对精确计算偏振模拟量至关重要。
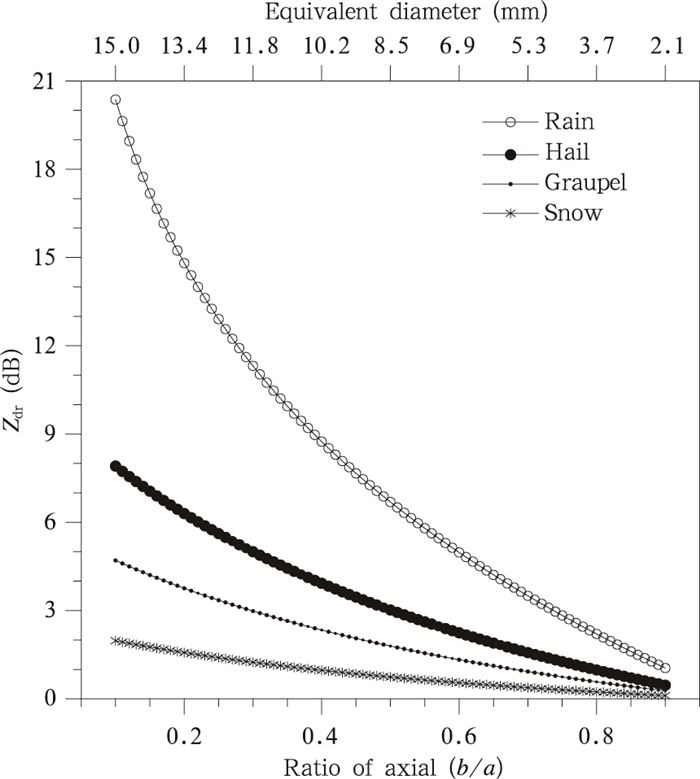 |
| 图 3 单个不同水凝物的差分反射率与轴比的关系 Fig. 3 Differential reflectivity as a function of the ratio of axial |
首先给定纯雨滴的εrain值为70.9,干冰雹的εdh值取为3.17。由于干雪的结构十分蓬松,粒子中包含一定量的空气,从而影响干雪的密度和相对介电常数。采用Tiuri等(1984)的研究结论,无论是旧干雪,还是新干雪,其εds都唯一依赖于干雪相对于水的密度比例ρd(ρd=ρds/ρw)的变化,两者的关系式为
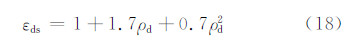
更复杂的相对介电常数计算是冰水二相物质混合时的情况(De Wolf et al,1990)。融化中的冰相粒子相对介电常数会出现剧烈变化,而且其变化幅度还随着融化程度的不同而改变。多数研究结果(Longtin et al,1987;Sihvola et al,1988)认为在计算雷达后向散射时使用Maxwell-Garnet公式效果更佳。Maxwell-Garnet公式如下
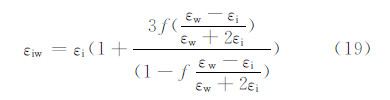
下落倾角定义为粒子对称轴与坐标系Z轴的夹角(见附图 1中θb)。但对于一群粒径为1 mm左右的微观粒子,要具体给出每一个粒子的θb值是不可能的,因此目前一般采用某种概率密度函数描述粒子对称轴的取向情况。已有的模拟器(Pfeifer et al,2008; Jung et al,2008a)多采用高斯分布来描述粒子下落倾角分布,但最新的模拟观测实验结果(Huang et al,2008)表明,相对于高斯分布,Fisher分布更适合于描述粒子下落倾角的分布(俞加伟等,2013)
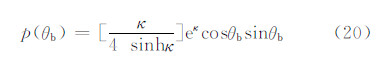
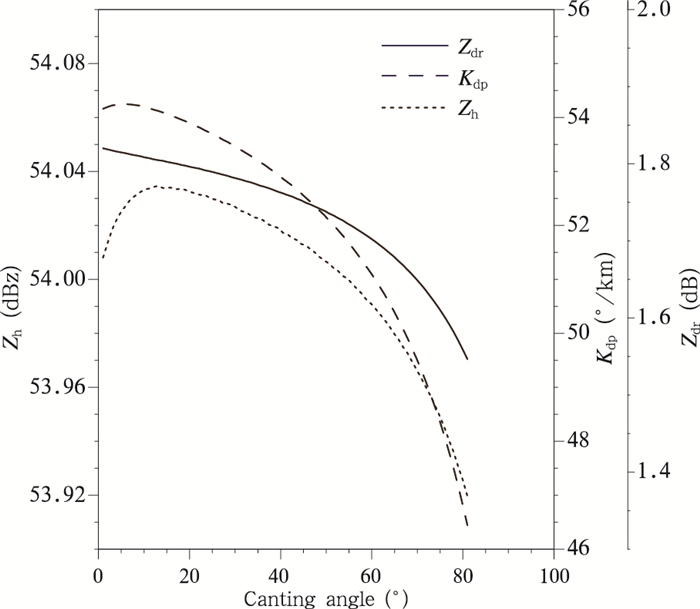 |
| 图 4 偏振量随下落倾角描述函数演变 Fig. 4 Changes in polarization with different functions of the canting angle |
为了验证已构建的模拟器,采用WRF模式V3.4.1 自带的二维理想飑线试验结果验证该模拟器。模拟区域水平网格数为1200,水平分辨率为250 m;垂直80层,模式顶高为20 km;积分时间步长3 s,累计积分7 h。该个例选用开放的侧边界条件,采用1.5阶TKE方案计算水平/垂直湍流扩散,采用阻尼系数为0.003 s-1的Rayleigh阻尼器抑制模式顶部5 km范围内的虚假回波。除云微物理过程选用Morrison方案(Morrison et al,2009)外,其他物理过程均不予考虑。
WRF的理想飑线试验的初始场由Weisman等(1982,1984)提供的温、湿度廓线提供。该温、湿度廓线属于典型的中纬度、大陆型飑线的背景环境场,其初始对流有效位能(CAPE)值为2200 J/kg,融化层高度是4 km,2.5 km以下的风垂直切变是0.0048 s-1。初始扰动为中心强度为3 K的热泡,其水平范围4 km,垂直范围1.5 km,中心位于离地面1.5 km高度处。
当积分250 min时,飑线达到成熟阶段(图 5a)。新单体不断在阵风锋前沿生成,强度也很快达到最强;同时由于其后部对流不稳定能量较低,属于层云区。在x=165—185 km之间有两个成熟的对流云单体C1和C2,其回波顶高度超过10 km;在单体C1左侧,单体C3处于减弱阶段,并逐渐转变为层云。因此下面将以此时刻为例分析评估模拟器对对流云及层云偏振特征的模拟能力。
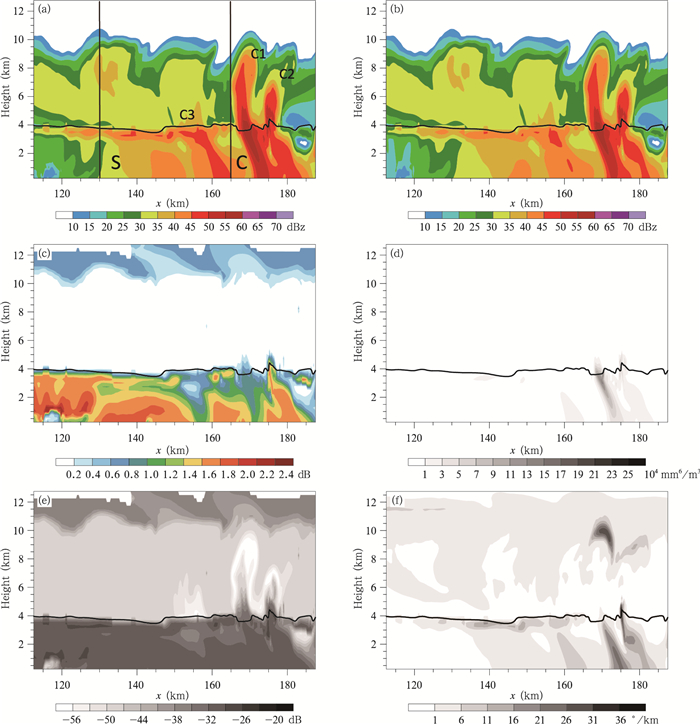 |
| 图 5 第250 min时二维理想飑线偏振量(a.Zh, b.ZV,c.Zdr,d.Zdp, e.LDR, f.Kdp)的水平-高度剖面 Fig. 5 Vertical cross sections of simulated (a) Zh, (b) ZV, (c) Zdr, (d) Zdp, (e) LDR, (f) Kdp after 250 min integration of the 2D ideal squall-line simulation |
在双线偏振雷达观测中常常出现如雹粒子偏振特征(孙丝雨等,2013)、Zdr柱(Brandes et al,1995)和0℃层亮带(Fabry et al,1995)等特征。二维理想飑线试验中,云冰、雪、雨和雹不同的微观特性(如轴比、相对介电常数、下落倾角等),和宏观特性(混合比和数浓度)导致模拟偏振量具有不同的性质。模拟偏振量是否具有双线偏振雷达观测特征将是评价模拟器优劣的重要指标。
3.2 雹粒子偏振特征在x=170、175 km处存在两个对流单体C1和C2,其中心Zh值超过了55 dBz(图 5a),而对应的雹粒子混合比(6.5 g/kg)也是极大值中心(图 7d)。但Zh极值中心高度在0℃层附近,而混合比极值中心则在0℃层以上约2 km。这是由于低层的雹粒子有效直径更大(图略),对反射率的贡献也更大;再者跃过0℃层后雹粒子开始融化,其εr值会急剧增大,进而导致反射率增大。由于大冰雹粒子在下落过程中会不断翻滚(见2.2节),在雷达扫描中近似为球形(轴比取为1),因此Zh极大值中心(x=170、175 km,z=4.1 km)附近出现了清晰的Zdr(≤1 dB)减小的窄垂直区域,该区域被称为“Zdr洞”(Wakimoto et al,1988),在Zdr洞周围Zdr迅速增大(图 5c)。主要是由大雨滴带来的Zdr值(约2 dB,图略)。Jung等(2008b)和Liu等(2005)的模拟偏振量结果也表明雹(霰)粒子会使Zh值增大,并同时减小Zdr值。另外,在冰雹混合比大值区附近随高度降低,LDR明显降低。这可能与低层雹粒子直径相对较大,轴比较小有关。
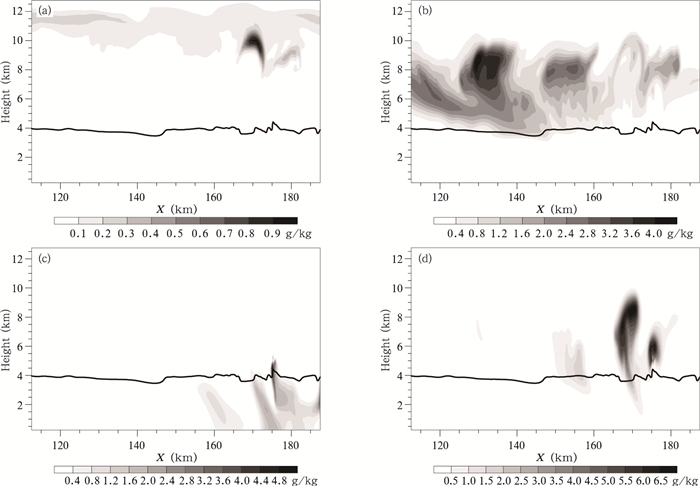 |
| 图 7 云冰(a)、雪(b)、雨(c)和雹(d)的混合比浓度 Fig. 7 Same as in Fig.5 but for the model mixing ratios (a) cloud ice, (b) snow, (c) rain, (d) hail |
许多观测研究(Brandes et al,1995;Kumjian et al,2008)表明,在对流风暴单体中,一般认为由于雨滴被上升气流带入云中较冷的区域后冻结且失去取向稳定性而导致Zdr值迅速减小,进而能够观测到正的Zdr呈垂直柱状分布。在本研究中,同样再现了弱Zdr柱(图 6a),该Zdr柱位于x=176 km处,中心强度为1.8 dB,水平范围约4 km,垂直扩展到5 km左右(即0℃层以上约500 m)。同时该Zdr柱对应着雨水混合比大值中心(4.8 g/kg),并伴随着约15 m/s的上升气流(图 6b)。这与上述Zdr柱形成原因猜想十分一致。但模拟的Zdr柱垂直扩展高度仍低于实际观测到的约7 km(Kumjian et al,2008),这可能是因为目前Morrison方案仍无法完全再现雨滴上升冻结的物理过程。
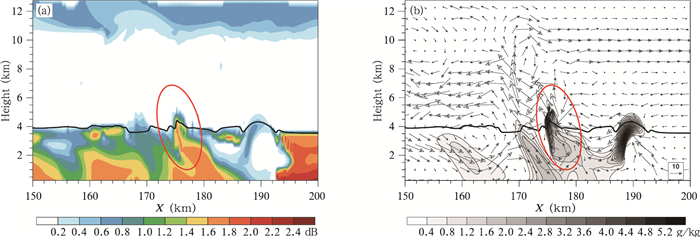 |
| 图 6 第250 min时差分反射率(a)及雨水混合比(b,矢量箭头为风场)的垂直剖面 Fig. 6 Vertical cross sections of (a) differential reflectivity and (b) rain mixing ratio overlapped with wind vector after 250 min integration of the ideal 2D squall-line simulation |
据雷达观测,层云降水的典型特征是拥有一条明显的Zh“亮带”。本模拟器同样模拟出了0℃层亮带(图 5a)。该亮带中心Zh强度超过40 dBz,垂直厚度约800 m,位于x=115至155 km之间,0℃等温线以下500 m处。而Jung等(2008b)模拟的0℃层亮带则位于0℃等温线以下1.5 km。另外分析各种水凝物粒子的反射率贡献(图略)发现,0℃层亮带主要由雪粒子贡献。跃过0℃层后,雪粒子开始融化,其εr值增大,进而导致Zh值迅速增大。另外雪粒子的不断融化变湿也使Kdp出现了明显亮带特征(图 5f),0℃层以上其值基本为6 °/km,随后逐渐增大到16 °/km,然后又随着雪粒子融化蒸发减小。
在本研究的Kdp模拟中,发现与云冰、雪和雨等Kdp主要贡献者相比,雹粒子的Kdp值要小两个数量级,仅为0.2 °/km左右。这主要是因为大冰雹粒子在下落过程中会出现翻滚,面对雷达观测可近似为球形,因而根据Kdp计算公式(式(15))可知,Kdp值也接近于0。飑线的不同位置,Kdp值的主要贡献粒子自然也不一样。在0℃等温线附近,Kdp值主要由融化的雪粒子贡献。雨滴下落过程中(离地面的3—4 km范围内),其有效直径不断变长,轴比也不断变小,使得Kdp,r值逐渐变大,极大值可达36.72 °/km。在云冰富集区(x=170 km,z=10 km),Kdp,i值同样较显著,极大值为29.89 °/km。这是因为云冰的轴比统一取为0.75,并且其下落倾角概率分布仍具有主导方向。
3.5 偏振量的统计特征为进一步评估模拟器对偏振量的模拟效果,计算了理想飑线个例层云区(x=130,160 km之间)和对流云区(x=165,185 km之间)的水平平均混合比及相应偏振量平均值。图 8、9中黑色直线为区域平均0℃等温线,位于4.1 km高度上。
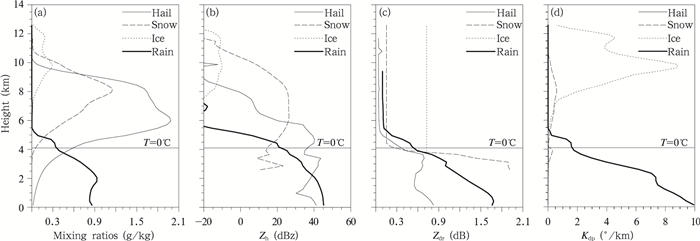 |
| 图 8 对流云区雨、云冰、雪和雹的混合比(a)、水平反射率(b,Zh)、差分反射率(c,Zdr)、 比差分相位(d,Kdp)的高度廓线 Fig. 8 Vertical profile of area-averaged (a) mixing ratio of several hydrometeors, (b) horizontal reflectivity, (c) differential reflectivity, and (d) specific differential phase over the convection region |
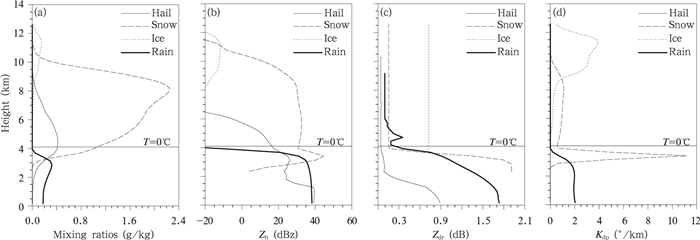 |
| 图 9 同图8,但计算区域为层云区 Fig. 9 Same as Fig.8 but for the stratiform region |
对流云区中,雹分布范围最广,一直从近地面扩展至10 km高度上,平均混合比也最大,最大值为1.9 g/kg(图 8a)。0℃层以下,雨和雹对对流云区的Zh贡献最大; 0℃层以上,则主要由雹和雪贡献。由于云冰粒径较小,因此仅在7.5—12.5 km范围内贡献约-10 dBz。而层云区的Zh廓线最明显的特征是雪粒子的贡献更大,尤其在0℃层附近出现了一个40 dBz的峰值,这正是层云区0℃层亮带的直接体现。
云冰、雪、雨和雹的轴比取值都在0—1,即假定所有粒子排列均为水平主导,因此各水凝物的平均Zdr(dB)值均为正值(图 8b、9b)。其次在0℃层以上,云冰和干雪的轴比均被取为常数0.75,并且两者的εr也为常数2.025和1.17,其Zdr计算式可简化为
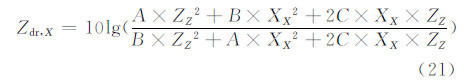
另外,无论是在对流云区,或是在层云区,0℃层以下的Zdr值都更大,其值主要由雹、雨和雪粒子贡献。在0℃层以下附近,由于融化导致雪粒子εr急剧增大,进而使得其Zdr值迅速增大,甚至超过雨和雹的Zdr值。
对于Kdp廓线,雹粒子基本没有贡献。对流云区的Kdp值主要由雨和云冰贡献。这主要是因为该时刻云冰混合比较高(图 7a),及雨滴在下落过程中固有的轴比变小趋势。对于层云区,雪对0℃层附近的Kdp值有主要贡献,平均值达到11.5 °/ km。
Bringi等(2001)结合理论推导和观测研究表明,Zdp对理论模型混合物中固定取向的椭球形雨滴十分敏感,而且雷达观测得到的Zh和Zdp的相关系数很高,接近1。二者之间的拟合关系又被称为“雨线”。在本研究的模拟结果中,Zdp的水平-高度剖面(图 5f)同雨水混合比(图 7c)在分布范围和形态上都十分相似。进一步分析二者的统计关系发现,Zh和10lg Zdp可用最小二乘法进行拟合,其拟合结果(图 10b)为
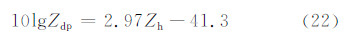
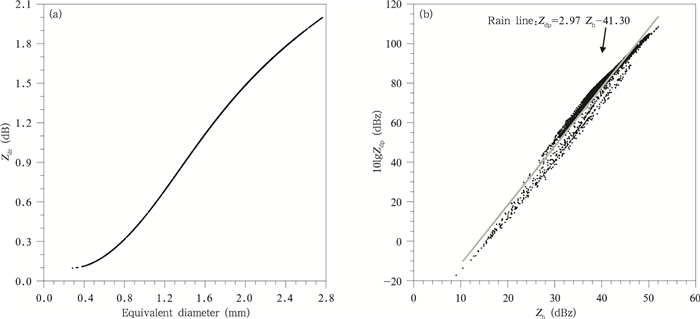 |
| 图 10 雨滴有效直径(De)与Zdr(a)及其Zh与10lgZdp(b)的散点图 Fig. 10 The scatter diagram of (a) effective diameter of rain drops’ and the differential reflectivity, (b) horizontal reflectivity of raindrops’ and the 10lg Zdp |
Zdr值大小与轴比有密切关系,而雨滴的轴比由式(19)—(20)决定。因此,随着有效直径增大,雨滴的Zdr值也基本呈线性增大(图 10a)。
表 1给出了云冰、雪、雨及雹的各种偏振量极大值统计结果。该结果与梁海河等(2005)给出S波段双线偏振雷达探测的各种降水类型的偏振量变化范围(其文中表 1)基本吻合。
| 水凝物类别 | Zh(dBz) | Zdr(dB) | Kdp(°/km) | LDR(dB) | Zdp(104mm6/m3) |
| 云冰 | -4.6 | 0.70 | 29.89 | -36.4 | 0.0 |
| 雪 | 48.6 | 1.90 | 22.32 | -27.8 | 20.0 |
| 雨 | 52.0 | 2.45 | 36.72 | -27.7 | 25.1 |
| 雹 | 60.1 | 1.80 | 0.34 | -26.3 | 24.5 |
以Rayleigh-Gans散射为基本原理构建了一个S波段双线偏振雷达模拟器。本模拟器考虑了云冰、雪、雨和雹4种水凝物,以水凝物的混合比和数浓度为基本输入量,并对包括混合相粒子在内的各种水凝物粒子的轴比、相对介电常数和下落倾角进行模型化处理,最终计算得到水平反射率、垂直反射率、差分反射率、线性退偏振比、差分反射率因子和比差分相位。通过上述流程,模拟器将模式变量与偏振雷达观测量有机地联系起来了。这为将偏振雷达观测资料用于模式预报效果评估提供了有效手段;同时该模拟器经过改进也可作为同化系统的观测算子,可真正实现在对流尺度模式中直接同化相应偏振量的目标。
模拟器构建完成后,利用二维理想飑线个例对模拟器进行测试评估。评估对象为积分250 min的成熟飑线系统,此时飑线既包含对流云区,又包含层云区。结果表明,模拟器能够如实再现飑线系统的主要偏振特征。如雹的高Zh值,低Zdr值(又称Zdr洞);由于雨滴冻结而形成的Zdr柱;0℃层附近雪粒子融化而导致的Zh和Kdp亮带特征;雨滴的Zh与10lgZdp的“雨线”统计特征等。另外模拟器计算的各水凝物的偏振量极大值也基本符合前人的研究结果。
需要指出的是,模拟结果与真实情况存在一定偏差。主要有以下3个方面的原因:一是由于假定所有粒子姿态都是水平主导的(0<R≤1),直接导致Zdr和Kdp无法取到负值;二是0℃层以上的云冰、雪的Zdr值为常数,这是因为其轴比和εr均被取为常数;三是对粒子轴比、下落倾角的处理都是基于国外的研究结果,这与东亚的云微物理事实是否一致还有待于进一步研究。
本模拟器仅考虑了水平入射情况下的偏振量计算,事实上双线偏振雷达是按多个仰角依次扫描的,不同的仰角将直接导致面对入射波时对粒子姿态处理方式的变化,进而影响偏振量计算的整个流程。因此在接下来的工作中将讨论有关多仰角模拟器的开发及其在实际天气个例中的应用。
附录:散射矩阵计算附图 1给出了单个椭球形粒子在电磁波场中的排列情况。在以椭球形粒子中心为原点的笛卡尔坐标中,平面波的入射方向由θi和φi确定,其中θi定义为雷达仰角的余角,φi一般取值π。θb和φb确定了椭球体对称轴的排列方向,θb即下落倾角,φb一般取值π/2。
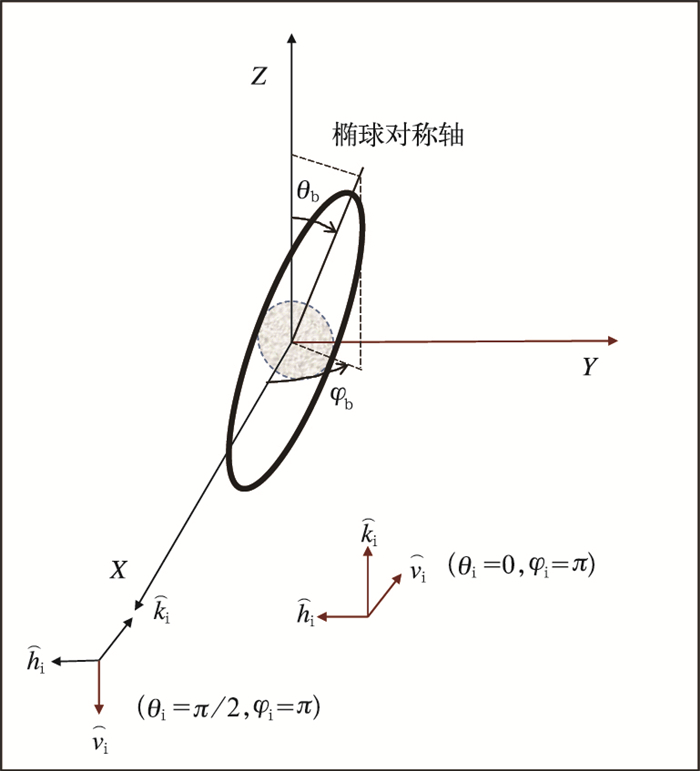 |
| 附图1 椭球形粒子排列示意图(Bringi, et al, 2001) Fig. 1 Posture of ellipsoidal particle (Bringi, et al, 2001) |
对于单个粒子的后向散射,Pfeifer等(2008)和Jung等(2008a,2008b)是基于T矩阵方法计算的。而本研究中则考虑在S波段下采用Rayleigh-Gans散射,其后向散射矩阵S为
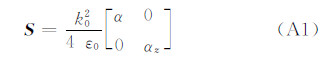

采用Van Bladel(1985)的退偏振因子计算式

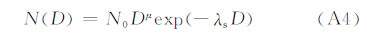
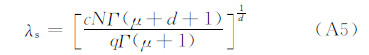
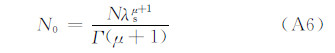
| 水凝物类别 | c | d | μ | ρ(kg/m3) |
| 云冰 | π ρi/6 | 3 | 0 | 500 |
| 雪 | π ρs/6 | 3 | 0 | 100 |
| 雨 | π ρw/6 | 3 | 0 | 997 |
| 雹 | π ρh/6 | 3 | 0 | 900 |
| 曹俊武, 刘黎平, 葛润生. 2005. 模糊逻辑法在双线偏振雷达识别降水粒子相态中的研究. 大气科学, 29(5): 827-836. Cao J W, Liu L P, Ge R S. 2005. A study of fuzzy logic method in classification of hydrometeors based on polarimetric radar measurement. Chinese J Atmos Sci, 29(5): 827-836 (in Chinese) |
| 陈德辉, 薛纪善, 杨学胜等. 2008. GRAPES新一代全球/区域多尺度统一数值预报模式总体设计研究. 科学通报, 53(20): 2396-2407. Chen D H, Xue J S, Yang X S, et al. 2008. New generation of multi-scale NWP system (GRAPES): General scientific design. Chin Sci Bull, 53(22): 3433-3445 |
| 郭凤霞, 马学谦, 王涛等. 2014. 基于X波段双线偏振天气雷达的雷暴云粒子识别. 气象学报, 72(6): 1231-1244. Guo F X, Ma X Q, Wang T, et al. 2014. An approach to the hydrometeors classification for thunderclouds based on the X-band dual-polarization Doppler weather radar. Acta Meteor Sinica, 72(6): 1231-1244 (in Chinese) |
| 梁海河, 徐宝祥, 刘黎平等. 2005. 偏振微波雷达探测大气研究进展及几个问题的考虑. 地球科学进展, 20(5): 541-548. Liang H H, Xu B X, Liu L P, et al. 2005. Evolvement of polarimetric technology detecting atmosphere and some consideration of it's problems. Adv Ear Sci, 20(5): 541-548 (in Chinese) |
| 刘黎平, 钱永甫, 王致君. 1996. 用双线偏振雷达研究云内粒子相态及尺度的空间分布. 气象学报, 54(5): 590-599. Liu L P, Qian Y F, Wang Z J. 1996. The study of spacial distribution of phase and size of hydrometeors in cloud by dual linear polarization radar. Acta Meteor Sinica, 54(5): 590-599 (in Chinese) |
| 刘黎平, 牟容, 许小永等. 2007. 一次飑线过程的动力和微物理结构及滴谱变化对降水估测的影响研究. 气象学报, 65(4): 601-611. Liu L P, Mou R, Xu X Y, et al. 2007. Dynamic and microphysical structures of a squall line system and effects of rain drop size distribution on precipitation. Acta Meteor Sinica, 65(4): 601-611 (in Chinese) |
| 孙丝雨, 沈永海, 霍苗等. 2013. 双线偏振雷达在一次强降雹过程中的初步应用. 暴雨灾害, 32(3): 249-255. Sun S Y, Shen Y H, Huo M, et al. 2013. Preliminary application of dual-polarization weather radar in a severe hail event. Torrential Rain Disaster, 32(3): 249-255 (in Chinese) |
| 王洪, 尹金方, 王东海. 2014. 单双参云微物理方案对华南暴雨的模拟对比分析. 高原气象, 33(5): 1341-1351. Wang H, Yin J F, Wang D H. 2014. Comparative analysis of single-moment and double-moment microphysics schemes on a local heavy rainfall in South China. Plateau Meteor, 33(5): 1341-1351 (in Chinese) |
| 王致君, 楚荣忠. 2004. 偏振天气雷达在气象中的应用简介. 干旱气象, 22(2): 62-68. Wang Z J, Chu R Z. 2004. A brief introduction about the application of polarization radar in meteorology. Arid Meteor, 22(2): 62-68 (in Chinese) |
| 尹金方, 王东海, 翟国庆. 2014. 区域中尺度模式云微物理参数化方案特征及其在中国的适用性. 地球科学进展, 29(2): 238-249. Yin J F, Wang D H, Zhai G Q. 2014. A study of characteristics of the cloud microphysical parameterization schemes in mesoscale models and its applicability to China. Adv Ear Sci, 29(2): 238-249 (in Chinese) |
| 俞加伟, 陈年泼, 郑志龙等. 2013. 气象雷达中雨滴谱回波参数建模技术研究. 杭州电子科技大学学报, 33(5): 114-117. Yu J W, Chen N P, Zheng Z L, et al. 2013. Raindrop echo parameter modeling technology research in weather radar. J Hangzhou Dianzi Univ, 33(5): 114-117 (in Chinese) |
| 俞小鼎, 姚秀萍, 熊廷南等. 2006. 多普勒天气雷达原理与业务应用. 北京: 气象出版社, 1-45. Yu X D, Yao X P, Xiong T N, et al. 2006. Principles and Applications of Doppler Weather Radar. Beijing: China Meteorological Press, 1-45 (in Chinese) |
| Andsager K, Beard K V, Laird N F. 1999. Laboratory measurements of axis ratios for large raindrops. J Atmos Sci, 56(15): 2673-2683 |
| Baldauf M, Seifert A, Förstner J, et al. 2011. Operational convective-scale numerical weather prediction with the COSMO model: Description and sensitivities. Mon Wea Rev, 139(12): 3887-3905 |
| Beard K V, Chuang C. 1987. A new model for the equilibrium shape of raindrops. J Atmos Sci, 44(11): 1509-1524 |
| Bluestein H B, Förench M M, Tanamachi R L, et al. 2007. Close-range observations of tornadoes in supercells made with a dual-polarization, X-band, mobile Doppler radar. Mon Wea Rev, 135(4): 1522-1543 |
| Brandes E A, Vivekanandan J, Tuttle J D, et al. 1995. A study of thunderstorm microphysics with multiparameter radar and aircraft observations. Mon Wea Rev, 123(11): 3129-3143 |
| Bringi V N, Chandrasekar V. 2001. Polarimetric Doppler Weather Radar: Principles and Applications. Cambridge: Cambridge University Press, 636pp |
| Caumont O, Ducrocq V, Delrieu G, et al. 2006. A radar simulator for high-resolution nonhydrostatic models. J Atmos Oceanic Technol, 23(8): 1049-1067 |
| Chandrasekar V, Keränen R, Lim S, et al. 2013. Recent advances in classification of observations from dual polarization weather radars. Atmos Res, 119: 97-111 |
| De Wolf D A, Russchenberg H W J, Ligthart L P. 1990. Modelling of particle distribution in the melting layer. IEE Proceedings H:Microwaves, Antennas and Propagation, 137(6): 389-395 |
| Fabry F, Zawadzki I. 1995. Long-term radar observations of the melting layer of precipitation and their interpretation. J Atmos Sci, 52(7): 838-851 |
| Green A W. 1975. An approximation for the shapes of large raindrops. J Appl Meteor, 14(8): 1578-1583 |
| Hall M P M, Cherry S M, Goddard J W F, et al. 1980. Raindrop sizes and rainfall rate measured by dual-polarization radar. Nature, 285(5762): 195-198 |
| Hong S Y, Dudhia J, Chen S H. 2004. A revised approach to ice microphysical processes for the bulk parameterization of clouds and precipitation. Mon Wea Rev, 132(1): 103-120 |
| Huang G J, Bringi V, van den Heever S, et al. 2005. Polarimetric radar signatures from RAMS microphysics// 32nd Int. Conf. on Radar Meteorology.Albuquerque: Amer Meteor Soc, P11R. 16 |
| Huang G J, Bringi V N, Thurai M. 2008. Orientation angle distributions of drops after an 80 m fall using a 2D video disdrometer. J Atmos Oceanic Technol, 25(9): 1717-1723 |
| Jung Y, Xue M, Zhang G F, et al. 2008a. Assimilation of simulated polarimetric radar data for a convective storm using the ensemble Kalman filter. Part Ⅱ: Impact of polarimetric data on storm analysis. Mon Wea Rev, 136(6): 2246-2260 |
| Jung Y, Zhang G F, Xue M. 2008b. Assimilation of simulated polarimetric radar data for a convective storm using the ensemble Kalman filter. Part Ⅰ: Observation operators for reflectivity and polarimetric variables. Mon Wea Rev, 136(6): 2228-2245 |
| Kumjian M R, Ryzhkov A V. 2008. Polarimetric signatures in supercell thunderstorms. J Appl Meteor Climatol, 47(7): 1940-1961 |
| Li X L, Mecikalski J R. 2010. Assimilation of the dual-polarization Doppler radar data for a convective storm with a warm-rain radar forward operator. J Geophys Res, 115(D16): D16208 |
| Li X L, Mecikalski J R. 2012. Impact of the dual-polarization Doppler radar data on two convective storms with a warm-rain radar forward operator. Mon Wea Rev, 140(7): 2147-2167 |
| List R. 1986. Properties and growth of hailstones//Thunderstorm Dynamics and Morphology. Oklahoma: University of Oklahoma Press, 259-276 |
| Liu L P, Zhang P F, Xu Q, et al. 2005. A model for retrieval of dual linear polarization radar fields from model simulation outputs. Adv Atmos Sci, 22(5): 711-719 |
| Longtin D R, Bohren C F, Battan L J. 1987. Radar backscattering by large, spongy ice oblate spheroids. J Atmos Oceanic Technol, 4(3): 355-358 |
| Michalakes J, Dudhia J, Gill D, et al. 2004. The weather research and forecast model: Software architecture and performance//The 11th ECMWF Workshop on the Use of High Performance Computing in Meteorology. Reading, UK: World Scientific, 156-168 |
| Morrison H, Curry J A, Khvorostyanov V I. 2005. A new double-moment microphysics parameterization for application in cloud and climate models. Part Ⅰ: Description. J Atmos Sci, 62(6): 1665-1677 |
| Morrison H, Thompson G, Tatarskii V. 2009. Impact of cloud microphysics on the development of trailing stratiform precipitation in a simulated squall line: Comparison of one-and two-moment schemes. Mon Wea Rev, 137(3): 991-1007 |
| Pfeifer M, Craig G C, Hagen M, et al. 2008. A polarimetric radar forward operator for model evaluation. J Appl Meteor Climatol, 47(12): 3202-3220 |
| Pruppacher H R, Beard K V. 1970. A wind tunnel investigation of the internal circulation and shape of water drops falling at terminal velocity in air. Quart J Roy Meteor Soc, 96(408): 247-256 |
| Ryzhkov A, Giangrande S, Schuur T. 2003. Rainfall measurements with the polarimetric WSR-88D radar. National Severe Storms Laboratory Report,98pp |
| Sihvola A H, Kong J A. 1988. Effective permittivity of dielectric mixtures. IEEE Trans Geosci Remote Sens, 26(4): 420-429 |
| Smith P L, Myers C G, Orville H D. 1975. Radar reflectivity factor calculations in numerical cloud models using bulk parameterization of precipitation. J Appl Meteor, 14(6): 1156-1165 |
| Straka J M, Zrnic D S, Ryzhkov A V. 2000. Bulk hydrometeor classification and quantification using polarimetric radar data: Synthesis of relations. J Appl Meteor, 39(8): 1341-1372 |
| Thurai M, Bringi V N. 2005. Drop axis ratios from a 2D video disdrometer. J Atmos Oceanic Technol, 22(7): 966-978 |
| Tiuri M E, Sihvola A H, Nyfors E, et al. 1984. The complex dielectric constant of snow at microwave frequencies. IEEE J Oceanic Eng, 9(5): 377-382 |
| Ulbrich C W, Atlas D. 1984. Assessment of the contribution of differential polarization to improved rainfall measurements. Radio Sci, 19(1): 49-57 |
| Van Bladel J G. 1985. Electromagnetic Fields. New York: Hemisphere, 1149pp |
| Vivekanandan J, Raghavan R, Bringi V N. 1993. Polarimetric radar modeling of mixtures of precipitation particles. IEEE Trans Geosci Remote Sens, 31(5): 1017-1030 |
| Vivekanandan J, Ellis S M, Oye R, et al. 1999. Cloud microphysics retrieval using S-band dual-polarization radar measurements. Bull Amer Meteor Soc, 80(3): 381-388 |
| Wakimoto R M, Bringi V N. 1988. Dual-polarization observations of microbursts associated with intense convection: The 20 July storm during the MIST project. Mon Wea Rev, 116(8): 1521-1539 |
| Weisman M L, Klemp J B. 1982. The dependence of numerically simulated convective storms on vertical wind shear and buoyancy. Mon Wea Rev, 110(6): 504-520 |
| Weisman M L, Klemp J B. 1984. The structure and classification of numerically simulated convective storms in directionally varying wind shears. Mon Wea Rev, 112(12): 2479-2498 |
| Wu B, Verlinde J, Sun J Z. 2000. Dynamical and microphysical retrievals from Doppler radar observations of a deep convective cloud. J Atmos Sci, 57(2): 262-283 |
| Yin J F, Wang D H, Zhai G Q. 2011. Long-term in situ measurements of the cloud-precipitation microphysical properties over East Asia. Atmos Res, 102(1-2): 206-217 |
| Yin J F, Wang D H, Zhai G Q. 2013. A comparative study of cloud-precipitation microphysical properties between East Asia and other regions. J Meteor Soc Japan Ser Ⅱ, 91(4): 507-526 |
| Yin J F, Wang D H, Zhai G Q. 2014. An investigation into the relationship between liquid water content and cloud number concentration in the stratiform clouds over north China. Atmos Res, 139: 137-143 |
 2016, Vol. 74
2016, Vol. 74


