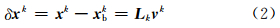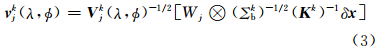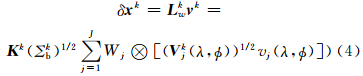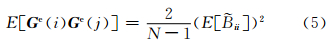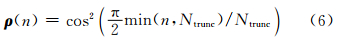中国气象学会主办。
文章信息
- 张卫民, 刘柏年, 曹小群, 赵延来, 朱孟斌, 赵文静. 2016.
- ZHANG Weimin, LIU Bainian, CAO Xiaoqun, ZHAO Yanlai, ZHU Mengbin, ZHAO Wenjing. 2016.
- 流依赖球面小波背景误差协方差模型设计和初步试验
- Development and preliminary application of a wavelet flow-dependent background error covariance model
- 气象学报, 74(3): 410-420
- Acta Meteorologica Sinica, 74(3): 410-420.
- http://dx.doi.org/10.11676/qxxb2016.024
-
文章历史
- 2015-06-18 收稿
- 2016-02-24 改回
2. 国防科学技术大学计算机学院, 长沙, 410073
2. College of Computer, National University of Defense Technology, Changsha 410073, China
数值天气预报技术的不断发展得益于数值预报模式的改进(陈德辉等,2004;沈学顺等,2011;王明欢,2011)、非常规资料的使用(马旭林,2015)和资料同化中背景误差协方差模型的优化等因素。背景误差协方差矩阵(B-矩阵)对变分同化系统的信息传播、信息平滑、平衡关系和流型结构的建立等具有十分重要的作用(Bannister,2008),精细刻画背景误差协方差已成为建立高水平资料同化系统的先决条件。由于B-矩阵的维数特别巨大,无法直接获取得到完整的背景场误差,对B-矩阵估计是一项十分困难的工作。通常的处理方法是引入简化和近似的背景误差协方差模型(B-矩阵模型),如假设背景误差协方差(B)具有各向同性、位置无关和不随时间变化等理想特性。在此基础上将B-矩阵转化为一组控制变量变换,利用变换将关于模式状态的目标泛函转化为控制变量的泛函,这样即可以消除显式定义B-矩阵的困难,也可以提高极小化目标泛函过程的收敛速度。业务同化系统中通常将控制变换分解为平衡变换、水平变换和垂直变换空间三部分,由平衡变换描述变量间的相关,而由水平变换和垂直变换来描述单个变量内部在水平、垂直方向的空间相关。
谱空间对角化和物理空间递归滤波方法是处理B-矩阵水平相关的两种典型方法(Parrish et al,1992; Rabier et al,1998; Derber et al,1999; Bannister,2008)。但是,单独用谱方法或者递归滤波方法都不能刻画 B 的所有特征。如谱方法不能刻画背景协方差在物理空间的变化特征,而递归滤波不能刻画协方差随波动尺度变化的特征。Fisher(2003,2004)利用小波函数在谱和格点空间中都具有局部性的特点(Ingleby,2001; Weaver et al,2001),引入了小波B-矩阵模型,弱化了模型的各向同性以及与位置无关假设,并考虑了单变量背景误差协方差在水平和垂直方向的不可分离性。欧洲中期天气预报中心(ECMWF)在2005年前后将小波B-矩阵模型应用到了四维变分同化系统(4DVar)中。张卫民等(2012)也成功将球面小波B-矩阵模型应用到了银河四维变分同化业务系统(YH4DVar)中。
上述模型仍假定B-矩阵是不随时间变化的常量,因此无法反映B-矩阵随流型变化的时变特性。一种弱化静态假设的可行方案是:在变分同化的基本框架中引入流依赖背景误差协方差的集合估计值,并与静态的B-矩阵进行线性加权(Hamill et al,2003; Lorenc,2003; Qiu et al,2006; Liu et al,2008; Isaksen et al,2010; 张蕾等,2009;庄照荣等,2011;冷洪泽等,2012)。如Hamill等(2003)将三维变分和集合卡尔曼滤波(EnKF)进行结合,形成了混合三维变分同化系统。Liu等(2008)使用一组集合预报实时统计流依赖背景误差协方差,并利用背景场扰动统计值代替增量算法中的预处理矩阵,使得目标泛函梯度计算过程中所需的伴随模式积分可以用观测空间中的背景场统计值代替。Isaksen等(2010)在ECMWF的四维变分同化系统中引入集合资料同化(EDA)方法,利用分析集合获取流依赖的背景场误差方差,并应用到确定性预报系统的四维变分同化中。但是上述研究的B-矩阵模型、同化系统和框架、控制变量等都与YH4DVar存在差别。刘柏年等(2015)主要侧重于流依赖的背景场误差方差的滤波处理,并没有涉及到整个B-矩阵模型的设计和实现。
设计流依赖球面小波背景误差协方差模型的关键是如何得到随大气状态变化的平衡系数、背景场误差方差、依赖于小波尺度和水平位置的局地垂直相关协方差的均方根矩阵及其伴随矩阵。本研究在张卫民等(2012)、刘柏年等(2015)的基础上,利用YH4DVar构造多个能反映背景误差分布特征的集合样本。基于这些样本统计流依赖背景误差方差和垂直相关矩阵,并以此设计和实现了流依赖球面小波背景误差协方差模型,给出基于流依赖球面小波背景误差协方差的目标泛函表达式和小波空间的控制变量转换关系式。并以背景误差方差统计和后处理、垂直相关矩阵算法设计为重点,叙述了流依赖球面小波背景误差协方差模型的实现过程,通过台风个例分析来检验该模型对同化效果的影响。
2 流依赖球面小波背景场误差协方差模型增量形式的流依赖四维变分资料同化目标泛函可表述为
控制向量 vk、控制变换 Lk和分析增量δ xk满足 式中,k是分析循环次数,xbk是第k次分析循环需要获取的大气状态分析场 xk的先验估计即背景场。 yk是第k次分析循环同化窗口内的所有观测组成的向量,Hk是将模式状态量映射到观测空间的算子。矩阵 O 是观测误差协方差矩阵。流依赖的背景误差协方差矩阵 P 在式(1)中并没有直接出现,而是由控制变换 Lk隐式地表示 P k= Lk LkT。 Lk可进一步分解为平衡变换和空间变换两部分。平衡变换也称物理变换,目的是分离变量之间的相关,将多变量分析问题简化为单变量分析问题;空间变换又分为水平和垂直变换,用来分离变量自身在水平和垂直方向的相关。
由于相关的局地化设计在具有各向异性和空间位置相关的B-矩阵模型设计中十分重要,传统的谱方法和格点很难同时在谱空间和物理空间中表征出局部化特性,基于球面小波函数构造的B-矩阵模型能够利用球面小波函数的多尺度分析能力可以刻画不同尺度大气运动的背景误差特征(Fisher,2003)。小波变换Wj将控制变量 vk转换到小波空间上的控制向量 vkT=(v1k,v2k… vjk,…,vJk)T
式中,j标识不同尺度的小波,Kk表示不同气象变量之间的物理变换,由它定义平衡约束关系,Σbk表示格点空间的背景场误差方差,Vjk(λ,ø)表示在j尺度小波空间和水平位置(λ,ø)上的垂直协方差矩阵。原则上,每个网格点都需要独自定义垂直协方差矩阵Wj⊗(Σbk)-1/2(Kk)-1δx 。而在实际计算中,为了减少B-矩阵的存储空间,通常是对一组相邻的格点应用同一个垂直协方差矩阵。将式(3)代入到式(2)可导出基于球面小波的流依赖控制变量转换关系式从式(4)可以看出,球面小波背景误差协方差模型需要定义的模型参数包括平衡系数、背景场误差方差以及依赖于小波尺度和水平位置的局地垂直相关协方差的均方根矩阵及其伴随矩阵。为了使模型能充分反映背景场误差的流依赖特性,需要使这些参数能随大气状态的流型特征而变化,因此在每次同化循环时,需要重新定义流依赖的平衡关系和背景场误差方差。
3 基于集合资料同化的流依赖背景场误差统计误差方差、依赖于小波尺度和水平位置的局地垂直相关协方差矩阵等模型参数的统计都需要数量足够大的背景场误差样本。对于气候态的模型参数,背景场误差集合可以自然地利用不同时次的背景场误差作为样本成员,但对于流依赖的模型参数必须反映当前流型状态的背景场误差特性,比较自然的做法就是利用集合方法来生成误差样本。
假设已得到某一分析时刻tk背景场 xbk的N个集合成员 xbik(i=1,…,N),令 xbk为这N个集合成员的平均,则流依赖的背景场误差协方差矩阵 Bk可以通过统计各集合成员与集合平均的方差和协方差近似得到
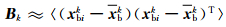
流依赖背景场误差协方差矩阵的这种统计与气候态的背景场误差协方差矩阵的主要区别是只利用当前时刻或最近一段时刻的背景场样本集合。另外一种近似统计方法是直接用集合成员之差
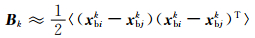
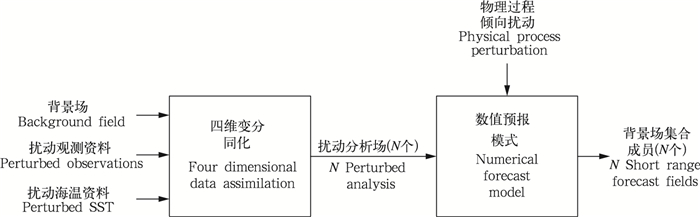
参照欧洲中期天气预报中心的集合资料同化方案(Bonavita et al,2012),N个背景场集合成员可以利用前一个时间窗口的观测资料通过集合资料同化方法生成,即通过扰动输入同化系统的观测资料、边界条件和背景场,然后对各扰动输入利用同化系统生成扰动分析成员,以此作为背景场集合成员。其中观测资料扰动通过在观测中加入观测误差概率密度函数的随机噪声得到,而分析的背景场扰动是通过预报模式的物理过程倾向扰动得到,而不是直接扰动背景场本身,流依赖背景场集合成员的生成流程见图 1。
|
| 图 1 流依赖背景场集合成员生成示意 Fig. 1 Schematic diagram for the ensemble of flow-dependent background fields generated through Ensemble Data Assimilation method |
要使这样统计得到的矩阵能真正近似于背景场误差协方差矩阵,必须得到足够的样本。背景场误差协方差矩阵对角线上的元素实际上就是背景场误差方差,对角线以外的元素组成了背景场误差的协方差。对于方差和协方差统计要求的集合样本数显然是可以不一样的,因此在实际处理时可以分开统计,在背景场误差协方差模型中也是分开使用的,可以看出,这种计算的代价很高。目前有两种思路减少计算量:(1) 减小集合资料同化的分辨率,(2) 采用小样本统计方法。欧洲中期天气预报中心目前设计的集合资料同化系统是同时采用这两种方法,首先将集合资料同化分辨率设为确定性同化的一半,然后引入滤波技术消除小样本带来的噪声(Isaksen et al,2010)。
3.1 流依赖背景场误差方差计算及小样本滤波流依赖背景误差方差可用扰动背景场集合成员的方差代替,但是会引入随机误差(Vran)和系统误差(Vsys)(Berre et al,2007,2010)。随机误差是因集合样本数偏少引起的,当集合成员足够大时,随机误差可以忽略;系统误差表示的是集合资料同化估计误差与真实误差的偏离程度,它反映了集合资料同化表征不确定性时存有缺失。实际业务系统中,集合样本数一般取10—50个,此时引入的随机误差项对样本估计值的精度造成了很大影响,需要引入计算量小的客观滤波方法(Raynaud et al,2011;Bonavita et al,2012)以提高样本误差估计精度。Mallat等(1998)和Raynaud等(2009)将样本噪声的协方差表示为集合误差协方差矩阵期望的简单函数,即
式中,N是集合大小,Raynaud等(2009)根据式(5)采用了以下低通滤波 式中,n是总谱波数,Ntrunc是滤波器的截断波数。在谱空间,应用此低通滤波相当于在格点空间的误差方差添加了一个加权平均,使得较大尺度信号通过,而较小尺度样本噪声被过滤掉(Buehner et al,2007)。 3.2 流依赖局地垂直相关矩阵计算
由式(3)定义的控制向量需要对每个尺度的每个水平位置引入一个局地垂直相关矩阵 V jk(λ,ø),该矩阵需要反映 Wj⊗[(Σbk)-1/2(Kk)-1δx ] 垂直廓线误差的相关。在控制变量变换中,需要同时使用局地垂直协方差矩阵的均方根矩阵及其伴随矩阵,因此在统计参数时直接计算出局地垂直协方差矩阵的均方根矩阵及其伴随矩阵。由于这部分统计参数需要巨大的资料存储空间,因此只能在相对于变分同化系统更低分辨率的格点上进行垂直相关矩阵的统计计算,而在分析过程中使用时,需要将低分辨率统计量插值到同化系统的格点上。另外由于(Σbk)-1/2是对角矩阵,在计算过程中可以与(Kk)-1的顺序互换。
局地垂直相关矩阵 Vjk(λ,ø)的统计计算需要一定数量的误差样本,一般要求样本数不能少于模式垂直层,欧洲中期天气预报中心认为,91层分析系统的样本数超过600,流依赖背景场误差统计要求这些样本都是同一时刻的,在实际应用时几乎是不可能得到这么大的集合资料同化样本,为了使局地垂直相关矩阵有足够的信息容量,采用流依赖局地垂直相关矩阵 Vjflow-dep(λ,ø)和气候态局地垂直相关矩阵 Vjclim(λ,ø)进行线性组合,即计算 Vjk(λ,ø)=α Vjflow-dep(λ,ø)+(1-α)Vjclim(λ,ø)。
Vjclim(λ,ø)和Vjflow-dep(λ,ø)的统计计算过程都是采用如下方法:
(1) 首先利用方差将背景场误差样本正规化,然后实施平衡变换K将所有正规化的背景场误差样本转换为中间控制向量,表示成矢量 vp;
(2) 对所有样本进行小波函数Wj和矢量 vp之间的卷积运算Wj⊗ vp。具体方法是将误差样本中的每个变量转换到谱空间中,并和Ŵj(n)进行乘积运算,然后进行逆球谐变换转换到格点空间中,就得到同时依赖于小波尺度和水平位置的新背景误差样本 vpj(λ,ø,k,t);
(3) 对所有样本应用内积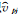 (λ,ø,k,t)=P(λ,ø,k,t)vpj(λ,ø,k,t),P(i,j,k,t)是权重,它实际上就是小波系数;
(λ,ø,k,t)=P(λ,ø,k,t)vpj(λ,ø,k,t),P(i,j,k,t)是权重,它实际上就是小波系数;
(4) 由公式 Vj(λ,ø,k,k′)=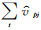 (λ,ø,k,t)
(λ,ø,k,t)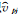 (λ,ø,k′,t)/T 计算误差样本空间上局地垂直协方差矩阵元素的平均值,其中T是误差样本个数。分别对k和k′进行循环,就能得到局地垂直协方差矩阵 Vj(λ,ø);
(λ,ø,k′,t)/T 计算误差样本空间上局地垂直协方差矩阵元素的平均值,其中T是误差样本个数。分别对k和k′进行循环,就能得到局地垂直协方差矩阵 Vj(λ,ø);
(5) 对所有的小波尺度j和不同的水平位置重复上面的步骤,就能得到所有的局地垂直协方差矩阵 Vj(λ,ø);
(6) 为了得到稳定的统计量和减小背景误差统计量的存储量,可以在水平位置上进行水平空间上的平均,从而认为相距较近的水平格点共用相同的局地垂直协方差矩阵。
Vjclim(λ,ø)和Vjflow-dep(λ,ø)统计计算的区别是输入的背景场误差样本不同,Vjclim(λ,ø)是利用一段时间内的背景场误差,其获取的是模型参数在气候意义下的平均效益,因此统计计算通过离线方式实施,在同化进行过程中不再变化。而 Vjflow-dep(λ,ø)则需要利用同一时刻的背景场误差的多个样本进行统计,它伴随每次同化时进行同步计算,在设置恰当的比率因子α后,对组合得到的流依赖局地垂直相关矩阵α Vjflow-dep(λ,ø)+(1-α)Vjclim(λ,ø)进行乔列斯(Chaolesky)分解,得到每个局地垂直协方差矩阵的均方根矩阵及其伴随,目前比率因子α还没有很好的计算方法,需要根据经验给定。
4 数值试验和结果分析为了验证流依赖球面小波背景场误差协方差模型的有效性,利用YH4DVar进行试验,集合资料同化试验系统配置如下:
(1) 在T399L91分辨率(谱三角截断波数为399、线性网格、91个混合坐标层)下运行一个控制分析和30个扰动分析,引入探空、地面、飞机、辐射率和GPS掩星弯曲角观测资料,为了避免复杂的观测扰动,卫星运动矢量资料AMV等没有引入到系统中。
(2) 四维变分的同化窗口设为12 h,配置两次最小化迭代,即两次外循环,第1次的分辨率设为T95,第2次的分辨率设为T159,第1次最小化迭代步固定为50步,第2次最小化迭代固定为30步。
(3) 每天同样运行两次集合资料同化,00时(世界时,下同)同化使用前一日21时至09时的观测资料,12时同化使用09时至次日21时的观测资料,控制和扰动分析采用同样的质量控制方式,分析循环中运行模式的15 h短期预报。
(4) 控制分析使用未加扰动的观测资料。扰动成员则使用加上了随机方法生成扰动的观测资料,观测扰动满足高斯分布,均值为0,标准偏差等于四维变分中使用的观测误差估计。
(5) 预报模式中引入了物理过程随机倾向扰动,因此不需要再显示扰动背景场。
将控制分析得到的分析场作为真实场,这样每个扰动分析得到的扰动分析场减去控制分析场就得到了误差样本。图 2给出流依赖球面小波背景场误差协方差的模拟流程。
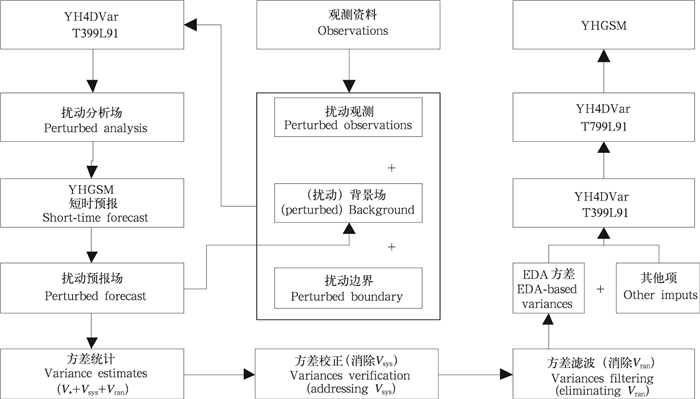
|
| 图 2 流依赖球面小波背景场误差协方差的模拟流程 Fig. 2 Schematic diagram for the generation of flow-dependent spherical wavelet background error covariance |
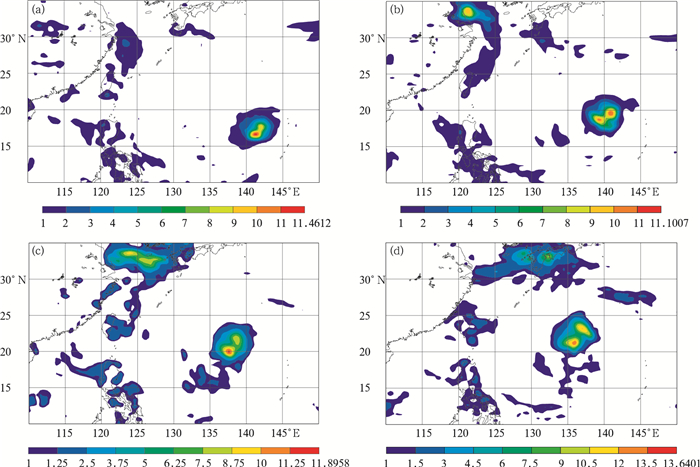
采用图 2的试验流程,计算得到了2015年9月22日09时至23日21时共4个时次所对应的西太平洋地区第91个模式层上涡度的背景误差方差,滤波的截断波数为150。从图 3可以看出,采用集合资料同化估计得到的流依赖涡度背景误差方差结构及中心位置随着台风中心位置的移动发生了相应的变化,主要体现为在台风影响区域背景场误差方差偏大,且极值位于台风中心位置附近。而原YH4DVar系统采用的静态背景误差方差在这段时间没有变化,且结构无法反映出台风影响区域由于剧烈垂直运动导致的误差偏大情况。在下一次同化循环中引入计算得到的流依赖背景场误差方差可以提高观测资料的使用效率,优化变分资料控制的阈值选择。使原本被拒绝的位于台风附近的观测量能够合理地进入到同化系统,提高对台风等剧烈天气的同化分析效果。
|
| 图 3 2015年9月22日09时(a)和21时(b)、23日09时(c) 和21时(d) 背景场误差方差 (单位:10-5s-1) 随时间的变化 Fig. 3 Evolution of the standard deviation of vorticity (unit:10-5s-1) at 09:00 UTC 22 (a), 21:00 UTC 22 (b), 09:00 UTC 23(c) and 21:00 UTC 23 (d) September 2015 |
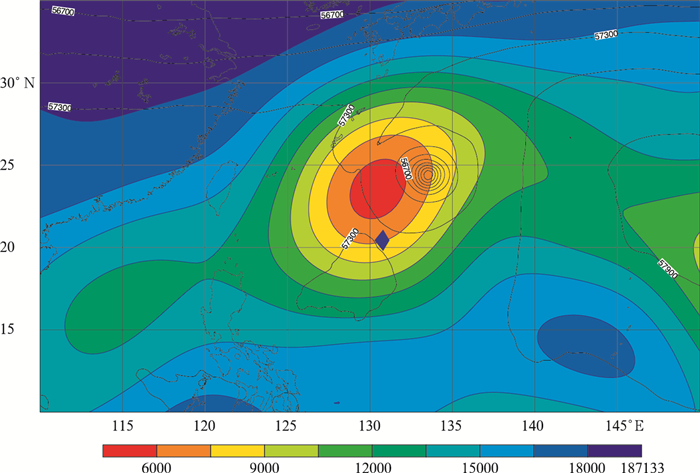
检验背景误差协方差矩阵是否具有流依赖特性的另一种直观方式是查看相关函数矩阵 C 能否反映出时间和空间变化的天气形势(Pereira et al,2006; Pannekoucke et al,2008; Varella et al,2011)。相对方差而言,对统计相关函数的统计则需要更多的样本,以T399L91为例,至少需要100个,计算代价非常大。因此,在构造样本时可采用滑动取样方法构造所需样本。利用集合样本可计算出风的局地相关长度尺度
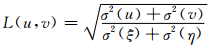
|
| 图 4 500 hPa高度上风的水平相关长度 (色阶,m) (等值线为500 hPa位势高度的9 h预报场,对应的时间为2015年9月25日21时,间隔为300 gpm,菱形对应台风中心的观察位置(20.8°N,130.8°E)) Fig. 4 Horizontal correlation length-scale (shaded, m) of winds near 500 hPa diagnosed from flow-dependent wavelet-based correlations for the period 20-25 September 2015, which is superimposed on 500 hPa geopotenti analysis field (contour with interval of 300 gpm; The diamond denotes the observed typhoon center (20.8°N,130.8°E)) |
为了分析流依赖背景场误差协方差模型对分析和预报的影响,在YH4DVar的基础上设计了一组对比试验,其中控制试验仍采用目前准静态的背景场误差估计值,而流依赖试验与控制的唯一区别在于,在最小化迭代中用到了上述流依赖球面小波背景误差协方差模型。
以2015年21号西北太平洋超强台风“杜鹃”作为试验个例。台风“杜鹃”的低压区最早生成于2015年9月15日,由于前期低压区发展缓慢、螺旋性差、结构杂乱无章,直至9月23日00时低压区才 形成热带气旋,中心最低海平面气压为1000 hPa位于(18.7°N,138.6°E)。中国中央气象台、韩国气象厅、日本气象厅和美国应用联合台风警报中心发布的9月23日00时台风路径预报结果均往东北北上,但由于西风槽的强度比预期的明显偏弱,副热带高压脊出现的弱点不足以让杜鹃突破北上。最终台风向西北运动,在台湾和福建登陆。9月23日晚各中心才修正了预报路径,YHGSM的10 d业务预报也出现了类似的翻转现象。为了与观测数据相对应,试验中选择9月23日00时作为同化分析时间,其中在流依赖同化试验中用到了9月22日12 时生成和统计得到的流依赖球面小波背景误差协方差和相关系数。
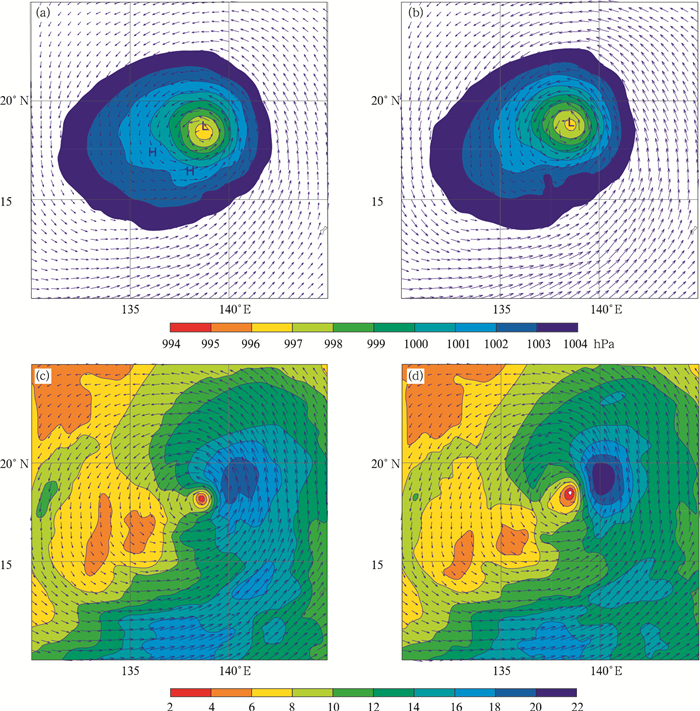
从9月23日00时海平面气压(图 5a、b)和2 m风场(图 5c、d)的同化分析结果可以看出,流依赖试验的涡旋中心位置向北偏移约15 km。从风场对比情况来看,流依赖试验给出的低层环流发展得更加对称,涡旋东北部气流发展更旺盛,最大风速约增大3 m/s,可以带来更丰富的海洋暖湿空气,促进台风发展。850 hPa水汽通量的分布情况与风场有很强的一致性(图略),改进后的分析场所给出的涡旋区域有更多的水汽通量流入。可见,新模型在一定程度上改变了涡旋中心位置和低层风场结构。此外,两者差异还体现在被同化到系统的有效资料数上,在观测资料总数不变的条件下,引入流依赖球面小波背景误差协方差模型的同化试验增加了240个有效观测。
|
| 图 5 2015年9月23日00时平均海平面气压(a、b)及2 m风场(c、b) (a、c. 控制试验即采用静态背景场误差协方差模型,b、d.同化过程中采用了流依赖模型;等值线为平均海平面气压,间隔为1 hPa,箭头表示风场分布,1 cm对应20 m/s) Fig. 5 Analysis of mean sea level pressure (a,b; shaded, with 1 hPa interval) and 2 m wind vectors (c,d; arrow head scaled by 20 m/s per cm) at 00:00 UTC 23 September 2015 (a,c. the control experiment, b,d. the flow-depended background-error covariance) |
为了进一步验证模型对预报的影响,在上述分析场对比试验的基础上,采用YHGSM业务谱模式进行了5 d预报,并与台风中心的最低平均海平面气压和位置的观测值进行了对比(图 6)。从图 6a可以看出,起报时刻的台风定位都出现了很大的偏差,经6 h修正后,流依赖试验的预报结果迅速靠向观测位置,并随着预报时间往前推进,两者差距逐渐缩小。而控制预报则保持原有走势,逐渐偏离观测。从台风强度5 d预报的对比结果(图 6b)可以看出,两个预报结果差别不大,在9月24日06时之前预报是偏强的,之后表现为偏弱,这一现象在后期发展为超强台风时(9月27日00时)更为明显,而此时流依赖试验的预报能得到更真实的平均海平面气压值。
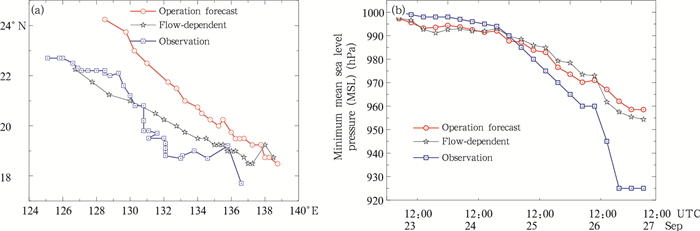
|
| 图 6 2015年9月22日00时起报的台风“杜鹃”路径(a)和强度(b)预报 (为了与观测保持一致,图中去掉了前24 h和8 d以后的预报数据,蓝线为中国天气台风网的观测数据) Fig. 6 Track (a) and intensity (b) forecasts of Typhoon Dujuan initialized at 00:00 UTC 22 September 2015 (for sick of consistency, forecast results before the first 24 h and after 8 d are not shown, the blue line corresponding to the observations from http://typhoon.weather.com.cn) |
以上试验表明,引入流依赖球面小波背景误差协方差模型后,能对台风“杜鹃”强度和路径预报有一定的正影响。但是,需要说明的是,“杜鹃”对前期初始条件非常敏感,改进带有一定的随机性。试验中仅对比分析了台风的强度和路径,引入流依赖球面小波背景误差协方差模型是否对其他指标也能产生正效果、模型的适用性和稳定性如何尚需要大量对比试验并进一步系统性地验证说明。
5 结 论恰当定义背景场误差是所有资料同化系统最为基础的先决条件,利用集合资料同化方法能够提供表征随天气状态变化的背景场误差统计,结合集合资料同化和球面小波的优势能够较好地定义流依赖背景场误差协方差模型,从而提供了克服当前协方差模型主要缺点的可能性。
设计和实现流依赖背景场误差协方差模型的关键是如何利用有限集合样本实时统计出流依赖平衡关系、背景误差方差和局地垂直相关协方差。对于流依赖平衡关系、垂直相关协方差的实时统计,虽然文中给出了具体的统计实现方法,但是目前的计算条件远达不到要求,只能采取如引入历史样本的折衷处理办法。而对于背景误差方差,可以通过引入谱滤波技术来减少对集合样本数的需求,因此可以完全实现流依赖的背景误差方差的实时统计。在流依赖球面小波背景场误差协方差模型的有效性验证试验中,10个集合资料同化成员在引入谱滤波后能有效提高背景误差方差估计值的质量,精确反映出大气状态的重要特征,显著改善了业务随机方法得到的背景误差方差和相关函数,并对预报场表现出一定的正效果。未来将进行更多的试验进一步系统评估该模型的有效性。
| 陈德辉, 薛纪善. 2004. 数值天气预报业务模式现状与展望. 气象学报, 62(5):623-633. Chen D H, Xue J S. 2004. An overview of the present status and prospect of the operational numerical weather prediction models. Acta Meteor Sinica, 62(5):623-633(in Chinese) |
| 冷洪泽, 宋君强, 曹小群等. 2012. 基于粒子滤波的一种改进的资料同化方法. 物理学报, 61(7):70501-070501. Leng H Z, Song J Q, Cao X Q, et al. 2012. An improved particle filter in data assimilation. Acta Phys Sinica, 61(7):070501(in Chinese) |
| 刘柏年, 张卫民, 曹小群等. 2015. 集合资料同化中方差滤波技术研究及试验. 地球物理学报, 58(5):1526-1534. Liu B N, Zhang W M, Cao X Q, et al. 2015. Investigations and experiments of variance filtering technology in the Ensemble Data Assimilation. Chinese J Geophys, 58(5):1526-1534, doi:10.6038/cjg20150506(in Chinese) |
| 马旭林, 于月明, 陈德辉. 2015. 适应性观测研究现状和展望. 气象学报, 73(2):221-235. Ma X L, Yu Y M, Chen D H. 2015. The present situation and prospect of the adaptive observation. Acta Meteor Sinica, 73(2):221-235(in Chinese) |
| 沈学顺, 王明欢, 肖锋. 2011. GRAPES模式中高精度正定保形物质平流方案的研究Ⅰ:理论方案设计与理想试验. 气象学报, 69(1):1-15. Shen X S, Wang M H, Xiao F. 2011. A study of the positive definite conformal advection scheme with high accuracy in the GRAPES model Ⅰ:Scientific design and idealized tests. Acta Meteor Sinica, 69(1):1-15(in Chinese) |
| 王明欢, 沈学顺, 肖锋. 2011. GRAPES模式中高精度正定保形物质平流方案的研究Ⅱ:连续实际预报试验. 气象学报, 69(1):16-25. Wang M H, Shen X S, Xiao F. A study of the positive definite conformal advection scheme with high accuracy in the GRAPES model Ⅱ:Continuous real-time rainfall prediction experiments. Acta Meteor Sinica, 69(1):16-25(in Chinese) |
| 张蕾, 邱崇践, 张述文. 2009. 在四维变分同化中运用集合协方差的试验. 气象学报, 67(6):1124-1132. Zhang L, Qiu C J, Zhang S W. 2009. Experiments of ensemble convariance application in the 4D variational system. Acta Meteor Sinica, 67(6):1124-1132, doi:10.11676/qxxb2009.108(in Chinese) |
| 张卫民, 曹小群, 宋君强. 2012. 以全球谱模式为约束的四维变分资料同化系统YH4DVAR的设计和实现. 物理学报, 61(24):249202. Zhang W M, Cao X Q, S J Q. 2012. Development and implementation of the four-dimensional variational data assimilation system constrained by the global spectral model. Acta Phys Sinica, 61(24):249202(in Chinese) |
| 庄照荣, 薛纪善, 李兴良. 2011. GRAPES集合卡尔曼滤波资料同化系统Ⅰ:系统设计及初步试验. 气象学报, 69(4):620-630. Zhuang Z R, Xue J S, Li X L. 2011. The GRAPES ensemble Kalman filter data assimilation system. Part I:Development and preliminary experiment. Acta Meteor Sinica, 69(4):620-630, doi:10.11676/qxxb2011.054(in Chinese) |
| Bannister R N. 2008. A review of forecast error covariance statistics in atmospheric variational data assimilation. Ⅰ:Characteristics and measurements of forecast error covariances. Quart J Roy Meteor Soc, 134(637):1951-1970 |
| Berre L, Pannekoucke O, Desroziers G, et al. 2007. A variational assimilation ensemble and the spatial filtering of its error covariances:Increase of sample size by local spatial averaging//Proc. ECMWF Workshop on Flow-Dependent Aspects of Data Assimilation. Reading, United Kingdom:ECMWF, 151-168 |
| Berre L, Desroziers G. 2010. Filtering of background error variances and correlations by local spatial averaging:A review. Mon Wea Rev, 138(10):3693-3720 |
| Bonavita M, Isaksen L, Hólm E, et al. 2012. On the use of EDA background error variances in the ECMWF 4D-Var. Quart J Roy Meteor Soc, 138(667):1540-1559 |
| Buehner M, Charron M. 2007. Spectral and spatial localization of background-error correlations for data assimilation. Quart J Roy Meteor Soc, 133(624):615-630 |
| Derber J, Bouttier F. 1999.A reformulation of the background error covariance in the ECMWF global data assimilation system. Tellus A, 51(2):195-221 |
| Fisher M. 2003. Background error covariance modeling//Proceedings of the ECMWF Seminar on Recent Developments in Data Assimilation for Atmosphere and Ocean. Reading, UK:ECMWF, 45-63 |
| Fisher M. 2004. On the equivalence between the Kalman smoother and long-window, weak-constraint 4D-Var//Proceedings of the Sixth Workshop on Adjoint Applications in Dynamic Meteorology. Maratea (It.), 45-64 |
| Hamill T M, Snyder C, Whitaker J S. 2003.Ensemble forecasts and the properties of flow-dependent analysis-error covariance singular vectors. Mon Wea Rev, 131(8):1741-1758 |
| Isaksen L, Bonavita M, Buizza R, et al. 2010. Ensemble of data assimilations at ECMWF. European Centre for Medium-Range Weather Forecasts, Technical Memorandum No. 636(http://www.ecmwf.int/en/elibrary/10125-ensemble-data-assimilations-ecmwf) |
| Ingleby N B. 2001. The statistical structure of forecast errors and its representation in The Met Office Global 3-D Variational Data Assimilation Scheme. Quart J Roy Meteor Soc, 127(571):209-231 |
| Lorenc A C. 2003.The potential of the ensemble Kalman filter for NWP:A comparison with 4D-Var. Quart J Roy Meteor Soc, 129(595):3183-3203 |
| Liu C S, Xiao Q N, Wang B. 2008. An ensemble-based four-dimensional variational data assimilation scheme. Part Ⅰ:Technical formulation and preliminary test. Mon Wea Rev, 136(9):3363-3373 |
| Mallat S, Papanicolaou G, Zhang Z F. 1998. Adaptive covariance estimation of locally stationary processes. Ann Statist, 26(1):1-47 |
| Pannekoucke O, Berre L, Desroziers G. 2008. Background-error correlation length-scale estimates and their sampling statistics. Quart J Roy Meteor Soc, 134(631):497-508 |
| Parrish D F, Derber J C. 1992.The national meteorological center's spectral statistical-interpolation analysis system. Mon Wea Rev, 120(8):1747-1763 |
| Pereira M B, BerreL. 2006. The use of an ensemble approach to study the background error covariances in a global NWP Model. Mon Wea Rev, 134(9):2466-89 |
| Qiu C, Chou J. 2006. Four-dimensional data assimilation method based on SVD:Theoretical aspect. Theor Appl Climatol, 83(1-4):51-57 |
| Raynaud L, Berre L, Desroziers G. 2011. An extended specification of flow-dependent background error variances in the Météo-France global 4D-Var system. Quart J Roy Meteor Soc, 137(656):607-619 |
| Raynaud L, Berre L, Desroziers G. 2009. Objective filtering of ensemble-based background-error variances. Quart J Roy Meteor Soc, 135(642):1177-1199 |
| Rabier F, Thépaut J N, Courtier P. 1998. Extended assimilation and forecast experiments with a four-dimensional variational assimilation system. Quart J Roy Meteor Soc, 124(550):1861-1887 |
| Varella H, Berre L, and Desroziers G. 2011. Diagnostic and impact studies of a wavelet formulation of background-error correlations in a global model. Quart J Roy Meteor Soc, 137(658):1369-1379 |
| Weaver A, Courtier P. 2001. Correlation modelling on the sphere using a generalized diffusion equation. Quart J Roy Meteor Soc, 127(575):1815-1846 |
 2016, Vol. 74
2016, Vol. 74