中国气象学会主办。
文章信息
- 景丞, 姜彤, 王艳君, 陈静, 蹇东南, 罗岚心, 苏布达 . 2016.
- JING Cheng, JIANG Tong, WANG Yanjun, CHEN Jing, JIAN Dongnan, LUO Lanxin, SU Buda . 2016.
- 中国区域性极端降水事件及人口经济暴露度研究
- A study on regional extreme precipitation events and the exposure of population and economy in China
- 气象学报, 74(4): 572-582.
- Acta Meteorologica Sinica, 74(4): 572-582.
- http://dx.doi.org/10.11676/qxxb2016.037
-
文章历史
- 2015-12-18 收稿
- 2016-04-02 改回
2. 中国气象局国家气候中心, 北京, 100081;
3. 中国科学院新疆生态与地理研究所, 荒漠与绿洲生态国家重点实验室, 乌鲁木齐, 830011;
4. 中国气象科学研究院, 北京, 100081
2. National Climate Center, China Meteorological Administration, Beijing 100081, China;
3. State Key Laboratory of Desert and Oasis Ecology, Xinjiang Institute of Ecology and Geography, Chinese Academy of Sciences, Urumqi 830011, China;
4. Chinese Academy of Meteorological Sciences, Beijing 100081, China
近百年来, 随着工业水平不断提高, 全球气温成持续上升的趋势。气候变化所带来的风险逐渐成为影响全球安全与发展的重大挑战。IPCC AR5(IPCC, 2013)指出, 1880—2012年全球平均气温升高0.85℃。伴随着全球气温的上升, 地表蒸发量增大, 空中含水量增大, 全球和区域水循环增强, 使得极端降水事件发生的概率有所增大。极端降水事件作为影响中国最为广泛的灾害性事件之一, 对人民生命财产和自然环境造成了极大的影响, 每年因暴雨洪涝造成的经济损失达气象灾害造成总经济损失的37.2%, 死亡的人数占灾害总数的11.7%(秦大河等, 2015)。因此, 对于极端降水事件的演变规律及暴露度研究具有十分重要的科学和现实意义。
早期的极端降水阈值选取主要采取绝对阈值法, 如, Groisman(1999)采用25.4和50.8 mm作为极端降水阈值;中国气象部门规定50—100 mm/d为暴雨, 不小了100 mm/d为大暴雨等。而灾害事件的致灾性不仅取决于灾害事件本身的物理特征, 还受地理环境、基础设施、居民意识等因素影响, 在干旱半干旱区, 一次不大的降水事件就有可能引发洪涝、滑坡、泥石流等灾害(黄建平等, 2014), 对于这类地区, 50 mm/d暴雨阈值已无法反映降水的极值情况。一些学者采用百分位法定义极端降水, 如, Plummer等(1999)提出采用日降水量的99百分位值作为强降水的阈值, 翟盘茂等(2003)利用降水序列的第99个百分位值的多年平均值作为极端降水事件的阈值, 潘敖大等(2010)将逐年湿日(日降水量不小于0.1 mm)降水量序列的第95个百分位值的多年平均值作为极端降水的阈值等。
目前对极端降水的演变规律研究多采用单站阈值(翟盘茂等, 1997;严中伟等, 2000;Groisman et al, 2005;杨金虎等, 2008;王志福等, 2009, 赵丽等, 2014)。有学者提出采用某站发生极端事件时中国其余台站发生极端事件的概率, 或某站发生极端降水事件时, 其周边出现极端降水可能性较大的台站数等指标研究区域性极端事件(黄丹青等, 2009;闵屾等, 2008);一些学者基于空间聚类方法, 或划定一定区域内多站超过降水阈值定义区域性或群发性事件, 并将事件的持续时间与影响范围联系起来, 识别中国的区域性极端降水(Tu et al, 2011;Ren et al, 2012;Chen et al, 2013;Zou et al, 2015)。
本研究利用1960—2014年中国771个地面观测站的逐日降水数据, 将既定持续时间尺度和连续面积上达到阈值的降水事件定义为区域性极端降水事件。以降水事件的极端程度作为相对强度, 通过建立强度-面积-持续时间(Intensity-Area-Duration, IAD)分析方法, 对1960—2014年中国区域性极端降水事件的相对强度、影响面积、最强中心进行研究, 并基于历次事件的影响面积, 将暴露于极端降水事件范围内的人口和国内生产总值作为人口经济的暴露度指标, 初步开展了中国人口经济对区域性极端降水事件的暴露度研究。
2 数据与方法 2.1 数据基于中国气象局国家气象信息中心整编的1960—2014年全国916个基准站的日降水数据, 选取其中的771个站作为研究对象(图 1)。选站标准为:将各站逐年资料缺测>5%(18 d/a)的年份作为无效年, 无效年不超过总年数的5%(3 a)的站予以保留。
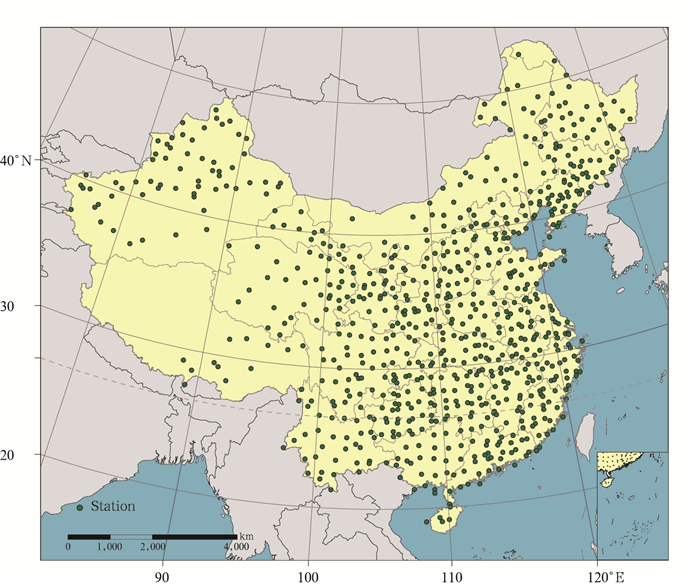
|
| 图 1 气象站空间分布 Figure 1 Location distribution of meteorological stations |
将中国大陆地区划分为4140个0.5°×0.5°的格点, 选用2010年中国第6次人口普查数据和2010年中国各省统计年鉴中县域人口和国内生产总值(GDP)数据, 按照各格点面积与所在县面积比值计算格点人口、国内生产总值, 得到中国大陆地区0.5°×0.5°的社会经济格点数据。为分析因极端降水事件演变而造成的社会经济暴露程度的变化, 假定社会经济维持在2010年的水平, 初步探讨暴露于极端降水事件下的人口、国内生产总值的演变规律。
2.2 方法 2.2.1 距平逼近值法考虑到日降水量在空间分布上具有很大的不连续性, 简单对要素场进行插值误差较大, 采用距平逼近法(New et al, 2000)进行插值, 其步骤为:首先利用ANUSPLIN软件, 采用薄板样条(TPS, Thin-plate splines)方法(Wahba, 1979;Hutchinson, 1995)对气候场进行插值, 并将海拔高度作为协变量, 以减少地形对插值结果的影响;第二步采用角距权重(ADW, Angular Distance Weighting)法(Shepard, 1984)对距平场进行插值, 主要考虑站点与格点之间角度与距离的权重;最后将气候场与距平场叠加得到格点化降水数据。此方法被应用于CRU(Climatic Research Unit)数据集的插值, 能够较好地反映日降水量的实际分布情况(Xu et al, 2009;吴佳等, 2013)。
2.2.2 极端降水阈值与相对强度为研究连续面积上的区域性降水事件, 利用距平逼近法将全中国台站降水插值到0.5°×0.5°的格点上, 定义每个格点上日降水量大于1 mm的值为有效降水, 选取1960—2014年逐年有效降水量序列第95百分位数的55 a平均值作为该格点极端降水的阈值。分别选取每个格点上持续3、5、7 d均为有效降水的序列做滑动累加, 将累加序列第95百分位数的55 a平均值分别作为持续3、5、7 d降水的极端事件阈值, 以分析持续多日的降水极值事件。计算百分位数采用Bonsal(2001)提出的方法, 即将序列中所有值按升序排列a1, a2, …, am…an, 序列中某值不大于am的概率
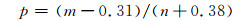
|
(1) |
式中, m为am的序号, n为样本数。若样本数为40, 则序列第95百分位数为升序排列后第38个值a38(p=93.3%)和第39个值a39(p=95.8%)的线形插值。此方法计算简便, 且不受样本数和样本分布的影响, 得到广泛的应用(翟盘茂等, 2003;杨金虎等, 2008)。
考虑到不同区域间降水量的差异, 降水量超过极端降水阈值的倍数作为评估区域性极端降水事件强弱的指标, 以反映降水事件的极端程度, 即所采用的相对强度。设每天每个格点上的降水量为P, 该格点阈值为T, 则定义该格点该日相对强度I=(P-T)/T, 低于阈值的格点相对强度为0;对于持续多日的极端降水, 定义多日总降水量为Pd, 多日极端降水阈值为Td, 则多日极端降水相对强度Id=(Pd-Td)/Td。
2.2.3 强度-面积-持续时间(IAD)方法改进Andreadis等(2005)创建的SAD方法(Severity-Area-Duration), 将极端事件的3个重要特征:强度、影响面积、持续时间联系起来, 选取既定时间尺度和连续面积上大于阈值的格点集合形成一次事件, 其中, 既定时间尺度指在这一尺度的时段内某一格点上持续发生了有效降水且降水总量超过了相应的极端降水阈值, 连续面积指在同一时段, 相邻格点上发生了超过阈值的降水, 强度则选用相对强度。改进后的方法称为强度-面积-持续时间(IAD)法。IAD方法可以针对区域性的极端降水事件, 研究既定持续时间下事件相对强度与影响面积的联系和变化, 并能通过包络线的形式对最强的区域性极端降水事件进行判别分析。具体步骤如下:
(1)提取事件范围, 首先, 选取既定时间尺度(1、3、5、7 d), 计算研究区域内所有格点各时段的降水总量和相对强度, 将区域内相对强度最大的格点作为一次区域性极端降水事件的“最强中心”, 并记录其相对强度与影响面积(图 2a);第二, 在当前时段内“最强中心”周围8个网格中寻找次强的格点, 将其与“最强中心”集合形成一个“次强中心”, 记录其相对强度和影响面积(图 2b), 其相对强度为所涉及连续格点相对强度的平均值, 面积为格点面积之和;第三, 继续寻找“次强中心”周围格点上的相对强度次强格点并记录相对强度与影响面积, 直至该连续面积上不再有超过阈值的格点, 则将该连续面积上所有格点集合形成一次区域性极端降水事件(图 2c、d);第四, 重新寻找其他“最强中心”, 重复上述步骤, 可找出当前时间尺度下所有区域性极端降水事件(图 2e)。
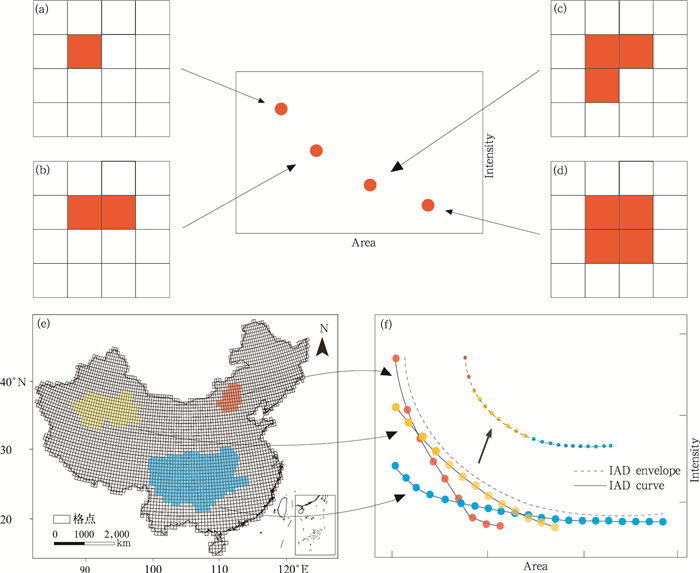
|
| 图 2 IAD曲线绘制过程 Figure 2 The construction of Intensity-Area-Duration (IAD) curve |
(2)构建IAD曲线, 将事件提取过程中所有记录的反映相对强度与面积关系的点相连接, 绘制成对应的一条反映面积和相对强度关系的曲线;选取同一时间尺度下所有事件曲线, 将不同影响面积上相对强度最大的点相连, 形成一条所有事件曲线最上方的包络曲线(图 2f), 即IAD包络线, 以反映既定持续时间和不同影响面积上, 极端降水事件能够达到的最大相对强度。
2.2.4 Mann-Kendall(M-K)非参数检验方法Mann-Kendall(M-K)检验方法(Mann, 1945;Kendall, 1975)是一种常用的对于时间序列趋势的非参数检验方法, 在水文、气象等方面有着广泛的应用(Tao et al, 2011;Gemmer et al, 2011)。文中采用M-K趋势检验法进行了极端降水事件的变化趋势分析。
3 区域性极端降水事件分析 3.1 极端降水空间分布图 3是1960—2014年中国多年平均极端降水日数空间分布, 年极端降水日数分布与降水量分布基本相似, 从东南向西北递减, 大值区主要分布在长江以南地区, 一般大于7 d, 最大值位于云南省西北部, 平均每年近13 d出现极端降水, 小值区主要位于西北地区, 一般小于1 d, 南疆最小值仅0.36 d。中国极端降水日数变化分布(图 4)与中国的干湿变化趋势相似, 极端降水日数明显减少的区域主要位于东北、华北和西南地区, 从东北到西南成带状分布, 极端降水日数明显增加的区域主要位于西北地区和东南沿海地区, 其中西北地区的增加趋势最为明显。
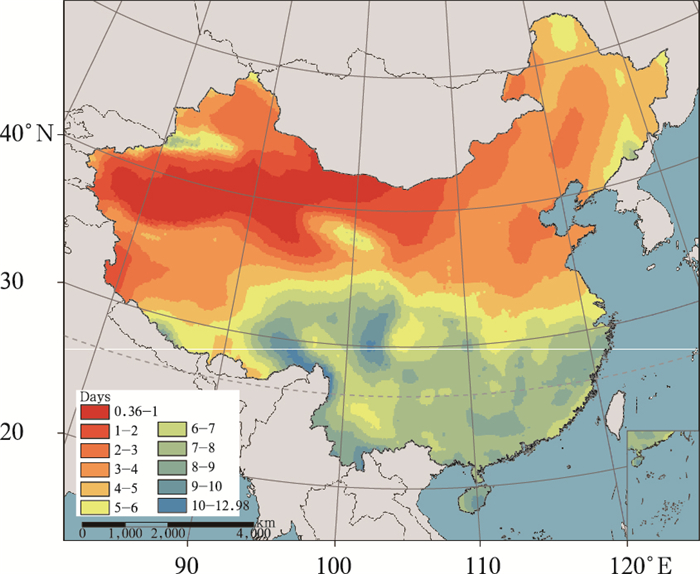
|
| 图 3 多年平均极端降水日数分布 Figure 3 The distribution of frequency of annual extreme precipitation event |
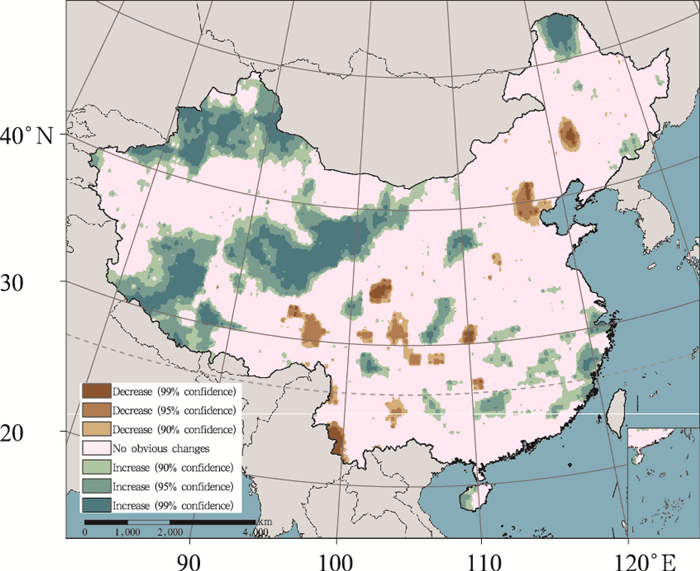
|
| 图 4 年极端降水日数变化趋势 Figure 4 Trends of frequency of annual extreme precipitation event |
1960—2014年不同时间尺度区域性极端降水事件的IAD包络线(图 5)显示, 极端降水事件相对强度最大的几个时段主要在1960—1968、1991—1999和2006—2013年。其中, 1 d的极端降水包络线主要由4个时段的事件组成, 影响面积为0—5万km2的最强事件发生在2010和2013年, 影响面积为5万—10万km2的最强事件发生在1965年, 影响面积10万—72万km2的最强事件主要发生在1994年, 影响面积72万—99万km2的最强事件发生在1981年;持续3 d的极端降水包络线主要由3个时段的事件组成, 影响面积0—14万km2的最强事件主要发生在2010和2013年, 影响面积14万—40万km2的最强事件发生在2006年, 影响面积40万—58万km2的最强事件发生在1968年;持续5 d的极端降水包络线主要由3个事件组成, 影响面积0—7万km2的最强事件发生在2010年, 影响面积7万—15万km2的最强事件发生在1963年, 影响面积在15万—44万km2的最强事件发生在1994年;持续7 d的极端降水包络线主要由3个时段的事件组成, 影响面积0—7万km2的最强事件发生在2010年, 影响面积7万—36万km2的最强事件主要发生在1998和1999年, 影响面积36万—42万km2的最强事件发生在1966年。
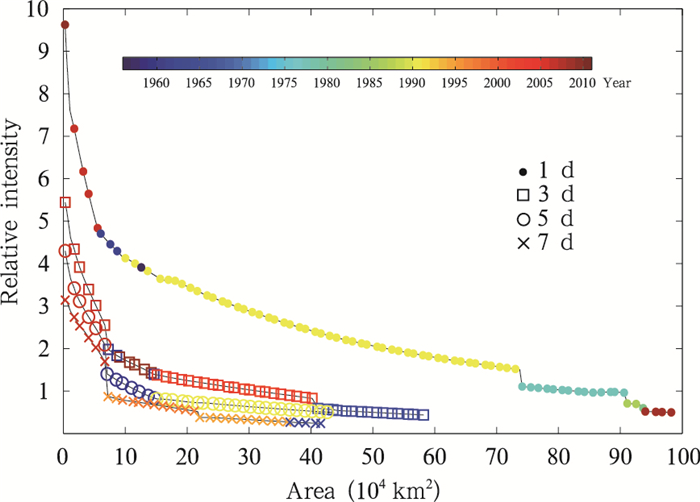
|
| 图 5 1960—2014年不同时间尺度极端降水IAD包络线 Figure 5 The IAD envelope of extreme precipitation events with different durations between 1960 and 2014 |
仅从影响面积上看, 不同持续时间下, 影响面积最大的极端降水事件为1 d事件, 发生在2012年9月1日, 达到98.7万km2, 持续3、5、7 d极端降水事件的最大影响面积分别在1968年8月3日达到58.2万km2, 1994年6月5日达到43.8万km2, 1966年8月28日达到41.6万km2。仅从事件相对强度上看, 不同持续时间下, 中心点相对强度最大的区域性极端降水事件均发生在2010年以后, 1 d降水和持续3、5、7 d最强事件中心点降水量分别达到其极端降水阈值的10.6、6.4、5.3、4.1倍。
1960—2014年区域性极端降水事件包络线所包含的事件中心的分布(图 6)显示, 1960—1968年事件中心主要分布在东北、华北和西南地区, 1991—1999年事件中心主要分布在华南和华东地区, 2006—2013年, 事件中心偏南, 主要分布在华南和西南地区, 其中大部分事件中心集中在海南省;持续时间上, 单日极端降水事件中心主要在四川中部和辽宁东部, 这里降水波动性大, 易形成短期的极端降水。持续多日的极端降水事件中心主要在江苏、广东、广西、云南、海南等地, 这里水汽充沛, 天气系统复杂, 易形成持续时间较长的极端降水。
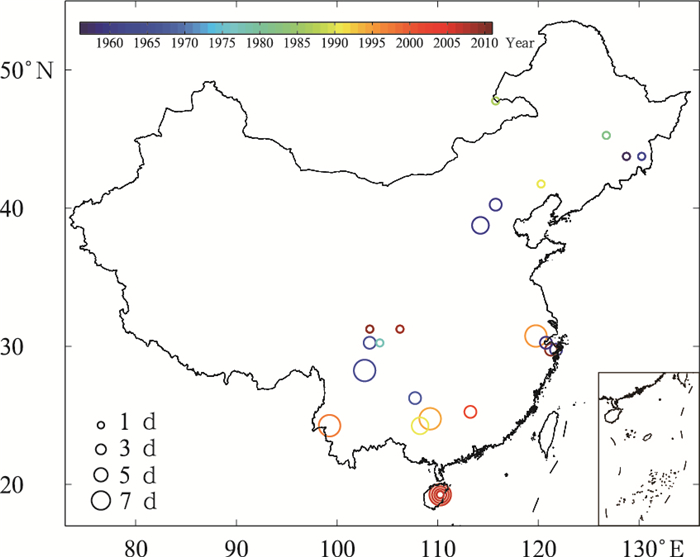
|
| 图 6 1960—2014年极端降水事件最强中心分布 Figure 6 Spatial distribution of the maximum intensity centers of extreme precipitation events during 1960-2014 |
图 7为1960—2014年所有1 d区域性极端降水事件的影响面积和相对强度变化趋势。可见, 区域性极端降水事件的影响面积有显著的增大(其M-K统计量为1.99, 达到95%信度水平), 尤其在1995年以后, 影响面积较大的年份明显增多, 其中, 最大的年份在1998年, 平均每日达到15.4万km2, 其次为2010年, 平均每日达到14.3万km2, 这两年中国范围内均发生了罕见的大洪水。55年来, 极端降水事件相对强度呈现不显著的增大趋势(其M-K统计量为0.25), 相对强度最大的年份在2007年, 为0.49, 表示每次事件日降水量超过阈值近50%, 相对强度最小的年份在1980年, 为0.34。
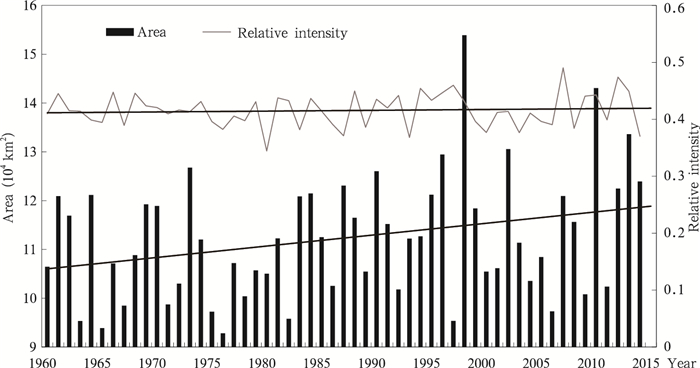
|
| 图 7 1960—2014年极端降水事件影响面积和相对强度变化 Figure 7 Trends of the areal coverage and relative intensity of extreme precipitation events during 1960-2014 |
为探究区域性极端降水事件可能带来的最大影响, 选取所有时间尺度为1 d的事件, 以2010年社会经济水平为基准, 绘制了暴露于极端降水事件影响区域内的人口和国内生产总值的散点图(图 8)。1960—2014年, 有16%的事件暴露人口超过了1000万, 378次事件暴露人口超过了1亿。共有3次事件暴露人口超过2.5亿, 暴露人口最多的事件发生在2013年5月6日, 最强中心位于湖北省, 暴露人口2.8亿, 占全国总人口的20.1%, 影响面积59.4万km2。另外两次发生在2003和1969年, 最强中心均位于北京市, 影响面积均大于50万km2(图 8a)。
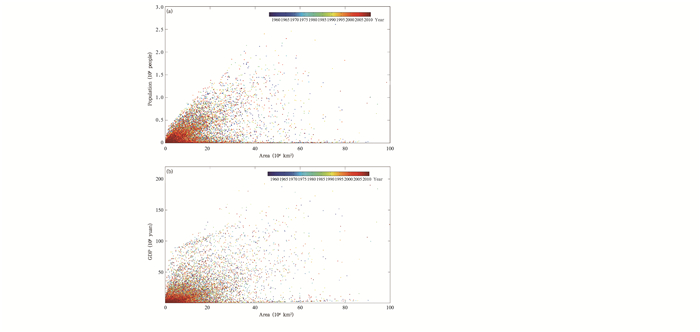
|
| 图 8 1960—2014年暴露于极端降水事件影响区域内的人口(a)、国内生产总值(b)散点图 Figure 8 Scatter plot of the population (a) and GDP (b) exposed to extreme precipitation events during 1960-2014 |
图 8b显示, 13%的事件暴露国内生产总值超过了10亿元, 247次事件超过了100亿元。共有两次事件暴露国内生产总值高于190亿元, 一次发生在1983年, 暴露国内生产总值达197亿元, 占全国国内生产总值总量的15.8%, 最强中心位于湖北省, 另一次发生在1997年, 暴露国内生产总值为192亿元, 最强中心位于江苏省。
当影响面积小于50 km2时, 人口与国内生产总值散点图分布有所不同, 人口图呈锥形发散, 暴露人口较多的事件影响面积一般较大;国内生产总值与面积的关系不明显, 而是更多的受最强中心所处区域经济状况的影响, 如1995年发生在广东省的极端降水事件, 暴露于事件影响范围的国内生产总值达到了82.2亿元, 而面积仅为2.5万km2。当影响面积大于50 km2时, 暴露于极端降水事件的人口和国内生产总值均表现出无规律的分布, 许多事件尽管有着很大的影响面积, 但因事件发生的区域人口较少, 经济落后, 暴露于事件的人口或国内生产总值并不多, 如1970年发生在新疆南部的极端降水事件, 面积达89万km2, 但暴露人口仅207万;1976年发生在西藏南部的极端降水事件暴露面积达到了90万km2, 但暴露国内生产总值仅4.4亿元。
选取20世纪60、70、80、90和21世纪初5个年代, 绘制不同年代, 反映不同影响面积上人口和国内生产总值暴露度最大值的包络曲线(图 9a、c)。20世纪60年代的事件影响面积在75万km2时暴露人口达到最多, 在63万km2时暴露国内生产总值最大;70年代和80年代的事件在50万km2上暴露人口和经济均达到最大;20世纪90年代的事件影响面积在52万km2时暴露人口达到最多, 在42万km2上暴露国内生产总值达到最大;21世纪初的事件影响面积在59万km2时暴露人口就可达2.8亿, 影响面积在90万km2时暴露国内生产总值最大。
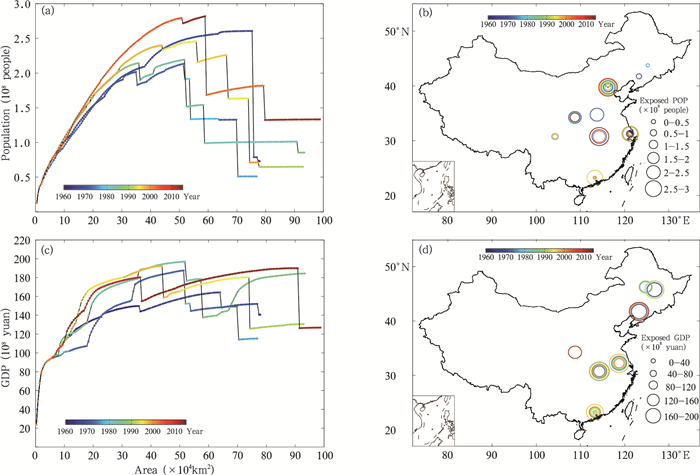
|
| 图 9 不同年代人口(a)、国内生产总值(c)暴露度包络线和构成包络线的事件位置(b、d) Figure 9 The envelopes of the population(a) and GDP(a) exposed to extreme precipitation events in different time and the locations of the events that constitute the envelopes(b, d) |
从不同年代构成包络线的事件位置看(图 9b、d), 暴露人口较多的事件主要分布在华东和华北, 其中20世纪60年代暴露人口较多的事件主要在东北和华北地区, 70和80年代则主要在华东、华中、华北, 90年代暴露人口较多的事件偏南, 主要分布在华南、西南、华东, 到21世纪初与20世纪70、80年代相似, 主要分布于华东、华中、华北;暴露国内生产总值较多的事件更为集中地分布于东北、华北和华南, 其中60年代的事件主要在东北, 70年代主要在华东, 80年代暴露国内生产总值最多的事件发生在东北, 90年代与暴露人口相似, 主要分布于华东和华南, 到21世纪初, 在华东、华中、华北均发生了暴露国内生产总值较大的事件。
逐年暴露于极端降水事件影响区域内的人口和国内生产总值(图 10)。1960—2014年, 暴露人口和国内生产总值均成显著增大趋势。暴露人口最多的年份在1983年, 平均为2408万人/d, 其次是1998年, 平均为2375万人/d, 最少的年份出现在1978年, 平均为1464万人/d。从年代际上看, 暴露于极端降水事件影响区域内的人口在20世纪70年代最少, 此后一直到21世纪初均成上升趋势, 进入21世纪后有所减少, 其中20世纪90年代暴露人口最多, 平均为1973万人/d。暴露于极端降水事件影响区域内的国内生产总值最大的年份在1998年, 达到20亿元/d, 其次是1983年, 为19.2亿元/d, 暴露国内生产总值最小的年份为1969年, 为16.9亿元/d。暴露于极端降水事件影响区域内的国内生产总值在年代际上变化与暴露人口的变化相似, 均表现为先减少再增加, 至2000年以后有所减少的态势。
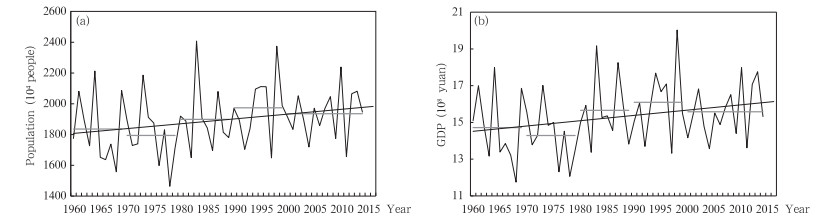
|
| 图 10 1960—2014年暴露于极端降水事件影响区域内的人口(a)和GDP(b) Figure 10 Population(a) and GDP(b) exposed to extreme precipitation events during 1960-2014 |
根据中国1960—2014年771个气象站的逐日观测降水, 将既定持续时间和连续面积上的超过阈值的极端降水事件定义为区域性极端降水事件, 采用强度-面积-持续时间(IAD)法, 对区域性极端降水事件极端程度、影响面积、最强中心进行了分析。并利用人口和GDP格点数据, 探讨了区域性降水事件对社会经济的可能影响。得到以下结论:
(1) 区域性极端降水事件相对强度最大的几个时段主要在1960—1968、1991—1999和2006—2013年。其中, 影响面积最大的1 d极端降水事件发生在2012年, 达到98.7万km2, 持续3、5、7 d极端降水事件的最大影响面积分别为58.2万、43.8万、41.6万km2。
(2) 仅从事件相对强度上看, 中心点相对强度最大的区域性极端降水事件均发生在2010年以后。1、3、5、7 d的最强区域性极端降水事件, 最大降水量分别达到其极端降水阈值的10.6、6.4、5.3、4.1倍。最强中心主要分布在长江以南和东北地区, 其中单日极端降水事件最强中心主要在四川中部和辽宁东部, 持续多日的极端降水事件最强中心主要在江苏、广东、广西、云南、海南等地。
(3) 1960—2014年区域性极端降水事件的影响面积成显著的增大趋势(95%信度水平), 尤其在1995年以后影响面积较大的年份明显增多, 其中, 最大的年份在1998年, 平均每天达到15.4万km2。55年来, 极端降水事件相对强度成不显著的增大趋势, 平均相对强度最大的年份在2007年, 为0.49, 表示每次事件日降水量超过阈值近50%。
(4) 1960—2014年, 暴露在极端降水事件影响区域的人口和国内生产总值变化情况基本相同, 均成显著增加趋势, 暴露人口最多的年份在1983年, 平均为2408万人/d, 暴露国内生产总值最多的年份在1998年, 平均为20亿元/d。年际变化上, 暴露在极端降水事件区域的人口和国内生产总值均在20世纪70年代有所降低, 后一直到21世纪初均成上升趋势, 在2000年以后有所减少。
采用的IAD方法主要基于格点降水数据, 利用距平逼近法虽能一定程度上减少格点插值带来的误差, 但在青藏高原和塔里木河地区可能对降水量有一定程度的高估, 带来一定的不确定性。区域性极端降水事件的成因及相关环流机制仍需通过进一步研究加以分析。通过IAD方法能够准确地找出区域性极端事件发生的时间和范围, 但还需通过与历史资料中具体事件记录进行对比与验证。此外, 未来气候变化环境下极端降水事件演变及其对流域水文资源的影响也是下一步研究重点问题。
| 黄丹青, 钱永甫. 2009. 极端温度事件区域性的分析方法及其结果. 南京大学学报(自然科学) , 45 (6) : 715–723. Huang D Q, Qian Y F. 2009. An analysis method for regional characteristics of extreme temperature and results. J Nanjing Univ (Nat Sci) , 45 (6) : 715–723. (in Chinese) |
| 黄建平, 冉津江, 季明霞. 2014. 中国干旱半干旱区洪涝灾害的初步分析. 气象学报 , 72 (6) : 1096–1107. Huang J P, Ran J J, Ji M X. 2014. A preliminary analysis of flood disasters in the arid and semi-arid regions of China. Acta Meteor Sinica , 72 (6) : 1096–1107. (in Chinese) |
| 闵屾, 钱永甫. 2008. 中国极端降水事件的区域性和持续性研究. 水科学进展 , 19 (6) : 763–771. Min S, Qian Y F. 2008. Regionality and persistence of extreme precipitation events in China. Adv Water Sci , 19 (6) : 763–771. (in Chinese) |
| 潘敖大, 范苏丹, 陈海山. 2010. 江苏省近45 a极端气候的变化特征. 气象科学 , 30 (1) : 87–92. Pan A D, Fan S D, Chen H S. 2010. Characteristics of changes in extreme climate over Jiangsu Province in the last 45 a. Scientia Meteor Sinica , 30 (1) : 87–92. (in Chinese) |
| 秦大河, 张建云, 闪淳昌, 等. 2015. 中国极端天气气候事件和灾害风险管理与适应国家评估报告. 北京: 科学出版社 : 66pp . Qin D H, Zhang J Y, Shan C C, et al. 2015. China National Assessment Report on Risk Management and Adaptation of Climate Extremes and Disasters. Beijing: Science Press : 66pp . |
| 王志福, 钱永甫. 2009. 中国极端降水事件的频数和强度特征. 水科学进展 , 20 (1) : 1–9. Wang Z F, Qian Y F. 2009. The frequency and intensity of extreme precipitation event in China. Adv Water Sci , 20 (1) : 1–9. (in Chinese) |
| 吴佳, 高学杰. 2013. 一套格点化的中国区域逐日观测资料及与其它资料的对比. 地球物理学报 , 56 (4) : 1102–1111. Wu J, Gao X J. 2013. A gridded daily observation dataset over China and its comparison with the other datasets. Chin J Geophys , 56 (4) : 1102–1111. (in Chinese) |
| 严中伟, 杨赤. 2000. 近几十年中国极端气候变化格局. 气候与环境研究 , 5 (3) : 267–272. Yan Z W, Yang C. 2000. Geographic patterns of extreme climate changes in China during 1951-1997. Climatic Environ Res , 5 (3) : 267–272. (in Chinese) |
| 杨金虎, 江志红, 王鹏祥, 等. 2008. 中国年极端降水事件的时空分布特征. 气候与环境研究 , 13 (1) : 75–83. Yang J H, Jiang Z H, Wang P X, et al. 2008. Temporal and spatial characteristics of extreme precipitation event in China. Climatic Environ Res , 13 (1) : 75–83. (in Chinese) |
| 翟盘茂, 任福民. 1997. 中国近四十年最高最低温度变化. 气象学报 , 55 (4) : 418–429. Zhai P M, Ren F M. 1997. Changes in China's maximum and minimum temperatures in the recent 40 years. Acta Meteor Sinica , 55 (4) : 418–429. (in Chinese) |
| 翟盘茂, 潘晓华. 2003. 中国北方近50年温度和降水极端事件变化. 地理学报 , 58 (S) : 1–10. Zhai P M, Pan X H. 2003. Changes in extreme temperature and precipitation over North China during the second half of the 20th century. Acta Geograph Sinica , 58 (S) : 1–10. (in Chinese) |
| 赵丽, 杨青, 韩雪云, 等. 2014. 1961-2009年新疆极端降水事件时空差异特征. 中国沙漠 , 34 (2) : 550–557. Zhao L, Yang Q, Han X Y, et al. 2014. Spatial and temporal differences in extreme precipitation during 1961-2009 in Xinjiang, China. J Desert Res , 34 (2) : 550–557. (in Chinese) |
| Andreadis K M, Clark E A, Wood A W, et al. 2005. Twentieth-century drought in the conterminous United States. J Hydrometeorol , 6 (6) : 985–1001. DOI:10.1175/JHM450.1 |
| Chen Y, Zhai P M. 2013. Persistent extreme precipitation events in China during 1951-2010. Climate Res , 57 (2) : 143–155. DOI:10.3354/cr01171 |
| Gemmer M, Fischer T, Jiang T, et al. 2011. Trends in precipitation extremes in the Zhujiang River Basin, South China. J Climate , 24 (3) : 750–761. DOI:10.1175/2010JCLI3717.1 |
| Groisman P Y. 1999. Changes in the probability of extreme precipitation: Important indicators of climatic change. Climatic Change , 42 (1) : 243–283. DOI:10.1023/A:1005432803188 |
| Groisman P Y, Knight R W, Easterling D R, et al. 2005. Trends in intense precipitation in the climate record. J Climate , 18 (9) : 1326–1350. DOI:10.1175/JCLI3339.1 |
| Hutchinson M F. 1995. Interpolating mean rainfall using thin plate smoothing splines. Int J Geograph Inf Syst , 9 (4) : 385–403. |
| IPCC. 2013. Climate Change 2013: The Physical Science Basis. Working Group I Contribution to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change. Cambridge, UK, New York, USA: Cambridge University Press |
| Kendall M G. 1975. Rank Correlation Methods. London: Griffin . |
| Mann H B. 1945. Nonparametric tests against trend. Econometrica , 13 (3) : 245–259. DOI:10.2307/1907187 |
| New M, Hulme M, Jones P. 2000. Representing twentieth-century space-time climate variability. Part Ⅱ: Development of 1901-96 monthly grids of terrestrial surface climate. J Climate , 13 (13) : 2217–2238. |
| Plummer N, Salinger M J, Nicholls N, et al. 1999. Changes in climate extremes over the Australian region and New Zealand during the Twentieth Century. Climatic Change , 42 (1) : 183–202. DOI:10.1023/A:1005472418209 |
| Ren F M, Cui D L, Gong Z Q, et al. 2012. An objective identification technique for regional extreme events. J Climate , 25 (20) : 7015–7027. DOI:10.1175/JCLI-D-11-00489.1 |
| Shepard D S. 1984. Computer Mapping: The SYMAP Interpolation Algorithm//Gaile G L, Willmott C J. Spatial Statistics and Models. Netherlands: Springer , 40 : 133–145. |
| Tao H, Gemmer M, Bai Y G, et al. 2011. Trends of streamflow in the Tarim River Basin during the past 50 years: Human impact or climate change?. J Hydrol , 400 (1-2) : 1–9. DOI:10.1016/j.jhydrol.2011.01.016 |
| Tu K, Yan Z W, Wang Y. 2011. A spatial cluster analysis of heavy rains in China. Atmos Oceanic Sci Lett , 4 (1) : 36–40. DOI:10.1080/16742834.2011.11446897 |
| Wahba G. 1979. How to smooth curves and surfaces with splines and cross-validation//24th Conf. on Design of Experiments. New York: Academic Press, 167-192 |
| Xu Y, Gao X J, Shen Y, et al. 2009. A daily temperature dataset over China and its application in validating a RCM simulation. Adv Atmos Sci , 26 (4) : 763–772. DOI:10.1007/s00376-009-9029-z |
| Zou X K, Ren F M. 2015. Changes in regional heavy rainfall events in China during 1961-2012. Adv Atmos Sci , 32 (5) : 704–714. DOI:10.1007/s00376-014-4127-y |
 2016, Vol. 74
2016, Vol. 74


