中国气象学会主办。
文章信息
- 程昕, 王咏薇, 胡诚, 王伟, 张弥, 肖启涛, 刘寿东, 李旭辉 . 2016.
- CHENG Xin, WANG Yongwei, HU Cheng, WANG Wei, ZHANG Mi, XIAO Qitao, LIU Shoudong, LEE Xuhui . 2016.
- 应用E-ε湍流动能闭合湖泊热力学过程模型对东太湖湖-气交换的模拟
- The lake-air exchange simulation of a lake model over eastern Taihu Lake based on the E-ε turbulent kinetic energy closure thermodynamic process
- 气象学报, 74(4): 633-645.
- Acta Meteorologica Sinica, 74(4): 633-645.
- http://dx.doi.org/10.11676/qxxb2016.043
-
文章历史
- 2015-12-17 收稿
- 2016-04-24 改回
2. 南京信息工程大学大气物理学院, 南京, 210044;
3. 中国科学院大气物理研究所大气边界层物理和大气化学国家重点实验室, 北京, 100029
2. School of Atmospheric Physics, Nanjing University of Information Science and Technology, Nanjing 210044, China;
3. State Key Laboratory of Atmospheric Boundary Layer Physics and Atmospheric Chemistry, Institute of Atmospheric Physics, Chinese Academy of Sciences, Beijing 100029, China
湖泊是气候系统的重要组成部分, 湖-气交换对流域气候、局地天气和环流影响显著。湖泊对周围地区的气候起到调节作用(Krinner, 2003;Long et al, 2007;Samuelsson et al, 2010;Subin et al, 2012), 在中高纬度地区, 湖泊会对周围陆地在冬季产生加热效应, 春夏季出现冷却效应。湖泊会干扰地面天气尺度系统, 影响湖体周围区域的天气形势, 致使湖泊周围产生强降雪(Hjelmfelt, 1990;Hjelmfelt et al, 1983;Laird et al, 2009)、湖陆风(Lyons et al, 1976;Lyons, 1972)、湖心云带(Hjelmfelt, 1990)等短期和局部天气现象, 也会造成雷暴(King et al, 2003)等强对流天气的发生。湖泊的存在会导致周围区域的局地环流发生改变, 使周围城市的热岛效应增强(杨健博等, 2013);同时湖泊周围风场的变化影响空气中污染物的传播和扩散(Keen et al, 1978)。因此, 急需认识湖-气相互作用机理及相关的湖泊物理过程。
采用数值模式来研究湖-气交换过程是一种可行的手段。目前国际上已经发展的湖泊模式大都为一维模式(Goudsmit et al, 2002), 即假定湖泊在水平方向上状态均一, 只考虑湖泊水体在垂直方向上的水热输送。当前大量研究采用对于水体内部涡流扩散进行参数化处理的一维热扩散模式, 如Hostetler的湖模式(Hostetler et al, 1990)、Minlake(Riley et al, 1988)、CHEMSEE(Ulrich, 1991)、LIMNMOD(Karagounis et al, 1993)等, 此类模型的优点在于模型的输入量少, 通过仅有的数据即可模拟出湖泊的生物物理化学过程, 但模型过于经验化, 很难确定模型中的相关经验参数(Goudsmit et al, 2002)。水体的湍流混合运动是湖泊重要的物理过程, 对湖泊温热变化、动力分布状况都产生重要的影响, 因此, 引入湍流闭合方案的湖泊模式也逐步发展, 如拉格朗日DYRESM模型(Imberger et al, 1981)、PROBE(Huttula et al, 1992; Elo et al, 1998)、 GOTM(Burchard et al, 1999)和其他一些k-ε湍流闭合模型(Burchard et al, 1995)。引入湍流闭合方案模型的优势是具有更高的时间分辨率(Goudsmit et al, 2002), 适用于研究湖泊内部水体的传输过程, 较为精确地模拟出湖泊混合层的湍流运动, 而且可以对湖泊进行长时间的模拟, 可用于研究气候变化对湖泊内部垂直混合的影响以及湖体物理过程和生物化学过程的交互作用。
中国湖泊模型也有一定的发展。周从直等(1994)、孙菽芬等(2008)应用一维涡流扩散模型估算湖泊水温, 王浩(1991)应用数值模式模拟出湖陆风的双环流现象, 指出在湖中心产生湖风和陆风, 然后扩展向两岸。Deng等(2013)利用气象数据驱动离线湖泊模型, 模拟浅湖湖泊的水热通量状况。古红萍等(2013)将一维湖泊模式耦合到WRF(Weather Research and Forecasting Model)中, 评估耦合模式模拟的湖温、湖冰及湖泊影响的降水。任晓倩等(2014)在湖泊模型的浅湖部分引入底部沉积层模块, 并较好地模拟出了洱海的水热变化。在当前全球气候异常的大环境背景下, 运用数值模式研究中国湖泊陆面过程对周围区域的影响, 具有不可替代的意义。
太湖是中国第三大淡水湖, 总面积2338 km2, 平均水深1.9 m。对太湖已有的研究中, Deng等(2013)、朴美花(2014)、古红萍等(2013)均采用对水体内部涡流扩散进行参数化处理的一维热扩散模式, 对太湖的湖温、热通量进行模拟。模拟结果表明, 太湖由于其湖水较浅, 具有与深水湖泊完全不同的水气交换特征。主要表现在湖-气通量的交换受到天气状况显著的影响, 具有明显的季节及日变化特征。同时, 水生植物作为湖泊生态系统的一部分, 对湖泊的物理、化学性质存在很大的影响。沉水植物作为水生群落的一部分, 可以改善水质, 修复生态系统(Nes et al, 2003);沉水植物能够减小沉积物的再悬浮(Horppila et al, 2003), 增强湖泊温度分层强度(Dale et al, 1977)等。太湖其湖-气交换也受到湖体中水生植物影响(Xiao et al, 2013), 太湖东部生长着大量的沉水植物, 由于沉水植物的存在, 东太湖的动量交换系数比西太湖低42%左右。湖泊中沉水植物也会改变湖水的透光性, 从而影响热量在湖体中的传输。但是当前已有的针对太湖的模拟研究工作中, 应用的湖模式并没有引入湍流闭合化方案, 也没有考虑到沉水植物对湖-气交换的影响。
基于以上研究背景, 本研究采用E-ε湍流动能闭合湖泊热力学过程模型(Herb et al, 2005), 对2013年8月东太湖沉水植物密集区域的湖-气交换进行模拟, 拟初步探索以下几个问题:(1)该E-ε模型是否能够准确模拟出东太湖的湖-气交换过程?(2)湖体湍流动能对于湖水热分层的影响?(3)湖体沉水植物的分布对水温存在怎样的影响?
2 观测数据及模式介绍 2.1 研究区域太湖是典型的大型浅水湖泊。由于地区经济的发展, 水生态环境遭到严重破坏, 且蓝藻水华频发导致水质的下降, 使西太湖区域水生植物逐渐减少甚至消失;相比较而言, 东太湖湖区内水生植物较多, 主要为沉水植物, 包括微齿眼子菜、穗花狐尾藻和伊乐藻等(雷泽湘等, 2006)。由于采用的模型考虑了沉水植物对湖-气交换的影响, 因此, 选择东太湖作为研究区域。
2.2 观测站点驱动及验证所用的数据来自于太湖中尺度通量网(Lee et al, 2014)的避风港站(31°16′N, 120°39′E)。此站点2011年12月建立, 位于东太湖, 距离太湖东岸4 km。主要的观测仪器包括:(1)距湖面8.5 m的涡度相关系统, 由开路式红外气体分析仪(EC150, Campbell Scientific Inc., Logan, UT, USA)和三维超声风速仪(CSAT3, Campbell Scientific Inc., Logan, UT, USA)组成, 观测大气中水汽、CO2浓度和三维风速/超声温度, 采样频率为10 Hz, 由数据采集器(CR3000, Campbell Scientific Inc.)在线计算30 min平均动量通量、感热通量、潜热通量和CO2通量;(2)四分量辐射仪(CNR4, Kipp & Zonen B. V., Delft, The Netherlands), 用于观测向上长波辐射、向下长波辐射、向上短波辐射、向下短波辐射;(3)小气候系统, 由温、湿度传感器(HMP155A, Vaisala Inc. Helsinki, Finland)和风速风向传感器(05103, R M Young Company, Traverse City, Michigan, USA)组成, 观测距湖面8.5 m高度的气温、湿度、风速等气象要素;(4)水温梯度观测系统(109-L, Compbell Scientific Inc., Logan, UT, USA), 分别得到湖深20、50、100、150 cm和底泥温度。
2.3 涡度相关数据处理使用的观测数据为2013年8月通量数据、小气候观测的风速、气温、相对湿度, 辐射数据和水温梯度观测数据。涡度相关系统测得的通量数据后处理包括:降水时刻野点的剔除、两次坐标旋转(Lee et al, 2004)、超声虚温订正和WPL校正(Lee et al, 2011; Webb et al, 1980)。
2.4 模型介绍所用的模型为E-ε湍流动能闭合湖泊热力学过程模型, 此模型是由明尼苏达大学Herb等(2005)建立的, 适用于开阔水域或有沉水植物生长的浅水湖泊区域。模型建立的基础是将垂直方向上的热力传输方程与一维的湍流扩散方程相耦合, 并将湖中的沉水植物参数化, 计算出湖体的温度以及湖体的湍流动能。
该模型不考虑积雪层和湖底沉积层, 湖水深度设置为2 m, 湖水分为50层, 每30 min读入驱动数据, 模拟出每30 min的各层水温、湍流动能等。模型中的主要计算方案为
(1)湖水表面辐射及湍流通量计算方案
湖泊热通量的边界条件即湖表的热量通量
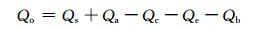
|
(1) |
式中, Qo为湖表热通量, Qs为湖表吸收的短波辐射, Qa为大气长波辐射, Qc为感热通量, Qe为潜热通量, Qb为向外长波辐射。其中, Qs的计算式为
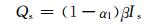
|
(2) |
式中, αl为湖水反照率, β为湖泊表层吸收太阳短波辐射的比例, Is为入射的太阳短波辐射。
大气长波辐射(Qa)和湖表向外长波辐射(Qb)分别用气温和湖温通过斯蒂芬-玻尔兹曼定律计算
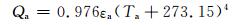
|
(3) |
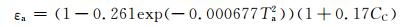
|
(4) |
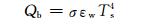
|
(5) |
式中, εa为大气辐射率, Ta为气温, Qc为云量, εw为湖水的辐射率, 取值为0.97, Ts为湖表温度, σ=5.6696×10-8W/(m2·K4), 是斯蒂芬-玻尔兹曼常数。
湖表的感热通量(Qc)和潜热通量(Qe)的计算式为
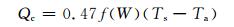
|
(6) |
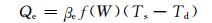
|
(7) |
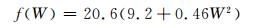
|
(8) |
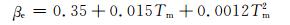
|
(9) |

|
(10) |
式中, W为风速, Td为露点温度。
(2)湖水温度的热扩散计算方案
运用垂直方向上的热力传输方程和一维的湍流扩散方程计算得到湖体的水温分布。垂直方向上的热力传输方程为
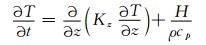
|
(11) |
式中, T为水温, t为时间, z为垂直坐标, Kz为湍流扩散系数, ρ为水的密度, cp为水的比热, H(z)为因太阳辐射产生的内部热量
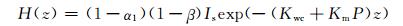
|
(12) |
式中, Kwc为水的消光系数, Km为因植物产生的消光系数, P为单位体积的植物生物量, α1为湖水反照率, β为湖泊表层吸收太阳短波辐射的比例。
(3)湖体E-ε闭合湍流动能计算方案
一维的湍流扩散方程表达式为
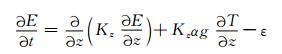
|
(13) |
式中, E为湍流动能, α为热扩散系数, g为重力加速度, ε为消散项
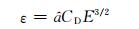
|
(14) |
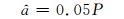
|
(15) |
式中, â为单位体积的植物表面积, CD为总的阻力系数, P为沉水植物生物量密度。
2.5 引入辐射观测数据和模型的下边界值文中基于Herb等(2005)原有的湖泊热力学过程模型, 又引入了辐射的观测数据和模型的下边界值:(1)湖泊模型驱动数据中, 引入了向下长波辐射和向外长波辐射的观测数据, 代替原模式中通过斯蒂芬-玻尔兹曼定律结合云量、湖表水温数据计算所得到的大气向下长波辐射和太湖表面向外长波辐射;(2)模式初始水温廓线由观测值给定;(3)模拟过程中, 引入湖水与底泥交界处的温度观测数据作为湖泊模型中水温计算的下边界值。在原模式中, Herb等(2005)模拟时将湖泊底泥与水交界处温度设为定值。当前的工作将该模式应用于太湖, 模拟较长时间尺度的湖体陆-气交换, 因此, 引入湖泊底泥与水交界处的温度观测值作为模式的下边界值。
2.6 研究时段及参数设置模拟算例时段为2013年8月1日00时—31日23时30分(北京时, 下同), 该时段东太湖沉水植物生长茂盛。
湖泊陆面过程模型中相关参数的设定对于模拟结果非常重要, 所用的模型中参数包括表征沉水植物相关参数以及湍流动能计算相关参数。然而模型中很多参数并无直接的观测值, 确定这些参数主要参考已有的文献。张运林等(2003, 2004)测定太湖水体的消光系数为1.5—4.6 m-1, 所以模型中消光系数(Kwc)的数值在此范围内调试确定。由于实验环境限制, 没有沉水植物生物量密度和沉水植物高度的观测数据。根据已有的关于东太湖水生植物生长的研究结果(雷泽湘等, 2006;何俊等, 2008), 了解东太湖水生植物生长状况, 设置模型中沉水植物生物量密度(P)、沉水植物高度(h)的参数值。表 1是该模型中相关参数的设置。
| 参数 | 物理量 | 数值(文献) |
| Kwc | 湖水的消光系数 | 2 m-1 |
| Km | 沉水植物的消光系数 | 0.02 m2 /gdw(Westlake,1964) |
| P | 沉水植物生物量密度 | 300 gdw/m3 |
| h | 沉水植物高度 | 1.2 m |
| d | 湖水深度 | 2 m |
| Ck | 混合长度系数 | 0.1 (Herb, et al, 2005) |
| CD | 阻力系数 | 1.0 (Finnigan, 2000) |
| Kh | 下层滞水带扩散率 | 0.03 m2 /d (Herb, et al, 2005) |
| Cw | 风修正系数 | 1.0 |
| nz | 湖水分层数 | 50 |
| △t | 时间步长 | 30 min |
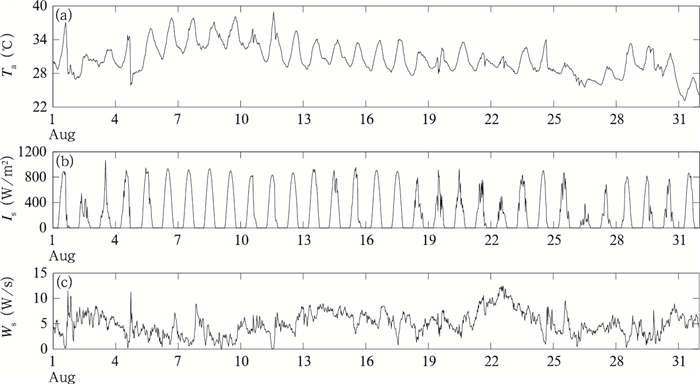
图 1给出了避风港站2013年8月每30 min气温、短波辐射和风速的变化趋势。8月气温平均值为30.6℃, 平均风速为5.01 m/s, 最大风速达到12.48 m/s, 出现在8月22日。8月上半月大部分时间天气晴好, 而下半月大多阴天, 由于太湖湖体较浅, 湖水温度的分布明显受到天气状况的影响。根据湖水温度随深度的变化(图 2a), 可将太湖避风港区域的水温分层分为3种情况, 即水温分层显著、水温分层不明显和水温分层较弱。
|
| 图 1 2013年8月太湖近湖面气温(a)、短波辐射(b)及风速(c)的分布 Figure 1 Time series of air temperature (a), downward shortwave radiation (b) and wind speed (c) over Taihu Lake in August 2013 |
|
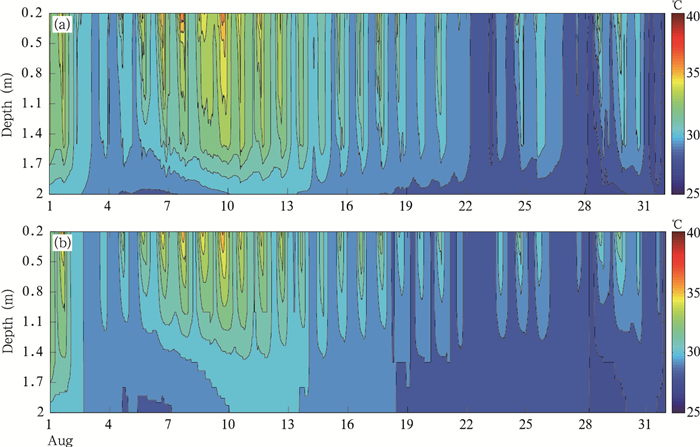
| 图 2 2013年8月观测(a)与模拟(b)的太湖垂直水温廓线 Figure 2 Observed (a) and simulated (b) water temperature in Taihu Lake in August 2013 |
当天气晴好, 风速较小时, 白天太湖水体受到太阳辐射的照射, 储存热量, 湖水上层温度高, 下层温度低, 分层非常明显。结合图 1所示的太湖避风港站近地层风速、气温的分布可知, 8月1、5—15日的最高气温达到38.92℃, 风速偏小, 平均风速为4.37 m/s;如图 2a所示, 这一时段热分层现象最为明显, 在8月7日距湖面0.2 m处的水温和湖水与底泥交界处的水温最大差值达到7.9℃。
阴天且风速较大时, 湖体表面接收到的辐射热量较小, 同时较大的风速使得湖体的动力混合增强, 到达湖体表面的热量迅速向下混合, 水温垂直方向上几乎均匀分布, 湖水热分层几乎消失。8月22—27日, 气温是处于逐渐降低的状态, 风速变大, 最大值为12.48 m/s, 此时段湖水热分层结构最不明显, 距湖表 0.2 m处的湖水温度与湖底水温平均相差不超过1℃。
而8月2—4、16—21、28—31日天气过程处于前两种状态的过渡带, 太湖水温有一定的分层, 但不明显。例如8月2—4日的气温开始降低, 风速变大, 湖水的热分层结构开始削弱。28—31日, 气温开始回升, 平均风速为4.44 m/s, 出现湖体的热分层现象, 但不太显著。
采用E-ε湍流动能闭合湖泊热力学过程模型能够较好地模拟出不同天气条件下太湖东部夏季的水温热分层结构(图 2b)。从图 2b模拟结果可以看出, 晴朗小风天气条件下(8月1、5—15日), 湖水温度随着深度具有明显的变化, 热分层结构最为明显, 阴天且风速较大时(8月22—27日), 湖水温度随深度变化不大, 模型的模拟结果很接近观测值。表 2是模型计算得到的各层水温与实际观测的湖水温度的均方根误差和平均误差, 0.2、0.5、1.0和1.5 m深水温的均方根误差均不超过1℃, 平均误差的绝对值也未超过1℃。
| 深度(m) | 相关系数 | 均方根误差(℃) | 平均误差(℃) |
| 0.2 | 0.97* | 0.46 | -0.45 |
| 0.5 | 0.96* | 0.44 | -0.37 |
| 1.0 | 0.96* | 0.40 | -0.60 |
| 1.5 | 0.89* | 0.63 | -0.97 |
| 注:*相关系数通过1%水平显著性检验。 | |||
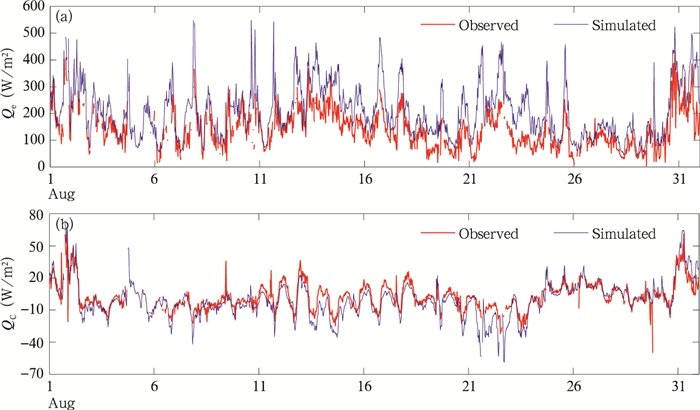
太湖避风港平台涡度相关系统观测得到8月感热通量和潜热通量, 观测结果显示潜热通量的月平均值为139.2 W/m2, 感热通量的月平均值为2 W/m2, 与感热通量相比, 在湖泊能量分配中潜热通量占主导。晴天, 湖泊的蒸发较强, 潜热通量较大, 8月1日潜热通量的观测值最大达到400.9 W/m2, 阴天, 8月22—27日, 该段时间潜热通量较低, 平均值为104.7 W/m2。
该E-ε湍流动能闭合湖泊热力学过程模型模拟出的东太湖表面8月感热通量和潜热通量与观测值的吻合较好。模型的模拟值与涡度相关系统观测得到的感热通量、潜热通量进行对比(图 3)。潜热通量的模拟值与观测值的相关系数为0.82, 均方根误差为55 W/m2, 而感热通量的相关系数为0.86, 均方根误差为8.4 W/m2(表 3)。感热通量、潜热通量的模拟值随时间的变化趋势与观测值较为吻合。2013年8月太湖湖表潜热通量与观测值相比, 有一定程度的偏高(图 3a)。究其原因, 可能与涡度相关系统观测的通量数据能量不闭合有关, Wang等(2014)研究表明, 太湖避风港区域湖泊能量平衡的闭合度的月平均值为71%。
| 相关系数 | 均方根误差(W/m2) | 平均误差(W/m2) | |
| 潜热通量 | 0.82* | 54.72 | 5.44 |
| 感热通量 | 0.86* | 8.41 | 0.43 |
| 注:*相关系数通过1%水平显著性检验。 | |||
|
| 图 3 2013年8月太湖表面潜热通量(a)、感热通量(b)模拟与观测的对比 Figure 3 Simulated and observed surface energy fluxes in Taihu Lake in August 2013 (a. latent heat, b. sensible heat) |
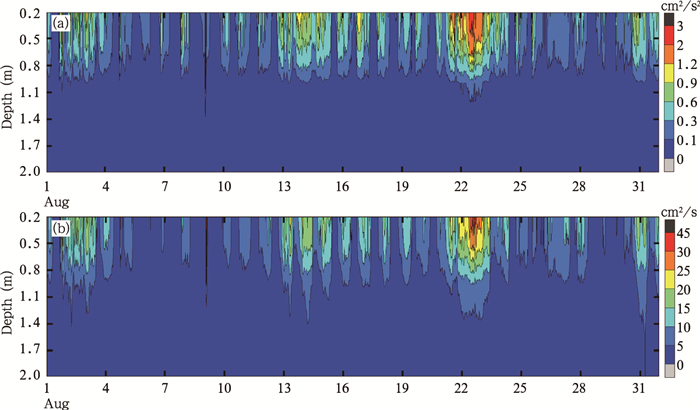
从3.1.1节的分析可以看出, 水体的热分层与天气状况密切相关。此外, 水体与其他陆地有着显著的不同, 当能量进入到湖体之后, 湖体湍流运动对于热量的传输以及水温的热分层也存在明显的影响。从E-ε湍流动能闭合湖泊热力学过程模型模拟出的2013年8月太湖避风港区域湍流动能和湍流扩散系数分布(图 4)可以看出, 晴天小风天气条件下(8月1、5—15日), 受天气条件影响, 白天湖水上层温度高, 下层温度低, 且风速较小, 湖水处于热力及动力湍流稳定状态, 湍流动能和湍流扩散系数的数值明显比较低。该时段大部分时间湍流动能小于0.1 cm2/s2, 湍流扩散系数小于5 cm2/s, 湖水的湍流混合运动弱。阴天大风时(8月22—27日), 湖表无强的辐射热源, 湖水呈现热力中性状态, 而较大的风速驱动了湖体内的湍流运动, 湖水的热分层现象不显著, 对应该时段湖体的湍流动能、湍流扩散系数明显比其他时段的数值大, 湖水的湍流混合最强, 8月22日出现了8月份湍流动能最大值2.8 cm2/s2, 湍流扩散系数最大值33.8 cm2/s。
|
| 图 4 2013年8月湍流动能(a)、湍流扩散系数(b)模拟的垂直分布 Figure 4 Simulated turbulent kinetic energy (a) and turbulent diffusivity coefficient (b) in August 2013 |
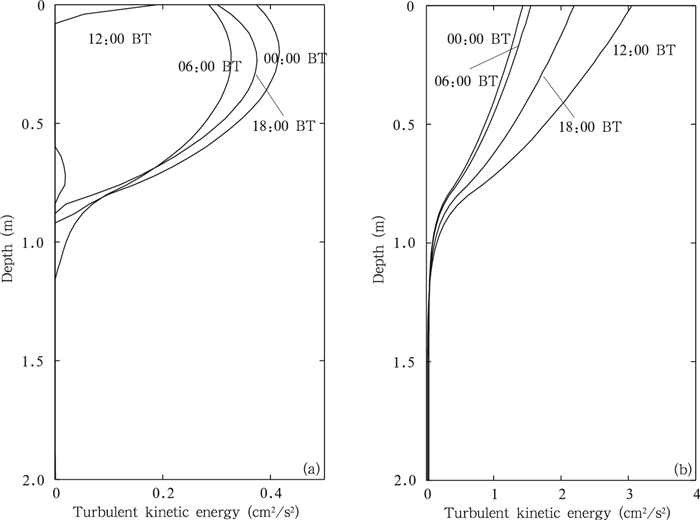
太湖湖体湍流强, 水体混合运动则较为剧烈, 热分层现象就不明显;当湍流动能较小时, 湖水的湍流运动变弱, 湖水热分层就会变得显著。在不同的气象条件下, 水体的温度层结存在明显的差异。文中进一步分析了代表性天气湍流动能垂直廓线(图 5)及对应的水体温度的日变化特征(图 6)。其中8月10日代表晴天小风天气, 平均气温33.4℃, 平均风速是4.5 m/s。8月22日代表阴天大风天气, 气温日变化不大, 平均为29.6℃, 平均风速达到10.4 m/s。
|
| 图 5 8月10日(a)与22日(b)湍流动能廓线随时间的变化 Figure 5 Turbulent kinetic energy profiles on 10 (a) and 22 August (b) |
|
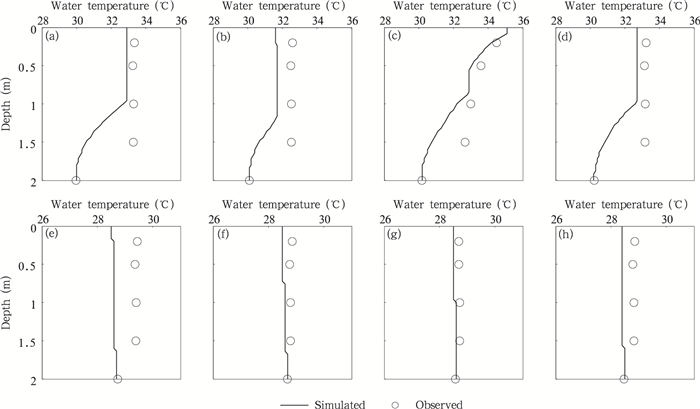
| 图 6 两种天气条件下湖体水温廓线(a、b、c、d.8月10日00、06、12、18时,晴天小风;e、f、g、h.8月22日00、06、12、18时,阴天大风) Figure 6 Water temperature profile in two weather conditions (a, b, c, d. 00:00, 06:00, 12:00, 18:00 BT 10 August, sunny condition with weak wind; e, f, g, h. 00:00, 06:00, 12:00, 18:00 BT 22 August, cloudy day with high wind speeds) |
晴天小风天气(图 5a), 8月10日00、06、18时太湖的湍流动能, 在湖深0.2 m处达到最大值, 之后随着湖水深度的增加逐渐减小, 在湖深1 m处为0 cm2/s2。湖表湍流动能在12时最小;湖体湍流动能最大值出现在00时, 湍流动能为0.41 cm2/s2。夜间湖水表层的湍流动能大于白天, 是由于白天太阳辐射向湖体的输入, 湖水表层吸收的热量比深层的热量多, 湖水的热层结比较稳定, 湍流混合运动不强;而夜晚湖表因长波辐射冷却, 浅层湖水温度下降, 湖水热层结的稳定性遭到干扰, 湖体内部的混合运动增强。
在大风天气下(图 5b), 8月22日00、06、12和18时湖表面风速分别为8.9、9.2、12和15 m/s, 湖表的湍流动能则分别为1.43、1.55、3.05和2.20 cm2/s2, 湖水的湍流动能随深度逐渐减小, 在水深1 m处接近0 cm2/s2。太湖作为浅水湖泊, 很容易受到湖表面风速的影响, 在大风天气条件下, 湖表的湍流动能都比较大。
图 6给出了8月10和22日两种天气条件下00、06、12、18时相应时段湖体水温廓线。可见晴天小风(图 6a、b、c、d)天气状况下, 温度层结明显, 12时太阳辐射强, 湖面吸收辐射温度升高, 此时的湖表面温度比其他3个时刻高, 又由于湍流动能很小, 湖水混合运动不明显, 导致湖水温度随深度的增加而减小, 湖面与湖底的水温相差5℃左右。而在阴天大风(图 6e、f、g、h)天气状况下, 由于湖水湍流动能较大, 湖体内部热量混合均匀, 使得4个时刻下的湖水温度随深度的增加, 变化均不大, 湖面的水温与湖底水温相差不到1℃。
3.3 沉水植物高度对湖水热分层的影响太湖东部的湖体沉水植物密集, 沉水植物的存在也对湖水的流体运动及热力层结产生影响, 因此, 分析了沉水植物高度对水温的影响。结果表明, 沉水植物高度对于湖水的辐射传输及湍流交换产生影响, 并进而影响到水体的热力分层。
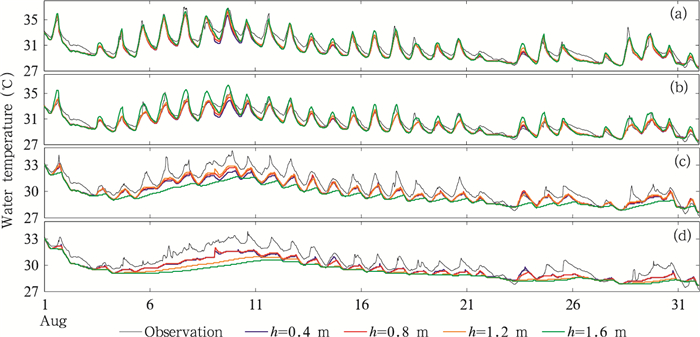
图 7是沉水植物高度对湖水温度的影响。沉水植物高度越高, 水体浅层的水温较高, 而水体深处的水温越低。水深0.5 m处, 沉水植物高度1.6 m时, 模拟的水温最高(图 7b), 水深1.5 m处, 沉水植物高度为1.6 m的算例模拟出的水温最高, 其平均值比0.4 m高度模拟的低0.43℃(图 7d)。分析其原因, 当沉水植物越高, 太阳短波辐射就越难到达湖水下层, 同时沉水植物的存在抑制了湍流混合运动, 这两方面的原因导致湖表接收的热量很难达到湖底, 随沉水植物高度的增高, 湖体底部的温度降低。同时也使热量更多地留在湖水上层, 使得沉水植物层顶部水温偏高。
|
| 图 7 沉水植物高度对不同深度水温的影响(a、b、c、d.湖深0.2、0.5、1.0、1.5 m) Figure 7 Effects of submersed macrophytes height on water temperature in different depths (a-d. Water depth: 0.2, 0.5, 1.0, 1.5m) |
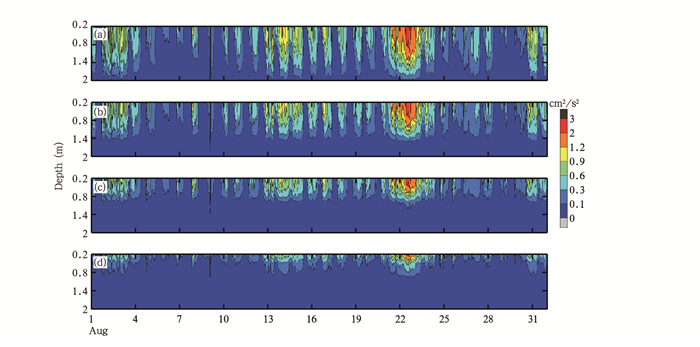
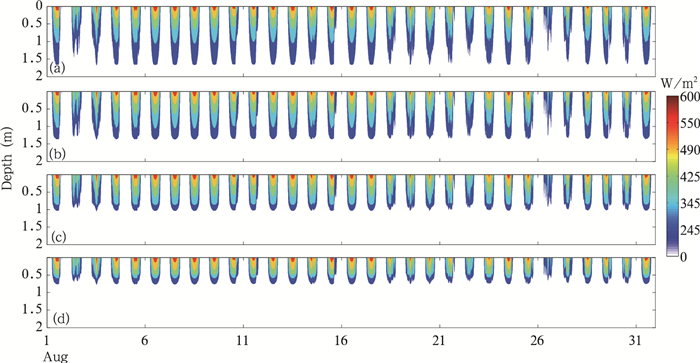
图 8是湖体内部的湍流动能对不同沉水植物高度的响应, 图 9给出了沉水植物高度分别为0.4、0.8、1.2和1.6 m时, 湖体内部接收到的热量变化, 当沉水植物高度为0.4 m时, 湖体有强烈的混合作用(图 8a), 湖深1.9 m处仍有较强的混合运动, 湖表接收到的热量可传递到湖深1.7 m处(图 9a), 湖深1.5 m处, 湖水白天接收的能量是32.3 W/m2。而沉水植物高度是1.6 m时, 湖深0.8 m以下, 湍流动能值也接近为0 cm2/s2(图 8d), 白天接受的能量几乎为0(图 9d)。
|
| 图 8 不同沉水植物高度对湖水湍流动能的影响(a—d.沉水植物高度0.4、0.8、1.2、1.6 m) Figure 8 Effects of submersed macrophytes height on turbulent kinetic energy in different depths (a-d. Height of submersed macrophyte: 0.4, 0.8, 1.2, 1.6 m) |
|
| 图 9 沉水植物高度对不同深度接收太阳辐射的影响(a、b、c、d.沉水植物高度0.4、0.8、1.2、1.6 m) Figure 9 Effects of submersed macrophytes height on solar radiation in different depths (a, b, c, d. Height of submersed macrophytes: 0.4, 0.8, 1.2, 1.6 m) |
采用E-ε湍流动能闭合湖泊热力学过程模型, 对2013年8月东太湖沉水植物密集区域的湖-气交换进行了模拟, 初步分析了夏季太湖湖水的热分层结构, 并评估了E-ε湍流动能闭合湖泊热力学过程模型中沉水植物及湍流动能对于湖水热分层的影响。得到了如下的结论:
(1)Herb等(2005)模型适用于太湖, 该模式能较好地模拟出湖水的温度, 各层温度模拟值与观测值的均方根误差不超过1℃。感热通量和潜热通量与观测值的趋势吻合较好, 潜热通量模拟值与观测值的均方根误差为54.72 W/m2, 感热通量均方根误差是8.41 W/m2。
(2)太湖属于浅水湖泊, 湖水温度的热分层状况受到天气状况的影响显著。晴天小风条件下, 湖表温度高, 湖底温度低, 湖水热力稳定, 风速对于湖体动力湍流产生的影响不大, 且受湖水中密集的沉水植物的影响, 湖水中湍流动能较小, 湖水的湍流混合作用小, 湖面0.2 m处的水温和湖水与底泥交界处的水温最大相差可达7.9℃。大风条件下, 湖水的湍流运动被驱动, 湖体内部的热量混合均匀, 湖水热分层结构不明显。
(3)太湖东部区域, 沉水植物的存在导致到达湖底的太阳辐射被削弱, 水体的内部热量减少, 水温降低。同时由于沉水植物对湖水流动的拖曳作用, 湖体内部的湍流混合动能减小。因此, 沉水植物高度越高, 到达湖底的热量越少, 湖水的热分层越明显。当沉水植物较高(1.6 m)时, 与沉水植物较低(0.4 m)相比, 湖体1.5 m深度处的8月平均温度降低0.43℃。
采用E-ε湍流动能闭合湖泊热力学过程模型对2013年8月东太湖沉水植物密集区域的湖-气交换及水温分布特征进行了模拟, 当前的研究表明模型模拟性能良好。然而模型中沉水植物生物量密度、沉水植物高度的设置仅来源于估计, 并没有实际观测的结果, 可能需要在接下来的工作中设计实验测量, 或从遥感数据中得到相应的值。此外, 陆面过程模型中对于表面能量采用闭合的方案, 然而观测值大多处于能量不闭合的状态, 如何更好地对比模拟值与观测值, 使得模拟方案更为准确, 尚需进一步探讨。
本次模拟选用的时段是沉水植物生长旺盛的8月, 对于其他季节的模拟, 模型中的相关参数还需要相应的做出调整, 分析模型在不同季节下的适用性将是接下来研究的重要内容。并且, 将E-ε湍流动能闭合湖泊热力学过程模型与CLM4中湖泊子模型(Deng et al, 2013)等已有的其他湖泊模型的对比工作有利于参数化方案的发展, 深化对湖泊过程的理解, 也将是今后研究工作的重要方向。
| 古红萍, 沈学顺, 金继明, 等. 2013. 一维热扩散湖模式在太湖的应用研究. 气象学报 , 71 (4) : 719–730. Gu H P, Shen X S, Jin J M, et al. 2013. An application of a 1-D thermal diffusion lake model to Lake Taihu. Acta Meteor Sinica , 71 (4) : 719–730. (in Chinese) |
| 何俊, 古孝鸿, 刘国锋. 2008. 东太湖水生植物及其与环境的相互作用. 湖泊科学 , 20 (6) : 790–795. He J, Gu X H, Liu G F. 2008. Aquatic macrophytes in East Lake Taihu and its interaction with water environment. J Lake Sci , 20 (6) : 790–795. DOI:10.18307/2008.0618 (in Chinese) |
| 雷泽湘, 徐德兰, 黄沛生, 等. 2006. 太湖沉水和浮叶植被及其水环境效应研究. 生态环境 , 15 (2) : 239–243. Lei Z X, Xu D L, Huang P S, et al. 2006. Submersed and floating-leaved macrophytes in Taihu Lake and their water environmental effect. Ecol Environ , 15 (2) : 239–243. (in Chinese) |
| 朴美花. 2014.浅水湖泊陆面过程模型的改进及耦合应用研究[学位论文].南京:南京信息工程大学. Piao M H. 2014. Research on the improvement and coupling application of shallow lakes land surface model[D]. Nanjing: Nanjing University of Information Science and Technology (in Chinese) http://cdmd.cnki.com.cn/article/cdmd-10300-1015566497.htm |
| 任晓倩, 李倩, 陈文, 等. 2014. 一个新的湖-气热传输模型及其模拟能力评估. 大气科学 , 38 (5) : 993–1004. Ren X Q, Li Q, Chen W, et al. 2014. A new lake model for air-lake heat exchange process and the evaluation of its simulation ability. Chin J Atmos Sci , 38 (5) : 993–1004. (in Chinese) |
| 孙菽芬, 颜金凤, 夏南, 等. 2008. 陆面水体与大气之间的热传输研究. 中国科学G辑:物理学力学天文学 , 51 (8) : 1010–1021. Sun S F, Yan J F, Xia N, et al. 2008. The model study of water mass and energy exchange between the inland water body and atmosphere. Sci China Ser G: Phys Mech Astron , 51 (8) : 1010–1021. DOI:10.1007/s11433-008-0121-7 (in Chinese) |
| 王浩. 1991. 湖陆风演变过程的数值模拟. 南京大学学报 , 27 (2) : 383–395. Wang H. 1991. A numerical study of the developing process of the lake and land breezes. J Nanjing Univ , 27 (2) : 383–395. (in Chinese) |
| 杨健博, 刘红年, 费松, 等. 2013. 太湖湖陆风背景下的苏州城市化对城市热岛特征的影响. 气象科学 , 33 (5) : 473–484. Yang J B, Liu H N, Fei S, et al. 2013. The impact of urbanization on the urban heat island in Suzhou under the influence of Taihu lake-land breeze. J Meteor Sci , 33 (5) : 473–484. (in Chinese) |
| 张运林, 秦伯强, 陈伟民, 等. 2003. 太湖水体光学衰减系数的分布及其变化特征. 水科学进展 , 14 (4) : 447–453. Zhang Y L, Qin B Q, Chen W M, et al. 2003. Analysis on distribution and variation of beam attenuation coefficient of Taihu Lake's water. Adv Water Sci , 14 (4) : 447–453. (in Chinese) |
| 张运林, 秦伯强, 陈伟民, 等. 2004. 太湖水体光学衰减系数的特征及参数化. 海洋与湖沼 , 35 (3) : 209–213. Zhang Y L, Qin B Q, Chen W M, et al. 2004. Regression analysis of beam attenuation coefficient under water in Lake Taihu. Ocean Limn Sinica , 35 (3) : 209–213. (in Chinese) |
| 周从直, ChapraS C. 1994. 湖泊热结构和蒸发的模拟计算. 环境科学 , 15 (2) : 33–37. Zhou C Z, Chapra S C. 1994. Simulation of thermal structure and evaporation for lakes. Environ Sci , 15 (2) : 33–37. (in Chinese) |
| Burchard H, Baumert H. 1995. On the performance of a mixed-layer model based on the k-ε turbulence closure. J Geophys Res , 100 (C5) : 8523–8540. DOI:10.1029/94JC03229 |
| Burchard H, Bolding K, Ruiz-Villarreal M. 1999. GOTM, a general ocean turbulence model: Theory, implementation and test cases. European Commission Report EUR 18745 EN, 103 pp |
| Dale H M, Gillespie T J. 1977. The influence of submersed aquatic plants on temperature gradients in shallow water bodies. Can J Bot , 55 (16) : 2216–2225. DOI:10.1139/b77-251 |
| Deng B, Liu S D, Xiao W, et al. 2013. Evaluation of the CLM4 lake model at a large and shallow freshwater lake. J Hydrometeor , 14 (2) : 636–649. DOI:10.1175/JHM-D-12-067.1 |
| Elo A R, Huttula T, Peltonen A, et al. 1998. The effects of climate change on the temperature conditions of lakes. Bor Environ Res , 3 (2) : 137–150. |
| Finnigan J. 2000. Turbulence in plant canopies. Annu Rev Fluid Mech , 32 (41) : 519–571. |
| Goudsmit G H, Burchard H, Peeters F, et al. 2002. Application of k-ε turbulence models to enclosed basins: The role of internal seiches. J Geophys Res , 107 (C12) : 23–1. |
| Herb W R, Stefan H G. 2005. Dynamics of vertical mixing in a shallow lake with submersed macrophytes. Water Resour Res , 41 (2) : 293–307. |
| Hjelmfelt M R, Braham R R. 1983. Numerical simulation of the airflow over Lake Michigan for a major lake-effect snow event. Mon Wea Rev , 111 (1) : 205–219. DOI:10.1175/1520-0493(1983)111<0205:NSOTAO>2.0.CO;2 |
| Hjelmfelt M R. 1990. Numerical study of the influence of environmental conditions on lake-effect snowstorms over Lake Michigan. Mon Wea Rev , 118 (1) : 138–150. DOI:10.1175/1520-0493(1990)118<0138:NSOTIO>2.0.CO;2 |
| Horppila J, Nurminen L. 2003. Effects of submerged macrophytes on sediment resuspension and internal phosphorus loading in Lake Hiidenvesi (southern Finland). Water Res , 37 (18) : 4468–4474. DOI:10.1016/S0043-1354(03)00405-6 |
| Hostetler S W, Bartlein P J. 1990. Simulation of lake evaporation with application to modeling lake level variations of Harney-Malheur Lake, Oregon. Water Resour Res , 26 (10) : 2603–2612. |
| Huttula T, Peltonen A, Bilaletin A, et al. 1992. The effects of climatic change on lake ice and water temperature. Aqua Fennica , 22 : 129–142. |
| Imberger J, Patterson J C. 1981. A dynamic reservoir simulation model-DYRESM: 5//Transport Models for Inland & Coastal Waters. New York: Academic Press, 310-361 |
| Karagounis I, Trösch J, Zamboni F. 1993. A coupled physical-biochemical lake model for forecasting water quality. Aquat Sci , 55 (2) : 87–102. DOI:10.1007/BF00877438 |
| Keen C S, Lyons W A. 1978. Lake/land breeze circulations on the western shore of Lake Michigan. J Appl Meteor , 17 (12) : 1843–1855. DOI:10.1175/1520-0450(1978)017<1843:LBCOTW>2.0.CO;2 |
| King P W S, Leduc M J, Sills D M L, et al. 2003. Lake breezes in southern Ontario and their relation to tornado climatology. Wea Forecasting , 18 (5) : 795–807. DOI:10.1175/1520-0434(2003)018<0795:LBISOA>2.0.CO;2 |
| Krinner G. 2003. Impact of lakes and wetlands on boreal climate. J Geophys Res , 108 (D16) : 4520. DOI:10.1029/2002JD002597 |
| Laird N F, Desrochers J, Payer M. 2009. Climatology of lake-effect precipitation events over Lake Champlain. J Appl Meteor Climatol , 48 (2) : 232–250. DOI:10.1175/2008JAMC1923.1 |
| Lee X, Finnigan J, Paw K T. 2004. Coordinate systems and flux bias error//Handbook of Micrometeorology: A Guide for Surface Flux Measurement and Analysis. Boston, USA: Kluwer Academic Publishers, 33-66 |
| Lee X, Massman W J. 2011. A perspective on thirty years of the Webb, Pearman and Leuning density corrections. Bound Layer Meteor , 139 (1) : 37–59. DOI:10.1007/s10546-010-9575-z |
| Lee X, Liu S D, Xiao W, et al. 2014. The Taihu eddy flux network: An observational program on energy, water, and greenhouse gas fluxes of a large freshwater lake. Bull Am Meteor Soc , 95 (10) : 1583–1594. DOI:10.1175/BAMS-D-13-00136.1 |
| Long Z, Perrie W, Gyakum J, et al. 2007. Northern lake impacts on local seasonal climate. J Hydrometeor , 8 (4) : 881–896. DOI:10.1175/JHM591.1 |
| Lyons W A. 1972. The climatology and prediction of the Chicago Lake breeze. J Appl Meteor , 11 (8) : 1259–1270. DOI:10.1175/1520-0450(1972)011<1259:TCAPOT>2.0.CO;2 |
| Lyons W A, Cole H S. 1976. Photochemical oxidant transport: Mesoscale lake breeze and synoptic-scale aspects. J Appl Meteor , 15 (7) : 733–743. DOI:10.1175/1520-0450(1976)015<0733:POTMLB>2.0.CO;2 |
| Nes E H V, Scheffer M, Berg M S V D, et al. 2003. Charisma: A spatial explicit simulation model of submerged macrophytes. Ecol Mod , 159 (2-3) : 103–116. DOI:10.1016/S0304-3800(02)00275-2 |
| Riley M J, Stefan H G. 1988. Minlake: A dynamic lake water quality simulation model. Ecol Mod , 43 (3) : 155–182. |
| Samuelsson P, Kourzeneva E, Mironov D. 2010. The impact of lakes on the European climate as simulated by a regional climate model. Bor Environ Res , 15 (2) : 113–129. |
| Subin Z M, Murphy L N, Li F Y, et al. 2012. Boreal lakes moderate seasonal and diurnal temperature variation and perturb atmospheric circulation: Analyses in the Community Earth System Model 1 (CESM1). Tellus A , 64 (3) : 53–66. |
| Ulrich M. 1991. Modeling of chemicals in lakes-development and application of user-friendly simulation software (MASAS & CHEMSEE) on personal computers. Zürich |
| Wang W, Xiao W, Cao C, et al. 2014. Temporal and spatial variations in radiation and energy balance across a large freshwater lake in China. J Hydrol , 511 : 811–824. DOI:10.1016/j.jhydrol.2014.02.012 |
| Webb E K, Pearman G I, Leuning R. 1980. Correction of flux measurements for density effects due to heat and water vapour transfer. Quart J Roy Meteor Soc , 106 (447) : 85–100. DOI:10.1002/(ISSN)1477-870X |
| Westlake D F. 1964. Light extinction, standing crop and photosynthesis within weed beds. Verh Int Verein Limnol Theor Angew , 15 : 415–425. |
| Xiao W, Liu S, Wang W, et al. 2013. Transfer coefficients of momentum, heat and water vapour in the atmospheric surface layer of a large shallow freshwater lake. Bound Layer Meteor , 148 : 479–494. DOI:10.1007/s10546-013-9827-9 |
 2016, Vol. 74
2016, Vol. 74


