中国气象学会主办。
文章信息
- 刘琨, 张峰, 吴琨, 周秀骥, 张华, 刘仁强 . 2016.
- LIU Kun, ZHANG Feng, WU Kun, ZHOU Xiuji, ZHANG Hua, LIU Renqiang . 2016.
- 大气粒子散射相函数的参数化方案比较及其改进
- Comparisons and improvement of parameterization schemes for the scattering phase function of atmospheric particles
- 气象学报, 74(5): 784-795.
- Acta Meteorologica Sinica, 74(5): 784-795.
- http://dx.doi.org/10.11676/qxxb2016.052
-
文章历史
- 2015-11-16 收稿
- 2016-05-20 改回
2. 中国气象科学研究院灾害天气国家重点实验室, 北京, 100081;
3. 中国气象局国家气候中心气候研究开放实验室, 北京, 100081
2. State Key Laboratory of Severe Weather, Chinese Academy of Meteorological Sciences, Beijing 100081, China;
3. National Climate Center, China Meteorological Administration, Beijing 100081, China
大气辐射传输过程在气候模拟、大气遥感反演及大气光化学过程中起着非常重要的作用。而辐射方案的精度差异会对大气数值模式模拟效果产生一定影响(杨学胜等,2009;许尤福等,2011;荆现文等,2012;张梦等,2014;Zhang H et al,2014)。辐射传输的物理过程通常由辐射传输方程来描述,而该方程属于积分-微分方程,很难获得解析解,因此,已经有大量研究发展了一些近似方案来求解大气辐射传输方程,如二流近似方案(King et al,1986;Kylling et al,1995;Fu et al,1997;邱金桓,1998;Qiu,1999;Li et al,2005;Lu et al,2009)和四流近似方案(Liou et al,1988;Stamnes et al,1988;Li et al,1996;Zhang F et al,2013a, 2013b, 2016;Zhang H et al,2015)。二流近似是指用两个自由度来表示辐射强度在球空间的分布特征。多年来,由于其形式简单、计算速度快,被广泛应用于参数化气候模式的辐射传输过程。但这种方法有明显的缺陷和不足。King等(1986)对各种单层的二流近似解的精度进行了评估,指出在不同的光学厚度、太阳天顶角和单次散射反照率的情况下,采用二流近似方法计算得到的大气透射率和反射率的相对误差高达15%—20%。Lu等(2009)指出二流近似可以导致10%以上的云顶加热率误差,而云顶加热率影响着云的发生、发展。随着气候模式时空分辨率的提高和物理过程的改进,其对一个高精度、高速度的辐射算法的需求显得越来越迫切。张峰(2013)及Zhang F等(2013a, 2013b, 2016)基于辐射传输的4个不变性原理,建立了四流累加辐射传输方案。该方案越来越受到重视,并能显著提高对气溶胶辐射强迫的评估精度,因此在气候模式中得到广泛应用(Zhang H et al,2015;Li et al,2015),在辐射传输计算过程中,各种近似方案都需要对散射相函数进行相应阶数的Legendre函数展开。例如,二流近似方案需要对散射相函数进行二阶Legendre函数展开,四流近似方案需要对散射相函数进行四阶Legendre函数展开。目前,无论是单柱的辐射模式,还是气候模式中的辐射方案,其四流近似方案通常采用Henyey-Greenstein(HG)方案(Henyey et al,1941)对散射相函数进行Legendre函数展开(Zhang F et al,2013a;Zhang H et al,2015)。Zhang F等(2013a)对新建的四流球谐函数展开累加方案的精度进行了较为全面的评估,认为该方案能显著提高辐射通量和加热率的计算精度,但以上结论同样是基于HG方案得到的。而在HG方案中,高阶展开采用的仅仅是非对称因子g的幂次方。这种单参数近似不能准确地表示相函数的特征,尤其是无法表述相函数的后向散射特性(Kattawar,1975),因此,HG方案会直接影响到辐射方案本身的计算精度(Li et al,2015)。为了改进这种近似方法,Kattawar(1975)提出了双Henyey-Greenstein(DHG)方案,是指用两个HG相函数的线性组合来表示散射相函数的变化特征,即用3参数来表示相函数。相比单参数近似的HG方案,该方案具有更大的自由度去刻画散射相函数各向异性的特性。DHG方案提出已经有40多年,但该方案在辐射传输计算中应用甚少。此外,相比HG方案,该方案在辐射计算中能多大程度的提高计算精度,也均未见有相关研究。本研究对DHG方案进行了较为系统的研究,提出了改进的DHG方案(MDHG),并评估了HG、DHG和MDHG这3种方案的计算精度。
2 相函数基本理论散射相函数是散射角的函数。对于球形粒子,可以利用米散射理论计算出其散射相函数;对于非球形粒子,可以利用T矩阵(Mishchenko et al,1994)、几何光学(Yang et al,2007)和Bridging(Zhao et al,2006)技术等方法计算出其散射相函数。为了便于辐射传输计算,文中将相函数用已知的数学函数表达,采用勒让德多项式展开的相函数可以写成(Henyey et al,1941)
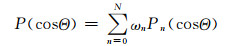
|
(1) |
式中,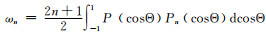
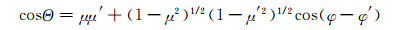
|
(2) |
式中,μ为光的入射方向,μ′为光的散射方向。对式(1)进行方位角平均可得
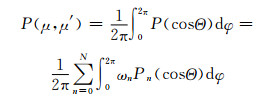
|
(3) |
式中,Pn(cosΘ)可以展开为
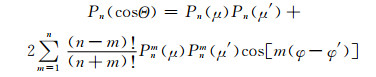
|
(4) |
根据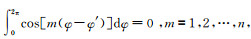
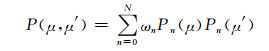
|
(5) |
目前,应用最为广泛的相函数是Henyey等(1941)提出的Henyey-Greenstein(HG)相函数。该方案采用非对称因子g表示相函数
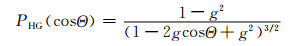
|
(6) |
式(6)可以展成为
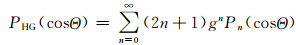
|
(7) |
根据式(3)、(5)和(7)可得方位角平均的HG近似相函数
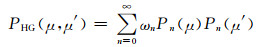
|
(8) |
式中,ωn=(2n+1)gn,并将这种方案记为HG。在该方案中,相函数的高阶展开ωn仅用非对称因子g表示,因此,在辐射传输计算中得到广泛应用(Lu et al,2009;Liou et al,1988;Stamnes et al,1988;Li et al,1996;Zhang F et al,2013a;Zhang H et al,2015)。
2.2 双Henyey-Greenstein近似双Henyey-Greenstein(DHG)(Kattawar,1975)近似是指由两个HG相函数的线性组合来表示相函数的散射特性。相比单参数的HG方案而言,DHG方案有3个待定参数,因此,有更多的自由度来表现相函数的真实特征。DHG方案采用两个HG方案的权重组合来计算相函数
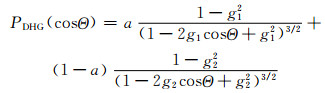
|
(9) |
根据上式,方位角平均的DHG近似相函数可表示为
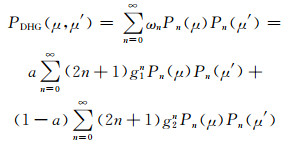
|
(10) |
根据式(5),可得到式(10)中3个参数a、g1和g2满足的方程
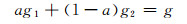
|
(11) |
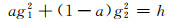
|
(12) |
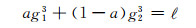
|
(13) |
式中,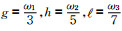
根据以上约束方程,Kattawar(1975)给出了a、g1和g2的解
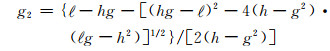
|
(14) |
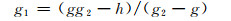
|
(15) |
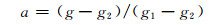
|
(16) |
为方便表述,将Kattawar(1975)提出的以上方案记为DHG。该方案的本质是采用相函数的展开项ω1、ω2、ω3来参数化相函数。在一些特定情况下,DHG方案得到的相函数存在异常峰值,而这并不符合相函数的真实特征(Kattawar,1975)。因此,该方案在辐射传输计算中几乎没有得到应用。为了解决这一问题,本研究采用ω1,ω2两项的相函数展开系数和相函数的整体特征来求解DHG方案的3个参数。具体步骤如下:
(1) 根据式(11)和(12)可得到包含有未知数a的方程的解
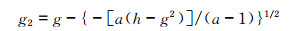
|
(17) |
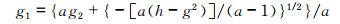
|
(18) |
(2) 权重a从0开始以0.001为间隔循环至2,利用式(17)、(18)能得到2000种不同的a、g1和g2组合;
(3) 从以上组合中挑选出满足|g1|>|g2|和|g1|<1的a、g1和g2组合。在|g1|和|g2|均小于1时,使得相函数的高阶展开项中包含的g1n和g2n在n趋向于无穷后仍收敛。
(4) 以上每一种组合均能利用式(9)构造相函数,把构造的相函数和真实的相函数(根据粒子的谱分布和已有的粒子散射理论,就能计算出真实的相函数。文中计算得到真实的相函数从0°开始以0.3°为间隔,共包含601个值)进行比较,求得相对误差最小的一组a、g1和g2组合,这种方案记为MDHG。
3 计算结果比较大气中气溶胶和云的强散射过程主要发生在短波波段。而在短波波段中,可见光波段的能量最强,通常采用波长0.55 μm来表示可见光波段的平均情况。因此,文中计算波长0.55 μm处的气溶胶和水云粒子的散射相函数,并分别利用HG、DHG和MDHG方案对其进行参数化,进一步讨论这几种参数化下相函数的精度。此外,利用四流球谐函数展开累加方案(Zhang F et al,2013a)比较分析以上3种不同相函数参数化方案下计算的反射率、透射率或吸收率的精度,将128流离散纵标的计算结果作为精确值(Stamnes et al,1988)。四流球谐函数展开累加方案的主要思想是用4个球谐函数来表示辐射强度在角度空间的分布特征,采用ω4来进行δ调整(Wiscombe,1977)。该方案能显著改善辐射通量和加热率的计算,并已在北京气候中心气候系统模式(BCC_AGCM2.0.1)和加拿大气候模拟与分析中心的气候模式(CanAM4)中得到应用(Zhang H et al,2015;Li et al,2015)。
3.1 沙尘气溶胶对于沙尘气溶胶,文中考虑随机取向的椭球粒子,并采用对数正态分布来描述沙尘粒子的分布。该分布函数曾为世界气象组织推荐(Sokolik et al,1998)
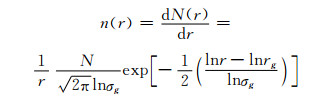
|
(19) |
式中,r为椭球沙尘等效为等体积球体的半径,rg为粒子群的模态半径,σg为标准偏差,N为气溶胶粒子的数浓度(cm-3)。其有效半径为re=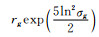
| a | g1 | g2 | ω4=9[ag14+(1-a)g24] | |
| DHG(核模态) | 0.995 | 0.690 | -1.485 | 2.213 |
| MDHG(核模态) | 0.989 | 0.696 | -0.635 | 2.213 |
| DHG(粗模态) | 0.981 | 0.850 | -1.015 | 4.796 |
| MDHG(粗模态) | 0.697 | 0.983 | 0.428 | 5.946 |
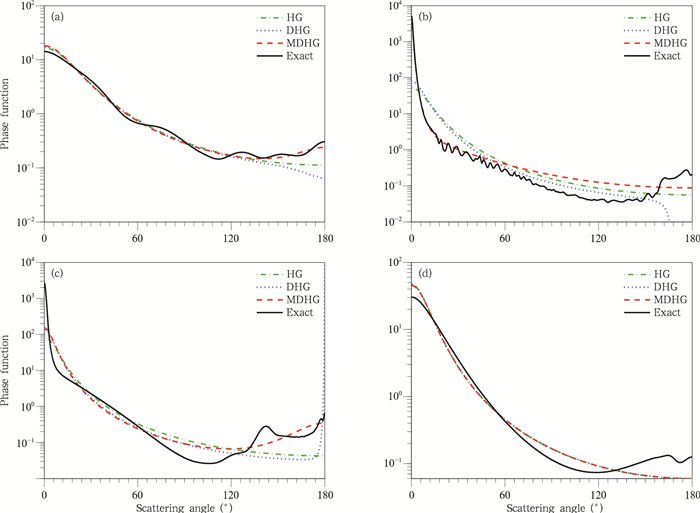
图 1a、b分别给出了核模态和粗模态沙尘气溶胶相函数的精确值(Exact)以及HG、DHG和MDHG方案的结果。可以看出,粗模态沙尘具有很强的前向峰值,其后向也有一个小的峰值。HG方案的相函数较平滑,但其在前向和后向并不接近真值,尤其没有表现出前向的强峰值。DHG方案的相函数在散射角为54°—170°时比其他两种方案更接近真值,但其在170°后出现了相函数为负数的情况,因此该方案没有体现出粗模态沙尘的后向峰值特征。本研究提出的MDHG方案的相函数在散射最强的前向几乎与精确值重合,对前向强峰值的模拟精度较高。此外,MDHG方案在后向也较HG和DHG方案更接近于真值。和粗模态沙尘相比,核模态沙尘没有很强的前向峰值。HG、DHG和MDHG这3种方案的相函数在前向均与真值较为接近,精度相近。而在后向,这3种方案的相函数有较大差异。DHG方案的相函数在后向出现了骤降,与真值差异最大,精度最差。HG方案的相函数虽然稳定,在后向的精度高于DHG方案,但与真值相比仍有较大的误差。而MDHG方案的相函数表现出了相函数的后向特征,更接近真实的相函数。
|
| 图 1 核模态沙尘气溶胶(a)、粗模态沙尘气溶胶(b)、水云(c)和霾(d)的相函数比较 Figure 1 Phase functions of nuclei mode dusts (a), coarse mode dusts (b), water clouds (c) and haze (d) |
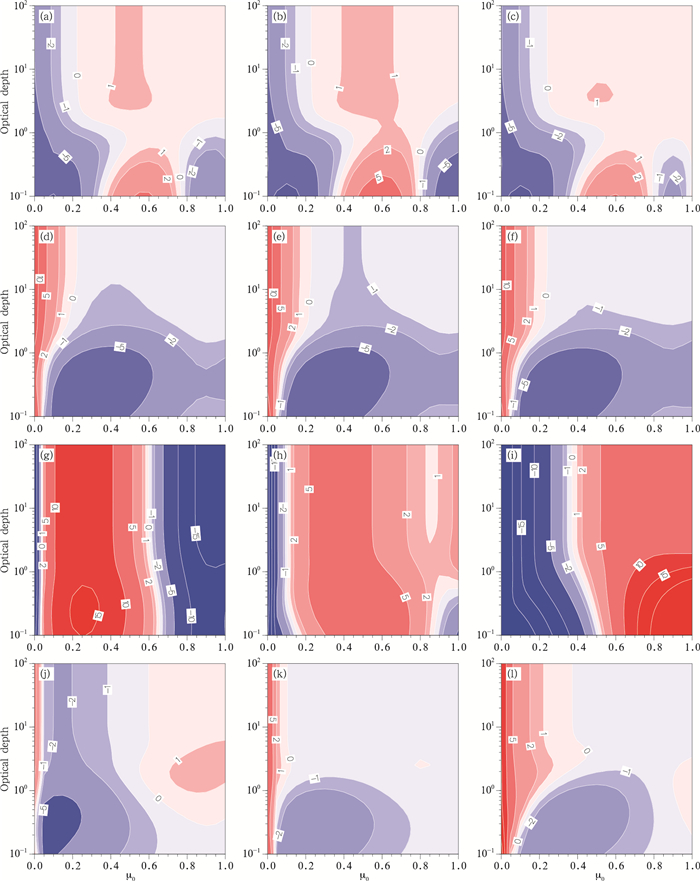
此外,还比较了不同相函数参数化方案下的四流球谐函数展开累加方案的反射率和吸收率的精度。核模态沙尘气溶胶的反射率和吸收率在不同方案下的精度如图 2a—f所示。从反射率的误差结果可以看出,DHG方案相比其他两种方案误差更大,尤其在光学厚度小于0.2且μ0为0.5—0.7和0.9—1.0时相对误差可达5%。而在此范围内,HG和MDHG方案的相对误差约为2%。当光学厚度大于1时,MDHG方案中相对误差小于1%的范围比HG和DHG方案大。从吸收率的误差结果来看,3种方案精度相当,MDHG方案在μ0为0.4—0.5且光学厚度大于3时,精度比HG和DHG方案略高。故总体而言,MDHG方案比HG和DHG方案精度更高。
|
| 图 2 核模态(a—f)和粗模态(g—l)沙尘气溶胶的反射率(a—c,g—i)和吸收率(d—f,j—k)的相对误差(a、d、g、j.HG,b、e、h、k.DHG,c、f、i、l.MDHG) Figure 2 Relative errors of reflection (a-c, g-i) and absorption (d-f, j-k) for dusts in nuclei mode (a-f) and coarse mode (g-l) |
粗模态沙尘气溶胶在不同方案下的反射率和吸收率的精度如图 2g—l所示。从反射率的误差结果来看,HG方案精度最低,在μ0为0.1—0.4和0.8—1.0时误差都大于10%。DHG方案误差最小,仅当在μ0小于0.1时相对误差大于10%。MDHG方案在μ0小于0.2时以及光学厚度小于2且μ0为0.8—1.0时的相对误差皆大于10%,但其相对误差大于10%的范围小于HG方案,故MDHG方案的精度高于HG方案。从吸收率的误差结果可以看出,这3种方案的精度都较高。HG方案在μ0为0.05—0.2且光学厚度在0.1—1时误差大于5%,而其他两种方案均小于5%。此外,HG方案在光学厚度大于2且μ0为0.25—0.45时相对误差大于1%,而其他两种方案均接近于0。相比之下,3种方案中HG方案精度最低。DHG方案在μ0小于0.1时,误差小于MDHG方案。故整体而言,DHG方案相对误差最小,精度略优于MDHG方案,HG方案误差最大。
3.2 水云水云的粒子尺度分布接近于Γ分布(Pruppacher et al,1996)
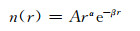
|
(20) |
式中,A、α和β为常数,r为水云粒子的半径,有效半径为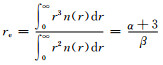
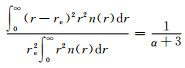
在计算云的光学特性的参数化试验中,为了方便计算,选用水云的有效方差为ve=0.172(Fu et al,1997),有效半径为re=5.89 μm(Fu et al,1997)。该水云可以代表典型的低云特征。水云的复折射指数为m=1.33+1.79×10-9i。计算得到波长0.55 μm处水云的ω和g分别为1和0.85。表 2中给出了在水云情况下,DHG和MDHG方案得到的a、g1、g2和ω4的值。
| a | g1 | g2 | ω4=9[ag14+(1-a)g24] | |
| DHG | 0.984 | 0.883 | -0.999 | 5.526 |
| MDHG | 0.975 | 0.891 | -0.616 | 5.557 |
由图 1c可以看出,水云的HG方案的相函数没有很好地反映出相函数的真实特征,特别是相函数的后向特征。DHG方案在0°—132°的散射角下精度较高,但在后向出现了异常增大,甚至超过了真实相函数的前向最大值。在3种方案中,MDHG方案的相函数是整体上最接近于真值的,尤其是其后向精度高于其他两种方案,能很好地反应出真实相函数的后向特征。
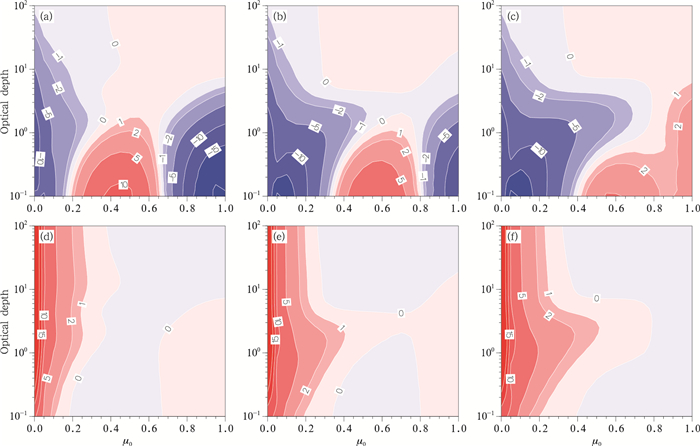
在波长0.55 μm处,水云的吸收作用非常小,因此只讨论其反射率和透射率的情况。图 3a—f为3种方案在水云情况下的反射率和透射率的精度比较。MDHG方案在μ0为0.4—1.0时相对误差小于2%,优于其他两种方案。这3种方案的透射率结果基本相同,在μ0为0.4—1.0时误差几乎为0。故总体来看,MDHG方案相对误差最小,DHG方案其次,这两种方案整体都要好于HG方案。
|
| 图 3 水云的反射率(a—c)和透射率(d—f)的相对误差(a、d.HG,b、e.DHG,c、f.MDHG) Figure 3 Relative errors of reflection (a-c) and transmission (d-f) for water clouds |
对于霾粒子,采用了Haze L的相函数散射模型,其非对称因子g=0.80(Garcia et al,1985)。从图 1d可以看出,HG、DHG和MDHG方案的相函数都几乎重合,均较为接近真实相函数。然而如表 3所示,将MDHG方案得到的最优a、g1、g2和ω4与DHG方案得到的值进行比较,发现DHG方案中,g2远大于g1。此外,DHG方案中ω4出现了较大负值,这导致了光学厚度在进行δ调整后反而增大,从而影响之后的反射率和透射率的计算精度,增大反射率和透射率的相对误差。而MDHG方案得到的g1、g2和ω4均非常合理。
| a | g1 | g2 | ω4=9[ag14+(1-a)g24] | |
| DHG | 1.0+1.98×10-7 | 0.804 | 57.827 | -16.156 |
| MDHG | 2.000 | 0.786 | 0.768 | 3.743 |
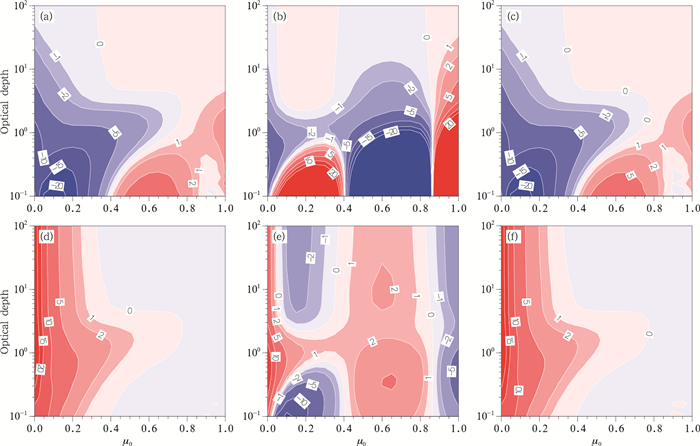
在计算HG、DHG和MDHG方案的反射率和透射率时,令单次散射反照率为1,从3种方案的反射率和透射率的精度(图 4a—f)可以看出,DHG方案下的反射率在光学厚度小于1时误差大于20%,精度明显低于其他两种方案;同样其透射率的相对误差也是3种方案中最大的。HG和MDHG方案的精度相当,这两种方案的透射率在μ0为0.5—1.0时的相对误差几乎为0。
|
| (a、d.HG,b、e.DHG,c、f.MDHG) 图 4 霾在单次反照率为1时的反射率(a—c)和透射率(d—f)的相对误差 Figure 4 Relative errors of reflection (a-c) and transmission (d-f) (ω=1) for haze |
本研究对DHG方案进行改进,提出了MDHG方案,并将HG、DHG和MDHG这3种方案的相函数进行了系统的对比。由相函数的比较结果发现:HG方案的结果虽然稳定但不能表现出相函数的前向或后向的峰值特征,例如该方案无法准确地描述粗模态沙尘气溶胶相函数的前向峰值和后向峰值以及水云相函数的后向峰值。DHG方案的相函数在后向易出现异常峰值或负值,例如该方案描述的水云相函数出现异常峰值以及粗模态沙尘气溶胶相函数出现负值。整体而言,MDHG方案精度最高,能表现出相函数的前、后向峰值的特征。此外,还利用四流球谐函数展开累加方案,进一步比较了不同相函数参数化方案下的反射率、透射率和吸收率的计算精度。由反射率、透射率和吸收率的计算结果发现:MDHG方案整体更为精确,而HG方案精度较低,例如在水云情况下其误差大于DHG和MDHG方案。DHG方案在沙尘气溶胶和水云情况下计算的结果都比较精确,但是对霾的计算误差较大。
综合比较相函数以及反射率、透射率和吸收率的计算精度,MDHG方案得到的相函数最能表现其前向和后向特征,且该方案计算的反射率、透射率和吸收率的精度也总体优于HG和DHG方案。因此,MDHG方案是理想的相函数参数化方案。
附录在无时间变化,弹性、独立散射的近似条件下,方位角平均的平面平行的辐射传输方程为
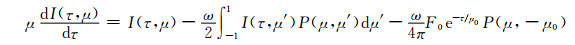
|
(A1) |
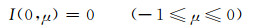
|
(A2) |

|
(A3) |
式中,I(τ, μ)是指介质中光学厚度为τ,天顶角的方向余弦为μ的辐射强度。F0为大气顶垂直于太阳光方向的辐射通量,τ0是该介质的总光学厚度,其中方位角平均的相函数为
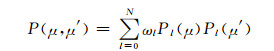
|
(A4) |
球谐函数谱展开的目的就是将辐射强度对角度的依赖进行分离,因此,假设散射强度为
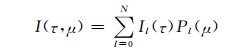
|
(A5) |
取N=3,将辐射强度的在角度空间分布用4个自由度来表示,即为四流球谐函数展开方法,根据辐射传输方程可得
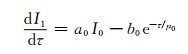
|
(A6) |
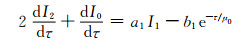
|
(A7) |
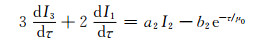
|
(A8) |
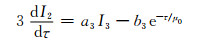
|
(A9) |
上式中,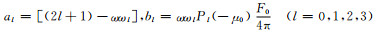
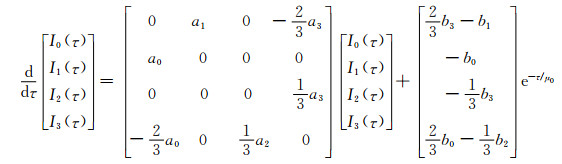
|
(A10) |
利用一阶线性微分方程组基本理论,求得以上方程的解
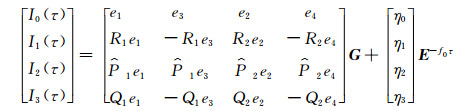
|
(A11) |
式中,参数f0=1/μ0,G=[C1 D1 C2 D2]T,e1=e-k1τ,e2=e-k2τ,e3=e-k1(τ0-τ),e4=e-k2(τ0-τ),R1, 2=-a0/k1, 2,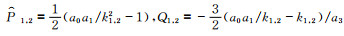
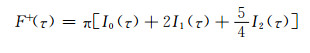
|
(A12) |
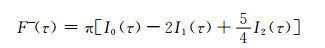
|
(A13) |
因此,该层介质的反射率r(τ0, μ0)、透射率t(τ0, μ0)、吸收率a(τ0, μ0)为
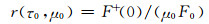
|
(A14) |
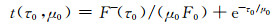
|
(A15) |
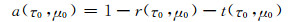
|
(A16) |
对于计算多层非均匀介质联合辐射通量,可采用累加法进行计算。首先,从第1层开始不断向下迭代,得到第1层至第k层联合的透射矩阵T1, k(μ0)和反射矩阵R1, k*
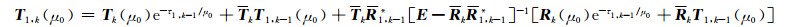
|
(A17) |
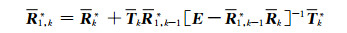
|
(A18) |
式中,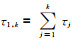
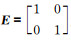
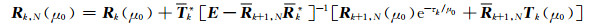
|
(A19) |
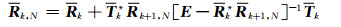
|
(A20) |
式中,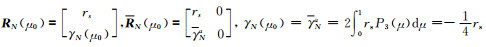
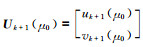
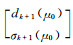
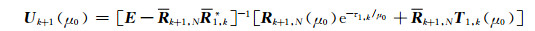
|
(A21) |
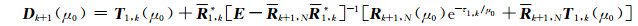
|
(A22) |
因此,在k+1层(第k层的下边界)处向上和向下的辐射通量分别
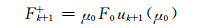
|
(A23) |
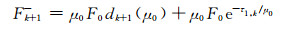
|
(A24) |
大气层顶向上和向下的辐射通量为
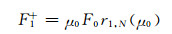
|
(A25) |
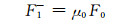
|
(A26) |
式中,uk+1、dk+1和r1, N为矩阵Uk+1(μ0)、Dk+1(μ0)和R1, N(μ0)的第1个元素。关于T1, k(μ0)、R1, k*、Rk, N(μ0)、R、Uk+1(μ0)和Dk+1(μ0)的相关定义见Zhang F等(2013a)和和张峰(2013)。
| 荆现文, 张华. 2012. McICA云-辐射方案在国家气候中心全球气候模式中的应用与评估. 大气科学 , 36 (5) : 945–958. Jing X W, Zhang H. 2012. Application and evaluation of McICA cloud-radiation framework in the AGCM of the national climate center. Chin J Atmos Sci , 36 (5) : 945–958. (in Chinese) |
| 邱金桓. 1999. 一个改进的δ-Eddington近似. 科学通报 , 44 (4) : 304–309. Qiu J H. 1999. An improved δ-Eddington approximation. Chin Sci Bull , 44 (4) : 304–309. DOI:10.1007/BF02885477 (in Chinese) |
| 许尤福, 赵凤生, 闵玉秋. 2011. 平面平行大气中偏振辐射传输的数值计算. 气象学报 , 69 (5) : 912–921. Xu Y F, Zhao F S, Min Y Q. 2011. Numerical calculations for the vector discrete-ordinate radiative transfer in a plane-parallel atmosphere. Acta Meteor Sinica , 69 (5) : 912–921. (in Chinese) |
| 杨学胜, 沈元芳, 徐国强. 2009. 辐射方案对GRAPES全球模式的影响. 大气科学 , 33 (3) : 593–599. Yang X S, Shen Y F, Xu G Q. 2009. The impacts of radiation schemes on the GRAPES global model. Chin J Atmos Sci , 33 (3) : 593–599. (in Chinese) |
| 张峰. 2013.气候变化中辐射传输计算与外强迫因子反演研究[D].北京:中国科学院大学, 122pp. Zhang F. 2013. Radiative transfer parameterizations and reconstruction of driving forces in climate change[D]. Beijing: University of Chinese Academy of Sciences, 122pp (in Chinese) http://cdmd.cnki.com.cn/article/cdmd-85101-1013212456.htm |
| 张梦, 王宏, 黄兴友. 2014. NASA/Goddard长波辐射方案在GRAPES_Meso模式中的应用研究. 大气科学 , 38 (3) : 603–614. Zhang M, Wang H, Huang X Y. 2014. Application research of the NASA/goddard longwave radiative scheme in the GRAPES_Meso model. Chin J Atmos Sci , 38 (3) : 603–614. (in Chinese) |
| Fu Q, Liou K N, Cribb M C, et al. 1997. Multiple scattering parameterization in thermal infrared radiative transfer. J Atmos Sci , 54 (24) : 2799–2812. DOI:10.1175/1520-0469(1997)054<2799:MSPITI>2.0.CO;2 |
| Fu Q, Thorsen T J, Su J, et al. 2009. Test of Mie-based single-scattering properties of non-spherical dust aerosols in radiative flux calculations. J Quant Spectrosc Radiat Transfer , 110 (14-16) : 1640–1653. DOI:10.1016/j.jqsrt.2009.03.010 |
| Garcia R D M, Siewert C E. 1985. Benchmark results in radiative transfer. Transp Theory Stat Phys , 14 (4) : 437–483. DOI:10.1080/00411458508211687 |
| Henyey L C, Greenstein J L. 1941. Diffuse radiation in the Galaxy. Astrophys J , 93 : 70–83. DOI:10.1086/144246 |
| Kattawar G W. 1975. A three-parameter analytic phase function for multiple scattering calculations. J Quant Spectrosc Radiat Transfer , 15 (9) : 839–849. DOI:10.1016/0022-4073(75)90095-3 |
| King M D, Harshvardhan. 1986. Comparative accuracy of selected multiple scattering approximations. J Atmos Sci , 43 (8) : 784–801. DOI:10.1175/1520-0469(1986)043<0784:CAOSMS>2.0.CO;2 |
| Kylling A, Stamnes K, Tsay S C. 1995. A reliable and efficient two-stream algorithm for spherical radiative transfer: Documentation of accuracy in realistic layered media. J Atmos Chem , 21 (2) : 115–150. DOI:10.1007/BF00696577 |
| Li J, Ramaswamy V. 1996. Four-stream spherical harmonic expansion approximation for solar radiative transfer. J Atmos Sci , 53 (8) : 1174–1186. DOI:10.1175/1520-0469(1996)053<1174:FSSHEA>2.0.CO;2 |
| Li J, Dobbie J S, Raisanen P, et al. 2005. Accounting for unresolved clouds in a 1-D solar radiative-transfer model. Quart J Roy Meteor Soc , 131 (608) : 1607–1629. DOI:10.1256/qj.04.31 |
| Li J, Barker H, Yang P, et al. 2015. On the aerosol and cloud phase function expansion moments for radiative transfer simulations. J Geophys Res , 120 (23) : 12128–12142. DOI:10.1002/2015JD023632 |
| Liou K N, Fu Q, Ackerman T P. 1988. A simple formulation of the delta-four-stream approximation for radiative transfer parameterizations. J Atmos Sci , 45 (13) : 1940–1947. DOI:10.1175/1520-0469(1988)045<1940:ASFOTD>2.0.CO;2 |
| Lu P, Zhang H, Li J. 2009. A new complete comparison of two-stream DISORT and Eddington radiative transfer schemes in a real atmospheric profile. J Quant Spectrosc Radiat Transfer , 110 (1-2) : 129–138. DOI:10.1016/j.jqsrt.2008.09.009 |
| Mishchenko M I, Travis L D. 1994. T-matrix computations of light scattering by large spheroidal particles. Opt Commun , 109 (1-2) : 16–21. DOI:10.1016/0030-4018(94)90731-5 |
| Pruppacher H R, Klett J D. 1996. Microphysics of Clouds and Precipitation. Dordrecht Boston: Kluwer Academic Publishers : 976pp . |
| Qiu J H. 1999. Modified delta-eddington approximation for solar reflection, transmission, and absorption calculations. J Atmos Sci , 56 (16) : 2955–2961. DOI:10.1175/1520-0469(1999)056<2955:MDEAFS>2.0.CO;2 |
| Sokolik I N, Toon O B, Bergstrom R W. 1998. Modeling the radiative characteristics of airborne mineral aerosols at infrared wavelengths. J Geophys Res , 103 (D8) : 8813–8826. DOI:10.1029/98JD00049 |
| Stamnes K, Tsay S C, Wiscombe W, et al. 1988. Numerically stable algorithm for discrete-ordinate-method radiative transfer in multiple scattering and emitting layered media. Appl Opt , 27 (12) : 2502–2509. DOI:10.1364/AO.27.002502 |
| Wiscombe W J. 1977. The delta-M method: Rapid yet accurate radiative flux calculations for strongly asymmetric phase functions. J Atmos Sci , 34 (9) : 1408–1422. DOI:10.1175/1520-0469(1977)034<1408:TDMRYA>2.0.CO;2 |
| Yang P, Feng Q, Hong G, et al. 2007. Modeling of the scattering and radiative properties of nonspherical dust-like aerosols. J Aerosol Sci , 38 (10) : 995–1014. DOI:10.1016/j.jaerosci.2007.07.001 |
| Zhang F, Li J. 2013a. Doubling-adding method for delta-four-stream spherical harmonic expansion approximation in radiative transfer parameterization. J Atmos Sci , 70 (10) : 3084–3101. DOI:10.1175/JAS-D-12-0334.1 |
| Zhang F, Shen Z, Li J, et al. 2013b. Analytical delta-four-stream doubling-adding method for radiative transfer parameterizations. J Atmos Sci , 70 (3) : 794–808. DOI:10.1175/JAS-D-12-0122.1 |
| Zhang F, Wu K, Li J, et al. 2016. Analytical infrared delta-four-stream adding method from invariance principle. J Atmos Sci, doi: http://dx.doi.org/10.1175/JAS-D-15-0317.1 |
| Zhang H, Jing X, Li J. 2014. Application and evaluation of a new radiation code under McICA scheme in BCC_AGCM2.0.1. Geosci Model Dev , 7 (3) : 737–754. DOI:10.5194/gmd-7-737-2014 |
| Zhang H, Wang Z L, Zhang F, et al. 2015. Impact of four-stream radiative transfer algorithm on aerosol direct radiative effect and forcing. Int J Climatol , 35 (14) : 4318–4328. DOI:10.1002/joc.4289 |
| Zhao J Q, Shi G Y, Che H Z, et al. 2006. Approximations of the scattering phase functions of particles. Adv Atmos Sci , 23 (5) : 802–808. DOI:10.1007/s00376-006-0802-y |
 2016, Vol. 74
2016, Vol. 74


