中国气象学会主办。
文章信息
- 曹伟华, 梁旭东, 赵晗萍, 段小刚, 张自银 . 2016.
- CAO Weihua, LIANG Xudong, ZHAO Hanping, DUAN Xiaogang, ZHANG Ziyin . 2016.
- 基于Copula函数的北京强降水频率及危险性分析
- Copula-based frequency analysis and its application in hazard risk assessment of heavy rainfall in Beijing
- 气象学报, 74(5): 772-783.
- Acta Meteorologica Sinica, 74(5): 772-783.
- http://dx.doi.org/10.11676/qxxb2016.056
-
文章历史
- 2015-10-27 收稿
- 2016-05-30 改回
2. 中国气象科学研究院灾害天气国家重点实验室, 北京, 100081;
3. 北京师范大学减灾与应急管理研究院, 北京, 100875;
4. 北京师范大学统计学院, 北京, 100875;
5. 北京市气象局, 北京, 100089
2. State Key Laboratory of Severe Weather, Chinese Academy of Meteorological Sciences, Beijing 100081, China;
3. Academy of Disaster Reduction and Emergency Management, Beijing Normal University, Beijing 100875, China;
4. School of Statistics, Beijing Normal University, Beijing 100875, China;
5. Beijing Meteorological Service, Beijing 100089, China
IPCC(2012)报告指出,在气候变暖背景下,21世纪全球许多地区强降水事件的频率和强度很可能增大。强降水作为中国许多城市的一种严重的致灾因子,容易诱发城市内涝、泥石流和山体滑坡等灾害,造成严重财产损失和人员伤亡。因此,强降水致灾因子频率及其危险性分析对于城市防灾、减灾规划以及灾害风险管理具有重要现实意义。
强降水持续时间、降水量和降水强度是描述强降水事件的重要指标(Kim et al, 2012)。强降水致灾因子危险性通常通过其致灾因子强度超过一定量级的频率(或重现期)来度量。目前常采用日降水量作为强降水危险性的指标,通过一元分布刻画强降水重现期(Adamowski, 2000)。然而,这种基于单因子的评价方法实际上把本质上为多个维度的强降水事件简化到一个维度,因此,丢失强降水致灾因子的许多重要信息,具有明显局限性。为克服这一缺点,已有研究尝试建立强降水的多变量联合分布(Yue et al, 2002)。然而,传统的多变量联合分布建模方法通常需要很强的假设条件,如变量间满足独立性假设、各变量服从相同边缘分布、多变量的联合分布服从正态分布或可以转化为正态分布等(Zhang et al, 2007),而强降水事件并不能保证变量之间的独立性,也很难满足服从相同边缘分布的假设,因此,传统的多变量联合分布方法并不适用于强降水事件的频率分析。为了体现强降水持续时间与降水量对其致灾后果的综合影响,近年来,中国已有学者开展了强降水指标加权的指数分析(扈海波等,2013;Zou et al, 2015),或通过日降水量和降水日数分析强降水频率时空特征(张强等,2011; Li et al, 2015)等相关研究。这些工作虽然从不同角度强调了多维指标变量对强降水频率及致灾因子危险性刻画的重要性,然而其对强降水致灾指标的考虑仍以传统的降水日数和降水量为主,而诸如短历时强降水的信息在分析中并不能得到凸显,因此,很难体现自然降水持续时间对于强降水危险性的影响。
相比于传统方法,由Sklar(1959)提出的Copula方法可更加灵活地构建具有依存关系的多变量联合分布,由于该方法中边缘分布类型不受约束,变量也无需满足独立性假设,因此,在刻画多变量的相互依存关系上更具有优势。目前,Copula方法在降水事件分析中已得到应用,De Michele等(2003)首次建立基于Copula的强降水频率模型,通过二元Copula函数并结合广义帕累托分布模拟了降水强度和持续时间的依存关系;Zhang等(2007)通过阿基米德Copula函数建立降水变量的二元分布,确定降水变量的联合重现期;Vandenberghe等(2011)利用二元Copula函数比较观测与模拟的降水事件重现期。同时,Copula还被广泛应用于干旱领域,如Rauf等(2014)研究了澳大利亚干旱强度与历时的联合分布及重现期;刘晓云等(2015)基于Copula函数建立中国南方干旱历时与严重程度的联合分布,并计算干旱条件重现期,比较干旱联合重现期的空间分布特征。这些研究为洪涝、干旱等极端事件的频率分析和风险研究提供了有效途径。
北京作为中国的政治、文化中心,强降水灾害频发,风险防范工作尤为重要。虽然已有相关研究通过一元分布探讨了个别站点的降水重现期(马京津等,2012),然而对强降水持续时间与降水量的二元联合分布,以及两者耦合作用下的强降水频率及致灾因子危险性空间特征的研究仍较为欠缺。已有研究表明,随着全球变暖与城市化进程的加剧,北京夏季短时强降水增多,少于12 h的强降水在总降水量中所占比例已超过75%(Li et al,2008)。因此,全面分析北京地区强降水的时空特征对于提升该区域精细化强降水灾害预警水平尤为重要。本研究将综合考虑北京地区强降水持续时间和过程降水量两个致灾因子,通过构建两者的二元Copula模型,刻画降水持续时间和过程降水量耦合作用下的强降水频率特性和致灾因子危险性空间特征,以期为北京地区强降水灾害的防灾、减灾规划与风险管理提供科学依据。
2 研究方法 2.1 二元Copula函数记连续型随机变量X、Y的二元累积分布函数为H(x, y),依据Sklar定理(Sklar, 1959),存在唯一的、定义在[0, 1]2上的二元分布函数C(·, ·),使得
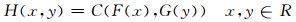
|
(1) |
式中,F(x)和G(y)为边缘累积分布函数,C(·, ·)为与(X, Y)对应的二元Copula函数,也称为连接函数(连接联合分布和边缘分布)。二元Copula函数具有不依赖于X, Y的边缘分布形式,完全刻画多变量间相依结构的显著特点(Genest,et al,2007),已成为多变量相依度分析的重要研究工具。
2.2 基于Copula的强降水致灾因子联合分布构建强降水的持续时间(D)和过程降水量(W)是体现强降水致灾的主要指标。基于Copula函数对(D, W)进行联合建模包括两个部分:一是确定降水持续时间、过程降水量的边缘分布函数及其参数,即确定F(d)、G(w);二是确定Copula函数和参数。下文将详细介绍强降水致灾因子联合分布模型的构建。
2.2.1 候选边缘分布边缘概率分布的确定是构建北京地区强降水致灾因子联合分布的重要前提。由于降水变量的概率分布具有地区差异性,采用目前强降水频率分析中应用最为广泛的6种概率分布作为拟合强降水持续时间和过程降水量的候选边缘分布(表 1)(Vandenberghe et al, 2011;Salvadori et al, 2015;Rauf et al, 2014),并采用最大似然估计法进行边缘分布函数的参数估计(Zhang et al, 2012)。通过K-S(Kolmogorov-Smirnov)检验(Massey, 1951)比较6种分布的拟合优度,以确定北京地区各站点降水持续时间和过程降水量的最佳边缘分布类型。6种候选分布分别为指数(Exp)、广义极值(GEV)、伽玛(Γ)、对数正态(LN)、韦伯分布(Weibull)和广义帕累托(GP)分布(表 1)。
| 分布 | 边缘分布函数 | 参数 |
| 指数 | F(x)=1-exp(-x/μ) | μ为均值 |
| 广义极值 | F(x)=exp(-[1+ξ(x-μ)/σ]-1/ξ) | ξ≠0为形状参数,σ>0为尺度参数,μ为位置参数 |
| 伽玛 | 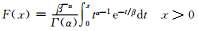 |
α为形状参数, β为尺度参数, Γ(α)为伽玛函数 |
| 对数正态 | F(x)=Φ((lnx-μ)/σ) | Φ(x)为标准正态分布函数, μ为均值, σ为标准差 |
| 韦伯 | F(x)=1-exp[-(x/α)β] | α>0为尺度参数, β>0为形状参数 |
| 广义帕累托 | F(x)=1-[1+ξ(x-μ)/σ]-1/ξ | ξ≠0为形状参数, σ>0为尺度参数, μ为位置参数 |
选择恰当的Copula函数族刻画强降水持续时间和过程降水量的相依结构是构建强降水致灾因子联合分布的另一个重要环节。在众多Copula函数族中,Gumbel、Clayton和Frank 3种阿基米德Copula函数对强降水频率特征的刻画应用最为广泛(De Michele et al, 2003; Zhang et al, 2007; Kao et al, 2007;Vandenberghe et al, 2011),因此,文中采用这3种候选Copula函数刻画强降水持续时间和过程降水量的相依结构(表 2)。Copula函数的参数采用最大似然估计法实现(Zhang et al, 2012)。通过CvM (Cramér-von Mises)检验(Genest et al, 2009, 2011)比较Copula函数的拟合优度,确定刻画降水持续时间和过程降水量相依结构的二元Copula函数。
| Copula | C(u, v) | 参数θ范围 |
| Gumbel | exp(-[(-lnu)1/θ+(-lnv)1/θ]θ) | θ∈(0, 1] |
| Clayton | (u-θ+v-θ-1)-1/θ | θ∈(0, ∞) |
| Frank | 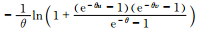 |
θ∈(-∞, ∞)\{0} |
重现期作为一种量化致灾因子危险性的指标,被广泛应用于灾害风险分析等领域(Kao et al, 2007;刘晓云等,2015),为城市防灾工程设计提供依据,对于城市灾害风险评估和管理具有重要意义。文中主要对以下两种重现期情景进行讨论:
(1) 无条件重现期情景:适用于单一因素对事件具有决定性作用,或者两个随机变量无相关性或相关性很弱的情况。假设强降水致灾因子的危险性完全取决于过程降水量,则通过过程降水量的重现期来刻画强降水致灾因子危险性是合理的。此时,无条件重现期定义为大于等于一定过程降水量的强降水事件平均出现的时间间隔,可表示为

|
(2) |
式中,μT是强降水事件的平均间隔时间,如,密云站在2005—2014年的10年间共出现46次强降水事件,由此推算强降水事件的平均间隔,μT=10/46=0.217 a/次,由于北京强降水一般集中于5—9月,其他月份很少出现强降水,这意味着密云夏季平均1.1个月出现一次强降水事件。
(2) 条件重现期情景:强降水作为一种致灾因子,其致灾特性受持续时间和降水量的共同影响。通过条件重现期可以更合理地刻画二重因素影响下的强降水事件的频率特征。通过边缘分布和二元Copula函数构建强降水条件概率表达式是计算条件重现期的基础。条件概率表达式和条件重现期的建立往往需结合致灾因子自身的实际特性。比如对干旱而言,通常干旱历时越长、干旱严重程度越重其致灾后果亦越重,进行致灾危险分析时主要考虑在历时较长条件下严重程度超过一定阈值的干旱条件概率和重现期(刘晓云等,2015);而对于强降水而言,往往在短时间内强度很大的降水事件的致灾后果很严重,因此,此类事件的频率分析主要考虑在一定持续时间时强度超过一定阈值的强降水条件概率(Kao et al, 2007)。
结合北京地区夏季短历时强降水较多的特点,将降水持续时间小于某阈值(d)条件下,过程降水量大于某阈值(w)的强降水条件概率定义为

|
(3) |
进一步,强降水条件重现期定义为一定持续时间内过程降水量超过一定阈值的强降水事件平均出现的时间间隔。假设持续时间在一定阈值d内,过程降水量超过某阈值w的强降水事件的条件重现期情景为TCOND,其计算公式可表示为(Kao et al, 2007)

|
(4) |
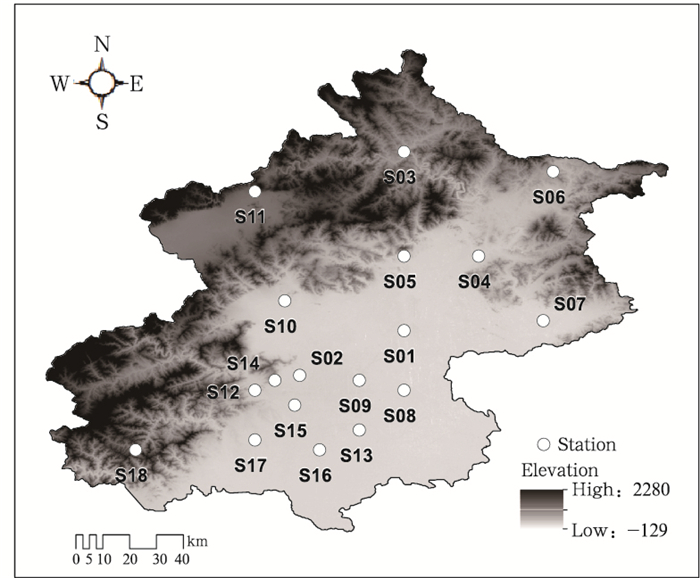
采用北京地区2005—2014年5—9月逐时台站(图 1)降水量资料进行分析。根据北京地区降水事件的持续性特征(Li et al, 2008),选取2 h作为无雨持续时间间隔来区分两次独立的降水事件,并将降水强度大于0.05 mm/h的降水过程判定为一次有效降水事件,同时,选取一次降水事件从开始至结束的累积小时数作为降水持续时间D(h),D小时内的累积降水量作为本次降水事件的过程降水量W(mm),并将过程降水量大于等于15 mm且平均降水强度大于等于5 mm/h的降水事件定义为强降水事件。
|
| 图 1 站点空间分布及北京地形高度分布 Figure 1 Locations of meteorological stations and the topography of Beijing |
从研究时段内北京地区各站点的强降水次数、降水持续时间以及过程降水量的基本统计特征(表 3)可以看出,北京地区强降水事件发生频次平均为33次,且存在很强的区域差异,其中密云地区发生最频繁,为46次。各站平均过程降水量在30 mm以上,最大过程降水量和最长持续时间都出现在霞云岭,分别达到338 mm和31 h,其他大部分站点的降水最长持续时间则小于24 h。总体而言,北京地区强降水事件持续时间较短,平均持续时间为4—6 h,短历时强降水特性明显。从过程降水量与持续时间的Kendall秩相关系数τ来看(表 3),强降水事件的过程降水量与持续时间成正相关,Kendall秩相关系数τ在0.41—0.75(达到0.01显著性水平)。并且,北京地区强降水过程降水量随着持续时间延长而增大,呈现出明显的相关关系(图 2),整体上τ可达到0.61。以上结果表明,北京地区强降水事件的过程降水量与降水持续时间存在显著的依存关系,适合采用Copula函数建立两者之间的联合分布。
| 站号 | 站名 | 次数 | 持续时间(h) | 过程降水量(mm) | Kendall秩相关系数 | ||||
| 最小值 | 最大值 | 平均值 | 最小值 | 最大值 | 平均值 | ||||
| S01 | 顺义 | 33 | 2 | 19 | 6 | 17 | 242 | 50 | 0.75 |
| S02 | 海淀 | 42 | 1 | 23 | 6 | 16 | 239 | 44 | 0.57 |
| S03 | 汤河口 | 21 | 1 | 15 | 4 | 16 | 78 | 30 | 0.58 |
| S04 | 密云 | 46 | 1 | 18 | 5 | 15 | 204 | 46 | 0.65 |
| S05 | 怀柔 | 32 | 1 | 26 | 6 | 16 | 154 | 45 | 0.69 |
| S06 | 上甸子 | 30 | 1 | 17 | 4 | 15 | 111 | 33 | 0.48 |
| S07 | 平谷 | 41 | 1 | 16 | 5 | 15 | 220 | 39 | 0.67 |
| S08 | 通州 | 38 | 1 | 16 | 5 | 15 | 171 | 39 | 0.63 |
| S09 | 朝阳 | 37 | 1 | 15 | 5 | 19 | 223 | 45 | 0.41 |
| S10 | 昌平 | 19 | 1 | 18 | 6 | 19 | 144 | 51 | 0.62 |
| S11 | 佛爷顶 | 17 | 1 | 14 | 5 | 17 | 91 | 34 | 0.72 |
| S12 | 门头沟 | 35 | 1 | 24 | 6 | 16 | 305 | 49 | 0.72 |
| S13 | 观象台 | 35 | 1 | 16 | 4 | 16 | 160 | 37 | 0.62 |
| S14 | 石景山 | 45 | 1 | 17 | 5 | 18 | 292 | 44 | 0.58 |
| S15 | 丰台 | 39 | 1 | 18 | 5 | 15 | 244 | 41 | 0.65 |
| S16 | 大兴 | 36 | 2 | 16 | 5 | 15 | 185 | 39 | 0.56 |
| S17 | 房山 | 33 | 1 | 17 | 5 | 15 | 254 | 41 | 0.58 |
| S18 | 霞云岭 | 26 | 1 | 31 | 6 | 15 | 338 | 51 | 0.65 |

|
| 图 2 北京地区强降水持续时间与过程降水量的散点分布 Figure 2 Scatter plot of correlated heavy rainfall variables in Beijing |
为确定强降水事件持续时间和过程降水量的边缘概率分布,采用最大似然法估计强降水变量的边缘分布参数,并采用K-S检验(Massey, 1951)对北京地区各站点强降水持续时间和过程降水量的6种概率分布进行拟合优度检验(表 4)。选取P值大于0.05且统计量最小的分布函数作为各站点降水变量的最佳边缘概率分布。以密云站为例,该站降水持续时间和过程降水量以对数正态和广义极值分布的K-S统计量最小,适合分别作为密云站降水持续时间和过程降水量的边缘分布。通过对比该站6种候选边缘分布拟合的理论累积分布与经验累积分布的匹配程度(图 3),也进一步证实了这两种边缘分布的选择是合适的。因此,密云站降水持续时间和过程降水量的边缘分布类型分别采用对数正态和广义极值分布。从表 4所给出的各站点选定的边缘分布可以看出,北京地区降水持续时间在多数站点以广义极值和对数正态分布为主,而过程降水量在绝大多数站点则更适用于广义极值分布。整体而言,广义极值分布和对数正态分布更适合作为北京地区强降水持续时间和过程降水量的边缘分布。
| 站名 | 持续时间 | 过程降水量 | ||||||
| 分布 | Dn | P值 | 参数值 | 分布 | Dn | P值 | 参数值 | |
| 顺义 | 韦伯 | 0.18 | 0.23 | α=6.54,β=1.44 | 广义极值 | 0.08 | 0.97 | ξ=0.65,σ=12.72,μ=29.00 |
| 海淀 | 对数正态 | 0.11 | 0.61 | μ=1.52,σ=0.60 | 广义极值 | 0.07 | 0.97 | ξ=0.40,σ=11.82,μ=29.14 |
| 汤河口 | 广义极值 | 0.19 | 0.39 | ξ=0.23,σ=1.5,μ=2.54 | 伽玛 | 0.17 | 0.51 | α=4.63,β=6.44 |
| 密云 | 对数正态 | 0.11 | 0.54 | μ=1.49,σ=0.65 | 广义极值 | 0.08 | 0.92 | ξ=0.55,σ=13.62,μ=27.72 |
| 怀柔 | 对数正态 | 0.11 | 0.75 | μ=1.37,σ=0.82 | 广义极值 | 0.10 | 0.84 | ξ=0.61,σ=12.11,μ=27.11 |
| 上甸子 | 对数正态 | 0.19 | 0.22 | μ=1.25,σ=0.51 | 广义极值 | 0.10 | 0.87 | ξ=0.58,σ=7.53,μ=22.04 |
| 平谷 | 广义极值 | 0.14 | 0.40 | ξ=0.32,σ=1.56,μ=3.07 | 广义极值 | 0.07 | 0.96 | ξ=0.62,σ=9.50,μ=23.51 |
| 通州 | 对数正态 | 0.12 | 0.61 | μ=1.47,σ=0.56 | 广义极值 | 0.08 | 0.96 | ξ=0.38,σ=10.99,μ=26.77 |
| 朝阳 | 广义极值 | 0.11 | 0.70 | ξ=0.14,σ=1.97,μ=3.48 | 广义极值 | 0.06 | 1.00 | ξ=0.61,σ=10.17,μ=28.14 |
| 昌平 | 广义极值 | 0.11 | 0.94 | ξ=0.52,σ=2.17,μ=3.19 | 广义极值 | 0.10 | 0.98 | ξ=0.73,σ=12.47,μ=29.29 |
| 佛爷顶 | 对数正态 | 0.16 | 0.72 | μ=1.24,σ=0.81 | 对数正态 | 0.14 | 0.82 | μ=3.55,σ=0.74 |
| 门头沟 | 广义极值 | 0.15 | 0.37 | ξ=0.53,σ=1.81,μ=3.02 | 广义极值 | 0.07 | 0.98 | ξ=0.78,σ=11.64,μ=25.47 |
| 观象台 | 广义极值 | 0.16 | 0.27 | ξ=0.44,σ=1.47,μ=2.59 | 广义极值 | 0.08 | 0.98 | ξ=0.73,σ=8.61,μ=22.85 |
| 石景山 | 广义极值 | 0.14 | 0.31 | ξ=0.34,σ=1.82,μ=3.31 | 广义极值 | 0.05 | 1.00 | ξ=0.69,σ=9.00,μ=26.52 |
| 丰台 | 广义极值 | 0.16 | 0.27 | ξ=0.41,σ=1.57,μ=2.94 | 广义极值 | 0.10 | 0.81 | ξ=0.83,σ=9.40,μ=22.53 |
| 大兴 | 对数正态 | 0.15 | 0.38 | μ=1.41,σ=0.58 | 广义极值 | 0.08 | 0.95 | ξ=0.53,σ=10.05,μ=24.82 |
| 房山 | 对数正态 | 0.14 | 0.51 | μ=1.31,σ=0.63 | 广义极值 | 0.08 | 0.97 | ξ=0.55,σ=10.54,μ=24.72 |
| 霞云岭 | 伽玛 | 0.15 | 0.51 | α=1.57,β=3.78 | 对数正态 | 0.14 | 0.65 | μ=3.55,σ=0.74 |
| 注:Dn表示K-S检验的统计量。 | ||||||||

|
| 图 3 密云站降水持续时间(a)和过程降水量(b)不同边缘分布的拟合效果 Figure 3 Comparisons of different CDFs of rainfall duration (a) and accumulated precipitation (b) for Miyun station |
强降水二元Copula分布首先采用最大似然法估计模型参数,然后根据CvM检验比较3种阿基米得Copula函数的拟合优度,从而确定北京地区各站点强降水事件的二元Copula函数类型。表 5给出了各站点3种候选Copula函数族对应的CvM检验统计量取值及其P值。P值越大表示拟合程度越高,P值越小说明该Copula函数族越不适于用来拟合目标站点数据。可以看出,在0.01的显著性水平下,Frank Copula函数基本上通过检验(表示现有数据不能拒绝候选Copula函数),但当显著性水平增大至实际中经常采用的0.05时,Frank Copula在绝大部分站点上不能通过检验。相反,在绝大多数情况下,Gumbel Copula函数P值最大,即使在0.05显著性水平上绝大多数站点也可以通过检验,说明Gumbel Copula函数对于多数站点拟合效果更好,因此,采用Gumbel Copula函数族刻画北京这些站点强降水持续时间和过程降水量的相依结构。北京东北部顺义、密云少数站点则是更适合用Frank Copula函数,说明这些地区的降水分布类型具有某种特殊性,其相关结构值得进一步分析研究。至此,建立了北京地区强降水二元Copula分布,为强降水条件重现期及危险性分析奠定了基础。
| 站号 | 站名 | 参数θ | Clayton | Frank | Gumbel | |||
| 统计量 | P值 | 统计量 | P值 | 统计量 | P值 | |||
| S01 | 顺义 | 12.746 | 0.154 | 0.000 | 0.029 | 0.349* | 0.045 | 0.018* |
| S02 | 海淀 | 0.471 | 0.175 | 0.000 | 0.051 | 0.012* | 0.033 | 0.105* |
| S03 | 汤河口 | 0.521 | 0.099 | 0.008 | 0.046 | 0.157* | 0.032 | 0.477* |
| S04 | 密云 | 8.100 | 0.139 | 0.000 | 0.031 | 0.181* | 0.035 | 0.089* |
| S05 | 怀柔 | 0.365 | 0.103 | 0.002 | 0.039 | 0.095* | 0.027 | 0.385* |
| S06 | 上甸子 | 0.656 | 0.137 | 0.000 | 0.053 | 0.035* | 0.038 | 0.115* |
| S07 | 平谷 | 0.404 | 0.138 | 0.000 | 0.044 | 0.030* | 0.030 | 0.185* |
| S08 | 通州 | 0.418 | 0.121 | 0.000 | 0.045 | 0.035* | 0.031 | 0.218* |
| S09 | 朝阳 | 0.618 | 0.105 | 0.002 | 0.053 | 0.014* | 0.036 | 0.125* |
| S10 | 昌平 | 0.414 | 0.107 | 0.008 | 0.062 | 0.041* | 0.036 | 0.387* |
| S11 | 佛爷顶 | 0.423 | 0.409 | 0.093* | 0.060 | 0.052* | 0.040 | 0.260* |
| S12 | 门头沟 | 0.358 | 0.166 | 0.000 | 0.069 | 0.002 | 0.046 | 0.016* |
| S13 | 观象台 | 0.444 | 0.167 | 0.000 | 0.044 | 0.042* | 0.028 | 0.306* |
| S14 | 石景山 | 0.471 | 0.220 | 0.000 | 0.070 | 0.001 | 0.042 | 0.028* |
| S15 | 丰台 | 0.411 | 0.156 | 0.000 | 0.046 | 0.030* | 0.024 | 0.450* |
| S16 | 大兴 | 0.480 | 0.151 | 0.000 | 0.052 | 0.016* | 0.037 | 0.099* |
| S17 | 房山 | 0.481 | 0.082 | 0.010* | 0.033 | 0.268* | 0.022 | 0.725* |
| S18 | 霞云岭 | 0.432 | 0.169 | 0.000 | 0.054 | 0.029* | 0.038 | 0.148* |
| 注:*表示在0.01显著性水平上通过检验,下划线代表拟合优度最高的Copula分布的P值。 | ||||||||
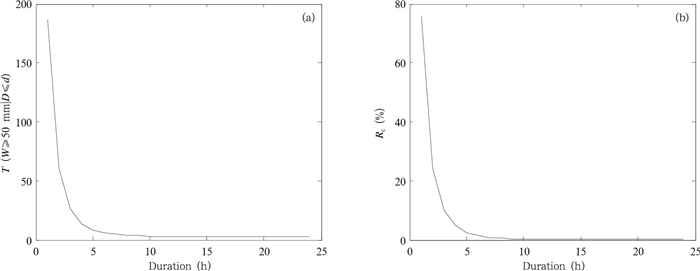
图 4a给出了北京地区平均的强降水持续时间与降水量超过50 mm的条件重现期关系。可以看出,条件重现期随着持续时间缩短而迅速增大,当持续时间很短时(小于6 h),条件重现期的变化尤其明显;而当持续时间在6 h以上时,强降水事件的条件重现期则相对稳定。强降水事件无条件重现期与条件重现期的差异率(RC=(TCOND-Tw)/Tw×100%)也反映出类似特征(图 4b),在降水持续时间较长时差异率相对较小,而当降水持续时间小于6 h时差异率较为明显,说明对于持续时间小于6 h这种短历时强降水事件,综合考虑强降水持续时间和过程降水量来刻画强降水频率显得尤为重要。
|
| 图 4 北京地区平均强降水持续时间与条件重现期(a)及差异率RC(b)对应关系 Figure 4 The relationship between the duration and the conditional return period (a), and that between the duration and the changing rate RC(b) |
根据《北京市气象灾害预警信号与防御指南》(北京市气象局,2013)对降水持续时间及降水量的界定标准,选取两种情景进行强降水致灾危险性分析:(1) 12 h以内降水量超过50 mm,此时达到暴雨蓝色预警标准;(2) 6 h降水量超过50 mm,此时达到暴雨黄色预警标准。这两类强降水都可能诱发城市内涝、山体滑坡及泥石流等灾害,对这两种情景条件重现期的分析有助于为城市强降水灾害的防灾、减灾提供依据。
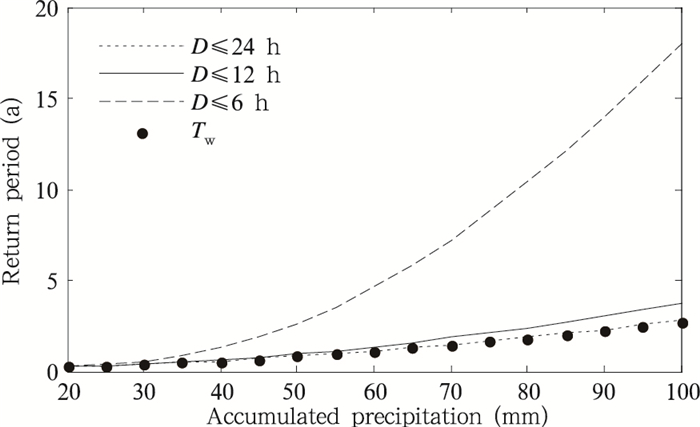
图 5以密云站为例,给出了持续时间阈值分别为12和6 h时,强降水条件重现期随过程降水量的变化。可见对于相同的降水持续时间,条件重现期随着过程降水量的增大而增大,而对于相同的过程降水量,条件重现期随着降水持续时间缩短而增大。实际上,同时考虑降水持续时间和过程降水量两个因素相当于考虑了降水事件的平均强度,即同样的过程降水量,持续时间越短,则平均强度越大,进而发生概率越低,重现期越长,表明此类事件在相同承灾条件下产生的灾害后果往往也越严重。因此,可以通过条件重现期区分不同强降水事件的致灾危险性。
|
| 图 5 密云站过程降水量的条件重现期及无条件重现期 Figure 5 Conditional return periods of accumulated precipitation with given durations and the unconditional return periods in Miyun |
图 5还给出了无条件重现期与持续时间阈值为24 h的条件重现期结果,可以发现,无条件重现期与24 h的条件重现期十分接近。根据各自定义,条件重现期是在持续时间低于一定的阈值(d)时,讨论某类致灾性强降水出现的频率,而无条件重现期是在所有样本中讨论该类事件出现的频率,因此,当持续时间阈值越来越大时,两类样本的差异越来越小,从而当阈值足够大时,对应的两类重现期的差异趋近于0。密云站强降水持续时间较短,最长降水持续时间(18 h)低于24 h阈值,因此,该站点的无条件重现期与条件重现期接近。
值得一提的是,在一些灾害风险评估中,日降水量常作为估算重现期或评价致灾危险性的指标,即在限定于持续时间≤24 h的这种情况做分析,这在北京地区相当于考虑无条件重现期情景,具有较大局限性。由于北京地区短历时强降水事件频发,其重现期与无条件重现期差别很大,因此,通过日降水量进行估算将导致对短历时强降水事件重现期及危险性的低估。相比而言,基于Copula函数的强降水事件的条件重现期由于刻画了降水持续时间和过程降水量的依存关系,可以综合反映不同强降水持续时间条件下的强降水事件频率信息,因此能更合理地刻画不同强降水事件的致灾因子危险性特征。
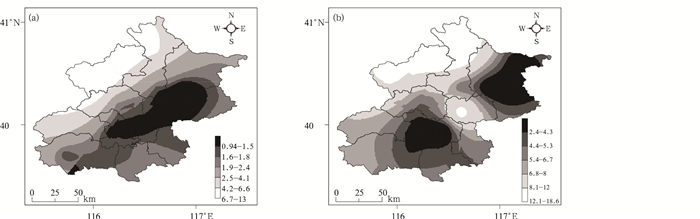
3.3.2 典型强降水的重现期空间分布特征在城市洪涝灾害防灾、减灾中,不仅需要了解某地典型强降水频率的整体信息,还需要了解该区域强降水致灾因子的空间分布,以便合理地开展区域防灾、减灾规划与救灾布局。为此,进一步分析持续时间阈值在12和6 h条件下,过程降水量超过50 mm的典型强降水重现期(记作TW≥50 mm|D≤12 h、TW≥50 mm|D≤6 h)在北京地区的空间分布(图 6)。可以看出,TW≥50 mm|D≤12 h情景下,重现期的空间分布呈明显的东北—西南走向,与北京地区的地形分布保持一致(图 1),表明在地形影响下,北京山前平原地区,此类强降水事件的发生频率较高, 而在西部、西北部山区,频率则较低。对于降水强度更大的TW≥50 mm|D≤6 h情景,重现期的低值中心则主要集中在北京城区及东北部,表明这些地区持续时间在6 h以内的50 mm以上强降水事件发生更为频繁,此类事件致灾因子危险性也相对更高,这一空间分布特征也印证了城市对局地强降水强度的影响(郑祚芳等,2015)。以上两种重现期情景的空间分布差异性表明,根据降水持续时间和过程降水量对强降水致灾因子进行综合分析,可以更全面地给出不同情景强降水致灾因子强度与频率的空间分布信息,从而为北京地区应对不同强降水的灾害风险提供科学依据。
|
| 图 6 过程降水量≥50 mm,持续时间≤12 h(a)、持续时间≤6 h(b)的强降水条件重现期的空间分布(单位:a) Figure 6 Spatial distributions of the conditional return period of accumulated precipitation greater than 50 mm with durations of D≤12 h (a) and D≤6 h (b) (unit: a) |
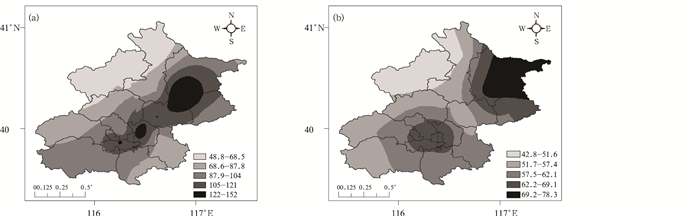
重现期对应的降水量阈值是城市雨水系统规划设计的重要依据。根据北京经济、人口及自然条件等的空间分布特征,目前,北京重点地区的雨水系统设计重现期为5—10 a(马洪涛等,2013)。本小节通过计算北京地区10年一遇(T=10 a)和5年一遇(T=5 a)的两种情景重现期的降水量阈值(表 6),作为强降水致灾因子危险性的重要指标,并给出北京地区不同情景强降水危险性的空间分布特征。以T=10 a情景为例(图 7),北京地区降水持续时间在12 h以内的过程降水量空间分布整体呈东北—西南走向的带状结构(图 7a),与北京地形分布比较一致,在北京城区朝阳站和东北远郊区密云站降水量分别达到132、154 mm。而降水持续时间在6 h以内的降水量在北京地区呈现两个明显高值中心,分别在东北远郊密云地区以及北京城区(图 7b)。密云站的过程降水量在78 mm以上,北京城区表现为另一降水量高值中心,朝阳、海淀、石景山、丰台、观象台、门头沟的过程降水量均在63 mm以上。以上分析表明,通过条件重现期刻画强降水危险性,能更好地体现致灾因子的过程降水量和持续时间的二维强度和频率信息。综合而言,不同情景强降水事件的危险性具有明显的地区差异特征,其中10年一遇强降水事件在北京城区及东北部密云地区的危险性最高,应在城市雨水系统设计和城市洪涝防灾减灾规划中予以重点考虑。
| 站号 | 站名 | 5年一遇 | 10年一遇 | ||||
| D≤6 h | D≤12 h | D≤24 h | D≤6 h | D≤12 h | D≤24 h | ||
| S01 | 顺义 | 41.39 | 85.66 | 132.11 | 46.22 | 121.74 | 198.46 |
| S02 | 海淀 | 54.25 | 76.90 | 96.97 | 62.85 | 94.37 | 127.47 |
| S03 | 汤河口 | 41.42 | 47.09 | 48.72 | 46.46 | 53.06 | 55.32 |
| S04 | 密云 | 63.87 | 114.00 | 131.59 | 78.88 | 154.19 | 197.87 |
| S05 | 怀柔 | 49.05 | 73.45 | 101.33 | 56.69 | 88.50 | 139.89 |
| S06 | 上甸子 | 58.45 | 69.99 | 70.80 | 82.80 | 98.32 | 103.77 |
| S07 | 平谷 | 50.82 | 78.66 | 100.18 | 59.11 | 97.94 | 144.15 |
| S08 | 通州 | 48.04 | 70.00 | 81.65 | 55.79 | 82.48 | 107.75 |
| S09 | 朝阳 | 62.58 | 94.70 | 106.64 | 76.98 | 132.19 | 161.54 |
| S10 | 昌平 | 49.31 | 67.21 | 84.56 | 58.64 | 86.96 | 115.89 |
| S11 | 佛爷顶 | 36.01 | 48.22 | 52.02 | 39.51 | 54.82 | 62.41 |
| S12 | 门头沟 | 52.55 | 82.81 | 107.87 | 62.65 | 105.89 | 153.82 |
| S13 | 观象台 | 52.07 | 72.17 | 90.49 | 63.05 | 97.95 | 134.79 |
| S14 | 石景山 | 55.64 | 81.07 | 106.61 | 65.56 | 104.79 | 157.29 |
| S15 | 丰台 | 54.32 | 90.53 | 122.70 | 65.14 | 125.34 | 188.87 |
| S16 | 大兴 | 48.17 | 74.28 | 91.05 | 57.83 | 92.17 | 127.49 |
| S17 | 房山 | 51.50 | 78.26 | 91.23 | 62.04 | 100.08 | 132.39 |
| S18 | 霞云岭 | 45.90 | 79.61 | 103.31 | 52.67 | 100.89 | 130.63 |
|
| 图 7 10年一遇重现期的过程降水量(mm)阈值(a.持续时间≤12 h,b.持续时间≤6 h) Figure 7 Accumulated precipitation (mm) for a ten-year return period with the duration less than 12 h (a) and 6 h (b) respectively |
在全球变暖背景下,城市极端强降水事件近年来频繁发生,准确分析其致灾频率和危险性对于城市防灾、减灾规划及风险管理具有重要意义。本研究以北京地区2005—2014年逐时降水资料为基础提取强降水事件案例,基于二元Copula函数,建立能反映强降水事件主要致灾因素——降水持续时间和过程降水量依存关系的二元联合分布模型,计算了北京地区强降水事件条件重现期,并通过条件重现期分析了该地区不同情景强降水事件致灾因子危险性及其空间分布特征。基于Copula函数的二元联合分布模型能更合理地反映不同情景强降水事件的危险性特征,为研究北京地区强降水灾害风险评估提供了一种新途径。主要结论如下:
(1) 北京地区强降水事件的降水持续时间与过程降水量存在显著相互依存关系,适于应用Copula函数刻画两者的联合分布。通过强降水变量边缘分布的K-S检验发现,广义极值和对数正态分布对多数站点的降水持续时间拟合效果较好,而过程降水量则更适用于广义极值分布。
(2) 北京地区强降水持续时间与过程降水量的二元Copula函数具有空间差异性,在绝大多数站点,Gumbel Copula函数能够较好地刻画强降水二元变量的相依结构,而少数站点则更适用Frank Copula函数。
(3) 同样的过程降水量,降水持续时间越短则平均降水强度越大,进而对应更低的发生概率和更长的重现期,持续时间在6 h以内的强降水条件重现期受持续时间影响较大。北京地区强降水事件的持续时间一般小于24 h,仅对日降水量进行估算将导致对短时强降水事件重现期及危险性的低估;基于Copula分布的强降水事件的条件重现期由于可以刻画降水持续时间和过程降水量的依存关系,能更合理地描述不同强降水事件的致灾因子危险性特征。
(4) 利用条件重现期刻画强降水危险性,体现了致灾因子的过程降水量和持续时间的二维强度和频率信息。不同情景强降水具有各自特定的空间分布结构,表明北京地区不同强降水事件的危险性具有明显的地区差异性特征,利用Copula函数可实现对不同情景特征的辨识,从而为北京地区局地强降水事件的防灾减灾规划及灾害风险管理提供科学依据。
| 北京市气象局. 2013. 北京市气象灾害预警信号与防御指南. 北京: 气象出版社 . Beijing Meteorological Service. 2013. The Guide of Beijing Meteorological Disasters Warning and Prevention. Beijing: China Meteorological Press . |
| 扈海波, 轩春怡, 诸立尚. 2013. 北京地区城市暴雨积涝灾害风险预评估. 应用气象学报 , 24 (1) : 99–108. Hu H B, Xuan C Y, Zhu L S. 2013. The pre-event risk assessment of Beijing urban flood. J Appl Meteor Sci , 24 (1) : 99–108. (in Chinese) |
| 刘晓云, 王劲松, 李耀辉, 等. 2015. 基于Copula函数的中国南方干旱风险特征研究. 气象学报 , 73 (6) : 1080–1091. Liu X Y, Wang J S, Li Y H, et al. 2015. Characteristics of drought risk in southern China based on the Copula function. Acta Meteor Sinica , 73 (6) : 1080–1091. (in Chinese) |
| 马洪涛, 王军, 张晓昕, 等. 2013. 北京市雨水系统规划设计重现期研究. 给水排水 , 39 (5) : 50–55. Ma H T, Wang J, Zhang X X, et al. 2013. Research return periods of planning and design standards for storm water system in Beijing city. Water Wastewater Eng , 39 (5) : 50–55. (in Chinese) |
| 马京津, 李书严, 王冀. 2012. 北京市强降雨分区及重现期研究. 气象 , 38 (5) : 569–576. Ma J J, Li S Y, Wang J. 2012. The study of Beijing's rainstorm division and its return periods. Meteor Mon , 38 (5) : 569–576. (in Chinese) |
| 张强, 李剑锋, 陈晓宏, 等. 2011. 基于Copula函数的新疆极端降水概率时空变化特征. 地理学报 , 66 (1) : 3–12. Zhang Q, Li J F, Chen X H, et al. 2011. Spatial variability of probability distribution of extreme precipitation in Xinjiang. Acta Geogr Sinica , 66 (1) : 3–12. (in Chinese) |
| 郑祚芳, 祁文, 李青春, 等. 2015. 基于自动站观测的北京夏季降水特征. 气候与环境研究 , 20 (2) : 201–208. Zheng Z F, Qi W, Li Q C, et al. 2015. Statistical characteristics of precipitation in summer in Beijing area during 2007-2011. Climatic Environ Res , 20 (2) : 201–208. (in Chinese) |
| Adamowski K. 2000. Regional analysis of annual maximum and partial duration flood data by nonparametric and L-moment methods. J Hydrol , 229 (3-4) : 219–231. DOI:10.1016/S0022-1694(00)00156-6 |
| De Michele C, Salvadori G. 2003. A generalized Pareto intensity-duration model of storm rainfall exploiting 2-copulas. J Geophys Res , 108 (D2) : 4067. DOI:10.1029/2002JD002534 |
| Genest C, Favre A C. 2007. Everything you always wanted to know about copula modeling but were afraid to ask. J Hydrol Eng , 12 (4) : 347–368. DOI:10.1061/(ASCE)1084-0699(2007)12:4(347) |
| Genest C, Rémillard B, Beaudoin D. 2009. Goodness-of-fit tests for copulas: A view and a power study. Insur Math Econ , 44 (2) : 199–213. DOI:10.1016/j.insmatheco.2007.10.005 |
| Genest C, Kojadinovic I, Nešlehová J, et al. 2011. A goodness-of-fit test for bivariate extreme-value Copulas. Bernoulli , 17 (1) : 253–275. DOI:10.3150/10-BEJ279 |
| IPCC.2012. Managing the Risks of Extreme Events and Disasters to Advance Climate Change Adaptation: Special Report of the Intergovernmental Panel on Climate Change. Vienna: IPCC |
| Kao S C, Govindaraju R S. 2007. A bivariate frequency analysis of extreme rainfall with implications for design. J Geophys Res , 112 (D13) : D13119. DOI:10.1029/2007JD008522 |
| Kim Y O, Seo S B, Jang O J. 2012. Flood risk assessment using regional regression analysis. Nat Hazards , 63 (2) : 1203–1217. DOI:10.1007/s11069-012-0221-6 |
| Li J, Yu R C, Wang J J. 2008. Diurnal variations of summer precipitation in Beijing. Chin Sci Bull , 53 (12) : 1933–1936. |
| Li J F, Zhang Q, David Chen Y Q, et al. 2015. Future joint probability behaviors of precipitation extremes across China: Spatiotemporal patterns and implications for flood and drought hazards. Global Planet Change , 124 : 107–122. DOI:10.1016/j.gloplacha.2014.11.012 |
| Massey F J. 1951. The Kolmogorov-Smirnov test for goodness of fit. J Ame Stat Assoc , 46 (253) : 68–78. DOI:10.1080/01621459.1951.10500769 |
| Rauf U F A, Zeephongsekul P. 2014. Copula based analysis of rainfall severity and duration: A case study. Theor Appl Climatol , 115 (1-2) : 153–166. DOI:10.1007/s00704-013-0877-1 |
| Salvadori G, De Michele C. 2015. Multivariate real-time assessment of droughts via copula-based multi-site hazard trajectories and fans. J Hydrol , 526 : 101–115. DOI:10.1016/j.jhydrol.2014.11.056 |
| Sklar A. 1959. Fonctions de repartition an dimensions etleursmarges. Publications de l'Institut de Statistique de l'Universit'e de Paris , 8 (1) : 229–231. |
| Vandenberghe S, Verhoest N E C, Onof C, et al. 2011. A comparative copula-based bivariate frequency analysis of observed and simulated storm events: A case study on Bartlett-Lewis modeled rainfall. Water Resour Res , 47 (7) : W07529. DOI:10.1029/2009WR008388 |
| Yue S, Rasmussen P. 2002. Bivariate frequency analysis: Discussion of some useful concepts in hydrological application. Hydrol Process , 16 (14) : 2881–2898. DOI:10.1002/(ISSN)1099-1085 |
| Zhang L, Singh V P. 2007. Bivariate rainfall frequency distributions using Archimedean copulas. J Hydrol , 332 (1-2) : 93–109. DOI:10.1016/j.jhydrol.2006.06.033 |
| Zhang L, Singh V P. 2012. Bivariate rainfall and runoff analysis using entropy and copula theories. Entropy , 14 (12) : 1784–1812. DOI:10.3390/e14091784 |
| Zou X K, Ren F M. 2015. Changes in regional heavy rainfall events in China during 1961-2012. Adv Atmos Sci , 32 (5) : 704–714. DOI:10.1007/s00376-014-4127-y |
 2016, Vol. 74
2016, Vol. 74

