中国气象学会主办。
文章信息
- 古红萍, 沈学顺, 金继明, 肖薇, 王咏薇. 2013.
- GU Hongping, SHEN Xueshun, J1N Jiming, X1A0 Wei, WANG Yongwei. 2013.
- 一维热扩散湖模式在太湖的应用研究
- An application of a 1-D thermal diffusion lake model to Lake Taihu
- 气象学报, 71(4): 719-730
- Acta Meteorologica Sinica, 71(4): 719-730.
- http://dx.doi.org/10.11676/qxxb2013.051
-
文章历史
- 收稿日期:2012-03-19
- 改回日期:2013-03-22
2. 中国科学院大学, 北京, 100049;
3. 中国气象局数值预报中心, 北京, 100081;
4. 犹他州立大学, 犹他, 84321, 美国;
5. 南京信息工程大学大气环境中心, 南京, 210044
2. University of Chinese Academy of Sciences, Beijing 100049, China;
3. Center for Numerical Prediction, China Meteorological Administration, Beijing 100081, China;
4. Utah State University, Utah 84321, USA;
5. Nanjink University of Information Science and Technology, Nanjing 210044, China
从20世纪50年代开始,湖泊对天气和气候的影响越来越为人们所重视(Laird et al,2010; Rouse et al,2008; Samuelsson et al,2001; Kristovich et al,1998; Bates et al,1993)。湖泊作为下垫面的一种,其水热性质与周围的陆面有明显不同,如水面的反照率,较大的比热容以及水的热传导性质和粗糙度。这些差异直接导致了湖泊与大气感、潜热交换与其他陆-气的感、潜热交换有着显著的差异。因此,模拟区域包含湖泊则必须把湖泊的这些特殊的下垫面性质以及湖-气的交互作用考虑进去,才能准确地预测出天气和区域气候的变化(Dutra et al,2010; Krinner,2003;Lofgren,1997)。
湖泊对天气和区域气候的影响是随季节和地理位置的不同而不同的。总的来说,不结冰的湖泊趋向于减少气温的日变化(Samuelsson et al,2010)。夏季初期一些温带和高纬度地区的湖泊表面温度要比周围的陆地低,再加上湖面的粗糙度比陆地要小,因此,在这个季节湖泊跟周围陆地相比趋向于减少向大气输送的热通量(Dutra et al,2010; Rouse et al,2008; Krinner,2003; Lofgren,1997)。在低纬度高温地区,湖泊与陆地相比在所有季节中都趋向于增加向大气输送的潜热通量(Dutra et al,2010)。秋季温带和高纬度地区的湖表温度要比周围的陆地温度高,将增大向大气输送的热通量(Dutra et al,2010; Samuelsson et al,2010; Rouse et al,2008; Lofgren,1997)。秋季和冬季初期发生的湖水翻转和冻结过程将对边界层起到加热和加湿的作用(Jeffries et al,1999),因此,常能够在湖泊的下风方向观测到由于湖泊作用产生的强降水和雪暴天气现象(Laird et al,2010; Samuelsson et al,2001; Goyette et al,2000; Kristovich et al,1998; Bates et al,1993)。相反,湖冰的消融过程则将对其上的边界层起冷却作用(Samuelsson et al,2010)。
当前的数值天气预报模式、区域气候模式和全球气候模式对湖泊的处理都过于简单。目前广泛使用的天气研究和预报模式(如,WRF3.0)对大面积湖区的湖温处理是采用类似海表温度的处理办法通过插值得到,而对次网格尺度的湖区则忽略不计(Skamarock,2005)。在已有的研究中,通常采用比较简单的混合层模式或热力传输模式来研究湖泊的作用,这些方法曾经被加拿大的区域气候模式(Goyette et al,2000; Plummer et al,2006)、地球物理流体动力学实验室的全球气候模式(Lofgren,1997)等采用。还有一些包含了对湖泊的复杂处理但是并没有考虑湖水的结冰过程(Bonan,1995)和雪对空气和湖水的绝热作用(Samuelsson et al,2010)。大部分耦合的陆面大气模式所使用的陆面数据低估了全球的湖面面积(Downing et al,2006),并把湖的深度和光学性质简单地处理成固定值。但实际上,湖的深度、光学特性以及湖水的相变对准确地模拟湖-气相互作用是非常重要的(Rouse et al,2005; Hocking et al,1999; Brown et al,2010; Dutra et al,2010)。
目前,把湖模式耦合到数值模式的工作正在开展(Res,2010a,2010b;Mironov et al,2010; MacKay et al,2009),是耦合数值模式发展的前沿问题之一。几种不同类型的一维湖泊模式已经被发展出来(Res,2010a;Perroud et al,2009),可以把湖模式归纳为以下3种类型:(1)基于相似理论发展起来的相对简单的2层模型(如: Flake,Mironov et al,2010);(2)对涡旋扩散系数进行参数化的热扩散模型(如:Hostetler的湖模式(Hostetler et al,1990)和Minlake(Fang et al,1996));(3)更加复杂的湍流模型(如:拉格朗日模型DYRESM(Yeates et al,2003)和k-ε湍流闭合模型SIMSTRAT(Goudsmit et al,2002))。
这些不同类型的一维湖泊模型都有其各自的优点和缺点(Martynov et al,2010; Perroud et al,2009; Stepanenko et al,2010)。Flake计算量较小,并且,模式可以基本合理地模拟出不同类型湖泊的湖表温度和结冰过程。但是,对于湖泊的季节性层结结构模拟得不是很好,由于该模式只有2层结构,很难合理地模拟出深湖的湖底温度。Hostetler等(1990)湖模式对较浅湖泊的模拟效果较好,但是,对于深湖的模拟则不理想,由于混合不够对湖表温度的模拟存在冬季降温过低和春节升温太快的特点(Martynov et al,2010; Stepanenko et al,2010)。湍流模型由于考虑了更多的因素(如:湖面波动等),可以更好地刻画出密西根湖和日内瓦湖的温度特征(Perroud et al,2009; Stepanenko et al,2010),但预报的苏必利尔湖的混合则过强。相比较而言,湍流模型所需要的计算量是非常大的,还需要读入额外的跟湖泊有关的数据,并且,这个模式的应用目前只限于离线运行,并没有被耦合到任何天气和气候模式中。
本研究基于区域气候模式CLM3.0中的湖模式(Bonan et al,2002;Zeng et al,2002)。该模式是在Hostetler等(1990)一维热扩散模型的基础上发展而来的(Bonan,1995;Dai et al,2003)。作为研究湖-气耦合模式的一环,应用可能获取的观测资料,评估了该湖模式对太湖的模拟能力,研究了湖模式对不同参数的敏感性以及大气强迫场的误差对模拟结果误差的影响。2 模式介绍2.1 湖模式
所用湖模式是一个一维的质量和能量守恒模式。该模式最初由Zeng等(2002)参考和借鉴了Bonan(1995)、Henderson-Sellers(1985,1986)、Hostetler等(1990,1993,1994)的工作发展而来的,在Hostetler等的一维热扩散模型的基础上,通过增加考虑三相变化的冰模块,该模式可以模拟出各种天气状况下的湖泊与大气的相互作用。
该模式对没有冻结的湖泊,其涡旋扩散系数的计算采用Hostetler湖模式中的参数化方法。任一层的湖水允许任意比例的冻结,湖水的冻结将释放潜热从而加热湖水或湖泊上层的空气。对流混合可以在湖水的任何一层发生,即使那一层的湖水已经冻结。模式中有雪层出现时没有太阳光进入湖泊,反之,湖面上没有雪层出现时,则太阳光可以穿透湖水到达湖泊的底部,到达底部的太阳光则被湖泊底部的第1层土壤层吸收。湖泊的深度可以根据实际情况有不同的深度,对任意深度的湖泊假设其物理过程都是适用的。
该湖模式主要由3部分组成。第1部分由大气的强迫场计算出湖水的表面温度,同时各种通量如动量通量、感热通量和水汽通量等也一并计算出来;第2部分是模式的核心部分,计算各个垂直层次(20—25层,包括最多5层雪层,以及10层湖水和湖底以下10层土壤)的温度,用Crank-Nicholson方法将一维的热扩散方程写成差分形式,离散化的方程组可以整理成3个对角矩阵的形式,很方便地求解出各层的温度;第3部分是湖泊的水文过程,详细考虑了湖泊中水的三相变化以及雪的挤压等,但是没有考虑雪的渗透。
预报湖水温度的控制方程是一维的热扩散方程,假设湖泊各个深度的截面积相等,则其控制方程为
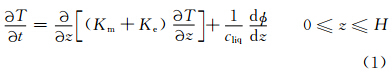
为了方便同时求出各层的温度,将上述热扩散方程的热扩散系数(Km+Ke)改为采用热容和热传导率的形式,以便使热量能够在不同界面中如土壤、湖水以及雪中进行无缝传导。因此,控制方程(1)可写成
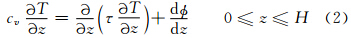
最顶层的边界条件是由表层进入湖泊的热量通量G决定,根据能量守恒方程可写成
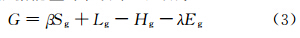
底部的边界条件设为0通量层,假设湖水最底层与其下的沉积物没有热量交换产生。方程(2)采用Crank-Nicholson方法写成差分形式,容易整理成三对角矩阵形式的差分方程组,求解出每一层的温度。
2.2 涡旋扩散系数垂直涡旋扩散系数采用Hostetler湖模式中用湍流扩散来考虑湖水湍流混合的方法进行参数化。该模式假设湖水水平均一,湖水中热量的水平交换是不重要的,热量的分配主要由垂直交换引起。垂直涡旋扩散系数的大小主要由稳定度参数——理查森数决定,计算该垂直涡旋扩散系数Ke,i的方程可以写成
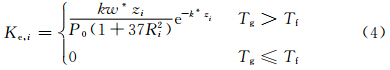
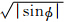 ,Tg为湖的表面温度,Tf为冻结温度(273.15 K),i为湖泊各层的索引数。关于垂直涡旋扩散系数计算的具体推导可以参看Henderson-Sellers(1985)。3 方法、数据和步骤
,Tg为湖的表面温度,Tf为冻结温度(273.15 K),i为湖泊各层的索引数。关于垂直涡旋扩散系数计算的具体推导可以参看Henderson-Sellers(1985)。3 方法、数据和步骤
为了定量评估该湖模式的模拟能力以及对不同参数的敏感性和大气强迫场的误差对模式模拟结果的影响,本研究选用太湖作为测试区。选取太湖评估模式的主要原因是湖泊的观测资料比较少,在此采用南京信息工程大学大气环境中心提供的2010年8月11—28日太湖观测资料,用来驱动湖模式以及检验模式的模拟能力。该观测资料的时间间隔为30 min,包括常规气象观测(气温、湖表面温度、气压、相对湿度、风向、风速)、各种通量的观测(感、潜热通量)、辐射观测(向上和向下的短波辐射和长波辐射)以及湖水不同深度(0.2、0.5、1.5和1.9 m)水温观测。使用的太湖观测点为梅梁湾(31°24′N,120°13′E),该观测点的水深为1.9 m。模式中的湖深设为该观测点的深度1.9 m,湖水的10层分层如下:最顶层因为温度变化大设的最薄,各层中心的深度分别为 0.05、 0.195、0.385、0.575、0.765、0.955、1.145、1.335、1.525和1.715 m。模拟的时段为2010年8月11日00时—29日00时,共18 d。每30 min读入一次观测资料,时间步长设为30 min,每1 h输出1次用来与观测资料比较。模式初始的各层水温资料用观测资料插值得到。在进行测试前,先把观测资料转成模式需要的量,并对观测值进行质量控制,排除了部分异常值。
本研究采用太湖观测的大气场资料驱动湖模式,并把模拟结果与观测资料进行了对比分析,评估该湖模式对太湖的模拟能力。在此基础上,通过对影响湖水温度模拟的关键过程的敏感性试验,确定了适用于太湖的湖模式的主要参数;通过改变大气强迫场,定量分析了由于大气强迫场误差所引起的模拟误差,为下一步将该湖模式耦合到大气模式中由于模式输入所引起误差的分析做准备。4 模式的改进与评估4.1 初始模拟结果和分析
为了研究湖-气相互作用,必须由湖模式预报出比较准确的湖水表面温度和湖面与大气的各种通量交换数据。因此,首先考察该湖模式对湖表温度的模拟能力,主要过程的参数采用模式缺省值。图 1给出了模式模拟的2010年8月11—28日逐时的湖水表面温度和观测资料的比较。从图 1可以看到,该湖泊模式能够模拟出湖泊表面温度的日变化,但模拟的湖表温度与观测资料相比除存在明显的系统性偏低以外,温度的日变化幅度比观测的也小。
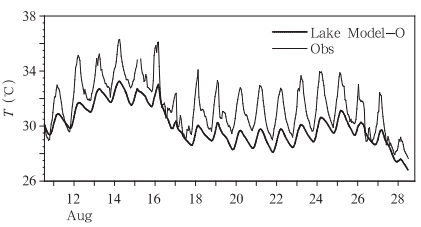 |
| 图 1 模拟的2010年8月11—28日逐时湖表面温度与观测(细线代表观测,粗线为湖模式模拟) Fig. 1 Hourly water surface temperature,11-28 August 2010,observed(thin line) and simulated by the original lake model(thick line) |
因此,需要进一步对该模式对太湖的模拟能力进行参数的敏感性测试,找出适用于太湖的各种湖泊参数。
对于太湖,蔡启铭等(1991)根据米散射理论,利用太湖水中悬浮质粒径谱分布的实测资料,计算了湖水的光散射相矩阵、消光系数和吸收系数等光学参量,并采用蒙特卡罗方法研究了湖面反照率和水体光吸收以及太阳高度角、入射光波长、底泥反射、悬浮质浓度和粒径谱分布的影响。数值计算结果表明:在研究湖泊水体对太阳辐射能量的反射和吸收时,水中悬浮质是一个不可忽视的重要因素。黄文钰等(2002)和沈建军等(2009)均指出,太湖存在严重的水污染问题,按综合营养状态指数评价,全湖富营养化程度平均处于中度富营养化,局部湖区处于高度富营养化状态。按照《地表水环境质量标准》(GB3838-2002),太湖湖水含磷总浓度平均达到四级,造成每年太湖蓝藻暴发。在本研究时段,2010年8月太湖有6 d水华(即蓝藻)面积超过300 km2,其中,8月15、17、18日水华面积分别为983.8、765.2、618.7 km2,蓝藻水华在8月的大规模暴发可能与该期间太湖较高的水温有关。
湖水中存在悬浮质和富营养化程度将会改变太阳辐射在湖水中的分布和传输,从而带来湖水中温度结构和能量的变化。该湖泊模式中依赖于湖泊的水质决定的参数有2个,分别为β(湖泊表层吸收的太阳辐射系数)和η(消光系数或衰减系数)。对于不结冰的湖泊,该湖模式中计算太阳辐射在湖水中的传输是采用类似Bonan(1995)的方法,认为入射的太阳光一部分被湖泊表层(<0.6 m)所吸收,该部分的大小等于射入湖泊中的太阳短波辐射中的红外部分(波长>700 nm),湖泊表层吸收以后剩下的太阳辐射在湖水中的吸收和传输则根据Beer-Lambert定律用一个固定的衰减系数(η)计算。太阳光通过湖水表层(0.6 m以上)的吸收和下层湖水(0.6 m以下)的吸收以后最后到达湖底的太阳光,则假设全部被湖底的土壤层吸收。这个假设基本是合理的,但是,对于浅湖和干净的没有任何污染的湖泊这个假设则不太合理,因为在这些湖泊中穿透到湖泊底部的太阳光可能被湖泊的底层反射,反射回去的太阳光一部分被湖水吸收而一部分则返回到大气中,结果是增加了湖表对太阳光的反照率。太湖属于浅湖,观测点所在的湖深为1.9 m,但是,太湖的污染严重,湖水中含的悬浮物质越多,对太阳辐射的吸收和散射越强。再加上8月大面积蓝藻的暴发,因此,太阳光被湖底反射然后重新返回大气的可能性很小。
β准确与否直接决定了湖表温度的预报准确程度。目前模式中β为0.4,而实际上β值是变化的,它的大小是随湖泊的表面杂质、污染等变化的。模式中所使用的β值为0.4是基于假设湖水是干净透明的,所以,考虑到太湖的污染严重以及8月大面积蓝藻的暴发,β值应该在0.4—1.0。 在当前的模拟中,由于条件所限,无法获得精确的太湖β值。在后面的测试中,将分别选取β等于0.6和0.8进行测试。
η是光在水中的衰减系数(m-1),穿透到深度z处的太阳辐射(φz)由进入水中的太阳辐射(φ0)和η决定。计算公式为

从该公式可以看出,当z=η-1时,该处吸收的太阳辐射减少为进入的太阳辐射的e-1倍。因此,衰减系数η越大,z越小,表明越多的太阳能被表层吸收。因此,η也是决定太阳能在湖水各层分布的重要参数。而这个参数的值是由湖水的浑浊度决定的。在湖模式中,如果没有提供额外的值给η读入的话,模式中会根据Hakanson(1995)在瑞典的88个湖泊中得到的观测资料拟合的一个简单的经验函数来计算η,该函数是湖深的函数。该经验公式为

决定湖泊能量分布的关键参数除了和太阳辐射的分布和传输有关的β与η两个参数外,还有一个重要的参数z0(湖水表面的动量粗糙长度)也是决定湖泊能量分布的重要参数。z0是风速等于0的高度,它是表征下垫面粗糙状况的一个特征长度。同时z0的大小又决定了湖面与大气动力和热力交换的程度。因此,能否取得正确的湖表面粗糙长度对能否正确模拟出湖表温度是非常关键的(Henderson-Sellers,1984)。根据Stull(1991)和Pielke(1990)提供的资料,广阔水域的粗糙长度(z0)的值域范围一般为10-4—10-3 m。原模式中z0取为固定值0.01 m,热量通量的粗糙长度和水汽通量的粗糙长度取为与z0相等。根据文献中所提供的水域的粗糙长度的取值范围以及试验结果,该值取为0.01 m显然不合理。因此,在本研究中将选取z0为0.001和0.0002 m(海洋中使用的值)分别进行测试。另外,除了z0设定固定值进行测试外,还试验了z0随湖深、风速而变化的情况(z0的计算公式参考Flake模式中计算粗糙长度的方法)
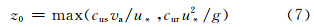
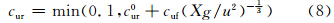
根据上面的分析结果,设计了如下的敏感试验,为了把η0和β的贡献区别开来,试验分成两组进行,第一组中计算η的系数η0不变,即η0为1.1925;第二组中计算η0取为3×1.1925。第一组进行9个测试(表 1),β分别取为0.4(a)、0.6(b)和0.8(c);z0分别为0.001 m(1)、0.0002 m(2)和用公式计算得到的值(3)。第二组将重复第一组的全部试验,除了η0变为3×1.1925。
| z0(m) | β=0.4 | β=0.6 | β=0.8 |
| 0.001 | 1a | 1b | 1c |
| 0.0002 | 2a | 2b | 2c |
| 公式计算 | 3a | 3b | 3c |
第一组试验的结果见图 2。从图 2可以看出,对β分别取为0.4、0.6和0.8,z0为0.0002 m和用公式计算得到的值比z0为0.001 m的模拟结果要好。而对相同的z0值,则β为0.8要比0.4和0.6的模拟结果要好。并且,从图 2中可以发现β分别取为0.4、0.6得到的模拟结果基本重合在一起。第二组试验的结果见图 3,从图 3可以看出,和第一组试验结果有相类似之处的地方是:对β分别取为0.4、0.6和0.8,z0为0.0002 m和用公式计算得到的值比z0为0.001 m的模拟结果要好。而对相同的z0值,则β为0.8要比0.4和0.6的模拟结果要好。图 3中β分别取为0.4、0.6得到的模拟结果也基本重合在一起。
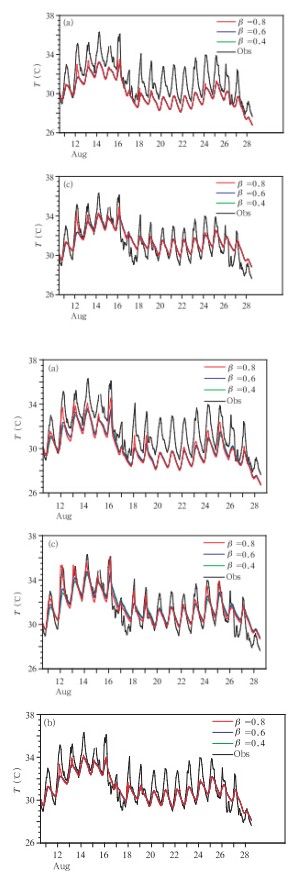 |
| 图 2 第一组试验η0=1.1925模拟的2010年8月11—28日逐时湖表面温度与观测的对比(a. z0=0.001 m,b. z0=0.0002 m,c. z0为公式计算) Fig. 2 Hourly water surface temperature,11-28 August 2010,observed and simulated by the lake model with η0=1.1925(a. z0=0.001 m,b. z0=0.0002 m,c. z0 is calculated roughtness length) |
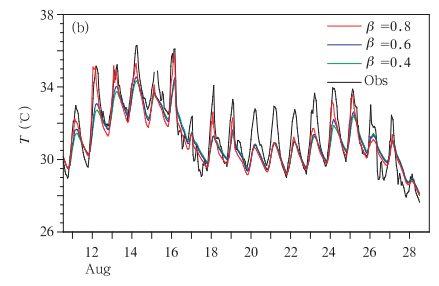 |
| 图 3 第二组试验η0=3×1.1925其他同图 2 Fig. 3 As in Fig. 2 but for η0=3×1.1925 |
为了定量地描写这两组试验模拟结果的好坏,分别计算出这两组试验得到的湖水表面温度和观测的相关系数及归一化的标准偏差,画成泰勒图直观地表示18组试验的优劣。由于β分别取为0.4和0.6的结果几乎重合在一起,因此,为了清晰起见,图 4和图 5中没有将β分别取为0.6的结果画在泰勒图上。第一组试验的泰勒图(图 4)上可以发现,这6组试验的相关系数都很接近0.9,说明这6组试验的模拟结果与观测相关性都很高。但是,β取为0.8(红点)比β取为0.4(蓝点)的结果要好。从归一化的标准偏差可发现,z0用公式计算得到的值(3)比z0=0.0002 m(2)的模拟结果要好,而z0=0.0002 m(2)比z0=0.001 m(1)的模拟结果要好。第二组试验的泰勒图(图 5)上发现,和第一组的泰勒图得出一致的结论,都是β取为0.8(红点)比β取为0.4(蓝点)的结果要好。z0用公式计算得到的值(3)比z0=0.0002 m(2)的模拟结果要好,而z0=0.0002 m(2)比z0=0.001 m(1)的模拟结果要好。因此,从图 4和5的结果可以得出适合于太湖的β值应取为0.8,z0用公式计算得到的值。
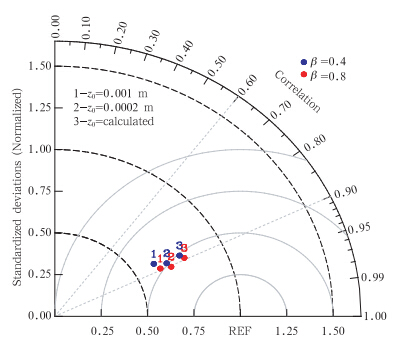 |
| 图 4 第一组试验η0=1.1925模拟的2010年8月11—28日逐时湖表面温度与观测值比较的泰勒图 Fig. 4 Normalized pattern statistics showing differences between observational and simulated hourly water surface temperatures 11-28 August 2010,with η0=1.1925 |
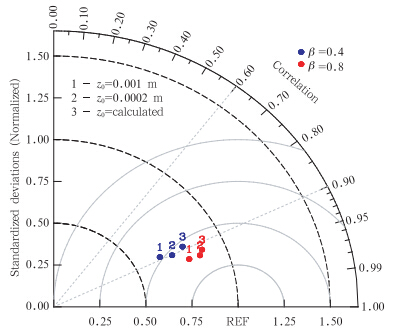 |
| 图 5 第二组试验η0=3×1.1925模拟的2010年8月11日—28日逐时湖表面温度与观测值比较的泰勒图 Fig. 5 As in Fig. 4 but for η0=3×1.1925 |
对比图 4(第一组试验:η0=1.1925)和图 5(第二组试验:η0=3×1.1925)可以发现,第二组试验模拟结果的均方根误差比第一组试验都要小,说明第二组试验优于第一组试验。因此,在太湖的模拟中,η0应取3×1.1925,这也与之前的分析结果一致,即在浅湖特别是污染严重的湖泊中,湖的浅层吸收了更多的太阳辐射。
4.3 参数优化后的模拟结果从4.2节对敏感性试验的结果分析可以知道,适用于太湖的依赖于湖泊类型而决定的3个参数的取值分别应为:η0=3×1.1925,β=0.8,z0用公式计算得到的值。这里重新用选定的3个参数值运行模式,得出新的模拟结果与最初模式的模拟结果作对比。图 6为湖模式用新的参数后模拟得出的2010年8月11—28日逐时的湖表温度与原始模拟结果和观测的对比。从图中可以看出,选用新的参数模拟得到的结果与观测的湖表温度很接近,能较好地模拟出湖温的逐时变化和日变化特征,比原来的模拟结果有了很大的提高。图 7是新模拟的2010年8月11—28日湖水垂直温度-时间序列剖面与原始模拟结果和观测的对比。从图 7可以看出,采用新的参数模拟的湖水温度-时间序列剖面与观测非常接近,从原始的模拟结果图上看出,上下层的水温一致,没有考虑太湖的实际情况,模拟的湖水温度剖面结构反映的是清澈的湖水应该有的温度结构。而新的模拟结果考虑了太湖的生态环境和污染情况,通过采用新的依赖湖泊决定的3个参数(β、η0和z0)可以较真实地考虑太湖的情况,让进入湖水的能量更多地集中在湖水浅层,通过跟观测的湖水温度图对比,与实际情况正好吻合。通过改进模拟的湖表温度和用计算的z0代替模式中固定的z0值后,从图 8中可以看出,模拟的感、潜热通量都比原始的模拟有了很大的改进,与观测更为接近。
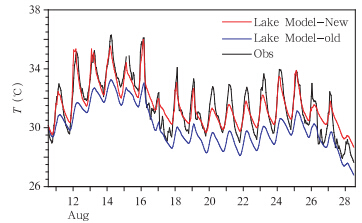 |
| 图 6 模拟的2010年8月11—28日逐时的湖表面温度与观测的对比(黑线代表观测,蓝线为最初模式模拟的结果,红线代表采用新的参数的模式模式结果) Fig. 6 Hourly water surface temperature,11-28 August 2010,observed and simulated by the original(blue line) and new lake model(red line) |
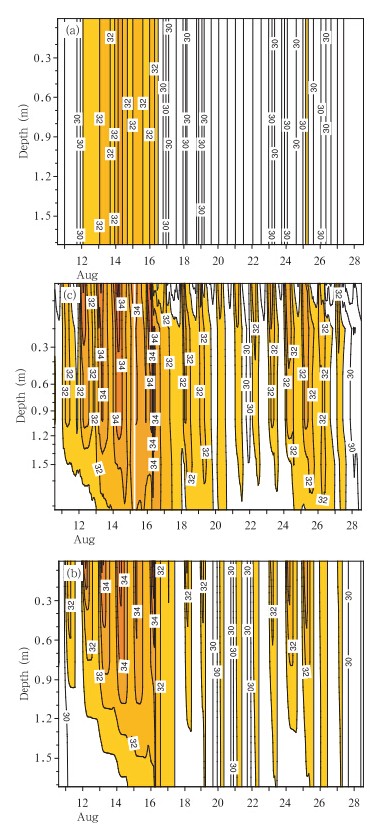 |
| 图 7 2010年8月11—28日湖水垂直温度-时间序列剖面(单位:℃)(a.原始的模拟结果,b.新的模拟结果,c.观测) Fig. 7 Hourly vertical water temperature(unit:℃),August 11-28 2010(a. simulated by the original lake model,b.simulated by the new lake model,c. the observed) |
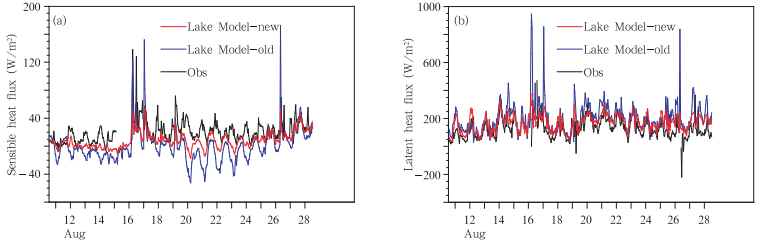 |
| 图 8 2010年8月11—28日逐时的感、潜热通量对比(a.感热通量,b.潜热通量;黑线:观测,蓝线:原模式模拟结果,红线代表新的模拟结果) Fig. 8 Hourly surface energy flux comparison between observational(black line),original simulation(blue line) and new simulation results(red line)for 11-28 August 2010(a. sensible heat flux,b. latent heat flux) |
为了研究该湖模式对主要大气强迫场的误差所引起的模式计算的湖表温度的误差,设计了如下的敏感性试验:第一组,太阳辐射的误差设为±10%(约±30 W/m2);第二组,强迫温度场的误差为±10%(约±3℃);第三组,强迫的u、v风场误差为±10%(约±0.35 m/s)。测试结果见图 9,图 9a为太阳辐射(S↓)+10%的误差引起的湖表面温度的误差为+1.2%,-10%的误差引起的湖表面温度的误差为-2.5%,图 9b为大气2 m的空气温度(T2m)的+10%误差引起的模拟的湖表温度的误差为+2.3%,-10%的误差引起的湖表面温度的误差为-2.0%,图 9c为u、v风场的+10%的误差引起的湖表面温度的误差为-0.4%,-10%的误差引起的湖表面温度的误差为+0.5%。从以上结果可以看出,总体来说,模式结果对大气强迫的误差敏感度不高;相比之下,模式结果对风场最不敏感,对辐射和气温的敏感度相当。
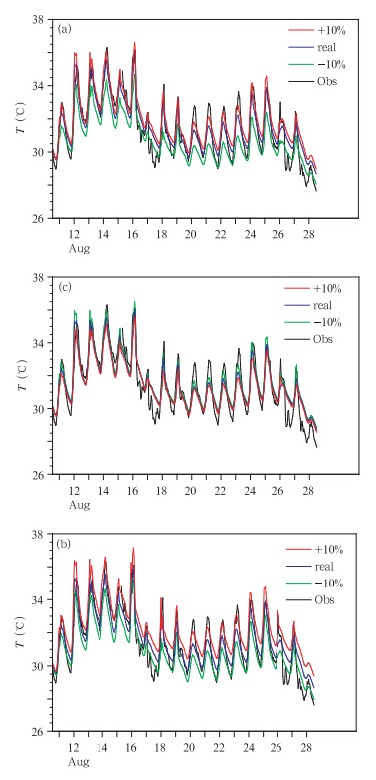 |
| 图 9 模拟的2010年8月11—28日逐时的湖表面温度与观测的对比(a.改变太阳辐射,b.改变2 m空气温度,c.改变u、v风场;黑线代表观测;绿线代表输入的强迫场误差为-10%,蓝线代表不改变强迫场,红线代表输入的强迫场误差为+10%;单位:℃) Fig. 9 Hourly water surface temperature for 11-28 August 2010,observed(black line) and sensitivity-simulated with the forcing error of +10%(red line)or -10%(green line)under changes in(a)solar radiation,(b)2 m air temperature,and (c)u and v. Blue line is for no change in the forcing(unit:℃) |
采用一个一维的质量和能量守恒湖模式,利用太湖区获得的2010年8月11—28日的观测资料作为模式的强迫场,得出该湖模式对太湖区的模拟效果,但原模式模拟结果并不理想,模拟的湖的湖表面温度与观测有较大的系统性偏差,并且温度的日变化幅度与观测相比也小。之后进一步分析了该模式对太湖的模拟效果较差的原因。具体分析了太湖的生态环境和污染情况,设计了18个测试参数的敏感性试验,从敏感性试验的结果分析得到,适用于太湖的依赖于湖泊类型决定的3个参数的取值分别应为:η0=3×1.1925,β=0.8,z0用公式计算得到的值。并且,用新得到的适用于太湖的3个参数重新进行了模拟,并与原模拟结果和观测资料作对比,发现采用新参数后的模拟结果比原模拟结果有了很大的改进,模拟的湖表温度基本接近观测,模拟的湖水温度垂直剖面时间序列与观测吻合得较好,而且感、潜热通量的模拟也都与观测接近。最后,对输入湖模式的主要大气参量(太阳辐射、2 m气温以及风场)的±10%的误差引起的模式模拟的湖表面温度的误差分析表明,模拟结果对大气强迫的误差敏感度不高;相比之下,模拟结果对风场最不敏感,对辐射和气温的敏感度相当。通过该湖模式对大气强迫场误差敏感度分析,为下一步把该湖模式耦合到WRF模式中,分析由于模式的输入误差所引起的误差做好了准备。该湖模式在太湖的研究得出的结果,对今后该湖模式在相同类型湖泊的应用研究具有一定的指导和借鉴意义,并为下一步发展湖-气耦合模式和开展湖-气相互作用的研究提供了必备的前提条件。
在本研究中,对于参数β和η0值的确定,由于条件所限,采用的是用模式测试方法,并不能代表太湖湖水的真实状态,也没有观测数据验证,所以,在下一步的工作中,通过该敏感性分析得知这两个参数的重要性之后,如果可以用实际的观测值来取代,则将获得更加理想和真实的模拟结果。另外需要指出的是,由于本研究的时段为2010年8月11—28日,对于太湖其他时段参数的确定则需要进一步通过不同季节的试验加以确认;并且,该参数的获得是通过研究太湖得到的,具有一定的局限性,对于其他相同类型的湖泊的适用性仍需进一步的验证。
致谢:研究所用的太湖水温、辐射及通量等各种观测资料要特别感谢江苏省基础研究计划(自然科学基金)面上研究项目(BK2011830),教育部长江学者和创新团队发展计划项目(PCSIRT)和江苏高校优势学科建设工程项目(PAPD);国家自然科学基金:浅水湖泊陆面模型的发展及耦合应用(41275024)的支持。
| 蔡启铭,杨平.1991.太湖悬浮质对湖面反照率及水体光吸收的影响.海洋与湖沼,22(5):458-466 |
| 黄昌春,李云梅,乐成峰等.2009.太湖梅梁湾漫衰减系数季节性差异及其主导因素.生态学报,29(6):3295-3306 |
| 黄文钰,高光.2002.太湖水污染近期变动趋势及对策建议.上海环境科学,21(003):149-152 |
| 张杏珍,杨长新译.1990.中尺度气象模拟.北京:气象出版社,677pp |
| 杨长新译.1991.边界层气象学导论.北京:气象出版社,405pp |
| 沈建军,李柏山,许海萍.2009.太湖水污染原因分析及治理措施.环境科学导刊,28(002):27-29 |
| 张运林,秦伯强,陈伟民等.2003.太湖水体光学衰减系数的分布及其变化特征.水科学进展,14(4):447-453 |
| 张运林,秦伯强,陈伟民等.2004.太湖水体光学衰减系数的特征及参数化.海洋与湖沼,35(3):209-213 |
| Bates G T, Giorgi F, Hostetler S W. 1993. Toward the simulation of the effects of the Ureat Lakes on regional climate. Mon Wea Rev,121(5):1373-1387 |
| Bonan GB.1995. Sensitivity of a UCM simulation to inclusion of inland water surfaces. J Climate, 8(11); 2691-2704 |
| Bonan U B,Levis S, Kergoat L,et al. 2002. Landscapes as patches of plant Iunctional types: An integrating concept for climate and ecosystem models. Ulob Biogeo Chem Cycles,16(2): 1021 |
| Brown L G,Duguay C R. 2010. The response and role of ice cover in lake-climate interactions. Prog Phys Ueogr, 34(5):671-704 |
| Cristolor S, Vadineanu A, Ignat G, et al. 1994. Factors affecting light penetration in shallow lakes. Hydrobiol, 275(1):493-498 |
| Dai Y, Zeng X, Dickinson R E, et al. 2003. The common land model. Bull Amer Meteor Soc, 84(8); 1013-1024 |
| Downing J A, Prairie Y T, Cole J J,et al. 2006. The global abundance and size distribution of lakes, ponds, and impoundments. Limnol Oceanogr, 51(5): 2388-2397 |
| Dutra E, Stepanenko V M,Balsamo U, et al. 2010. An online study of the impact of lakes on the performance of the ECMWF surface scheme. Boreal Env Res,15(2): 100-112 |
| Fang X, Stelan H(;.1996. Long-term lake water temperature and ice cover simulation-measurements. Cold Reg Sci Technol, 24 (3):289-304 |
| Goyette S, McFarlane N A, Flato G M. 2000. Application of the Canadian Regional Climate Model to the Laurentian Great Lakes region: Implementation of a lake model. Atmos-Ocean, 38(3): 481-503 |
| Goudsmit G H, Burchard H,Peeters F,et al. 2002. Application of Canadian Regional Climate Model to the Laurentian Ureat Lakes region: Implementation of a lake model. Atmos-Ocean, 38(3):481-503 |
| Hakanson L. 1995. Optimal size of predictive models. Ecol Model, 78(3):195-204 |
| Henderson-Sellers B. 1984. Engineering Limnology. Boston, MA, Pitman Advanced Publishing Program, 356pp |
| Henderson-Sellers B. 1985. New formulation of eddy dillusion ther-mocline models. Appl Math Modell, 9(6):441-446 |
| Henderson-Sellers B. 1986. Calculating the surlace energy balance for lake and reservoir modeling: A review. Rev Ueophys, 24 (3):625-649 |
| Hocking G C,Straskraba M. 1999. The ellect of light extinction on thermal stratilication in reservoirs and lakes. Int Rev Hydrobiol, 84(6):535-556 |
| Hostetler S W, Bartlein P J. 1990. Simulation of lake evaporation with application to modeling lake level variations of Harney-Malheur Lake, Oregon. Water Resour Res, 26(10): 2603-2612 |
| Hostetler S W, Bates U T, Uiorgi F. 1993. Interactive coupling of a lake thermal model with a regional climate model. J Ueophys Res, 98(D3):5045-5057 |
| Hostetler S W, Uiorgi F, Bates U T. 1994. Lake-atmosphere Teed backs associated with Paleolakes Bonneville and Lahontan. Science, 263(5147):665 |
| JeIIries M O,Zhang T, Frey K, et al. 1999. Estimating late-winter heat Ilow to the atmosphere Irom the lake-dominated Alaskan North Slope. J Ulaciol, 45(150):315-324 |
| Krinner G. 2003. Impact of lakes and wetlands on boreal climate. J Ueophys Res, 108, 18 |
| Kristovich D A R, Graham R R. 1998. Mean proliles of moisture fluxes in snow-Tilled boundary layers. Bound Layer Meteor,87 195-215 |
| Laird N F, Desrochers J,PayerM,et al. 2010. Climatology of lake-ellect precipitation events over Lake Champlain. J Appl Meteor Climatol, 48(2): 232-250 |
| Lolgren B M.1997. Simulated ellects of idealized laurentian great lakes on regional and large-scale climate. J Climate, 10(11) 2847-2858 |
| MacKay MD, Neale P J,Arp C D, et al. 2009. Modeling lakes and reservoirs in the climate system. Limnol Oceanogr, 54(6) 2315-2329 |
| Mironov D, Heise E, Kourzeneva E, et al. 2010. Implementation of the lake parameterisation scheme FLake into the numerical weatherprediction model COSMO. Boreal Env Res,15:218-230 |
| Perroud M, Uoyette S, Martynov A, et al. 2009. Simulation of multiannual thermal proliles in deep Lake Ueneva; A comparison of one-dimensional lake models. Limnol Oceanogr, 54(5) 1574-1594 |
| Plummer D A, Caya D, Frigon A,et al. 2006. Climate and climate change over North America as simulated by the Canadian RCM. 1 Climate, 19(13):3112-3132 |
| Res B E. 2010a. Implementation of the lake parameterisation scheme FLake into the numerical weather prediction model COSMO. Boreal Env Res,15:218-230 |
| Res B E. 2010b. Simulation of temperate Ireezing lakes by one-dimensional lake models; Performance assessment for interactive coupling with regional climate models. Boreal Env Res, 15 143-164 |
| Rouse W R, Oswald C J,Binyamin J,et al. 2005. The role of Northern lakes in a regional energy balance. J Hydrometeorol, 6 291-305 |
| Rouse W R, Blanken P D, Bussieres N,et x1.2008. Investigation of the thermal and energy balance regimes of Ureat Slave and Great Bear Lakes. J Hydrometeorol, 9;1318-1333 |
| Samuelsson P,Tjernstrim M. 2001. Mesoscale Ilow modification in-duced by land-lake surface temperature and roughness dinerences. J Ueophys Res,106(D12):12419-12435 |
| Samuelsson P,Kourzeneva E, Mironov D. 2010. The impact of lakes on the European climate as simulated by a regional climate model. Boreal Env Res, 15(2):113-129 |
| Skamarock W C,Klemp J B, Dudhia J,et al. 2008. A Description of the Advanced Research WRF Version3. Mesoscale and Microscale Meteorology Division, National Center for Atmospheric Research, NCAR/TN-475+STR, http://www.mmm.ucar.edu/wrf/user/docs/arw_v3.pdf |
| Stepanenko V M,Goyette S, Martynov A,et al, 2010. First steps of a Lake Model Intercomparison Project; Lake MIP. Boreal Env Res, 15:191-202 |
| Subin Z M,Riley W J,Mironov D V. 2012. An improved lake model for climate simulations: model structure sensitivity analyses in CESM1.J Adv Mad Ezrth Sys, 4,M02001 |
| Yeates P S, Imberger J. 2003. Pseudo two-dimensional simulations of internal and boundary Iluxes in stratified lakes and reservoirs. Int J River Basin Manag, 1(4); 297-319 |
| Zeng X, Shaikh M, Dai Y,et al. 2002. Coupling of the common land model to the NCAR community climate model. J Climate, 15(14):1832-1854 |
 2013, Vol. 71
2013, Vol. 71

