中国气象学会主办。
文章信息
- 赵建华, 张强, 隆霄. 2013.
- ZHAO Jianhua, ZHANG Qiang, LONG Xiao. 2013.
- 中性层结下局地平缓地形起沙的次网格参数化研究
- Study of the subgrid scale parameterization of dust emissions caused by gentle local terrain under the neutrally stratified atmosphere
- 气象学报, 71(4): 731-742
- Acta Meteorologica Sinica, 71(4): 731-742.
- http://dx.doi.org/10.11676/qxxb2013.064
-
文章历史
- 收稿日期:2012-07-21
- 改回日期:2013-04-22
2. 兰州大学大气科学学院, 兰州, 730000
2. College of Atmospheric Sciences, Lanzhou University, Lanzhou 730000, China
在实际沙尘过程中,经常发生一些局地的沙尘天气过程,比如拉萨贡嘎机场周边河谷地带、河西走廊龙首山一带的狭谷地带、内蒙古巴丹吉林沙漠北侧拐子湖附近(郭铌等,2004)以及新疆吐鲁番至珍珠泉之间的三十里风区、鄯善县红旗坎到哈密县了墩的百里风区、阿拉山口风口和托里的老风口等四大风口引起的沙尘天气过程。这些过程由于其空间尺度较小,不能被沙尘数值模式所分辨,一定程度上制约了模式的应用与发展。
理论研究、数值模拟、风洞试验与野外试验均揭示,气流经过起伏地形时风速会发生一定变化(Chepil et al,1964; Jackson et al,1975; Maurizi,2000; Ding et al,2003; Garvey et al,2005; Liu et al,2011; Ameur et al,2012)。气流吹过山丘时,山顶风速将增大,在下游可能形成分离点,产生涡旋。Rokenes(2009)发现气流经过圆形山丘时会增大平均速度、降低湍流强度。Ameur等(2012)指出,斜坡会增大气流速度与其倾角。Parsons等(2004)和Liu等(2011)发现,沙丘的不同部位其风速是不同的。气流进入山谷时,风速与风向均会发生变化,在一定条件下还会出现部分空气从主气流中分离,并进而产生回流的现象(Tampieri,1987; Snyder et al,1991; Garvey et al,200; 李双权等,2012)。Maurizi(2000)对气流经过两维山谷的数值模拟发现,不同位置水平风速的垂直廓线不同。Snyder等(1991)对3组坡度不同山谷的风洞试验指出,最陡的山谷会产生分离流,分离的切变层中湍流切应力比上游边界层的大。Garvey等(2005)通过孤立山谷的风洞试验指出,风垂直吹过山谷时,山谷对上风与下风方向气流的影响距离分别至少为其宽度的一半与两倍;风斜吹过山谷时,可能会产生沿山谷的气流。除了上述中性层结,在其他稳定度条件下地形对气流也有一定的影响。在不稳定条件下,气流经过地形时,会形成不同性质的对流系统和不同特征的地形流结构,对对流触发产生重要作用(董继立等,2008;李唐棣等,2012)。对2008年“7.22”襄樊特大暴雨的研究指出,地形会对气流产生阻碍、促进上升运动(廖移山等,2011)。在稳定条件下,Bouwmeester(1978)风洞试验发现,陡坡对气流的扰动随着中性稳定到稳定的轻微过度而呈现出剧烈变化;Hunt等(1988)指出,地形对气流的扰动与上风向平均速度、山的坡度、层结对上风向风速廓线的效应以及层结的动力效应有关;Uchida等(2001)数值试验发现,山体周围的气流是不稳定的,稳定度不同,气流稳定度也不同。
地形对气流的强迫进而对起沙产生一定影响(宣捷,1998; Parsons et al,2004; 姜学恭等,2008; Liu et al,2011)。Xuan等(1994)发现湍流与复杂地形可使临界起尘风速显著降低、尘排放量增大、平均沉降量增大以及沉降分布发生改变。朱好等(2010)也认为,临界起沙摩擦速度与地形有一定关系。郭铌等(2004)与王建鹏等(2006)指出,西北特殊地形可促进气流加速和抬升,有利于沙尘暴的形成与触发。李得禄等(2012)发现,丘间低地不同部位风沙流结构存在明显差异。另外,地形对沙尘的传输与沉降也有一定影响(Belcher et al,1998; Goossens,2006;沈建国等,2007; Hoffmann et al,2008)。
对沙尘天气而言,起沙占有重要地位,是沙尘天气能否发生的先决条件,也是影响沙尘天气强度与范围的重要因素。沙尘数值模式是研究沙尘天气规律、沙尘天气对环境与生态的影响以及沙尘气溶胶效应的重要工具,受到学术界的重视。不过,沙尘数值模式具有一定的分辨率,这决定了次网格局地地形引起的起沙无法被分辨。但是,一些局地地形对局地沙尘天气乃至大范围沙尘天气都有一定影响。如果忽视此影响,显然会使沙尘数值模式出现部分局地沙尘天气预报无效、对大范围沙尘天气局部预报性能偏低的问题。如何在模式中考虑这种过程,对模式预报性能的提高具有重要意义。本研究即是从局地地形起沙的次网格参数化问题展开。2 方 法2.1 狭管效应与下滑效应
狭管和斜坡是两种重要地形,其主要效应分别为狭管效应和下滑效应。当大气非中性时将会引起背风波、水跃以及局地热力环流等其他动力学现象,而且,坡度较大时,还会出现分离点与涡旋。为了简单,主要研究中性层结下局地平缓地形的起沙参数化问题。
狭管效应指的是风平行狭管轴向流经狭管时由于横截面积的变化引起风速的变化。下滑效应是空气沿地形从高处下沉到低处时引起风速的变化,比如气流翻过山脉后下滑。下滑效应与斜坡有关,而狭管两侧的山丘具有一定的坡度,故下滑效应可以在狭管中体现出来:气流平行于狭管轴向时,产生狭管效应;沿狭管两侧山丘下滑时则产生下滑效应。两种效应均可以通过狭管一种地形来研究。
狭管效应一般与质量守恒方程有关,后者在气层厚度变化不大,并忽略密度变化时体现为质量通量守恒。理想不可压流体做定常运动时,下滑效应根据伯努利方程可知,其与压力及重力做功之和有关。本文首先采用这两种效应对风速影响的已有研究成果,然后再考虑中性层结下地形引起的速度变化。
《新疆短期天气预报指导手册》编写组(1986)、蒋维楣等(1994)、祝学范(2004)、王式功等(2010)的研究认为,假设在近地面不厚的气层内无空气质量的辐合、辐散,且高低层空气质量不交换的条件下,风通过狭管时其大小变化为(暂不计温度的局地变化)


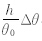 ,θ0为地面位温,g为重力加速度,h为坡高,即空气下降的垂直距离,Δθ为地面位温与越山冷空气位温之差。
,θ0为地面位温,g为重力加速度,h为坡高,即空气下降的垂直距离,Δθ为地面位温与越山冷空气位温之差。显然,该下滑效应仅考虑了浮力效应。实际上,理论研究、数值模拟与风洞试验均揭示,在没有浮力作用下,风经过斜坡、山丘或山谷时风速自身就会发生变化(Jackson et al,1975; Maurizi,2000; Ding et al,2003;Garvey et al,2005; Liu et al,2011; Ameur et al,2012),故尚需考虑地形引起的变化。
由于地形对气流的影响具有一定的复杂性,研究起步较晚。风洞试验指出,对于粗糙度较大的山丘,只要其坡度不超过10°,即使在强风条件下,也不会出现流体分离现象;对于光滑的自然形状与三角形状的两维山脊,产生平稳分离流的临界角为18°(Kaimal et al,1994)。许多不考虑分离现象的理论研究成果即局限在此坡度之内。Jackson等(1975)首先给出了中性层结下两维孤立平缓山脉上速度分布的解析解。后来,Mason等(1979)与Warmsley等(1982)给出了三维地形上升速度分布的解析解。Taylor等(1984)、Walmsley等(1989)以及Weng等(2000)给出了计算山顶加速比的指示法,该法适用于孤立山丘与规则起伏地形。Lemelin等(1988)基于数值模拟结果给出了LSD(Lemelin Surry Davenport)方法,该法可以近似计算出包括陡坡与大堤在内的加速比。工程科学数据组织(Engineering Sciences Data Unit,ESDU)基于纳维-斯托克斯方程的解给出了适用于简单堤岸的简化方法(按工程科学数据组织的缩写记为ESDU方法,下同)和适用于圆形山丘、不规则山丘及多个山丘等复杂地形的复杂方法,这些方法可以计算二维与三维地形的加速因子(ESDU,1993)。Pellegrini等(2005)在中性层结下采用流线坐标的二维平稳流动支配方程解出了平缓山脉完全湍流区中的风速廓线公式,即修正的对数律。本研究采用效果较好的ESDU方法(ESDU,1993; Rokenes,2009),该法采用等效堤岸的概念。所谓等效堤岸是假设气流流经山丘时受到的地形效应可以在一个相应的堤岸上体现出来,风经过地形时其速度变化为
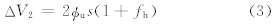
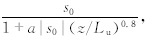 s0需要从ESDU(1993)给出的两维堤岸在z=0时s的取值图中读取,z为垂直高度,a取值为
s0需要从ESDU(1993)给出的两维堤岸在z=0时s的取值图中读取,z为垂直高度,a取值为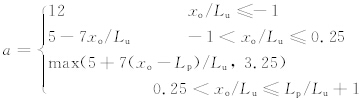
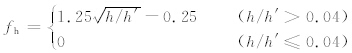
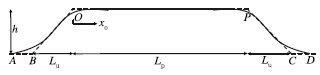 |
| 图 1 ESDU等效堤岸与长度定义示意图 (定义只对风从左向右吹有效) Fig. 1 Equivalent embankment concept and the length definitions for the ESDU model (The definitions are valid only for the wind from left to right) |
这样,假设整个下滑效应产生的风速变化(ΔV)可用线性叠加的形式表示
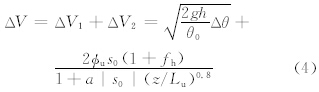
如前所述,狭管和斜坡可以利用狭管地形一并处理。当只考虑狭管效应时,可以认为横穿狭管的风速为0;当只考虑下滑效应时,可认为平行于狭管的风速为0,狭管两侧山脉的高度可以不等。
研究两效应主要是如何确定狭管内的风速。确定风速可以采用两种方法,一种是求取狭管的平均风速,另一种是在已知狭管具体形状的情况下,根据气流通过狭管的规律,求取狭管内每一点处的速度分布。由于第二种方法较复杂,故下面以第一种方法解决。
为简单计,以一个平直等效狭管反映实际狭管地形对风的影响。在地形追随坐标下,不考虑垂向速度,设网格内10 m高平均风速为V,狭管的平均风速为Vp,狭管外部的速度为Ve;相应表面积分别为A、Ap和Ae,A=Ap+Ae,则

考虑定常过程和不可压流体,不计地面摩擦。以狭管底部和10 m高风速所在高度之间的空气为控制体。如图 2所示,设进入狭管入口处气流的平均风速为Vi,Vi//V1。在地形追随坐标下,设气流宽度为l,狭管入口处气流宽度为lp1(即狭管入口处的弧长),狭管入口处两侧外部总宽度为le1,lp1+le1=l。为简单计,取l为气流在流过狭管时其宽度保持不变的最小值。狭管内部平均宽度为lp2,狭管外部平均宽度为le2,lp2+le2=l。狭管中的轴向平均风速分量为Vpr,Vpr//V1,横向平均风速分量为Vps,Vps//V2,狭管外部环境的轴向与横向速度为Ver和Ves。
 |
| 图 2 狭管示意图 (a.网格内狭管平面图,b.狭管横向剖面图(lp21=  lp22=PQ,lp23= lp22=PQ,lp23=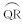 )) Fig. 2 Sketch of the narrow-pipe )) Fig. 2 Sketch of the narrow-pipe (a. ichnography of a narrow pipe within a grid; and b. cross section of a narrow pipe. lp21=  lp22=PQ and lp23= lp22=PQ and lp23=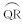 in(b)) in(b)) |
根据连续性方程易得



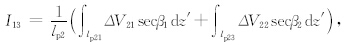 为地形自身引起的速度变化;
为地形自身引起的速度变化;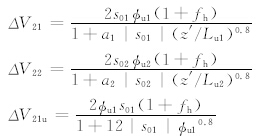
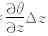 ,Δθ1和Δθ2是狭管谷底空气与两侧山顶部的位温差;h1、h2、β1和β2亦然,两两分别为两侧山高和山坡与垂向的平均夹角(图 2b);
,Δθ1和Δθ2是狭管谷底空气与两侧山顶部的位温差;h1、h2、β1和β2亦然,两两分别为两侧山高和山坡与垂向的平均夹角(图 2b); 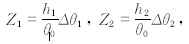 lp2=lp21+lp22+lp23; tanβ1=
lp2=lp21+lp22+lp23; tanβ1=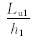 =Øu1-1,tanβ2=
=Øu1-1,tanβ2=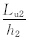 =Øu2-1,Lu1与Lu2见图 2b,Øu1与Øu2分别对应Lu1与Lu2; l′p21=
=Øu2-1,Lu1与Lu2见图 2b,Øu1与Øu2分别对应Lu1与Lu2; l′p21=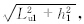 ,l′p23=
,l′p23=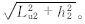 显然,式(8)形式比较复杂。
显然,式(8)形式比较复杂。由式(5)—(8)便可知狭管中的速度。下面对其进行一些简化。
为简单计,设Vt1=Vt3=Vt。将式(6)—(8)代入式(5),可得
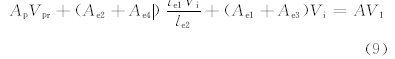
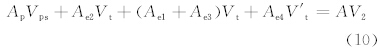
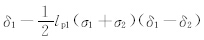 ,当轴出流与网格两条边相交时,λ1=δ1-[lp1σ3-
,当轴出流与网格两条边相交时,λ1=δ1-[lp1σ3-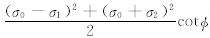 ](δ1-δ2)。其中δ1=le1/(l-
](δ1-δ2)。其中δ1=le1/(l-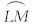 ),δ2=lp1/
),δ2=lp1/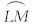 ,σ0=HBsinØ,当轴出流只与AB边相交时,σ1=HMtanØ,σ2=HLtanØ;当轴出流只与BC边相交时,σ1=ILtanØ,σ2=IMtanØ;当轴出流与AB、BC两条边均相交时,σ1=HMtanØ,σ2=IMtanØ。λ2与迎风坡侧山脉的高度沿狭管轴向的变化有关,比较复杂,可以暂高为1。Ap=Llp1,L为狭管的长度。V′t为风横穿狭管后抵达对面山顶的速度,由式(4)可得
,σ0=HBsinØ,当轴出流只与AB边相交时,σ1=HMtanØ,σ2=HLtanØ;当轴出流只与BC边相交时,σ1=ILtanØ,σ2=IMtanØ;当轴出流与AB、BC两条边均相交时,σ1=HMtanØ,σ2=IMtanØ。λ2与迎风坡侧山脉的高度沿狭管轴向的变化有关,比较复杂,可以暂高为1。Ap=Llp1,L为狭管的长度。V′t为风横穿狭管后抵达对面山顶的速度,由式(4)可得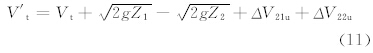
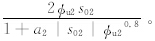
由式(6)、(9)可得
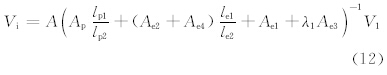
由式(10)可得
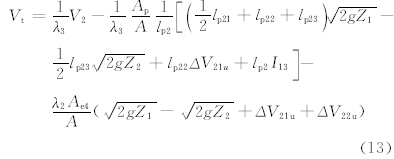
下面再给出式(6)、(8)、(12)和(13)中涉及的常数。对于l,可以假设l为狭管最大宽度的数倍,考虑到网格的尺度,可取值
l=max(nlp1,lgrid)
其中,n为一自然数,lgrid为网格对角线的长度。对于Aei(i=1,2,3,4),鉴于Ae2与Ae4为梯形,可简单求出,此处只给出Ae1与Ae3的公式。Ae1为
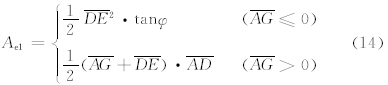
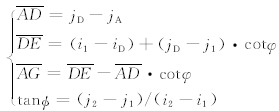
设狭管出口和入口平行,则Ae3与Ae1呈正比,易得
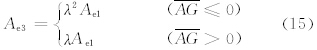
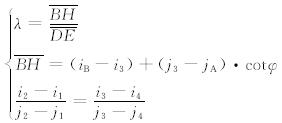
风速是起沙的决定因素。在起沙次网格参数化中,关键是如何得到次网格风速。本研究以跃移沙粒的跃移通量为例。根据White(1979)和Marticorena等(1997)的研究,跃移层在粒径范围ΔDp内的跃移通量ΔFh(单位: g/(cm·s))的公式为
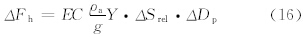
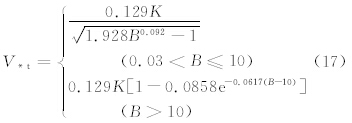
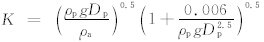 ,其中,0.006的单位为g·cm0.5/s;B=1331Dp1.56+0.38为无量纲的雷诺数,ρp是沙粒密度(单位:g/cm3)。整个粒径范围内的跃移通量为式(16)的积分。
,其中,0.006的单位为g·cm0.5/s;B=1331Dp1.56+0.38为无量纲的雷诺数,ρp是沙粒密度(单位:g/cm3)。整个粒径范围内的跃移通量为式(16)的积分。以中性层结下近地面层风速廓线公式,将2.2节得到的Vp换算为摩擦速度Vp*,以体现局地地形对起沙的影响。Pellegrini等(2005)在假设中性层结下、小山丘近地表处垂直动量通量随高度变化不大的情况下,得到了摩擦速度与速度的关系式
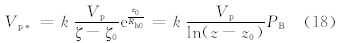
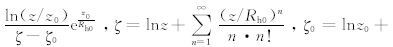
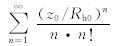 ,ζ与ζ0中的求和部分是指数积分函数,Rh0是山脉的有效曲率半径。显然,相比于均匀地形,式(18)多了一修正项PB。
,ζ与ζ0中的求和部分是指数积分函数,Rh0是山脉的有效曲率半径。显然,相比于均匀地形,式(18)多了一修正项PB。起沙量与ΔFh成正比,后者在一定程度上可以表征前者的相对大小,为简单计,以下所指的起沙量均以ΔFh代替。
用Vp*替代式(16)的V*,R′=V*tVp*-1代替R,即可得到狭管跃移通量。考虑到狭管中沙源分布不均,而且,狭管的平均风速与流经狭管沙源上的风速也有一定差别,故引入一参数C′来表征这种差异。此时狭管中粒径在Dp—Dp+ΔDp的起沙量ΔF′h为
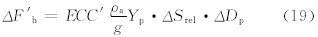
式(16)与(19)求商,可得地形效应(局地地形引起跃移通量的相对变化)(Q)为
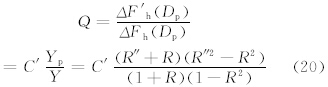
分狭管效应、地形效应以及两种地形的叠加效应3种方案进行试验。3.1 狭管效应
此时Vps=0,Vp=Vpr。设V1=V,lp1=xlp2,x为常数,则由式(6)和(12)可知
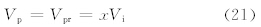
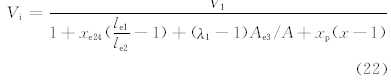
易得
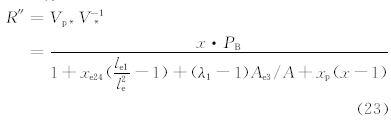
ΔF′h与Q的表达式形式同式(19)和(20)(下同)。
考虑两种情况,一种是狭管入口大、出口小,即风从狭管的阔口进、窄口出,此时x>1;另一种是狭管入口小、出口大,即风从狭管的窄口进、阔口出,此时x≤1。由图 3可见,在给定xe24=0.4,xp=0.2,且lp1=l/3(x≤1)或lp1=2l/3(x>1)的条件下,当x>1时,狭管中的速度是增大的;x≤1时,狭管中的速度是减小的。这显然是符合常识判断的。跃移通量中与速度有关的量Y在x≤1时(图 4a)是减少的,相伴随的是,跃移通量和起沙量减少(图 4b),而且,大粒径沙粒不再跃移。x>1时,Y(图 4c)和地形效应Q(图 4d)无论粒径大小均是增大的,而且,当速度大于一定程度时,大粒径沙粒跃移通量开始超过较小粒径沙粒跃移通量(图 4c),而Q随速度趋向于常值。这意味着,狭管效应既可以导致风速、跃移通量和起沙量的变化,又可以改变沙尘中的粒径结构。
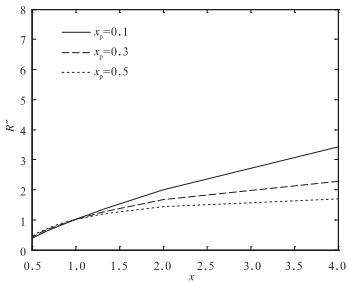 |
| 图 3 R″随x的变化 Fig. 3 Changes in R″ with x |
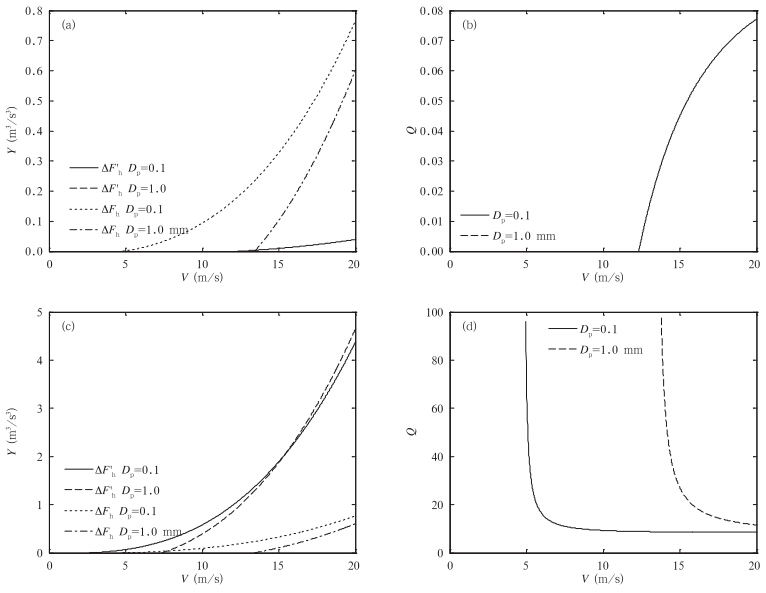 |
| 图 4 狭管效应下(a、c)Y与(b、d)Q随V的变化(a、b. x=0.5,c、d. x=2) Fig. 4 Changes in Y and Q with V under the narrow-pipe effect(x=0.5 in(a) and (b) and x=2 in(c) and (d)) |
此时狭管一侧高,一侧水平,满足h2=0,β2= ,lp23=0,Vi=0、Vp=Vps以及V=V2。此时由式(8)和(11)可得
,lp23=0,Vi=0、Vp=Vps以及V=V2。此时由式(8)和(11)可得
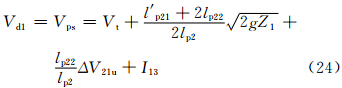
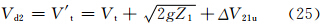
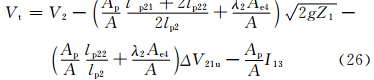
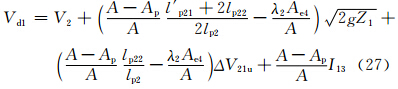
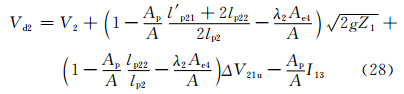
考虑两种情况,一种是沙源位于山坡上,另一种是沙源位于山脚下。此时lp22=0,简单取l′p21=lp21,则式(27)和(28)变为
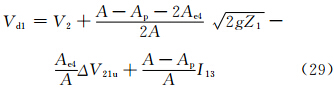
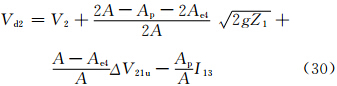
对于沙源位于山坡上的情况,风速采用Vd1,其R″记为R″d1;对于沙源位于山脚下的情况,风速采用Vd2,其R″记为R″d2。R″d1和R″d2分别为
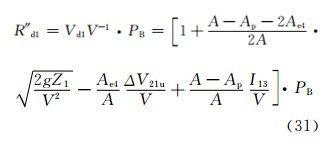
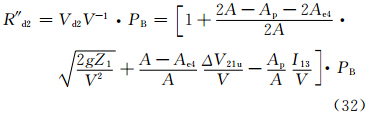
如此(图略)。
考虑下滑效应,山坡越高,位温差越大,地面位温越低,则风速越大(图 5a);风速越大,Y也越大(图 5b、c),跃移通量和起沙量也越大。不过,Q随风速的增大而减小(图 5d),故地形效应是逐渐降低的。而且,山脚风速和起沙量明显大于山坡,细粒子跃移通量又大于粗粒子。
 |
| 图 5 沙源位于山坡与山脚时的下滑效应(a. R″随Z1的变化,b. Z1=2 m时Y随V的变化,c. Z1=5 m时Y随V的变化,d. Q随V的变化) Fig. 5 Downslide effects for the cases in which the s and -dust source is located on hill side/hill foot(a. R″ vs. Z1; b. Y vs. V with Z1=2 m; c. Y vs. V with Z1=5 m; and d. Q vs. V)(see the text for further details) |
由式(21)、(29)和(30)可得狭管效应和下滑效应 叠加后的风速
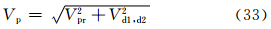
取3.1—3.3节对各变量的取值,但只取Z1=2 m,并设V1⊥V2,V1与V夹角30°。由图 6可见,对于入口大、出口小的狭管,风速、跃移通量和起沙量明显增大,在同样的风速下,较大粒径沙粒的跃移通量增幅大于较小粒径沙粒;而且,山脚的风速大于山坡的风速,但在一定条件下,较小粒子在山坡的跃移通量要大于在山脚的跃移通量(图 6b、c中Dp=0.1 mm的曲线,差别很细微)。
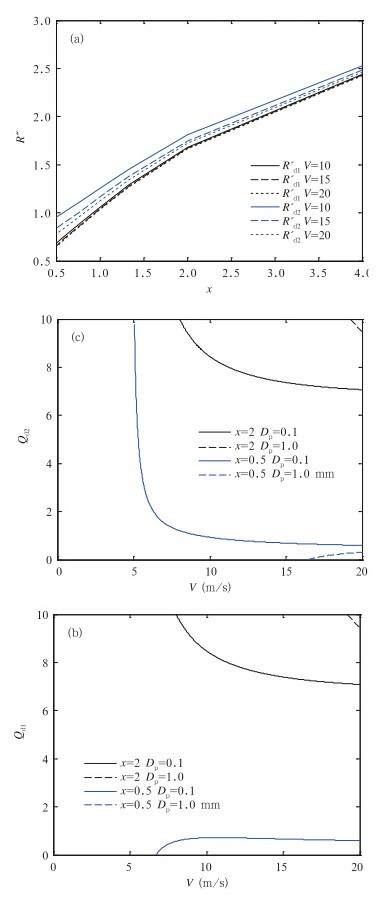 |
| 图 6 狭管效应与下滑效应的耦合 (a. R″随x的变化,b. 沙源位于山坡时Q 随V的变化,c. 沙源位于山脚时Q随V的变化) Fig. 6 Coupled effects of the narrow-pipe effect with the downslide effect(a. R″ vs. x,b. changes in Q with V when the dust source is located on the hill side,and c. changes in Q with V when the dust source is located on the hill foot) |
以上方案基于狭管正好处于网格中的情况,实际上狭管很可能与网格相交,此时可以狭管为中心,在原有网格上重新插值出一个网格,使此狭管正好处于新网格之中;然后以此新网格为基础,得到其地形起沙量;最后以下面两套方案得到各原有网格次网格的起沙量。
至于新网格中如何将参数化结果加到整个网格起沙量上,有两套方法实现。4.1 分算法
第一套方法是将网格中的地形看成是平坦地形与狭管地形的叠加,分别计算各自的起沙量,然后求出整个网格的起沙量。狭管地形的起沙量采用本研究得到的结果,均匀地形的起沙量通过将算出的狭管地形的速度Vp代入式(5),得到平坦地形的速度Ve,再通过将Ve代入式(16)—(20)得到网格中平坦地形的跃移通量ΔF′he
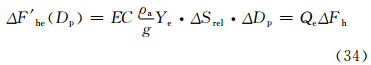

 。
。考虑次网格过程之后网格中的跃移通量ΔF″h则为
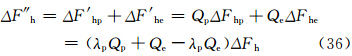
对于均匀平坦地形,狭管可以看成是进出口截面积相等、且狭管两侧山高为0的情形,而且,Pellegrini等(2005)的修正对数律公式可以应用到均匀地形,因此,可以在本研究的方法下得到网格中的速度Vp和Ve后,直接以式(18)算出摩擦速度,再以式(19)求出跃移通量,并最终得到起沙量。此法是重新计算起沙量,不再采用模式原来的计算方法。5 结 论
本研究基于对狭管效应与下滑效应(《新疆短期天气预报指导手册》编写组,1986;蒋维楣等,1994;祝学范,2004; 王式功等,2010)以及气流过山(ESDU,1993)现有研究成果,研究了局地地形下风速与起沙的次网格参数化问题,得到相应的参数化方案,并进行了理想数值试验。试验结果表明:
(1)对于狭管效应,风从狭管的阔口进、窄口出时,风速、跃移通量和起沙量均增大;反之,窄口进、阔口出时,风速、跃移通量和起沙量均减小,且大粒径沙粒跃移受到抑制。
(2)对于下滑效应,风速、跃移通量和起沙量也均增大,增幅与山坡高度、位温差大小以及地面位温有关;山脚的风速、跃移通量与起沙量大于山坡的风速、跃移通量与起沙量。
(3)狭管效应与下滑效应叠加时,当风从狭管的阔口进、窄口出时,风速、跃移通量和起沙量均增大,大粒径沙粒跃移通量增加率大于小粒径沙粒。反之,当窄口进、阔口出时,出入口宽度之比与网格风速大小存在一临界值,当出入口宽度比大于此临界值时,狭管中风速开始减小,反之增大;而且,如果沙源位于山坡,跃移通量减小,大粒径沙粒甚至不再跃移;如果沙源位于山脚,大粒径沙粒的跃移量也减少,但小粒径沙粒在风速大于某一临界值时才减小,反之则会增加。
(4)对于局地地形起沙的次网格参数化方案与沙尘数值模式的耦合,给出了分算法与整算法两套方法。
所以,考虑地形效应后,风速、跃移通量、起沙量和跃移沙粒的粒径结构均会发生一定的变化。考虑到沙尘气溶胶对辐射和云的影响,显然,考虑地形效应后,除了沙尘模式对局地地形造成的沙尘天气的预报精度会有一定的提升外,还会提高沙尘模式对沙尘气溶胶气候效应的模拟。
| 董继立,谈哲敏.2008.条件不稳定湿大气中三维理想地形上空对流的动力学特征.气象学报,66(3):293-309 |
| 郭铌,张杰,韩涛等.2004.西北特殊地形与沙尘暴发生的关系探讨.中国沙漠,24(5):576-581 |
| 李得禄,满多清,朱国庆等.2012.丘间低地不同部位风沙流结构特征.中国沙漠,32(5):1210-1215 |
| 李双权,哈斯,杜会石等.2012.沙质草地蝶形风蚀坑形态-气流相互作用.中国沙漠,32(5):1201-1209 |
| 李唐棣,谈哲敏.2012.条件不稳定大气中二维小尺度双脊地形上空对流及降水特征.气象学报,70(3):536-548 |
| 姜学恭,陈受钧.2008.地形影响沙尘传输的观测和模拟研究.气象学报,66(1):1-12 |
| 蒋维楣,徐玉貌,于洪彬.1994.边界层气象学基础.南京:南京大学出版社,50-150 |
| 廖移山,冯新,石燕等.2011.2008年“7.22”襄樊特大暴雨的天气学机理分析及地形的影响.气象学报,69(6):945-955 |
| 沈建国,姜学恭,孙照渤.2007.地形对沙尘暴的影响及敏感试验研究.高原气象,26(5):1013-1022 |
| 王建鹏,沈桐立,刘小英等.2006.西北地区一次沙尘暴过程的诊断分析及地形影响的模拟试验.高原气象,25(2):259-267 |
| 王式功,周自江,尚可政等.2010.沙尘暴灾害.北京:气象出版社,117-119 |
| 《新疆短期天气预报指导手册》编写组.1986.新疆短期天气预报指导手册.乌鲁木齐:新疆人民出版社,150-457 |
| 宣捷.1998.低层大气中固体粒子运动及其物理模拟.环境科学学报,18(4):350-355 |
| 朱好,张宏升.2010.中国西北不同沙源地区起沙阈值的对比分析与研究.气象学报,68(6):977-984 |
| 祝学范.2004.大风出现的位置与地形的关系.新疆气象,27(6):1-2 |
| Ameur K, Masson C.2012. Effects of terrain slope on nacelle anemometry. J Sol Energy Eng, 134(3),31003, doi:10.1115 /1.4006039 |
| Belcher S E, Hunt J C R. 1998. Turbulent Ilow over hills and waves. Annu Rev Fluid Mech, 30(1): 507-538 |
| Bouwmeester R J B. 1978. Wind Characteristics over Ridges[D]. Colorado; Colorado State University, 1-53 |
| Chepil W S, Siddoway F H,Armbrust D V. 1964. Wind Erodibility of Knolly Terrain. J Soil Water Conserv, 19(5):179-181 |
| Ding L, Ssreet R L. 2003. Numerical study of the wake structure behind a three-dimensional hill. J Atmos Sci, 60(14):1678-1690 |
| ESDU. 1993. Mean Wind Speeds over Hills and Other Topography (Item no. 91043). London: ESDU International PLC, 1-45 |
| Uarvey B, Castro I P, Wiggs U F S, et al. 2005. Measurements of Mows over isolated valleys. Bound Layer Meteor, 117(3):417-446 |
| Uoossens D. 2006. Aeolian deposition of dust over hills; the effect of dust grain size on the deposition pattern. Earth Surl Proc Land, 31(6):762-776 |
| Hoffmann C,Funk R, Wieland R, et al. 2008. EIIects of grazing and topography on dust Ilux and deposition in the Xilinggele grassland, Inner Mongolia. J Arid Environ, 72(5):792-807 |
| Hunt J C R, Richards K J,Brighton P W M. 1988. Stably stratified shear flow over low hills. Quart J Roy Meteor Soc, 114(482):859-886 |
| Jackson P S, Hunt .J C R. 1975. Turbulent wind Ilow over a low hill Quart J Roy Meteor Soc, 101(430):929-955 |
| Kaimal J C,Finnigan J J. 1994. Atmospheric Boundary Layer Flows:Their Structure and Measurement. New York:Oxford University Press, 1-289 |
| Lemelin D R, Surry D, Davenport A (}. 1988. Simple approximations for wind speed-up over hills. J Wind Eng Ind Aerodyn, 28(1-3):117-127 |
| Liu B, Qu J,Zhang W, et al. 2011. Numerical simulation of wind flow over transverse and pyramid dunes. J Wind Eng Ind Aerodyn, 99(8):879-888 |
| Marticorena B, Bergametti U, Aumont B. 1997. Modeling the atmospheric dust cycle: 2. Simulation of Saharan dust sources. J Ueophys Res, 102(D4):4387-4404 |
| Mason P J,Sykes R I. 1979. Flow over an isolated hill of moderate slope. Quart J Roy Meteor Soc, 105(444):383-395 |
| Maurizi A. 2000. Numerical simulation of turbulent Mows over 2D valleys using three versions of the k-a closure model. J Wind Eng Ind Aerodyn, 85(1):59-73 |
| Parsons D R, Walker I J,Wiggs U F S. 2004. Numerical modeling of Ilow structures over idealized transverse aeolian dunes of varying geometry. Ueomorph, 59(1-4):149-164 |
| Pellegrini C C,Bodstein G C R. 2005. A modified logarithmic law for neutrally stratified Ilow over low-sloped hills. J Appl Meteor, 44(6):900-916 |
| Rokenes K. 2009. Investigation of Terrain EIIects with Respect to Wind Farm Siting[D]. Norway: Norwegian University of Science and Technology, 31-140 |
| Snyder W H,Khurshudyan L H, Nekrasov R E, et al. 1991. Flow and dispersion of pollutants within two-dimensional valleys. J Atmos Environ, 25(7); 1347-1375 |
| Tampieri F. 1987. Separation Ieatures of boundary layer flow over valleys. Bound Layer Meteor, 40(3):295-307 |
| Taylor P A, Lee R J. 1984. Simple Uuidelines for estimating wind speed variations due to small scale topographic leathers. (Climatol Bull, 18(2): 3-22 |
| Uchida T, Okya Y. 2001. Numerical study of stably stratified flows over a two-dimensional hill in a channel of Iinite depth. Fluid Res, 29(4):227-250 |
| Walmsley J L, Salmon J R, Taylor P A. 1982. On the application of a model of boundary layer Ilow over low hills to real terrain. Bound Layer Meteor, 23(1):17-46 |
| Walmsley J L, Taylor P A, Salmon J R. 1989. Simple guidelines for estimating wind speed variations due to small-scale topographic leathers-an update. Climatol Bull, 23(1):3-14 |
| Weng W S, Taylor P A, Walmsley J L. 2000. Uuidelines for airllow over complex terrain; model developments. J Wind Eng Ind Aerodyn, 86(2-3):169-186 |
| White B R. 1979. Soil transport by winds on Mars. J Ueophys Res, 84(B9):4643-4651 |
| Xuan J,Robins A. 1994. The ellects of turbulence and complex terrain on dust emissions and depositions Irom coal stockpiles. Atmos Environ, 28(11):1951-1960 |
 2013, Vol. 71
2013, Vol. 71

