中国气象学会主办。
文章信息
- 刘琳, 陈静, 程龙, 林春泽, 吴志鹏. 2013.
- LIU Lin, CHEN Jing, CHENG Long, LIN Chunze, WU Zhipeng. 2013.
- 基于集合预报的中国极端强降水预报方法研究
- Study of the ensemble-based forecast of extremely heavy rainfalls in China:Experiments for July 2011 cases
- 气象学报, 71(5): 853-866
- Acta Meteorologica Sinica, 71(5): 853-866.
- http://dx.doi.org/10.11676/qxxb2013.044
-
文章历史
- 收稿日期:2012-08-01
- 改回日期:2013-05-22
2. 成都信息工程学院, 成都, 610225;
3. 中国气象局数值预报中心, 北京, 100081
2. Chengdu University of Information Technology, Chengdu 610225, China;
3. Numerical Weather Prediction Center, Beijing 100081, China
极端天气事件对人类社会和环境有很大的影响,甚至可造成严重灾害,极端天气事件的定义方法很多(Easterling et al,2000),Beniston(2007)认为大致分为3种:(1)事件有相对较大或较小的强度;(2)事件发生的频率相对较低;(3)事件导致了严重的社会经济损失。政府间气候变化专门委员会(IPCC)第3、4次报告(IPCC,2001,2007)从第2种角度对极端天气气候事件作了明确的定义:对一特定地点和时间,极端天气事件就是发生概率极小的事件,通常发生概率只占该类天气现象的10%或者更低。这样避免了事件的绝对强度随区域不同而差异较大的问题。
在极端天气事件中,极端降水事件预报一直是气象学家们高度重视的研究领域。极端降水事件预报研究主要分为两类:一是通过观测资料定义与极端降水事件相关的代用气候指数,分析极端降水变化特征,反映极端降水事件变化情况。对降水或强降水长期变化特征研究发现,极端降水有明显增多趋势(Yamamoto et al,1999; Groisman et al,1999; Osborn et al,2000)。严中伟等(2000)指出,中国北方干旱化问题主要反映在微量降水事件显著减少。黄荣辉等(2003)发现了自1976年以来中国华北地区持续干旱及长江、淮河流域夏季季风降水明显增多的特征。翟盘茂等(2003)、Qian等(2005)、张婷等(2009)对中国各区域极端降水变化特征的研究结论基本一致,即西南、西北北部和华东极端降水事件频率呈增加趋势,华北、华中呈减少趋势。李红梅等(2008)发现,中国东部地区盛夏降水变化主要受暴雨降水强度变化的影响,占总降水变化的60%以上;盛夏长江流域降水量、降水频率、极端降水频率以及暴雨降水强度均呈增大趋势,在华北地区则呈减小趋势。二是通过数值模式对极端天气事件进行数值模拟预报研究。王志福等(2008)使用区域海-气耦合模式对中国夏季极端降水进行模拟研究,结果表明区域海-气耦合模式基本能够模拟出气候平均极端降水阈值的空间分布型。卢萍等(2009)研究结果表明,初始水汽条件对最大降水发生时间产生明显影响。江志红等(2009)考察政府间气候变化专门委员会第4次评估报告的7个全球模式及5个集合预报模式对极端降水指数的模拟能力,指出全球模式能较好地模拟极端降水指数气候场空间分布,较好地反映中国线性趋势,且集合预报能力优于大部分单个模式。
大气是一个混沌系统,天气预报的不确定性是其根本属性之一(叶笃正等,2006)。极端降水事件属于小概率事件,天气预报的不确定性给降水预报、特别是极端降水这一类小概率事件的预报带来了极大的困难。集合预报作为一种新兴的概率预报方法,是未来研究小概率极端天气事件的发展方向(陈静等,2005,李泽椿等,2002)。利用概率预报的思路来研究极端降水天气事件由来已久。Steven等(2001)利用美国国家环境预测中心(NCEP)短期集合预报系统(SREF),对2000年7月25日发生在美国北卡罗莱纳州的一次暴雪进行模拟研究,结果显示大多数集合预报中的成员成功预报出了这次暴雪。Sobash等(2011)利用邻域法(Theis et al,2005),将确定性对流模式预报结果转换为极端天气概率预报产品,提高了模式对极端天气的预报能力。中国在这方面的研究尚少,陈朝平(2010)基于贝叶斯理论,利用四川147个站点暴雨的气候概率订正暴雨集合概率预报产品,在一定程度上消除暴雨空报。李芳(2012)采用4种多模式集合方案,制作1960—2005年中国东部夏季降水概率密度函数(PDF)季度预测,结果表明最优集合方案的概率密度函数预测产品均具有高校准度,且其锐度不低于气候学预测。
Lalaurette(2002)基于欧洲中期天气预报中心(ECMWF)集合预报发展了一种极端天气预报方法——极端天气预报指数(EFI)。极端天气预报指数原理是计算模式气候与集合预报(EPS)累积概率分布函数连续概率差异。结果表明,极端天气预报指数对于极端天气事件具有较好预报效果,能提前5 d预报出极端天气事件。Lalaurette(2003)又基于Anderson-Darling检验原理,对极端天气预报指数公式进行修订,提高极端天气预报指数对于极端天气的敏感度。Evrin(2006)基于ERA-40再分析资料重新生成模式气候累积概率分布,从而提高了极端天气预报指数的预报技巧。
基于集合预报的极端天气预报方法在中国处于初步研究阶段,夏凡等(2012)基于中国T213集合预报系统资料,研究极端低温天气预报方法,对2008年1月极端低温天气进行了预报试验和评估检验。结果表明,极端天气预报指数对极端低温天气具有较高的识别能力,可提前3—5 d发出极端低温预警信号。随着预报时效的延长,识别技巧逐渐降低。而利用极端天气预报指数对其他极端天气(极端强降水、极端大风等)的预报还有待进一步的研究,尤其是降水这种非连续变量与气温有很大的差别,极端天气预报指数是否也能很好地识别极端强降水天气?有鉴于此,本研究将充分考虑中国T213集合预报的降水预报特征,研究基于T213集合预报的极端降水天气预报指数(EPFI)数学模型,并根据T213模式降水预报累积概率分布特征,确定极端降水预报临界阈值,利用极端降水天气预报指数对2011年7月的多次极端强降水过程进行预报试验和检验。2 资料简介
本研究所用降水资料包括中国观测降水资料和中国气象局(CMA)T213集合预报降水资料:观测降水资料采用中国国家气象信息中心整编的中国2412个测站2001—2011年6—8月00时(世界时,下同)的逐日24 h累积降水。T213集合预报资料时间为该系统资料存档之日至2011年,即2007年7月和2008—2011年6—8月00时起报的中国降水预报资料,预报时效为24—168 h,水平分辨率为0.5625°。
图 1a为观测站点分布,图 1b为中国区域内T213模式预报网格点分布。可见观测站点分布不均匀,东部和南部观测站较密集,而西北部尤其是新疆和西藏等地观测站稀疏,采用Cressman插值方法(陈飞等,2010),将全中国2412个站点的观测降水资料插值到T213模式网格点上(n=3182),如图 1b。
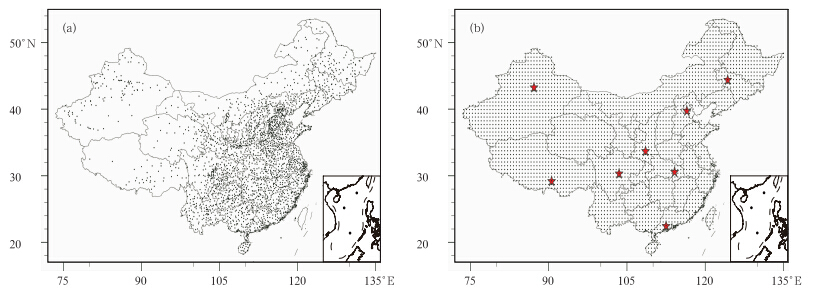 |
| 图 1 观测站点和模式网格点的空间分布 (a.2412个观测站点,b.模式网格点;五角星为8个区域的代表格点) Fig. 1 Spatial distributions of(a)the 2412 rainfall observation stations and (b)the model grids (The stars in(b)denote the grid points that are representative for the eight sub-regions under study,respectively) |
在研究极端强降水预报方法之前,先对观测和模式极端强降水特征进行对比分析,考察二者分布特征差异以及模式极端强降水的误差分布,为建立更符合中国集合预报模式特征的极端天气预报模型和预报指数提供依据。
考虑到中国地形复杂,不同地区极端降水累积概率分布特征差异很大,因此,在中国8个不同气候区域(陈隆勋等,1991)内各选取一个典型代表格点进行研究分析,图 1b中的五角星即为各区域的代表格点,表 1为8个不同气候区域的划分和代表格点位置。
| 代表格点编号 | 代表区域 | 格点经度(°E) | 格点纬度(°N) |
| 1 | 东北 | 124.31 | 44.44 |
| 2 | 西北西部 | 87.19 | 43.31 |
| 3 | 西北东部 | 108.56 | 33.75 |
| 4 | 华北 | 115.88 | 39.38 |
| 5 | 长江中下游 | 114.19 | 30.38 |
| 6 | 西南 | 103.50 | 30.38 |
| 7 | 华南 | 112.50 | 22.50 |
| 8 | 青藏高原 | 90.56 | 29.25 |
参照翟盘茂等(2003)对极端强降水事件定义的百分位法,将2001—2010年6—8月中国每个格点的观测日降水量(n=920)按照升序排列,定义第99个百分位上降水量的10年平均为该格点的极端强降水阈值。当某日降水量超过该格点的极端强降水阈值时,则称该格点出现极端强降水,否则无极端强降水发生。
对于模式极端强降水的确定,选取2008—2010年6—8月的集合预报降水预报结果,组成中国每个格点的模式降水气候序列,长度为4140(3 a × 92 d/a × 15个集合预报成员),定义气候序列第99个百分位或者以上的降水为模式极端强降水。
中国夏季雨日降水量的概率分布明显为偏态分布,用Г分布能较好地拟合(刘学华等,2006),故利用Г分布来拟合模式降水序列分布。图 2为8个区域代表格点的模式降水气候序列的概率密度分布曲线,预报时效为24—168 h。可见8个代表格点24—168 h的降水概率密度分布表现出一致的趋势,但不同预报时效的概率密度分布略有差异。总体上看,10—40 mm降水,不同预报时效的概率密度分布差异较大,24 h的降水概率密度最大,随着预报时效延长至144 h,模式气候降水概率密度逐渐减小,而168 h的降水概率密度反而比144 h有所提升。随着预报时效的延长,大于40 mm的降水概率密度逐渐减小并趋于0,降水概率密度有向10 mm以下雨量集中的趋势。值得注意的是,168 h以后,降水概率密度曲线基本不变。这说明模式预报的降水结果随着时效的延长,大雨和中雨的频率有减小趋势,小雨的频率逐渐增大。至168 h以后,各量级降水的概率密度开始趋于稳定。
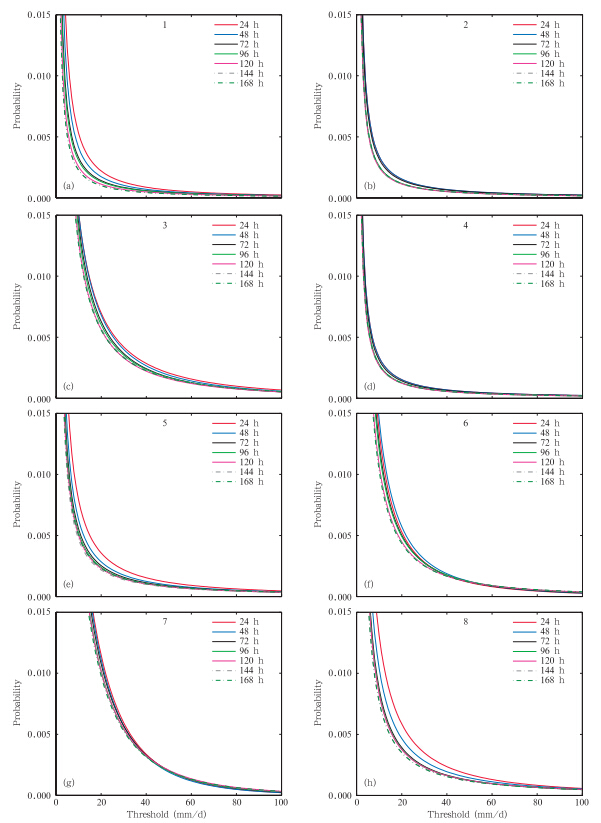 |
| 图 2 集合预报模式降水序列的概率密度分布(a—h:8个代表格点) Fig. 2 Precipitation probability distribution of the ensemble forecast system at the representative grid points of theeight sub-regions(a-h),respectively |
为了研究观测与模式极端强降水的差异,资料长度均为2008—2010年6—8月,根据3.1节中对观测和模式极端强降水的定义,得出观测与模式极端强降水的空间分布(图 3)。其中,图 3a为观测极端强降水分布,图 3b—d为24、96和168 h的模式极端强降水分布。可以看出,模式预报的极端强降水分布与观测十分接近,雨带从东南向西北递减。但模式预报的极端强降水大值中心与观测存在一定的偏差,观测极端强降水有5个大值中心:四川和陕西交界处、湖北湖南交界的恩施和张家界地区、大别山地区、安徽黄山附近以及广东等沿海地带;而模式预报极端强降水中心与观测存在一定差异,如青藏高原东南部存在虚假极端降水高值区,广东沿海地区极端强降水大值中心偏向江苏、浙江和福建一带,其他极端强降水的大值中心基本上与观测比较接近。此外,模式极端强降水较观测明显偏弱,尤其是东部地区,并且,随着预报时效的延长,模式极端强降水呈减弱趋势。
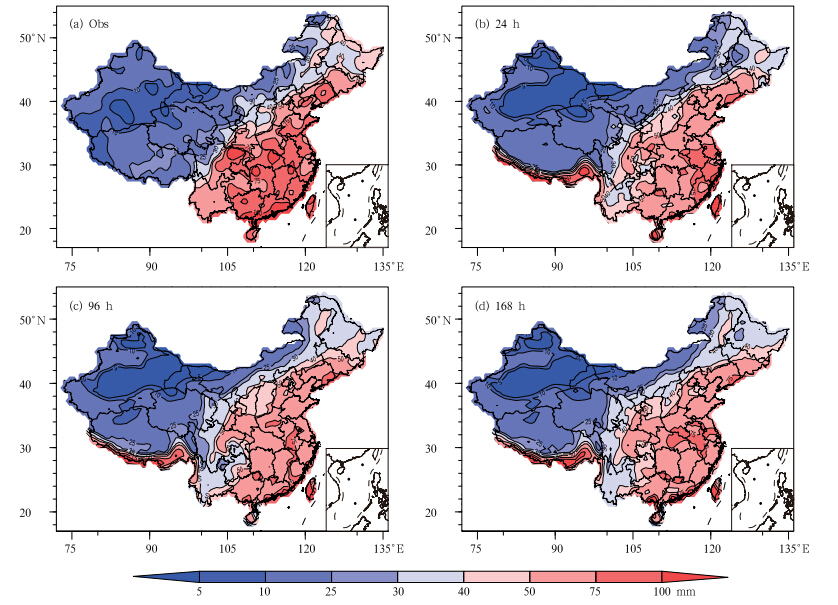 |
| 图 3 观测和模式极端强降水空间分布(a.观测,b、c、d.24、96、168 h 模式) Fig. 3 Spatial distributions of(a)the observed and (b)24-,(c)96-,and (d)168-h ensemble forecast extreme precipitation |
利用集合预报进行极端强降水预报原理是根据模式历史气候与集合预报各成员降水预报累积概率分布函数的连续差异大小以获取极端强降水是否发生的预报信息。以48和96 h集合预报降水累积概率分布为例,结合相应的模式历史气候累积概率分布情况,从两者连续差异特征解释基于集合预报的极端强降水预报原理。
图 4为极端降水天气预报指数原理示意图,图 4a横坐标为降水量,纵坐标为累积概率,实线分别为48(绿色)和96 h(黑色)模式气候累积概率曲线,虚线为48(绿色)和96 h(黑色)集合预报累积概率曲线,图 4b为相应的概率密度分布曲线。48和96 h 的模式历史气候分别是由2007—2010年7月的48和96 h 的T213 集合预报各成员降水预报结果组成,长度为1860(4 a × 31 d/a ×15个集合预报成员);对应预报时效的集合预报分布序列则选取T213集合预报2011年7月20日的48和96 h降水预报结果,序列样本长度为15个集合预报成员。
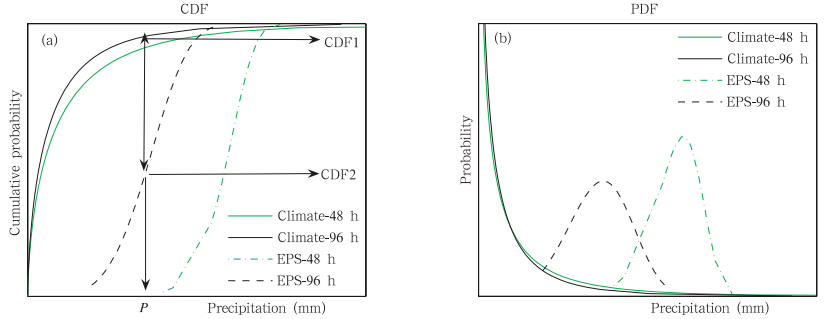 |
| 图 4 极端降水天气预报指数原理示意(a.降水量-累积概率,b.降水量-概率密度) Fig. 4 Schematic diagrams of the ensemble-based extreme precipitation forecast(in(a)the vertical axis represents cumulative probability and the horizontal axis represents precipitation; solid line represents the CDF curve of the model climate; dashed line represents the CDF curve of the ensemble forecasts(green line is for 48 h and black line for 96 h); and in(b)the vertical axis represents probability density and the horizontal axis represents precipitation; solid line represents the PDF curve of the model climate; dashed line represents the PDF curve of the ensemble forecasts(green line is for 48 h and black line for 96 h)) |
从图 4a可见,降水量为P时,对应96 h的模式气候累积概率为CDF1,集合预报累积概率为CDF2,二者之差(CDF1- CDF2)大于0,表明降水量级大于P的集合预报概率大于模式历史情况,96 h 集合预报与模式历史气候累积概率曲线之间的面积值,即96 h预报降水量区间内二者差异的连续积分,如积分值大于0,表明集合预报降水较模式历史气候偏多。如集合预报降水累积概率越趋于分布在尾端部分(即大降水端),则集合预报与模式历史气候累积概率分布曲线之间面积越大,从图 4a的48 h集合预报可见,48 h集合预报与模式气候累积概率分布曲线间的面积大于96 h。图 4b给出了与图 4a对应的48和96 h的概率密度分布,可见其48 h集合预报降水集中区间的量级明显大于96 h,48 h降水强度较96 h偏强。因此,48 h集合预报对大降水量级的预报信号较96 h强。
以上分析表明,模式气候与集合预报各成员预报结果的累积概率分布函数连续差异大小可以用来衡量降水量级强度,当二者连续差异为正,表明降水偏多,当二者连续差异为负,则表明降水偏少。两者差异正值越大,即两者分布曲线间面积越大,降水量级越大,达到一定程度后就可以判断为极端强降水。 4.2 基于Anderson-Darling检验的极端降水预报指数数学模型
基于Aderson-Darling检验原理(Anderson et al,1952),Lalaurette(2002)定义了极端降水天气预报指数
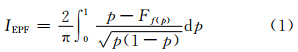
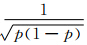 为权重系数,当p=1/2时,权重系数最小,当p=0或1时,权重系数最大,可提高极端降水天气预报指数对累积概率分布尾端的极端天气(p接近于0或1)的敏感程度,更大程度预报可能发生的极端强降水天气。离散化后的极端降水预报指数计算公式为
为权重系数,当p=1/2时,权重系数最小,当p=0或1时,权重系数最大,可提高极端降水天气预报指数对累积概率分布尾端的极端天气(p接近于0或1)的敏感程度,更大程度预报可能发生的极端强降水天气。离散化后的极端降水预报指数计算公式为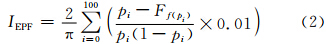
从式(1)可知,极端降水天气预报指数为-1—1的实数,如所有的集合预报成员小于气候概率的最小值(即对于所有分位数p,Ff(pi)均为1),极端降水天气预报指数取-1,表明可能出现极端干旱事件;如果所有的集合预报成员的结果大于气候概率的最大值(即对于所有分位数p,Ff(pi)均为0),则极端降水天气预报指数为1,就有可能出现极端强降水事件。极端降水天气预报指数越接近-1(1),极端干旱(强降水)天气发生的可能性越大。
模式气候累积概率分布是极端降水天气预报指数的重要组成部分。参照Lalaurette(2002)的方法,采用2007—2010年T213集合预报生成降水的模式气候累积概率分布,夏凡等(2012)研究发现,T213模式的预报结果在不同预报时效的误差不同,在4.1节的分析中也发现,不同预报时效的降水概率密度分布并不一致。随着预报时效的延长,模式所预报的小雨频率增多。故选取T213集合预报模式2007—2010年7月00时发布的中国区域内格点的逐日降水资料,每个格点上生成独立的7个(24—168 h)模式气候序列,序列长度为1860(n=4 a×31 d/a×15个集合预报成员),为了与第6节的模式气候产生方案有所区别,将此处的气候累积概率方案简称为T213-P1。
采用2007—2010年7月T213集合预报逐日降水资料,生成中国区域24—168 h共7个预报时效的集合预报累积概率分布,序列长度为15,由式(2)计算出2007—2010年逐日7个预报时效的极端降水天气预报指数,为计算极端强降水预报指数临界阈值提供基础数据。
4.3 极端强降水预报指数临界阈值确定方法由上述可知,极端降水天气预报指数为正值时,表明有可能会出现极端强降水天气。但预报员更迫切需要明确极端降水天气预报指数取哪一个值,可以发出极端强降水预警信号,本节重点研究极端降水预报指数阈值的确定方法,极端强降水事件可视为发生和不发生的二分类事件,通过一定方法确定某一极端降水天气预报指数值为极端强降水预报临界阈值,如果极端降水天气预报指数大于这一临界阈值,则预报有极端强降水,若极端降水天气预报指数小于临界阈值,则预报无极端强降水。如何确定临界阈值是预报极端强降水的一个重要环节。
众所周知,TS评分和预报偏差(Bias)是评估二分类事件预报水平的重要评分参数,考虑极端强降水事件实况和极端降水天气预报指数预报的双态列联表(表 2),可以计算出预报的TS评分、预报偏差,同时获得命中率和虚警率。
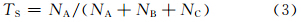
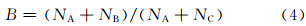
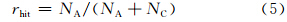
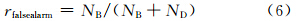
| EPFI预报出现 | EPFI预报不出现 | |
| 实况发生 | NA | NC |
| 实况不发生 | NB | ND |
确定极端降水天气预报指数临界阈值的方法是综合考虑TS评分和预报偏差评分的物理意义,设计一个S判识指数

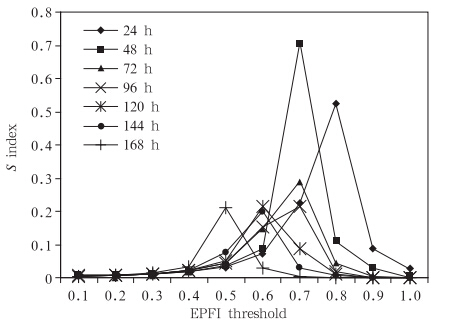 |
| 图 5 S值随不同极端降水天气预报指数阈值变化曲线(时效:24—168 h) Fig. 5 Variations of the S index with the different EPFI thresholds for the 24-168 h forecast periods of validity |
| 时效(h) | EPFI阈值 |
| 24 | 0.8 |
| 48 | 0.7 |
| 72 | 0.7 |
| 96 | 0.7 |
| 120 | 0.6 |
| 144 | 0.6 |
| 168 | 0.5 |
基于上述2011年7月15—31日T213集合预报的7个预报时效的集合预报累积概率分布和模式气候累积概率分布,利用式(2)计算出中国每个格点7个预报时效的极端降水预报指数。表 4为极端降水预报统计检验平均值。可以看出,TS评分随着时效的延长而逐渐降低,24 h的TS评分最高,为0.150。预报偏差基本上随预报时效的延长而增大,随时效的延长空报稍微增多。命中率随时效的延长而逐渐降低(由0.321降至0.139)。虚警率逐渐升高,168 h达到0.044。
相对作用特征(ROC)曲线是用来评估概率预报的有效方法(Mason et al,2002),将不同概率分类(极端降水天气预报指数可分成10个等级)的命中率和虚警率所组成的点绘成一条曲线,曲线在对角线以上,则有正的技巧。曲线和坐标轴围成的面积(AROC)越大,预报效果越好。图 6为极端降水天气预报指数试验的平均相对作用特征曲线,可见24—168 h预报的相对作用特征曲线都在对角线以上,随着时效的延长,曲线越来越偏向对角线,这表明24—168 h的预报结果都存在正的预报技巧,并且,随着时效的延长,预报技巧逐渐降低,各时效相对作用特征面积见表 4。
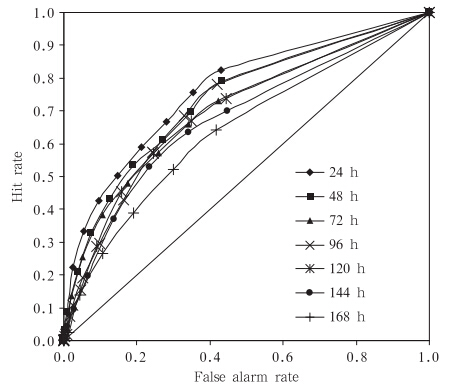 |
| 图 6 极端降水天气预报指数试验的平均相对作用特征曲线 (不同点代表不同的极端降水天气预报指数阈值) Fig. 6 Average relative operating characteristic curve valid for the EPFI test. Each point of the curve corresponds to a different EPFI threshold |
| 24 h | 48 h | 72 h | 96 h | 120 h | 144 h | 168 h | |
| TS评分 | 0.150 | 0.111 | 0.107 | 0.094 | 0.084 | 0.069 | 0.055 |
| 预报偏差 | 1.168 | 1.156 | 1.723 | 1.573 | 1.298 | 1.911 | 1.589 |
| 命中率 | 0.321 | 0.309 | 0.240 | 0.209 | 0.175 | 0.196 | 0.139 |
| 虚警率 | 0.025 | 0.038 | 0.023 | 0.024 | 0.016 | 0.028 | 0.044 |
| 相对作用特征曲线面积 | 0.759 | 0.727 | 0.703 | 0.716 | 0.697 | 0.678 | 0.642 |
以2011年7月24日为例对极端强降水预报进行细致分析,当日最大降水中心位于北京、天津和辽宁一带,其中,北京地区局部的降水量超过100 mm,平均降水量为62 mm,累积最大降水量出现在密云北山下(244 mm),造成2人死亡,1人失踪。内蒙古东部和山东也出现了50 mm以上降水。通过统计,7月24日发生极端强降水的格点数为76个,占总格点数的2.39%(图 7),主要发生在内蒙古北部的大兴安岭,北京、河北、天津以及山东中部,西藏西部和南部等地。
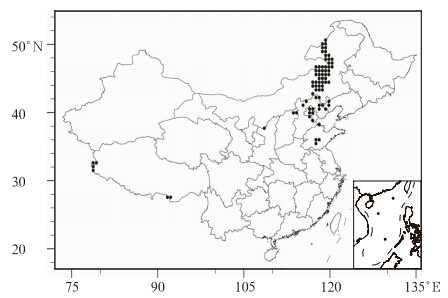 |
| 图 7 2011年7月24日发生极端强降水的格点分布 Fig. 7 Distribution of the extreme precipitation grids on 24 July 2011 |
图 8为与7月24日实况对应的48—120 h极端强降水预报指数分布,即预报起报时间分别为2011年7月22日00时的48 h预报,7月21日00时的72 h预报,依此类推。阴影区域为极端降水天气预报指数判断有极端强降水发生的区域。对比极端强降水实况(图 7b)可以看出,48和72 h的极端降水天气预报指数预报出了内蒙古东部、北京、河北、天津和西藏西部的大片区域,而漏报了山东中部和西藏南部等地,96与72 h的预报情况类似。120—144 h也是报出了内蒙古东部、北京、河北、天津、西藏西部等地的极端强降水,但是华南地区出现了一定的空报,并且,随着预报时效的延长,华南地区空报增多。在24—96 h的极端降水天气预报指数图中,极端强降水的雨带分布和实况非常接近(前几个时效的极端降水天气预报指数图省略),而120 h以后的预报效果有所降低,但是,大部分的极端强降水区域还是能报出。
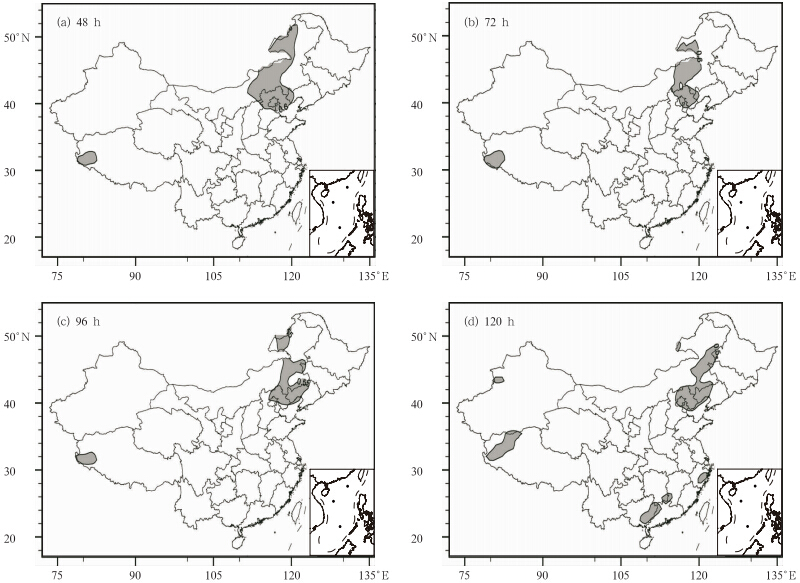 |
| 图 8 2011年7月24日极端降水天气预报指数分布(a.48 h,b.72 h,c.96 h,d.120 h) Fig. 8 Distributions of EPFI on 24 July 2011 at(a)48-,(b)72-,(c)96-,and (d)120-h forecast lead times |
从上述极端降水天气预报指数的预报效果和检验结果可以看出,极端降水天气预报指数对于极端强降水具有一定的预报能力,能提前3—7 d发出正确的极端强降水预警信号。但是,南方地区的极端降水天气预报指数预报值偏大,120 h预报图中华南地区出现了一些空报;48—120 h的预报图中都漏报了山东中部。造成这样的原因可能是模式气候累积概率只包含了7月的降水信息,此时雨带随副热带高压北跳到华北地区,造成华北降水增多,华南和长江中下游降水减少,表现在华南和华中的模式气候累积概率分布中小雨概率增多,北方的模式气候累积概率中大雨概率增多,导致华南和华中的极端降水天气预报指数偏大,北方极端降水天气预报指数偏小。6 模式气候累积概率对极端强降水预报效果的影响
从式(1)、(2)可以看出,模式气候对极端降水预报指数有重要影响。众所周知,中国的雨季主要集中在6—8月(称为主汛期),包含的降水信息比一个月更全面,而目前中国的模式资料的历史时段相对于欧洲中期天气预报中心比较短,根据这种情况,设计了第2套模式气候资料。选取T213集合预报2008—2010年6—8月00时发布的中国格点的逐日降水资料,每个格点上生成独立的7个(24—168 h)模式气候序列,每个序列长度为4140(n=3 a × 92 d/a ×15个集合预报成员),简称T213-P2。
图 9为华北、华南和长江中下游3个区域代表格点72 h的两套模式气候序列的累积概率分布曲线对比(其他时效的情况与之类似)。可以看出,华北代表格点的T213-P2与T213-P1相比,中、小量级雨量的频率增大,累积概率曲线更偏向纵轴;长江中下游和华南代表格点的中雨和大雨的频率增大,累积概率曲线更趋向横轴,华南的这种趋势更加明显,中雨和大雨的频率增大的更多。这表明T213-P2使得北方的小雨增多,中南部的中雨和大雨频率增大。
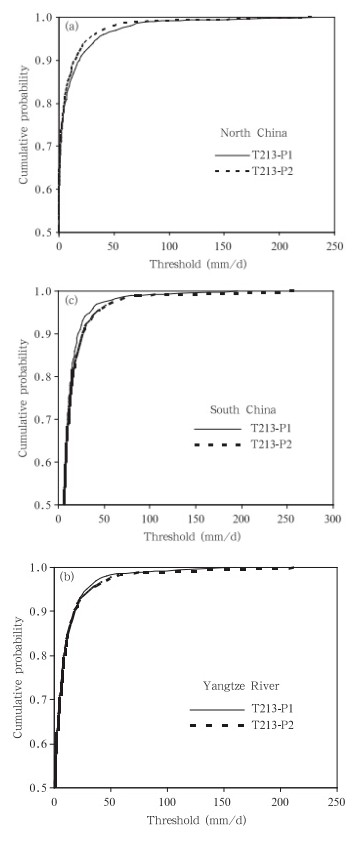 |
| 图 9 两种模式降水气候累积概率分布曲线(a.华北,b.长江中下游,c.华南) Fig. 9 Cumulative probability curves from the 72-h model climate precipitation datasets T213-P1(solid) and T213-P2(dashed)for(a)North China,(b)the mid-lower reaches of the Yangtze River,and (c)South China |
图 10为两种方案对7月24日极端强降水的预警效果对比。图 10a、b分别对应48 h的T213-P1和T213-P2两种模式气候方案计算出的极端降水天气预报指数预警分布,可以看出T213-P1方案漏报了山东中部的极端强降水(如上文中所述),T213-P2方案则成功预报出该地的极端强降水。
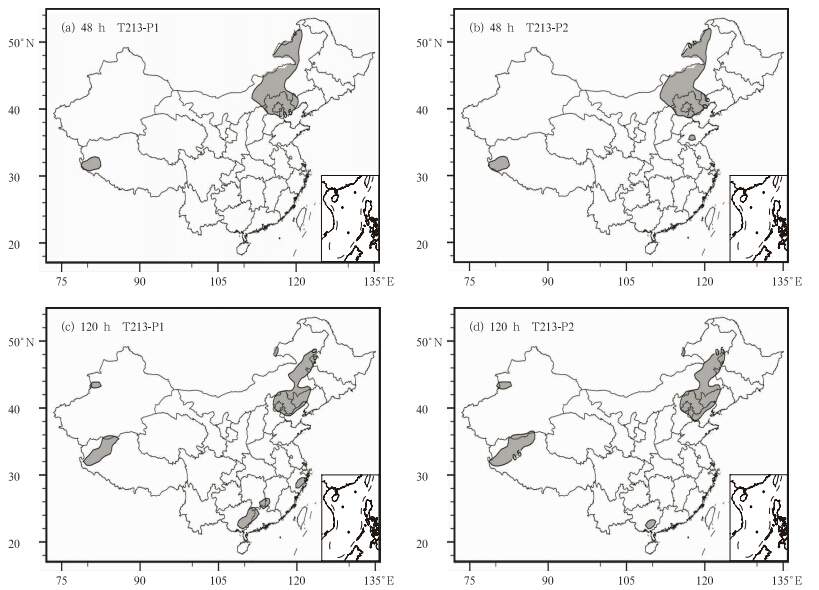 |
| 图 10 2011年7月24日T213-P1(a、c)和T213-P2(b、d)两种模式气候的极端降水天气预报指数对比(a、b.48 h,c、d.120 h) Fig. 10 EPFI maps derived from the two model climate precipitation datasets T213-P1(a,c) and T213-P2(b,d)on 24 July 2011 for 48-(a,b) and 120-h(c,d)forecasts |
图 10c、d分别对应120 h的T213-P1和T213-P2两种方案的极端强降水预警分布,T213-P1方案在华南地区出现了大片的空报,而T213-P2方案则有很大的改进,华南区域的空报情况明显减小。对比批量试验的其他个例,情况与上述相似,即T213-P2方案改进了北方区域由于极端降水天气预报指数偏小所造成的漏报,并且,使得华南地区极端降水天气预报指数减小,空报情况得到了很大的改善。
图 11为两种方案的检验效果对比。T213-P2的TS评分、命中率都明显高于T213-P1,对比两种方案的相对作用特征曲线(表 5),前者高于后者。但T213-P2的虚警率和预报偏差也稍微高于T213-P1,这表明T213-P2方案的命中率高于T213-P1方案,能更多地预报出极端降水,但也存在空报稍多的情况。整体来说T213-P2方案优于T213-P1方案。
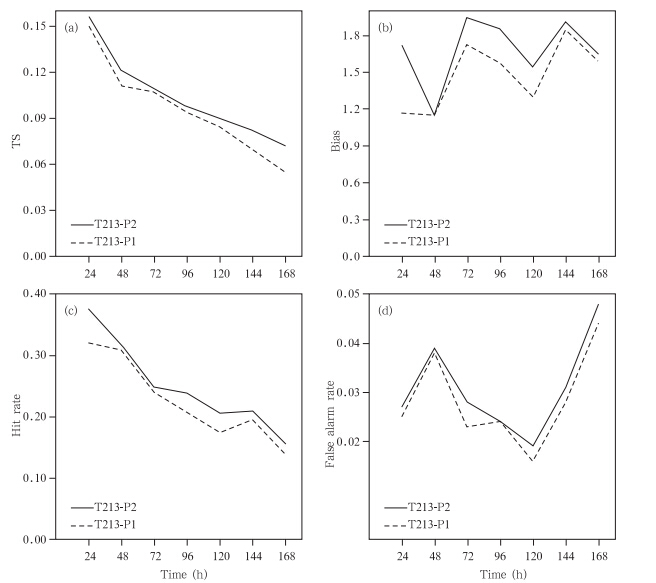 |
| 图 11 两种模式降水气候方案的平均检验结果(a.TS评分,b.预报偏差,c.命中率,d.虚警率) Fig. 11 Average test results of the two model climates of precipitation(a. TS scores,b. forecast bias,c. hit rate,d. false alarm rate) |
| AROC | 24 h | 48 h | 72 h | 96 h | 120 h | 144 h | 168 h |
| T213-P1 | 0.759 | 0.727 | 0.703 | 0.716 | 0.697 | 0.678 | 0.642 |
| T213-P2 | 0.762 | 0.724 | 0.711 | 0.731 | 0.710 | 0.696 | 0.661 |
通过两种不同模式气候累积分布方案试验的对比可知,T213-P2在T213-P1的基础上提高了极端降水天气预报指数对极端强降水的预报技巧,命中率更高,预报出极端强降水的可能性更大。究其原因,可能是中国的雨季具有一定的连续性(主要分布在6—8月),T213-P2包含的降水信息比T213-P1更全面,但是也存在空报略高的情况,所以,气候累积概率分布要尽可能全面的反映气候的客观真实状况。7 结论和讨论
极端强降水天气属于小概率事件,其发生具有很多不确定的因素,预报难度很大。本研究从极端强降水累积概率密度函数角度出发,充分考虑中国T213集合预报的降水预报特征,分析观测与数值预报模式产生的降水累积概率密度分布函数的特征差异,根据Anderson-Darling检验原理,设计基于中国气象局T213集合预报的极端降水天气预报指数,对2011年7月中国极端强降水天气进行预报试验,并分析模式历史降水预报累积概率密度分布函数对极端降水天气预报指数的影响。结论如下:
(1)T213集合预报的降水预报结果,对10—40 mm降水,不同预报时效概率密度分布差异较大,随着预报时效延长,降水概率密度逐渐减小;超过40 mm降水,不同预报时效的降水概率密度逐渐减小并趋于0,小于10 mm的降水,不同预报时效概率密度逐渐增大,并向10 mm以下雨量集中,至168 h以后,各量级降水的概率开始趋于稳定。
(2)对比中国区域内模式预报和观测极端强降水分布可知,模式预报的极端强降水分布特征与实况非常接近,但模式预报的极端强降水明显偏弱,并随着预报时效的延长,极端强降水逐渐减小。模式极端强降水的大值中心也存在一定的偏差:广东沿海地区的大值中心偏向了江苏、浙江和福建一带;西藏南部则出现了虚假的大值中心。
(3)极端天气预报指数可以充分利用集合降水累积概率密度分布的尾端信息,为极端强降水提供科学合理的预报,试验结果表明,极端降水天气预报指数对极端强降水具有较好的识别能力,可提前3—7 d发出极端强降水预警信号,随着预报时效的延长,预报技巧逐渐降低。
(4)通过对两种模式气候累积分布方案试验的对比可知,模式气候累积概率包含6—8月模式历史资料的预报技巧高于仅包含7月模式历史预报资料,这是因为中国的雨季具有一定的连续性(主要分布在6—8月),6—8月模式历史资料包含的降水信息比7月模式历史资料更全面。所以,气候累积概率分布要尽可能全面的反映气候的真实状况。
| 陈飞, 施平, 杜岩等. 2010. 基于Cressman客观分析的南海北部海区数据同化实验. 热带海洋学报, 29(4): 1-7 |
| 陈隆勋, 邵永宁. 1991. 近40年我国气候变化的初步分析研究. 应用气象学报, 2(2): 164-174 |
| 陈静, 薛纪善, 颜宏. 2005. 一种新型的中尺度暴雨集合预报初值扰动方法研究. 大气科学, 29(5): 717-726 |
| 陈朝平, 冯汉中, 陈静. 2010. 基于贝叶斯方法的四川暴雨集合概率预报产品释用. 气象, 36(5): 22-39 |
| 黄荣辉, 陈际龙, 周连童等. 2003. 关于中国重大气候灾害与东亚气候系统之间关系的研究. 大气科学, 27(4): 770-788 |
| 江志红, 陈威霖, 宋洁等. 2009. 7个IPCC AR4模式对中国地区极端降水指数模拟能力的评估及其未来情景预估. 大气科学, 33(1): 109-120 |
| 李芳. 2012. 基于多模式集合方案的中国东部夏季降水概率季度预测. 气象学报, 70(2): 183-191 |
| 李红梅, 周天军, 宇如聪. 2008. 近四十年我国东部盛夏日降水特性变化分析. 大气科学, 32(2): 358-370 |
| 李泽椿, 陈德辉. 2002. 国家气象中心集合数值预报业务系统的发展及应用. 应用气象学报, 13(1): 1-15 |
| 刘学华, 吴洪宝. 2006. 中国夏季雨日降水量的概率分布. 南京气象学院学报, 29(2): 173-180 |
| 卢萍, 宇如聪, 周天军. 2009. 四川盆地西部暴雨对初始水汽条件敏感性的模拟研究. 大气科学, 33(2): 241-250 |
| 王志福, 钱永甫, 林惠娟. 2008. 区域海气耦合模式对我国极端降水模拟分析. 高原气象, 27(1): 113-121 |
| 夏凡, 陈静. 2012. 基于T213集合预报的极端天气预报指数及温度预报应用试验. 气象, 38(12): 1492-1501 |
| 严中伟, 杨赤. 2000. 近几十年中国极端气候变化格局. 气候与环境研究, 5(3): 267-272 |
| 叶笃正, 严中伟, 戴新刚等. 2006. 未来的天气气候预测体系. 气象, 32(4): 3-8 |
| 翟盘茂, 潘晓华. 2003. 中国北方近50 年温度和降水极端事件变化. 地理学报, 58(增刊): 1-10 |
| 张婷, 魏凤英. 2009. 华南地区汛期极端降水的概率分布特征. 气象学报, 67(3): 442-451 |
| Anderson T, Darling D. 1952. Asymptotic theory of certain goodness of fit criteria based on stochastic processes. The Annals of Mathematical Statistics, 23(2): 193-212 |
| Beniston M, Stephenson D B, Christensen O B, et al. 2007. Future extreme events in European climate: An exploration of regional climate model projections. Climatic Change, 81(S1): 71-95 |
| Easterling D R, Meehl G A, Parmesan C, et al. 2000. Climate extremes: Observations, modeling and impacts. Science, 289(5487): 2068-2074 |
| Evrin Z. 2006. Recent developments in extreme weather forecasting. ECMWF Newsletter No. 107-Spring: 8-17 |
| Groisman P Y, Karl T R, Easterling D R, et al. 1999. Changes in the probability of heavy precipitation: Important indicators of climatic change. Climatic Change, 42(1): 243-283 |
| IPCC. 2001. Climate Change 2001: The Science of Climate Change. Contribution of Working Group I to the Third Assessment Report of the Intergovernmental Panel on Climate Change//Houghton J T, Ding Y, Griggs D J, et al. Cambridge, United Kingdom and New York, NY, USA, Cambridge University Press, 881 pp |
| IPCC. 2007. Climate Change 2007: The Physical Science Basis. Contribution of Working Group I to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change//Solomon S, Qin D, Manning M, et al. Cambridge, United Kingdom and New York, NY, USA, Cambridge University Press, 996 pp |
| Lalaurette F. 2002. Early detection of abnormal weather conditions using a probabilistic extreme forecast index. Quart J Roy Meteor Soc, 129(594): 3037-3057 |
| Lalaurette F. 2003. Two proposals to enhance the EFI re-sponse near the tails of the climate distribution. http://www.ecmwf.int/products/forecasts/efi_guide.pdf, 1-8 |
| Mason S J, Graham N E. 2002. Areas beneath the relative operating characteristics (ROC) and relative operating level (ROL) curves: Statistical significance and interpretation. Quart J Roy Meteor Soc, 128(584): 2145-2166 |
| Osborn T J, Hnhne M, Jones P D, et al. 2000. Observed trends in the daily intensity of United Kingdom precipitation. Int J Climatol, 20(4): 347-364 |
| Qian W H, Lin X. 2005. Regional trends in recent precipitation indices in China. Meteor Atmos Phys, 90(3-4): 193-207 |
| Steven T M, Jun D. 2001. Application of the NCEP/EMC short range ensemble forecast system (SREF) to predicting extreme precipitation events//The 81st AMS Annual Meeting. Amer Meteor Soc, Albuquerque, NM, July, 25: 64-70 |
| Sobash R A, Kain J S, Bright D R, et al. 2011. Probabilistic forecast guidance for severe thunderstorms based on the identification of extreme phenomena in convection-allowing model forecasts. Wea Forecasting, 26(5): 714-728 |
| Theis S E, Hense A, Damrath U. 2005. Probabilistic precipitation forecasts from a deterministic model: A pragmatic approach. Meteor Appl, 12(3): 257-268 |
| Yamamoto R, Sakurai Y. 1999. Long term intensification of extremely heavy rainfall intensity in recent 100 years. World Resour Rev, 11: 271-281 |
 2013, Vol. 71
2013, Vol. 71


