中国气象学会主办。
文章信息
- 谭学, 刘黎平, 范思睿. 2013.
- TAN Xue, LIU Liping, FAN Sirui. 2013.
- 新一代天气雷达海浪回波特征分析和识别方法研究
- Statistical characteristics of sea clutter and its identification with the CINRAD
- 气象学报, 71(5): 962-975
- Acta Meteorologica Sinica, 71(5): 962-975.
- http://dx.doi.org/10.11676/qxxb2013.074
-
文章历史
- 收稿日期:2012-07-09
- 改回日期:2013-05-22
2. 中国气象科学研究院灾害天气国家重点实验室, 北京, 100081;
3. 四川省人工影响天气办公室, 成都, 610072
2. State Key Laboratory of Severe Weather Chinese Academy of Meteorological Sciences, Beijing 100081, China;
3. Weather Modification Office of Sichuan Province, Chengdu 610072, China
在沿海地区,雷达经常会探测到海浪回波,这种回波属于非气象回波,主要是由超折射现象所引起,而非气象回波将干扰降水回波,影响雷达降水产品的准确性,导致临近预报出现偏差,因此,要在降水估计之前将其识别并剔除。一些专家提出了自动处理雷达基数据的方法,如早期的海浪回波识别主要依靠回波的垂直变化(Fulton et al,1998),Alberoni等(2001)利用区域非断裂廓线的出现频率剔除超折射海浪回波,Steiner等(2002)利用决策树方法研究一系列反射率参数,认为雷达回波的垂直伸展、反射率因子场的水平变化和反射率的垂直梯度识别海浪回波最有效。Kessinger等(2002,2003)在Steiner的技术基础上,提出了采用模糊逻辑算法的雷达资料分类技术。综合使用回波强度、径向速度和速度谱宽识别地物、海浪回波模糊逻辑方法已应用于WSR-88D天气雷达产品生成子系统(ORPG)。Zhang等(2004)提出在计算反射率垂直梯度时,将Steiner算法中的仰角改为高度,实际高度的使用显著减小了波速随距离的展宽影响。Berenguer等(2005,2006)通过分析受超折射回波影响区域,将其作为参数加入模糊逻辑算法中识别海浪回波。Lakshmanan等(2003)提出了基于神经网络的雷达资料质量控制技术。随着双线偏振雷达技术不断发展,在模糊逻辑方法中加入双线偏振参量,能较好地识别地物、超折射等非气象回波(Ryzhkov et al,2002; Gourley et al,2007)。一些专家(Lakshmanan et al,2004; Michelson et al,2004; Bøvith et al,2006)综合利用卫星和雷达资料进行地物、海浪和晴空回波的识别和剔除。
中国建成的雷达网已逐步投入业务运行,并在此基础上开展了灾害性天气监测、风场反演、定量估测降水和临近预报等工作(俞小鼎等,2006;张亚萍等,2007)。所以,对雷达基数据的质量控制是非常必要的。刘黎平等(2007)、江源等(2009)进行了多普勒天气雷达地物回波模糊识别方法的研究,有效地识别了地物及超折射回波。目前,中国对基数据中海浪回波的识别及剔除尚未开展,虽然未经质量控制的雷达探测资料用于天气过程的定性分析和使用问题还不大,有经验的预报员能凭借经验判别海浪回波,但对于雷达资料的定量应用,如雷达资料的同化、水文预报等,海浪回波必须进行处理,否则会出现严重误差。
本研究首先对福州、温州SA雷达收集到的海浪回波进行分类,分析了两类海浪回波的特征,给出了识别两类海浪回波的隶属函数。针对第1类海浪回波,采用了基于回波分块和模糊逻辑的分步式海浪回波识别方法;针对第2类海浪回波,采用了基于模糊逻辑的分步式海浪回波识别方法。通过识别效果分析,回波分块和分步式方法对海浪回波的识别有明显的改善。2 个例选取及特征分析2.1 个例选取
所选个例数据为福州、温州CINRAD/SA雷达观测的基数据。利用人为方法对资料进行判断,确定海浪、降水回波的“真值”。判断的依据是:海浪回波出现在海面区域,由许多针状的回波体组成,呈扇形向外辐散,回波高度比较低,很少达到第2个仰角,径向速度偏小,主要集中在-10—5 m/s,对应区域卫星观测的TBB(Black Body Temperature)温度高于273 K;对于降水回波,可从回波形状、垂直结构、演变和移动等方面加以判断。应该注意的是:用人工方法严格区分海浪回波和降水回波有时是非常困难的,特别是对晴空回波和远处的弱降水回波更是如此。
根据上述方法收集到6992个海浪回波体扫资料,按照出现时间将其分为两类:
(1)第1类海浪回波
第1类海浪回波主要出现在非台风期间,在平面位置显示器(以下简称PPI)上,由许多针状的回波体组成,呈扇形向外辐散,强度一般较强、不均匀性较明显,回波顶高很低,很少能到达第2个仰角,与降水回波很少混合,第1类海浪回波的出现一般都伴随着超强地物回波存在。这类回波通常是由于超折射现象引起,降水过程前后出现概率较大,回波范围大,这种海浪回波比较常见(图 1a,图中时间为世界时,下同)。
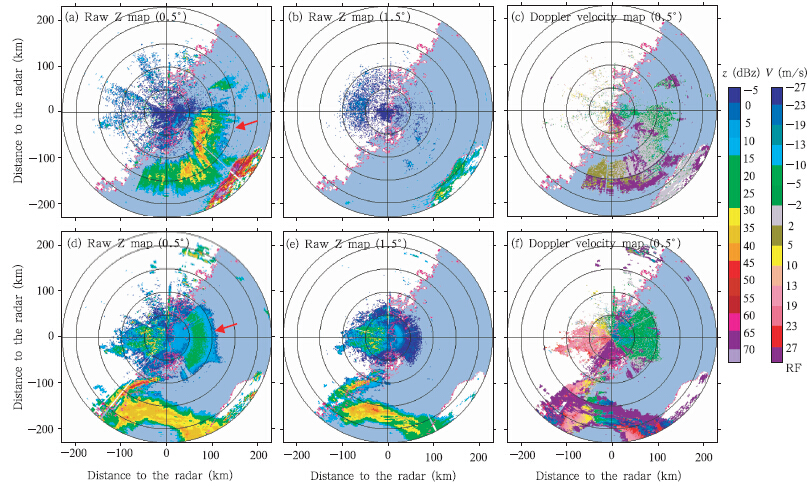 |
| 图 1 福州雷达2009年5月6日20时21分第1类海浪回波(a—c)与2010年9月19日17时20分台风凡亚比来临前的第2类海浪回波(d—f)PPI (a、d.0.5°仰角反射率因子,b、e.1.5°仰角反射率因子,c、f.0.5°仰角径向速度;红色箭头指向超折射海浪回波,距离圈:50 km,淡蓝色为海面) Fig. 1 PPI of the first kind of sea clutter at 2021 UTC 6 May 2009(a-c) and the second kind of sea clutter during Typhoon Fanapi at 1720 UTC 19 Sep 2010(d-f)from Fuzhou radar(red rows point to sea clutter,interval of range circles:50km,light blue shows the sea area) (a,d.reflectivity at 0.5° elevation; b,e.reflectivity at 1.5° elevation; c,f.radial velocity at 0.5° elevation) |
(2)第2类海浪回波
第2类海浪回波仅在台风期间出现;在PPI上,也由许多针状的回波体组成,呈扇形向外辐散,但强度一般较弱且均匀,回波顶高很低,没有明显移动。这类回波主要在雷达位置的近海域出现(图 1d)。
6992个海浪回波体扫资料,包括福州2009—2011年收集到的3336个第1类海浪回波体扫资料、2008—2010年收集到3238个第2类海浪回波体扫资料,温州2008—2010年收集到的418个第2类海浪回波体扫资料。通过分析这些数据发现,第1类海浪回波最早出现在3月中旬,并一直持续到10月下旬,春末夏初(5—6月)出现概率最大,并且,夜晚的出现概率明显大于白天;第2类海浪回波出现时间主要在6—10月,因其出现一般伴随台风,所以,与台风的出现季节类似。2.2 海浪回波强度、速度阈值划分
由于两类海浪回波的回波顶高都较低,径向速度较小,通过收集到的海浪回波数据统计分析得到海浪回波的强度、速度阈值(表 1)。其中Z1、Z2为对应的第1个仰角(0.5°仰角)和第2个仰角(1.5°仰角)PPI的回波强度,V为对应的第1个仰角PPI的径向速度。对不同类型的降水回波,凡超过其阈值的回波可直接认定为降水回波。
| 强度阈值 | 速度阈值 | ||
| 第1类海浪回波 | Z1<30 dBz Z1≥30 dBz | Z2<0 dBz或无值 Z1-Z2<15 dBz | -10 m/s<V<5 m/s |
| 第2类海浪回波 | R<50 km 5 0 km≤R<100 km R≥100 km | Z2<10 dBz Z2<5 dBz Z2<0 dBz | -15 m/s<V<5 m/s |
针对第1类海浪回波,考虑到海浪回波和降水回波通常是成块出现,很少混合,其回波强度的局地变化、径向速度等也有明显差异。首先对回波进行分块,判断每个回波块的属性,确定一个判断阈值,对超过阈值的回波块直接认定为降水回波,然后对小于阈值的回波块和零散回波,利用模糊逻辑方法对每个格点回波进行判断,最后将每个格点回波识别为海浪回波或降水回波。针对第2类海浪回波,直接利用模糊逻辑方法进行逐点识别。3.1 回波块识别方法
针对第1类海浪回波,将强度在5 dBz以上的回波利用风暴单体识别与跟踪(SCIT)算法组合成块。从收集到的降水回波和海浪回波样本中,选取面积在100 km2以上的回波块,共选取2160个降水回波块和1536个第1类海浪回波块,使用降水回波频率(FOBP)参量用于计算回波块属性值

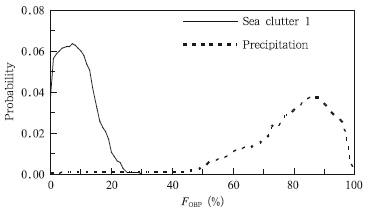 |
| 图 2 FOBP的概率分布 Fig. 2 Probability distribution curves of FOBP |
从图 2可知,降水回波的降水回波频率参数明显大于海浪回波的降水回波频率。其中,降水回波的FOBP绝大部分值主要集中在50%—100%,而海浪回波的FOBP主要集中在0%—20%。3.2 基于模糊逻辑的逐点识别方法
模糊逻辑方法就是从雷达资料(回波强度、径向速度和速度谱宽)中提取用于区分不同雷达回波(如降水回波、地物和海浪回波等)的物理量,然后根据降水回波、地物和海浪回波的特征设置隶属函数,对这些物理量进行模糊化处理,得到所有物理量对于不同类型回波的0—1取值范围的判据,该判据越大,回波点属于这种类型回波的可能性就越大。对这些判据进行加权累加,当某点的海浪回波的判据超过指定的阈值时,该点就被识别为海浪回波。
分析海浪回波和降水回波差异的7个物理量,包括从回波强度中提取的5个物理量:回波强度的纹理(TdBz)、垂直变化(GdBz)、沿径向的库间变化程度(SPIN)、降水回波频率(FOBP)、时间变化(VT-dBz);从径向速度和速度谱宽中提取的2个物理量:径向速度的区域平均值(MDVE)和速度谱宽的区域平均值(MDSW)。这些量的定义为
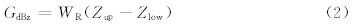
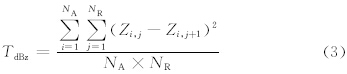

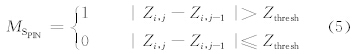


利用实际的雷达降水、海浪回波资料,分析这些回波的上述物理量特征,在此基础上确定隶属函数。
针对第1类海浪回波,选用福州雷达2009年5月6日、2010年5月26日,厦门雷达2009年5月14日,汕头雷达2009年5月6日,温州雷达2009年5月10日,舟山雷达2009年5月29日,共有1232851个海浪回波点;福州雷达2011年6月28日混合性降水过程、2010年5月7日对流过程、2011年3月26日层状云降水过程资料,舟山雷达2010年9月22日对流过程资料,烟台雷达2009年5月22日混合降水过程资料,共有3395344个降水回波点,分析降水回波和第1类海浪回波的特征差异。
针对第2类海浪回波,选用福州雷达2008年7月27日(强台风“凤凰”期间)、2010年9月19日(超强台风“凡亚比”期间),舟山雷达2011年8月5日(强台风“梅花”期间),汕头雷达2010年10月19日(超强台风“鲇鱼”期间)、2011年10月1日(强台风“尼格”期间),湛江雷达2010年7月21日(热带风暴“灿都”期间)的第2类海浪回波,共有2145683海浪回波点;福州雷达2008年9月15日、2010年9月19日,温州雷达2008年7月28日、2008年9月13日,湛江雷达2010年7月21日,青岛雷达2012年8月20日台风降水回波资料,共有1852342个降水回波点,分析台风降水回波和第2类海浪回波的特征差异。
对符合表 1中强度阈值内的海浪回波和降水回波统计分析,给出两类海浪回波、降水回波的GdBz、TdBz、SPIN、FOBP、VT-dBz、MDSW和MDVE的概率分布(图 3)。可以看到,两类海浪回波的径向速度值都偏负,速度较小;第1类海浪回波的TdBz和SPIN值明显大于降水回波,垂直变化也明显大于降水回波,FOBP在0值附近概率最大;第2类海浪回波的TdBz和SPIN值明显小于台风降水,VT-dBz值也明显小于台风降水。此外,对不同类型的降水回波经过强度阈值滤除后统计分析,超过阈值的回波直接认定为降水回波,这样直接去除了特征较明显的回波(回波顶高较高),如大部分对流云、混合降水,所以,统计分析出来的海浪回波与降水回波概率分布更具有可比性;而台风降水回波的回波顶高较高,经过强度阈值判定后,剩余的主要是台风降水的外沿部分或距离较远的回波,而强回波的外沿部分强度变化一般比较大,距离较远的回波可以通过距离判定进行处理。
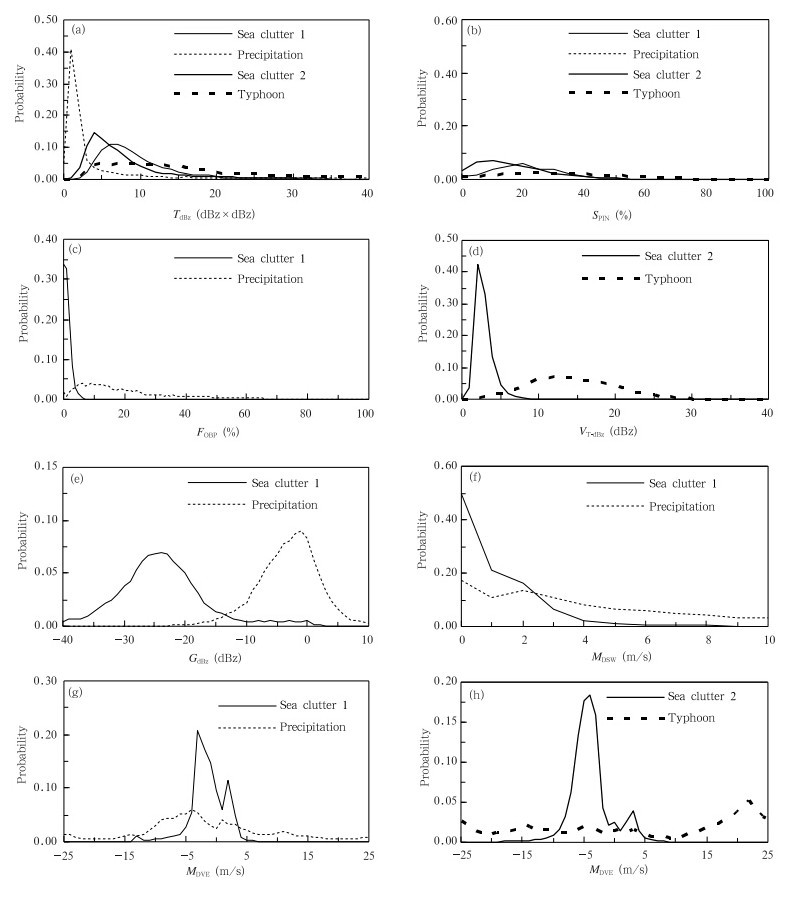 |
| 图 3 海浪和降水回波的概率分布 (a.TdBz,b.SPIN,c.FOBP,d.VT-dBz,e.GdBz,f.MDSW,g.MDVE,h.MDVE) Fig. 3 Probability distribution curves of the characteristic parameters for the sea clutters and precipitation (a.TdBz,b.SPIN,c.FOBP,d.VT-dBz,e.GdBz,f.MDSW,g.MDVE,h.MDVE) |
根据这些参量的概率分布,就可以确定用梯形折线表示的各个量的隶属函数(图 4)。
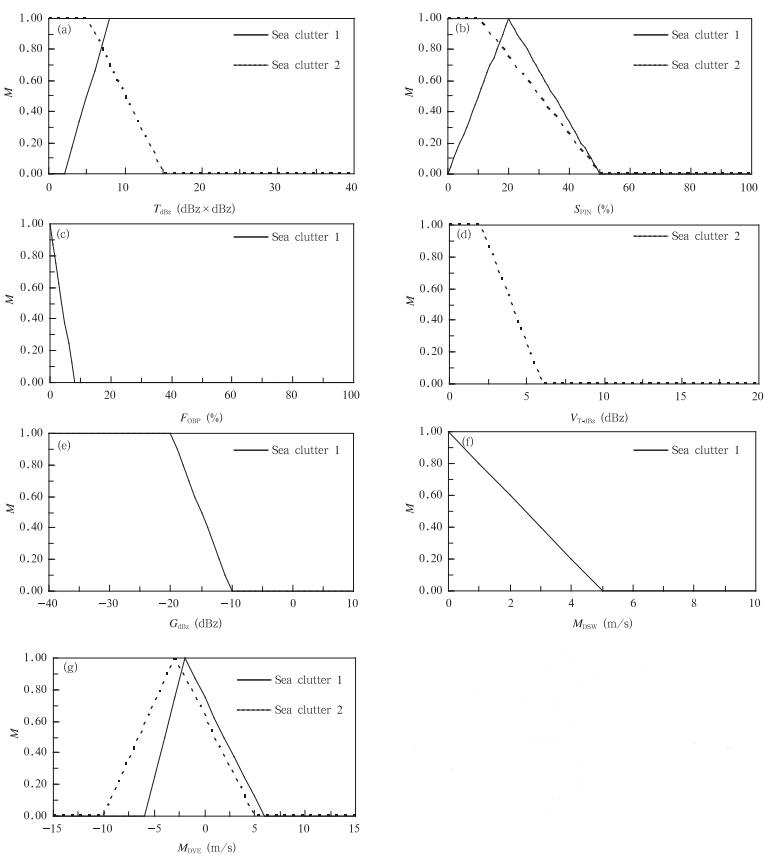 |
| 图 4 海浪回波识别的隶属函数 (a.TdBz,b.SPIN,c.FOBP,d.VT-dBz,e.GdBz,f.MDSW,g.MDVE) Fig. 4 P Membership functions for the first kind of sea clutter and the second kind of sea clutter (a.TdBz,b.SPIN,c.FOBP,d.VT-dBz,e.GdBz,f.MDSW,g.MDVE) |
在实际计算这些参数过程中,针对SA雷达观测模式的特点,采用了如下计算方法:
(1) 识别海面区域
由于海浪回波只发生在海面上,为了避免对陆地上的误判,采用90 m×90 m分辨率数字地形高程模型(DEM)对雷达观测范围内的海面和陆地区域进行区分,并且,所有算法只在海面区域进行识别。
(2)资料的配对
由于DEM资料、TBB资料、SA雷达的回波强度和径向速度资料分辨率不同,为此将雷达的两层回波强度、径向速度资料、DEM资料和TBB资料进行经纬度处理,按照经纬度排列这些资料,以满足同一回波点回波强度、径向速度资料、DEM资料、TBB资料的对应。
(3)海浪回波识别算法(SCDA)预处理
(a)只分析海浪回波主要出现的季节,例如3月1日—10月31日。因此,只对这个时间段的雷达基数据进行海浪回波识别。
(b)由于第2类海浪回波出现与台风有关,所以第2类海浪回波识别算法只应用于台风期间,其余时间均进行第1类海浪回波识别。
(4)海浪回波识别方法
(a)回波块识别方法
针对第1类海浪回波,面积为100 km2以上的回波块,如果FOBP>FLIM(0.3),则该回波块直接识别为是降水回波,然后对小于阈值的回波块和零散回波进行逐点识别。
(b)基于模糊逻辑的逐点识别方法
为了滤掉噪声对径向速度参量计算的影响,用中值滤波方法,处理径向速度资料,并用于计算径向速度值(MDVE)。根据表 2,可以分别计算各个回波点的特征量,并根据相应的隶属函数,计算各自的判据,对每个点的判据进行累加平均,对每个隶属函数均给予相应的权重(表 2),这样就得到了每个点海浪的判别值(0—1),该值越大,是海浪回波的可能性就越大,反之,是降水回波或其他回波的可能性就越大。对于径向速度的距离模糊区,只计算回波强度物理量。
| 特征量 | 权重 | |
| 第1类 | 第2类 | |
| MDVE | 1 | 1 |
| MDSW | 1 | 0 |
| TdBz | 1 | 1 |
| SPIN | 1 | 1 |
| GdBz | 1 | 0 |
| FOBP | 1 | 0 |
| VT-dBz | 0 | 1 |
(5)分步式海浪回波判断步骤
第1步,设定3个阈值T1、TS、T2(T1<TS<T2),其中,TS为标准的阈值(如0.5),T1为第1步判断非海浪回波的阈值(例如0.4),T2为第1步判断为海浪回波的阈值(0.6),T1和T2用于第1步判断,判据大于T2的为海浪回波,判据小于T1的为非海浪回波,判据介于这两个阈值之间的进入下一步判断。
第2步,设定计算范围NA×NR,对应每个判据介于T1和T2之间的点,在影响距离库数范围内,计算已判断为海浪和非海浪回波的加权判据与TS的差
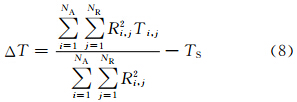
利用未统计部分的“真值”资料,分析了各个参量对海浪回波识别效果的影响。特别是分析了分步式方法和回波分块方法在识别过程中起的作用。
以“真值”资料为目标,分别对两类海浪回波和降水回波进行识别,以准确率、误判率和漏判率来分析识别效果。即对海浪回波资料,该方法正确地识别为海浪回波点数目占整个资料的比例为识别准确率,没有识别出海浪回波的点的比例为漏判率,降水回波识别为海浪回波为误判率。
首先分析阈值为0.5时各参量的识别准确率(表 3),其中,GdBz参量只统计上下层都有强度的回波点。此外,分析了分步式方法对两类海浪回波识别效果的影响。表 4给出了采用固定阈值为0.5与分步式方法对两类海浪回波、降水回波识别的准确率和误判率。
| 隶属函数 | MDSW | MDVE | TdBz | SPIN | GdBz | FOBP | VT-dBz |
| 第1类 | 70.64 | 85.15 | 70.23 | 73.42 | 88.64 | 92.85 | - |
| 第2类 | - | 89.33 | 75.15 | 72.85 | - | - | 87.34 |
| 方法 | 隶属函数 | 海浪、降水 总样本识别 准确率 | 降水识别 误判率 | 台风降水 识别误判率 |
| 固定阈 值为0.5 | 第1类 | 93.46 | 2.83 | - |
| 第2类 | 90.45 | - | 6.32 | |
| 分步式 | 第1类 | 95.33 | 1.78 | - |
| 第2类 | 92.53 | - | 5.27 |
针对第1类海浪回波,分别统计了综合采用回波分块和基于模糊逻辑的逐点识别方法时,降水回波的误判率和只采用模糊逻辑的逐点识别的误判率。对综合采用回波分块识别方法和只采用模糊逻辑的识别方法的降水回波误判率分别是1.78%和6.45%,可以看出,利用回波分块的方法可以很好的改善对降水回波的误判。4.2 第1类海浪回波个例分析
分析2009年5月14日07时03分福州雷达观测到的一次超折射海浪回波的识别效果(图 5)。可见海面区域出现了大面积回波(图 5a),将仰角抬高到1.5°后(图 5b),回波基本消失,这些回波的径向速度很小(图 5d);在东南方向约200 km的陆地(台湾地区)上出现了强超折射地物回波,说明海面区域有很强的逆温;并且,从同时相对应区域FY-2C红外亮温图像(图 5c)上可以看到,该回波区域的TBB较高,即该区域处于无云或少云状态。说明海面上这些回波基本为超折射海浪回波。采用本算法识别出了绝大部分超折射海浪回波(图 5f),但仍然保留着一些弱海浪回波点,主要原因是该区域回波强度变化较小,没有径向速度观测资料。
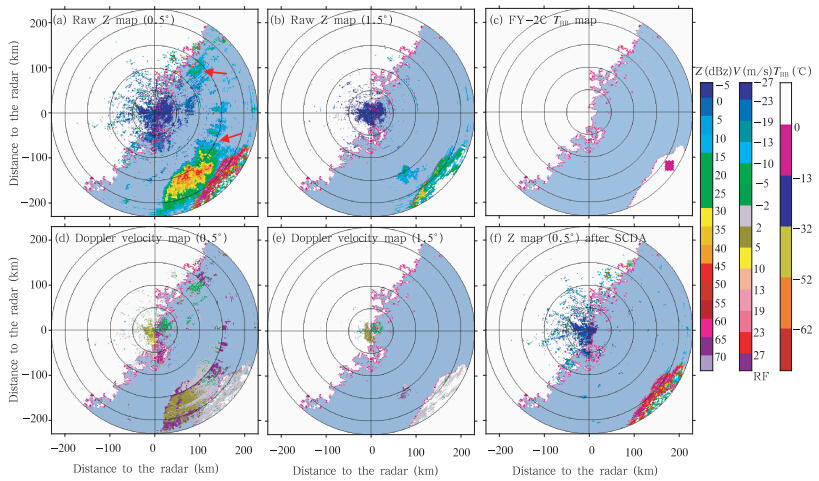 |
| 图 5 2009年5月14日07时03分福州雷达PPI (a、b.回波识别前0.5°、1.5°仰角反射率因子,c.FY-2C TBB,d、e.回波识别前0.5°、1.5°仰角径向速度,f.SCDA识别后的0.5°仰角反射率因子;红色箭头指向超折射海浪回波) Fig. 5 PPI from the Fuzhou radar scan measured at 07:03 UTC 14 May 2009 (a,b.reflectivity at 0.5°,1.5° elevation before echo identification; c.FY-2C TBB;d,e.radial velocity at 0.5°,1.5° elevation before echo indentification;f.reflectivity at 0.5° elevation after SCDA; red rows point to sea clutter) |
为了更好地分析降水回波位置与第1类海浪回波变化的关系,下面分析2010年5月30日—6月1日福州一次降水过程与海浪回波的演变及其识别结果。30日07时32分,在雷达站东南方约150 km有混合降水回波,并向东南方逐渐离开雷达区域,同时在东北方向200 km处开始出现海浪回波,10时35分降水回波全部离开雷达区域,海浪回波逐渐增多、增强,直至31日21时31分,西北方有小对流的出现,逐渐向东南方海面区域移动,随着降水回波的逐渐靠近,海浪回波逐渐变弱,6月1日10时08分对流云逐渐增强,并向正东移动,逐渐覆盖海面区域,海浪回波开始逐渐减弱最后消失。
分析不同时刻的降水回波位置和海浪回波的变化,可以看出,随着降水回波逐渐离开雷达站,海浪回波开始出现,并逐渐的增多、增强;降水回波逐渐向海面区域移动,海浪回波逐渐减弱,并最后消失。
为了分析超折射海浪回波时的大气折射条件,利用美国国家环境预测中心(NCEP)再分析资料对图 7中红色三角形位置的大气折射模数N和大气修正折射模数M进行了计算。表 5为2010年6月1日06时温度、湿度、大气折射模数N、大气修正折射模数M的计算结果。图 6为根据上述要素计算结果绘制的垂直廓线,可见在950—900 hPa出现逆温,湿度也随高度递减,大气修正折射模数M在1000—950 hPa随高度升高而增大,950—925 hPa随高度升高减小,925 hPa以上随高度升高增大。因此,在950—925 hPa存在dMdh<0情况,满足大气超折射现象的生成条件。
| 气压(hPa) | 高度(m) | 温度(K) | 相对湿度(%) | 水汽压(hPa) | N | M |
| 1000 | 74 | 294.5 | 80 | 21.16 | 354.55 | 366.27 |
| 975 | 302 | 292.5 | 85 | 19.65 | 344.38 | 391.49 |
| 950 | 553 | 290.8 | 82 | 16.41 | 327.31 | 413.64 |
| 925 | 720 | 292.5 | 52 | 12.16 | 298.45 | 411.46 |
| 900 | 998 | 292.8 | 39 | 9.95 | 281.84 | 437.99 |
| 850 | 1485 | 290 | 44 | 9.53 | 265.31 | 500.75 |
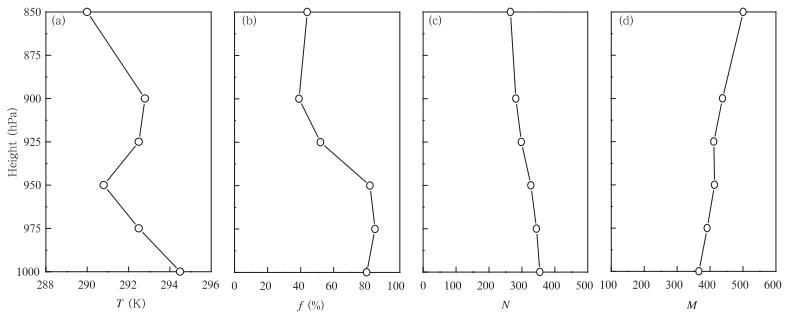 |
| 图 6 2010年6月1日06时温度(a)、相对湿度(b)、大气折射模数N(c)、大气修正折射模数M(d)的垂直廓线 Fig. 6 Profile distributions of temperature,relative humidity,N and M at 06:00 UTC 1 June 2010 |
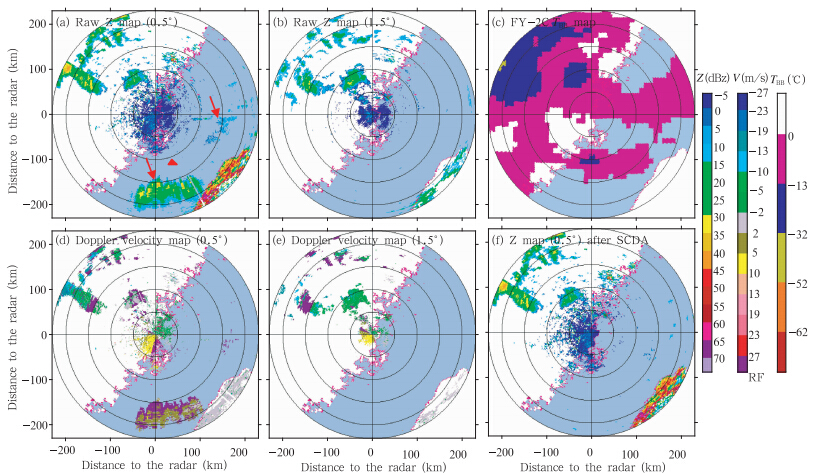 |
| 图 7 22010年6月1日04时32分福州雷达PPI (a、b.回波识别前0.5°、1.5°仰角反射率因子,c.FY-2C的TBB,d、e.回波识别前0.5°、1.5°仰角径向速度,f.SCDA识别后的0.5°仰角反射率因子;红色箭头指向超折射海浪回波,红色三角形为计算大气波导的位置) Fig. 7 PPI from the Fuzhou radar scan measured on 04:32 UTC 1 Jun 2010(a,b.reflectivity at 0.5°,1.5° elevation before echo identification; c.FY-2C TBB; d,e.radial velocity at 0.5°,1.5° elevation before echo identification;f.reflectivity at 0.5°elevation after SCDA; red rows point to sea clutter,red triangles show the point at which M is calculated) |
图 7给出了福州2010年6月1日04时32分回波强度和速度原始资料及海浪回波识别后的结果(0.5°仰角)。在雷达站正南方150—200 km有一片回波,从第2层与第1层回波强度的对比、径向速度场、对应的红外亮温及其回波区域有大气波导现象来看,这些回波为海浪回波。从图 7f可以看出,这些回波基本被准确识别,应该注意的是:少量强度比较弱的海浪回波,未被识别出来,主要原因是该回波强度整体较弱,强度变化较小,而且,没有径向速度观测资料。 4.3 第2类海浪回波个例分析
分析2010年9月19日12时27分福州雷达观测超强台风凡亚比来临前的一次超折射海浪回波的识别效果(图 8)。在雷达站东边0—100 km区域有一块扇形回波,并且,从第2层与第1层回波强度的对比、径向速度场、对应的红外亮温及其前一时刻的回波变化来看,这些回波大部分为海浪回波,该方法能将绝大部分海浪回波识别出来,但由于雷达周围存在着一些弱非降水回波(如晴空回波)与海浪回波混合无法区分,本方法一并将其识别并滤除。应该注意的是:降水回波中少量的外沿部分被识别为海浪回波,主要原因是该区域回波在海浪回波影响的区域范围内,并且强度变化较小,没有径向速度观测资料,前后时刻回波变化不明显。
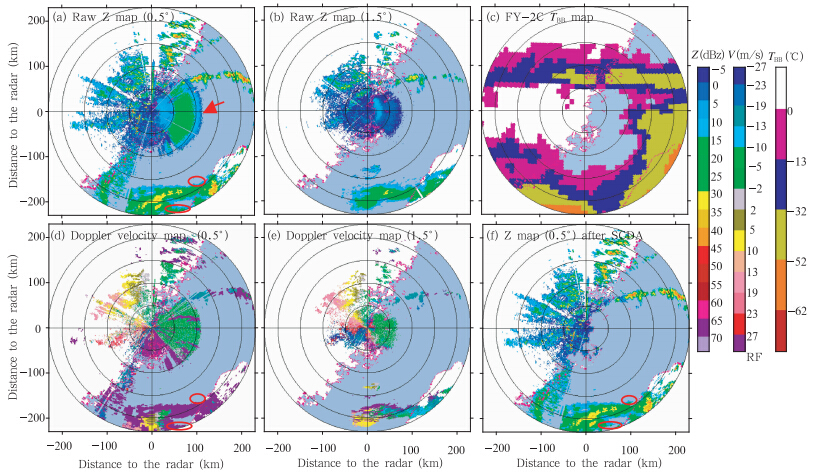 |
| 图 8 2010年9月19日12时27分福州雷达观测图 (a、b.回波识别前0.5°、1.5°仰角反射率因子,c.FY-2C TBB,d、e.回波识别前0.5°、1.5°仰角径向速度,f.SCDA识别后的0.5°仰角反射率因子;红色箭头指向超折射海浪回波,实线圈为误识别回波) Fig. 8 PPI from the Fuzhou radar scan measured on 12:27 UTC 19 Sep 2010 (a,b.reflectivity at 0.5°,1.5° elevation before echo identification; c.FY-2C TBB;d,e.radial velocity at 0.5°,1.5° elevation before echo identification;f.reflectivity at 0.5°elevation after SCDA; red rows point to sea clutter,real line circles are for to the wrongly idenified echo) |
为了更好地考查台风降水与第2类海浪回波同时存在时该方法识别海浪回波的效果,下面分析2008年9月11—15日福州一次与森拉克超强台风过程伴随的海浪回波的演变及其识别结果。从这次过
程分析,11日06时19分,在雷达位置的近海区域开始出现了弱超折射海浪回波,此时在福州雷达站东南方400 km处出现台风周围的螺旋雨带,并向雷达站点方向移动,随着台风的不断靠近,海浪回波逐渐增强,直到15日11时32分随着台风的逐渐远去,海浪回波开始逐渐变弱,并最后消失。
分析不同时刻的海浪回波变化,可以明显看出,随着台风逐渐靠近,海浪回波强度越来越强;台风逐渐远离,海浪回波越来越弱,并最后消失。图 9给出了福州2008年9月13日10时51分回波强度和速度原始资料和海浪回波识别后的结果(0.5°仰角)。从第1层径向速度和第2层回波强度PPI来看,雷达近海域100 km范围内大部分径向速度较小,与降水回波速度有很大区别,回波强度相对较弱且较均匀,回波高度较低,并且与前一时刻2008年9月13日10时45分回波相比,没有明显移动,这些回波基本被准确识别。
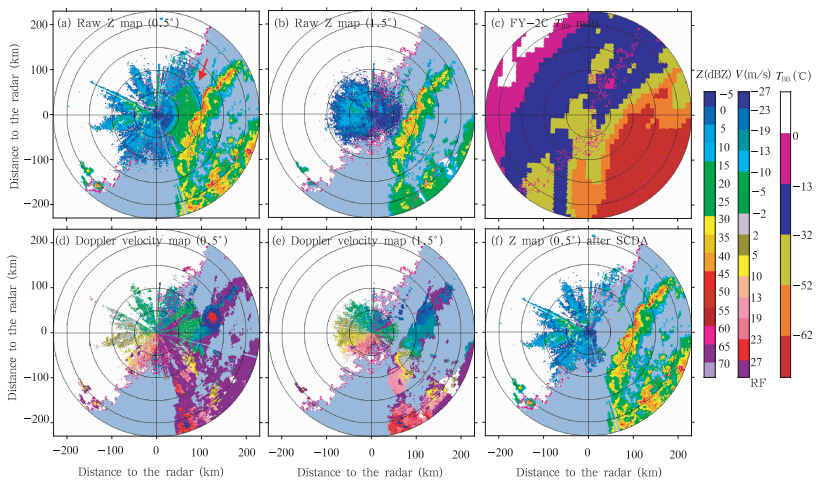 |
| 图 9 2008年9月13日10时51分福州雷达PPI (a、b.回波识别前0.5°、1.5°仰角反射率因子,c、FY-2C TBB,d、e.回波识别前0.5°仰角径向速度,f.SCDA识别后的0.5°仰角反射率因子;红色箭头指向超折射海浪回波) Fig. 9 PPI from the Fuzhou radar scan measured at 10:51 UTC 13 Sep 2008 (a,b.reflectivity at 0.5°,1.5° elevation before echo identification; c.FY-2C TBB;d,e.radial velocity at 0.5°,1.5° elevation before echo identification;f.reflectivity at 0.5°elevation after SCDA; red rows point to sea clutter) |
根据中国SA福州雷达观测的降水和海浪回波强度、径向速度资料,分析了两类海浪回波的特征,针对第1类海浪回波,采用了基于回波块和模糊逻辑的海浪回波识别方法;针对第2类海浪回波,直接采用了基于模糊逻辑的分步式海浪回波识别方法。并利用实际观测的雷达资料进行了两类海浪回波和降水回波的识别试验,结果表明:
(1)第1类海浪回波和降水回波的TdBz、SPIN、GdBz、FOBP、MDVE和MDSW这6个参量取值范围有明显区别,用这6个参量能够反映第1类海浪回波和降水回波特征并加以识别;第2类海浪回波和台风降水回波的TdBz、SPIN、VT-dBz和MDVE这4个参量取值范围有明显区别,用这4个参量能够反映第二类海浪回波和台风降水回波特征并加以识别。
(2)两种方法均能够分别有效识别两类海浪回波和对应的降水回波,在识别第1类海浪回波时,对于一般强度的海浪回波,本方法识别效果较好,可以识别出绝大部分回波;对于强度较弱(小于10 dBz)的第1类海浪回波,识别效果不是很好,有少量的剩余;在识别第2类海浪回波中,海浪回波的识别效果较好,可以识别出绝大部分回波,并且海浪回波的误判率和漏判率较小。
(3)利用回波块的识别方法明显减少了对降水回波的误判;而利用分步式方法能进一步改善海浪回波的识别效果,特别是减少了没有径向速度资料的降水回波被误判为海浪回波的现象。
| 江源, 刘黎平, 庄薇. 2009. 多普勒天气雷达地物回波特征及其识别方法改进. 应用气象学报, 20(2): 203-213 |
| 刘黎平, 吴林林, 杨引明. 2007. 基于模糊逻辑的分步式超折射地物回波识别方法的建立和效果分析. 气象学报, 65(2): 252-260 |
| 俞小鼎, 张爱民, 郑媛媛等. 2006. 一次系列下击暴流事件的多普勒天气雷达分析. 应用气象学报, 17(4): 385-393 |
| 张亚萍, 程明虎. 徐慧等. 2007. 雷达定量测量降水在佛子岭流域径流模拟中的应用. 应用气象学报, 18(3): 295-305 |
| Alberoni P P, Andersson T, Mezzasalma P, et al. 2001. Use of the vertical reflectivity profile for identification of anomalous propagation. Meteor Appl, 8(3): 257-266 |
| Berenguer M, Sempere-Torres D, Sánchez-Diezma R, et al. 2005. Identification of clutter echoes using a fuzzy logic technique//Proceedings of the 32nd Conference on Radar Meteorology, CD-ROM: P4R. 1 |
| Berenguer M, Sempere-Torres D, Corral C, et al. 2006. A fuzzy logic technique for identifying nonprecipitating echoes in radar scans. J Atmos Oceanic Technol, 23(9): 1157-1180 |
| B?vith T, Gill R S, Overgaard S, et al. 2006. Detecting weather radar clutter using satellite-based nowcasting products//Proceedings of the 4th European Conference on Radar in Meteorology and Hydrology,4pp |
| Fulton R A, Brcidenbach J P, Seo D J, et al. 1998. The WSR-88D rainfall algorithm. Wea Forecasting, 13: 377-395 |
| Gourley J J, Tabary P, Parent-du-Chatelet J. 2007. A fuzzy logic algorithm for the separation of precipitating from nonprecipitating echoes using polarimetric radar observations. J Atmos Oceanic Technol, 24(8): 1439-1451 |
| Kessinger C, Ellis S, van Andel J, et al. 2002. NEXRAD Data Quality Optimization-Annual Report for Fiscal Year 2002, National Center for Atmospheric Research, Boulder, CO. 89pp |
| Kessinger C, Ellis S, van Andel J, et al. 2003. The AP clutter mitigation scheme for the WSR-88D//Proceedings of the 31st International Conference on Radar Meteorology. Amer Meteor Soc, 526-529 |
| Lakshmanan V, Hondl K, Stumpf G, et al. 2003. Quality control of weather radar data using texture features and a neural network//Proceedings of the 5th International Conference on Advances in Pattern Recognion. Kolkota: IEEE, 15-18 |
| Lakshmanan V, Valente M. 2004. Real-time quality control of reflectivity data using satellite infrared channel and surface observations//Proceedings of the 20th International Conference on Information and Processing Systems (IIPS) for Meteorology, Oceanography, and Hydrology. Amer Meteor Soc |
| Michelson D B, Sunhede D. 2004. Spurious weather radar echo identification and removal using multisource temperature information. Meteor Appl, 11(1): 1-14 |
| Ryzhkov A, Zhang P, Doviak R, et al. 2002. Discrimination between weather and sea clutter using Doppler and dual-polarization weather radars//Proc of the Open Symposium on Propagation and Remote Sensing,4pp |
| Steiner M, Smith J A. 2002. Use of three-dimensional reflectivity structure for automated detection and removal of nonprecipitating echoes in radar data. J Atmos Ocean Tchnol, 19(5): 673-686 |
| Zhang J, Wang S, Clarke B. 2004. WSR-88D reflectivity quality control using horizontal and vertical reflectivity structure//Proceedings of the 11th Conference on Aviation. Amer Meteor Soc, P5. 4 |
 2013, Vol. 71
2013, Vol. 71

