中国气象学会主办。
文章信息
- 江川, 沈学顺. 2013.
- JIANG Chuan, SHEN Xueshun. 2013.
- 基于大涡模拟评估GRAPES模式对对流边界层的模拟性能
- Assessment of the simulative performance of the GRAPES model on the convective boundary layer based on the large eddy simulations
- 气象学报, 71(5): 879-890
- Acta Meteorologica Sinica, 71(5): 879-890.
- http://dx.doi.org/10.11676/qxxb2013.079
-
文章历史
- 收稿日期:2013-04-23
- 改回日期:2013-06-04
2. 中国气象局数值预报中心, 北京, 100081
2. Center for Numerical Prediction, China Meteorological Administration, Beijing 100081
大气边界层是地-气系统物质和能量交换的桥梁,是数值模式中重要的次网格尺度过程之一。随着大型计算机的快速发展,数值预报模式希望通过提高网格分辨率以提高模式预报的准确性。然而,单纯通过提高模式分辨率对模拟边界层湍流、积云对流及飑线等中小尺度系统效果仍然不佳(Lean et al,2008)。造成这种问题的原因主要来自两个方面:(1)由于中尺度数值模式中的次网格方案多建立在粗分辨率网格假设的基础上,对于细网格尺度并不适用(Cullen et al,2009);(2)数值模式的动力框架存在隐含耗散问题,在模式中耗散一般来自水平扩散和平流方案两方面,GRAPES模式在计算时需要得到拉格朗日轨迹上游点的物理量值,而上游点大多不在网格点上,此时就需要通过周围点的插值得到,这就造成了GRAPES模式的隐含耗散问题。Mccalpin等(1989)对不同插值方法的半拉格朗日方案的耗散进行定量分析发现,半拉格朗日方案存在不同程度的数值耗散和计算频散,这种耗散在模式分辨率提高到百米及千米尺度时尤为凸显。GRAPES半拉格朗日动力框架在中尺度数值预报及全球中期预报中已得到了很好的应用,但从未在大涡尺度上考察过其性能。所以,在未来发展千米及其以下高分辨尺度的GRAPES模式时,有必要首先检验GRAPES半拉格朗日动力框架在大涡尺度上的性能,了解GRAPES模式在高分辨率情形下的模拟精度。同时,由于目前模式中的次网格物理过程方案都基于粗分辨率假设,如GRAPES中的边界层参数化是一个一维垂直方向上K闭合方案,当分辨率提高到千米尺度之后,水平方向上的湍流扩散不能忽视,所以GRAPES大涡模式的构造能进一步为发展三维边界层湍流扩散方案提供模拟验证工具。在云可分辨尺度上,模式如何考虑边界层湍流对模式预报对流的发生、发展将起关键的作用,构建GRAPES大涡模式了解边界层内的湍流特点,并研究边界层湍流参数化对未来中小尺度数值预报的发展具有重要意义。
自Deardorff(1970,1972)将大涡模拟(LES)技术引入对大气边界层的研究后,大涡模拟已被广泛地用于边界层湍流的模拟研究中(Moeng,1984;Mason et al,1986;Schmidt et al,1989),并得到一系列详实可靠的高分辨率大气湍流信息。大涡模拟的基本思想认为湍流运动是由许多大小不同的涡旋组成,采用充分精细的网格尺度(100 m以下)将大涡和小涡分开处理,由于大湍涡携带大部分湍流能量,对其进行直接模拟;而小尺度的湍涡是通过非线性相互作用产生,它们与运动的不稳定性和边界问题不直接相关,并多起耗散作用,更易进行参数化闭合处理。Sullivan等(1994)总结了大涡模拟中常用的次网格闭合方案(SGS):(1)传统的Smagorinsky-Lilly次网格闭合方案(Smagorinsky,1963;Lilly,1967),该方案计算量小,且仅包含一个无量纲常数CS;(2)TKE闭合方案(Deardorff,1973),该方案计算量适中,但模拟得到的近地面平均风速不满足相似理论;(3)高阶闭合方案(Deardorff,1974),该方案能较大程度保持模式物理框架的完整性,但是计算量较大;(4)动力学闭合方案,该闭合方案中的参数CS根据局地流体的状况而变化,其值由动力学方法确定(Germano et al,1991; Porté-Agel et al,2000; Huang et al,2008)。
最早的大涡模拟研究都针对大涡特征明显的典型对流边界层,随着计算机水平的提高,大涡模拟拓展至边界更复杂、大涡特征较不明显的稳定边界层和不均匀下垫面上(Mason et al,1990;Hadfield et al,1991;Walko et al,1992)。同时大涡模拟模式具有极高的格点分辨率和对边界层湍流的三维模拟效果,这些特点使它很适用于各类物理过程的研究,如深、浅对流、暖云降水对流等过程(Petch et al,2008; Reinert et al,2009)。基于大涡模拟技术在边界层研究中的独特优势,越来越多的中尺度模式希望能将高分辨率边界层方案(大涡模拟机制)引入数值预报模式中。Robert等(2003)考察了英国气象局Met Office Unified Model在大涡尺度上模拟的可行性,指出引入高分辨率边界层方案后的中尺度模式对边界层的模拟效果有大幅度改进,同时也指出对中尺度模式平流方案中的固有耗散问题引入补偿机制十分关键。Drikakis(2003)指出中尺度模式中的平流方案所造成的隐含耗散与次网格方案所造成的耗散在大涡尺度上同等重要。
本研究通过将GRAPES中尺度模式分辨率提高至大涡模拟尺度,同时引入Smagorinsky-Lilly小尺度湍涡参数化,构建可用于大涡模拟的GRAPES_LES模式,并通过与广泛应用的UCLA_LES模式的模拟结果进行比较,考察GRAPES模式在大涡分辨率情形下的模拟能力。该研究以干对流边界层为例进行模拟试验,不考虑湿过程以重点考察模式的动力性能及框架中所隐含的耗散问题。同时,在GRAPES_LES的次网格方案设计中对不同的Smagorinsky常数(对应不同的滤波尺度)进行敏感性试验,以考察滤波尺度的改变能否有效地补偿半拉格朗日框架隐含耗散的问题。 2 GRAPES_LES的构造及试验设计2.1 GRAPES_LES的构造
GRAPES是中国自主研发的一个多尺度通用模式,该模式采用球坐标系下的全可压非静力方程组及半隐式半拉格朗日时间积分方案,水平方向采用Arakawa-C跳点网格,垂直方向采用Charney-Philips变量跳层设计,垂直坐标为地形高度追随坐标。半拉格朗日轨迹计算考虑了球面效应,轨迹上游点的物理量插值采用准三次插值方案。GRAPES具有完备的物理过程,本研究由于重点测试GRAPES动力框架在大涡尺度上的性能,不对模式物理过程做详细阐述,详细物理过程可以参考薛纪善等(2008)的文章。此外,由于不考虑地形的作用,本研究中GRAPES模式的垂直坐标为高度坐标。
GRAPES_LES是在原GRAPES动力框架的基础上,加入大涡模拟中常用的次网格参数化方案,并提高分辨率以直接模拟大尺度涡旋(100 m以下)。本研究采用Smagorinsky-Lilly次网格闭合方案,方程组(1)是GRAPES_LES在球坐标系下的预报方程组,方程组(3)给出次网格闭合方案公式。
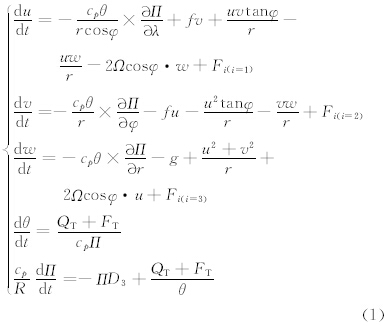
方程组(1)中包含运动方程、连续方程及热力学方程,分别为风速及位温的时间倾向,λ、φ、r分别为球坐标系的坐标,cp为定压比热容,R为气体常数,g为重力加速度,在该方程组中引入埃克斯纳气压变量Π=pp0Rcp,D3为三维散度,QT为非绝热加热项,对于Fi、FT,若假设i,j分别取1、2、3,即代表x、y、z三个方向,则代表动量及热量的湍流扩散项,其表达式如方程组(2)

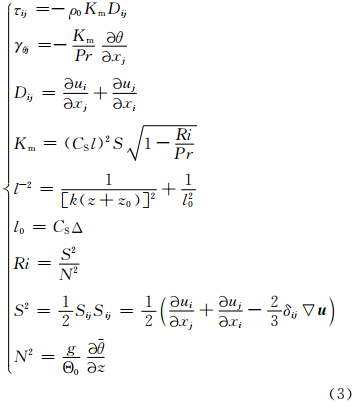
方程组(2)和(3)中的τij与γθj分别代表次网格动量通量及热量通量,Km为涡动系数,Pr为涡动普朗特数,S为形变张量,Ri为里查森数,N为浮力通量,δij为克罗内克符号,l0为混合长(滤波尺度),l为该闭合方案中定义的长度尺度,z为垂直高度,ρ为密度,z0为粗糙度长度,Θ0为参考状态的位温,ρ0为背景密度,Δ=(ΔxΔyΔz)1/3为格点尺度,k为卡尔曼常数,取为0.35,CS为Smagorinsky常数。Nieuwstadt等(1993)指出CS为次网格方案中一个极为重要的量,由小涡闭合方案的公式l0=CSΔ可看出,CS与混合长及格点尺度有关,在大涡模拟技术中需对大尺度湍涡和小尺度湍涡进行划分,因此就涉及到滤波尺度的问题,在Smagorinsky-Lilly方案的假设中混合长与滤波尺度相当,即代表大的滤波尺度,能够减少高波数(小尺度)湍涡部分的方差值,同理小的CS值可以增加小尺度湍涡部分的能量,即产生所需要的补偿耗散效果。同时还指出大的CS的取值会造成大尺度热量的略微增加,然而相对而言,CS的取值对大尺度湍涡影响较小。一般在大涡模拟中若假设各向同性的惯性子区并且采用截谱型滤波,则CS一般取0.17(Lilly,1967)。但是,多数情况下湍流并非各向同性,而且,模式中包含有除了次网格过程之外的耗散(特别是平流过程),所以,在不同的大涡模式中CS取值并不相同。该数的取值要求应该足够大以阻尼格点尺度数值运算的噪音(例如有限差分误差),又不应该浪费大涡模式高的分辨率(Mason et al,1986)。因此,本研究同时设计了对CS的敏感性试验,用于考察GRAPES_LES模式的响应,从而选择合适的CS使GRAPES_LES达到较为合理的模拟效果。
2.2 试验设计本研究选取独立的大涡模拟模式UCLA_LES(Stenvens,2010)用以评估GRAPES_LES的模拟性能。UCLA_LES是一个应用广泛的三维大涡模式,该模式不但可用于对对流、中性、稳定边界层的模拟,同时模式中也提供了不同复杂程度的微物理过程,如Seifert等(2001,2008)的暖云微物理方案,Stevens等(2008)的浅积云对流参数化方案。表 1给出了UCLA_LES与GRAPES_LES模式框架的对比。
| 模式 | GRAPES_LES | UCLA_LES |
| 动力假设 | 可压缩;非静力平衡 | 滞弹性;非静力平衡 |
| 坐标系 | 球坐标系 | 笛卡尔坐标系 |
| 平流方案 | 动量:半拉格朗日平流方案;标量:分段有理函数法(PRM) | 动量:四阶中央差;标量:单调中央差 |
| 时间步长 | 5 s | 可变(最大时间步长5 s) |
| 时间积分 | 半隐式积分方案 | 三阶龙格-库塔方案 |
| 气压算子 | 广义共轭余差(GCR)法迭代求亥姆霍兹方程 | 快速傅立叶变换(FFT)的泊松算子 |
| 垂直格点设置 | Charney-Philips跳层 | 洛仑兹 |
| 水平格点设置 | Arakawa-C | Arakawa-C |
| Smagorinsky系数 | 0.23,0.46,0.115 | 0.23 |
如前所述,本研究选取一个理想的均匀地表下的干对流边界层个例,其初始状态由式(4)确定。
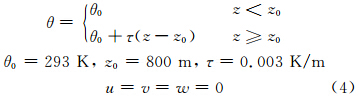
为使GRAPES_LES与UCLA_LES的模拟结果具有可比性,两模式的边界条件都设为周期边界条件,上、下边界条件都为刚体边界,模式在上部5层加入了重力波的阻尼吸收层,并在计算下边界强迫时运用了莫宁-奥布霍夫相似理论。对于网格距和模拟范围的取法,参考了一些文献中的做法,如Schmit等(1989)、Moeng(1984)、Cuxart等(2000)利用大涡模拟对边界层模拟时的取值;同时也参考了Robert等(2003)对英国气象局Met Office Unified Model模式大涡尺度上的性能评估时的分辨率取法,水平垂直分辨率都取为50 m。同时,由于Agee等(1999)指出大涡模拟区域的大小必须大于特征水平长度尺度的2.5倍,文中模拟4 h边界层高度约为1350 m,则模拟区域大于3375 m应该能满足大涡模拟对区域的基本要求。所以,在初步模拟中给定5 km×5 km×2.7 km的模拟区域,水平分辨率为50 m,垂直方向不等距分为50层,在1200 m上有比率为1.02的垂直格距拉伸,模式层顶取为2700 m。取模式在积分达到准定常态后的结果进行分析。这里,积分达到准定常态的判别标准是积分时间超过6倍对流边界层的特征时间尺度(吴涧等,1999),即:
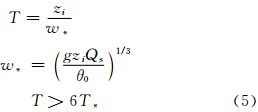
图 1给出了达到准定常态后(1.33—4 h)边界层高度的变化情况,边界层顶值的位置由位温梯度最大值确定。由图 1可以看出,GRAPES_LES能够模拟出与UCLA_LES相近的边界层顶的高度及层顶变化趋势,尤其以CS=0.115时与UCLA_LES模拟结果最为接近。
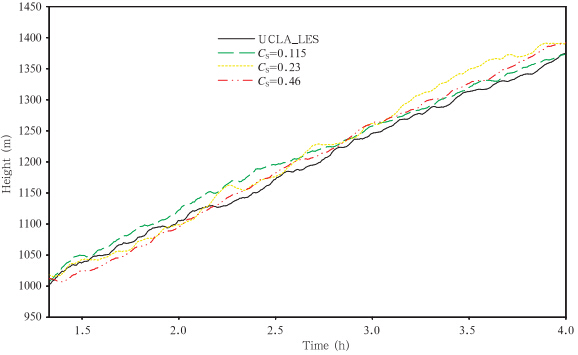 |
| 图 1 UCLA_LES与GRAPES_LES边界层高度的时间演变 Fig. 1 Evolution of the boundary-layer height from the UCLA_LES and GRAPES_LES simulations |
图 2给出了GRAPES_LES与UCLA_LES模式在4 h后的垂直速度X-Z剖面,选取了两个模式中部同一个格点y=45处的值。图中也分别给出了GRAPES_LES取CS=0.115,0.23,0.46时与UCLA_LES模拟结果的对比。由图 2可以看出,在相同CS(CS=0.23)的条件下,GRAPES_LES能够模拟出与UCLA_LES模式相似的边界层垂直速度分布特征,即在对流边界层中由于重力波的作用所引起的垂直上升和下沉区的相间分布特征;以及边界层顶附近的夹卷效应等。但也可以明显看到,GRAPES_LES的模拟结果要光滑得多,这主要是由于GRAPES半拉格朗日平流计算时上游点物理量的插值带来的隐含耗散造成。因此,为使GRAPES_LES的模拟结果更加合理,需要在小尺度涡旋次网格参数化方案设计中考虑对这部分耗散加以补偿。为此,图 2中也给出了GRAPES_LES对不同CS的响应,考察不同滤波尺度的选择是否能提高GRAPES_LES的模拟性能(图 2b、d)。图 2b和d分别给出了缩小和放大滤波尺度的结果,可以看到不同CS值的选取对结果有较为明显的影响。当选取小的CS(CS=0.115)值即滤波尺度缩小时,所模拟出的垂直速度场与UCLA_LES的模拟结果更为相近,而大的CS(CS=0.46)值模拟的垂直速度场则进一步平滑了边界层本身应有的小尺度湍涡分布特征(图 2d)。
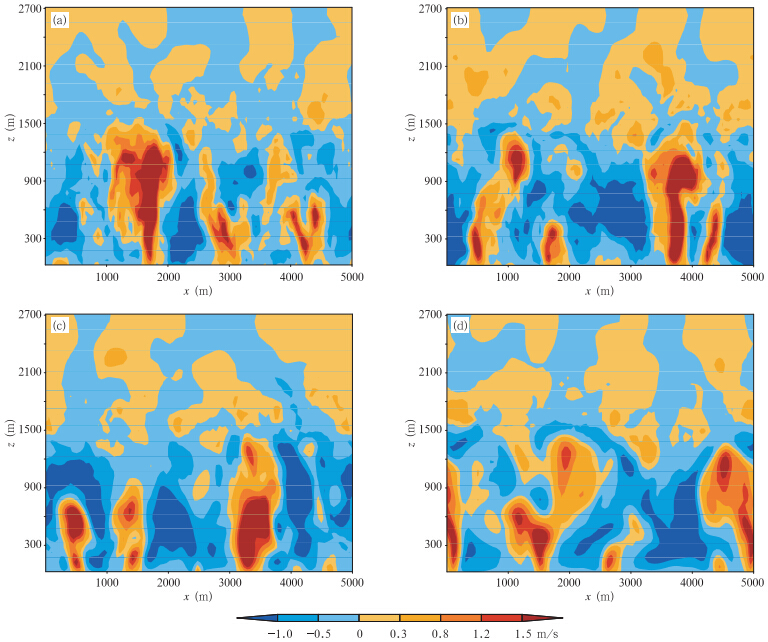 |
| 图 2 UCLA_LES与GRAPES_LES垂直速度垂直剖面分布(a. UCLA_LES的模拟结果,b. CS=0.115时GRAPES_LES的模拟结果,c. CS=0.23时GRAPES_LES的模拟结果,d. CS=0.46时GRAPES_LES的模拟结果) Fig. 2 Vertical cross-sections of the instantaneous vertical velocity from the UCLA_LES and GRAPES_LES simulations(a. UCLA_LES,b. GRAPES_LES when CS is 0.115,c. GRAPES_LES when CS is 0.23,d. GRAPES_LES when CS is 0.46) |
相同的模拟特征在垂直速度的水平剖面上更为明显,从GRAPES_LES与UCLA_LES在模拟4 h后第15层(650 m)的垂直速度分布(图 3)可以看出,当取相同的滤波尺度时,GRAPES_LES垂直速度分布较为平滑,模拟出的细致的小尺度湍涡结构与UCLA_LES的结果相比不那么显著。但将CS值调整至0.115 后,模拟结果变得更为接近,这时GRAPES_LES能模拟出更小结构的湍涡,并且垂直速度的蜂窝状结构也更为明显,模拟效果显著提高。
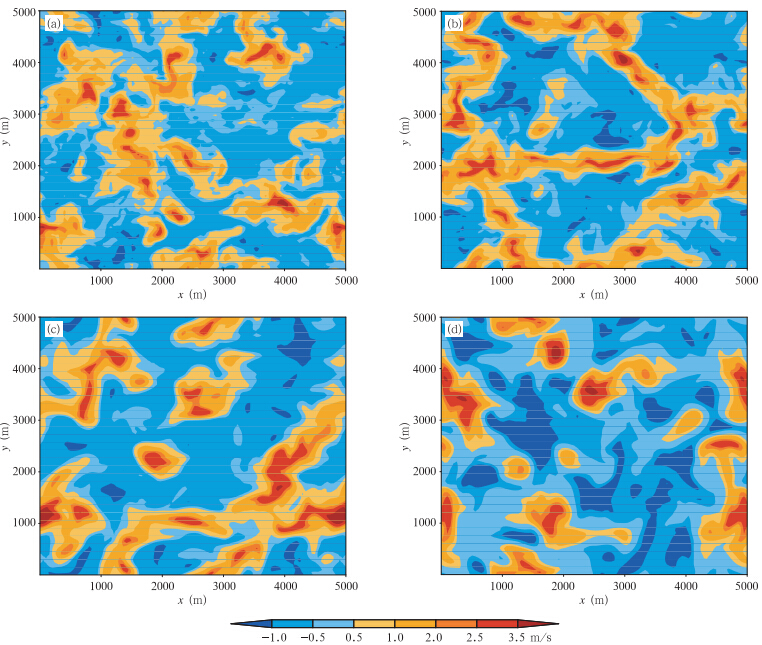 |
| 图 3 UCLA_LES与GRAPES_LES垂直速度水平截面(z=650 m)的分布 (a. UCLA_LES的模拟结果,b. CS=0.115时GRAPES_LES的模拟结果,c. CS=0.23时GRAPES_LES的模拟结果,d. CS=0.46时GRAPES_LES的模拟结果) Fig. 3 Horizontal distribution of the instantaneous vertical velocity at height 650 m simulated by UCLA_LES and GRAPES_LES(a. UCLA_LES,b. GRAPES_LES when CS is 0.115,c. GRAPES_LES when CS is 0.23,d. GRAPES_LES when CS is 0.46) |
物理量的方差和偏斜量是湍流研究中的重要参数,方差可用于度量湍流的强度,偏斜量则是用于度量随机过程与均匀、各向同性湍流概率分布(高斯分布)的偏离程度(王雪梅,2001)。图 4—6中分别给出了3—4 h平均的位温方差、垂直速度方差及垂直速度偏斜量w′3/(w2*)3/2的垂直分布。从图 4和图 5中可以看出,GRAPES_LES与UCLA_LES位温方差及垂直速度方差分布无论是形状或者方差极大值的位置都极为相似,只是相同滤波尺度时,GRAPES_LES模拟的湍流能量略偏弱,位温方差则偏强。进一步从图 6中可以发现,GRAPES_LES能够模拟出偏斜量的不断增大及边界层顶附近的极大值分布特征,GRAPES_LES模拟出的偏斜量偏大,尤其以CS=0.46时偏离最为明显。
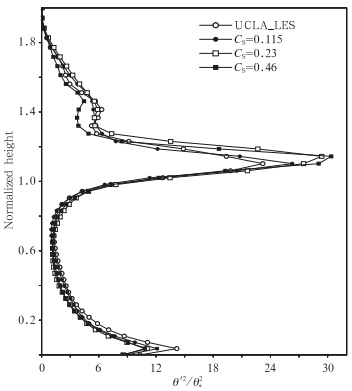 |
| 图 4 UCLA_LES与GRAPES_LES归一化时间平均位温方差(θ′2/θ2*)分布 Fig. 4 Normalized time-area averaged profiles for the potential temperature variance for UCLA_LES and GRAPES_LES |
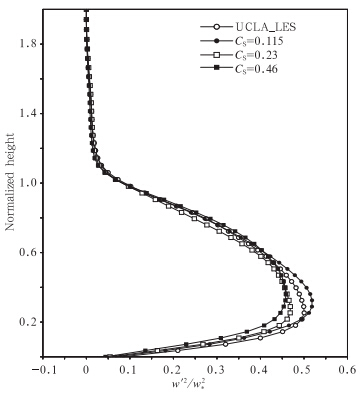 |
| 图 5 UCLA_LES与GRAPES_LES归一化时间平均垂直速度方差(w′2/w2*)分布 Fig. 5 Normalized time-area averaged profiles for the vertical velocity variance for UCLA_LES and GRAPES_LES |
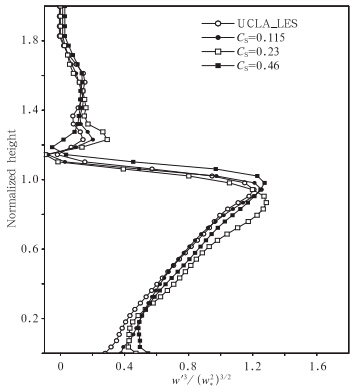 |
| 图 6 UCLA_LES与GRAPES_LES归一化时间平均垂直速度偏斜量(w′3/(w2*)3/2)分布 Fig. 6 Normalized time-area averaged profiles for the skewness of vertical velocity for UCLA_LES and GRAPES_LES |
图 7和图 8分别给出了4 h时,大涡动能、小涡动能、大涡位温垂直通量及小涡位温垂直通量,其中,TKE代表湍流动能,w′θ′表示大涡尺度的位温垂直通量,w″θ″为小涡尺度的位温垂直通量。通过4幅图可以看出,GRAPES_LES中的大涡、小涡与UCLA_LES中的大涡、小涡扮演相同的角色,大涡包含大部分的能量并且负责大部分的物质传输,小涡主要起耗散作用。同时,对比相同CS值可发现GRAPES_LES中小尺度湍涡的耗散作用强于UCLA_LES的结果。而在选取较小CS值时,模拟曲线则更接近UCLA_LES的结果。
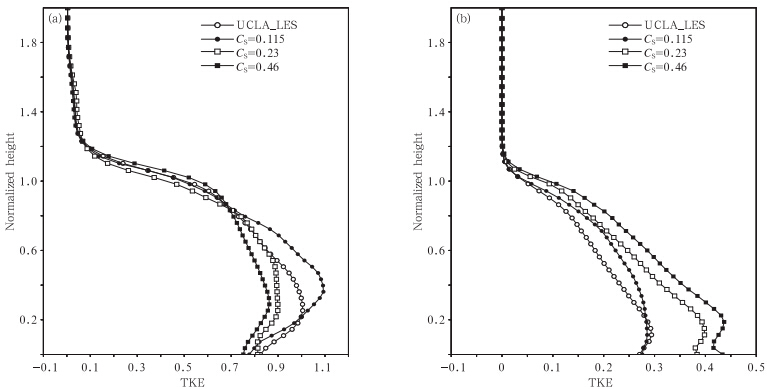 |
| 图 7 大涡(a)及小涡(b)部分归一化湍流动能(TKE)的分布 Fig. 7 Normalized turbulent kinetic energy profiles by large eddy(a) and small eddy(b) |
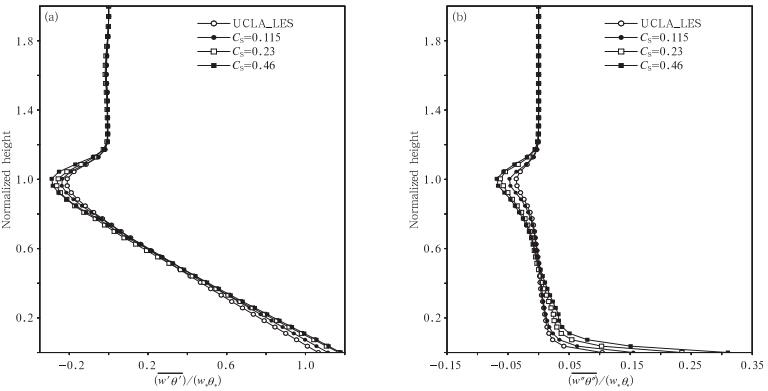 |
| 图 8 大涡(a)及小涡(b)部分归一化垂直位温通量的分布 Fig. 8 Normalized vertical potential temperature flux profiles by large eddy(a) and small eddy(b) |
为进一步考察GRAPES_LES对干对流边界层湍流的模拟能力,图 9给出了UCLA_LES和GRAPES_LES在1000 m高度处3—4 h平均的垂直速度湍流能谱。模式能谱与实际大气能谱分布规律进行对比分析,是评估一个模式动力框架合理性的有效手段。通过计算GRAPES_LES的湍流能谱并与UCLA_LES进行比较,可以更全面地了解和评估GRAPES_LES的模拟性能,同时也可以考察不同滤波长度(CS)的选择能否有效补偿GRAPES_LES半拉格朗日动力框架插值所产生的隐含耗散。本研究采用Denis等(2002)提出的离散余弦变换(DCT)方法对二维有限区域气象场进行谱分析,该方法不限定气象场的周期性,也不用去除倾向,能够较真实地反映实际湍流能谱的信息。郑永骏等(2008)曾利用该方法对半隐式半拉格朗日的GRAPES模式进行了动能谱的分析,并得到了合理的动能谱分布。
该方法的具体操作利用2D-DCT正变换公式
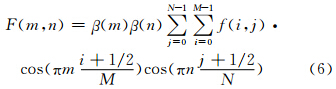
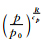
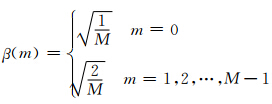
该公式可以将二维气象场展开为二维谱系数F(m,n),它是二维波数(m,n)的函数,该气象场的方差公式为
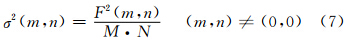
为了将其表示一维波数k的函数,定义归一化波数
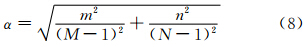
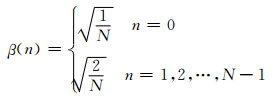
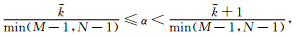 =1,2,…,min(M-1,N-1)-1,将其对应的方差σ2(m,n)加入S(),并化为用圆频率表示的波数
=1,2,…,min(M-1,N-1)-1,将其对应的方差σ2(m,n)加入S(),并化为用圆频率表示的波数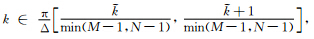 相对应的功率谱密度
相对应的功率谱密度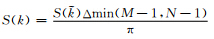
图 9给出了5条线,直线代表惯性子区中的-5/3斜率,另外4条折线分别代表UCLA_LES、CS=0.115,0.23,0.46时GRAPES_LES的能谱密度曲线。该湍流能谱做了相应的归一化处理,其中,k代表波数,zi取为逆温层高度1350 m,kzi=1就相当于波长为27倍格距的波,为对流边界层的特征速度尺度,S(k)代表能谱密度。由图 9可以看出,UCLA_LES在kzi=2的时候达到最大,之后曲线沿着-5/3的斜率下降至kzi=6,约为5倍格距的波长处,然后随着波数的增大平缓地下降。对比取相同CS时GRAPES_LES的能谱分布,可以看到GRAPES_LES能谱密度随着波数的增大下降较为剧烈,验证了GRAPES半拉格朗日动力框架耗散更强。进一步考察滤波尺度分别为CS=0.115和CS=0.46时对应的能谱密度,可以看出CS=0.46时耗散更强,说明过高估计了小尺度湍涡的耗散作用。而当CS=0.115时,GRAPES模式隐含的耗散与小尺度湍涡部分的耗散其共同作用使GRAPES_LES可以得到与UCLA_LES较为吻合的结果,这也说明在发展大涡模式时应充分考虑所基于模式的计算精度来完善其大涡模拟性能。
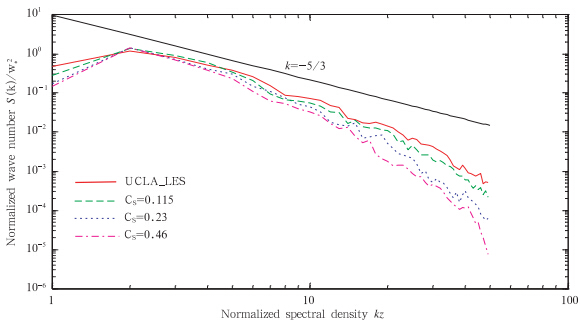 |
| 图 9 UCLA_LES与GRAPES_LES归一化湍流能谱分布 Fig. 9 Normalized power spectra of vertical velocity simulated by UCLA_LES and GRAPES_LES |
通过湍流能谱的比较,可以看出在半拉格朗日动力框架下构造大涡模式是可行的,能够模拟出能量与波数的E∝k-5/3(Kolmogorov,1941)定律;但是湍流能谱的分析也揭示GRAPES模式所隐含的耗散问题值得重视,尤其是在发展云分辨尺度的GRAPES模式时应予以重视。通过试验可以看出,不同的滤波长度(CS)的选择的确能较好地缓和GRAPES半拉格朗日动力框架
中产生的部分隐含耗散,但在高波数部分这种耗散仍然存在,这就需要进一步研究耗散的形成机制,或者构造更加适合的次网格闭合方案,从而提高GRAPES在大涡尺度上对边界层湍流的模拟能力。4 结论与展望
利用独立的大涡模式UCLA_LES作为参考,评估了中国自主研发的GRAPES模式在大涡尺度上对对流边界层的模拟性能,并得到以下结论:
(1)GRAPES_LES模式能够模拟出与已有广泛运用的大涡模式模拟的相似边界层湍流特征,如水平剖面的网状结构、垂直剖面的热对流活动、方差的分布情况、湍涡的湍流动能及垂直热通量分布特征,显示出良好的模拟性能。
(2)模拟结果显示GRAPES模式存在隐含耗散问题,在使用相同的滤波尺度(Smagorinsky常数)时,GRAPES_LES模拟出的速度场更为平滑,与UCLA_LES的结果相比模拟出的小尺度湍流结构过于光滑,湍流能谱图中的耗散也更为明显。
(3)对不同的Smagorinsky常数(对应不同的滤波尺度)进行了敏感性试验,表明可以通过改变滤波尺度,有效地缓解半拉格朗日框架隐含的耗散问题,得到更接近UCLA_LES模拟的湍流特征。
本研究是GRAPES_LES的第一步工作,即加入小涡的闭合方案后评估GRAPES模式的动力框架在大涡尺度模拟中的性能,检验高分辨率GRAPES模式构造中应该注意的问题。后续工作中将逐步加入水汽条件、云微物理过程、复杂地形、非均匀下垫面等内容,构建更为完备的GRAPES_LES模式,从而为检验和发展边界层湍流参数化提供科学工具。
| McCalpin J D, 林峰. 1989. 半拉格朗日平流内在耗散的定量分析. 气象科技, (6): 32-38 |
| 王雪梅. 2001. 用大涡模式研究对流边界层湍流. 气候与环境研究, 6(4): 473-477 |
| 吴涧, 蒋维楣. 1999. 对流边界层的大涡模拟研究. 气象科学, 19(1): 33-41 |
| 薛纪善, 陈德辉. 2008. 数值预报系统 GRAPES 的科学设计与应用. 北京: 科学出版社,383pp |
| 郑永骏, 金之雁, 陈德辉. 2008. 半隐式半拉格朗日动力框架的动能谱分析. 气象学报, 66(2): 143-157 |
| Agee E, Gluhovsky A. 1999. LES model sensitivities to domains,grids, and large-eddy timescales. J Atmos Sci, 56(4): 599-604 |
| Cullen M J P, Brown A R. 2009. Large eddy simulation of the atmosphere on various scales. Philos Trans Roy Soc A: Math Phys Eng Sci, 367(1899): 2947-2956 |
| Cuxart J, Bougeault P, Redelsperger J L.2000. A turbulence scheme allowing for mesoscale and large-eddy simulations. Quart J Roy Meteor Soc, 126(562): 1-30 |
| Deardorff J W. 1970. Convective velocity and temperature scales for the unstable planetary boundary layer and for Rayleigh convection. J Atmos Sci, 27(8): 1211-1213 |
| Deardorff J W. 1972. Numerical investigation of neutral and unstable planetary boundary layers. J Atmos Sci, 29(1): 91-115 |
| Deardorff J W. 1973. The use of subgrid transport equations in a three-dimensional model of atmospheric turbulence. J Fluid Eng, 95: 429-438 |
| Deardorff J W. 1974. Three-dimensional numerical study of the height and mean structure of a heated planetary boundary layer. Bound Layer Meteor, 7(1): 81-106 |
| Denis B J, Cté J, Laprise R. 2002. Spectral decomposition of two-dimensional atmospheric fields on limited-area domains using the Discrete Cosine Transform (DCT). Mon Wea Rev, 130(7): 1812-1829 |
| Drikakis D. 2003. Advances in turbulent flow computations using high-resolution methods. Prog Aerosp Sci, 39(6-7): 405-424 |
| Germano M, Piomelli U, Moin P, et al. 1991. A dynamic subgrid-scale viscosity eddy model. Phys Fluids A, 3: 1760-1765 |
| Hadfield M G, Cotton W R, Pielke R A. 1991. Large eddy simulation of thermally forced circulations in the convective boundary layer, Part I: Eddy simulations of thermally. Bound-Layer Meteor, 57: 79-114 |
| Huang H Y, Stevens B, Margulis S A. 2008. Application of dynamic subgrid-scale models for large-eddy simulation of the daytime convective boundary layer over heterogeneous surfaces. Bound-Layer Meteor, 126(3): 327-348 |
| Kolmogorov A N. 1941. Dissipation of energy in a locally isotropic turbulence. Dokl ANSSSR, 32: 141 |
| Lean H W, Clark P A, Dixon M, et al. 2008. Characteristics of high-resolution versions of the Met Office Unified Model for forecasting convection over the United Kingdom. Mon Wea Rev, 136(9): 3408-3424 |
| Lilly D K. 1967. The representation of small-scale turbulence in numerical simulation experiments. IBM Scientific Computing Symposium Environ Sci, 195-201 |
| Mason P J, Callen N S. 1986. On the magnitude of the subgrid-scale eddy coefficient in large-eddy simulations of turbulent channel flow. J Fluid Mech, 162(1): 439-462 |
| Mason P J, Derbyshire S H. 1990. Large-eddy simulation of the stably-stratified atmospheric boundary layer. Bound-Layer Meteor, 53(1-2): 117-162 |
| Moeng C H. 1984. A large-eddy simulation model for the study of planetary boundary layer turbulence. J Atmos Sci, 41(13): 2052-2062 |
| Nieuwstadt F T M, Mason P J, Moeng C H, et al. 1993. Large-eddy simulation of the convective boundary layer: A comparison of four computer codes. Turbulent Shear Flow, 8: 343-367 |
| Petch J C, Blossey P N, Bretherton C S. 2008. Differences in the lower troposphere in two-and three-dimensional cloud-resolving model simulations of deep convection. Quart J Roy Meteor Soc, 134(636): 1941-1946 |
| Porté-Agel F, Meneveau C, Parlange M B. 2000. A scale-dependent dynamic model for large-eddy simulation: Application to a neutral atmospheric boundary layer. J Fluid Mech, 415: 261-284 |
| Reinert D, Wirth V. 2009. A new large-eddy simulation model for simulating air flow and warm clouds above highly complex terrain. Part II: The moist model and its application to banner clouds. Bound-Layer Meteor, 133(1): 113-136 |
| Robert J B, Richard M F, Carol E H. 2003. Can a semi-Lagrangian model simulate convective boundary layer turbulence? NWP Forecasting Research Technical Report No. 507 |
| Schmit H, Schumann U. 1989. Coherent structure of the convective boundary layer derived from large eddy simulations. J Fluid Mech, 200: 511-562 |
| Seifert A, Beheng K D. 2001. A double-moment parameterization for simulating autoconversion, accretion and self collection. Atmos Res, 59-60: 265-281 |
| Seifert A. 2008. On the parameterization of evaporation of raindrops as simulated by a one-dimensional rainshaft model. J Atmos Sci, 65(11): 3608-3619 |
| Smagorinsky J. 1963. General circulation experiments with the primitive equations. Mon Wea Rev, 91(3): 99-164 |
| Stevens B, Seifert A. 2008. Understanding macrophysical outcomes of microphysical choices in simulations of shallow cumulus convection. J Meteor Soc Japan, 86: 143-162 |
| Stenvens B. updated by Malte Rieck. 2010. Introduction to UCLA_LES: Version 3. 2. 1 |
| Sullivan P P, McWilliams J C, Moeng C H. 1994. A subgrid-scale model for large-eddy simulation of planetary boundary-layer flows. Boundary-Layer Meteor, 71(3): 247-276 |
| Walko R L, Cotton W R, Pielke R A. 1992. Large eddy simulations of the effects of hilly terrain on the convective boundary layer. Bound-Layer Meteor, 58(1-2): 133-150 |
 2013, Vol. 71
2013, Vol. 71


