2013, Vol. 71
中国气象学会主办。
文章信息
- 张祎, 宇如聪, 李建, 陈昊明. 2013.
- ZHANG Yi, YU Rucong, LI Jian, CHEN Haoming. 2013.
- 两步保形平流方案在高分辨率球面经纬网格下的跳点差分试验
- An implementation of a leaping-point Two-step Shape-Preserving Advection Scheme in the high-resolution spherical latitude-longitude grid
- 气象学报, 71(6): 1089-1102
- Acta Meteorologica Sinica, 71(6): 1089-1102.
- http://dx.doi.org/10.11676/qxxb2013.085
-
文章历史
- 收稿日期：2013-03-25
- 改回日期：2013-06-24
2. 中国科学院大学, 北京, 100049;
3. 中国气象局, 中国气象科学研究院灾害天气国家重点试验室, 北京, 100081
2. Graduate University of Chinese Academy of Sciences, Beijing 100049, China;
3. LaSW, Chinese Academy of Meteorological Sciences, China Meteorological Administration, Beijing 100081, China
在大气环流模式中，水物质的平流传输计算对模式水循环的模拟有重要影响，并进而影响模式的能量平衡。一般地，平流方案可分为拉格朗日和欧拉类型。半拉格朗日传输(SLT)方案由于可以允许较大时间步长以及具有较低的数值耗散，国际上的许多模式都采用该类方案进行标量物质传输的计算，而欧拉型差分方案的应用则较少。
Codron等(2002)曾指出，当前大气环流模式存在一个与水汽传输相关的系统性误差。由于模式普遍将传输过程和凝结过程分开处理，因此，传输过程中发生的凝结现象则无法在模式中出现。由于模式在近地面层一般采用地形追随坐标，水平相邻格点的温度在复杂地形处差异明显，当水汽由暖格点向冷格点输送时，在实际的传输过程中就可能由于降温而发生饱和凝结致雨，但在模式中只能在输送过程结束后才发生降水，从而产生系统性的降水偏差。
由于半拉格朗日传输类方案对目标网格点求解时存在跨格点问题，当上(下)游点距目标网格点过远时，水汽输送的轨迹过长，则会更易于加剧这一系统性误差，影响降水等模拟的正确性。而欧拉型方案由于仅使用相邻网格的信息，可能会相对抑制该现象的产生(Codron et al，2002)。
当前，国际上的大气环流模式对复杂地形区域的气候模拟普遍存在较大偏差(Yu et al，2000；Kim et al，2008；Su et al，2012；Zhang et al，2013a，2013b)。东亚地区地形复杂，包括了世界上最高的高原，许多气候特征都与青藏高原及周边地形密切相关(叶笃正等，1979；曾庆存等，1994；张耀存等，1999；Yu et al，2004a，2004b)。因此，适合复杂地形的数值计算方案对提高模式对该地区的模拟性能显得至关重要。美国国家大气研究中心的第5版公用大气模式(NCAR-CAM5)(Neale et al，2010)由于具有良好的开放性和底层结构而被广泛应用于研究工作，该模式中欧拉-谱动力框架采用了经典的半拉格朗日传输方案(Williamson et al，1989，1994)求解平流方程。为了考察平流方案对模拟结果的影响，改进模式对大地形地区降水的模拟能力，本研究尝试采用一个欧拉差分型平流方案替换原始的半拉格朗日传输方案。同时，鉴于提高分辨率是改善地形效应的重要途径之一(Gent et al，2010)，希望能够在高分辨率(格距不大于0.5°)下实现这一目标。
两步保形平流方案(TSPAS)是Yu(1994)提出的一个欧拉型差分方案。该方法建立在二阶精度的Lax-Wendroff方案和一阶精度的迎风格式上。Lax-Wendroff方案的特点是耗散低、但频散高，易产生上冲下溢的现象。迎风格式频散低而耗散大，产生的计算解过分平滑。TSPAS的思想是在满足保形性的前提下，尽量提高数值精度。通过一个保形判据，TSPAS将Lax-Wendroff和迎风格式结合起来。当满足保形判据时，采用Lax-Wendroff方案；违反保形判据时，则采取迎风格式。TSPAS在保持较小计算量的同时，也能保持较好的计算效果(刘洪涛等，2002)，因而已被广泛地运用于中国的一些数值模式：如η坐标区域天气模式(AREM)(宇如聪等，2004)，η坐标区域气候模式(CREM)(Shi et al，2009)，中国科学院大气物理研究所(IAP)大气科学和地球流体力学数值模拟国家重点试验室(LASG)格点版本大气环流模式(GAMIL)(Wang et al，2004)，LASG/IAP气候系统海洋模式(LICOM)(肖潺等，2006)等。但是，在基于经纬网格的高分辨率全球大气环流模式中，该方案的应用面临瓶颈：由于高分辨率模式高纬度纬向格距过小，差分法为了满足Courant-Friedrichs-Lewy(CFL)条件必须采用很短的时间步长，因而增大了计算量。为了能够在高分辨率的CAM5中应用该方案，本研究设计了一个跳点差分版本的TSPAS，使得积分步长可以与CAM5中的半拉格朗日传输方案接近，而较原TSPAS则提高了一个数量级。并通过理想试验，对比了原TSPAS和跳点TSPAS，跳点TSPAS和CAM5-SLT方案的特性。通过实际模式结果，验证了跳点TSPAS的可行性，确保了其在高分辨率CAM5中的稳定积分。采用跳点TSPAS的高分辨率CAM5初步显示出对东亚等地形复杂地区降水模拟有所改进，为后续发展奠定了基础。2 方案介绍
在CAM5中，通量形式的传输物质预报方程为
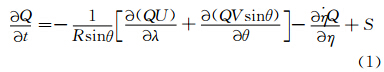
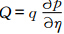(q为混合比，p为气压，η为混合垂直坐标系数)，表示传输物质。U和V表示纬向和经向风场，λ表示经度，θ表示余纬(记由南向北为正向，则南极点θ=0，北极点θ=π)，R为地球半径。模式中主要的传输物质包括水汽、云水、云冰、云水数浓度、云冰数浓度。式(1)等号右边分别为通量形式的水平平流项(
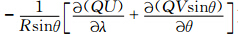)、垂直平流项(
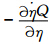)以及湿物理过程对格点尺度标量物的调整项(S)。平流方案主要求解水平和垂直平流项对Q造成的影响。
2.1 水平平流
如图 1所示，方程的离散建立在C网格，实心圆、方块和五角星分别为标量点、U风速点、V风速点位置。由于原高斯网格的风场和标量点均在实心圆处，假设风场呈线性分布，则U(V)风场为东西(南北)相邻高斯格点的平均值。对于i=1，2，…，pLON，j=2，3，…，pLAT-1，TSPAS可作如下表述。
 |
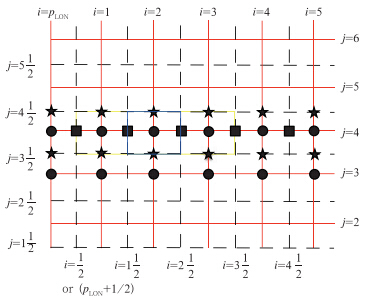| 图 1 非极圈处C网格标量点和风场分布 (i、j表示纬向和经向序号，红色实线表示整数纬圈(原高斯纬圈)，黑色虚线表示半数纬圈，实心圆表示标量点即原高斯格点位置，方块表示U风场位置，五角星表示V风场位置，蓝色方框表示非跳点时计算实心圆处标量值的网格范围，黄色方框表示同一位置，第一次跳点后的计算网格范围) Fig. 1 Distribution of scalar and wind vector on a C grid(i，j denote the indexes along latitude and longitude，the red solid line denotes an integer latitude(the original Gaussian grid)，the black dashed line denotes a half latitude，the solid circle denotes scalar point (i.e. the original Gaussian grid)，the solid square denotes the U point，the solid pentacle denotes V point，the blue rectangular shows one original grid distance for calculating scalar at the center，while the yellow rectangular shows the grid distance after the first leaping point) |
(1)采用Lax-Wendroff格式进行预估
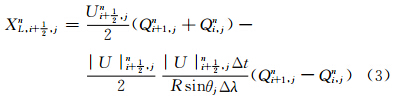
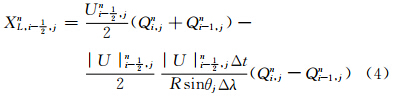
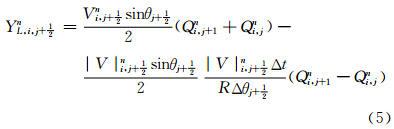
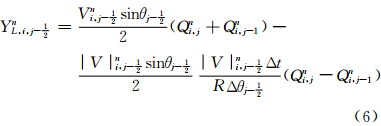
(2)建立判据，确定合适的积分格式
=
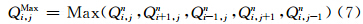
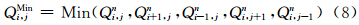
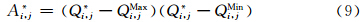
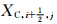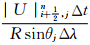(Lax-Wendroff)，否则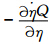=1(迎风)；当且仅当A*i-1，j和A*i，j均小于0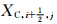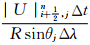，=(Lax-Wendroff)，否则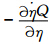=1(迎风)；当且仅当A*i，j和A*i，j+1均小于0，
=
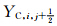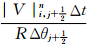(Lax-Wendroff)，否则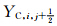=1(迎风)；当且仅当A*i，j-1和A*i，j均小于0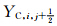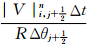，=(Lax-Wendroff)，否则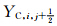=1(迎风)。
(3)实际积分步
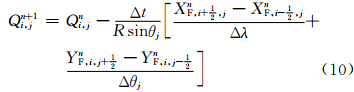
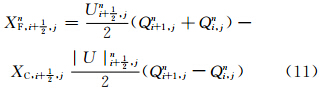
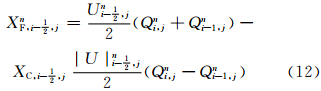
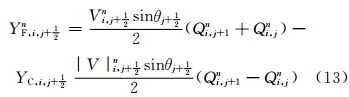
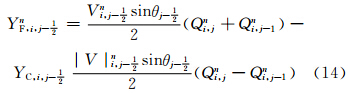
以上为非极圈处的TSPAS计算流程，对于高斯网格南、北极圈(j=1和j=pLAT)，同样采用以上处理流程，只是预估和积分方程的形式不同。下面以积分方程为例，简要介绍。对于i=1，2，…，pLON，j=2，3，…，pLAT-1，以ΔSi，j=R2ΔλΔθjsinθj代表以Qi，j为中心的网格面积，对式(10)等号两侧同乘以ΔSi，j，进行不包括南、北极圈的全球积分。X方向的通量由于周期边界条件全部抵消(图 1)，Y方向的通量经过累加抵消后，剩余
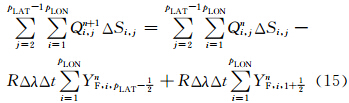
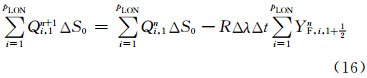
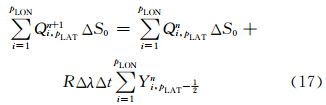
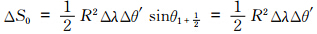
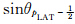，表示构成极帽(图 2)的每一个三角形的面积(图 2中点线和虚线圆弧构成的区域)，整个极帽由pLON个三角形构成(Burridge et al，1977)。Δθ′表示极帽边缘到极点弧距，Δθ′=θ1+
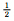(南极圈)，Δθ′=π-θpLAT-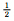(北极圈)。假设在南、北极圈上，Q值始终保持均匀分布，则有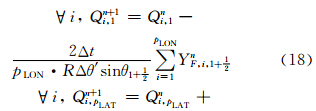
 |
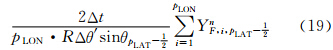
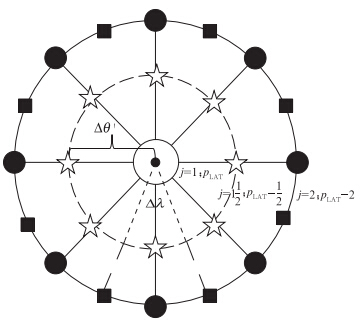| 图 2 极帽示意图 (纬圈的序号由j表示，实线表示整数纬圈，虚线表示半数纬圈，极帽为虚线圆部分，由pLON个三角形(点线和虚线圆弧)构成，实心圆表示标量点，方块表示U风速点位置，五角星表示V风速点位置，Δθ′为极帽边缘到极点的弧距，Δλ为纬向分辨率) Fig. 2 Schematic diagram for a polar cap(south polar) (the order number of the latitude is documented as j，the solid line denotes an integer latitude，the dashed line denotes a half latitude; the polar cap is the dashed circle region，which is constituted by pLON triangles(formed by two dotted lines and the dashed arc)，the solid circle denotes scalar point，the solid square denotes U wind point，the pentacle denotes the V wind point) |
垂直方向的平流计算是TSPAS的一维通量应用形式，仍然包括预估、判断、积分3个步骤。CAM5采用混合σ-p垂直坐标(Simmons et al，1981)，变量的分布如图 3所示。记模式垂直层数为K，则界面层数为K+1。以k(k=1，2，3，…，K)表示标量物所处的整层，k±表示垂直速度W所处的界面层，η表示垂直坐标，对任意位置(i，j)处的Qk有
 |
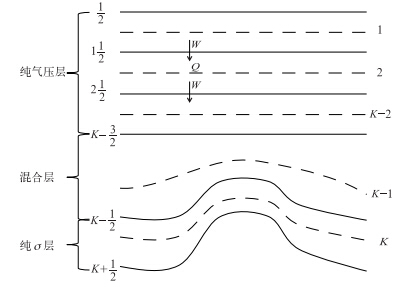| 图 3 模式变量垂直分布示意图 (实线表示界面半层，虚线表示模式整层，K为垂直总层数) Fig. 3 Distribution of variables on a hybrid vertical coordinate (the solid line denotes the model interface level，the dashed line denotes the model middle level，K denotes the total number of vertical levels) |
预估步
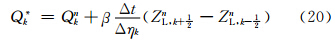
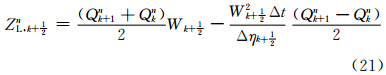
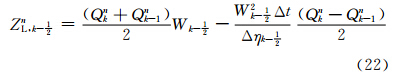
判据步
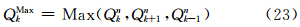
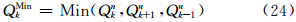
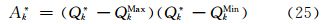
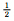=Wk+·
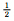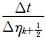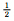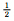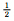
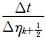(Lax-Wendroff)，否则ZC，k+=1(迎风)；当且仅当A*k和A*k-1均小于0，ZC，k-=Wk-(Lax-Wendroff)，否则ZC，k-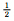=1(迎风)；
积分步
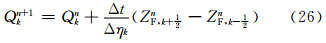
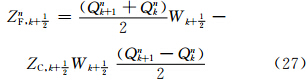
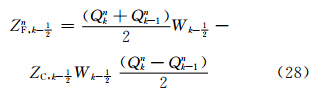
2.1和2.2节中介绍了原始三维TSPAS在CAM5中的计算过程。为了保证大时间步长下的计算稳定性，当纬向球面单位距离(dx)小于一个阈值时则进行跳点差分。纬向的通量和通量差的计算建立在扩大后的新格距下。如图 1所示，蓝色方框的纬向范围为不跳点时一个单位的计算格距，而黄色方框的纬向范围则表示进行第一次跳点后的新格距。计算方框中心的标量点时，所需的纬向通量位置应关于该点对称，间距为当前格距。计算某半网格点上的XF时，所使用的标量点位置同样应关于该半格点对称，间距为当前格距。同时，跳点并不意味着减少纬向的计算格点数，对于每一个格点，都以扩大后的新格距进行纬向的计算。以下作详细表述：
(1)确定阈值，一般取为赤道纬向单位距离的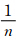
(本研究n=2)，同时确定当前的计算格距，记为k(k=1即不跳点)。需要注意的是k须为奇数，才能保证跳点后C网格上标量点两侧的风场仍然关于标量点对称，且保持交错性。这样纬向的守恒性仍然可以由于XF的累加抵消而得以成立。
(2)对于每一纬圈j，应满足跳点后的纬向单位距离(dxj)与赤道单位距离(dxtr)之比大于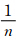，即：
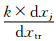>1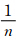，若不满足条件则需要改变跳点个数，k=F(n×k)，函数F对括号内的值仅返回奇数(若为偶数，则返回值加1)。
(3)确定每个纬圈的跳点个数后，将主要方程改写为
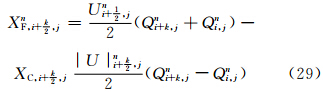
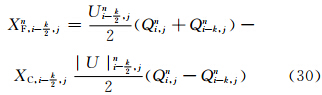
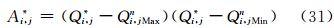
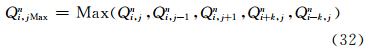
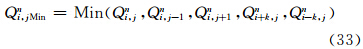
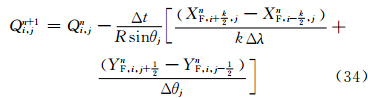
理想试验为检验和比较算法性能提供了较为方便的手段。采取刚体平移试验来进行球面经纬网格上的测试，该试验中圆周内的标量值在球面上绕某一旋转轴进行位移。试验的详细介绍可见Williamson等(1992)，此处仅给出必要说明。
风场和初始标量场由式(35)和(36)给出
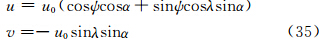
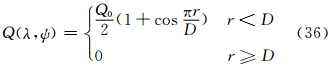
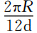，R为地球半径，u0约为40 m/s。α为刚体旋转轴与球坐标极轴的夹角，λ和ψ表示经度和纬度。Q0取为1，r为圆周上的点到圆心的球面距离，D为
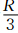。本研究中，初始圆周中心分别位于赤道分界线和南极圈，即α为0和
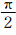，每12 d圆周绕转轴旋转一周回到初始位置。所有试验积分72 d，给出旋转1、3、5周的结果进行分析，记为R1、R3、R5(初值为R0)。
首先比较原TSPAS和跳点TSPAS的结果，由于赤道上的位移并不涉及跳点。因此，仅进行初值位于南极处的绕赤道轴旋转的试验，并分别考察了T42、T106和T266三种分辨率下的情况。原TSPAS的时间步长分别为400 s(T42)、100 s(T106)、10 s(T266)，跳点TSPAS的时间步长设为1200 s(T42)、600 s(T106)、180 s(T266)。该组试验为串行运行，CPU频率为2.67 GHz。
鉴于篇幅所限，仅给出T266分辨率下两组试验的计算结果(图 4)。由圆周在不同时刻的形状可知，两组试验在相同的初值下(图 4a、b)，在旋转1(图 4c、d)、3(图 4e、f)、5(图 4g、h)周后，圆周的中心数值、梯度和扩散范围都比较接近。同时，二组试验的圆周内数值都没有出现大于初值最大值(1)或小于初值最小值(0)的情况，即满足保形规则。表 1给出了两组试验的计算误差，守恒性和耗时的对比。总误差的计算参照Yu(1994)，由式(37)给出
 |
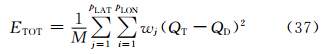
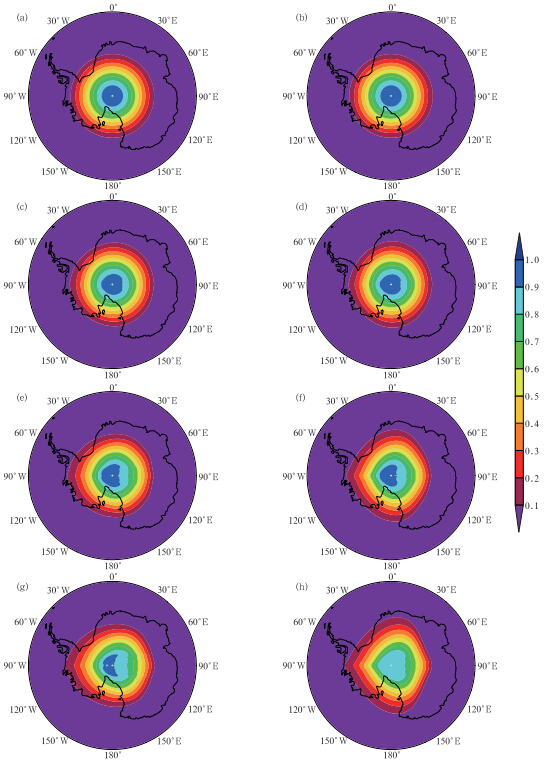| 图 4 原TSPAS(a、c、e、g)和跳点TSPAS(b、d、f、h)在T266分辨率下刚体平移试验结果 (初值(a、b)和旋转1(c、d)、3(e、f)、5(g、h)圈后的结果) Fig. 4 Solid body rotation tests of the original TSPAS(a，c，e，g) and leaping-point TSPAS(b，d，f，h)under T266 resolution (initial values(a，b)，and the values after 1(c，d)，3(e，f) and 5(g，h)times rotations，respectively) |
| T42 | T106 | T266 | |||
| 数值误差 | 原TSPAS | R1 | 3.54×10-5 | 1.61×10-6 | 3.70×10-8 |
| R3 | 6.93×10-5 | 6.70×10-6 | 2.18×10-7 | ||
| R5 | 8.50×10-5 | 1.16×10-5 | 4.67×10-7 | ||
| R1 | 3.83×10-5 | 1.84×10-6 | 5.42×10-8 | ||
| 跳点 | R3 | 7.64×10-5 | 8.22×10-6 | 3.44×10-7 | |
| R5 | 9.38×10-5 | 1.48×10-5 | 7.72×10-7 | ||
| 守恒性ε | R0 | 2.10 | 5.26 | 13.16 | |
| 原TSPAS | R1 | 2.11 | 5.26 | 13.16 | |
| R3 | 2.11 | 5.26 | 13.16 | ||
| R5 | 2.11 | 5.26 | 13.16 | ||
| R0 | 2.10 | 5.26 | 13.16 | ||
| 跳点 | R1 | 2.11 | 5.26 | 13.16 | |
| R3 | 2.11 | 5.26 | 13.16 | ||
| R5 | 2.11 | 5.26 | 13.16 | ||
| 耗时(s) | 原TSPAS | 16.43 | 495.21 | 36795.67 | |
| 跳点 | 5.59 | 83.91 | 2298.07 | ||
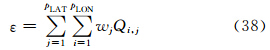
从表 1来看，跳点TSPAS与原TSPAS的总计算误差较为接近。总体上，跳点TSPAS较原TSPAS的误差稍大。这一方面是由于跳点后高纬度地区分辨率损失造成的，另一方面跳点TSPAS采用了更多迎风格式，也增大了耗散(以T42为例，跳点与原TSPAS迎风差使用次数占总计算次数的百分比分别为14.79%和14.26%)。从守恒性来看，基于高斯权重的检验方式下，TSPAS在小数点后1至2位仍然保持一致，跳点TSPAS并未改变原TSPAS的守恒性。然而，跳点TSPAS由于时间步长提高近一个量级，相同时间内的计算速度大幅度提高。基于此，下面进一步对比跳点TSPAS与CAM5-SLT的结果。
表 2给出了在赤道上绕极轴旋转和初值位于南极的绕赤道轴旋转的误差、守恒性和耗时对比。限于篇幅，这里略去运算效果图。赤道上旋转的试验由于并未涉及跳点，可以反映原始TSPAS与CAM5-SLT的计算精度对比，初值位于南极的试验则反映了实际跳点TSPAS的情况。作为拉格朗日型方案，CAM5-SLT相较欧拉型的TSPAS计算精度更高。但其无法满足守恒性，ε在两组试验中，无论高分辨率或低分辨率，均呈明显的衰减；而跳点TSPAS则是守恒的。在耗时方面，由于相同分辨率下，跳点TSPAS和半拉格朗日传输方案采用相同的时间步长，耗时则主要取决于算法一个时步计算量的累加。可以看出，跳点TSPAS比CAM5-SLT要更省时。
 |
根据理想试验的结果，单从计算精度来看，TSPAS的误差要高于半拉格朗日传输。但在实际模式计算中，由于风场和水汽的不均匀分布与非线性变化，二者的差异不如理想试验明显。更重要的是，一个物质传输方案必须综合考虑守恒性、保形性和计算精度等，并结合真实的模拟结果进行评价。尽管当前已有一些满足守恒性的半拉格朗日传输型方案(Nair et al，2002；Zerroukat et al，2004； Peng et al，2005；Lauritzen et al，2010；Skamarock et al，2010；Wong et al，2013)，但是国际上的许多大气环流模式仍然采用了类似CAM5-SLT的非守恒半拉格朗日传输型方案。同时，在实际模式计算中，由于水汽变化涉及到复杂的湿物理过程调整，整个水汽过程的计算结果是多个方案计算的综合，而不是由传输过程单方面的计算精度所决定。下一节将给出实际模式运行结果。4 CAM5中的应用
本研究进行了两组CAM5运行试验，一组为T42分辨率下，采用原TSPAS和跳点TSPAS的模式积分；另一组为T266分辨率，采用半拉格朗日传输的原模式与采用跳点TSPAS模式模拟(分别记为T266和T266.TSPAS)。所有试验均为历史海温强迫，从1979年开始积分，选择1981—1990年结果进行分析。T42下，原TSPAS平流步长为150 s，跳点TSPAS为800 s。T266下，半拉格朗日传输和跳点TSPAS的时间步长均为180 s。
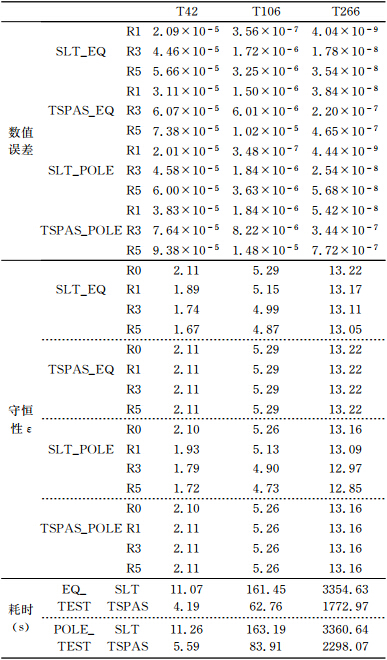
图 5给出的是T42下跳点与原始TSPAS模拟的年平均850 hPa的比湿场(图 5a、b)、温度场(图 5c、d)和总降水场(图 5e、f)。二者对水汽场和温度场的大值中心及梯度分布的模拟均较为接近，位于赤道地区和几个大陆上的雨带在两组模式中也有相似的再现。同时，跳点TSPAS在高纬度地区并未出现模拟异常。这组试验证实了跳点TSPAS具有与原TSPAS相同的模拟效果。
 |
| 图 5 跳点(a、c、e)与原始TSPAS(b、d、f)在CAM5-T42分辨率下的模拟结果(年平均的850 hPa(a、b)比湿场(kg/kg)、(c、d)温度场(K)和(e、f)总降水场(mm/d)) Fig. 5 Simulations from the CAM5 with the leaping-point(a，c，e) and original(b，d，f)TSPAS under T42 resolution(annual mean(a，b)specific humidity(kg/kg)(c，d)temperature at 850 hPa(K)，and (e，f)total precipitation(mm/d) |
图 6分别是采用半拉格朗日传输和跳点TSPAS的两组高分辨率(T266)试验模拟的850 hPa的年平均比湿场(图 6a、b)、温度场(图 6c、d)、纬向(图 6e、f)和经向(图 6g、h)风场。对于直接被平流的水汽场，两套平流方案模拟的赤道地区水汽大值中心，以及梯度分布仍较为一致。同时，平流方案的改变也并未影响大气控制方程中其他的热力(温度)和动力(风场)变量的气候态。两组结果均模拟出全球温度场的大值中心和梯度分布，中纬度西风带，南美、北美洲西海岸的经向风大值中心。
 |
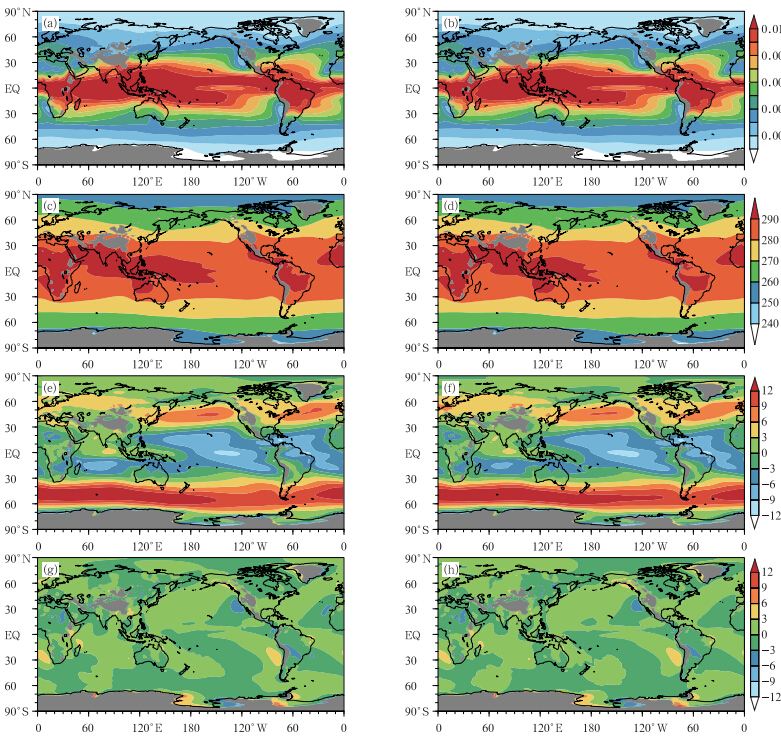| 图 6 T266分辨率，采用半拉格朗日传输平流方案的原模式(a、c、e)与使用跳点TSPAS(b、d、f)模式的850 hPa年平均气候态(a、b.比湿场(kg/kg)，c、d.温度场(K)，e、f. 纬向风(m/s)，g、h.经向风场(m/s)) Fig. 6 Simulations from the CAM5 with SLT(a，c，e) and the leaping-point TSPAS(b，d，f)under T266 resolution.((a，b)annual mean specific humidity(kg/kg)，(c，d)temperature(K)，(e，f)zonal wind(m/s) and (g，h)meridional wind at 850 hPa(m/s)) |
图 7进一步给出了模拟大气可降水量(垂直积分的总水汽场)的对比。再分析资料(图 7a)中的主要水汽分布中心和梯度在原T266(图 7b)中已经有较好的再现。由二者偏差(图 7c)可见，原模式模拟的可降水量较大的正偏差出现在南北赤道太平洋、非洲东岸、澳洲北部及南美洲东部；主要的负偏差位于非洲大陆西侧、印度洋和西太平洋交界、孟加拉湾北部等地区。采用TSPAS的模式与原模式的偏差(图 7d)在全球的大部分地区都很小(±1之间)。
 |
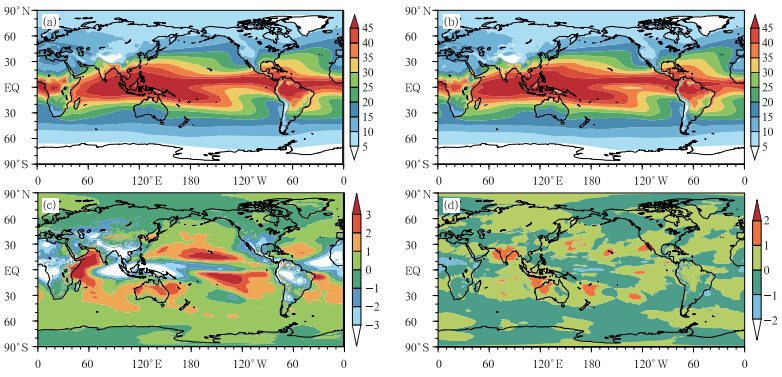| 图 7 大气可降水量气候态，(a)ERA-Interim再分析资料结果，(b)原T266模式结果，(c)T266与再分析差值，(d)T266.TSPAS与T266差值(单位：kg/m2) Fig. 7 Climatological mean of column precipitable water((a)ERA-Interim reanalysis data，(b)original T266，(c)the difference between T266 and ERA-Interim，and (d)the difference between TSPAS and T266) |
图 8给出了总降水率的气候态分布。观测中(图 8a)，位于赤道地区的降水大值中心在T266模式中已有较好再现(图 8b)。由二者差异可知(图 8c)，降水的正偏差出现在南北赤道太平洋、非洲东海岸、南美洲东北海岸和安第斯山脉，以及青藏高原南侧狭长的虚假降水大值带。负偏差则出现在印度洋和太平洋交界、孟加拉湾西部和北部地区、南美安第斯山脉以东。与可降水量的模拟差异一致，在全球大部分地区，降水的模拟差异在T266.TSPAS和T266中仍然较小(图 8d)。为了说明采用TSPAS方案后，对东亚地区降水的改进，图 8e给出了放大至东亚地区的降水气候态。可以看出，T266.TSPAS与T266在青藏高原南侧呈一条狭长的负偏差，而原模式在此处与观测为狭长的正偏差，这说明T266.TSPAS抑制了原模式该处过度的降水。如Codron等(2002)所论述，平流和凝结过程的分离造成的传输过程中无法产生降水这一现象在半拉格朗日传输型方案中易表现得更明显，而在基于欧拉通量差分的TSPAS中则相对得到抑制。这可能是采用TSPAS的模式在高原南侧出现降水负偏差的一个原因。诚然，仅以本研究结果尚不足以充分论证这一观点，还有待确凿的深入模式内部过程的试验加以验证，这一现象的原因仍然值得探讨。
 |
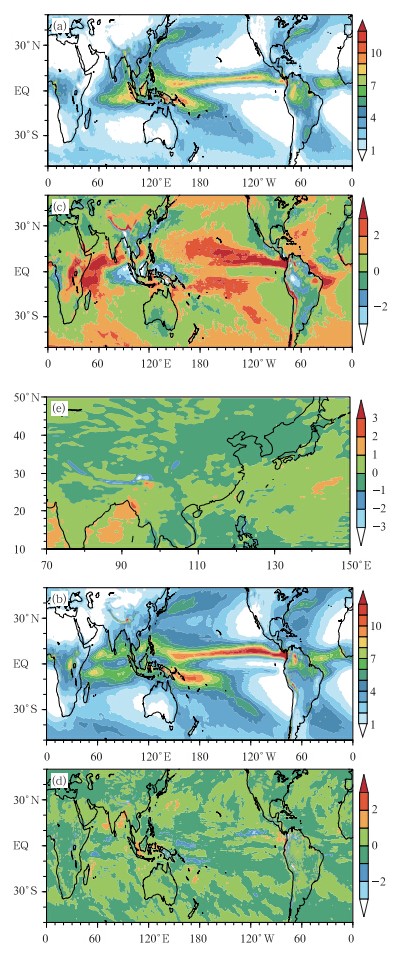| 图 8(a-d)同图 7a-d，但为南北纬50°间的年平均总降水量，观测资料取自TRMM-3B42，(e)为图 8d在东亚地区的放大 Fig. 8(a-d)as in Fig. 7(a-d)but for annual mean total precipitation between 50°S-50°N，the observational data are taken from TRMM-3B42，(e)is the East Asia region as is zoomed in from(d) |
设计了一个跳点差分版本的TSPAS，解决了原TSPAS在高分辨率球面经纬网格上的应用瓶颈，并将该方案引入CAM5替换模式原半拉格朗日传输方案。跳点TSPAS在高分辨率CAM5中可以采用与半拉格朗日传输方案一致的时间步长，而较原TSPAS的时间步长则提高了一个量级。主要结论为
(1)跳点TSPAS在保持原TSPAS守恒性、保形性、计算精度量级的基础上，大大提高了时间步长。TSPAS与CAM5-SLT方案相比，尽管耗散更高，但是改善了半拉格朗日传输方案的不守恒的问题，并且，计算效率更高。
(2)CAM5-T42下的模拟结果表明跳点TSPAS和原TSPAS对基本量(如温度、湿度等)的气候态模拟差异不大，跳点TSPAS在高纬度地区并未出现模拟异常。在高分辨率下，T266.TSPAS和原T266模拟的基本量的气候态也较为接近。与原模式相比，采用TSPAS的模式初步显示出对东亚青藏高原南侧的虚假降水有所抑制，为后续发展奠定了基础。
本研究提出的跳点方案可被用于球面经纬网格下任意欧拉类型标量物平流方案。应当指出，由于跳点后纬向差分不再包含相邻网格的信息，可能会造成计算解分离，导致虚假计算波的产生。然而，在理想试验和实际模式使用中，均未发现此类情况。可能的原因是：(1)实际问题不是一个纬向闭合的一维周期边界问题，可能有利于缓解该类情况；(2)经向积分和极点最近纬圈的均匀处理都对缓解这个问题的出现有抑制作用；(3)在不同纬圈上的跳点数变化也有利于抑制这个问题发生。采用该方案的高分辨率模式初步显示出对青藏高原南侧地区降水模拟有所改进，值得进一步的研究和思考，也为比较和讨论水汽传输方案对气候模式模拟结果的影响提供启示，为后续针对东亚复杂地形区的高分辨率气候模式的改进奠定了基础。
致谢：感谢国防科技大学-国家超级计算长沙中心提供的天河一号的计算节点，使得本研究的高分辨率长期积分试验得以顺利展开。| 刘洪涛, 王斌, 薛峰等. 2002. 大气环流模式降水的模拟对水汽方程差分方案的敏感性试验. 气候与环境研究, 7(1):121-134, doi:10.3878/j.issn.1006-9585.2002.01.12 |
| 肖潺, 俞永强. 2006. 保形平流方案在海洋环流模式中的应用. 自然科学进展, 16(11):1442-1448 |
| 叶笃正, 高由禧. 1979. 青藏高原气象学. 北京: 科学出版社, 278pp |
| 宇如聪, 薛纪善, 徐幼平. 2004. AREMS中尺度暴雨数值预报模式系统. 北京: 气象出版社, 233pp |
| 曾庆存, 宇如聪, 彭贵康等. 1994. "雅安天漏"研究Ⅲ: 特征、物理量结构及其形成机制. 大气科学, 18(6):649-659 |
| 张耀存, 钱永甫. 1999. 青藏高原隆升作用于大气临界高度的数值研究. 气象学报, 57(2):157-167 |
| Burridge D M, Haseler J. 1977. A model for medium range weather forecasting-adiabatic formulation. ECMWF Technical Report, No.4 |
| Codron F, Sadourny R. 2002. Saturation limiters for water vapour advection schemes: Impact on orographic precipitation. Tellus A, 54(4), doi: 10.1034/j.1600-0870.2002.01265.x |
| Gent P, Yeager S, Neale R, et al. 2010. Improvements in a half degree atmosphere/land version of the CCSM. Climate Dyn, 34(6):819-833 |
| Kim H J, Wang B, Ding Q. 2008. The global monsoon variability simulated by CMIP3 coupled climate models. J Climate, 21(20):5271-5294 |
| Lauritzen P H, Nair R D, Ullrich P A. 2010. A conservative semi-Lagrangian multi-tracer transport scheme (CSLAM) on the cubed-sphere grid. J Comput Phys, 229(5):1401-1424 |
| Nair R D, Machenhauer B. 2002. The mass-conservative cell-integrated semi-lagrangian advection scheme on the sphere. Mon Wea Rev, 130:649-667 |
| Neale R B, Andrew G, Sungsu P, et al. 2010. Description of the NCAR Community Atmosphere Model (CAM 5. 0). NCAR Technical Note, NCAR/TN-486+STR |
| Peng X, Xiao F, Ohfuchi W, et al. 2005. Conservative semi-lagrangian transport on a sphere and the impact on vapor advection in an atmospheric general circulation model. Mon Wea Rev, 133(3):504-520 |
| Shi H B, Yu R, Li J, et al. 2009. Development of a regional climate model (CREM) and evaluation on its simulation of summer climate over eastern China. J Meteor Soc Japan, 87(3):381-401 |
| Simmons A J, Burridge D M. 1981. An energy and angular-momentum conserving vertical finite-difference scheme and hybrid vertical coordinates. Mon Wea Rev, 109(4):758-766 |
| Skamarock W C, Menchaca M. 2010. Conservative transport schemes for spherical geodesic grids: High-order reconstructions for forward-in-time schemes. Mon Wea Rev, 138(12):4497-4508 |
| Su F, Duan X, Chen D, et al. 2012. Evaluation of the global climate models in the CMIP5 over the Tibetan Plateau. J Climate, 26, 3187-3208 |
| Wang B, Wan H, Ji Z, et al. 2004. Design of a new dynamical core for global atmospheric models based on some efficient numerical methods. Sci China Ser A: Math, 47(7):4-21 |
| Williamson D L, Rasch P J. 1989. Two-dimensional semi-lagrangian transport with shape-preserving interpolation. Mon Wea Rev, 117(1):102-129 |
| Williamson D L, Drake J, Hack J, et al. 1992. A standard test set for numerical approximations to the shallow water equations in spherical geometry. J Comput Phys, 102(1):211-224 |
| Williamson D L, Rasch P J. 1994. Water vapor transport in the NCAR CCM2. Tellus A, 46(1):34-51 |
| Wong M, Skamarock W C, Lauritzen P H, et al. 2013. A cell-integrated semi-Lagrangian semi-implicit shallow-water model (CSLAM-SW) with conservative and consistent transport. Mon Wea Rev, doi: 10.1175/MWR-D-12-00275.1 |
| Yu R C. 1994. A Two-step shape-preserving advection scheme. Adv Atmos Sci, 11(4):479-490 |
| Yu R C, Li W, Zhang X, et al. 2000. Climatic features related to eastern China summer rainfalls in the NCAR CCM3. Adv Atmos Sci, 17(4):503-518 |
| Yu R C, Wang B, Zhou T J. 2004a. Tropospheric cooling and summer monsoon weakening trend over East Asia. Geophys Res Lett, 31(22):L22212 |
| Yu R C, Wang B, Zhou T. 2004b. Climate effects of the deep continental stratus clouds generated by the Tibetan Plateau. J Climate, 17(13):2702-2713 |
| Zerroukat M, Wood N, Staniforth A. 2004. SLICE-S: A semi-lagrangian inherently conserving and efficient scheme for transport problems on the sphere. Quart J Roy Meteor Soc, 130(602):2649-2664 |
| Zhang Y, Li J. 2013a. Shortwave cloud radiative forcing on major stratus cloud regions in AMIP-type simulations of CMIP3 and CMIP5 models. Adv Atmos Sci, 30(3):884-907 |
| Zhang Y, Yu R, Li J, et al. 2013b. Dynamic and thermodynamic relations of distinctive stratus clouds on the lee side of the Tibetan Plateau in the cold season. J Climate, doi:10.1175/JCLI-D-13-00009.1 |