中国气象学会主办。
文章信息
- 魏伟, 张宏升. 2013.
- WEI Wei, ZHANG Hongsheng. 2013.
- 希尔伯特-黄变换技术及在边界层湍流研究中的应用
- The Hilbert-Huang transform technique and its applications to the study of the turbulence boundary layer
- 气象学报, 71(6): 1183-1194
- Acta Meteorologica Sinica, 71(6): 1183-1194.
- http://dx.doi.org/10.11676/qxxb2013.096
-
文章历史
- 收稿日期:2013-03-15
- 改回日期:2013-09-09
湍流是行星边界层中主要的运动形态,对地表与大气间动量、水热和物质输送与交换起着重要作用。湍流表现为叠加在平均运动上的阵性流动现象。通常,湍流可以视为由许多不同大小的湍涡相互叠加而成,可利用各种统计学方法(如谱分析等)描述湍涡的无序分布,通过将时间序列分解成频率(或波长)与能谱的关系可以进一步获取不同时空尺度的湍流特征。
20世纪60年代以来,随着观测手段和计算能力的提高,对于边界层湍流谱分布特征的分析愈发深入。1968年Kansas实验利用快速响应仪器给出了平坦均一下垫面风速和温度序列(Haugen et al,1971);Businger 等(1971)给出了经典的近地层通量廓线关系;Wyngaard 等(1971)提出了温度结构函数和风、温垂直梯度与稳定度关系的半经验公式;Kaimal 等(1972)证实了无量纲化的速度谱和温度谱在惯性副区的一致性,且满足科尔莫哥罗夫(Kolmogorov)局地各向同性理论。
中国学者针对大气边界层的湍流理论也进行了一系列的研究(刘鹏飞等,2010;全利红等,2007a;胡非等,2005;刘树华等,2001;吕乃平等,1985),并对不同下垫面条件下的湍流特征进行了深入的分析(李英等,2009;宋丽莉等,2009;张艳武等,2009;张强等,2008;卞林根等,2001;刘辉志等,2007,2003;Zhang et al,2001;许丽人等,2001;高志球等,1999;王存忠等,1994;王介民,1992)。但是,经典的湍流能谱分析多建立在傅里叶分解得到的功率谱基础上,其前提条件是假设时间序列线性且平稳。而大气流动是高雷诺数流动,边界层中湍流呈无规则的随机性和非线性,使用傅里叶分解进行湍流能谱分析具有一定的局限性。此后,有学者利用小波变换分析了大气对流边界层的湍流特性(全利红等,2007b;陈子赟等,2004;胡非,1998)。但和傅里叶分解一样,小波变换对于非线性、非均匀信号的分析也具有一定的局限性。大气和海洋现象多是非平稳、非线性的,传统分析方法的使用多基于一定的假设条件。
希尔伯特-黄变换(Hilbert-Huang Transform,HHT)是一种能自适应地将非平稳、非线性信号分解成单分量信号的经验算法,可以用于研究非平稳、非线性的大气湍流问题。鉴于其在非平稳、非线性信号分析中的优势,希尔伯特-黄变换方法已经被中外学者应用于气候变化、中小尺度天气现象、环境监测和海洋现象的研究中。Molla 等(2006)、Peel等(2006)、Iyengar等(2006)、Xie 等(2002)利用希尔伯特-黄变换分别对降水预测、印度季风和热带气旋进行了分析。Gloersen等(2004)、El-Askary 等(2004)将希尔伯特-黄变换应用到海-气相互作用领域。Lundquist(2003)、Karipot等(2009)利用希尔伯特-黄变换对低空急流进行了分析。此外,希尔伯特-黄变换还广泛用于世界各地边界层风场结构的分析中(Vincent et al,2011;Tatli et al,2005;Abarca-Del-Rio et al,2006;Janosi et al,2005)。中国学者也利用希尔伯特-黄变换技术对大气和海洋现象开展了相关研究(张瑞等,2011;孙勇等,2009;秦旭等,2009;邓伟涛等,2008;万仕全等,2005;熊学军等,2002)。鉴于希尔伯特-黄变换技术在大气湍流研究中应用的报道尚不多见。本研究选取中国北方内蒙古科尔沁地区2011年4月16日大气湍流探测资料,应用希尔伯特-黄变换技术对边界层湍流能谱进行分析,并探讨希尔伯特-黄变换在边界层湍流研究中的应用。2 资料获取与处理
大气湍流试验站位于中国北方内蒙古自治区科尔沁地区南部,地理位置为(42°56′N,120°42′E),平均海拔363 m,南距奈曼旗市区约20 km,属于典型的半干旱地区。超声风温仪架设在气象塔8 m高度处,传感器安装支臂为正西方向。湍流资料采样频率为10 Hz,为连续自动观测(李晓岚等,2012)。
选取2011年4月16日00—01时(北京时,下同)、05—06时、12—13时的湍流数据,分别代表大气边界层从夜间稳定层经过日出发展成为混合层过程中不同的大气层结特征,且满足谱分析方法所要求的数据具有良好连贯性的条件(Vincent et al,2010),也避免了缺失数据对原始数据波动周期的干扰(Stull,1988)。采用张宏升等(2001)提出的湍流数据处理流程,对10 Hz的大气湍流原始数据进行质量控制和坐标旋转等预处理。图 1给出了3个时段U、V、W和T的时间变化。
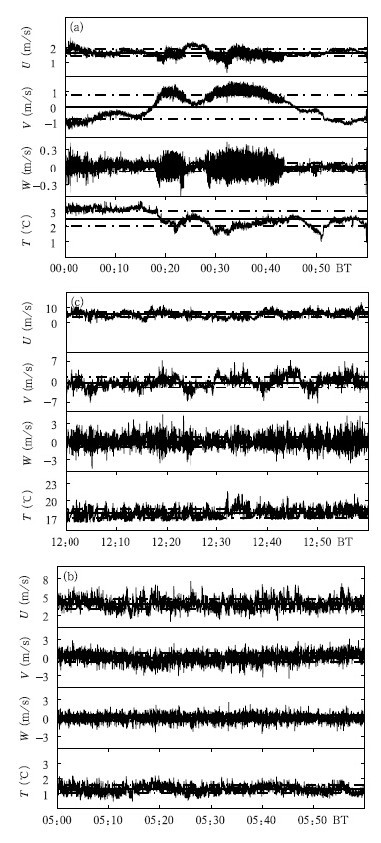 |
| 图 1 2011年4月16日科尔沁地区8 m高度水平纵向风速U、水平横向风速V、垂直风速W和温度T随时间的变化 (a.00—01时,b.05—06时,c.12—13时;横直线为均值,横虚线为标准差) Fig. 1 Time distribution of horizontal longitudinal speed U,cross speed V,vertical speed W and temperature T at 8 m level in the Horqin S and y L and on 16 April 2011(a. 00:00-01:00,b. 05:00-06:00,c. 12:00-13:00 BT; Straight lines represent the mean and the dashed lines represent the st and ard deviation) |
传统的信号分析方法一般可以分为傅里叶分析和时频分析方法。傅里叶分析假设非周期信号是一系列频率0—∞的正弦波的加权和,即傅里叶变换中的基函数是全局性的,信号的任何突变其频谱将散布在整个频率区间,这样可能会因强制拟合而产生实际并不存在的噪声信号。因此,傅里叶变换只适合平稳、线性信号的分析。此外,傅里叶分析只有唯一的基函数,即三角函数,这使得在不同信号的分析中缺乏适应性。后来发展出来的一系列时频分析方法在一定程度上提高了对不同信号的适应性。如:短时傅里叶变换/Gabor变换(谭为民等,2003),Wigner-Ville分布(Barbarossa,1995)和小波变换(周林等,2006;文鸿雁等,2006;王玉平等,1996)等。但在非平稳、非线性信号的分析中都具有一定的局限性。
针对传统信号分析方法的不足,Huang于1996年首次提出了一种能自适应地将非平稳、非线性信号分解成单分量信号的经验算法——经验模态分解(Empirical Mode decomposition,EMD),并于1998年给出了完整的分析方法——希尔伯特-黄变换(Huang et al,1998)。
针对非平稳信号的非周期性,定义全局上的傅里叶频率失去了意义,而瞬时频率可以描述频率峰值随时间的变化。瞬时频率的定义有多种,其中,对解析信号位相求导数得到的具有频率量纲的参量与傅里叶变换的频率定义是一致的。为了构造满足瞬时频率定义的复信号需要确定信号的虚部,Gabor(1946)提出的解析信号方法其复信号可以表示为
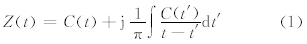
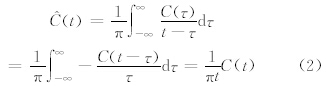
完整的希尔伯特-黄变换方法主要分为两步:第1步,对原始的非平稳、非线性时间序列进行经验模态分解,得到一组内在模函数(Intrinsic Mode Function,IMF),每个内在模函数满足以下两个特征:(1)在整个信号中的极值点数和过0点数相等或最多相差1;(2)由局地极大值和局地极小值确定的上下包络线的均值在任一点上均为0。前者保证了与原始时间序列相比,每一个内在模函数都可以视为一个单分量信号,后者保证了信号对时间轴的局部对称,防止瞬时频率受到非对称波形的干扰。第2步,对各内在模函数分量进行希尔伯特变换,得到解析信号和瞬时频率,进而得到三维希尔伯特谱。对可以同时反映信号振幅、时间和频率分布的三维希尔伯特谱进行时间积分,即得到振幅随频率的分布——希尔伯特边际谱;同理,对频率积分则可得到能量随时间的变化——瞬时能量(Instantaneous Energy Density Level,IE)。
用经验模态分解方法得到内在模函数的过程称为筛过程。该过程基于3个假设:(1)信号至少有一个极大值和一个极小值;(2)信号的特征时间尺度是由极值点之间的间隔确定的;(3)如果整个信号不包含极值点只包含曲折点(即奇异点)可以通过差分获得极值点。整个分解过程分3步:
(1)找出原始序列X(t)的所有局部极大值,插值得到其上包络线eMax(t);同理得到局部极小值的下包络线eMin(t)。对上下包络线进行平均得到原序列的平均包络线m1(t)=(eMax(t)+eMin(t))/2,利用原序列X(t)与m1(t)求差得到第1个分量h1(t)=X(t)-m1(t)。
(2)由于h1(t)不满足内在模函数的定义,需进行第2次筛选:将h1(t)作为原始序列计算上、下包络线和平均包络线m11(t),得到h11=h1-m11。重复上述过程k次,直到h1k满足内在模函数的定义,h1k=h1(k-1)-m1k,就得到了原始序列的第1个内在模函数,c1=h1k。
(3)c1包含了信号的最高频部分,用原始信号减去c1就得到第1个剩余项

r1一般仍包含一些更长周期的波动,所以,将r1作为新的非平稳、非线性时间序列重复上述(1)和(2)的筛过程,得到若干内在模函数信号cn和剩余项rn:r1-c2=r2,…,rn-1-cn=rn。
当cn或rn的振幅足够小,或者rn为单调函数,无法进一步提取出内在模函数时,整个经验模态分解过程终止,原始时间序列可以表示为
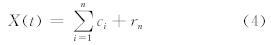
经过以上3个步骤,将原始非平稳、非线性时间序列分解为n个经验模态函数与剩余趋势项rn之和。
经验模态分解过程由若干个筛过程组成。筛过程主要有两个目的:消除载波,使波形更加对称。前者是为保证瞬时频率有意义,后者是为防止与邻近波动的振幅差异过大。但如果过分强调后者,得到的内在模函数就是一个常振幅的调制波,使波动振幅失去其物理意义。为了保证内在模函数结果有物理意义和防止过筛,Huang等(1998)和Rilling等(2003)分别提出了不同的筛算法终止准则。Huang 等(1998)提出通过计算相邻两次筛过程的标准差DS来限制过筛,其定义式为
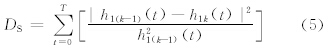
Huang等(1999)提出了可以称做S值终止准则的第2种方法,这是一种较为简单的标准,只需确定达到极值点数等于过0点数时的筛选次数S即可。但不同的S值会造成不同的筛选结果。一般情况下,S越大,筛选的次数越多。为了防止过筛,一般取3≤S≤5作为终止条件。
Rilling等(2003)提出的终止准则是基于两个阈值θ1和θ2。首先定义模态振幅a(t)=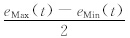 和估计函数σ(t)=
和估计函数σ(t)=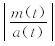 。当选定的(1-α)波段满足σ(t)<θ1且剩余波段满足σ(t)<θ2,一次筛过程终止。一般情况下,σ≈0.05,θ1≈0.05,θ2≈10θ1。
。当选定的(1-α)波段满足σ(t)<θ1且剩余波段满足σ(t)<θ2,一次筛过程终止。一般情况下,σ≈0.05,θ1≈0.05,θ2≈10θ1。
经验模态分解过程最重要的一步是确定信号的“包络线”。波动的上下包络线由局地极值点插值得到,常用的插值方法有三次样条插值、线性插值、多项式插值和阿克玛插值等。三次样条插值既能避免突变现象又能保证一定程度的光滑性,但对于非均匀的插值点容易造成过冲和欠冲,且计算速度较慢。其他插值法如线性插值和多项式插值会导致过筛;阿克玛插值虽然能适应非均匀插值点,但光滑性较差(钟佑明等,2005)。这里采用三次样条插值。
在得到一系列可视为单分量信号的内在模函数的基础上,即可进行希尔伯特变换。对每一个内在模函数ci(t)做希尔伯特变换得到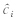 (t),则ci(t)的解析信号可以表示为
(t),则ci(t)的解析信号可以表示为
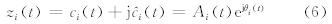
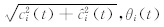 =arctg[
=arctg[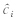 (t)/ci(t)]。可以看出,希尔伯特变换是通过正弦曲线的频率和幅值调制进而获得信号局地的最佳逼近,瞬时振幅Ai(t)和瞬时位相θi(t)都是时间的函数,可以很好地反映出信号的瞬时性。进一步对瞬时位相求导数即得到瞬时频率ωi(t)=
(t)/ci(t)]。可以看出,希尔伯特变换是通过正弦曲线的频率和幅值调制进而获得信号局地的最佳逼近,瞬时振幅Ai(t)和瞬时位相θi(t)都是时间的函数,可以很好地反映出信号的瞬时性。进一步对瞬时位相求导数即得到瞬时频率ωi(t)=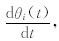 这样得到的瞬时频率不再受海森伯格测不准原理的限制,可以同时在时域和频域上达到很高的分辨率。
这样得到的瞬时频率不再受海森伯格测不准原理的限制,可以同时在时域和频域上达到很高的分辨率。对解析信号的实部求和得到原始信号X(t)=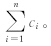 考虑剩余趋势项rn周期的不确定性,为避免虚假能量的计算,这里的X(t)略去了非内在模函数分量rn。波动振幅在频率-时间平面上的表示,即为希尔伯特谱H(ω,t)
考虑剩余趋势项rn周期的不确定性,为避免虚假能量的计算,这里的X(t)略去了非内在模函数分量rn。波动振幅在频率-时间平面上的表示,即为希尔伯特谱H(ω,t)
定义希尔伯特边际谱
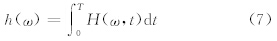
希尔伯特边际谱中的频率和傅里叶分析中的频率意义不同。傅里叶分析中每一个非0振幅的频率ω对应着一个存在于全局上的三角函数,而希尔伯特边际谱中某一频率ω的能量仅仅意味着在信号的局地有存在该频率波动的可能性,其发生的具体时间要结合三维希尔伯特谱确定。Huang等(1998)指出,希尔伯特边际谱实际上是一种非标准化的振幅-频率-时间的加权联合分布,每个时间-频率点上的权重就是振幅。希尔伯特边际谱中给出的频率分布仅代表了某特定频率波动存在的可能性。希尔伯特边际谱作为频率和振幅的函数,可以很好地表征不同频率的波动所对应的振幅大小。
瞬时能量(EI)定义为
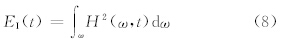
以水平纵向风速U为例,图 2给出2011年4月16日午夜、日出和正午不同时段经验模态分解的结果,包括若干个内在模函数分量和1个剩余项Res:午夜时段得到14个内在模函数分量;日出和正午时段得到13个内在模函数。图中内在模函数分量的纵坐标为振幅,同一时段的各内在模函数分量的纵坐标表示的振幅范围相同。
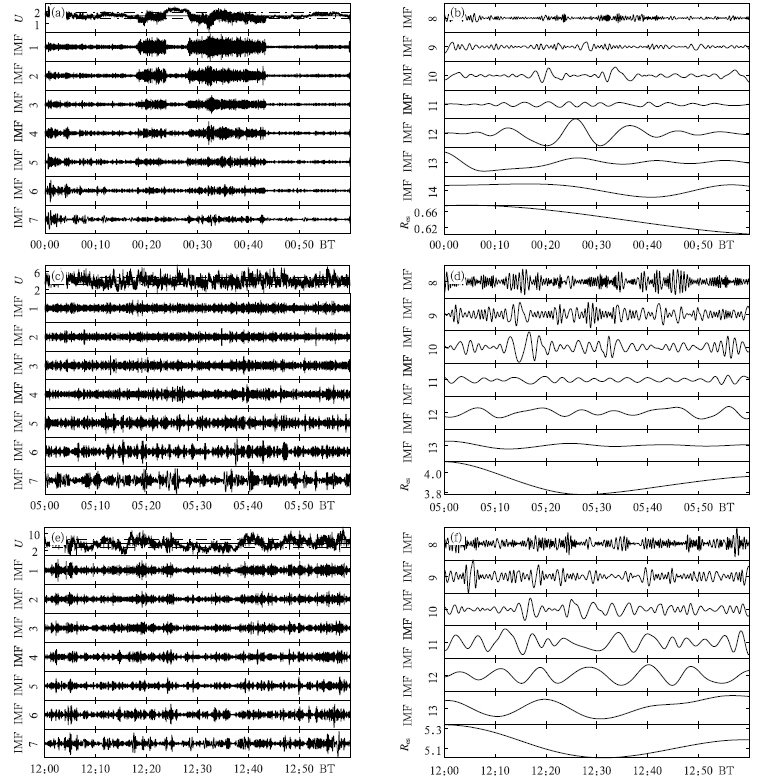 |
| 图 2 科尔沁地区2011年4月16日水平纵向风速U(m/s)、各内在模函数分量及剩余项Res (a、b. 00—01时,内在模函数纵轴振幅0.3 m/s;c、d. 05—06时,内在模函数纵轴振幅1.2 m/s;e、f. 12—13时,内在模函数纵轴振幅2.1 m/s;IMF1分量的平均瞬时频率最大,其他内在模函数分量的平均瞬时频率依次减小) Fig. 2 Horizontal longitudinal speed U(m/s) and IMF components and the residual term Res in the Horqin S and y L and on 16 April 2011 (a,b. 00:00-01:00 BT,the longitudinal range of IMF is 0.3 m/s; c,d. 05:00-06:00 BT,the longitudinal range of IMF is 1.2 m/s; e,f. 12:00-13:00 BT,the longitudinal range of IMF is 2.1 m/s. IMF1 has the largest instantaneous frequency and the instantaneous frequencies of the other IMF components reduce gradually) |
总体上,午夜时段的水平纵向风速U最小;日出时段次之;正午最大,湍流发展最为充分。3个不同时段的各内在模函数分量和剩余项Res的振幅也依次增大,振幅最大值从夜间、日出到正午分别为0.3、1.2和2.1 m/s。由图 2a、b可见,午夜时段水平纵向风速U存在周期约10 min的振荡,且有3个波动较为强烈的时段,分别是00时00—04分、18—23分、28—43分。高频分量IMF1-IMF8在3个时间段内均呈现较大的振幅,可以认为边界层内的湍流运动是由较高频的波动组成的。IMF8 的瞬时频率对应着约1 min的振荡周期,意味着比IMF8更高频的IMF7—IMF10为周期小于1 min的湍流运动分量。另外,IMF11的波动周期约为4 min,与能谱分析中阵风对应的3—5 min的周期一致(程雪玲等,2007;李倩等,2004;董双林,2001)。IMF12的瞬时振幅在14个内在模函数分量中最大,相应的能量也最强,对应着约13 min的波动周期,代表了重力内波(Finnigan et al,1984,1988;Einaudi et al,1989,1993;Poulos et al,2002)。剩余项Res的周期超过了原始数据的采样长度,可以认为是趋势项,其波动振幅远大于各内在模函数分量的振幅。考虑到剩余趋势项周期的不确定性,为避免虚假能量的计算,下文希尔伯特谱的计算不包含剩余项。图 2c、d和e、f分别给出日出和正午时段的湍流经验模态分解结果。对比图 2a、b,日出和正午时刻的湍流能量更强,对应的各内在模函数分量和剩余项Res的瞬时振幅更大,波动更强烈。与图 2a、b类似,日出和正午时段也存在着波动周期为3—5和10—13 min的内在模函数分量,分别为IMF11和IMF12。
图 3给出了3个时段的三维希尔伯特谱,显示了不同频率信号的振幅能量随时间的变化。为方便起见,振幅以分贝(dB)的形式给出。从时间轴角度,希尔伯特谱的结果与原始湍流信号以及内在模函数分解结果一致。由图 3a可见,00时00—04分、18—23分、28—43分时段的高频段波动振幅相对较大,进一步说明该3个时段的水平纵向风速信号是由较高频的湍流波动叠加而成。从频率轴角度,相对于高频段,频率小于0.5 Hz的波动振幅更大,意味着频率越低湍流能量越强。由图 3b可见,日出时边界层内的风速较大,但波动较为均匀,相应希尔伯特谱的波动振幅随时间的分布也比较均匀,但仍然可以看出波动相对比较剧烈的时刻对应的希尔伯特谱能量较强。与图 3a的分布规律一致,图 3b显示的主要能量也集中在低频段。此外,3.3—4.2 Hz波段也有较强的能量分布。由图 3c可见,正午的湍流波动更频繁,12时02、05、20分等时刻均存在明显的波动峰值,相对应的希尔伯特谱也呈现出较大的波动能量。
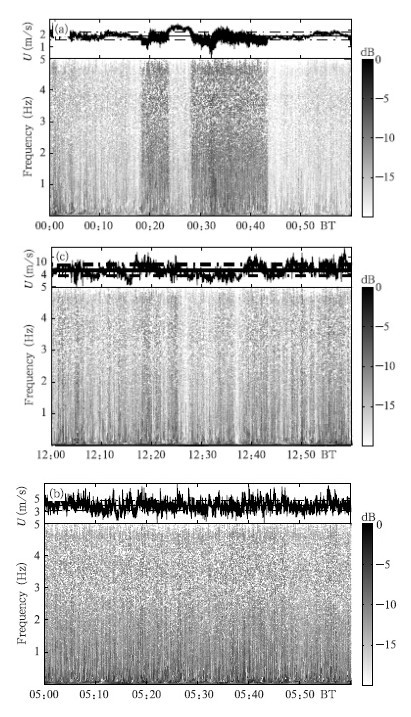 |
| 图 3 科尔沁地区2011年4月16日水平纵向风速U和希尔伯特谱 (a.00—01时,b.05—06时;c.12—13时) Fig. 3 Horizontal longitudinal speed U and the Hilbert spectrum (a. 00:00-01:00,b. 05:00-06:00, c. 12:00-13:00 BT 16 April 2011) |
为了进一步分析某些特定频率波动存在的可能性,对三维希尔伯特谱进行时间积分,得到希尔伯特边际谱。鉴于超声风温仪的采样频率为10 Hz,希尔伯特-黄变换方法所能分辨的最大振动频率为5 Hz。图 4给出了分辨率为2.5×10-3 Hz三个不同时段的希尔伯特边际谱。可以看出,3个时段均显示由低频段到高频段,湍流能量逐渐减小。图 2中内在模函数分量有几个明显的周期波动,如4 min左右的阵风、10—13 min的重力内波均在图中有体现。为了进一步得到低频段的能谱分布,仅对频率大于0.1 Hz的希尔伯特谱进行时间积分,得到低频波段的希尔伯特边际谱,分辨率达到5.0×10-5 Hz(图 5)。可以看出,在10—13 min范围内存在明显的谱峰,对应着重力内波的周期;另一个谱峰位于3—5 min范围内,与阵风的波动周期一致。
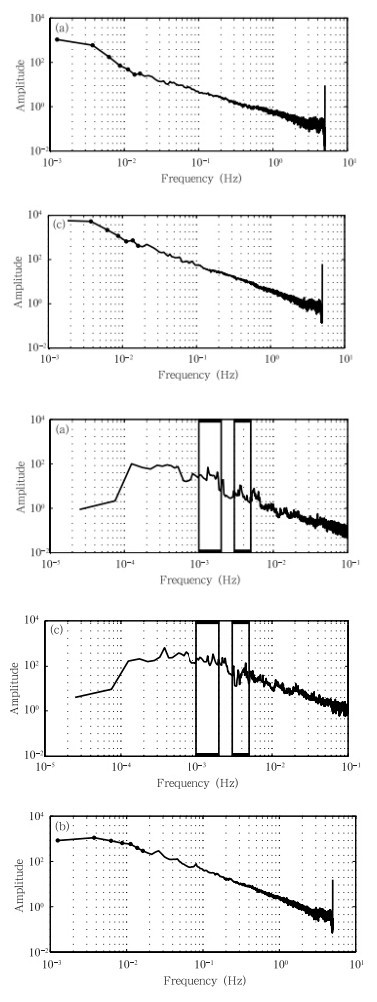 |
| 图 4 科尔沁地区2011年4月16日的希尔伯特边际谱(分辨率为2.5×10-3 Hz) (a. 00—01时,b. 05—06时,c. 12—13时) Fig. 4 Hilbert marginal spectrum with a resolution of 2.5×10-3 Hz (a. 00:00-01:00,b. 05:00-06:00,c. 12:00-13:00 BT 16 April 2011) |
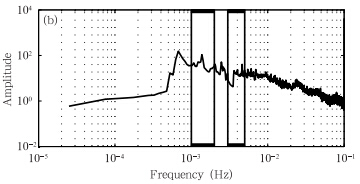 |
| 图 5 科尔沁地区2011年4月16日的希尔伯特边际谱(分辨率为5×10-5 Hz) (a. 00—01时,b. 05—06时,c. 12—13时;矩形框内的频段为10—13和3—5 min的振动周期) Fig. 5 Hilbert marginal spectrum with aresolution of 5×10-5 Hz (a. 00:00-01:00,b. 05:00-06:00,c. 12:00-13:00 BT 16 April 2011. Rectangles manifest the b and s of 10-13 min and 3-5 min) |
为了验证希尔伯特-黄变换在大气湍流研究中的可靠性,对2011年4月14—18日00、05、12时共15 h的U、V、W、T湍流数据分别进行希尔伯特-黄变换,也得到了相似的结果(图略)。
希尔伯特-黄变换方法与传统的频谱分析方法最大的区别在于前者没有特定的基函数,而是根据信号本身的变化自动适应分析过程,避免了固定的基函数引入的虚假波动分量。作为对比,以科尔沁地区2011年4月16日00—01时的水平纵向风速为例,图 6给出了希尔伯特-黄变换和快速傅里叶变换(FFT)结果的对比。由于湍流数据的有限采样时间间隔和采样长度对湍流统计量有一定的影响,对湍流谱作了相应修正(张宏升等,2001)。因为希尔伯特边际谱中某一频率的能量仅仅意味着在信号的局地有存在该频率波动的可能性,所以,希尔伯特边际谱中的能量和傅里叶分析中的能量意义不同,两者不具有可比性。本研究仅仅对比不同方法得到的频谱分布形态,可以看出,在快速傅里叶变换能谱中峰值波段被噪声信号所掩盖,希尔伯特边际谱能更有效地提取出湍流谱信息。
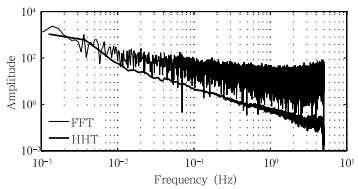 |
| 图 6 科尔沁地区2011年4月16日00—01时希尔伯特-黄变换和快速傅里叶变换计算的能谱对比 Fig. 6 Comparison of energy spectrums between HHT and FFT in the Horqin s and y l and during 00:00-01:00 BT 16 April 2011 |
湍流信号处理和分析的傅里叶方法与小波变换方法对于非线性、非均匀信号具有一定的局限性。希尔伯特-黄变换是一种能自适应地将非平稳、非线性信号分解成单分量信号的经验算法,适用于研究非平稳、非线性的大气湍流问题。利用希尔伯特-黄变换技术对中国北方科尔沁地区2011年4月16日午夜、日出和正午不同时段的湍流探测数据进行分析,得到:
(1)经验模态分解过程将原始的湍流信号分解成一系列单分量的内在模函数,与原始信号中的强波动信号相对应,各内在模函数分量在相应的时段内也具有较强的振幅;内在模函数中存在着周期约为4和13 min的波动,对应了阵风和重力内波的振动周期,并在希尔伯特边际谱中体现。
(2)三维希尔伯特谱同时反映了湍流信号能量在时域和频域上的变化。总体上,能量大都集中在频率小于0.5 Hz的低频波段。在原始信号和内在模函数分量中存在较大波动的时段,希尔伯特谱也对应着相对较大的能量。
(3)希尔伯特边际谱相当于传统的快速傅里叶变换计算的能量谱。从希尔伯特边际谱可以看出,受到阵风和重力内波的影响,在3—5和10—13 min周期的波段内边际谱存在着明显的谱峰。
作为一个非平稳、非线性信号的分析工具,希尔伯特-黄变换具有很好的完备性、正交性、局地性和自适应性。需要说明的是,虽然希尔伯特-黄变换具有一定的优势,但由于是一种经验的分析方法,还存在一些问题亟待解决。第一,经验模态分解过程得到的各内在模函数分量并不是严格意义上的单模态信号,存在一定程度的模态混叠。Huang等(1999)提出通过限制内在模函数分量的最小频率来解决模态混叠;Yang 等(2003a,2003b)建议用傅里叶变换筛选信号中的主要成分,先做带通滤波后再进行经验模态分解过程;Chen等(2003)提出了一种适用于自由衰减信号的解决方法。第二,端点效应。有两种解决思路,一是改进样条函数;二是对信号两端的数据进行延拓。除了本研究使用的镜像延拓法(Zhao et al,1999)外,目前广泛应用的还有神经网络延拓法(Deng,2001),多项式拟合延拓,利用自回归模型进行延拓,信号包络的极值延拓和平行直线延拓法(熊学军等,2002)等。第三,包络拟合方法。前文提到的若干种包络拟合方法如三次样条插值、线性插值、多项式插值和阿克玛插值,在实际应用中都存在一定程度的缺陷,为了得到更接近真实的包络线需要引入更高效的插值方法。第四,希尔伯特-黄变换结果与信号采样频率关系方面的研究有待进一步深入。
致谢:感谢中国科学院大气物理研究所高守亭研究员的鼓励和指导。感谢北京大学物理学院李晓岚博士提供观测资料。
| 卞林根, 陆龙骅, 陈彦杰等. 2001. 青藏高原东南部昌都地区近地层湍流输送的观测研究. 应用气象学报, 12(1): 1-13 |
| 陈子赟, 孙鉴泞, 袁仁民等. 2004. 对流槽湍流涡旋结构特征的小波分析. 地球物理学报, 47(6): 964-970 |
| 程雪玲, 曾庆存, 胡非等. 2007. 大气边界层强风的阵性和相干结构. 气候与环境研究, 12(3): 227-243 |
| 邓伟涛, 孙照渤, 倪东鸿等. 2008. 夏季北半球环状模态及其周期分析. 南京气象学院学报, 31(4): 539-545 |
| 董双林. 2001. 中国的阵风极值及其统计研究. 气象学报, 59(3): 327-333 |
| 高志球, 苏中波, 王介民等. 1999. 不同下垫面大气边界层湍流的混沌特性研究. 南京气象学院学报, 22(4): 680-684 |
| 胡非. 1998. 大气边界层湍流涡旋结构的小波分解. 气候与环境研究, 3(2): 97-105 |
| 胡非, 程雪玲, 赵松年等. 2005. 城市冠层中温度脉动的硬湍流特性和相似性级串模型. 中国科学(D辑: 地球科学), 35(增刊): 66-72 |
| 李倩, 刘辉志, 胡非等. 2004. 大风天气下北京城市边界层阵风结构特征. 中国科学院研究生院学报, 21(1): 40-44 |
| 李晓岚, 张宏升. 2012. 内蒙古科尔沁沙地起沙近地层动力学阈值的试验研究. 高原气象, 31(1): 38-46 |
| 李英, 李跃清, 赵兴炳. 2009. 青藏高原东坡理塘地区近地层湍流通量与微气象特征研究. 气象学报, 67(3): 417-425 |
| 刘辉志, 洪钟祥, 张宏升等. 2003. 内蒙古奈曼流动沙丘下垫面湍流输送特征初步研究. 大气科学, 27(3): 389-398 |
| 刘辉志, 冯健武, 邹捍等. 2007. 青藏高原珠峰绒布河谷地区近地层湍流输送特征. 高原气象, 26(6): 1123-1140 |
| 刘鹏飞, 刘树华, 胡非等. 2010. 湍流通量计算方法和误差的比较研究. 气象学报, 68(4): 487-500 |
| 刘树华, 文平辉, 张云雁等. 2001. 陆面过程和大气边界层相互作用敏感性实验. 气象学报, 59(5): 533-548 |
| 吕乃平, 李兴生. 1985. 稳定大气边界层中风向脉动的特征. 气象学报, 43(3): 35-44 |
| 秦旭, 张讲社, 延晓冬. 2009. 基于改进的EMD的运城市持续极端气温的初步分析. 大气科学学报, 32(5): 645-651 |
| 全利红, 胡非, 程雪玲. 2007a. 用小波系数谱方法分析湍流湿度脉动的相干结构. 大气科学, 31(1): 57-63 |
| 全利红, 胡非, 王迎春. 2007b. 强天气过程中近地面层风速的非线性动力学特征. 气候与环境研究, 12(3): 287-295 |
| 宋丽莉, 吴战平, 秦鹏等. 2009. 复杂山地近地层强风特性分析. 气象学报, 67(3): 452-460 |
| 孙勇, 卢晓亭, 程健. 2009. HHT方法在海水温度时间序列分析中的应用. 声学技术, 28(6): 4-7 |
| 谭为民, 彭东林, 郭小渝. 2003. 三种典型信号处理方法浅析. 测控技术, 22(6): 15-22 |
| 万仕全, 封国林, 周国华等. 2005. 基于EMD方法的观测数据信息提取与预测研究. 气象学报, 63(4): 516-525 |
| 汪璇, 曹万强. 2008. Hilbert变换及其基本性质分析. 湖北大学学报(自然科学版), 30(1): 53-55 |
| 王存忠, 曹文俊. 1994. 天津市郊大气边界层湍谱特征分析. 气象学报, 52(4): 484-491 |
| 王介民. 1992. 山谷城市的近地层大气湍流谱特征. 大气科学, 16(1): 11-17 |
| 王玉平, 蔡元龙, 耿中行. 1996. 基于小波变换的滤波方法. 信息与控制, 25(4): 235-241 |
| 文鸿雁, 张正禄. 2006. 小波分析与傅里叶变换相结合在探测周期性变形中的应用. 测绘通报, (3): 18-21 |
| 熊学军, 郭炳火, 胡筱敏等. 2002. EMD方法和Hilbert谱分析法的应用与探讨. 黄渤海海洋, 20(2): 12-21 |
| 许丽人, 李宗恺, 张宏升. 2000. 不同下垫面上近地层湍流的多尺度属性研究. 气象学报, 58(1): 83-94 |
| 张宏升, 康凌, 张霭琛. 2001. 大气湍流数据处理系统及计算方法的讨论. 气象水文海洋仪器, (1): 1-11 |
| 张强, 王胜. 2008. 西北干旱区夏季大气边界层结构及其陆面过程特征. 气象学报, 66(4): 599-608 |
| 张瑞, 汪亚平, 潘少明. 2011. 近50年来长江入海径流量对太平洋年代际震荡变化的响应. 海洋通报, 30(5): 572-577 |
| 张艳武, 黄静, 吴统文. 2009. 黑河下游额济纳绿洲近地层湍流输送特征研究. 气象学报, 67(3): 433-441 |
| 钟佑明, 金涛, 秦树人. 2005. 希尔伯特-黄变换中的一种新包络线算法. 数据采集与处理, 20(1): 13-17 |
| 周林, 夏雪, 万蕴杰等. 2006. 基于小波变换的谐波测量方法综述. 电子技术学报, 21(9): 67-74 |
| Abarca-Del-Rio R, Mestre O. 2006. Decadal to secular time scales variability in temperature measurements over France. Geophys Res Lett, 33: L13705, doi: 10.1029/2006GL026019 |
| Barbarossa S. 1995. Analysis of multicomponent LFM signals by a combined Wigner-Hough transform. IEEE Trans Signal Processing, 43(6): 1511-1515 |
| Businger J A, Wyngaard J C, Izumi Y, et al. 1971. Flux-profile relationships in the atmospheric surface layer. J Atmos Sci, 28(2): 181-189 |
| Chen Y B, Feng M Q. 2003. A technique to improve the empirical mode decomposition in the Hilbert-Huang transform. Earthquake Engineering and Engineering Vibration, 2(1): 75-85 |
| Cohen L. 1995. Time-Frequency Analysis. New Jersey: Prentice Hall PTR |
| Deng Y J, Wang W, Qian C C, et al. 2001. Boundary processing technique in EMD method and Hilbert transform. Chinese Sci Bull, 46(11): 954-961 |
| Einaudi F, Bedard A J Jr, Finnigan J J. 1989. A climatology of gravity waves and other coherent disturbances at the boulder atmospheric observatory during March-April 1984. J Atmos Sci, 46(3): 303-329 |
| Einaudi F, Finnigan J J. 1993. Wave-turbulence dynamics in the stably stratified boundary layer. J Atmos Sci, 50(13): 1841-1864 |
| El-Askary H, Sarkar S, Chiu L, et al. 2004. Rain gauge derived precipitation variability over Virginia and its relation with the El Nino Southern Oscillation. Adv Space Res, 33(3): 338-342 |
| Finnigan J J, Einaudi F, Fua D. 1984. The interaction between an internal gravity wave and turbulence in the stably-stratified nocturnal boundary layer. J Atmos Sci, 41(16): 2409-2436 |
| Finnigan J J. 1988. Kinetic energy transfer between internal gravity waves and turbulence. J Atmos Sci, 45(3): 486-505 |
| Gabor D. 1946. Theory of communication: Part 1: The analysis of information. J Institution of Electrical Engineers-Part Ⅲ: Radio and Communication Engineering, 93(26): 429-457 |
| Gloersen P, Huang N E. 2004. Interannual waves in the sea surface temperatures of the Pacific Ocean. Int J Remote Sens, 25(7-8): 1325-1330 |
| Haugen D A, Kaimal J C, Bradley E F. 1971. An experimental study of Reynolds stress and heat flux in the atmospheric surface layer. Quart J Roy Meteor Soc, 97(412): 168-180 |
| Huang N E, Shen Z, Long S R, et al. 1998. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc Roy Soc, 454(1971): 903-955 |
| Huang N E, Shen Z, Long S R. 1999. A new view of nonlinear water waves: the Hilbert spectrum. Annu Rev Fluid Mech, 31(1): 417-457 |
| Iyengar R N, Kanth S T G R. 2006. Forecasting of seasonal monsoon rainfall at subdivision level. Current Sci, 91(3): 350-356 |
| Janosi I M, MÜller R. 2005. Empirical mode decomposition and correlation properties of long daily ozone records. Phys Rev E, 71(5): 56126, doi: 10.1103/PhysRevE.71.056126 |
| Kaimal J C, Wyngaard J C, Izumi Y, et al. 1972. Spectral characteristics of surface-layer turbulence. Quart J Roy Meteor Soc, 98(417): 563-589 |
| Karipot A, Leclerc M Y, Zhang G. 2009. Characteristics of nocturnal low-level jets observed in the north Florida area. Mon Wea Rev, 137(8): 2605-2621 |
| Lundquist J K. 2003. Intermittent and elliptical inertial oscillations in the atmospheric boundary layer. J Atmos Sci, 60(21): 2661-2673 |
| Molla M K I, Rahman M S, Sumi A, et al. 2006. Empirical mode decomposition analysis of climate changes with special reference to rainfall data. Discrete Dyn Nature Soc |
| Peel M C, McMahon T A. 2006. Recent frequency component changes in interannual climate variability. Geophys Res Lett, 33(16): L16810, doi: 10.1029/2006GL025670 |
| Poulos G S, Blumen W, Fritts D C, et al. 2002. A comprehensive investigation of the stable nocturnal boundary layer. Bull Amer Meteor Soc, 83(4): 555-581 |
| Rilling G, Flandrin P, Goncalvès P. 2003. On empirical mode decomposition and its algorithms. IEEE-EURASIP Workshop on Nonlinear Signal and Image Processing NSIP, 3: 8-11 |
| Stull R B. 1988. An Introduction to Boundary Layer Meteorology. New York: Kluwer Academic Publishers, 218pp |
| Tatli H, Dalfes H N, Mentes S S. 2005. Surface air temperature variability over Turkey and its connection to large-scale upper air circulation via multivariate techniques. Int J Climatol, 25(3): 331-350 |
| Vincent C L, Giebel G, Pinson P, et al. 2010. Resolving nonstationary spectral information in wind speed time series using the Hilbert-Huang transform. J Appl Meteor Climatol, 49: 253-267 |
| Vincent C L, Giebel G, Pinson P. 2011. Wind fluctuations over the North Sea. Int J Climatol, 31(11): 1584-1595 |
| Wyngaard J C, Coté O R, Izumi Y. 1971. Local free convection, similarity, and the budgets of shear stress and heat flux. J Atmos Sci, 28(7): 1171-1182 |
| Xie L A, Pietrafesa L J, Wu K J. 2002. Interannual and decadal variability of landfalling tropical cyclones in the southeast coastal states of the United States. Adv Atmos Sci, 19(4): 677-686 |
| Yang J N, Lei Y, Pan S W, et al. 2003a. System identification of linear structures based on Hilbert-Huang Spectral analysis. Part 1: normal modes. Earthquake Engineering Structural Dyn, 32(9): 1443-1467 |
| Yang J N, Lei Y, Pan S W, et al. 2003b. System identification of linear structures based on Hilbert-Huang Spectral analysis. Part 2: complex modes. Earthquake Engineering Structural Dyn, 32(10): 1533-1554 |
| Zhang H S, Chen J Y, Park S U. 2001. Turbulence structure in unstable conditions over various surfaces. Bound Layer Meteor, 100(2): 243-261 |
| Zhao J P, Huang D J. 1999. Mirror extending and circular spline function for empirical mode decomposition method. J Zhejiang Univ, 2(3): 247-252 |
 2013, Vol. 71
2013, Vol. 71


