中国气象学会主办。
文章信息
- 张芳, 董敏, 吴统文. 2014.
- ZHANG Fang, DONG Min, WU Tongwen. 2014.
- CMIP5模式对ENSO现象的模拟能力评估
- Evaluation of the ENSO features simulations as done by the CMIP5 models
- 气象学报, 72(1): 30-48
- Acta Meteorologica Sinica, 72(1): 30-48.
- http://dx.doi.org/10.11676/qxxb2014.011
-
文章历史
- 收稿日期:2013-05-15
- 改回日期:2013-10-22
1 引 言
厄尔尼诺-南方涛动(ENSO)是全球气候系统中最显著的年际变化现象,尽管其发生于热带,但对全球的天气和气候都会产生影响,例如,干旱、洪涝及台风(热带风暴)等(王小玲等,2009;Lin,et al,2009)。研究ENSO现象的机制,预测厄尔尼诺、拉尼娜的发生、发展和相互转换具有极其重要的科学价值和社会效益,因此,ENSO现象的研究受到中外科学家的广泛关注(Trenberth,et al,2002;李崇银等,2008;任福民等,2012)。
海-气耦合模式是研究ENSO机制和预测ENSO现象的有效工具,也是研究气候变化的重要手段,各国气象学家都在为海-气耦合模式的发展和完善进行着不懈的努力。中国国家气候中心也在2005年开始研发第2代气候系统模式(Wu,et al,2008,2010,2013;Wu,2012;吴统文等,2014),并对模式的性能进行了多方的评估和应用(董敏等,2009;王璐等,2009;陈海山等,2011;高峰等,2012;张莉等,2013)。为了给耦合模式的评估和后续发展提供一个重要的平台,世界气候研究计划(WCRP)发起了国际耦合模式比较计划(CMIP)。在经历了CMIP1、CMIP2和CMIP3 几个阶段之后,于2008年9月启动了第5阶段试验计划(CMIP5)(Taylor,et al,2012)。中国国家气候中心气候系统模式BCC_CSM1.1和BCC_CSM1.1m也参与了这一计划(Wu,et al,2013;辛晓歌等,2012)。CMIP5计划提供了大量模式试验的最新成果,试验的评估研究将为政府间气候变化委员会(IPCC)第5次评估报告(AR5,计划在2013年发布)提供有价值的科学参考信息。同时CMIP5试验也为ENSO模拟研究提供了良好条件。
近10年来,海-气耦合模式在模拟和对ENSO进行季节预测方面已取得了长足进步。模式中物理过程参数化更加复杂和完善,模式的水平和垂直分辨率变得更精细,使用模式进行预测时,初始场的同化方案更加完整。这些使对ENSO的模拟得到了进一步的改进(Randall,et al,2007;AchutaRao,et al,2002,2006),模拟的中东太平洋海表温度距平的分布型更加接近实际,不仅模拟的基本气候态及季节变化与观测大体一致,模拟的厄尔尼诺现象的周期也与观测大体一致,而且能在一定程度上模拟出ENSO现象的年际变化(Guilyardi,et al,2009b)。
尽管如此,正如IPCC 第4次评估报告所指出的,模式模拟的ENSO与现实世界的ENSO现象相比,无论是气候背景场还是变率仍然存在着严重的、系统性的误差(van Oldenborgh,et al,2005;Capotondi,et al,2006;Guilyardi,2006;Wittenberg,et al,2006;Watanabe,et al,2010;Stevenson,2012;Yeh,et al,2012)。而造成这些问题的原因可能与对流参数化方案、信风强度的模拟、云反馈过程等有关(Braconnot,et al,2007;L′Ecuyer,et al,2007;Guilyardi,et al,2009a;Lloyd,et al,2009,2011;Sun,et al,2009;Zhang,et al,2012)。此外,尽管各种模式具有一些共同的问题,但模式的差异仍很大,且不同模式的差异比历史上曾经出现的不同的ENSO事件的差异还要大。所有这些问题均需要进一步研发解决。
CMIP5试验在2012年起陆续完成,同时开始针对ENSO现象对CMIP5模式进行评估。Bellenger等(2013)指出,尽管CMIP5模式与CMIP3相比在ENSO现象的模拟上没有质的飞跃,但CMIP5模式模拟的ENSO的振幅却不像CMIP3模式那样分散。65%的CMIP5模式模拟的ENSO振幅与观测值相差在25%以内,而CMIP3模式模拟的ENSO振幅与观测值相差则在50%以内。CMIP5模式模拟的ENSO生命周期及锁相也均比CMIP3略有改进。在热带太平洋平均海表温度和赤道太平洋纬向风应力的模拟方面,CMIP5模式也比CMIP3有所改进。Zhang等(2012,2013)检查了CMIP5模式模拟的厄尔尼诺发生时海温距平场的经向宽度,指出虽然CMIP5模式模拟的海温距平带要比实际狭窄,但比CMIP3模式略有改进。并指出这种改进与信风模拟的改善及ENSO周期性模拟的改善密切相关。Kim等(2012)评估了CMIP5模式对东太平洋型和中太平洋型两种不同的厄尔尼诺现象的模拟能力,同时也给出了3种试验,即工业革命前试验、历史试验和温室气体代表性浓度路径4.5(RCP4.5)的结果比较。Yeh等(2012)用CMIP5模式历史试验的集合结果研究了东太平洋热带海温的趋势及ENSO振幅并与CMIP3的结果进行比较。结果显示海温趋势的量级从CMIP3到CMIP5有明显的减小。这可能与CMIP5模式较高地估计了自然强迫和气溶胶的作用有关,因为CMIP5中有更多的模式是地球系统模式。此外,在20世纪的后半段海温距平的空间分布在CMIP3中是拉尼娜型,而在CMIP5则变成厄尔尼诺型。
当前有关ENSO的模拟研究和模式验证工作缺少对热带地区海温时空演变的分析;也缺少对反映ENSO的另一面,即热带太平洋地区大气南方涛动变化特征的模拟分析以及海洋和大气关系的分析。本研究将重点针对热带太平洋海温和大气海平面气压的时空分布及其演变特征,以及两者的相互关联,评估参与CMIP5的气候模式在ENSO现象模拟方面的能力和不足,为改进气候系统模式提供一些依据。
2 模式、资料和方法本研究采用了参加CIMP5计划的17个海-气耦合模式对20世纪历史气候的模拟(即CMIP5的 历史试验)的输出结果,各模式分辨率见表 1。
| 模式名称 | 所属国家和研究单位 | 大气模式分辨率 | 海洋模式分辨率 |
| BCC_CSM1.1 | 国家气候中心(中国) | T42(2.8°×2.8°)L26 | (0.3°—1.0°)×1.0°L40 |
| BCC_CSM1.1m | 国家气候中心(中国) | T106(1.1°×1.1°)L26 | (0.3°—1.0°)×1.0°L40 |
| CanESM2 | CCCma(加拿大) | T63(1.9°×1.9°)L35 | 0.9°×1.4°L40 |
| CCSM4 | NCAR(美国) | 0.9°×1.25°L27 | (0.3°—0.6°)×1.1°L60 |
| CNRM-CM5 | CNRM(法国) | TL127(1.4°×1.4°)L31 | 0.7°L42 |
| CSIRO-Mk3-6-0 | CSIRO(澳大利亚) | T63(1.9°×1.9°)L18 | 0.9°×1.875°L31 |
| FGOALS-g2 | 中国科学院大气物理研究所和清华大学(中国) | 2.8125°×3°L26 | (0.5°—1.0°)×1°L30 |
| FGOALS-s2 | 中国科学院大气物理研究所(中国) | R42(1.7°×2.8°)L26 | (0.5°—1.0°)×1°,L30 |
| GFDL-ESM2M | GFDL/NOAA(美国) | M45(2.0°×2.5°)L24 | 1°×1°L50 |
| GISS-E2-R | GISS/NASA(美国) | 2°×2.5°L40 | 1°×1.25°L32 |
| HadGEM2-CC | Hadley Centre(英国) | N96(1.25°×1.9°)L60 | (0.3°—1.0°)×1.0°L40 |
| inmcm4 | INM(俄罗斯) | 1.5°×2.0°L21 | 0.5°×1.0°L40 |
| IPSL-CM5A-LR | IPSL(法国) | 1.9°×3.75°L39 | (0.5°—2°)×2°L31 |
| MIROC5 | AORI/NIES/JAMSTE(日本) | T85(1.4°×1.4°)L40 | (0.5°—1.4°)×1.4°L50 |
| MPI-ESM-LR | MPI(德国) | T63(1.9°×1.9°)L47 | GR15(1.5°)L40 |
| MRI-CGCM3 | MRI(日本) | TL159(1.15°×1.1°)L48 | 0.5°×1°L51 |
| NorESM1-M | NCC(挪威) | F19(1.9°×2.5°)L26 | 1.125°L53 |
各个模式试验的详情见http://www.earthsystemgrid.org/search.html。各模式都按统一的试验方案进行模拟试验。首先,将温室气体等外强迫固定在工业革命前的状态运行模式数百年(各模式运行的时间可能不同,但多在500年以上)使模式达到平衡,然后在给定的1850—2005年实际观测的温室气体、气溶胶、火山灰等外强迫资料及太阳常数等条件下,从1850年大气-海洋的初始状态开始运行至2005年。本研究重点评估1958—2001年的全球月平均海表温度和海平面气压的模拟试验结果,为验证模式的模拟结果,选用同期的欧洲中心ERA-40再分析资料的海平面气压场(Kallberg,et al,2005)和全球海冰及海温数据集(GISST)的海表温度资料(Rayner,et al,1996)与模式输出进行对比分析。
3 结果分析 3.1 海温气候平均特征的模拟从17个模式模拟的热带海温气候平均场与观测场的差值分布(图 1)可以看出,参加CMIP5计划的模式绝大多数可以较好地模拟出热带海温的气候平均态。图中左列第1行多模式集合(MME)代表所有模式模拟结果的平均值与观测的误差。平均来看,模式与观测的海温相差约为-2—2℃,而大多数地方为-1—1℃。在160°E—115°W赤道附近的狭长地区为-1—-2℃的冷偏差,这说明模式模拟的赤道东太平洋地区的冷舌比观测的略强。在赤道以南的东太平洋上存在一片正偏差区,靠近南美西岸的地方正偏差达1—2℃。在赤道以北的东太平洋上也存在一片正偏差区,与赤道以南的正偏差区几乎呈对称分布,但其范围要小得多,强度也弱一些。在20°—30°N的北太平洋上有明显的负偏差,其中心可达-2—-3℃。在30°S以南的南太平洋上有1℃以内的正偏差。印度洋海温模拟的误差较小,除马达加斯加岛以北的印度洋西部和30°S以南的地方有1℃以内的正偏差以外,其他地方的误差为-1℃以内。
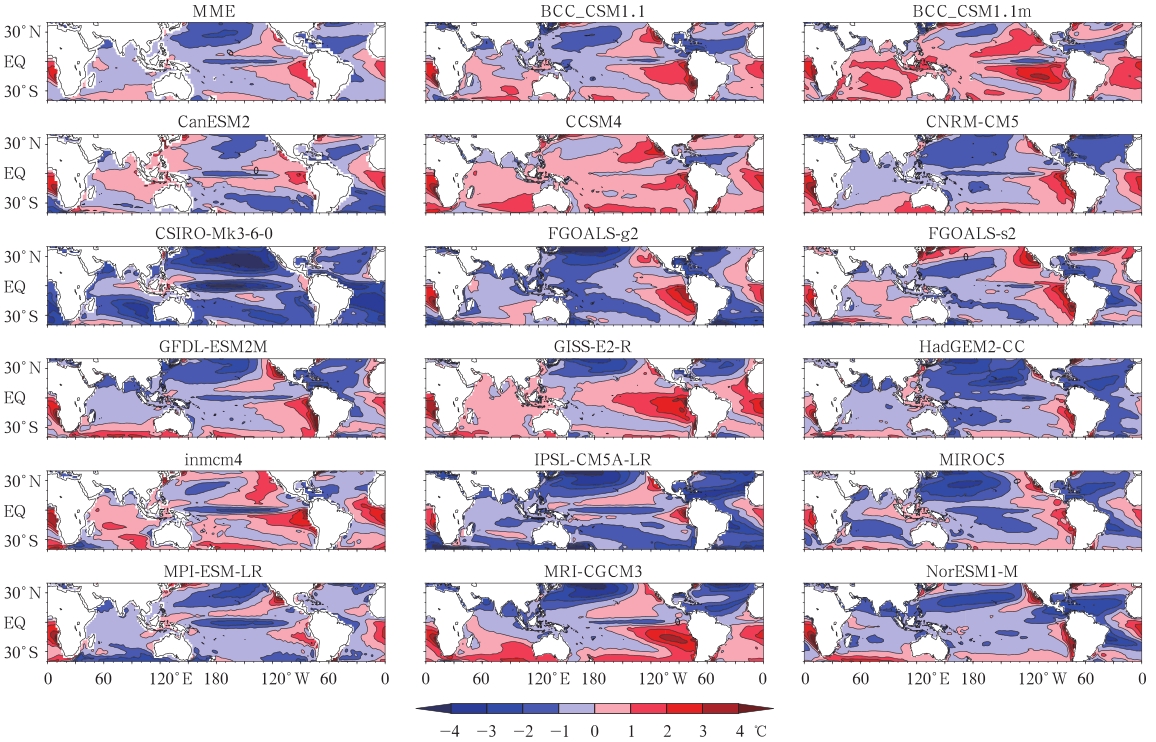 |
| 图 1 模式模拟1958—2001年海温气候平均场与GISST观测气候的偏差(模式的名称标在每个图的上方,下同) Fig. 1 Biases of the simulated and observed(GISST)SST averaged over 1958 to 2001(The model name is labeled at the top of each panel; the same below) |
从图 1还可以明显地看出各个模式模拟的误差 是不一样的。其中,BCC_CSM1.1、CNRM-CM5模式的误差分布与MME比较接近,但两者均在东太平洋的赤道南北两侧、南太平洋、南印度洋有比多模式平均更高的误差。在所有模式中,CSIRO-Mk3-6-0模式和IPSL-CM5-LR以及HadGEM2-CC偏冷最明显,而GISS-E2-R、CCSM4和BCC_CSM1.1m则明显偏暖。
表 2给出所有模式在20°S—20°N和10°S—10°N及Nino3.4区模拟与观测月平均海温的均方根误差,同时也给出了模式模拟的Nino3.4指数与观测的Nino3.4指数本身的均方差。可以看出,CCSM4、BCC_CSM1.1和CanESM2模拟的热带平均海温的误差较小,模式与观测的均方根误差在1.3℃以下,而CSIRO_Mk-3-6-0、BCC_CSM1.1m、GFDL-ESM2M和NorESM1-M的均方根误差则超过1.47℃,包括两个FGOALS在内的其他模式的误差处于中间水平。值得注意的是,BCC_CSM1.1m与BCC_CSM1.1模式在所有物理过程和动力过程上都是一样的,只是分辨率有所不同。BCC_CSM1.1m 模拟的热带太平洋海温及Nino3.4指数的误差比BCC_CSM1.1模式还大,说明要改进模式模拟ENSO的能力仅仅提高分辨率是不够的。
| 模式 | 海温均方根误差 | Nino3.4指数均方差 | ||
| 10°S—10°N | 20°S—20°N | Nino3.4区 | ||
| MME | 0.984 | 0.991 | 1.283 | 0.776 |
| BCC_CSM1.1 | 1.241 | 1.294 | 1.641 | 0.812 |
| BCC_CSM1.1m | 1.504 | 1.483 | 1.980 | 1.425 |
| CanESM2 | 1.237 | 1.147 | 1.735 | 1.343 |
| CCSM4 | 1.268 | 1.238 | 1.379 | 1.186 |
| CNRM-CM5 | 1.399 | 1.441 | 1.638 | 1.418 |
| CSIRO-Mk3-6-0 | 2.011 | 2.024 | 3.259 | 0.849 |
| FGOALS-g2 | 1.442 | 1.469 | 1.406 | 1.763 |
| FGOALS-s2 | 1.358 | 1.393 | 1.894 | 1.180 |
| GFDL-ESM2M | 1.474 | 1.477 | 1.836 | 1.720 |
| GISS-E2-R | 1.535 | 1.408 | 1.815 | 0.902 |
| HadGEM2-CC | 1.317 | 1.484 | 1.833 | 1.741 |
| inmcm4 | 1.573 | 1.392 | 2.026 | 0.725 |
| IPSL-CM5A-LR | 1.417 | 1.561 | 1.832 | 1.820 |
| MIROC5 | 1.413 | 1.461 | 2.010 | 2.886 |
| MPI-ESM-LR | 1.390 | 1.299 | 2.230 | 1.215 |
| MRI-CGCM3 | 1.273 | 1.426 | 1.589 | 0.745 |
| NorESM1-M | 1.473 | 1.625 | 1.609 | 2.081 |
从表 2还可以看出,(1)无论是热带平均海温还是Nino3.4指数,多模式平均的误差要小于单个模式的误差,这是因为各个模式误差的方向是不同的,有正有负。平均之后可抵消一部分误差。因此,这预示多模式集合预报可以改善模拟和预测的结果。(2)计算表明,观测的10°S—10°N、20°S—20°N区域海温的均方差及Nino3.4区海温的均方差分别为0.801、0.727、1.210℃。因此,不论是模拟的热带平均海温还是Nino3.4区海温,其与观测的均方根误差比所模拟的观测量本身的均方差都大。即使多模式平均的误差小一些,但也大于观测量本身的均方差,说明模式仍然需要做进一步的改进。
物理量均方差的大小表示该物理量的变率。计算表明,观测的Nino3.4指数的均方差为0.856,多模式平均的变率小于观测,为0.776℃。在所考察的模式中有13个模式的Nino3.4指数的变率比观测大,4个比观测小。CSIRO-Mk3-6-0、BCC_CSM1.1、CCSM4、CanESM2、GISS-E2-R、inmcm4、MRI-CGCM3、FGOALS-s2和MPI-ESM-LR等9个模式的变率与观测最接近,相差小于0.5℃。BCC _CSM1.1m、GFDL-ESM2M、FGOALS-g2、IPSL-CM5A-LR、CNRM-CM5和HadGEM2-CC等6个模式模拟的Nino3.4指数的变率与观测相差小于1℃,属中等。MIROC5、NorESM1-M模拟的Nino3.4指数的变率与观测相差超过1℃。MIROC5模式的变率最大,达2.886℃,为观测的3倍多,是模拟得较差的。
3.2 热带地区气压场大气与海洋是耦合在一起的一个系统,因此,海洋模拟的误差应该在大气中也有反映。图 2给出各个模式模拟的海平面气压与观测的误差以及多模式平均结果与观测的误差。从多模式平均的误差(图 2中的MME)上可以看出,在160°E—180°的南北纬30°附近的南北太平洋上各有一个1—2 hPa的正偏差。这就导致其与赤道间的气压梯度加大,从而导致赤道北侧的东北信风和南侧的东南信风加强,赤道附近向西的风应力作用使赤道东太平洋冷水西移、海温冷舌西伸以及东赤道地区深层冷水的上翻。此外,在南太平洋的东部,模式模拟的气压场与观测有负偏差,而这在南半球会引起吹向南美大陆的气流偏差,因此有利于产生正的海温偏差。
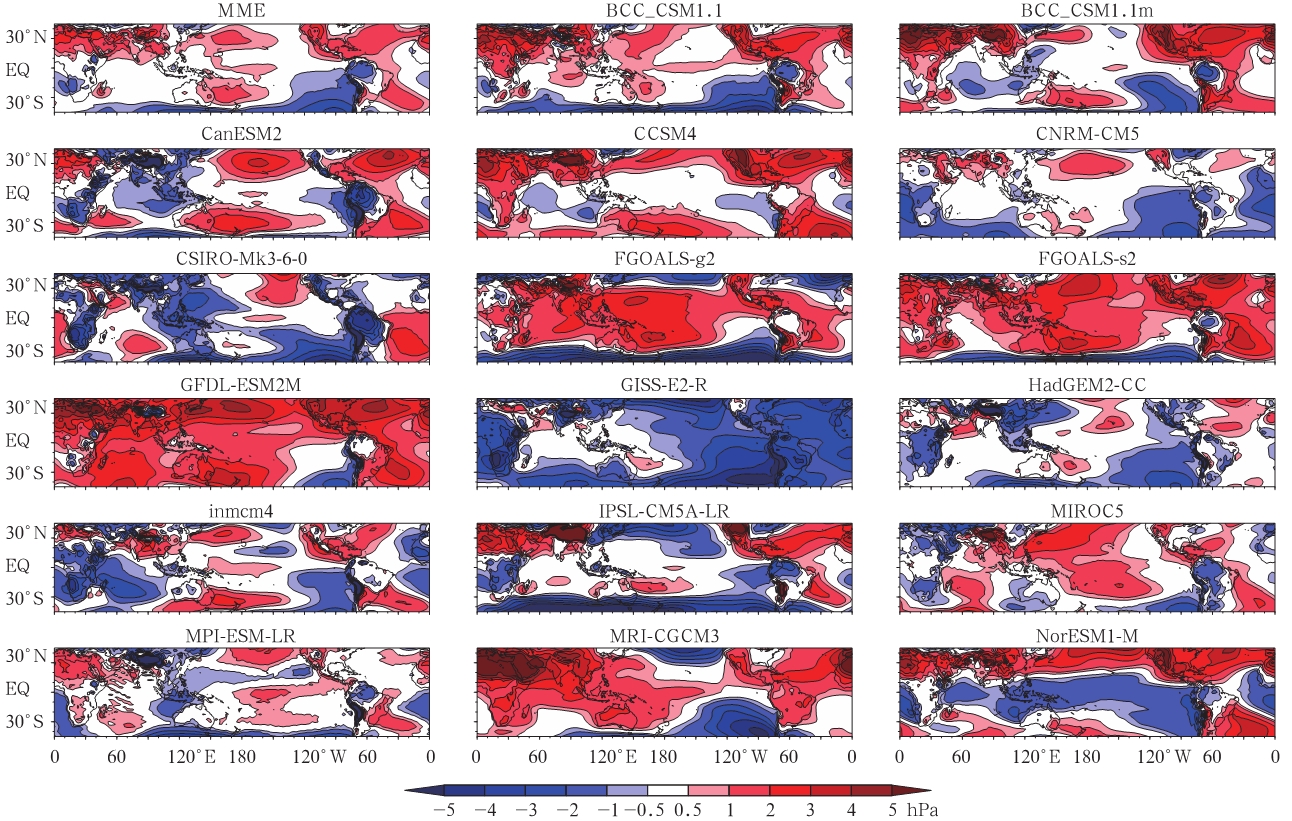 |
| 图 2 CMIP5各模式模拟的1958—2001年平均的海平面气压气候场与相应的ERA-40再分析场的误差空间分布 Fig. 2 Biases of the simulated and observed(ERA-40)sea level pressure averaged over 1958 to 2001 |
上述分析是对多模式平均的模拟结果而言的。而对某个具体模式,海温距平模拟误差与气压距平模拟误差的关系不一定与多模式平均的情况完全一致,需具体情况具体分析。例如,GISS-E2-R模式模拟的海平面气压场在东太平洋的南北半球都是负偏差,且离赤道越远负偏差越大,这就导致在东赤道太平洋地区西风偏差的加大,抑制东太平洋赤道地区海水的上翻,因此会使东太平洋模拟海温升高。
3.3 赤道地区海温季节循环图 3给出了赤道附近(2°S—2°N)多年平均状态下海温的季节变化。观测(OBS)结果显示,赤道海温有明显的半年和1年的周期变化。在西印度洋和西太平洋赤道海温呈半年周期,高温出现在4月和11月,低海温则出现在1月和8月。而东太平洋和大西洋的赤道海温则只有年变化,高温出现在3—4月,而低温则出现在8月。CMIP5模式大体上可以模拟出赤道附近上述海温的季节性变化,但具体细节上有差异。例如,IPSL-CM5-LR、CanESM2、FGOALS-s2、inmcm4等模式模拟的赤道东部海温则表现出半年的周期。
 |
| 图 3 CMIP5各模式模拟的沿赤道地区(2°S—2°N)的海表温度的年循环特征(已扣除1958—2001年多年年平均值)与同期GISST观测值的比较 Fig. 3 Annual cycle of monthly mean SST across the equator averaged over 2°S to 2°N for the observation(GISST) and simulation(the values are the deviations from the annual means over 1958 to 2001) |
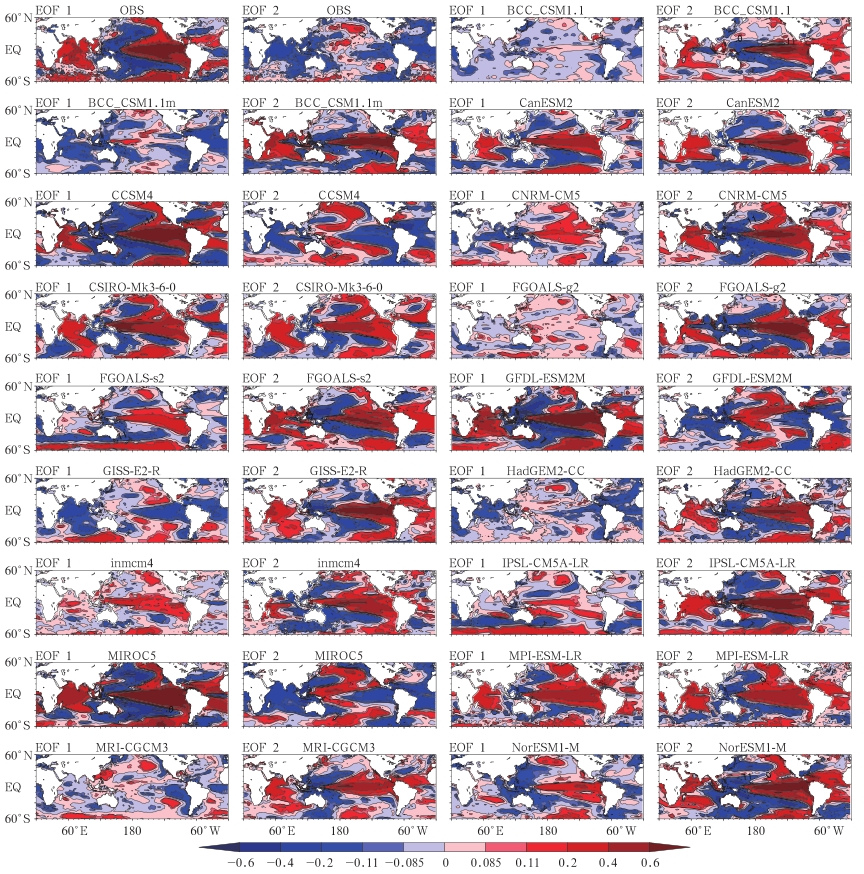
对1958—2001年各月热带太平洋区域(30°S—30°N,120°E—90°W)海温距平进行经验正交函数分解,从而可以了解海温距平场的时空演变特征。图 4给出GISST观测及各模式模拟的海温距平的空间特征向量,图 5则是与之对应的时间系数。观测的GISST海温距平的第1特征向量呈东正西负的分布,正值区从美洲西岸呈楔形向西伸到日界线西侧,而负值区则从印度尼西亚成杈状向东北及东南伸向北太平洋及南太平洋。这一模态与厄尔尼诺发生时热带太平洋海温距平分布型相似,因此,可称为ENSO模态,它可以解释海温距平总方差的25%。观测海温距平的第2特征向量是一个总体上为正值而局部为弱负值的模态。西太平洋热带的正值最大并向东部伸展,但在180°—90°W的赤道附近的一个狭窄的区域存在着弱的负值,此外,在中北太平洋上也有一小块自西南向东北伸展的负值区。由于这一模态是以正值为主,在时间系数的配合下可以反映海温的总体升高或降低,这一模态可称为趋势模态,其方差贡献约为12.7%。表 3中给出了观测及模拟的海温距平两个模态的时间系数的主要周期和随时间变化的趋势,主要周期均通过了0.05信度的红噪声检验,时间变化趋势中通过0.05信度检验的用黑体字表示。从表 3可以看出,观测海温距平的第1模态有4年周期,没有明显的趋势,这与通常所说的ENSO有2—7年周期是一致的,观测海温距平的第2模态有约0.15℃/a的趋势。在模拟的海温距平场的经验正交函数分解中,只有少数模式模拟的海温距平的主要特征向量与观测比较接近。例如CCSM4模拟的第1特征向量为ENSO模态,时间系数有6年的周期,但无明显的趋势,第2特征向量为趋势模态,时间系数有0.16℃/a的明显趋势,这两个特征向量所能解释的总方差比观测的略大,分别为29%和15.7%。这是所有模式中最接近观测的结果。其他大部分模式与观测的上述结果有较大的差异。BCC_CSM1.1模拟的海温距平的第1特征向量是一个总体上为正值的模态,占总方差的20.7%,第2特征向量则是东太平洋为正而西太平洋为负的模态,方差贡献为10.6%,与观测相比第1、第2特征向量的顺序正好相反。结合图 5的时间系数可知,BCC_CSM1.1模拟的海温距平场时空变化的第1特征向量反映的是海温近半个世纪的上升趋势,而第2特征向量则反映了厄尔尼诺-拉尼娜式的振荡变化。与观测相比,模式高估了由于全球变暖引起的海温升高趋势,但低估了ENSO式的振荡现象。与BCC_CSM1.1类似,BCC_CSM1.1m、CanESM2、CSIRO-Mk3-6-0、FGOALS-g2、FGOALS-s2、GISS-E2-R、HadGEM2-CC、inmcm4、IPSL-CM5A-LR、MPI-ESM-LR及NorESM1-M等模式也存在类似的问题。从表 3也可以看出,这些模式海温距平第1模态的时间系数均有正趋势,且都超过了0.05信度的显著性检验。GFDL-ESM2M、MIROC5、MRI-CGCM3、CNRM-CM5等模式模拟的海温距平的第1特征向量虽然与厄尔尼诺模态很接近,但其第2模态不是总体上为正值,而是以负值占优势,对应的时间系数也有负的趋势(表 3),因此,这些模式的第2特征向量反映的也是总体上升趋势,但其趋势达不到0.05信度显著性检验所要求的值。此外,GFDL-ESM2M、MRI-CGCM3、CNRM-CM5的第1模态是有明显趋势的,这也与观测不符。综上所述,只有CCSM4模式模拟的热带海温距平场的时空变化特征较为接近实际,其他模式均与实际有较大差距,需要努力改进。
 |
| 图 4 观测(GISST)和CMIP5各模式模拟的1958—2001年热带太平洋地区海表温度经验正交函数分解的前两个主要模态空间分布(图中左上角EOF1、EOF2分别表示第1、第2模态,右上角百分数表示各模态解释的对应方差贡献值) Fig. 4 First two EOF modes of the observed(GISST) and simulated SST over the tropical Pacific over 1958-2001(EOF1 and EOF2 at the top left of each panel indicate the first EOF mode and the second EOF mode,respectively. Variance explained by each mode is labeled at the top right of each panel) |
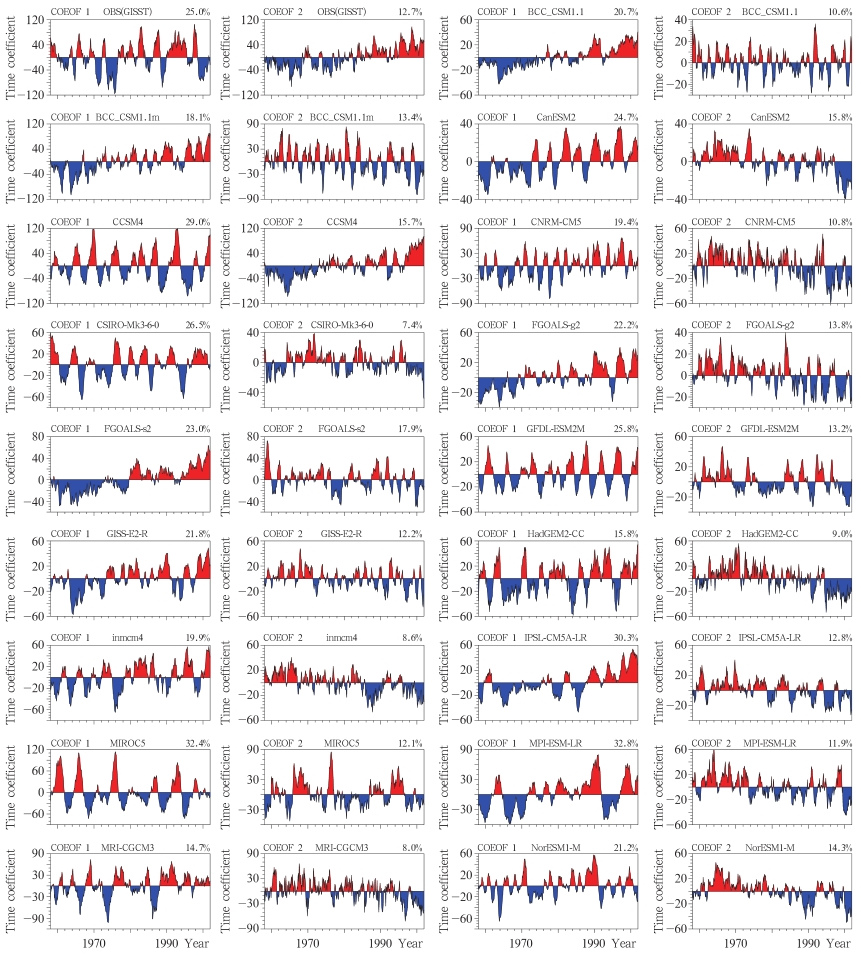 |
| 图 5 观测(GISST)和CMIP5各模式模拟的热带太平洋(30°S—30°N)1958—2001年逐月海表温度的经验正交函数分解前两个模态的时间系数(说明同图 4) Fig. 5 Time series of the first two EOF modes for the observed(GISST) and simulated SST over the tropical Pacific over 1958-2001 |
| 模式 | 海平面气压场 | 海温距平 | ||||||
| 主周期 | 线性趋势 | 主周期 | 线性趋势 | |||||
| 模态1 | 模态2 | 模态1 | 模态2 | 模态1 | 模态2 | 模态1 | 模态2 | |
| OBS | 4.0 | 14.7 | 0.0127 | -0.0274 | 4.0 | 44.0 | 0.0253 | 0.1528 |
| MME | 4.4 | 3.1 | -0.0306 | 0.0202 | 22.0 | 4.4 | 0.4058 | -0.0247 |
| BCC_CSM1.1 | 0.2 | 2.6 | -0.0132 | 0.0027 | 22.0 | 2.59 | 0.0833 | -0.0082 |
| BCC_CSM1.1m | 44.0 | 3.1 | -0.0395 | 0.0055 | 2.75 | 3.14 | 0.1612 | -0.0663 |
| CanESM2 | 4.9 | 4.9 | -0.0094 | -0.0001 | 4.89 | 3.38 | 0.0620 | -0.0503 |
| CCSM4 | 6.3 | 7.3 | -0.0064 | -0.0326 | 6.29 | 44.0 | -0.0027 | 0.1669 |
| CNRM-CM5 | 3.1 | 2.9 | -0.0038 | 0.0197 | 2.93 | 14.67 | 0.0758 | -0.0683 |
| CSIRO-Mk3-6-0 | 4.9 | 4.4 | -0.0011 | 0.0026 | 4.89 | 22.0 | 0.0157 | -0.0101 |
| FGOALS-g2 | 44.0 | 3.4 | 0.0014 | 0.0003 | 11.0 | 3.38 | 0.0734 | -0.0435 |
| FGOALS-s2 | 14.7 | 6.3 | -0.0105 | 0.0034 | 14.67 | 2.2 | 0.1157 | -0.0300 |
| GFDL-ESM2M | 4.4 | 4.4 | 0.0074 | -0.0050 | 4.4 | 5.5 | 0.0214 | -0.0244 |
| GISS-E2-R | 3.1 | 3.1 | -0.0314 | 0.0056 | 11.0 | 2.75 | 0.0620 | -0.0330 |
| HadGEM2-CC | 14.7 | 4.0 | -0.0142 | -0.0037 | 4.89 | 22.0 | 0.0449 | -0.0688 |
| inmcm4 | 8.8 | 44.0 | 0.0077 | 0.0014 | 5.5 | 44.0 | 0.0598 | -0.0615 |
| IPSL-CM5A-LR | 6.3 | 7.3 | -0.0145 | 0.0006 | 14.67 | 4.4 | 0.0825 | -0.0376 |
| MIROC5 | 6.3 | 7.3 | -0.0424 | -0.0191 | 6.29 | 7.33 | -0.0417 | -0.0075 |
| MPI-ESM-LR | 14.7 | 6.3 | -0.0044 | 0.0078 | 14.67 | 3.67 | 0.0844 | -0.0520 |
| MRI-CGCM3 | 2.1 | 3.7 | -0.0336 | 0.0154 | 8.8 | 44.0 | 0.0537 | -0.0685 |
| NorESM1-M | 2.9 | 2.8 | -0.0196 | -0.0030 | 7.33 | 22.0 | 0.0227 | -0.0621 |
与海温场的时空演变相配合,海平面气压场也有相应的时空演变。图 6给出海平面气压场距平经验正交函数分解前两个特征向量的分布,而图 7则是相应的时间系数。同时,为了考察上述两个模态时间系数的周期性和变化趋势,也计算了其周期和线性趋势(表 3)。对观测来说海平面气压场的第1特征向量反映的是热带地区气压的东西振荡。西太平洋(180°E以西)是正值区,而东太平洋则是负值区,配合相应的时间系数,反映东、西太平洋海平面气压场的振荡特征,它与南方涛动一致,这一模态所能解释的方差占总方差的25.4%。观测海平面气压场的第2特征向量具有全部热带太平洋为负值的特征,其中心在中太平洋,这一模态所能解释的方差占总方差的23.0%。由表 3可以看出,海平面气压场的第1模态的时间系数有4年的震荡周期,这与海温距平的变化是一致的。第1模态时间系数的线性趋势是正的,且通过了0.05信度显著性检验,这表明近50年来南方涛动有所加强。
 |
| 图 6 CMIP5各模式模拟的热带太平洋1958—2001年海平面气压场经验正交函数分解的前两个主要模态的空间分布特征和同期ERA-40资料的分析比较(说明同图 4) Fig. 6 First two EOF modes of the observed(ERA-40) and simulated SLP over the tropical Pacific over 1958-2001(the illustration is the same as in Fig. 4) |
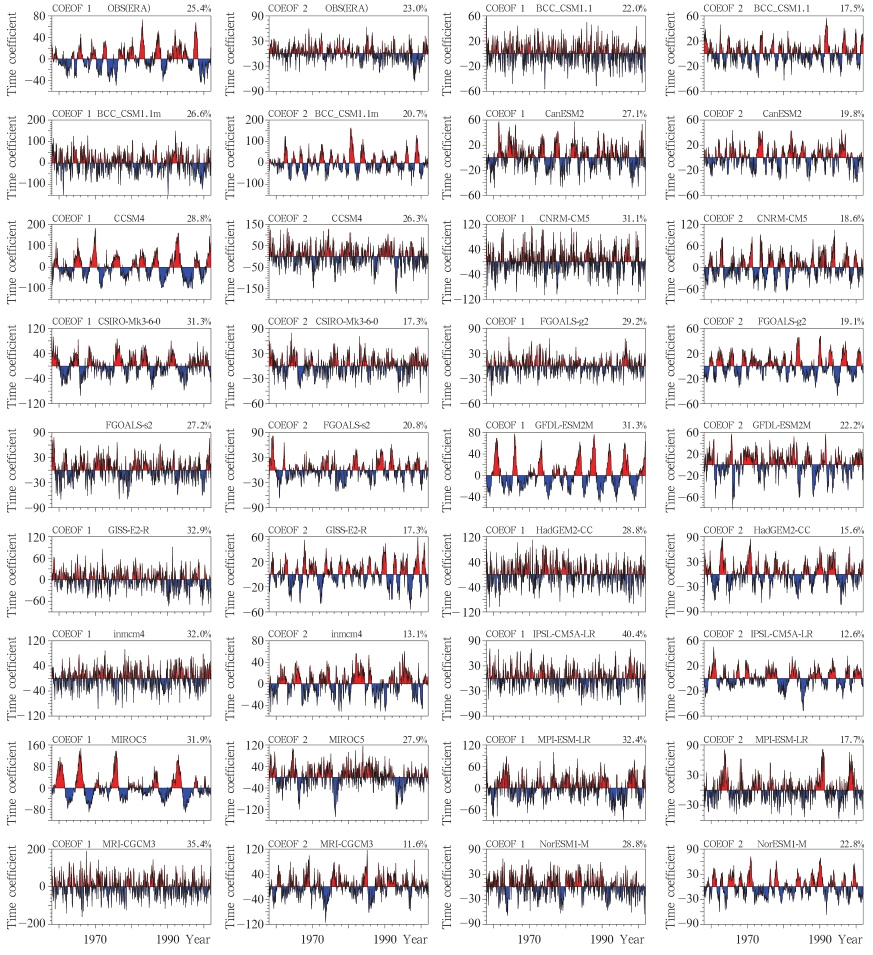 |
| 图 7 观测(ERA-40)和CMIP5各模式模拟的热带太平洋(30°S—30°N)1958—2001年逐月海平面气压的经验正交函数分解前两个模态的时间系数(说明同图 4) Fig. 7 Time series of the first two EOF modes for the observed(ERA-40) and simulated SLP over the tropical Pacific over 1958-2001 |
比较观测和17个模式模拟的海平面气压距平的时空模态发现,少数模式(如CCSM4、GFDL-ESM2M、MIROC5)模拟的海平面气压距平的模态与观测比较接近。即南方涛动模态为主模态,它所能解释的方差为28%—31%,而第2模态是一个负中心形状的分布型,其方差贡献为22.2%—27.9%。其他大多数模式,包括中国国家气候中心的模式所模拟的热带太平洋海平面气压距平场的主要时空模态的顺序与观测相反,即第1特征向量在整个热带太平洋为一个负中心的分布型,与观测海平面气压距平场的第2特征向量一样。而第2特征向量则是西太平洋为正中心而东太平洋为负中心的分布型,这与观测的第1特征向量是一致的。由于第2特征向量所能解释的方差比第1特征向量少,因此,对这些模式来说南方涛动类型的时空变化被低估了。
3.6 大气和海洋之间的相互关联大气与海洋是一个相互作用的耦合系统,在应用海-气耦合模式模拟气候时亦应该能模拟出大气与海洋的关系。众所周知,之所以有ENSO现象的名称正是因为厄尔尼诺现象与南方涛动是紧密联系在一起的。图 8给出了海平面气压距平场的第1、第2两个模态的时间系数与海温距平的相关系数。从前面的分析可知,观测海平面气压场距平的第1特征向量代表的是南方涛动的变化,而海温距平的正负指示的是厄尔尼诺和拉尼娜的交替变化。图 8很好地反映出南方涛动与厄尔尼诺的密切关系,可以看出,海平面气压距平第1模态的系数与热带Nino 3和Nino 4区的海温距平的相关系数达到0.6以上,远超过了信度0.01所要求的临界值,在模式模拟的结果中这种关系也有很好的体现。CCSM4、GFDL-ESM2M、MIROC5等3个模式的第1特征向量能很好地表示海平面气压距平的南方涛动模态,因此,第1特征向量的时间系数与热带地区海温距平有和观测类似的相关关系,即与赤道中东太平洋海温距平有显著的正相关关系,而与西太平洋海温距平为显著的负相关。包括BCC_CSM1.1在内的9个模式其第2特征向量能反映南方涛动的变化,因此,第2特征向量的系数与热带中东太平洋海温距平有显著的正相关,而与西太平洋海温距平则为显著的负相关。另有5个模式(CanESM2、FGOALS-s2、CSIRO-Mk3-6-0、MPI-CGCM3和NorESM1-M),其海平面气压距平场的第1、第2特征向量的系数均与热带海温距平密切相关,赤道中、东太平洋为正相关而与西太平洋海温距平为负相关,但这种相关对第2特征向量更明显。
 |
| 图 8 观测(图左上角)和CMIP5各模式模拟的热带太平洋1958—2001年海平面气压场的经验正交函数分解前两个模态时间系数与同期该区域海温距平的相关系数分布(图中相关系数大于0.11即达到了99%信度水平) Fig. 8 Correlations of the time series of the first two EOF modes for SLP with respect to the SST anomaly for observation(top left) and simulation over 1958-2001(the correlation coefficient larger than 0.11 is significant at the 95% confidence level) |
直接计算南方涛动指数(SOI)与Nino指数的相关系数也可以检验两者的关系,表 4给出观测及CMIP5模式中南方涛动指数与Nino3.4指数的相关系数。可以看出,观测的南方涛动指数与Nino3.4指数的相关系数为0.595。相关系数是基于1876—2003年即128年的1536个样本计算的。显著性检验结果表明,相关系数远大于0.001信度所要求的值,相关是非常显著的。所有CMIP5模式结果中南方涛动指数与Nino 3.4指数的相关系数均在0.3以上,相关系数也远大于0.001信度所要求的值。其中,BCC_CSM1.1m、CCSM4、CNRM-CM5、FGOALS-s2、GFDL-ESM2M、MIROC5和NorESM1-M等7个模式的相关系数在0.5以上。 而BCC_CSM1.1、IPSL-CM5A_LR和MRI-CGCM3的相关系数则为0.3—0.4,相对较小。其他模式介于两者之间。
| 模式 | 相关系数 | 模式 | 相关系数 |
| OBS | 0.595 | GFDL-ESM2M | 0.664 |
| BCC_CSM1.1 | 0.300 | GISS-E2-R | 0.417 |
| BCC_CSM1.1m | 0.500 | HadGEM2-CC | 0.491 |
| CanESM2 | 0.498 | inmcm4 | 0.497 |
| CCSM4 | 0.603 | IPSL-CM5A-LR | 0.370 |
| CNRM-CM5 | 0.607 | MIROC5 | 0.663 |
| CSIRO-Mk3-6-0 | 0.414 | MPI-ESM-LR | 0.453 |
| FGOALS-g2 | 0.486 | MRI-CGCM3 | 0.333 |
| FGOALS-s2 | 0.513 | NorESM1-M | 0.614 |
ENSO现象具有准周期性,通常2—7年发生一次。为了考察模式模拟ENSO周期的能力,对模式模拟的南方涛动指数进行了功率谱分析,并将其与观测进行对比(图 9),谱分析的时段为1876—2004年(129年,1548个月)。图 9左列的最上图为观测结果,其他分别为各模式的结果,图中实线为南方涛动指数的功率谱,3条虚线的中间一条是红噪声的谱,另外两条则分别是95%置信区间的上下边界。观测结果显示南方涛动指数在这一时段具有45、67、83、37及30个月的周期,约为4、5.6、7、3及2.5年的周期,即通常所说的ENSO现象有2—7年的准周期,其中,4年左右的周期最明显。17个模式所模拟的南方涛动指数均表现出明显周期性,而且,模拟的南方涛动指数周期基本都在观测所涵盖的范围之内,只有少数例外,但不同模式模拟的南方涛动指数主要周期还有所不同。CCSM4、CanESM2、GFLOALS-g2、GFDL-ESM2M、MRI-CGCM3、NorESM1-M等6个模式的南方涛动指数主周期约为4年,与观测的南方涛动指数主周期非常接近,这是模拟较好的。另有6个模式模拟的南方涛动指数的周期与观测相差较大,如CSIRO-Mk3-6-0、FGOALS-s2、HadGEM2-CC、MPI-ESM、inmcm4等模拟的南方涛动指数周期则偏长,其模拟的最强的周期为8—11年。GISS-E2-R模式的南方涛动指数周期从17(18)个月至80—90个月,即1.5—7年的各种周期均存在,由于总能量分布在各种不同的周期上,因此,每个周期的波动的方差贡献都较小。剩下的5个模式处于中间状态,BCC_CSM1-1、BCC-CSN1-1m和CNRM-CM5模拟的南方涛动指数周期偏短,以2—3年为主,IPSL-CM5A-LR和MIROC5则以6—7年周期为主,略偏长,但其主周期均在2—7年的范围内。
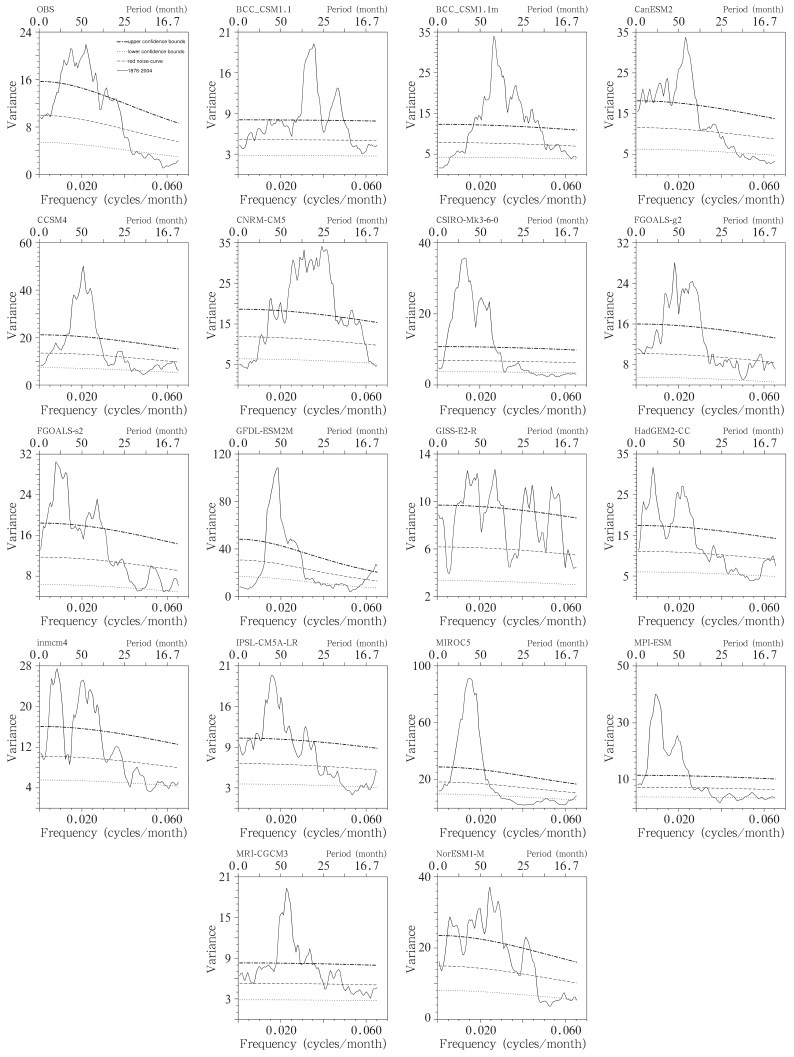 |
| 图 9 观测和CMIP5各模式模拟的1876—2004年南方涛动指数的谱分析(图中南方涛动指数观测资料来自澳大利亚气象局,网址http://www.bom.gov.au/climate/current/soihtm1.shtml) Fig. 9 Power spectrum of monthly mean SOI time series for the observation and simulations from 1876 to 2004(the observation of SOI are from Australian Government Bureau of Meteorology,http://www.bom.gov.au/climate/current/soihtm1.shtml) |
从观测得知,ENSO现象存在着锁相特征。厄尔尼诺峰值正距平一般出现在冬季,而拉尼娜的峰值也出现在冬季(李晓燕等,2000)。为了验证模式是否能模拟出ENSO现象的这种特征,计算了Nino 3.4区的Nino指数,从观测和每个模式的结果中选出5个强厄尔尼诺事件和5个强拉尼娜事件,分别计算Nino3.4指数的平均值。图 10给出这些厄尔尼诺和拉尼娜事件发生前后一段时间的平均Nino指数,表 5则给出观测及各个模式模拟的5个强厄尔尼诺/拉尼娜事件Nino3.4指数峰值平均出现的月份。可以看出MIROC5、CCSM4以及FGOALS-g2、FGOALS-s2等12个模式的厄尔尼诺峰值出现在11—2月,与观测基本一致。BCC_CSM1.1、BCC_CSM1.1m、GFDL-ESM2M、IPSL-CM5A-LR等4个模式模拟的厄尔尼诺峰值比观测略早,出现在9—10月。只有CSIRO-Mk-3-6-0模拟厄尔尼诺峰值出现在6月,与观测相差太大。
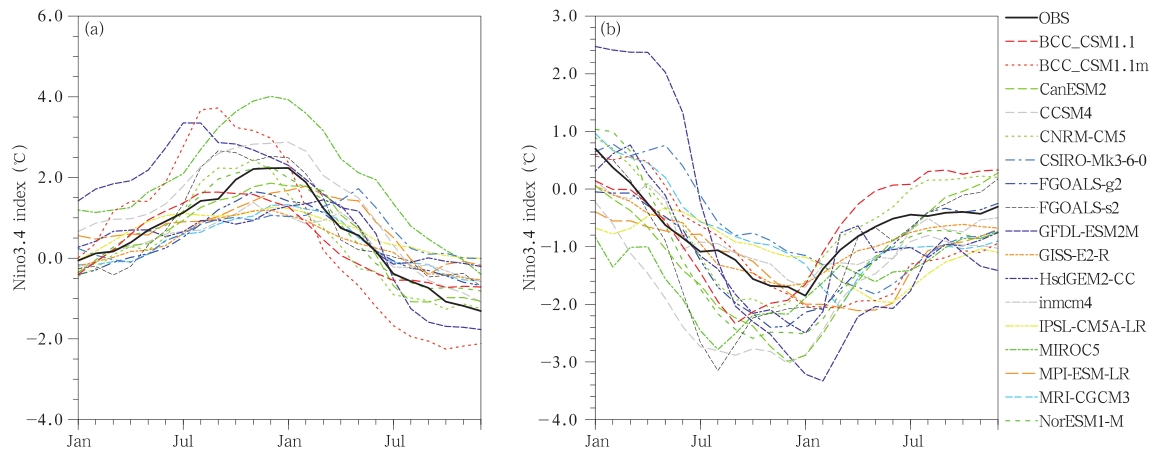 |
| 图 10 CMIP5各模式模拟和由GISST观测海温计算的1870—2003年5个最强的厄尔尼诺(a)和5个最强的拉尼娜(b)事件分别合成的Nino3.4指数 Fig. 10 Composite Nino3.4 index for the 5 strongest El Ni o events(a) and the 5 strongest La Ni a events(b)during 1870-2003 |
| 模式 | 极值出现月份 | |
| 厄尔尼诺 | 拉尼娜 | |
| OBS | 12 | 12 |
| BCC_CSM1.1 | 10 | 10 |
| BCC_CSM1.1m | 9 | 11 |
| CanESM2 | 1 | 11 |
| CCSM4 | 12 | 10 |
| CNRM-CM5 | 11 | 11 |
| CSIRO-Mk3-6-0 | 6 | 5 |
| FGOALS-g2 | 11 | 11 |
| FGOALS-s2 | 11 | 8 |
| GFDL-ESM2M | 9 | 1 |
| GISS-E2-R | 12 | 12 |
| HadGEM2-CC | 2 | 1 |
| inmcm4 | 11 | 1 |
| IPSL-CM5A-LR | 9 | 4 |
| MIROC5 | 12 | 8 |
| MPI-ESM-LR | 2 | 3 |
| MRI-CGCM3 | 2 | 3 |
| NorESM1-M | 11 | 10 |
模拟的拉尼娜现象的峰值与观测符合的程度不如厄尔尼诺的峰值。包括BCC_CSM1.1m、FGOALS-g2、GFDL-ESM2M、GISS-E2-R、HadGEM2-CC在内的9个模式模拟的拉尼娜峰值出现在11—2月,与观测基本一致。BCC_CSM1.1、CCSM4和NorESM1-M等3个模式模拟拉尼娜峰值出现在10月,比观测略偏早。IPSL-CM5A-LR、MPI-ESM-LR和MRI-CGCM3等3个模式模拟的拉尼娜峰值比观测略晚,出现在3—4月。只有CSIRO-Mk-3-6-0、MIROC5和FLOALS-s2模拟拉尼娜峰值出现在5—8月,与观测相差太大。
4 结论与讨论从参与CMIP5计划的17个海-气耦合模式对20世纪气候的模拟结果分析来看,当前的海-气耦合模式基本上能模拟出ENSO现象的一些主要特征,如热带太平洋地区的平均海温分布、海温距平的时空演变特征、热带大气的南方涛动特征、大气与海洋变化的密切联系、ENSO现象的周期性及锁相特征。但是,所考察的各模式在模拟能力上是有差异的,对ENSO的某个特征,有的模式模拟的结果好一些,而有的则略差,对某一模式来说则有可能模拟某一特征好一些而模拟另外的特征则不够。与以前的评估结果(AchutaRao,et al,2002,2006;Guilyardi,et al,2009b)相比,总体来看CMIP5模式模拟ENSO的能力比IPCC_AR4中报告的结果有明显的改进。尽管当前的模式在物理过程的描述或参数化方面有了很大提高,模式分辨率也更高了,但模拟的能力仍有很多地方需要进一步改进:
(1)模式模拟的海温距平仍然存在着不同程度的误差。多模式平均值的均方根误差小于1.0℃,但单个模式的误差要大一些,均方根误差较小的为1.2—1.3℃,多数模式在1.6℃以下,但也有个别模式的均方根误差超过2.0℃。无论是热带平均海温还是Nino3.4指数,其与观测的均方根误差比所模拟的观测量本身的均方差都大,说明模式仍然需要进一步改进。
(2)少数模式模拟的海温距平时空变化特征与观测非常接近。其第1模态为ENSO模态,对应的时间系数反映ENSO的时间演变特征,第2模态反映的是海温的长期变化趋势。多数模式模拟的海温距平时空变化的第1、第2特征向量分布顺序与观测相反,反映海温趋势的模态成了方差贡献最大的主模态,而ENSO模态成了第2模态。这说明目前多数模式模拟温室气体增温效应的机制太强,而模拟ENSO的机制偏弱。温室效应是对人类活动产生的温室气体通过辐射过程实现的,而ENSO类型的振荡则是模式内部过程和自然因素造成的。因此,对于以趋势模态为第1模态的模式来说其温室效应太强了,或者气溶胶的作用太弱了,调整模式中温室气体辐射效应和气溶胶的辐射效应可能是改进这类模式的一个切入点。此外,在研究全球变暖和对未来升温进行预估时,对于此类模式的升温结果应适当减小。
(3)对所有被考察的模式来说,海平面气压距平场的时空分解结果中也存在着反映南方涛动的主分量。对于某些模式来说,它是方差贡献最大的第1主分量,而对多数模式来说,它是第2主分量。计算结果表明,无论是第1还是第2特征向量,这种反映南方涛动模态的时间系数与海温距平有显著的相关。说明所有的模式均能很好地反映南方涛动与厄尔尼诺-拉尼娜的关系。
(4)大多数模式模拟结果显示,ENSO具有2—7年的周期,其中,4年周期最明显。但少数模式模拟的周期偏短,约为2年,也有个别模式模拟的周期偏长(11年)。AchutaRao 等(2006)指出,CMIP3模式在模拟ENSO现象周期方面比CMIP2有明显进步(见该文图 2),而与本研究图 9比较,可以发现CMIP5多数模式模拟的ENSO现象的周期比CMIP3总体上又有改进。
(5)多数模式模拟的厄尔尼诺及拉尼娜的峰值出现在冬季(11—2月),与观测基本吻合。另有少数模式模拟的峰值出现在9—10月,比观测略提前。只有个别模式模拟的峰值出现在夏季,与观测相差很大。
(6)总结以上CMIP5模式模拟ENSO的各项特征可以看出,CCSM4模式模拟的热带海温的误差较小,变率接近观测,模拟的热带海温年变化、年际变化的特征与实际接近,南方涛动指数与Nino3.4指数的相关与观测接近,模拟的南方涛动指数周期、ENSO峰值出现的季节也与观测接近,因此,是17个模式中模拟ENSO现象能力最强的一个。BCC_CSM1.1模式对热带海温及变率的模拟结果接近观测,但模拟的海温时空年际变化中升温趋势偏强而ENSO模态偏弱,模拟的ENSO周期偏短,峰值出现的时间偏早,在参加比较的17个模式中处于中等—偏好的水平。
为了正确模拟ENSO现象的一些基本特征还有很多工作要做,特别是有关ENSO机制方面的研究和改进。由于热带海温距平与气压距平的误差是紧密相关的,因此,大气基本状态的模拟,例如赤道太平洋附近东风带的模拟可能是至关重要的。Watanabe等(2011)指出Nino4区的纬向风应力对Nino3区的对流活动很敏感,因而模式中对流参数化的改进对正确模拟ENSO现象也可能是重要的。Marti等(2010)认为改进大气模式的水平分辨率可以改进大气-海洋的皮叶克尼斯反馈作用,本研究中BCC_CSM1.1m的水平分辨率高于BCC_CSM1.1,但在模拟ENSO现象方面没有明显的改进,说明光只有分辨率的提高还不够,模式的物理过程需要进一步改进,并与分辨率的提高协调一致才能起到作用。为了进一步诊断海气界面上的能量交换和反馈过程以及它们对ENSO变率的影响,皮叶克尼斯稳定度指数(Jin,et al,2006)可能是一个有用的工具。
| 陈海山, 施恩, 周晶. 2011. BCC气候模式对中国近50a极端气候事件的模拟评估. 大气科学学报, 34(5): 513-528 |
| 董敏, 吴统文, 王在志等. 2009. 北京气候中心大气环流模式对季节内振荡的模拟. 气象学报, 67(6): 912-922 |
| 高峰, 辛晓歌, 吴统文. 2012. BCC_CSM1.1对10 年尺度全球及区域温度的预测研究. 大气科学, 36(6): 1165-1179 |
| 李崇银, 穆穆, 周广庆等. 2008. ENSO机理及其预测研究. 大气科学, 32(4): 761-781 |
| 李晓燕, 翟盘茂. 2000. ENSO事件指数与指标研究. 气象学报, 58(1): 102-109 |
| 任福民, 袁媛, 孙丞虎等. 2012. 近30年ENSO研究进展回顾. 气象科技进展, 2(3): 17-24 |
| 王璐, 周天军, 吴统文等. 2009. BCC大气环流模式对亚澳季风年际变率主导模态的模拟. 气象学报, 67(6): 973-982 |
| 王小玲, 宋文玲. 2009. ENSO与登陆我国热带气旋的关系研究. 热带气象学报, 25(5): 576-580 |
| 吴统文, 宋连春, 李伟平等. 2014. 北京气候中心气候系统模式研发进展——在气候变化研究中的应用. 气象学报, 72(1): 12-29 |
| 辛晓歌, 吴统文, 张洁. 2012. BCC气候系统模式开展的CMIP5试验介绍. 气候变化研究进展, 8(5): 378-382 |
| 张莉, 吴统文, 辛晓歌等. 2013. BCC_CSM模式对热带降水年循环模态的模拟. 大气科学, 37(5): 994-1012 |
| AchutaRao K, Sperber K R. 2002. Simulation of the El Nio Southern Oscillation: Results from the Coupled Model Intercomparison Project. Climate Dyn, 19(3-4): 191-209 |
| AchutaRao K, Sperber K R. 2006. ENSO simulation in coupled ocean-atmosphere models: Are the current models better? Climate Dyn, 27(1): 1-15 |
| Bellenger H, Guilyardi E, Leloup J, et al. 2013. ENSO representation in climate models: from CMIP3 to CMIP5. Climate Dyn, doi: 10.1007/s00382-013-1783-z |
| Braconnot P, Hourdin F, Bony S, et al. 2007. Impact of different convectivecloud schemes on the simulation of the tropical seasonal cycle in a coupled ocean-atmosphere model. ClimateDyn, 29(5): 501-520 |
| Capotondi A, Wittenberg A, Masina S. 2006. Spatial and temporal structure of tropical Pacific interannualvariability in 20th century coupled simulations. Ocean Model, 15(3-4): 274-298 |
| Guilyardi E. 2006. El Nio-mean state-seasonal cycle interactions in a multi-model ensemble. Climate Dyn, 26(4): 329-348 |
| Guilyardi E, Braconnot P, Jin F F, et al. 2009a. Atmosphere feedbacksduring ENSO in a coupled GCM with a modified atmospheric convection scheme. J Climate, 22(21): 5698-5718 |
| Guilyardi E, Wittenberg A, Fedorov A, et al. 2009b. Understanding El Nio in ocean-atmosphere general circulation models: Progress and challenges. Bull Amer Meteor Soc, 90(3): 325-340 |
| Jin F F, Kim S T, Bejarano L. 2006. A coupled-stability index for ENSO. Geophys Res Lett, 33(23): L23708, doi: 10.1029/2006GL027221 |
| Kallberg P, Berrisford P, Hoskins B, et al. 2005. ERA-40 Atlas (ERA-40 Project Report Series). 19. ECMWF, 191 pp |
| Kim S T, Yu J Y. 2012. The two types of ENSO in CMIP5 models. Geophys Res Lett, 39(11): L11704, doi: 10.1029/2012GL052006 |
| L'Ecuyer T S, Stephens G L. 2007. The tropical atmospheric energy budget from the TRMM perspective. Part Ⅱ: Evaluating GCM representations of the sensitivity of regionalenergy and water cycles to the 1998-99ENSO cycle. J Climate, 20(18): 4548-4571 |
| Lin Z D, Lu R Y. 2009. The ENSO's effect on Eastern China rainfall in the following early summer. Adv Atmos Sci, 26(2): 333-342 |
| Lloyd J, Guilyardi E, Weller H, et al. 2009. The role of atmosphere feedbacks during ENSO in the CMIP3 models. Atmos Sci Lett, 10(3): 170-176 |
| Lloyd J, Guilyardi E, Weller H. 2011. The role of atmosphere feedbacks during ENSO in the CMIP3 models. Part Ⅱ: Using AMIP runs to understand the heat flux feedback mechanisms. Climate Dyn, 37(7-8): 1271-1292 |
| Marti O, Braconnot P, Dufresne J L, et al. 2010. Key features of the IPSL ocean atmosphere model and its sensitivity to atmospheric resolution. Climate Dyn, 34(1): 1-26 |
| Randall D A, Wood R A, Bony S, et al. 2007. Climate Models and Their Evaluation//Solomon S, Qin D, Manning M, et al. Climate Change 2007: The Physical Science Basis. Contribution of Working Group I to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change. Cambridge, United Kingdom and New York: Cambridge University Press |
| Rayner N A, Horton E B, Parker D E, et al. 1996. Version 2. 2 of Global Sea-Ice and Sea Surface Temperature Data Set, 1903-1994. Climate Research Technical Note (CRTN) No 74, Hadley Centre, Met Office, 47 pp |
| Stevenson S L. 2012. Significant changes to ENSO strength and impacts in the twenty-first century: Results fromCMIP5. Geophys Res Lett, 39, L17703, doi:10.1029/2012GL052759 |
| Sun D Z, Yu Y Q, Zhang T. 2009. Tropical water vapor and cloud feedbacks in climate models: A further assessment using coupled simulations. J Climate, 22(5): 1287-1304 |
| Taylor K E, Stouffer R J, Meehl F A. 2012. An overview of CMIP5 and the experiment design. Bull Amer Meteor Soc, 93(4): 485-498 |
| Trenberth K E, Caron J M, Stepaniak D P, et al. 2002. The evolution of ENSO and global atmospheric surface temperatures. J Geophys Res, 107: D8, doi:10.1029/2000JD000298 |
| van Oldenborgh G J, Philip S Y, Collins M. 2005. El Nio in a changing climate: A multi-model study. OceanSci, 1: 81-95 |
| Watanabe M, Suzuki T, O'ishi R, et al. 2010. Improved climate simulation by MIROC5: Mean states, variability, and climate sensitivity. J Climate, 23(23): 6312-6335 |
| Watanabe M, Chikira M, Imada Y, et al. 2011. Convective control of ENSO simulated in MIROC. J Climate, 24(2): 543-562 |
| Wittenberg A T, Rosati A, Lau N C, et al. 2006. GFDL's CM2 global coupled climate models. PartⅢ: Tropical Pacific climate and ENSO. J Climate, 19(5): 698-722 |
| Wu T W, Yu R C, Zhang F. 2008. A modified dynamic framework for the atmospheric spectral model and its application. J Atmos Sci, 65(7): 2235-2253 |
| Wu T W, Yu R C, Zhang F, et al. 2010. The Beijing Climate Center atmospheric general circulation model: Description and its performance for the present-day climate. Climate Dyn, 34(1): 123-147 |
| Wu T W. 2012. A mass-flux cumulus parameterization scheme for large-scale models: Description and test with observations. Climate Dyn, 38(3-4): 725-744 |
| Wu T W, Li W P, Ji J J, et al. 2013. Global carbon budgets simulated by the Beijing Climate Center Climate System Model for the last century. J Geophys Res Atmos, 118(10): 4326-4347 |
| Yeh S W, Ham Y G, Lee J Y. 2012. Changes in the tropical Pacific SST trend from CMIP3 to CMIP5 and itsimplication of ENSO. J Climate, 25(21): 7764-7771 |
| Zhang W J, Jin F F. 2012. Improvements in the CMIP5 simulations of ENSO-SSTA meridional width. Geophys Res Lett, 39(23): L23704, doi:10.1029/2012GL053588 |
| Zhang W J, Jin F F, Zhao J X, et al. 2013. On the bias in simulated ENSO SSTA meridional widths of CMIP3 models. J Climate, 26(10): 3173-3186 |
 2014, Vol. 72
2014, Vol. 72


